DEX: self-healing expanders

Abstract

We present a fully-distributed self-healing algorithm dex that maintains a constant degree expander network in a dynamic setting. To the best of our knowledge, our algorithm provides the first efficient distributed construction of expanders—whose expansion properties hold deterministically—that works even under an all-powerful adaptive adversary that controls the dynamic changes to the network (the adversary has unlimited computational power and knowledge of the entire network state, can decide which nodes join and leave and at what time, and knows the past random choices made by the algorithm). Previous distributed expander constructions typically provide only probabilistic guarantees on the network expansion which rapidly degrade in a dynamic setting; in particular, the expansion properties can degrade even more rapidly under adversarial insertions and deletions. Our algorithm provides efficient maintenance and incurs a low overhead per insertion/deletion by an adaptive adversary: only $O(\log n)$ rounds and $O(\log n)$ messages are needed with high probability (n is the number of nodes currently in the network). The algorithm requires only a constant number of topology changes. Moreover, our algorithm allows for an efficient implementation and maintenance of a distributed hash table on top of dex  with only a constant additional overhead. Our results are a step towards implementing efficient self-healing networks that have guaranteed properties (constant bounded degree and expansion) despite dynamic changes.

1 Introduction

Modern networks (peer-to-peer, mobile, ad-hoc, Internet, social, etc.) are dynamic and increasingly resemble self-governed living entities with largely distributed control and coordination. In such a scenario, the network topology governs much of the functionality of the network. In what topology should such nodes (having limited resources and bandwidth) connect so that the network has effective communication channels with low latency for all messages, has constant degree, is robust to a limited number of failures, and nodes can quickly sample a random node in the network (enabling many randomized protocols)? The well known answer is that they should connect as a (constant degree) expander (see e.g., [1]). How should such a topology be constructed in a distributed fashion? The problem is especially challenging in a dynamic network, i.e., a network exhibiting churn with nodes and edges entering and leaving the system. Indeed, it is a fundamental problem to scalably build dynamic topologies that have the desirable properties of an expander graph (constant degree and expansion, regardless of the network size) in a distributed manner such that the expander properties are always maintained despite continuous network changes. Hence it is of both theoretical and practical interest to maintain expanders dynamically in an efficient manner.

Many previous works (e.g., [10, 18, 23]) have addressed the above problem, especially in the context of building dynamic P2P (peer-to-peer) networks. However, all these constructions provide only probabilistic guarantees of the expansion properties that degrade rapidly over a series of network changes (insertions and/or deletions of nodes/edges)—in the sense that expansion properties cannot be maintained ad infinitum due to their probabilistic nature¹ which can be a major drawback in a dynamic setting. In fact, the expansion properties can degrade even more rapidly under adversarial insertions and deletions (e.g., as in [18]). Hence, in a dynamic setting, guaranteed expander constructions are needed. Furthermore, it is important that the network maintains its expander properties (such as high conductance, robustness to failures, and fault-tolerant multi-path routing) efficiently even under dynamic network changes. This will be useful in efficiently building good overlay and P2P network topologies with expansion guarantees that do not degrade with time, unlike the above approaches.

Self-healing is a responsive approach to fault-tolerance, in the sense that it responds to an attack (or component failure) by changing the topology of the network. This approach works irrespective of the initial state of the network, and is thus orthogonal and complementary to traditional non-responsive techniques. Self-healing assumes the network to be reconfigurable (e.g., P2P, wireless mesh, and ad-hoc networks), in the sense that changes to the topology of the network can be made on the fly. Our goal is to design an efficient distributed self-healing algorithm that maintains an expander despite attacks from an adversary.

Our model We use the self-healing model which is similar to the model introduced in [12, 29] and is briefly described here (the detailed model is described in Sect. 2). We assume an adversary that repeatedly attacks the network. This adversary is adaptive and knows the network topology and our algorithm (and also previous insertions/deletions and all previous random choices), and it has the ability to delete arbitrary nodes from the network or insert a new node in the system which it can connect to any subset of nodes currently in the system. We also assume that the adversary can only delete or insert a single node at a time step. The neighbors of the deleted or inserted node are aware of the attack in the same time step and the self-healing algorithm responds by adding or dropping edges (i.e., connections) between nodes. The computation of the algorithm proceeds in synchronous rounds and we assume that the adversary does not perform any more changes until the algorithm has finished its response. As typical in self-healing (see e.g., [12, 24, 29]), we assume that no other insertion/deletion takes place during the repair phase² (though our algorithm can be potentially extended to handle such a scenario). The goal is to minimize the number of distributed rounds taken by the self-healing algorithm to heal the network.

Our contributions In this paper, we present dex, in our knowledge the first distributed algorithm to efficiently construct and dynamically maintain a constant degree expander network (under both insertions and deletions) under an all-powerful adaptive adversary. Unlike previous constructions (e.g., [2, 10, 15, 18, 23]), the expansion properties always hold, i.e., the algorithm guarantees that the dynamic network always has a constant spectral gap (for some fixed absolute constant) despite continuous network changes, and has constant degree, and hence is a (sparse) expander. The maintenance overhead of dex is very low. It uses only local information and small-sized messages, and hence is scalable. The following theorem states our main result:

Table 1 Comparison of distributed expander constructions

Theorem 1

Consider an adaptive adversary that observes the entire state of the network including all past random choices and inserts or removes a single node in every step. Algorithm dex maintains a constant degree expander network that has a constant spectral gap. The algorithm takes $O(\log n)$ rounds and messages in the worst case (with high probability)³ per insertion/deletion where n is the current network size. Furthermore, dex requires only a constant number of topology changes.

Note that the above bounds hold w.h.p. for every insertion/deletion (i.e., in a worst case sense) and not just in an amortized sense. Our algorithm can be extended to handle multiple insertions/deletions per step in (cf. Sect. 5). We also describe (cf. Sect. 4.4.4) how to implement a distributed hash table (DHT) on top of our algorithm dex, which provides insertion and lookup operations using $O(\log n)$ messages and rounds.

Our results answer some open questions raised in prior work. In [10], the authors ask: Can one design a fully decentralized construction of dynamic expander topologies with constant overhead? The expander maintenance algorithms of [10, 18] handle deletions much less effectively than additions; [10] also raises the question of handling deletions as effectively as insertions. Our algorithm handles even adversarial deletions as effectively as insertions.

Technical contributions Our approach differs from previous approaches to expander maintenance (e.g., [10, 18, 23]). Our approach simulates a virtual network (cf. Sect. 3.1) on the actual (real) network. At a high level, dex works by stepping between instances of the guaranteed expander networks (of different sizes as required) in the virtual graph. It maintains a balanced mapping (cf. Definition 2) between the two networks with the guarantee that the spectral properties and degrees of both are similar. The virtual network is maintained as a p-cycle expander (cf. Definition 1). Since the adversary is fully adaptive with complete knowledge of topology and past random choices, it is non-trivial to efficiently maintain both constant degree and constant spectral gap of the virtual graph. Our maintenance algorithm dex uses randomization to defeat the adversary and exploits various key algorithmic properties of expanders, in particular, Chernoff-like concentration bounds for random walks ([9]), fast (almost) uniform sampling, efficient permutation routing ([28]), and the relationship between edge expansion and spectral gap as stated by the Cheeger Inequality (cf. Theorem 2 in “Appendix”). Moreover, we use certain structural properties of the p-cycle and staggering of “complex” steps that require more involved recovery operations over multiple “simple” steps to achieve worst case $O(\log n)$ complexity bounds. It is technically and conceptually much more convenient to work on the (regular) virtual network and this can be a useful algorithmic paradigm in handling other dynamic problems as well.

Related work and comparison Expanders are a very important class of graphs that have applications in various areas of computer science (e.g., see [14] for a survey) e.g., in distributed networks, expanders are used for solving distributed agreement problems efficiently [3, 16]. In distributed dynamic networks (cf. [3]) it is particularly important that the expansion does not degrade over time. There are many well known (centralized) expander construction techniques see e.g., [14]).

As stated earlier, there are a few other works addressing the problem of distributed expander construction; however all of these are randomized and the expansion properties hold with probabilistic guarantees only. Table 1 compares our algorithm with some known distributed expander construction algorithms. Law and Siu [18] give a construction where an expander is constructed by composing a small number of random Hamiltonian cycles. The probabilistic guarantees provided degrade rapidly, especially under adversarial deletions. Gkantsidis et al. [10] builds on the algorithm of [18] and makes use of random walks to add new peers with only constant overhead. However, it is not a fully decentralized algorithm. Both these algorithms handle insertions much better than deletions. Spanders [8] is a self-stabilizing construction of an expander network that is a spanner of the graph. Cooper et al. [6] shows a way of constructing random regular graphs (which are good expanders, w.h.p.) by performing a series of random ‘flip’ operations on the graph’s edges. Reiter et al. [26] maintains an almost d-regular graph, i.e., with degrees varying around d, using uniform sampling to select, for each node, a set of expander-neighbors. The protocol of [23] gives a distributed algorithm for maintaining a sparse random graph under a stochastic model of insertions and deletions. Melamed and Keidar [20] gives a dynamic overlay construction that is empirically shown to resemble a random k-regular graph and hence is a good expander. Gurevich and Keidar [11] gives a gossip-based membership protocol for maintaining an overlay in a dynamic network that under certain circumstances provides an expander.

In a model similar to ours, [17] maintains a distributed hash table (DHT) in the setting where an adaptive adversary can add/remove $O(\log n)$ peers per step. Another paper which considers node joins/leaves is [15] which constructs a SKIP+ graph within $O(\log ^2 n)$ rounds starting from any graph whp. Then, they also show that after an insert/delete operation the system recovers within $O(\log n)$ steps (like ours, which also needs $O(\log n)$ steps whp) and with $O(\log ^4 n)$ messages (while ours takes $O(\log n)$ messages whp). SKIP+ assumes the $\mathcal {LOCAL}$ model [25] and thus requires large-sized messages, unlike DEX, that works in the CONGEST model (small, i.e., logarithmic-sized, messages). However, the SKIP+ graph has an advantage that it is self-stabilizing, i.e., can recover from any initial state (as long as it is weakly connected). Jacob et al. [15] assume (as do we) that the adversary rests while the network converges to a SKIP+ graph. It was shown in [2] that skip graphs contain expanders as subgraphs w.h.p., which can be used as a randomized expander construction. Skip graphs (and its variant $\hbox {SKIP}+$ [15]) are probabilistic structures (i.e., their expansion holds only with high probability) and furtherm ore, they are not of constant degree, their degree grows logarithmic in the network size. The work of [22] has guaranteed expansion (like ours). However, as pointed out in [2], its main drawback (unlike ours) is that their algorithm has a rather large overhead in maintaining the network.

A variety of self-healing algorithms deal with maintaining topological invariants on arbitrary graphs [12, 13, 24, 27, 29]. The self-healing algorithm Xheal of [24] maintains spectral properties of the network (while allowing only a small increase in stretch and degree), but it relied on a randomized expander construction and hence the spectral properties degraded rapidly. Using our algorithm as a subroutine, Xheal can be efficiently implemented with guaranteed spectral properties.

2 The self-healing model

The model we are using is similar to the models used in [12, 24]. We now describe the details. Let $G = G_0$ be a small arbitrary graph$^{3}$ where nodes represent processors in a distributed network and edges represent the links between them. Each step $t\geqslant 1$ is triggered by a deletion or insertion of a single⁴ node from $G_{t-1}$ by the adversary, yielding an intermediate network graph $U_t$. The neighbors of the (inserted or deleted) node in the network $U_{t}$ react to this change by adding or removing edges in $U_t$, yielding $G_{t}$—this is called recovery or repair. The distributed computation during recovery is structured into synchronous rounds. We assume that the adversary rests until the recovery is complete, and subsequently triggers the next step by inserting/deleting a node. During recovery, nodes can communicate with their neighbors (i.e., along the edges) by sending messages of size $O(\log n)$, which are neither lost nor corrupted. We assume that local computation (within a node) is free, which is a standard assumption in distributed computing (e.g., [25]). Our focus is only on the cost of communication (time and messages).

Initially, a newly inserted node v only knows its unique id (chosen by the adversary) and does not have any a priori knowledge of its neighbors or the current network topology. In particular, this means that a node u can only add an edge to a node w if it knows the id of w. If node u knowing the id of w desires to make an edge with w, it requests the underlying system which establishes a connection i.e., an edge between u and w.

In case of an insertion, we assume that the newly added node is initially connected to a constant number of other nodes. This is merely a simplification; nodes are not malicious but faithfully follow the algorithm, thus we could explicitly require our algorithm to immediately drop all but a constant number of edges. The adversary is fully adaptive and is aware of our algorithm, the complete state of the current network including all past random choices. As typically the case (see e.g., [12, 24]), we assume that no other node is deleted or inserted until the current step has concluded (though our algorithm can be modified to handle such a scenario).

3 Preliminaries and overview of algorithm DEX

It is instructive to first consider the following natural (but inefficient) algorithms:

Flooding First, we consider a naive flooding-based algorithm that also achieves guaranteed expansion and node degree bounds, albeit at a much larger cost: Whenever a node is inserted (or deleted), a neighboring node floods a notification throughout the entire network and every node, having complete knowledge of the current network graph, locally recomputes the new expander topology. While this achieves a logarithmic runtime bound, it comes at the cost of using $\varTheta (n)$ messages in every step and, in addition, might also result in O(n) topology changes, whereas our algorithms requires only polylogarithmic number of messages and constant topology changes on average.

Fig. 1

A 4-balanced virtual mapping of a p-cycle expander to the network graph. On the left is a (virtual) 3-regular 23-cycle expander on $\mathbb {Z}_{23}$; on the right is the network $G_t$ with (real) nodes $\{A,\ldots ,G\}$

Maintaining global knowledge As a second example of a straightforward but inefficient solution, consider the algorithm that maintains a global knowledge at some node p, which keeps track of the entire network topology. Thus, every time some node u is inserted or deleted, the neighbors of u inform p of this change, and p then proceeds to update the current graph using its global knowledge. However, when p itself is deleted, we would need to transfer all of its knowledge to a neighboring node q, which then takes over p’s role. This, however, requires at least $\varOmega (n)$ rounds, since the entire knowledge of the network topology needs to be transmitted to q.

Our approach—algorithm DEX As mentioned in Sect. 2, the actual (real) network is represented by a graph where nodes correspond to processors and edges to connections. Our algorithm maintains a second graph, which we call the virtual graph where the vertices do not directly correspond to the real network but each (virtual) vertex in this graph is simulated by a (real) node⁵ in the network. The topology of the virtual graph determines the connections in the actual network. For example, suppose that node u simulates vertex $z_1$ and node v simulates vertex $z_2$. If there is an edge $(z_1,z_2)$ according to the virtual graph, then our algorithm maintains an edge between u and v in the actual network. In other words, a real node may be simulating multiple virtual vertices and maintaining their edges according to the virtual graph.

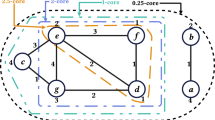
Figure 1 on page 5 shows a real network (on the right) whose nodes (shaded rectangles) simulate the virtual vertices of the virtual graph (on the left). In our algorithm, we maintain this virtual graph and show that preserving certain desired properties (in particular, constant expansion and degree) in the virtual graph leads to these properties being preserved in the real network. Our algorithm achieves this by maintaining a “balanced load mapping” (cf. Definition 3) between the virtual vertices and the real nodes as the network size changes at the will of the adversary. The balanced load mapping keeps the number of virtual nodes simulated by any real node to be a constant—this is crucial in maintaining the constant degree bound. We next formalize the notions of virtual graphs and balanced mappings.

3.1 Virtual graphs and balanced mappings

Consider some graph G and let $\lambda _G$ denote the second largest eigenvalue of the adjacency matrix of G. The contraction of vertices $z_1$ and $z_2$ produces a graph H where $z_1$ are $z_2$ merged into a single vertex z that is adjacent to all vertices to which $z_1$ or $z_2$ were adjacent in G. We extensively make use of the fact that this operation leaves the spectral gap $1-\lambda _G$ intact, cf. Lemma 10 in “Appendix”.

As mentioned earlier, our virtual graph consists of virtual vertices simulated by real nodes. Intuitively speaking, we can think of a real node simulating $z_1$ and $z_2$ as a vertex contraction of $z_1$ and $z_2$. The above stated contraction property motivates us to use an expander family (cf. Definition 4 in “Appendix”) as virtual graphs. We now define the p-cycle expander family, which we use as virtual graphs in this paper. Essentially, we can think of a p-cycle as a numbered cycle with some chord-edges between numbers that are multiplicative inverses of each other. It was shown in [19] that this yields an infinite family of 3-regular expander graphs with a constant eigenvalue gap. Figure 1 shows a 23-cycle.

Definition 1

(${\varvec{p}}$ -cycle, cf. [14]) For any prime number p, we define the following graph $\mathcal {Z}(p)$. The vertex set of $\mathcal {Z}(p)$ is the set $\mathbb {Z}_p=\{0,\ldots ,p-1\}$ and there is an edge between vertices x and y if and only if one of the following conditions hold: (1) $y = (x + 1) \mod p$, (2) $y = (x - 1) \mod p$, or (3) if $x,y>0$ and $y = x^{-1}$. Moreover, vertex 0 has a self-loop.

At any point in time t, our algorithm maintains a mapping from the virtual vertices of a p-cycle to the actual network nodes. We use the notation $\mathcal {Z}_t(p)$ when $\mathcal {Z}(p)$ is the p-cycle that we are using for our mapping in step t. (We omit p and simply write $\mathcal {Z}_t$ if p is irrelevant or clear from the context.) At any time t, each real node simulates at least one virtual vertex (i.e., a vertex in the p-cycle) and all its incident edges as required by Definition 1, i.e., the real network can be considered a contraction of the virtual graph; see Fig. 1 on page 5 for an example. Formally, this defines a function that we call a virtual mapping:

Definition 2

(Virtual mapping) For step $t\geqslant 1$, consider a surjective map $\varPhi _{t} : V(\mathcal {Z}_t) \rightarrow V(G_t)$ that maps every virtual vertex of the virtual graph $\mathcal {Z}_t$ to some (real) node of the network graph $G_t$. Suppose that there is an edge $(\varPhi _t(z_1), \varPhi _t(z_2)) \in E(G_t)$ for every edge $(z_1,z_2) \in E(Z_t)$, and these are the only edges in $Z_t$. Then we call $\varPhi _{t}$ a virtual mapping. Moreover, we say that node $u \in V(G_t)$ is a real node that simulates virtual vertices $z_1,\ldots ,z_k$, if $u=\varPhi _t(z_1)=\cdots =\varPhi _t(z_k)$.

In the standard metric spaces on $\mathcal {Z}_t$ and $G_t$ induced by the shortest-path metric $\varPhi$ is a surjective metric map since distances do not increase:

Fact 1

Let $\mathrm {dist}_H(u,v)$ denote the length of the shortest path between u and v in graph H. Any virtual mapping $\varPhi _t$ guarantees that $\mathrm {dist}_{Z_t}(z_1,z_2) \geqslant \mathrm {dist}_{G_t}(\varPhi (z_1),\varPhi (z_2))$, for all $z_1, z_2 \in \mathcal {Z}_t$.

We simply write $\varPhi$ instead of $\varPhi _t$ when t is irrelevant.

We consider the vertices of $\mathcal {Z}_t$ to be partitioned into disjoint sets of vertices that we call clouds and denote the cloud to which a vertex z belongs as $\textsc {cloud}(z)$. Whereas initially we can think of a cloud as the set of virtual vertices simulated at some node in $G_t$, this is not true in general due to load balancing issues, as we discuss in Sect. 4. We are only interested in virtual mappings where the maximum cloud size is bounded by some universal constant $\zeta$, which is crucial for maintaining a constant node degree. For our p-cycle construction, it holds that $\zeta \leqslant 8$.

We now formalize the intuition that the expansion of the virtual p-cycle carries over to the network, i.e., the second largest eigenvalue $\lambda _{G_t}$ of the real network is bounded by $\lambda _{Z_t}$ of the virtual graph. Recall that we can obtain $G_t$ from $\mathcal {Z}_t$ by contracting vertices. That is, we contract vertices $z_1$ and $z_2$ if $\varPhi (z_1)=\varPhi (z_2)$. According to Lemma 10 (in the “Appendix”), these operations do not increase $\lambda _{G_t}$ and thus we have shown the following:

Lemma 1

Let $\varPhi _t:\mathcal {Z}_t\rightarrow G_t$ be a virtual mapping. Then it holds that $\lambda _{G_t} \leqslant \lambda _{\mathcal {Z}_t}$.

Next we formalize the notion that our real nodes simulate at most a constant number of nodes. Let $\textsc {Sim}_{t}(u)=\varPhi _t^{-1}(u)$ and define the load of a node u in graph $G_t$ as the number of vertices simulated at u, i.e., $\textsc {Load}_{t}(u)=|\textsc {Sim}_{t}(u)|$. Note that due to locality, node u does not necessarily know the mapping of other nodes.

Definition 3

(Balanced mapping) Consider a step t. If there exists a constant C s.t. $\forall u \in G_t:\textsc {Load}_{t}(u) \leqslant C,$ then we say that $\varPhi _{t}$ is a C -balanced virtual mapping and say that $G_t$ is C -balanced.

Figure 1 on page 5 shows a balanced virtual mapping. At any step t, the degree of a node $u\in G_t$ is exactly $3\cdot \textsc {Load}_t(u)$ since we are using the 3-regular p-cycle as a virtual graph. Thus our algorithm strives to maintain a constant bound on $\textsc {Load}_t(u)$, for all t. Given a virtual mapping $\varPhi _t$, we define the (not necessarily disjoint) sets

$$\begin{aligned}&\textsc {Low}_{t}=\{u\in G_t:\textsc {Load}_{t}(u)\leqslant 2\zeta \};\end{aligned}$$

(1)

$$\begin{aligned}&\textsc {Spare}_{t}=\{u\in G_t:\textsc {Load}_{t}(u)\geqslant 2\}. \end{aligned}$$

(2)

Intuitively speaking, $\textsc {Low}_{t}$ contains nodes that do not simulate too many virtual vertices, i.e., have relatively low degree, whereas $\textsc {Spare}_t$ is the set of nodes that simulate at least 2 vertices each. When the adversary deletes some node u, we need to find a node in $\textsc {Low}_t$ that takes over the load of u. Upon a node v being inserted, on the other hand, we need to find a node in $\textsc {Spare}_t$ that can spare a virtual vertex for v, while maintaining the surjective property of the virtual mapping.

4 Expander maintenance algorithm

We describe our maintenance algorithm dexand prove the performance claims of Theorem 1. We start with a small initial network $G_0$ of some appropriate constant and assume there is a virtual mapping from a p-cycle $\mathcal {Z}_0(p_0)$ where $p_0$ is the smallest prime number in the range $(4n_0,8n_0)$. The existence of $p_0$ is guaranteed by Bertrand’s postulate [4]. (Since $G_0$ is of constant size, nodes can compute the current network size $n_0$ and $\mathcal {Z}_0(p_0)$ in a constant number of rounds in a centralized manner. For example, nodes can broadcast their information to each other in the constant sized graph. Each node now has a picture of the complete constant sized graph and can compute the required information.) Starting out from this initial expander, we seek to guarantee expansion ad infinitum, for any number of adversarial insertions and deletions.

As suggested earlier, we always maintain the invariant that each real node simulates at least one (i.e., the virtual mapping is surjective) and at most a constant number of virtual p-cycle vertices. The adversary can either insert or delete a node in every step. In either case, our algorithm reacts by doing an appropriate redistribution of the virtual vertices to the real nodes with the goal of maintaining a C-balanced mapping (cf. Definition 3).

Depending on the operations employed by the algorithm, we classify the response of the algorithm for a given step t as being either a type-1 recovery or a type-2 recovery and call t a type-1 recovery step (resp. type-2 recovery step). At a high level, a type-1 recovery is a simple redistribution of the virtual vertices with the virtual graph remaining the same. Type-1 recovery is very efficient, as (w.h.p.) it suffices to execute a single random walk of $O(\log n)$ length.

However, a type-2 recovery is significantly more complex than type-1 and requires replacement of the entire virtual graph by another virtual graph and subsequent redistribution i.e., moving from a p-cycle of a prime number p to another p-cycle for a higher p (we call this inflation)or lower p (we call this deflation). It is somewhat more complicated to show a worst case $O(\log n)$ performance for type-2 recovery: Here, the current virtual graph is either inflated or deflated to ensure a C-balanced mapping (i.e., bounded degrees). For the sake of exposition, we first present a simpler way to handle inflation and deflation, which yields amortized complexity bounds. We then describe a more complicated algorithm for type-2 recovery that yields the claimed worst case complexity bounds of $O(\log n)$ rounds and messages, and O(1) topology changes per step with high probability.

The first (simplified) approach (cf. Sect. 4.2) replaces the entire virtual graph by a new virtual graph of appropriate size in a single step. This requires O(n) topology changes and $O(n\log ^2 n)$ message complexity, because all nodes complete the inflation/deflation in one step. Since there are at least $\varOmega (n)$ steps with type-1 recovery between any two steps where inflation or deflation is necessary, we can nevertheless amortize their cost and get the amortized performance bounds of $O(\log n)$ rounds and $O(\log ^2 n)$ messages (cf. Cor. 1). We then present an improved (but significantly more complex) way of handling inflation (resp. deflation), by staggering these inflation/deflation operations across the recovery of the next $\varTheta (n)$ following steps while retaining constant expansion and node degrees. This yields a $O(\log n)$ worst case bounds for both messages and rounds for all steps as claimed by Theorem 1. In terms of expansion, the (amortized) inflation/deflation approach yields a spectral gap no smaller than of the p-cycle, the improved worst case bounds of the 2nd approach come at the price of a slightly reduced, but still constant, spectral gap. Algorithm 4.1 presents a high-level pseudo code description of our approach.

4.1 Type-1 recovery

When a node u is inserted, a neighboring node v initiates a random walk of length at most $\varTheta (\log n)$ to find a “spare” virtual vertex, i.e., a virtual vertex z that is simulated by a node $w \in \textsc {Spare}_{G_{t-1}}$ (see Algorithm 4.2 for the detailed pseudo code). Assigning this virtual vertex z to the new node u, ensures a surjective mapping of virtual vertices to real nodes at the end of the step.

When a node u is deleted, on the other hand, the notified neighboring node v also initiates random walks, except this time with the aim of redistributing the deleted node u’s virtual vertices to the remaining real nodes in the system (cf. Algorithm 4.3). We assume that every node v has knowledge of $\textsc {Load}_{G_{t-1}}(w)$, for each of its neighbors u. (This can be implemented with constant overhead, by simply updating neighboring nodes when the respective $\textsc {Load}_{G_{t-1}}$ changes.) Since the deleted node u might have simulated multiple vertices, node v initiates a random walk for each $z \in \textsc {Load}_{G_{t-1}}(u)$, to find a node $w \in \textsc {Low}_{G_{t-1}}$ to take over virtual vertex z. In a nutshell, type-1 recovery consists of (re)balancing the load of virtual vertices to real nodes by performing random walks. Rebalancing the load of a deleted node succeeds with high probability, as long as at least $\theta n$ nodes are in $\textsc {Low}_{G_{t-1}}$, where the rebuilding parameter $\theta$ is a fixed constant. For our analysis, we require that

$$\begin{aligned} \theta \leqslant 1/(68\zeta +1), \end{aligned}$$

(3)

where $\zeta \leqslant 8$ is the maximum (constant) cloud size given by the p-cycle construction. Analogously, for insertion steps, finding a spare vertex will succeed w.h.p. if $\textsc {Spare}_{G_{t-1}}$ has size $\geqslant \theta n$. If the size is below $\theta n$, we handle the insertion (resp. deletion) by performing an inflation (resp. deflation) as explained below. Thus we formally define a step t to be a type-1 step, if either

• (1) a node is inserted in t and $|\textsc {Spare}_{G_{t-1}}|\geqslant \theta n$ or

• (2) a node is deleted in t and $|\textsc {Low}_{G_{t-1}}|\geqslant \theta n$.

If a random walk fails to find an appropriate node, we do not directly start an inflation resp. deflation, but first deterministically count the network size and sizes of $\textsc {Spare}_{G_{t-1}}$ and $\textsc {Low}_{G_{t-1}}$ by simple aggregate flooding (cf. Procedures $\texttt {computeLow}$ and $\texttt {computeSpare}$). We repeat the random walks, if it turns out that the respective set indeed comprises $\geqslant \theta n$ nodes. As we will see below, this allows us to deterministically guarantee constant node degrees. The following lemma shows an $O(\log n)$ bound for messages and rounds used by random walks in type-1 recovery:

Lemma 2

Consider a step t and suppose that $\varPhi _{t-1}$ is a $4\zeta$-balanced virtual map. There exists a constant $\ell$ such that the following hold w.h.p:

• (a) If $|\textsc {Spare}_{G_{t-1}}|\geqslant \theta n$ and a new node u is attached to some node v, then the random walk initiated by v reaches a node in $\textsc {Spare}_{G_{t-1}}$ in $\ell \log n$ rounds.

• (b) If $|\textsc {Low}_{G_{t-1}}|\geqslant \theta n$ and some node u is deleted, then, for each of the (at most $4\zeta \in O(1)$) vertices simulated at u, the initiated random walk reaches a node in $\textsc {Spare}_{G_{t-1}}$ in $\ell \log n$ rounds.

That is, w.h.p. type-1 recovery succeeds in $O(\log n)$ messages and rounds, and a constant number of edges are changed.

Proof

We will first consider the case where a node is deleted [Case (b)]. The main idea of the proof is to instantiate a concentration bound for random walks on expander graphs [9]. By assumption, the mapping of virtual vertices to real nodes is $4\zeta$-balanced before the deletion occurs. Thus we only need to redistribute a constant number of virtual vertices when a node is deleted.

We now present the detailed argument. By assumption we have that $|\textsc {Low}| = a n \geqslant \theta n$, for a constant $0< a< 1$. We start a random walk of length $\ell \log n$ for some appropriately chosen constant $\ell$ (determined below). We need to show that (w.h.p.) the walk hits a node in $\textsc {Low}$. According to the description of type-1 recovery for handling deletions, we perform the random walk on the graph $G'_t$, which modifies $G_{t-1}{\setminus }\{u\}$, by transferring all virtual vertices (and edges) of the deleted node u to the neighbor v. Thus, for the second largest eigenvalue $\lambda =\lambda _{G'_{t}}$, we know by Lemma 1 that $\lambda \leqslant \lambda _{G_{t-1}}$. Consider the normalized $n\times n$ adjacency matrix M of $G'_{t}$. It is well known (e.g., Theorem 7.13 in [21]) that a vector $\pi$ corresponding to the stationary distribution of a random walk on $G_{t-1}$ has entries $\pi (x) = \frac{d_x}{2|E(G'_t)|}$ where $d_x$ is the degree of node x. By assumption, the network $G_{t-1}$ is the image of a $4\zeta$-balanced virtual map. This means that the maximum degree $\varDelta$ of any node in the network is $\varDelta \leqslant 12 \zeta$, and since the p-cycle is a 3-regular expander, every node has degree at least 3. If the adversary deletes some node in step t, the maximum degree of one of its neighbors can increase by at most $\varDelta$. Therefore, the maximum degree in $U_t$ and thus $G'_t$ is bounded by $2\varDelta$, which gives us the bound

$$\begin{aligned} \pi (x) \geqslant {3}/({2\varDelta n}), \end{aligned}$$

(4)

for any node $x \in G'_t$. Let $\rho$ be the actual number of nodes in $\textsc {Low}$ that the random walk of length $\ell \log n$ hits. We define $\mathbf {q}$ to be an n-dimensional vector that is 0 everywhere except at the index of u in M where it is 1. Let $\mathcal {E}$ be the event that $\ell \log n \cdot \pi (\textsc {Low}) - \rho \geqslant \gamma ,$ for a fixed $\gamma \geqslant 0$. That is, $\mathcal {E}$ occurs if the number of nodes in $\textsc {Low}$ visited by the random walk is far away ($\geqslant \gamma$) from its expectation.

In the remainder of the proof, we show that $\mathcal {E}$ occurs with very small probability. Applying the concentration bound of [9] yields that

$$\begin{aligned} \Pr \left[ \mathcal {E}\right] \leqslant \left( 1+\frac{\gamma (1-\lambda )}{10\ell \log n}\right) \cdot \left\| \frac{\mathbf {q}}{\sqrt{\pi }}\right\| _2 \cdot e^{\frac{-\gamma ^2(1-\lambda )}{20\ell \log n}}, \end{aligned}$$

(5)

where $\mathbf {q}/\sqrt{\pi }$ is a vector with entries $(\mathbf {q}/\sqrt{\pi })(x)=\mathbf {q}(x)/\sqrt{\pi (x)}$, for $1\leqslant x\leqslant n$. By (4), we know that $\pi (\textsc {Low}) \geqslant 3 a / 2\varDelta$. To guarantee that we find a node in $\textsc {Low}$ w.h.p. even when $\pi (\textsc {Low})$ is small, we must set $\gamma = \frac{ 3 a \ell }{2\varDelta } \log n$. Moreover, (4) also gives us the bound $\Vert {\mathbf {q}/\sqrt{\pi }}\Vert _2 \leqslant \sqrt{2\varDelta /3}\sqrt{n}.$ We define

$$\begin{aligned} C=\left( 1 + \frac{ 3 a}{20\varDelta }\right) \sqrt{2\varDelta /3}. \end{aligned}$$

Plugging these bounds into (5), shows that

$$\begin{aligned} \Pr \left[ \mathcal {E}\right]&\leqslant C\sqrt{n} e^{\left( -\frac{(3 a \ell / 2\varDelta )^2(1-\lambda )\log n}{20\ell }\right) } \\&= C n^{\left( \frac{1}{2}-\frac{9 a^2 \ell (1-\lambda ) }{ 80\varDelta ^2}\right) }. \end{aligned}$$

To ensure that event $\mathcal {E}$ happens with small probability, it is sufficient if the exponent of n is smaller than $-C$, which is true for sufficiently large $\ell$. Since $\theta$, $\varDelta$, and the spectral gap $1-\lambda$ are all O(1), it follows that $\ell$ is a constant too and thus the running time of one random walk is $O(\log n)$ with high probability. Recall that node v needs to perform a random walk for each of the virtual vertices that were previously simulated by the deleted node u; there are at most $4\zeta \in O(1)$ such vertices, since we assumed that $\varPhi _{t-1}$ is $4\zeta$ balanced. Therefore, all random walks take $O(\log n)$ rounds in total (w.h.p.).

Now consider Case (a), i.e., the adversary inserted a new node u and attached it to some existing node v. By assumption, $|\textsc {Spare}| = a n \geqslant \theta n$, and the random walk is executed on the graph $G_{t-1}$ (excluding newly inserted node u). Thus (4) and the remaining analysis hold analogously to Case (b), which shows that the walk reaches a node in $\textsc {Spare}$ in $O(\log n)$ rounds (w.h.p.).

Note that we only transfer a constant number of virtual vertices to a new nodes in type-1 recovery steps, i.e., the number of topology changes is constant. $\square$

The following lemma summarizes the properties that hold after performing a type-1 recovery:

Lemma 3

(Worst Case Bounds Type-1 Rec.) If type-1 recovery is performed in t and $G_{t-1}$ is $4\zeta$-balanced, it holds that

• (a) $G_t$ is $4\zeta$-balanced,

• (b) step t takes $O(\log n)$ (w.h.p.), rounds,

• (c) nodes send $O(\log n)$ messages in step t (w.h.p.), and

• (d) the number of topology changes in t is constant.

Proof

For (a), we first argue that the mapping $\varPhi _t$ is surjective: This follows readily from the above description of type-1 recovery (see $\texttt {insertion}(u,\theta )$ and $\texttt {deletion}(u,\theta )$ for the full pseudo code): In the case of a newly inserted node, the algorithm repeatedly performs a random walk until it finds a node in $\textsc {Spare}$ since $|\textsc {Spare}|\geqslant \theta n$. If some node u is deleted, then a neighbor initiates random walks to find a new host for each of u’s virtual vertices, until it succeeds. Thus, at the end of step t, every node simulates at least 1 virtual vertex. To see that no node simulates more than $4\zeta$ vertices, observe that the load of a node can only increase due to a deletion. As we argued above, however, the neighbor v that temporarily took over the virtual vertices of the deleted node u, will attempt to spread these vertices to nodes that are in $\textsc {Low}$ and is guaranteed to eventually find such nodes by repeatedely performing random walks.

Properties (b), (c), and (d) follow from Lemma 2. $\square$

4.2 Type-2 recovery: inflating and deflating

We now describe an implementation of type-2 recovery that yields amortized polylogarithmic bounds on messages and time. We later extend these ideas (cf. Sect. 4.4) to give $O(\log n)$ worst case bounds. Recall that we perform type-1 recovery in step t, as long as at least $\theta n$ nodes are in $\textsc {Spare}_{G_{t-1}}$ when a node is inserted, resp. in $\textsc {Low}_{G_{t-1}}$, upon a deletion.

Fact 2

If the algorithm performs type-2 recovery in t, the following holds:

• (a) If a node is inserted in t, then $|\textsc {Spare}_{G_{t-1}}| <\theta n$.

• (b) If a node is deleted in t, then $|\textsc {Low}_{G_{t-1}}|<\theta n$.

4.2.1 Inflating the virtual graph

If node v fails to find a spare node for a newly inserted neighbor and computes that $|\textsc {Spare}_{G_{t-1}}|<\theta n$, i.e., only few nodes simulate multiple virtual vertices each, it invokes Procedure $\texttt {simplifiedInfl}$ (cf. Algorithm 4.5 for the detailed pseudo code), which consists of two phases:

Phase 1: Constructing a larger p -Cycle Node v initiates replacing the current p-cycle $\mathcal {Z}_{t-1}(p_i)$ with the larger p-cycle $\mathcal {Z}_{t}(p_{i+1})$, for some prime number $p_{i+1} \in (4p_i,8p_i)$. This rebuilding request is forwarded throughout the entire network to ensure that after this step, every node uses the exact same new p-cycle $\mathcal {Z}_t$. Intuitively speaking, each virtual vertex of $\mathcal {Z}_{t-1}$ is replaced by a cloud of (at most $\zeta \leqslant 8$) virtual vertices of $\mathcal {Z}_{t}$ and all edges are updated such that $G_t$ is a virtual mapping of $\mathcal {Z}_t$.

For simplicity, we use x to denote both: an integer $x \in \mathbb {Z}_p$ and also the associated vertex in $V(\mathcal {Z}_t(p))$. At the beginning of step t, all nodes are in agreement on the current virtual graph $\mathcal {Z}_{t-1}(p_i)$, in particular, every node knows the prime number $p_i$. To get a larger p-cycle, all nodes deterministically compute the (same) smallest prime number $p_{i+1} \in (4p_i,8p_i)$, i.e., $V(\mathcal {Z}_t(p_{i+1})) = \mathbb {Z}_{p_{i+1}}$. [Local computation happens instantaneously and does not incur any cost (cf. Sect. 2).] Bertrand’s postulate [4] states that for every $n>1$, there is a prime between n and 2n, which ensures that $p_{i+1}$ exists. Every node u needs to determine the new set of vertices in $\mathcal {Z}_{t}(p_{i+1})$ that it is going to simulate: Let $\alpha = \frac{p_{i+1}}{p_i} \in O(1)$. For every currently simulated vertex $x\in \textsc {Sim}_{G_{t-1}}(u)$, node u computes the constant

$$\begin{aligned} c(x) = \lfloor \alpha (x+1)\rfloor - \lfloor \alpha x\rfloor - 1, \end{aligned}$$

(6)

and replaces x with the new virtual vertices $y_0,\ldots ,y_{c(x)}$ where

$$\begin{aligned} y_j=(\lfloor \alpha x \rfloor + j)\quad \mod p_{i+1},\,\hbox {for}\,0 \leqslant j \leqslant c(x). \end{aligned}$$

(7)

Note that the vertices $y_0,\ldots ,y_{c(x)}$ form a cloud (cf. Sect. 3.1) where the maximum cloud size is $\zeta \leqslant 8$. This ensures that the new virtual vertex set is a bijective mapping of $\mathbb {Z}_{p_{i+1}}$.

Next, we describe how we find the edges of $\mathcal {Z}_t(p_{i+1})$: First, we add new cycle edges (i.e., edges between x and $x+1\mod p_{i+1}$), which can be done in constant time by using the cycle edges of the previous virtual graph $\mathcal {Z}_{t-1}(p_i)$. For every x that u simulates, we need to add an edge to the node that simulates vertex $x^{-1}$. Since this needs to be done by the respective simulating node of every virtual vertex, this corresponds to solving a permutation routing instance. Corollary 7.7.3 of [28] (cf. Corollary 3) states that, for any bounded degree expander with n nodes, n packets, one per node, can be routed (even online) according to an arbitrary permutation in $O(\frac{\log n (\log \log n)^2}{\log \log \log n})$ rounds w.h.p. Note that every node in the network knows the exact topology of the current virtual graph (but not necessarily of the network graph $G_t$), and can hence calculate all routing paths in this graph, which map to paths in the actual network (cf. Fact 1). Since every node simulates a constant number of vertices, we can find the route to the respective inverse by solving a constant number of permutation routing instances.

The following lemma follows from the previous discussion

Lemma 4

Consider a $t\geqslant 1$ where some node performs type-2 recovery via $\texttt {simplifiedInfl}$. If the network graph $G_{t-1}$ is a C-balanced image of $\mathcal {Z}_{t-1}(p_i)$, then Phase 1 of $\texttt {simplifiedInfl}$ ensures that every node computes the same virtual graph in $O(\log n (\log \log n)^2)$ rounds such that the following hold:

• (a) $p_{i+1} = |\mathcal {Z}_{t}(p_{i+1})| \in (4p_i,8p_i)$, the network graph is $(C\zeta )$-balanced, and the maximum clouds size is $\zeta \leqslant 8$.

• (b) There is a bijective map between $\mathbb {Z}_{p_{i+1}}$ and $V(\mathcal {Z}_{t}(p_{i+1}))$.

• (c) The edges of $\mathcal {Z}_{t}(p_{i+1})$ adhere to Definition 1.

Proof

Property (a) follows from the previous discussion. For Property (b), we first show set equivalence. Consider any $z \in \mathbb {Z}_{p_{i+1}}$ and assume in contradiction that $z \notin V(\mathcal {Z}_t(p_{i+1}))$. Let $\alpha = {p_{i+1}} / {p_i}$ and let x be the greatest integer such that $z = \lfloor \alpha x \rfloor + k$, for some integer $k \geqslant 0$. If $k \geqslant \alpha$, then

$$\begin{aligned} z = \lfloor \alpha x + k \rfloor \geqslant \lfloor \alpha x + \alpha \rfloor = \lfloor \alpha (x+1) \rfloor , \end{aligned}$$

which contradicts the maximality of x, therefore, we have that $k < \alpha$. It cannot be that $x < p_i$, since otherwise $z \in V(Z(p_{i+1}))$ according to (7), which shows that $x \geqslant p_i$. This means that

$$\begin{aligned} z = \lfloor \alpha x \rfloor + k \geqslant \lfloor \alpha p_i \rfloor + k = \lfloor p_{i+1} \rfloor + k \geqslant p_{i+1}, \end{aligned}$$

which contradicts $z \in \mathbb {Z}_{p_{i+1}}$, thus we have shown $\mathbb {Z}_{p_{i+1}} \subseteq V(\mathcal {Z}_t(p_{i+1}))$. The opposite relation, i.e. $V(\mathcal {Z}_t(p_{i+1})) \subseteq \mathbb {Z}_{p_{i+1}}$, is immediate since the values associated to vertices of $\mathcal {Z}_t(p_{i+1})$ are computed modulo $p_{i+1}$.

To complete the proof of (b), we need to show that no two distinct vertices in $V(\mathcal {Z}_t(p_{i+1}))$ correspond to the same value in $\mathbb {Z}_{p_{i+1}}$, i.e., $V(\mathcal {Z}_t(p_{i+1}))$ is not a multi-set. Suppose, for the sake of a contradiction, that there are $y = (\lfloor \alpha x \rfloor + k) \mod \ p_{i+1}$ and $y' = (\lfloor \alpha x' \rfloor + k') \mod \ p_{i+1}$ with $y = y'$. By (7), we know that $k' \leqslant c(x)$, hence to bound $k'$ it is sufficient to show that $c(x) < \alpha$: By (6), we have that

$$\begin{aligned} c(x) = \lfloor \alpha x+\alpha - (\lfloor \alpha x \rfloor + 1)\rfloor < \lfloor \alpha x + \alpha - \alpha x \rfloor \leqslant \alpha . \end{aligned}$$

Note that the same argument shows that $k \leqslant \alpha$. Thus it cannot be that $y' = \lfloor \alpha x \rfloor + k + m p_{i+1}$, for some integer $m\geqslant 1$. This means that $x \ne x'$; wlog assume that $x > x'$. As we have shown above, $k' \leqslant c(x) < \alpha$, which implies that

$$\begin{aligned} y' = \lfloor \alpha x' \rfloor + k' < \lfloor \alpha (x'+1) \rfloor \leqslant \lfloor \alpha x \rfloor \leqslant y, \end{aligned}$$

yielding a contradiction to $y=y'$.

For property (c), observe that all new cycle edges (i.e., of the form $(x,x\pm 1))$ of $\mathcal {Z}_t(p_{i+1})$ are between nodes that were already simulating neighboring vertices of $\mathcal {Z}_{t-1}(p_{i})$, thus every node u can add these edges in constant time. Finally, we argue that every node can efficiently find the inverse vertex for its newly simulated vertices: Corollary 7.7.3 of [28] states that for any bounded degree expander with n nodes, n packets, one per processor, can be routed (online) according to an arbitrary permutation in $T=O(\frac{\log n (\log \log n)^2}{\log \log \log n})$ rounds w.h.p. Note that every node in the network knows the exact topology of the current virtual graph (nodes do not necessarily know the network graph $G_t$!), and can hence calculate all routing paths, which map to paths in the actual network (cf. Fact 1). Since every node simulates a constant number of vertices, we can find the route to the respective inverse by performing a constant number of iterations of permutation routing, each of which takes T rounds. $\square$

Phase 2: Rebalancing the load Once the new virtual graph $\mathcal {Z}_t(p_{i+1})$ is in place, each real node simulates a greater number (by a factor of at most $\zeta$) of virtual vertices and now a random walk is guaranteed to find a spare virtual vertex on the first attempt with high probability, according to Lemma 2(a). At the beginning of the step, the virtual mapping $\varPhi _{t-1}$ was $4\zeta$-balanced. This, however, is not necessarily the case after Phase 1, i.e., replacing $\mathcal {Z}_{t-1}$ by $\mathcal {Z}_t$. A node could have been simulating $4\zeta$ virtual vertices before $\texttt {simplifiedInfl}$ was invoked and now might be simulating $4\zeta ^2$ vertices of $\mathcal {Z}_t(p_{i+1})$. In fact, this can be the case for a $\theta$-fraction of the nodes. To ensure a $4\zeta$-balanced mapping at the end of step t, we thus need to rebalance these additional vertices among the other (real) nodes. Note that this is always possible, since $(1-\theta )n$ nodes had a load of 1 before invoking $\texttt {simplifiedInfl}$ and simulate only $\zeta$ virtual vertices each at the end of Phase 1. A node v that has a load of $k'>4\zeta$ vertices of $\mathcal {Z}_t(p_{i+1})$, proceeds as follows, for each vertex z of the (at most constant) vertices that it needs to redistribute: Node v marks all of its vertices as full and initiates a random walk of length $\varTheta (\log n)$ on the virtual graph $\mathcal {Z}_{t}(p_{i+1})$, which is simulated on the actual network. If the walk ends at a vertex $z'$ simulated at some node w that is not marked as full, and no other random walk simultaneously ended up at $z'$, then v transfers z to w. This ensures that z is now simulated at a node that had a load of $<4\zeta$. A node w immediately marks all of its vertices as full, once its load reaches $2\zeta$. Node v repeatedly performs random walks until all of the $k'-4\zeta$ vertices are transfered to other nodes.

Lemma 5

(Simplified type-2 recovery) Suppose that $G_{t-1}$ is $4\zeta$-balanced and type-2 recovery is performed in t via $\texttt {simplifiedInfl}$ or $\texttt {simplifiedDefl}$. The following holds:

• (a) $G_t$ is $4\zeta$-balanced.

• (b) With high probability, step t completes in $O(\log ^3 n )$.

• (c) With high probability, nodes send $O(n\log ^2 n)$ messages.

• (d) The number of topology changes is O(n).

Proof

Here we will show the result for $\texttt {simplifiedInfl}$. In Sect. 4.2.2, we will argue the same properties for $\texttt {simplifiedDefl}$ (described below).

Property (d) follows readily from the description of Phase 1. For (a), observe that, in Phase 1, $\texttt {simplifiedInfl}$ replaces each virtual vertex with a cloud of virtual vertices. Moreover, nodes only redistribute vertices such that their load does not exceed $4\zeta$. It follows that every node simulates at least one vertex, thus $\varPhi _{t}$ is surjective. What remains to be shown is that every node has a load $\leqslant 4\zeta$ at the end of t.

Consider any node u that has $\textsc {Load}(v)\in (2\zeta ,4\zeta )$ after Phase 1. To see that u’s load does not exceed $4\zeta$, recall that, according the description of Phase 2, u will mark all its vertices as full and henceforth will not accept any new vertices. By Fact 2.(a), at most $\theta n$ nodes have a load $>1$ in $U_{t}$. Let $Balls_0$ be the set of vertices that need to be redistributed. Lemma 4.(a) tells us that the every vertex in $\mathcal {Z}_{t-1}(p_i)$ is replaced by (at most) $\zeta$ new vertices in $\mathcal {Z}_t(p_{i+1})$, which means that $|Balls_0| \leqslant 4\theta (\zeta ^2 - \zeta )n,$ since every such high-load node continues to simulate $4\zeta$ vertices by itself.

To ensure that this redistribution can be done in polylogarithmic time, we need to lower bound the total number of available places (i.e. the bins) for these virtual vertices (i.e. the balls). By Fact 2.(a), we know that $\geqslant (1-\theta )n$ nodes have a load of at most $\zeta$ after Phase 1. These nodes do not mark their vertices as full, and thus accept to simulate additional vertices until their respective load reaches $2\zeta$. Let Bins be the set of virtual vertices that are not marked as full; It holds that $|Bins| \geqslant (1-\theta )\zeta n.$

We first show that with high probability, a constant fraction of random walks end up at vertices in |Bins|. Since $\mathcal {Z}_t(p_{i+1})$ is a regular expander, the distribution of the random walk converges to the uniform distribution (e.g., [21]) within $O(\log \sigma )$ random steps where $\sigma = |Z^{i+1}| \in \varTheta (n)$. More specifically, the distance (measured in the maximum norm) to the uniform distribution, represented by a vector $(1/\sigma ,\ldots ,1/\sigma )$, can be bounded by $\frac{1}{100\sigma }$. Therefore, the probability for a random walk token to end up at a specific vertex is within $[\frac{99}{100\sigma },\frac{101}{100\sigma }]$. Recall that, after Phase 1 all nodes have computed the same graph $\mathcal {Z}_t(p_{i+1})$ and thus use the same value $\sigma$.

We divide the random walks into epochs where an epoch is the smallest interval of rounds containing $c\log n$ random walks. We denote the number of vertices that still need to be redistributed at the beginning of epoch i as $Balls_i$.

Claim

Consider a fixed constant c. If $|Balls_i| \geqslant c\log n$, then epoch i takes $O(\log ^2 n)$ rounds, w.h.p. Otherwise, if $|Balls_j| < c\log n$, then j comprises $O(\log ^3 n)$ rounds w.h.p.

Proof

We will now show that an epoch lasts at most $O(\log ^3 n)$ rounds with high probability. First, suppose that $|Balls_i| \geqslant c\log n$. By Lemma 11, we know that even a linear number of parallel walks (each of length $\varTheta (\log n)$) will complete within $O(\log ^2 n)$ rounds w.h.p. Therefore, epoch i consists of $O(\log ^2 n)$ rounds, since $\varOmega (\log n)$ random walks are performed in parallel. In the case where $|Balls_j| <c\log n$, it is possible that an epoch consists of random walks that are mostly performed sequentially by the same nodes. Thus we add a $\log n$ factor to ensure that epoch j consists of $c\log n$ walks. By Lemma 11 we get a bound of $O(\log ^3 n)$ rounds. $\square$

Next, we will argue that after $O(\log n)$ epochs, we have $|Balls_j| <c\log n$. Thus consider any epoch i where $|Balls_i| \geqslant c\log n$. We bound the probability of the indicator random variable $Y_k$ that is 1 iff the walk associated with the k-th vertex ends up at a vertex that was already marked full when the walk was initiated. (In particular, $Y_k=0$ if the k-th walk ends up at z and z became full in the current iteration but was not marked full before.) Note that all $Y_k$ are independent. While the number of available bins (i.e. non-full vertices) will decrease over time, we know from (3) that $|Bins| - |Balls_0| > \frac{9}{10}|Bins|$; thus, at any epoch, we can use the bound $|Bins| \geqslant ({9}/{10})(1-\theta )\zeta n.$ This shows that

$$\begin{aligned} \text {Pr}\left[ Y_k=1\right]&\leqslant \frac{101}{100\sigma }\left( \sigma - |Bins|\right) \\&\leqslant \frac{101}{100}\left( 1-\frac{9(1-\theta )\zeta n}{10\sigma }\right) . \end{aligned}$$

From $\sigma \leqslant \zeta (1-\theta )n + 4\zeta ^2\theta n$ and the fact that (3) implies $1-\frac{9 (1-\theta ) \zeta }{10 ((1-\theta ) \zeta +4 \zeta ^2 \theta )}<3/20,$ we get that $\text {Pr}\left[ Y_k=1\right] \leqslant ({101}/{100}) \cdot ({3}/{20})$. Let $Y = \sum _{k\in Balls_i} Y_k$. Since $|Balls_i|=\varOmega (\log n)$, we can use a Chernoff bound (e.g. [21]) to show that

$$\begin{aligned} \Pr \left[ Y \geqslant ({909}/{1000})|Balls_i| \geqslant 6 \mathrm {E}[Y]\right] \leqslant 2^{-\frac{909}{1000}|Balls_i|}, \end{aligned}$$

thus with high probability (in n), a constant fraction of the random walks in epoch i will end up at non-full vertices. We call these walks good balls and denote this set as $Good_i$.

We will now show that a constant fraction of good balls do not end up at the same bin with high probability, i.e., we are able to successfully redistribute the associated vertices in this epoch. Let $X_k$ be the indicator random variable that is 1 iff the k-th ball is eliminated. We have $\Pr [X_k=1] \geqslant (1-\frac{101}{100|Bins|})^{|Good_i|-1} \geqslant e^{-\varTheta (1)}$, i.e., at least a constant fraction of the balls in $Good_i$ are eliminated on expectation.

Let W denote the number of eliminated vertices in epoch i, which is a function $f(B_1,\ldots ,B_{|Good_i|})$ where $B_j$ denotes the bin chosen by the j-th ball. Observe that changing the bin of some ball can affect the elimination of at most one other ball. In other words, W satisfies the Lipschitz condition and we can apply the method of bounded differences. By the Azuma-Hoeffding Inequality (cf. Theorem 12.6 in [21]), we get a sharp concentration bound for W, i.e., with high probability, a constant fraction of the balls are eliminated in every epoch.

We have therefore shown that after $O(\log n)$ epochs, we are left with less than $c\log n$ vertices that need to be redistributed, w.h.p. Let j be the first epoch when $|Balls_j| <c\log n$. Note that epoch j consists of $\varOmega (\log n)$ random walks where some nodes perform multiple random walks. By the same argument as above, we can show that with high probability, a constant fraction of these walks will end up at some non-full vertices without conflicting with another walk and are thus eliminated. Since we only need $c\log n$ walks to succeed, this ensures that the entire set $Balls_j$ is redistributed w.h.p. by the end of epoch j, which shows (a).

By Claim 4.2.1, the first $O(\log n)$ epochs can each last $O(\log ^2 n)$ rounds, while only epoch j takes $O(\log ^3 n)$ rounds. Altogether, this gives a running time bound of $O(\log ^3 n)$, as required for (b). For Property (c), note that the flooding of the inflation request to all nodes in the network requires O(n) messages. This, however, is dominated by the time it takes to redistribute the load: each epoch might use $O(n\log n)$ messages. Since we are done w.h.p. in $O(\log n)$ epochs, we get a total message complexity of $O(n \log ^2 n)$. For (d), observe that the sizes of the virtual expanders $\mathcal {Z}_{t-1}(p_i)$ and $\mathcal {Z}_t(p_{i+1})$ are both in O(n). Due to their constant degrees, at most O(n) edges are affected by replacing the edges of $\mathcal {Z}_{t-1}(p_i)$ with the ones of $\mathcal {Z}_t(p_{i+1}$, yielding a total of O(n) topology changes for) $\texttt {simplifiedInfl}$. $\square$

4.2.2 Deflating the virtual graph

When the load of all but $\theta n$ nodes exceeds $2\zeta$ and some node u is deleted, the high probability bound of Lemma 2 for the random walk invoked by neighbor v no longer applies. In that case, node v invokes Procedure $\texttt {simplifiedDefl}$ to reduce the overall load (cf. Algorithm 4.6). Analogously as $\texttt {simplifiedInfl}$, Procedure $\texttt {simplifiedDefl}$ consists of two phases:

Phase 1: Constructing a smaller p -Cycle To reduce the load of simulated vertices, we replace the current p-cycle $Z_{t-1}(p_i)$ with a smaller p-cycle $\mathcal {Z}_t(p_s)$ where $p_s$ is a prime number in the range $(p_i/8,p_i/4)$.

Let $\alpha = {p_i}/{p_s}$. Any virtual vertex $x \in \mathcal {Z}_{t-1}(p_i)$, is (surjectively) mapped to some $y_x \in \mathcal {Z}_t(p_{s})$ where $y = \lfloor {x}/{\alpha } \rfloor$. Note that we only add y to $V(\mathcal {Z}_t(p_s))$ if there is no smaller $x' \in \mathcal {Z}_{t-1}(p_i)$ that yields the same y. This mapping guarantees that, for any element in $\mathbb {Z}_{p_s}$, we have exactly 1 virtual vertex in $\mathcal {Z}_{t}(p_s)$: Suppose that there is some $y \in \mathbb {Z}_{p_s}$ that is not hit by our mapping, i.e., for all $x \in \mathbb {Z}_{p_i}$, we have $y > \lfloor \frac{x}{\alpha } \rfloor$. Let $x'$ be the smallest integer such that $y = \lfloor \frac{x'}{\alpha } \rfloor$. For such an $x'$, it must hold that $\alpha y \leqslant x' < \alpha (y+1)$. Since $\alpha >1$, clearly $x'$ exists. By assumption, we have $x' \geqslant p_i$, which yields $\left\lfloor {p_i}/{\alpha } \right\rfloor \leqslant \left\lfloor {x'}/{\alpha } \right\rfloor = y < p_s.$ Since $p_s = {p_i}/\alpha$, we get $\left\lfloor p_s\right\rfloor < p_s,$ which is a contradiction to $p_s \in \mathbb {N}$. Therefore, we have shown that $\mathbb {Z}_{s}\subseteq V(\mathcal {Z}_t(p_s))$. The opposite set inclusion can be shown similarly.

For computing the edges of $\mathcal {Z}_t(p_s)$, note that any cycle edge $(y,y\pm 1) \in E(\mathcal {Z}_t(p_s))$, is between nodes u and v that were at most $\alpha$ hops apart in $G_t$, since their distance is at most $\alpha$ in the virtual graph $\mathcal {Z}_{t-1}(p_i)$. Thus any such edge can be added by exploring a neighborhood of constant-size in O(1) rounds via the cycle edges (of the current virtual graph) $\mathcal {Z}_{t-1}(p_i)$ in $G_t$. To add the edge between y and its inverse $y^{-1}$, we proceed along the lines of Phase 1 of $\texttt {simplifiedInfl}$, i.e., we solve permutation routing on $\mathcal {Z}_{t-1}(p_i)$, taking $O(\frac{\log n (\log \log n)^2}{\log \log \log n})$ rounds.

The following lemma summarizes the properties of Phase 1:

Lemma 6

If the network graph $G_{t-1}$ is a balanced map of $\mathcal {Z}_{t-1}(p_i)$, then Phase 1 of $\texttt {simplifiedDefl}$ ensures that every node computes the same virtual graph $\mathcal {Z}_t(p_s)$ in $O(\log n (\log \log n)^2)$ rounds such that

• (a) $p_s = |\mathcal {Z}_t(p_s)| \in (p_i/8,p_i/4)$, for some prime $p_s$;

• (b) there is a 1-to-1 mapping between $\mathbb {Z}_{p_s}$ and $V(\mathcal {Z}_t(p_s))$;

• (c) the edges of $\mathcal {Z}_t(p_s)$ adhere to Definition 1.

Proof

Property (a) trivially holds. For (b), observe that by description Phase 1, we map $x \in \mathcal {Z}_{t-1}(p_i)$ surjectively to $y_x \in \mathcal {Z}_t(p_{s})$ using the mapping $y_x = \lfloor \frac{x}{\alpha } \rfloor$ where $\alpha = \frac{p_i}{p_s}$. Note that we only add $y_x$ to $V(\mathcal {Z}_t(p_s))$ if there is no smaller $x \in \mathcal {Z}_{t-1}(p_i)$ that yields the same value in $\mathbb {Z}_{p_s}$, which guarantees that $V(\mathcal {Z}_t(p_s))$ is not a multiset. Suppose that there is some $y \in \mathbb {Z}_{p_s}$ that is not hit by our mapping, i.e., for all $x \in \mathbb {Z}_{p_i}$, we have $y > \lfloor \frac{x}{\alpha } \rfloor$. Let $x'$ be the smallest integer such that $y = \lfloor \frac{x'}{\alpha } \rfloor$. For such an $x'$, it must hold that $\alpha y \leqslant x' < \alpha (y+1)$. Since $\alpha >1$, clearly $x'$ exists. By assumption we have $x' \geqslant p_i$, which yields

$$\begin{aligned} \left\lfloor \frac{p_i}{\alpha } \right\rfloor \leqslant \left\lfloor \frac{x'}{\alpha } \right\rfloor < p_s. \end{aligned}$$

Since $\alpha = \frac{p_i}{p_s}$, we get

$$\begin{aligned} \left\lfloor p_s\right\rfloor = \left\lfloor \frac{p_i}{\alpha } \right\rfloor < p_s, \end{aligned}$$

which is a contradiction to $p_s \in \mathbb {N}$. Therefore, we have shown that $\mathbb {Z}_{s}\subseteq V(\mathcal {Z}_t(p_s))$. To see that $V(\mathcal {Z}_t(p_s))\subseteq \mathbb {Z}_{s}$, suppose that we add a vertex $y \geqslant p_s$ to $V(\mathcal {Z}_t(p_s))$. By the description of Phase 1, this means that there is an $x \in V(\mathcal {Z}_{t-1}(p_{i}))$, i.e., $x \leqslant p_i - 1$, such that $y = \lfloor \frac{x}{\alpha } \rfloor$. Substituting for $\alpha$ yields a contradiction to $y\geqslant p_s$, since

$$\begin{aligned} y = \left\lfloor \frac{x}{\alpha } \right\rfloor \leqslant \left\lfloor \frac{p_{i}-1}{\alpha } \right\rfloor = \left\lfloor p_s - \frac{p_s}{p_i}\right\rfloor < p_s. \end{aligned}$$

For property (c), note that any cycle edge $(y,y\pm 1) \in E(\mathcal {Z}_t(p_s))$, is between nodes u and v that were at most $\alpha$ hops apart in $G_t$, since their distance can be at most $\alpha$ in $\mathcal {Z}_{t-1}(p_i)$. Thus any such edge can be added by exploring a neighborhood of constant-size in O(1) rounds via the cycle edges of $\mathcal {Z}_{t-1}(p_i)$ in $G_t$. To add an edge between y and its inverse $y^{-1}$, we proceed along the lines of the proof of Lemma 4, i.e., we solve permutation routing on $\mathcal {Z}_{t-1}(p_i)$, taking $O(\frac{\log n (\log \log n)^2}{\log \log \log n})$ rounds. $\square$

Phase 2: Ensuring a virtual mapping After Phase 1 is complete, the replacement of multiple virtual vertices in $\mathcal {Z}_{t-1}(p_i)$ by a single vertex in $\mathcal {Z}_t(p_s)$, might lead to the case where some nodes are no longer simulating any virtual vertices. A node that currently does not simulate a vertex, marks itself as contending and repeatedly keeps initiating random walks on $\mathcal {Z}_t(p_s)$ (that are simulated on the actual network graph) to find spare vertices. Moreover, a node w that does simulate vertices, marks an arbitrary vertex as taken and transfers its other vertices to other nodes if requested. To ensure a valid mapping $\varPhi _t$, we need to transfer non-taken vertices to contending nodes if the random walk of a contending node hits a non-taken vertex z and no other walk ends up at z simultaneously. A similar analysis as for Phase 2 of $\texttt {simplifiedInfl}$ shows Lemma 5 for deflation steps.

Lemmas 3 and 5 imply the following:

Lemma 7

At any step t, the network graph $G_t$, is $4\zeta$-balanced, i.e., $G_t$ has constant node degree and $\lambda _{G_t} \leqslant \lambda$ where $1-\lambda$ is the spectral gap of the p-cycle expander family.

Proof

The result follows by induction on t. For the base case, note that we initialize $G_0$ to be a virtual mapping of the expander $\mathcal {Z}_0(p_0)$, which obviously guarantees that the network is $4\zeta$-balanced. For the induction step, we perform a case distinction depending on whether t is a simple or inflation/deflation step and apply the respective result, i.e. Lemmas 3 or 5. $\square$

4.3 Amortizing (simplified) type-2 recovery

We will now show that the expensive inflation/deflation steps occur rather infrequently. This will allow us to amortize the cost of the worst case bounds derived in Sect. 4.2. Suppose that step t was an inflation step. By Fact 2(a), this means that at least $(1-\theta )n$ nodes had a load of 1 at the beginning of t, and thus a load of $\leqslant \zeta$ at the end of t. Thus, even after redistributing the additional load of the $\theta n$ nodes that might have had a load of $>4\zeta$, a large fraction of nodes are in $\textsc {Low}$ and $\textsc {Spare}$ at the end of t. This guarantees that we perform type-1 recovery in $\varOmega (n)$ steps, before the next inflation/deflation is carried out. A similar argument applies to the case when $\texttt {simplifiedDefl}$ is invoked, thus yielding amortized polylogarithmic bounds on messages and rounds per every step.

Lemma 8

There exists a constant $\delta$ such that the following holds: If $t_1$ and $t_2$ are steps where type-2 recovery is performed (via $\texttt {simplifiedInfl}$ or $\texttt {simplifiedDefl}$), then $t_{1}$ and $t_{2}$ are separated by at least $\delta n \in \varOmega (n)$ steps with type-1 recovery where n is the size of $G_{t_1}$.

For the proof of Lemma 8 we require the following 2 technical results:

Claim

Suppose that t is an inflation step. Then $|\textsc {Low}_{t}| \geqslant (\theta + \frac{1}{2})n$.

Proof (of Claim 4.3)

First, consider the set of nodes $S=U_t{\setminus }\textsc {Spare}_{U_t}$, i.e., $\textsc {Load}_{U_t}(u)=1$ for all $u \in S$. By Fact 2(a), we have $|S| \geqslant (1-\theta )n$. Clearly, any such node $u \in S$ simulates at most $\zeta$ virtual vertices after generating its own vertices for the new virtual graph, hence the only way for u to reach $\textsc {Load}_{t}(u)>2\zeta$ is by taking over vertices generated by other nodes. By the description of procedure $\texttt {simplifiedInfl}$, only (a subset of) the nodes in $\textsc {Spare}_{U_t}$ redistribute their load by performing random walks. By Lemma 7, we can assume that $G_{t_1-1}$ is $4\zeta$-balanced. Since $|\textsc {Spare}_{U_t}|<\theta n$, we have a total of $\leqslant (4\zeta -4) \theta n$ clouds that need to be redistributed. Observe that v continues to simulate 4 clouds (i.e. $4\zeta$ nodes) by itself. Since every node that is in S, has at most $\zeta$ virtual nodes, we can bound the size of $\textsc {Low}_{t}$ by subtracting the redistributed clouds from |S|. For the result to hold we need to show that

$$\begin{aligned} (\theta + {1} / {2}) \leqslant 1-\theta - (4\zeta - 4)\theta , \end{aligned}$$

which immediately follows by Inequality (3). $\square$

Claim

Suppose that t is a deflation step. Then $|\textsc {Spare}_{t}| \geqslant (\theta +\frac{1}{4\zeta })n$.

Proof (of Claim 4.3)

Consider the set $S=\{u:\textsc {Load}_{U_t}(u)>2\zeta \}$. Since $S=U_t {\setminus } \textsc {Low}_{U_t}$, Fact 2(b) tells us that $|S|\geqslant (1-\theta )n$ and therefore we have a total load of least $(1-\theta )(2\zeta +1)n + \theta n$ in $U_t$. By description of procedure $\texttt {simplifiedDefl}$, every cloud of virtual vertices is contracted to a single virtual vertex. After deflating we are left with

$$\begin{aligned} \textsc {Load}(G_t) \geqslant \left( (1-\theta )\left( 2+\frac{1}{\zeta }\right) + \frac{\theta }{\zeta }\right) n. \end{aligned}$$

To guarantee the sought bound on $\textsc {Spare}_{t}$, we need to show that $\textsc {Load}(G_t) \geqslant (1 + \theta + \frac{1}{4\zeta })n$. This is true, since by (3) we have $\theta \leqslant \frac{1}{3}+\frac{1}{4\zeta }$. Therefore, by the pigeon hole principle, at least $\theta +\frac{1}{4\zeta }$ nodes have a load of at least 2.

Proof of Lemma 8

Observe that the values computed by procedures $\texttt {computeSpare}$ and $\texttt {computeLow}$ cannot simultaneously satisfy the thresholds of Fact 2, i.e., $\texttt {simplifiedInfl}$ and $\texttt {simplifiedDefl}$ are never called in the same step. Let ${t_1,t_2,\ldots }$ be the set of steps where, for every $i\geqslant 1$, a node calls either Procedure $\texttt {simplifiedInfl}$ or Procedure $\texttt {simplifiedDefl}$ in $t_i$. Fixing a constant $\delta$ such that

$$\begin{aligned} \delta \leqslant {1} / {4\zeta }, \end{aligned}$$

(9)

we need to show that $t_{i+1} - t_{i} \geqslant \delta n$.

We distinguish several cases:

• 1. $t_i$ simplifiedInfl; $t_{i+1}$ simplifiedInfl:

  By Fact 2(a) we know that $\textsc {Spare}_{U_{t_i}}$ contains less than $\theta n$ nodes. Since we inflate in $t_i$, every node generates a new cloud of virtual vertices, i.e., the load of every node in $U_{t_i}$ is (temporarily) at least $\zeta$ (cf. Phase 1 of $\texttt {simplifiedInfl}$). Moreover, the only way that the load of a node u can be reduced in $t_i$, is by transferring some virtual vertices from u to a newly inserted node w. However, by the description of $\texttt {simplifiedInfl}$ and the assumption that $\zeta >2$, we still have $\textsc {Load}_{t}(u)>1$ (and $\textsc {Load}_{t}(w)\geqslant 1$), and therefore $\textsc {Spare}_{G_{t_{i}}}\supseteq V(G_{t_i}){\setminus }\{w\}$. Since the virtual graph (and hence the total load) remains the same during the interval $(t_i,t_{i+1})$, it follows by Lemma 7 that $\textsc {Spare}$ can shrink by at most the number of insertions during $(t_i,t_{i+1})$. Since $|\textsc {Spare}_{U_{t_{i+1}}}|<\theta n$, more than $(1-\theta )n-1 > \delta n$ insertions are necessary.

• 2. $t_i$ simplifiedDefl; $t_{i+1}$ simplifiedDefl: We first give a lower bound on the size of $\textsc {Low}_{G_{t_i}}$. By Lemma 5, we know that load at every node is at most $4\zeta$ in $U_{t_i}$. Since every virtual cloud (of size $\zeta$) is contracted to a single virtual zertex in the new virtual graph, the load at every node is reduced to at most 4. Clearly, the nodes that are redistributed do not increase the load of any node beyond 4, thus $\textsc {Low}_{t}=G_t$. Analogously to Case 1, the virtual graph is not changed until $t_{i+1}$ and Lemma 7 tells us that $\textsc {Low}$ is only affected by deletions, i.e., $(1-\theta )n \geqslant \delta n$ steps are necessary before step $t_{i+1}$.

• 3. $t_i$ simplifiedInfl; $t_{i+1}$ simplifiedDefl:

  By Claim 4.3, we have $|\textsc {Low}_{G_{t_i}}| \geqslant (\theta + 1/2) n$, while Fact 2(b) tells us that $|\textsc {Low}_{G_{t_{i+1}}}|<\theta n$. Again, Lemma 7 implies that the adversary must delete at least $n/2 \geqslant \delta n$ nodes during $(t_i,t_{i+1}]$.

• 4. $t_i$ simplifiedDefl; $t_{i+1}$ simplifiedInfl:

  By Claim 4.3, we have $|\textsc {Spare}_{G_{t_i}}| \geqslant (\theta + \frac{1}{4\zeta })n$, and by Fact 2(a), we know that $|\textsc {Spare}_{G_{t_{i+1}}}|<\theta n$. Applying Lemma 7 shows that we must have more than $\frac{1}{4\zeta }n \geqslant \delta n$ deletions before $t_{i+1}$. $\square$

The following corollary summarizes the bounds that we get when using the simplified type-2 recovery:⁶

Corollary 1

Consider the (simplified) variant of dex that uses Procedures 4.5 and 4.6 to handle type-2 recovery. With high probability, the amortized running time of any step is $O(\log n )$ rounds, the amortized message complexity of any recovery step is $O(\log ^2 n)$, while the amortized number of topology changes is O(1).

4.4 Worst case bounds for type-2 recovery

Whereas Lemma 3 shows $O(\log n)$ worst case bounds for steps with type-1 recovery, handling of type-2 recovery that we have described so far yields amortized polylogarithmic performance guarantees on messages and rounds w.h.p. per step (cf. Cor. 1). We now present a more complex algorithm for type-2 recovery that yields worst case logarithmic bounds on messages and rounds per step (w.h.p.). The main idea of Procedures $\texttt {inflate}$ and $\texttt {deflate}$ is to spread the type-2 recovery over $\varTheta (n)$ steps of type-1 recovery, while still retaining constant node degrees and spectral expansion in every step.

The coordinator The node w that currently simulates the virtual vertex with integer-label $0 \in V(\mathcal {Z}_{t-1}(p_i)) = \mathbb {Z}_{p_i}$ is called coordinator and keeps track of the current network size n and the sizes of $\textsc {Low}$ and $\textsc {Spare}$ as follows: Recall that we start out with an initial network of constant size, thus initially coordinator w can compute these values with constant overhead. If an insertion or deletion of some neighbor of v occurs and the algorithm performs type-1 recovery, then v informs coordinator w of the changes to the network size and the sizes of $\textsc {Spare}$ and $\textsc {Low}$ (by routing a message along a shortest path in $\mathcal {Z}_{t-1}(p_i)$) at the end of the type-1 recovery. Node v itself simulates some vertex $x \in \mathbb {Z}_{p_i}$ and hence can locally compute a shortest path from x to 0 (simulated at w) according to the edges in $\mathcal {Z}_t(p_i)$ (cf. Fact 1). The neighbors of w replicate w’s state and update their copy in every step. If the coordinator w itself is deleted, the neighbors transfer its state to the new coordinator that subsequently simulates 0. The coordinator state requires only $O(\log n)$ bits and thus can be sent in 1 message. Keep in mind that the coordinator does not keep track of the actual network topology or $\textsc {Spare}$ and $\textsc {Low}$, as this would require $\varOmega (n)$ rounds for transferring the state to a new coordinator. Algorithm 4.7 contains the pseudo code describing the operation of the coordinator.

4.4.1 Staggering the inflation

We proceed in 2 phases each of which is staggered over $\lceil \theta n\rceil$ steps. Let PC denote the p-cycle at the beginning of the inflation step. If, in some step $t_0$ the coordinator is notified (or notices itself) that $|\textsc {Spare}| < 3\theta n$, it initiates (staggered) inflation to build the new p-cycle $PC'$ on $\mathbb {Z}_{p_{i+1}}$ by sending a request to the set of nodes I that simulate the set of vertices $S=\{1,\ldots ,\lceil 1/\theta \rceil \}$. The $\lceil 1/\theta \rceil$ nodes in I are called active in step $t_0$.

Phase 1: Adding a larger p -cycle For every $x \in S$, the simulating node in I adds a cloud of vertices as described in Phase 1 of $\texttt {simplifiedInfl}$. More specifically, for vertex x we add a set $Y \subset V(PC')$ of c(x) vertices, as defined in Eq. (7) on page 9. We denote this set of new vertices by $\textsc {NewSim}(v)$. That is, node v now simulates $|\textsc {Load}(v)| + |\textsc {NewSim}(v)|$ many vertices. In contrast to $\texttt {simplifiedInfl}$, however, vertex $x\in PC$ and its edges are not replaced by Y (yet). For each node in $y \in Y$, the simulating node v computes the cycle edges and inverse $y^{-1}\in PC'$. It is possible that $y^{-1}$ is not among the vertices in S, and hence is not yet simulated at any node in I. Nevertheless, by Eq. (7), v can locally compute the vertex $x'\in PC$ that is going to be inflated to the cloud that contains $y^{-1} \in PC'$. Therefore, we add an intermediate edge $(y,x')$, which requires $O(\log n)$ messages and rounds. Note that $|\textsc {NewSim}(v)|$ could be as large as $4\zeta ^2$. Therefore, similarly as in Phase 2 of $\texttt {simplifiedInfl}$, a node in I needs to redistribute newly generated vertices if $|\textsc {NewSim}| > 4\zeta$ as follows: The nodes in I proceed by performing random walks to find node with small enough $\textsc {NewSim}$. Note that, even though $\texttt {inflate}$ has not yet been processed at nodes in $V(G_t) {\setminus } I$, any node that is hit by this random walk can locally compute its set $\textsc {NewSim}$ and thus check if it is able to simulate an additional vertex in the next p-cycle $PC'$. Since we have O(1) nodes in I each having O(1) vertices in their $\textsc {NewSim}$ set, these walks can be done sequentially, i.e., only 1 walk is in progress at any time, which takes $O(\log n)$ rounds in total.

After these walks are complete and all nodes in I have $|\textsc {NewSim}|\leqslant 4\zeta$, the coordinator is notified and forwards the inflation request to nodes $I'$ that simulate vertices $S'=\{\lceil 1/\theta \rceil + 1,\ldots ,2\lceil 1/\theta \rceil \}$. (Again, this is done by locally computing the shortest path in PC.) In step $t_0+1$, the nodes in $I'$ become active and proceed the same way as nodes in I in step $t_0$, i.e., clouds and intermediate edges are added for every vertex in $S'$.

Phase 2: Discarding the old p -cycle. Once Phase 1 is complete, i.e., all nodes are simulating the vertices in their respective $\textsc {NewSim}$ set, the coordinator sends another request to the set of nodes I—the active nodes in the next step—that are still simulating the set S of the first $\lceil 1/\theta \rceil$ vertices in the old p-cycle PC. Every node in I drops all edges of PC and stops simulating vertices in V(PC). In the next step, this request is forwarded to the nodes that simulate the next $\lceil \theta n\rceil$ vertices and reaches all nodes within $\theta n$ steps. After $T= 2\theta n$ steps⁷, the inflation has been processed at all nodes.

Finally, we need to argue that type-1 recovery succeeds with high probability while the staggered inflation is ongoing: If the adversary inserts a node w in any of these T steps, we can simply assign one of the newly inflated vertices to w. If, on the other hand, the adversary deletes nodes, we need to show that, for any $t \in [t_0,t_0+T]$, it holds that $|\textsc {Low}_t| \geqslant \theta n$. Recalling that the coordinator invoked the inflation in step $t_0$ because $|\textsc {Spare}_{t_0}| < 3\theta n$, it follows that $|\textsc {Low}_{t_0}| \geqslant n - 3\theta n$. In the worst case, the adversary deletes 1 node in every one of the following T steps, which increases the load of at most $2\theta n$ nodes. This yields that $|\textsc {Low}_t| \geqslant |\textsc {Low}_{t_0}| - 2\theta n = n - 5\theta n \geqslant \theta n$, due to (3). Thus, since the assumption of Lemma 2(b) holds throughout steps $[t_0,t_0+T]$, type-1 recovery succeeds with high probability as required.

4.4.2 Staggering the deflation

We now describe the implementation of $\texttt {deflate}$ that yields a worst case bound of $O(\log n)$ for the recovery in every step. Similarly to $\texttt {inflate}$, the coordinator initiates a staggered deflation whenever the threshold $|\textsc {Low}| < 3\theta$ is reached and the algorithm proceeds in two phases:

Phase 1: Adding a smaller p -cycle Phase 1 is initiated during the recovery in some step $t_0$ by the (current) coordinator w who sends a message to nodes S that simulate vertices $I=\{1,\ldots ,\lceil 1/\theta \rceil \}$. The nodes in S become active in the recovery of step $t_0$ and will start simulating the (smaller) p-cycle $\mathcal {Z}(p_s)$ in addition to the current p-cycle $\mathcal {Z}_{t_0}(p_i)$ by the end of the step, as described below. As in the case of $\texttt {inflate}$, w can efficiently find S (requiring only $O(\log n)$ messages and rounds) by following the shortest path in the current p-cycle $\mathcal {Z}_{t_0}(p_{i})$. Let $\alpha = p_i / p_s$ and consider some node $v \in S$. For every $x \in \textsc {Sim}(v)$, node v computes $y_x = \lfloor x/\alpha \rfloor$ and starts simulating $y_x \in \mathcal {Z}(p_s)$, if there is no $x' < x$ such that $x' = \lfloor x' / \alpha \rfloor$. That is, the new vertices are determined exactly the same way as in Phase 1 of $\texttt {simplifiedDefl}$ and node v adds $y_x$ to $\textsc {NewSim}(v)$.

Assuming that there is a $y_x \in \textsc {NewSim}(v)$, node v marks all $x_1,\ldots ,x_k \in \mathcal {Z}_{t_0}(p_i)$ that satisfy $y_x = \lfloor x_j / \alpha \rfloor$, for $1\leqslant j \leqslant k$, as taken. We say that x dominates $x_1,\ldots ,x_k$ and we call the set $\{x_1,\ldots ,x_k\}$ a deflation cloud. Note that some of the vertices of a deflation cloud might be simulated at other nodes. Nevertheless, according to the edges of $\mathcal {Z}_{t_0}(p_i)$, these nodes are in an O(1) neighborhood of v and can thus be notified to mark the corresponding vertices as taken. Intuitively speaking, if a node v simulates such a dominating vertex x, then v is guaranteed to simulate a vertex in the new p-cycle $\mathcal {Z}(p_s)$, and the surjective requirement of the virtual mapping is satisfied at v. Thus our goal is to ensure that every node in S simulates a dominating vertex by the end of the recovery of this step.

The problematic case is when none of the vertices currently simulated at node v dominates for some $y_x \in \mathcal {Z}(p_s)$. To ensure that v simulates at least 1 vertex of the new p-cycle $\mathcal {Z}(p_s)$, node v initiates a random walk on the graph $\mathcal {Z}(p_s)$ to find a dominating vertex that has not been marked taken. We thus lower-bound the size of dominating vertices that are never marked as taken, in any of the $\theta n$ steps during which $\texttt {deflate}$ is in progress:

Recall that the coordinator invoked $\texttt {deflate}$ because $|\textsc {Low}|<3\theta$. This means that $\geqslant (1-3\theta )n$ nodes have $\textsc {Load}_{t_0} > 2\zeta$ and the total load in the network is at least $(2\zeta (1-3\theta )+3\theta )n$ since every node simulates at least 1 vertex. If some node simulates a dominating vertex x, then all of the (at most $\alpha \leqslant 8$) dominated vertices $x'>x$ that also satisfy $y_x = \lfloor x' / \alpha \rfloor$ are marked as taken. Considering that $\zeta \leqslant 8$, the number of dominating vertices is at least $(2\zeta (1-3\theta )+3\theta )n/8 \geqslant (2 - \theta (6+3/\zeta ))n$. In each of the $\theta n$ steps while Phase 1 of $\texttt {deflate}$ is in progress, the adversary might insert some node that starts simulating a dominating vertex. Thus, in total we must give up $n+\theta n$ dominating vertices. It follows that the number of dominating vertices that are available (i.e. not needed by any node) is at least

$$\begin{aligned} (2 - \theta (6+3/\zeta ))n - n - \theta n = (1-\theta (6+3/\zeta +1))n. \end{aligned}$$

Recalling (3) on page 7, the right hand size is at least a constant fraction of n, i.e., the set of available dominating vertices D has size $\geqslant \varepsilon n$ while $\texttt {deflate}$ is in progress, for some $\varepsilon >0$. Similarly to the proof of Lemma 2, we can use the concentration bound of [9] to show that a random walk of v of length $O(\log n)$ hits a vertex in D with high probability. To avoid clashes between nodes in S, we perform these walks sequentially. Since there are only O(1) nodes in S, this takes overall $O(\log n)$ time and messages.

In step $t_0+1$, the nodes that simulate the next $1/\theta$ vertices become active and so forth, until the request returns to the (current) coordinator after $\lceil \theta n\rceil$ steps.

Phase 2: Discarding the old p -cycle Once the new (smaller) p-cycle $\mathcal {Z}(p_s)$ has been fully constructed, the coordinator sends another request to the nodes in I—which again become active nodes—that simulate the $\lceil 1/\theta \rceil$ vertices in S. Every node in I drops all edges of $E(\mathcal {Z}(p_{i}))$ and stops simulating vertices in $V(\mathcal {Z}(p_{i}))$. This request is again forwarded to the nodes that simulate the next $\theta n$ vertices and finally has reached all nodes within $\theta n$ steps. Thus, after $T=\lceil 2\theta n \rceil$ steps, the deflation has been completed at all nodes.

Since the coordinator initiated the deflation because $|\textsc {Low}_{t_0}| < 3\theta n$, it follows that $|\textsc {Spare}_{t_0}|\geqslant n - 3\theta n$, and thus $|\textsc {Spare}_t|\geqslant \theta n$, for all steps $t \in [t_0,t_0+T]$. Therefore, by an argument similar to Procedure $\texttt {inflate}$, it follows that type-1 recovery succeeds w.h.p. until the new virtual graph is in place.

Lemma 9

(Worst case bounds type-2 recovery) Suppose that the coordinator initiates either $\texttt {inflate}$ of $\texttt {deflate}$ during recovery in some step $t_0$ and $G_{t_0-1}$ is $4\zeta$-balanced. Then, for all steps $t \in [t_0,t_0+T]$ where $T=\lceil 2\theta n \rceil$ the following hold:

• (a) Every node simulates at most $8\zeta$ vertices and the recovery in t requires at most $O(\log n)$ rounds and messages (w.h.p.), while making only O(1) changes to the topology.

• (b) The spectral gap of $G_t$ is at least $\frac{(1-\lambda )^2}{8}$ where $1-\lambda$ is the spectral gap of the p-cycle expander family.

Proof

First consider (a): The bound of $8\zeta$ vertices follows from the fact that, during $\texttt {inflate}$ and $\texttt {deflate}$, any node simulates at most $4\zeta$ vertices from both p-cycles. This immediately implies a constant node degree. Recalling the description of Phases 1 and 2 for $\texttt {inflate}$ and $\texttt {deflate}$, we observe that either phase causes an overhead of $O(\log n)$ messages and rounds for each of the O(1) active nodes during recovery in some step $t \in [t_0,t_0+T]$; the worst case bounds of (a) follow.

We now argue that, at any time during the staggered inflation, we still guarantee a constant spectral gap. By the left inequality of Theorem 2 (“Appendix”), a spectral expansion of $\lambda _{G_{t_0-1}}$ yields an edge expansion (cf. Definition 5 in “Appendix”) $h(G_{t_0-1}) \geqslant (1-\lambda _{G_{t_0-1}})/2$, which is O(1). For both, $\texttt {inflate}$ and $\texttt {deflate}$, it holds that during Phase 1, nodes still simulate the full set of vertices and edges of the old p-cycle and some intermediate edges of the new p-cycle. In Phase 2, on the other hand, nodes simulate a full set of vertices and edges of the new p-cycle and some edges of the old p-cycle. Thus, during either phase, the edge expansion is bounded from below by the edge expansion of the p-cycle expander family. That is, we have $h(G_{t}) \geqslant h(G_{t_0-1})$, for any step $t \in [t_0,t_0+T]$. It is possible, however, that the additional intermediate edges decrease the spectral expansion. Nevertheless, we can apply the right inequality of Theorem 2 to get

$$\begin{aligned} 1-\lambda _{G_{t}} \geqslant \frac{h^2(G_{t_0-1})}{2} \geqslant (1-\lambda _{G_{t_0-1}})^2 / 8, \end{aligned}$$

as required. $\square$

4.4.3 Proof of Theorem 1

Lemmas 3 and 9 imply the sought worst case bounds of Theorem 1. The constant node degree follows from Lemma 3(a) and Lemma 9(a). Moreover, Lemma 9(b) shows a constant spectral gap for (the improved) type-2 recovery steps and the analogous result for type-1 recovery follows from Lemma 1 and Lemma 3(a).

4.4.4 Implementing a distributed hash table (DHT)

We can leverage our expander maintenance algorithm to implement a DHT as follows: Recall that the current size s of the p-cycle is global knowledge. Thus every node uses the same hash function $h_s$, which uniformly maps keys to the vertex set of the p-cycle.

We first look at the case where no staggered inflation/deflation is in progress: If some node u wants to store a key value pair (k, val) in the DHT, u computes the index $z:=h_s(k)$. Recall that u can locally compute a shortest path $z_1,z_2,\ldots ,z$ (in the p-cycle) starting at one of its simulated virtual vertices $z_1$ and ending at vertex z. Even though node u does not know how this entire path is mapped to the actual network, it can locally route by simply forwarding (k, val) to the neighboring node $v_2$ that simulates $z_2$; node $v_1$ in turn forwards the key value pair to the node that simulates $z_3$ and so forth. The node that simulates vertex z stores the entry (k, val). If z is transferred to some other node w at some point, then storing (k, val) becomes the responsibility of w. Similarly, for finding the value associated with a given key $k'$, node u routes a message to the node simulating vertex $h_s(k')$, who returns the associated value to u. It is easy to see that insertion and lookup both take $O(\log n)$ time and $O(\log n)$ messages and that the load at each node is balanced.

We now consider the case where a staggered inflation (cf. Procedure 4.8) has been started and some set of nodes have already constructed the next larger p-cycle of size $s'$. Let PC be the old (but not yet discarded) p-cycle and let $PC'$ denote the new p-cycle that is currently under construction. For a given vertex $z_i \in PC$ we use the notation $z_i'$ to identify the unique vertex in $PC'$ that has the same integer label as $z_i$.

Note that all nodes have knowledge of the hash function $h_{s'}$, which maps to the vertices of $PC'$. Suppose that a node $u \in S$ becomes active during Phase 1 of the staggered inflation and starts simulating vertices $z_1',\ldots ,z_\ell ' \in PC'$. (For clarity of presentation, we assume that $\ell \leqslant 4\zeta$, thus u does not need to redistribute these vertices. The case where $\ell > 4\zeta$ can be handled by splitting the operations described below among the nodes that end up simulating $z_1',\ldots ,z_\ell '$.) At this point, some set S of j nodes might still be simulating the corresponding vertices $z_1,\ldots ,z_\ell \in PC$, where $j\leqslant \ell \in O(1)$. Thus node u contacts the nodes in S (by routing a message to vertices $z_1,\ldots ,z_\ell$ along the edges of PC) and causes these nodes to transfer all data items associated with $z_1,\ldots ,z_\ell$ to u. From this point on until the staggered inflation is complete, the nodes in S forward all insertion and lookup requests regarding $z_1,\ldots ,z_\ell$ to node u. Note that the above operations require at most $O(\log n)$ rounds and messages, and thus only increase the complexity of the staggered inflation by a constant factor.

The case where a staggered deflation is in progress is handled similarly, by transferring key value pairs of vertices that are contracted to a single vertex in the new (smaller) p-cycle, whenever the simulating node becomes active.

5 Extension: handling multiple insertions and deletions

Our framework can be extended to a model where the adversary can insert or delete multiple nodes in each step, with certain assumptions:

Insertions The adversary can insert or delete a set N of up to $\varepsilon n$ many nodes in each step, for some small $\varepsilon >0$. We restrict the adversary to attach only a constant number of nodes in N to any node—dropping this restriction will allow the adversary to place the whole set N at the same node u, causing significant congestion due to u’s constant degree and our restriction of having messages of $O(\log n)$ size. Note that this might cause type-1 recovery to fail more frequently, since the number of available spare vertices is depleted within a constant number of insertion steps. Nevertheless we can still handle such large-scale insertions via type-2 recovery by using Procedure $\texttt {simplifiedInfl}$.

Deletions For deletions, we only allow the adversary to delete nodes that leave the remainder graph connected, i.e., if the adversary removes nodes N at time t, $G_{t-1}{\setminus } N$ is still connected. Moreover, for each deleted node there must remain at least one neighbor in the set $G_{t-1}{\setminus } N$. As in the case of insertions, such large-scale deletions might require Procedure $\texttt {simplifiedDefl}$ to be invoked every constant number of steps.

Corollary 2

(Multiple insertions/deletions) Suppose that the adversary can insert or delete $\leqslant \varepsilon n$ nodes, for some small $\varepsilon > 0$ in every step adhering to the following conditions: In case of insertions, the adversary attaches O(1) nodes to any existing node in the network. In case of deletions, the remaining graph is connected and, for each deleted node u, some neighbor of u is not deleted. There exists a distributed algorithm that requires $O(n\log ^2 n)$ messages and $O(\log ^3 n)$ rounds (w.h.p.) for recovery in every step.

6 Conclusion

We have presented a distributed algorithm for maintaining an expander efficiently using only $O(\log n)$ messages and rounds in the worst case. Moreover, our algorithm DEX guarantees a constant spectral gap and node degrees deterministically at all times. There are several open questions: How can we deal with malicious nodes in this setting? Is there an $\varOmega (\log n)$ lower bound on the number of rounds and/or messages that are necessary per adversarial action on average? It will be interesting to explore if our approach can be extended to other problems such as maintaining routing tables in an adversarial setting.

Appendix: Previous results and definitions

For completeness, we restate some definitions and results from literature that we reference in the paper.

We use the notation $G = \langle n,d,\lambda _G\rangle$ to denote a d-regular graph G of n nodes where the second largest eigenvalue of the adjacency matrix is $\lambda _G$.

Definition 4

(Expanders, spectral gap) Let d be a constant and let $\mathcal {G}=(\langle n_0,d,\lambda _0\rangle ,\langle n_1,d,\lambda _1\rangle ,\ldots )$ be an infinite sequence of graphs where $n_{i+1}> n_i$ for all $i\geqslant 0$. We say that $\mathcal {G}$ is an expander family of degree d if there is a constant $\lambda <1$ such that $\lambda _i\leqslant \lambda$, for all $i\geqslant 0$. Moreover, the individual graphs in $\mathcal {G}$ are called expanders with spectral gap $1-\lambda$.

Lemma 10

(cf. Lemma 1.15 in [5]) If H is formed by vertex contractions from a graph G, then $\lambda _H \leqslant \lambda _G$.

Lemma 11

Consider an expander network and suppose that every node initiates a random walk of length $\varTheta (\log n)$ and only 1 random walk token can be sent over an edge in each direction in a round. Then all random walks have completed with high probability after $O(\log ^2 n)$ rounds.

Proof

The result follows by instantiating Lemma 2.2 of [7], which shows that, if every node initiates $\eta$ random walks of length $\mu$, then all walks complete within $O(\frac{\eta \mu \log n}{\delta })$ rounds where $\delta$ is the minimum node degree. $\square$

Corollary 3

(Corollary 7.7.3 in [28]) In any bounded degree expander of n nodes, n packets, one per node, can be routed according to an arbitrary permutation in $O\left( \frac{\log n (\log \log n)^2}{\log \log \log n}\right)$ rounds.

Lemma 12

(Mixing Lemma, cf. Lemma 2.5 [14]) Let G be a d-regular graph of n vertices and spectral gap $1-\lambda$. Then, for all set of nodes $S,T \subseteq V(G)$, we have that $\left| |E(S,T)| - \frac{d|S||T|}{n} \right| \leqslant \lambda d \sqrt{|S||T|}$.

Definition 5

(Edge expansion, [14]) Consider a graph G of n nodes and a set $S \subseteq V(G)$. Let $E(S,\bar{S})$ be the set of edges between S and $G{\setminus } S$. The edge expansion of G is defined as

$$\begin{aligned} h(G):= \min \left\{ \frac{|E(S,\bar{S})|}{|S|}: S\subseteq V(G)\,\text {and}\,|S| \leqslant n/2\right\} . \end{aligned}$$

Theorem 2

(Cheeger Inequality, Theorem 2.6 in [14]) Let G be an expander with spectral gap $1-\lambda$ and edge expansion h(G). Then

$$\begin{aligned} \frac{1-\lambda }{2} \leqslant h(G) \leqslant \sqrt{2(1-\lambda )}. \end{aligned}$$