There is no stationary cyclically monotone Poisson matching in 2d

Abstract

We show that there is no cyclically monotone stationary matching of two independent Poisson processes in dimension $d=2$. The proof combines the harmonic approximation result from Goldman et al. (Commun. Pure Appl. Math. 74:2483–2560, 2021) with local asymptotics for the two-dimensional matching problem for which we give a new self-contained proof using martingale arguments.

1 Introduction

Consider two locally finite¹ point sets $\{X\},\{Y\}\subset \mathbb {R}^d$ in d-dimensional space. We are interested in their matching, which we think of as a bijection T from $\{X\}$ onto $\{Y\}$. More specifically, we are interested in their matching by cyclically monotone maps T, which means that for any finite subset²$\{X_n\}_{n=1}^{N}$ we have

$$\begin{aligned} \sum _{n=1}^N T(X_n)\cdot (X_n-X_{n-1})\ge 0\quad \text{ with }\quad X_0:=X_N. \end{aligned}$$

(1.1)

It is elementary to see that (1.1) is equivalent to local optimality, meaning

$$\begin{aligned} \sum _X(|T(X)-X|^2-|\widetilde{T}(X)-X|^2)\le 0 \end{aligned}$$

(1.2)

for any other bijection $\widetilde{T}$ that differs from T only on a finite number of points.³ This makes a connection to the optimal transportation between the measures

$$\begin{aligned} \mu =\sum _{X}\delta _X \quad \text{ and } \quad \nu =\sum _{Y}\delta _Y \end{aligned}$$

(1.3)

related via $T\#\mu =\nu$, which we shall explore in this paper. Note however that because of the (typically) infinite number of points, we cannot view T as a minimizer.

Before proceeding to the random setting, we make two simple observations that show that the set of $(\{X\},\{Y\},T)$ is rich: For $d=1$, (1.1) is easily seen to be equivalent to plain monotonicity. Every single matching $T(X_0)=Y_0$ can obviously be extended in a unique way to a monotone bijection T of $\{X\}$ and $\{Y\}$, so that for $d=1$, the set of monotone bijections T has the same magnitude as $\{X\}$ itself. Returning to general d, we note that for any monotone bijection T of $\{X\}$ and $\{Y\}$, and for any two shift vectors ${\bar{x}},{\bar{y}}\in \mathbb {R}^d$, the map $x\mapsto T(x-{\bar{x}})+{\bar{y}}$ is a monotone bijection of the shifted point sets $\{{\bar{x}}+X\}$ and $\{{\bar{y}}+Y\}$.

We are interested in the situation when the sets $\{X\}$, $\{Y\}$ and their cyclically monotone bijection T are random. More precisely, we consider the case when $\{X\}$ and $\{Y\}$ are independent Poisson point processes of unit intensity. We assume that the $\sigma$-algebra for $(\{X\},\{Y\},T)$ is rich enough so that the following elementary observables are measurable, namely the number $N_{U,V}$ of matched pairs $(X,Y)\in U\times V$ for any two Lebesgue-measurable sets $U,V\subset \mathbb {R}^d$ (with U or V having finite Lebesgue measure⁴):

$$\begin{aligned} N_{U,V}:=\#\{(X,Y)\in U\times V|Y=T(X)\}\in \{0,1,\ldots \}. \end{aligned}$$

We now come to the crucial assumption on the ensemble: In view of the above remark, the additive group $\mathbb {Z}^d\ni {\bar{x}}$ acts on $(\{X\},\{Y\},T)$ via

$$\begin{aligned} (\{X\},\{Y\},T)\mapsto (\{{\bar{x}}+X\},\{{\bar{x}}+Y\},T(\cdot -{\bar{x}})+{\bar{x}}). \end{aligned}$$

We assume that this action is stationary and ergodic.⁵ On the one hand, stationarity is a structural assumption; we shall only use it in following form: For any shift vector ${\bar{x}}$, the random natural numbers $N_{{\bar{x}}+U,{\bar{x}}+V}$ and $N_{U,V}$ have the same distribution. On the other hand, ergodicity is a qualitative assumption⁶; we will only use it in form of the following application of Birkhoff’s ergodic theorem:

$$\begin{aligned} \lim _{R\uparrow \infty }\frac{1}{R^d}\sum _{{\bar{x}}\in \mathbb {Z}^d\cap [0,R)^d}N_{{\bar{x}}+U,{\bar{x}}+V} =\mathbb {E}N_{U,V}\quad \text{ almost } \text{ surely }. \end{aligned}$$

Theorem 1.1

For $d\le 2$, there exists no stationary and ergodic ensemble of $(\{X\},$ $\{Y\},T)$, where $\{X\}$, $\{Y\}$ are independent Poisson point processes and T is a cyclically monotone bijection of $\{X\}$ and $\{Y\}$.

Our interest in this problem is motivated on the one hand by work on geometric properties of matchings by Holroyd [13] and Holroyd et al. [14, 15], and on the other hand by work on optimally coupling random measures by the first author and Sturm [17] and the first author [16]. In [14], Holroyd, Janson, and Wästlund analyze (stationary) matchings satisfying the local optimality condition (1.2) with the exponent 2 replaced by $\gamma \in [-\infty ,\infty ].$ They call matchings satisfying this condition $\gamma$-minimal and derive a precise description of the geometry of these matchings in dimension $d=1$. In dimension $d>1$ much less is known. In particular, in the critical dimension $d=2$ they could only show existence of stationary $\gamma$-minimal matchings for $\gamma <1$. The cases $\gamma \ge 1$ were left open, but see [15] and [13] for several open questions for $d=2$ and in particular $\gamma =1$. On the other hand, the first author and Sturm [16, 17] develop an optimal transport approach to these (and related) problems. They identify the point sets $\{X\},\{Y\}$ with the counting measures (1.3) and seek a stationary coupling Q⁷ between $\mu$ and $\nu$ minimizing the cost

$$\begin{aligned} \mathbb {E}\int _{B_1\times \mathbb {R}^d} |x-y|^\gamma dQ, \end{aligned}$$

where we denote by $B_R$ the unit ball of radius R. (Note that any (stationary) bijection $T:\{X\}\rightarrow \{Y\}$ induces a (stationary) coupling between $\mu$ and $\nu$ by setting $Q=(\textsf{id},T)_\#\mu$.) If this cost functional is finite there exists a stationary coupling which is necessarily locally optimal in the sense of (1.2) with the exponent 2 replaced by $\gamma$. In dimension 2 for $\mu$ and $\nu$ being two independent Poisson processes, this functional is finite if and only if $\gamma <1$, which is in line with the results of [14].

In view of these results, it is natural to conjecture that Theorem 1.1 also holds for $\gamma$-minimal matchings with $\gamma \ge 1$. However, our proof crucially relies on the harmonic approximation result of [10] which so far is only available for $\gamma =2$.

Before we explain the main steps of the proof of Theorem 1.1 in Sect. 1.1 we would like to give a few remarks on extensions and variants of Theorem 1.1.

Remark 1.2

Theorem 1.1 remains true if we replace the bijection T by the a priori more general object of a stationary coupling Q. This can be seen by either using that matchings are extremal elements in the set of all couplings of point sets or by directly writing the proof in terms of couplings which essentially only requires notational changes.

Remark 1.3

Very well studied siblings of stationary matchings are stationary allocations of a point process $\{X\}$, i.e. a stationary map $T:\mathbb {R}^d\rightarrow \{X\}$ such that $\textsf{Leb}(T^{-1}(X))$ equals $\mathbb {E}[\#\{X\in (0,1)^d\}]^{-1}$. There are several constructions of such an allocation, for instance by using the stable marriage algorithm in [12], the flow lines of the gravitational force field exerted by $\{X\}$ in [8], an adaptation of the AKT scheme in [22], or by optimal transport methods in [17].

By essentially the same proof as for Theorem 1.1, one can show that in $d=2$ there is no cyclical monotone stationary allocation to a Poisson process. The only place where we need to change something in the proof is the $L^\infty$ estimate Lemma 2.2.

Remark 1.4

We do not use many particular features of the Poisson measures $\mu$ and $\nu$ in the proof of Theorem 1.1 since ergodicity and stationarity allow us to argue on a pathwise level via the harmonic approximation result (cf. Sect. 1.1).

We use two properties of the Poisson measure. The first property is concentration around the mean. The second property is more involved. Denote by $W_p$ the $L^p$ Wasserstein distance. We use that⁸ diverges at the same rate for $R\rightarrow \infty$ as for some $\varepsilon >0$ (here we use $\varepsilon =1$).

As Remark 1.3 indicates stationary matchings are closely related to the bipartite matching problem, which is the natural variant of the problem studied in this paper with only a finite number of points $\{X_1,\ldots ,X_n\},\{Y_1,\ldots ,Y_n\}$. Note that then the local optimality condition (1.2) turns into a global optimality condition.⁹ This (finite) bipartite matching problem has been the subject of intense research in the last 30 years, see e.g. [1] for the first proof of the rate of convergence in the case of iid points in dimension $d=2$, [24] for sharp integrability properties for matchings in $d\ge 3$, [7] for a new appraoch based on the linearization of the Monge-Ampère equation, and [5] for a thorough analysis of the bipartite matching problem in $d=1$.

We rely on this connection in two ways. On the one hand we use the asymptotics of the cost of the bipartite matching which are known since [1]. However, we need a local version for which we give a self-contained proof using martingale techniques (see Sect. 2.5) which is new and interesting on its own. On the other hand we exploit a large scale regularity result for optimal couplings, the harmonic approximation result, developed in [10]. This regularity result was inspired by the PDE approach proposed by [7], see also [2, 3, 11, 21] for remarkable results for the bipartite matching problem using this approach.

1.1 Main steps in the proof of Theorem 1.1

In the following we will describe the main steps in the proof of Theorem 1.1. For the detailed proofs we refer to Sect. 2.

We argue by contradiction. We assume that there is a locally optimal stationary matching T between $\left\{ X \right\}$ and $\left\{ Y \right\}$. On the one hand, we will show that

$$\begin{aligned} \frac{1}{R^d}\sum _{X \in B_R\;\text{ or }\;T(X) \in B_R} |T \left( X \right) - X| \le o(\ln ^{\frac{1}{2}}R). \end{aligned}$$

(1.4)

On the other hand, it is known (we will prove the local version needed for our purpose) that any bipartite matching satisfies

$$\begin{aligned} \frac{1}{R^d}\sum _{X \in B_R\;\text{ or }\;T(X) \in B_R} |T \left( X \right) - X| \ge \Omega (\ln ^{\frac{1}{2}}R) \end{aligned}$$

(1.5)

leading to the desired contradiction.

Let us now describe the different steps leading to (1.4) and (1.5) in more detail. Our starting point is the observation that by stationarity and ergodicity the following $L^0$-estimate on the displacement $T \left( X \right) - X$ holds

$$\begin{aligned} \# \left\{ X \in (-R,R)^d \ :\ \left| T \left( X \right) - X\right| \gg 1 \right\} \le o (R^d), \end{aligned}$$

(1.6)

see Lemma 2.1 for a precise statement. This is the only place where stationarity and ergodicity enter. Since T is locally optimal, its support is in particular monotone, which means that for any $X, X' \in \left\{ X \right\}$ we have

$$\begin{aligned} (T \left( X' \right) - T \left( X \right) )\cdot (X'-X) \ge 0. \end{aligned}$$

By (1.6), we know that most of the points in $(-R,R)^d$ are not transported by a large distance. Combining this with monotonicity allows us to also shield the remaining points from being transported by a distance of order R, so that

$$\begin{aligned} \left| T \left( X \right) - X\right| \le o(R)\; \text{ provided } \text{ that } \; X \in (-R,R)^d, \end{aligned}$$

(1.7)

see Lemma 2.2 for a precise statement. By concentration properties of the Poisson process we may assume that $\frac{\# \left\{ X \in B_R \right\} }{\left| B_R\right| }\in \left[ \frac{1}{2},2 \right]$ for $R\gg 1$. Summing (1.7) over $B_R$ we obtain

$$\begin{aligned} \frac{1}{R^d} \sum _{X \in B_R} |T \left( X \right) - X|^2 \le o(R^2). \end{aligned}$$

(1.8)

Now comes the key step of the proof. We want to exploit regularity of T to upgrade (1.8) to an $O(\ln R)$ bound. The tool that allows us to do this is the harmonic approximation result [10, Theorem 1.4] (see also [19] for a simplified exposition of the theory) which quantifies the closeness of the displacement $T \left( X \right) - X$ to a harmonic gradient field $\nabla \varphi$, taking as input only the local energy

$$\begin{aligned} E(R) :=\frac{1}{R^d} \sum _{X \in B_R \ \text{ or } \ T \left( X \right) \in B_R} |T \left( X \right) - X|^2 \end{aligned}$$

(1.9)

and the distance of and to the Lebesgue measure on $B_R$

$$\begin{aligned} D(R) := \frac{1}{R^d}W^2_{(-R,R)^d}(\mu ,n_\mu ) + \frac{R^2}{n_\mu }(n_\mu -1)^2 +\frac{1}{R^d}W^2_{(-R,R)^d}(\nu ,n_\nu ) + \frac{R^2}{n_\nu }(n_\nu -1)^2, \end{aligned}$$

(1.10)

where $n_\mu = \frac{\# \left\{ X \in B_R \right\} }{\left| B_R\right| }$ and $n_\nu = \frac{\# \left\{ Y \in B_R \right\} }{\left| B_R\right| }$, and . By (1.8) (together with its counter part arising from exchanging the roles of $\left\{ X \right\}$ and $\left\{ Y \right\}$) we have $E(R)\le o\left( R^2\right)$. By the well-known bound for the matching problem in $d=2$ and by concentration properties of the Poisson process we have $D(R)\le O(\ln R)$, see Lemma 2.6. Iteratively exploiting the harmonic approximation result on an increasing sequence of scales we obtain that the local energy E inherits the asymptotic of D:

$$\begin{aligned} \frac{1}{R^d}\sum _{X \in B_R \; \text{ or } \; T \left( X \right) \in B_R} |T\left( X \right) - X|^2 \le O(\ln R), \end{aligned}$$

(1.11)

see Lemma 2.3. Combining this with the $L^0$-estimate yields

$$\begin{aligned} \frac{1}{R^d} \sum _{X\in B_R \;\text{ or }\; T\left( X \right) \in B_R}|T \left( X \right) - X| \le o ( \ln ^{\frac{1}{2}} R), \end{aligned}$$

see Lemma 2.4.

It remains to establish the lower bound (1.5), which is essentially known. However, for our purpose we need the local version (1.5). Our proof is very similar to the proof of the lower bound in the seminal paper [1]. Both approaches construct candidates for the dual problem based on dyadic partitions of the cube. However, instead of using a quantitative embedding result into a Gaussian process as in [1] we use a natural martingale structure together with a concentration argument. More precisely, we show that there exists $\zeta$ with $\textrm{supp} \zeta \in \left( 0,R \right) ^2$ and $\left| \nabla \zeta \right| \le 1$ such that

$$\begin{aligned} \frac{1}{R^d} \sum _{X \in (0,R)^2\;\text{ or }\;T(X) \in (0,R)^2} \zeta \left( T \left( X \right) \right) - \zeta \left( X \right) \ge \Omega (\ln ^\frac{1}{2} R), \end{aligned}$$

see Lemma 2.5. Note that this is sufficient for the contradiction stated at the beginning of the subsection, indeed

$$\begin{aligned} \begin{aligned} O(\ln ^\frac{1}{2} R)&\le \frac{1}{R^d} \sum _{X \in (0,R)^2\;\text{ or }\;T(X) \in (0,R)^2} \zeta \left( T \left( X \right) \right) - \zeta \left( X \right) \\&\le \frac{1}{R^d}\sum _{X \in (0,R)^2\;\text{ or }\;T(X) \in (0,R)^2} \left| T \left( X \right) - X\right| \\&\le \frac{1}{R^d}\sum _{X \in B_{\sqrt{2}R}\;\text{ or }\;T(X) \in B_{\sqrt{2}R}} \left| T \left( X \right) - X\right| \\&\le o(\ln ^\frac{1}{2} R). \end{aligned} \end{aligned}$$

2 Proofs

For the rest of the paper we let $\{X\}$ and $\{Y\}$ be two Poisson point processes and we let T be their matching, i. e. a bijection from $\{X\}$ to $\{Y\}$.

2.1 The ergodic estimate

Lemma 1.5

For any $\varepsilon >0$ there exist a deterministic L and a random radius $r_* < \infty$ a. s. such that for all $R\ge r_*$

$$\begin{aligned} \# \left\{ X \in (-R,R)^d \,|\,\left| T \left( X \right) - X\right| > L \right\} \le \left( \varepsilon R \right) ^d. \end{aligned}$$

(2.1)

Proof

Let $Q_R = (-R,R)^d$ and consider the number of points in $Q_R$ which are transported by a distance greater than L, namely

$$\begin{aligned} N_{Q_R}^{>L}:= \# \left\{ X \in Q_R \,|\,\left| T \left( X \right) - X\right| > L \right\} . \end{aligned}$$

We show that stationarity together with the ergodic theorem implies as $R \rightarrow \infty$ that

$$\begin{aligned} \frac{1}{R^d} N_{Q_R}^{>L}\rightarrow \mathbb {E} N_{Q_1}^{>L} \quad \text{ a. } \text{ s. }. \end{aligned}$$

(2.2)

Then, taking $L \rightarrow \infty$ we have

$$\begin{aligned} \mathbb {E} N_{Q_1}^{>L} \rightarrow 0. \end{aligned}$$

(2.3)

Note that (2.2) together with (2.3) imply the existence of a random radius $r_*$ and a deterministic L as in the Lemma. Indeed, for any fixed $\varepsilon >0$ we can choose L large enough so that $\mathbb {E} N_{Q_1}^{>L} \le \frac{\varepsilon ^d}{2}$, and then choose $r_*$ large enough so that for $R \ge r_*$

$$\begin{aligned} \left| \frac{1}{R^d} N_{Q_R}^{>L} - \mathbb {E} N_{Q_1}^{>L}\right| \le \frac{\varepsilon ^d}{2}, \end{aligned}$$

which turns into the equivalent assertion $\frac{1}{R^d} N_{Q_R}^{>L} \le \varepsilon ^d$.

We now turn to (2.2). For $i \in \mathbb {Z}^d$ note that

$$\begin{aligned}{ \begin{aligned} N_{Q_R}^{>L}&= \sum _{\left| i\right|< R} N_{Q_1+i}^{>L} \\&= \sum _{\left| i\right| <R} \# \left\{ X \in { \left( i_1 -1,i_1+1 \right) \times \dots \times \left( i_d -1, i_d+1 \right) } \,|\,\left| T \left( X \right) - X\right| > L \right\} . \end{aligned}} \end{aligned}$$

Since $\mu$ is stationary and ergodic, by the Birkhoff-von Neumann ergodic theorem [18, Theorem 9.6] for any divergent sequence of integer radii

$$\begin{aligned} { \frac{1}{R^d} \sum _{\left| i\right| < R} N_{Q_1+i}^{>L} \rightarrow \mathbb {E} N_{Q_1}^{>L}.} \end{aligned}$$

(2.4)

Note that for integer R the term on the left hand side amounts to $\frac{1}{R^d} N_{Q_R}^{>L}$. Since for every real R there exists an integer $\bar{R}$ such that $\bar{R} \le R \le \bar{R}+1$ and the ratio between $\bar{R}$ and $\bar{R}+1$ goes to 1 as $R \rightarrow \infty$, (2.4) holds also for any divergent sequences of real radii.

Finally we turn to (2.3). By dominated convergence it suffices to show that

$$\begin{aligned} N_{Q_1}^{>L} \rightarrow 0 \ \ a.~s.. \end{aligned}$$

(2.5)

Indeed, since $N_{Q_1}^{>L} \le \# \{X \in Q_1 \}$ by dominated convergence (2.3) holds. Note that $N_{Q_1}^{>L}$ is finite for every realization of $\left\{ X \right\}$ and there exists L large enough such that $N_{Q_1}^{>L} =0$, which implies the almost sure convergence (2.5) since $\mathbb {E}N_{Q_1}^{>L}$ is finite by the properties of the Poisson process. $\square$

2.2 The $L^\infty$-estimate

The proof is very similar to the $L^\infty$ estimate in [10, Lemma 2.9]. However, note that in [10, Theorem 1.4] a local $L^2$ estimate was turned into a $L^\infty$ estimate whereas in the current setup we want to turn a $L^0$ estimate into a $L^\infty$ estimate. The key property that allows us to do this is the monotonicity of the support of T. This translates the partial control given by (2.1) into the claimed $L^\infty$ estimate.

Lemma 1.6

For every $\varepsilon >0$ there exists a random radius $r_*<\infty$ a. s. such that for every $R \ge r_*$

$$\begin{aligned} \left| T \left( X \right) - X\right| \le \varepsilon R \quad \text{ provided } \text{ that } \; X \in (-R,R)^d. \end{aligned}$$

(2.6)

Proof

Step 1. Definition of $r_*=r_*(\varepsilon )$ as the maximum of three random scales. Fix $0< \varepsilon \ll 1$. First, by Lemma 2.1, there exists a (deterministic) length $L<\infty$ and a (random) length $r_*<\infty$ such that for $4R\ge r_*$, the number of the Poisson points in $(-2R,2R)^d$ transported further than the “moderate distance” L is small in the sense of

$$\begin{aligned} \#\{\,X\in (-2R,2R)^d\,|\,|T(X)-X|>L\,\}\le (\varepsilon 4R)^d. \end{aligned}$$

(2.7)

Second, by Lemma 2.6 we may also assume that $r_*$ is so large that for $R\ge r_*$, the non-dimensionalized transportation distance of $\mu$ to its number density

$$\begin{aligned} n_{Q_{2R}}:= \frac{\mu ((-2R,2R)^d)}{(4R)^d} \end{aligned}$$

is small, and that $n_{Q_{2R}}\approx 1$, in the sense of

$$\begin{aligned} W^2_{(-2R,2R)^d}(\mu ,n_{Q_{2R}})+\frac{(4R)^{d+2}}{n_{Q_{2R}}}(n_{Q_{2R}}-1)^2\le (\varepsilon 4 R)^{d+2}. \end{aligned}$$

(2.8)

Third, w. l. o. g. we may assume that $r_*$ is so large that

$$\begin{aligned} L\le \varepsilon r_*. \end{aligned}$$

(2.9)

We now fix a realization and $R\ge r_*$.

Step 2. There are enough Poisson points on mesoscopic scales. We claim that for any cube $Q\subset (-2R,2R)^d$ of “mesoscopic” side length

$$\begin{aligned} r\gg \varepsilon R \end{aligned}$$

(2.10)

we have¹⁰

$$\begin{aligned} \#\{\,X\in Q\,\}\gtrsim r^d. \end{aligned}$$

(2.11)

Indeed, it follows from the definition of $W_{(-2R,2R)}(\mu ,n_{Q_{2R}})$ that for any Lipschitz function $\eta$ with support in Q we have

$$\begin{aligned} \left| \int \eta d\mu -\int \eta n_{Q_{2R}} dy\right| \le (\textrm{Lip}\eta )\left( \int _Qd\mu +n_{Q_{2R}}|Q|\right) ^\frac{1}{2} W_{(-2R,2R)^d}\left( \mu ,n_{Q_{2R}}\right) . \end{aligned}$$

We now specify to an $\eta \le 1$ supported in Q, to the effect of $\int \eta d\mu$ $\le \int d\mu$ $=\#\{\,X\in Q\,\}$, so that by Young’s inequality

$$\begin{aligned} \int \eta n_{Q_{2R}} dy&\lesssim \#\{\,X\in Q\,\}+(\textrm{Lip}\eta )^2W_{(-2R,2R)^d}^2(\mu ,n_{Q_{2R}})\nonumber \\&+(\textrm{Lip}\eta )\big (n_{Q_{2R}} |Q|\big )^\frac{1}{2} W_{(-2R,2R)^d}(\mu ,n_{Q_{2R}}). \end{aligned}$$

(2.12)

At the same time, we may ensure $\int _{(-2R,2R)^d}\eta \gtrsim r^d$ and $\textrm{Lip}\eta \lesssim r^{-1}$, so that by (2.8), which in particular ensures $n_{Q_{2R}} \approx 1$, (2.12) turns into

$$\begin{aligned} r^d\lesssim \#\{\,X\in Q\,\}+r^{-2}(\varepsilon R)^{d+2}+r^{\frac{d}{2}-1}(\varepsilon R)^{\frac{d}{2}+1}. \end{aligned}$$

Thanks to assumption (2.10) we obtain (2.11).

Step 3. Iteration. There are enough Poisson points of moderate transport distance on mesoscopic scales. We claim that for any cube $Q\subset (-2R,2R)^d$ of side-length satisfying (2.10) we have

$$\begin{aligned} \text{ there } \text{ exists }\;X\in Q\;\text{ with }\;|T(X)-X|\le L. \end{aligned}$$

(2.13)

We suppose that (2.13) were violated for some cube Q. By (2.11), there are $\gtrsim r^d$ of such points. By assumption (2.10), there are thus $\gg (\varepsilon R)^d$ Poisson points in $(-2R,2R)^d$ that get transported by a distance $>L$, which contradicts (2.7).

Step 4. At mesoscopic distance around a given point $X\in (-R,R)^d$, there are sufficiently many Poisson points that are transported only over a moderate distance. More precisely, we claim that provided (2.10) holds, there exist $d+1$ Poisson points $\{X_n\}_{n=1}^{d+1}$ that are transported over a moderate distance, i. e.

$$\begin{aligned} |T(X_n)-X_n|\le L, \end{aligned}$$

(2.14)

but on the other hand lie in “sufficiently general” directions around X, meaning that

$$\begin{aligned} \begin{array}{l} \text{ the } \text{ convex } \text{ hull } \text{ of }\;\left\{ \frac{X_n-X}{|X_n-X|}\right\} _{n=1}^{d+1}\;\text{ contains }\;B_\rho \end{array} \end{aligned}$$

(2.15)

for $\rho \ll 1$, while the distances to X are of order r

$$\begin{aligned} |X_n-X|\sim r. \end{aligned}$$

(2.16)

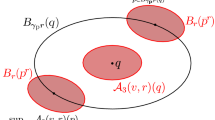
Indeed, this can be seen as follows: Consider the symmetric tetrahedron¹¹ with barycenter at X. For each of its $d+1$ vertices, consider a rotationally symmetric cone with apex at X and with axis passing through the vertex. Provided the opening angles $\alpha$ are $\ll 1$, by continuity, any selection $e_n$ of unit vectors in this cones still has the property that their convex hull contains $B_\rho$ for $\rho \ll 1$. Consider the intersection of these cones with the (dyadic) annulus centered at X of radii r and 2r. These $d+1$ intersections are contained in $(-2R,2R)^d$, and each contains a cube of side-length $\sim r$. Hence (2.13) applies and we may pick a Poisson point $X_n$ with (2.14) in each of these intersections, see Fig. 1. Condition (2.16) is satisfied because the points $X_n$ lie within the chosen annulus, and condition (2.15) is satisfied because the points $X_n$ lie within the chosen cones.

Fig. 1

Construction of good points in moderate distance in $d=2$

Step 5. All Poisson points are transported over distances $\ll R$. We claim that for all Poisson points X

$$\begin{aligned} |T(X)-X|\lesssim \varepsilon R\quad \text{ provided }\;X\in (-R,R)^d. \end{aligned}$$

(2.17)

Given the Poisson point $X\in (-R,R)^d$, let $\{X_n\}_{n=1}^{d+1}$ be as in Step 4. By cyclical monotonicity (1.1), which implies monotonicity of the map T, we have $(T(X_n)-T(X))\cdot (X_n-X)\ge 0$, which we use in form of

$$\begin{aligned} (T(X)-X)\cdot (X_n-X)&\le (T(X_n)-X_n)\cdot (X_n-X)+|X_n-X|^2\nonumber \\&\lesssim |T(X_n)-X_n|^2+|X_n-X|^2. \end{aligned}$$

(2.18)

We now appeal to (2.14), which by (2.9) and and (2.10) implies

$$\begin{aligned} |T(X_n)-X_n|\le r. \end{aligned}$$

Inserting this and (2.16) into (2.18), we obtain

$$\begin{aligned} (T(X)-X)\cdot \frac{X_n-X}{|X_n-X|}\lesssim r \end{aligned}$$

for all $n=1,\ldots ,d+1$. Since by (2.15), any unit vector e can be written as a linear combination of $\left\{ \frac{X_n-X}{|X_n-X|}\right\} _{n=1}^{d+1}$ with non-negative weights $\le \frac{1}{\rho }\sim 1$, this implies $|T(X)-X|\lesssim r$. Since (2.10) was the only constraint on r, we obtain (2.17). $\square$

2.3 Key step: Harmonic approximation

Lemma 1.7

There exist a constant C¹² and a random radius $r_* < \infty$ a. s. such that for every $R\ge r_*$ we have

$$\begin{aligned} \frac{1}{R^d}\sum _{X \in B_R \; \text{ or } \; T \left( X \right) \in B_R} |T\left( X \right) - X|^2 \le C \ln R. \end{aligned}$$

(2.19)

Proof of Lemma 2.3

The proof relies on the harmonic approximation result from [10, Theorem 1.4]. This result establishes that for any $0<\tau \ll 1$, there exists an $\varepsilon >0$ and a $C_\tau <\infty$ such that provided for some R

$$\begin{aligned} \frac{1}{R^2} E(6R) + \frac{1}{R^2} D(6R)\le \varepsilon \end{aligned}$$

(2.20)

(recall (1.9) and (1.10) for the definition) there exists a harmonic gradient field $\Phi$ such that

$$\begin{aligned} \begin{aligned}&\frac{1}{R^d} \sum _{X\in B_R\;\text{ or }\;T(X)\in B_R} \left| T \left( X \right) - X -\nabla \Phi (X)\right| ^2 \le \tau E(6R) + C_\tau D(6R),\\&\sup _{B_{2R}} |\nabla \Phi |^2 \le C_\tau \left( E(6R) + D(6R) \right) . \end{aligned} \end{aligned}$$

(2.21)

The fraction $\tau$ will be chosen at the end of the proof. Note that in (1.10) $D \left( R \right)$ is defined on boxes $(-R,R)^d$ while [10, Theorem 1.4] (2.20) requires balls. Since $B_{6R} \subseteq (-6R, 6R)^d$ we may assume that (2.20) holds also for $B_{6R'}$ for $R'$ close to R, see [10, Lemma 2.10] for this type of restriction property.

Step 1. Definition of $r_*$ depending on $\tau$. For $0< \tau \ll 1$ let $\varepsilon = \varepsilon \left( \tau \right)$ be as above. By Lemma 2.6 we may assume that $r_*$ is large enough so for any dyadic $R\ge r_*$

$$\begin{aligned} D(R) \le C \ln R \end{aligned}$$

(2.22)

and

$$\begin{aligned} \frac{D(6R)}{R^2} \le \frac{\varepsilon }{2}. \end{aligned}$$

(2.23)

Note that the estimate (2.23) is not sharp, but it is enough for our purpose. Moreover, only the bound (2.22) is specific to $d=2$. From now on, we restrict ourselves to dyadic R, which we may do w. l. o. g.  for (2.19). Note that by the bound on $D\left( 6R \right)$ in (2.23) and the second and fourth term in the definition of $D\left( R \right)$ in (1.10)

$$\begin{aligned} \# \left( \left\{ X \in B_R \right\} \cup \left\{ T(X) \in B_R \right\} \right) \le C R^d. \end{aligned}$$

(2.24)

Moreover, we may assume that $r_*$ is large enough so that (2.6) holds. Since $B_{6R}\subset (-6R,6R)^d$ we may sum (2.6) over $B_R$ to obtain for $R\ge r_*$

$$\begin{aligned} \frac{1}{R^d}\sum _{X\in B_{6R}} |T \left( X \right) - X|^2 \le \frac{\varepsilon }{4} R^2. \end{aligned}$$

By symmetry, potentially enlarging $r_*$, we may also assume that (2.6) holds with X replaced by $T \left( X \right)$ so that both

$$\begin{aligned} T \left( X \right) \in B_R \Rightarrow X \in B_{2R} \end{aligned}$$

(2.25)

and

$$\begin{aligned} \frac{1}{R^d}\sum _{T\left( X \right) \in B_{6R}} |T \left( X \right) - X|^2 \le \frac{\varepsilon }{4} R^2, \end{aligned}$$

thus

$$\begin{aligned} E \left( 6R \right) = \frac{1}{R^d}\sum _{X\in B_{6R}\;\text{ or }\;T(X)\in B_{6R}} |T \left( X \right) - X|^2 \le \frac{\varepsilon }{2} R^2, \end{aligned}$$

and in particular (2.20) holds. Finally by Lemma 2.1 we may assume, possibly enlarging $r_*$, that there exists a deterministic constant $L_\tau$ and for $R\ge r_*$ we both have

$$\begin{aligned} \# \left( \left\{ X \in Q_R \ | \ \left| T \left( X \right) - X\right|> L_\tau \right\} \cup \left\{ T(X) \in Q_R \ | \ \left| T \left( X \right) - X\right| > L_\tau \right\} \right) \le \tau R^d. \end{aligned}$$

(2.26)

and

$$\begin{aligned} L_\tau ^2 \le \ln R. \end{aligned}$$

(2.27)

Step 2. Application of harmonic approximation. For all $R \ge r_*$

$$\begin{aligned} E \left( R \right) \le {\tau } E \left( 6 R \right) + C_\tau \ln R. \end{aligned}$$

(2.28)

We split the sum according to whether the transportation distance is moderate or large. On the latter we use the harmonic approximation:

$$\begin{aligned}&{\frac{1}{R^{d}} \sum _{\left( X\in B_R\;\text{ or }\;T(X)\in B_R \right) \,\text{ and }\; \left| T\left( X \right) -X\right|>L_\tau } |T\left( X \right) - X|^2}\\&\quad \le \frac{2}{R^{d}} \sum _{{X\in B_R\;\text{ or }\;T(X)\in B_R}} |T \left( X \right) -X -\nabla \Phi \left( X \right) |^2 \\&\quad \quad + \frac{2}{R^{d}} \sum _{\left( X\in B_R\;\text{ or }\;T(X)\in B_R \right) \,\text{ and }\; \left| T\left( X \right) -X\right| >L_\tau } |\nabla \Phi (X)|^2 \\&\quad \quad {\mathop {\le }\limits ^{(2.21), (2.25), (2.26)}} 2 \tau E(6R) + 2 C_\tau D(6R) + 2\tau C_\tau (E(6R)+D(6R))\\&\quad = 2 \tau \left( 1 + C_\tau \right) E(6R) + 2 C_\tau \left( 1+\tau \right) D(6R). \end{aligned}$$

The last estimate combines to

$$\begin{aligned}&{\frac{1}{R^d}\sum _{X\in B_R\;\text{ or }\;T(X)\in B_R}|T \left( X \right) - X|^2}\\&= \frac{1}{R^d} \sum _{\left( X\in B_R\;\text{ or }\;T(X)\in B_R \right) \,\text{ and }\; \left| T\left( X \right) -X\right| \le L_\tau } |T \left( X \right) - X|^2 \\&\quad \quad + \frac{1}{R^d}\sum _{\left( X\in B_R\;\text{ or }\;T(X)\in B_R \right) \,\text{ and }\; \left| T\left( X \right) -X\right| >L_\tau } |T \left( X \right) -X|^2\\&\quad \quad {\mathop {\le }\limits ^{(2.24)}} C L_\tau ^2 +2 \tau \left( 1 + C_\tau \right) E(6R) + 2 C_\tau \left( 1+\tau \right) D(6R) \\&\quad \quad {\mathop {\le }\limits ^{(2.22),(2.27)}} 2 \tau \left( 1 + C_\tau \right) E \left( 6R \right) + \left( 2 C_\tau \left( 1 + \tau \right) +C \right) \ln R. \end{aligned}$$

Relabeling $\tau$ and $C_\tau$, this implies (2.28).

Step 3. Iteration. Iterating (2.28), we obtain for any $k\ge 1$

$$\begin{aligned} E(R)&\le \tau E(6R) + C_\tau \ln R \\&\le \tau ^2 E(6^2R) + \tau C_\tau \ln R + C_\tau \ln R\\&\le \tau ^k E(6^k R) + C_\tau \sum _{l=0}^{k-1} \tau ^l \ln R \\&{\mathop {\le }\limits ^{(2.20)}} \varepsilon \left( 36 \tau \right) ^k R^2 + C_\tau \sum _{l=0}^{k-1} \tau ^l \ln R. \end{aligned}$$

We now fix $\tau$ such that $36\tau < 1$ to the effect of

$$\begin{aligned} E \left( R \right) \le C \sum _{l=0}^{\infty } \tau ^l \ln R \le C \ln R. \end{aligned}$$

$\square$

2.4 Trading integrability against asymptotics

Lemma 1.8

For every $\varepsilon >0$ there exists a random radius $r_* < \infty$ a. s. such that for every $R \ge r_*$ we have

$$\begin{aligned} \frac{1}{R^d} \sum _{X\in B_R \;\text{ or }\;T\left( X \right) \in B_R}|T \left( X \right) - X| \le \varepsilon \ln ^{\frac{1}{2}} R. \end{aligned}$$

Proof

By Lemma 2.3, we know that there exists a random radius $r_*$ such that for $R\ge r_*$ we have

$$\begin{aligned} E \left( R \right) = \frac{1}{R^d}\sum _{X\in B_R \;\text{ or }\; T\left( X \right) \in B_R}|T\left( X \right) - X|^2 \le C\ln R. \end{aligned}$$

(2.29)

Let $0 < \varepsilon \ll 1$. Possibly enlarging $r_*$, we may also assume by Lemma 2.1 that there exists a deterministic constant L such that for $R \ge r_*$

$$\begin{aligned} \# \left( \left\{ X \in B_R \ | \ \left| T \left( X \right) - X\right|> L \right\} \cup \left\{ T(X) \in B_R \ | \ \left| T \left( X \right) - X\right| > L \right\} \right) \le \varepsilon R^d. \end{aligned}$$

(2.30)

Furthermore, note that by Lemma 2.6 and the second and fourth term in the definition of $D \left( R \right)$ in (1.10) we may also assume possibly enlarging $r_*$ again that for $R \ge r_*$ (2.24) holds. Finally, we may also assume possibly enlarging $r_*$ that for $R \ge r_*$

$$\begin{aligned} L \le \varepsilon ^\frac{1}{2} \ln ^\frac{1}{2} R. \end{aligned}$$

(2.31)

We split again the sum into moderate and large transportation distance and apply Cauchy-Schwarz:

$$\begin{aligned} \frac{1}{R^d}\sum _{X\in B_R \;\text{ or } \; T\left( X \right) \in B_R} |T\left( X \right) -X|&\le \frac{1}{R^d}\sum _{\left( X\in B_R\;\text{ or }\;T(X)\in B_R \right) \,\text{ and }\; \left| T\left( X \right) -X\right| \le L} |T\left( X \right) - X| \\&+\frac{1}{R^d}\sum _{\left( X\in B_R\;\text{ or }\;T(X)\in B_R \right) \,\text{ and }\; \left| T\left( X \right) -X\right| >L} |T\left( X \right) - X|\\&{\mathop {\le }\limits ^{(2.24), (2.29), (2.30)}} C L + \varepsilon ^\frac{1}{2} E(R)^\frac{1}{2}\\&{\mathop {\le }\limits ^{(2.31)}} C \varepsilon ^\frac{1}{2} \ln ^\frac{1}{2} R. \end{aligned}$$

Relabeling $\varepsilon$ proves the claim. $\square$

2.5 Asymptotics for the bipartite matching problem in dimension $d=2$

In this section we give a self-contained proof of the upper and lower bounds on the asymptotics in the matching problem in the critical dimension $d=2$.

The intuition why $d=2$ is critical for optimal transportation is clear: the fluctuations of the number density of the Poisson point process of unit intensity, i. e. its deviation from 1 on some mesoscopic scale $r\gg 1$ are of size $O(\frac{1}{\sqrt{r^d}})$. To compensate these fluctuations, one has to displace particles by a distance $O(r\times \frac{1}{\sqrt{r^d}})$, which is O(1) iff $d=2$. Hence taking care of the fluctuations on every dyadic scale r requires a displacement of O(1). Naively, this suggests a transportation cost per particle that is logarithmic in the ratio between the macroscopic scale R and the microscopic scale 1. However, by the independence properties of the Poisson point process, the displacements on every dyadic scale are essentially independent, so that there are the usual cancellations when adding up the dyadic scales. Hence the displacement behaves like the square root of the logarithm.

The proof of the lower bound is similar to the original proof in [1]. However, in the final step we use martingale arguments instead of Gaussian embeddings. The proof of the upper bound has some similarities to the proof in [3]. Again we use martingale arguments and crucially the Burkholder-Davis-Gundy inequality. It would be interesting to see whether our technique for the upper bound allows to get the precise constant as in [3].

Lemma 1.9

Let $\mu , \nu$ denote two independent Poisson point processes in $\mathbb {R}^2$ of unit intensity. There exists a constant C, and a random radius $r_* < \infty$ a. s. such that for any dyadic radii $R \ge r_*$

$$\begin{aligned} \sup \left\{ \int \zeta \left( d\mu -d\nu \right) \quad \big |\;\textrm{supp}\zeta \subset (0,R)^2,\;|\nabla \zeta |\le 1,\; \int \zeta dx=0 \right\} \ge C R^2 \ln ^\frac{1}{2} R. \end{aligned}$$

Lemma 1.10

Let $\mu , \nu$ be as in Lemma 2.5. Then there exists a constant C, and there exists a random radius $r_*<\infty$ a. s. such that for any dyadic radii $R \ge r_*$

$$\begin{aligned} D(R) \le C \ln ^\frac{1}{2} R. \end{aligned}$$

For the lower as well as the upper bound, our proof proceeds in two stages. First we show the desired estimate in expectation. Then we use concentration arguments to lift it to a pathwise estimate.

2.5.1 Lower bound on $W_1$

Lemma 1.11

Let $\mu$ denote the Poisson point process in $\mathbb {R}^2$ of unit intensity. Then it holds for $R\gg 1$

$$\begin{aligned} \mathbb {E}{\sup \left\{ \int \zeta d\mu \quad \big |\;\textrm{supp}\zeta \subset (0,R)^2,\;|\nabla \zeta |\le 1,\; \int \zeta dx=0 \right\} }\gtrsim R^2\ln ^\frac{1}{2}R. \end{aligned}$$

(2.32)

Proof

W. l. o. g. we may assume that $R\in 2^\mathbb {N}$, and will consider the (finite) family of all dyadic cubes $Q\subset (0,R)^2$ of side-length $\ge 1$. For such Q, we call $Q_r$ and $Q_l$ the right and left half of Q and consider the integer-valued random variable

$$\begin{aligned} N_Q=\mu (Q_r)-\mu (Q_l). \end{aligned}$$

(2.33)

Fixing a smooth mask (or reference function) ${\hat{\zeta }}$ with

$$\begin{aligned} \textrm{supp}{\hat{\zeta \in }}(0,1)^2,\quad \int {\hat{\zeta }},d{\hat{x}}=0,\quad \int _{{\hat{x}}_1>\frac{1}{2}}{\hat{\zeta }} d{\hat{x}} -\int _{{\hat{x}}_1<\frac{1}{2}}{\hat{\zeta }} d{\hat{x}}=1, \end{aligned}$$

(2.34)

for every Q we define $\zeta _Q$ via the simple transformation

$$\begin{aligned} \zeta _Q(A_Q{\hat{x}})={\hat{\zeta }}({\hat{x}})\;\text{ where }\;A_Q\;\text{ is } \text{ the } \text{ affine } \text{ map } \text{ with }\;Q=A_Q(0,1)^2. \end{aligned}$$

(2.35)

For later purpose we note that by standard properties of the Poisson process (see [20, equation (4.23)]) we have (recall that we consider dyadic cubes only)

$$\begin{aligned} \mathbb {E}N_Q^2=|Q|,\quad \mathbb {E}N_QN_{Q'}=0\;\text{ for }\;Q\not =Q',\quad \mathbb {E}N_Q\int \zeta _Qd\mu =|Q|. \end{aligned}$$

(2.36)

For every dyadic $r=R,\frac{R}{2},\frac{R}{4},\ldots ,1$ we consider the function

$$\begin{aligned} \zeta _r:=\sum _{Q\;\text{ of } \text{ level }\;\ge r}N_Q\zeta _Q \end{aligned}$$

(2.37)

and note that for a fixed point $x\in (0,R)^d$, we have

$$\begin{aligned} \nabla \zeta _r(x)=\sum _{R\ge \rho \ge r}\sum _{Q\;\text{ of } \text{ level }\;\rho }N_Q\nabla \zeta _Q(x), \end{aligned}$$

(2.38)

observing that the sum over Q restricts to the one cube of dyadic level/side-length $\rho$ that contains x. We now argue that (2.38) is a martingale, where $r=R,\frac{R}{2},\frac{R}{4},\ldots$, plays the role of a discrete time. More precisely, it is a martingale with respect to the filtration generated by $\{\{N_Q\}_{Q\;\text{ of } \text{ level }\;r}\}_r$. It suffices to show that when conditioned on $\{N_{{\bar{Q}}}\}_{{\bar{Q}}\;\text{ of } \text{ level }\;\rho }$ for $\rho \ge 2r$, the expectation of $N_Q$ for every Q of level r vanishes. To this end, apply a Lebesgue-measure preserving transformation of $\mathbb {R}^2$ that swaps the left and right half of Q; when applied to point configurations, it preserves the law of the Poisson point process, it leaves $N_{{\bar{Q}}}$ for ${\bar{Q}}$ of level $\rho \ge 2r$ invariant, in particular also the $\sigma -$algebra generated by these random variables, and it converts $N_Q$ into $-N_Q$. Hence, $\mathbb {E}[N_Q|\{N_{{\bar{Q}}}\}_{{\bar{Q}}\;\text{ of } \text{ level }\;\rho }, \rho \ge 2r]=0.$

As the sum over Q in (2.38) reduces to a single summand, this martingale has (total) quadratic variation¹³

$$\begin{aligned} \sum _{R\ge r\ge 1} \sum _{Q\;\text{ of } \text{ level }\;r} N_Q^2|\nabla \zeta _Q(x)|^2, \end{aligned}$$

and we claim that it satisfies

$$\begin{aligned} \mathbb {E}\int \sum _{R\ge r\ge 1}\sum _{Q\;\text{ of } \text{ level }\;r}N_Q^2|\nabla \zeta _Q(x)|^2dx \lesssim R^2\ln R. \end{aligned}$$

(2.39)

Indeed, by (2.36) we obtain that the l. h. s. of (2.39) is given by $\sum _{Q}$ $|Q| \int |\nabla \zeta _Q(x)|^2dx$. By (2.35), this in turn is estimated by $\sum _{Q}$ |Q| $=\sum _{R\ge r\ge 1}R^2$ $=R^2\log _2R$. We also claim that the last item in (2.36) implies

$$\begin{aligned} \mathbb {E}\int \zeta _1d\mu \gtrsim R^2\ln R. \end{aligned}$$

(2.40)

Indeed, the l. h. s. of (2.40) is again given by $\sum _{Q}$ |Q|. We now appeal to the (quadratic) Burkholder inequality [23, Theorem 6.3.6] (exchanging $\mathbb {E}$ and $\int dx$) to obtain from (2.39)

$$\begin{aligned} \mathbb {E}\int \sup _{R\ge r\ge 1}|\nabla \zeta _r(x)|^2dx\lesssim R^2\ln R. \end{aligned}$$

(2.41)

We now are in the position to define $\zeta$ via a stopping “time”. Given an $M<\infty$, which we think of as being large and that will be chosen later, we keep subdividing the dyadic cubes (recall that we restrict to those of side length $\ge 1$) as long as

$$\begin{aligned} { \int _Q|\nabla \sum _{{{\bar{Q}}\subset Q}}N_{{\bar{Q}}}\zeta _{{\bar{Q}}}(x)|^2dx\le M |Q|\ln R\quad \text{ and }\quad |N_Q|^2\le M |Q| \ln R . } \end{aligned}$$

(2.42)

This defines a nested sub-family of dyadic cubes, and thereby a random (spatially piecewise constant) stopping scale $r_*=r_*(x)$ (note that $\frac{r_*}{2}$ is a stopping time but we will not need that in this proof). We then set

$$\begin{aligned} \zeta (x):=\zeta _{r_*(x)}(x). \end{aligned}$$

(2.43)

We first argue that we have the Lipschitz condition

$$\begin{aligned} |\nabla \zeta |^2\lesssim M\ln R. \end{aligned}$$

(2.44)

Indeed, consider one of the finest cubes Q in the family constructed in (2.42); by definition (2.43), the first item in (2.42) amounts to

$$\begin{aligned}{ \int _Q|\nabla \zeta (x)|^2dx\le M|Q|\ln R,} \end{aligned}$$

so that (2.44) follows once we show for arbitrary point x

$$\begin{aligned} r_*(x)|\nabla ^2\zeta (x)|\lesssim \sqrt{M \ln R}. \end{aligned}$$

(2.45)

Indeed, by definitions (2.35), (2.37) and (2.43), the l. h. s. is estimated by

$$\begin{aligned} |\nabla ^2\zeta (x)| \le \sum _{r_*(x)\le r\le R} \sum _{Q\ni x\;\text{ level }\;r} |N_Q| | \nabla ^2 \zeta _Q(x)| {\mathop {\lesssim }\limits ^{(2.35)}} \sum _{r_*(x)\le r\le R}r^{-2}\sum _{Q\ni x\;\text{ level }\;r} \left| N_Q\right| . \end{aligned}$$

By construction of $r_*(x)$ in form of the second item in (2.42) the latter is estimated by

$$\begin{aligned} \sum _{r_*(x)\le r\le R}r^{-2}\sum _{Q\ni x\;\text{ level }\;r} \left| N_Q\right| {\mathop {\lesssim }\limits ^{(2.42)}} \sum _{r_*(x)\le r\le R} r^{-1} \sqrt{M \ln R}. \end{aligned}$$

This is a geometric series that is estimated by $\lesssim r_*^{-1}(x) \sqrt{M \ln R}$, as desired.

We now argue that the “exceptional” set

$$\begin{aligned} E:=\{\,x\in (0,R)^2\,|\,r_*(x)>1\,\}, \end{aligned}$$

where the dyadic decomposition stops before reaching the minimal scale $r=1$, has small volume fraction in expectation:

$$\begin{aligned} M\mathbb {E}|E|\lesssim R^2. \end{aligned}$$

(2.46)

Indeed, by definitions (2.37) and (2.42), E is the disjoint union of dyadic cubes Q that have at least one (out of four) children $Q'$ of level $r=\frac{r_*(x)}{2}$ with

$$\begin{aligned}{ \int _{Q'}|\nabla \zeta _r(x)|^2dx>M|Q'|\ln R\quad \text{ or }\quad |N_{Q'}|^2>M|Q'| \ln R,} \end{aligned}$$

which combines to

$$\begin{aligned}{ |N_{Q'}|^2+\int _{Q'}\sup _{1\le r\le R}|\nabla \zeta _r(x)|^2dx>M\frac{|Q|}{4}\ln R.} \end{aligned}$$

Summing over all Q covering E, this yields

$$\begin{aligned}{ \sum _{\text{ all }\;Q}|N_{Q}|^2+\int \sup _{1\le r\le R}|\nabla \zeta _r(x)|^2dx>M\frac{|E|}{4}\ln R.} \end{aligned}$$

Taking the expectation we obtain from (2.36) and (2.41)

$$\begin{aligned} R^2\ln R\gtrsim M\mathbb {E}|E|\ln R, \end{aligned}$$

which yields (2.46).

We finally argue that

$$\begin{aligned} M^\frac{1}{4}\mathbb {E}|\int (\zeta _1-\zeta )d\mu |\lesssim R^2\ln R. \end{aligned}$$

(2.47)

Together with (2.40) this implies $\mathbb {E}\int \zeta d\mu \gtrsim R^2\ln R$ for $M\gg 1$, which we fix now. In combination with (2.44) this implies the claim of the lemma. Indeed, $\frac{\zeta }{\nabla \zeta }$ is an admissible candidate for (2.32) and the statement follows once M in (2.47) is chosen to be large enough. The dyadic decomposition defines a family of exceptional cubes Q (a cube Q is exceptional if and only if for any $x\in Q$ we have that its level r satisfies $r<r_*(x)$). In view of (2.37) and (2.43), we thus have to estimate $\sum _{Q} I(Q\;\text{ exceptional}) N_Q\int \zeta _Q d\mu$. Applying $\mathbb {E}|\cdot |$ and using Hölder’s inequality in probability we obtain

$$\begin{aligned} \mathbb {E}|\int (\zeta _1-\zeta )d\mu |\le \sum _Q (\mathbb {P}Q\;\text{ exceptional})^\frac{1}{4} (\mathbb {E}N_Q^4)^\frac{1}{4} (\mathbb {E}(\int \zeta _Q d\mu )^2)^\frac{1}{2}. \end{aligned}$$

As for (2.36), we have for the last factor $\mathbb {E}(\int \zeta _Q d\mu )^2$ $=\int \zeta _Q^2$ $\lesssim |Q|$. For the middle factor, we recall that the two numbers in (2.33) are Poisson distributed with mean $\frac{1}{2}|Q|$, so that $\mathbb {E}N_Q^4$ $\lesssim |Q|^2$ by elementary properties of the Poisson distribution. Hence we gather

$$\begin{aligned} \mathbb {E}|\int (\zeta _1-\zeta )d\mu |&\lesssim \sum _Q (\mathbb {P}Q\;\text{ exceptional})^\frac{1}{4}|Q|\nonumber \\&\le \big (\sum _Q (\mathbb {P}Q\;\text{ exceptional})|Q|\big )^\frac{1}{4} \big (\sum _Q|Q|\big )^\frac{3}{4}. \end{aligned}$$

As we noted before, we obtain for the second factor $\sum _Q|Q|\lesssim R^2\ln R$. For the first factor, we note

$$\begin{aligned} \sum _{Q\;\text{ level }\;r}(\mathbb {P}Q\;\text{ exceptional})|Q| =\mathbb {E}|\cup _{Q\;\text{ exceptional } \text{ level }\;r}Q|. \end{aligned}$$

(2.48)

Since $\cup _{Q\;\text{ exceptional }}Q\subset E$, we have that the sum in r of the l. h. s. of (2.48) is $\lesssim \mathbb {E}|E|\ln R$. Now (2.47) follows from (2.46). $\square$

Proof of Lemma 2.5

Step 1. From one to two measures. We claim that for $R\gg 1$ the following inequality holds

$$\begin{aligned} \mathbb {E}{\sup \left\{ \int \zeta (d\mu - d\nu ) \quad \big |\;\textrm{supp}\zeta \subset (0,R)^2,\;|\nabla \zeta |\le 1,\; \int \zeta dx=0 \right\} }\gtrsim R^2\ln ^\frac{1}{2}R. \end{aligned}$$

(2.49)

Indeed, write ${\mathcal {F}}=\left\{ \zeta : \textrm{supp}\zeta \subset (0,R)^2,\;|\nabla \zeta |\le 1,\; \int \zeta dx=0 \right\}$ and $S=\sup _{\zeta \in {\mathcal {F}}} \int \zeta d\mu ,$ where the supremum has to be understood as an essential supremum. By basic results on essential suprema, there exists a countable subset $\{\zeta _n, n\ge 1\}\subset {\mathcal {F}}$ such that $S=\sup _{n\ge 1} \int \zeta _n d\mu$. Setting, $S_n=\max _{k\le n} \int \zeta _k d\mu$ we have $S_n\nearrow S$ and by monotone convergence $\mathbb {E}S_n\nearrow \mathbb {E}S.$ Hence, there is n such that $\mathbb {E}S_n\gtrsim R^2\ln ^\frac{1}{2} R$ by Lemma 2.7. By definition of $S_n$, $S_n=\int \zeta d\mu$ for some ${\mathcal {F}}$-valued random variable $\zeta$ (that takes finitely many values $\zeta _1, \dots , \zeta _n$ w. r. t. $\mu$), which is admissible in (2.49). Clearly, $\zeta$ is measurable w. r. t. $\mu$ alone. However, $\zeta$ is measurable only dependent on $\mu$ and not on $\nu$. Since $\nu$ has intensity measure dx we obtain by independence of $\mu$ and $\nu$

$$\begin{aligned} \mathbb {E}\left[ \int \zeta (d\mu -d\nu ) \right]&= \mathbb {E}_\mu \left[ \mathbb {E}_\nu \left[ \int \zeta (d\mu -d\nu ) \right] \right] = \mathbb {E}_\mu \left[ \int \zeta d\mu - \int \zeta dx \right] \\&= \mathbb {E}_\mu \left[ \int \zeta d\mu \right] \gtrsim R^2 \ln ^\frac{1}{2} R \end{aligned}$$

which proves (2.49).

Step 2. Concentration around expectation. We claim that

$$\begin{aligned} S_R \left( \mu , \nu \right) := \sup \left\{ \int \zeta \left( d\mu -d\nu \right) \quad \big |\;\textrm{supp}\zeta \subset (0,R)^2,\;|\nabla \zeta |\le 1,\; \int \zeta dx=0 \right\} \nonumber \\ \end{aligned}$$

(2.50)

satisfies

$$\begin{aligned} \lim _{\begin{array}{c} R \rightarrow \infty \\ \text{ R } \text{ dyadic } \end{array}} \frac{1}{R^2 \ln ^{\frac{1}{2}} R} \left| S_R \left( \mu , \nu \right) - \mathbb {E} S_R \left( \mu , \nu \right) \right| = 0 \quad \mathbb {P}- \text {a.~s.}. \end{aligned}$$

(2.51)

Indeed, by the triangle inequality, we split the statement into two:

$$\begin{aligned} \left| S_R \left( \mu , \nu \right) - \mathbb {E} S_R \left( \mu , \nu \right) \right| \le \left| S_R \left( \mu , \nu \right) - \mathbb {E}_\mu S_R \left( \mu , \nu \right) \right| + \left| \mathbb {E}_\mu S_R \left( \mu , \nu \right) - \mathbb {E} S_R \left( \mu , \nu \right) \right| . \end{aligned}$$

By a Borel-Cantelli argument it suffices to show that for any fixed $\varepsilon >0$ and $R \gg 1$ the following statements hold

$$\begin{aligned}{} & {} \mathbb {P} \left( \frac{1}{R^2 \ln ^\frac{1}{2}R} \left| S_R \left( \mu , \nu \right) - \mathbb {E}_\mu S_R \left( \mu , \nu \right) \right| > \varepsilon \right) \lesssim \exp \left( - \frac{\varepsilon ^2}{4} \ln R \right) , \end{aligned}$$

(2.52)

$$\begin{aligned}{} & {} \mathbb {P} \left( \frac{1}{R^2 \ln ^\frac{1}{2}R} \left| \mathbb {E}_\mu S_R \left( \mu , \nu \right) - \mathbb {E} S_R \left( \mu , \nu \right) \right| > \varepsilon \right) \lesssim \exp \left( - \frac{\varepsilon ^2}{4} \ln R \right) . \end{aligned}$$

(2.53)

We first turn to (2.52). For $z \in \mathbb {R}^2$ we consider the difference operator

$$\begin{aligned} D_{z} S_R \left( \mu , \nu \right) := S_R \left( \mu + \delta _z, \nu \right) - S_R \left( \mu , \nu \right) . \end{aligned}$$

Since the $\zeta$’s in the definition (2.50) satisfy $\sup \left| \zeta \right| \le \sqrt{2}R$, we have

$$\begin{aligned} \left| D_{z} S_R \left( \mu , \nu \right) \right| \le \sup \left\{ \left| \zeta \left( z \right) \right| \big |\;\textrm{supp}\zeta \subset (0,R)^2,\;|\nabla \zeta |\le 1,\; \int \zeta dx=0 \right\} \le R. \end{aligned}$$

(2.54)

Hence,

$$\begin{aligned} \int _{\mathbb {R}^2} \left( D_{z} S_R \left( \mu , \nu \right) \right) ^2 dz \le \int _{\left( 0,R \right) ^2} R^2 dz \le R^4. \end{aligned}$$

Applying [26, Proposition 3.1] with $\beta = R$ and $\alpha ^2 = R^4$ we obtain for $R \gg 1$

$$\begin{aligned} \begin{aligned} \mathbb {P} \left( \left| S_R \left( \mu , \nu \right) - \mathbb {E}_\mu S_R \left( \mu , \nu \right) \right| > \varepsilon R^2 \ln ^\frac{1}{2}R \right)&\lesssim \exp \left( - \frac{\varepsilon R^2 \ln ^\frac{1}{2} R}{2 \beta } \ln \left( 1+ \frac{\beta \varepsilon R^2 \ln ^\frac{1}{2} R}{\alpha ^2} \right) \right) \\&= \exp \left( - \frac{\varepsilon R \ln ^{\frac{1}{2}} R}{2} \ln \left( 1 + \frac{\varepsilon \ln ^{\frac{1}{2}} R}{R} \right) \right) \\&\lesssim \exp \left( - \frac{\varepsilon ^2}{4} \ln R \right) . \end{aligned} \end{aligned}$$

The argument for (2.53) is almost identical: For arbitrary $w \in \mathbb {R}^2$ we need to consider

$$\begin{aligned} D_w \mathbb {E}_\mu S_R \left( \mu , \nu \right) = \mathbb {E}_\mu S_R \left( \mu , \nu + \delta _w \right) - \mathbb {E}_\mu S_R \left( \mu , \nu \right) . \end{aligned}$$

Because of $D_w \mathbb {E}_\mu S_R \left( \mu , \nu \right) = \mathbb {E}_\mu D_w S_R \left( \mu , \nu \right)$ we obtain as above

$$\begin{aligned} \left| D_w \mathbb {E}_\mu S_R \left( \mu , \nu \right) \right| = \left| \mathbb {E}_\mu D_w S_R \left( \mu , \nu \right) \right| \le R. \end{aligned}$$

Then applying once more [26, Proposition 3.1] with $\beta = R$ and $\alpha = R^2$ implies (2.53). $\square$

2.5.2 Upper Bound

Lemma 1.12

Let $\mu$ denote the Poisson point process in $\mathbb {R}^2$ of unit intensity. Then it holds for $R\gg 1$

$$\begin{aligned} \mathbb {E}W_{(0,R)^2}^2(\mu ,n)\lesssim R^2\ln R, \end{aligned}$$

(2.55)

where $n=\frac{\mu ((0,R)^2)}{R^2}$ is the (random) number density.

Proof

Clearly, the intuition mentioned at the beginning of Sect. 2.5 suggests to uncover a martingale structure. W.l.o.g. we may assume that $R\in 2^\mathbb {N}$, and will consider the family of all dyadic squares Q. For such Q, we consider the number density

$$\begin{aligned} n_Q:=\frac{\mu \left( Q \right) }{|Q|}. \end{aligned}$$

(2.56)

Note that $n_Q|Q|\in \mathbb {N}_0$ is Poisson distributed with expectation |Q|. Note that if, for a fixed point x, we consider the sequence of nested squares Q that contain x, the corresponding random sequence $n_Q$ is a martingale. We want to stop the dyadic subdivision just before the number density leaves the interval $[\frac{1}{2},2]$ of moderate values. This defines a scale:

$$\begin{aligned} r_*(x):= 2 \sup \{r \ | \ \text{ is } \text{ the } \text{ sidelength } \text{ of } \text{ dyadic } \text{ square }\,Q\ni x\;\text{ with }\; n_Q\not \in [\frac{1}{2},2]\}. \end{aligned}$$

(2.57)

Since on a square Q of side length $r=\frac{1}{2}$ we have $n_Q\in 4\mathbb {N}_0$ we trivially obtain

$$\begin{aligned} r_*(x) \ge 1. \end{aligned}$$

(2.58)

As we shall argue now, it follows from the properties of the Poisson distribution that (the stationary) $r_*(x)$ is O(1) with overwhelming probability, in particular

$$\begin{aligned} \mathbb {E}r_*^4(x)\lesssim 1. \end{aligned}$$

(2.59)

Indeed, by the concentration properties of the Poisson distribution we have for any $\rho \in 2^\mathbb {N}$

$$\begin{aligned} \begin{aligned} \mathbb {P}\left( r_*(x) > \rho \right)&\le \sum _{Q \ni x, r_Q \ge \rho } \mathbb {P}\left( n_{Q_\rho } \notin \left[ \frac{1}{2}, 2 \right] \right) \\&\lesssim \sum _{r \ge \rho \;\text{ dyadic }} \exp \left( - C r^2 \right) \lesssim \exp \left( -C \rho ^2 \right) . \end{aligned} \end{aligned}$$

Thus we may estimate

$$\begin{aligned} \begin{aligned} \mathbb {E}r_*^4 (x)&= 4 \int _0^\infty \rho ^{3} \mathbb {P}\left( r_* (x)> \rho \right) d\rho \lesssim \int _0^\infty \rho ^{3} \exp \left( -C \rho ^2 \right) d\rho \lesssim 1. \end{aligned} \end{aligned}$$

We now distinguish the case of $r_* \le R$ on $(0,R)^2$ and its complement. In the last case, there exists a $y \in (0,R)^2$ such that $r_*(y) > R$, which by (2.57) means that there exists a dyadic cube $Q \ni y$ of sidelength $r_Q \ge R$ and $n_Q \notin \left[ \frac{1}{2}, 2 \right]$, which in turn implies that $r_* > R$ on the entire $(0,R)^2$. Now fix a deterministic $y \in (0,R)^2$. Since $n_{(0,R)^2} R^2$ is the number of particles we use the brutal estimate of the transportation distance

$$\begin{aligned} W^2_{(0,R)^2} \left( \mu , n_{(0,R)^2} \right) \le n_{(0,R)^2} R^22R^2. \end{aligned}$$

(2.60)

Since by assumption, $(0,R)^2 \subset (0, r_*(y))^2$, this yields $W^2_{(0,R)^2}$ $\left( \mu , \right.$ $\left. n_{(0,R)^2}\right)$ $\le n_{(0,r_*(y))^2}$ $r_*^2 (y) 2 R^2$. Hence by definition of $r_*(y)$, see (2.57) we obtain $W^2_{(0,R)^2} \left( \mu , n_{(0,R)^2} \right) \le 2 r_*^2 (y) 2 R^2$ $\lesssim r_*^4 (y)$. By (2.59), taking the expectation yields as desired

$$\begin{aligned} \mathbb {E}W^2_{(0,R)^2} \left( \mu , n_{(0,R)^2} \right) I \left( r_*(y) > R \right) \lesssim 1, \end{aligned}$$

where $I \left( r_*(y) > R \right)$ denotes the indicator function of the event $\left\{ r_*(y) > R \right\}$.

In the more interesting case of $r_* \le R$, we define a partition of $(0,R)^2$. A cube $Q_*$ is an element of the partition if and only if its sidelength $r_{Q_*}$ satisfies

$$\begin{aligned} r_{Q_*}=\max \{r_*(x) : x \in Q_*\}. \end{aligned}$$

(2.61)

In words, this means that the number density of $Q_*$ is still within $[\frac{1}{2},2]$ but the number density of at least one of its four children leaves the interval $[\frac{1}{2},2]$. This implies the following reverse of (2.61)

$$\begin{aligned} \frac{1}{|Q_*|}\int _{Q_*} r^2_{*} \ge \frac{1}{4} r^2_{Q_*}. \end{aligned}$$

(2.62)

Equipped with this partition, we define the density $\lambda$ by

$$\begin{aligned} \lambda =n_{Q_*}\quad \text{ on }\;Q_*. \end{aligned}$$

We consider the transportation distance between $\mu$ and the measure $\lambda dx$. By definition of $\lambda$, there exists a coupling where the mass is only redistributed within the partition $\{Q_*\}$. This implies the inequality

$$\begin{aligned} W_{(0,R)^2}^2(\mu ,\lambda )\le \sum _{Q_*}2r_{Q_{*}}^2 n_{Q_*}|Q_*| {\mathop {\le }\limits ^{(2.57),(2.62)}}16\sum _{Q_*} \int _{Q_*} r^2_{*} = 16\int _{(0,R)^2}r_*^2. \end{aligned}$$

Taking the expectation, by (2.59) and Jensen’s inequality,

$$\begin{aligned} \mathbb {E}W_{(0,R)^2}^2(\mu ,\lambda ) I \left( r_* \le R \right) \lesssim 1. \end{aligned}$$

Hence in view of (2.59) and the triangle inequality for the transportation distance it remains to show

$$\begin{aligned} {\mathbb {E}} W_{(0,R)^2}^2(\lambda ,n_{(0,R)^2}) I \left( r_* \le R \right) \lesssim R^2\ln R. \end{aligned}$$

(2.63)

The purpose of the stopping (2.57) is that we have the lower bound $\lambda , n_{(0,R)^2}\ge \frac{1}{2}$ on the two densities, which implies the inequality

$$\begin{aligned} W_{(0,R)^2}^2(\lambda ,n_{(0,R)^2})\le 2\int _{(0,R)^2}|j|^2 \end{aligned}$$

(2.64)

for all distributional solutions j of

$$\begin{aligned} \nabla \cdot j=n_{(0,R)^2}-\lambda \;\;\text{ in }\;(0,R)^2,\quad \nu \cdot j=0\;\;\text{ on }\;\partial (0,R)^2. \end{aligned}$$

(2.65)

Inequality (2.64) can be easily derived from the Eulerian description of optimal transportation (see for instance [4, Proposition 1.1] or [25, Theorem 8.1]). Indeed, the couple $\left( \rho , j \right)$, with $\rho = t n_{(0,R)^2} + \left( 1-t \right) \lambda \ge \frac{1}{2}$ and j satisfying (2.65) is an admissible candidate for the Eulerian formulation of $W_{(0,R)^2}^2(\lambda ,n_{(0,R)^2})$.

We now construct a j: For a dyadic square Q we define its four children $Q'$ as the four squares that we obtain by dyadically decomposing Q and we (distributionally) solve the Poisson equation with piecewise constant r. h. s. and no-flux boundary data

$$\begin{aligned} -\Delta \varphi _Q=n_Q-n_{Q'}\;\;\text{ in }\;Q',\quad \nu \cdot \nabla \varphi _Q=0\;\;\text{ on }\;\partial Q. \end{aligned}$$

(2.66)

Note that (2.66) admits a solution since the integral of the r. h. s. over Q vanishes by definition of $\{n_Q\}$. Since the no-flux boundary condition allows for concatenation of $-\nabla \varphi _Q$ without creating singular contributions to the divergence,

$$\begin{aligned} j(x):=-\sum _{Q\ni x,R \ge r_Q\ge 2r_{Q_*}\;\text{ for }\; Q_* \ni x}\nabla \varphi _Q(x) \end{aligned}$$

(2.67)

which means that the sum¹⁴ extends over all dyadic cubes $Q \subset \left( 0,R \right) ^2$ containing x and being strictly coarser than $\left\{ Q_* \right\}$, defines indeed a distributional solution of (2.65).

The Poincaré inequality gives the universal bound

$$\begin{aligned} \int _Q dx|\frac{1}{r_Q}\nabla \varphi _Q|^2\lesssim |Q|\sum _{Q'\;\text{ child } \text{ of }\;Q}(n_{Q'}-n_Q)^2. \end{aligned}$$

Appealing to the trivial estimate $\sum _{Q'\text{ child } \text{ of }\;Q}(n_{Q'}-n_Q)^2$ $\lesssim$ $\sum _{Q'\;\text{ child } \text{ of }\;Q}$ $(n_{Q'}-1)^2$, and to the standard estimate on the variance of the Poisson process, namely $\mathbb {E}(n_Q-1)^2\lesssim \frac{1}{|Q|}$, we obtain

$$\begin{aligned} \mathbb {E}\int _Q|\nabla \varphi _Q|^2\lesssim |Q|. \end{aligned}$$

(2.68)

Now comes the crucial observation: We momentarily fix a point x and consider all squares $Q\ni x$. We note that $\nabla \varphi _Q(x)$ depends on the Poisson point process only through $\{n_{Q'}\}$ where $Q'$ runs through the children of Q. Moreover, since the expectation of the r. h. s. of the Poisson equation (2.66) vanishes, also the expectation of $\nabla \varphi _Q(x)$ vanishes. Hence the sum

$$\begin{aligned} \sum _{Q\ni x,R \ge r_Q\ge r}\nabla \varphi _Q(x) \end{aligned}$$

is a martingale in the scale parameter $r=R,\frac{R}{2},\frac{R}{4},\ldots$ w. r. t. to the filtration generated by the $\{n_Q\}_{Q}$. Since $r_* \ge 1$, we thus obtain by the Burkholder inequality [23, Theorem 6.3.6]

$$\begin{aligned} \mathbb {E}\big |\sum _{Q\ni x,R \ge r_Q\ge 2r_{Q_*}\;\text{ for }\; Q_* \ni x}\nabla \varphi _Q(x)\big |^2&\le \mathbb {E}\sup _{r \ge 1}\big |\sum _{Q\ni x,R \ge r_Q\ge r}\nabla \varphi _Q(x)\big |^2 \\&\lesssim \mathbb {E}\sum _{Q\ni x,R \ge r_Q\ge 1}|\nabla \varphi _Q(x)|^2. \end{aligned}$$

Inserting definition (2.67) into the l. h. s., using triangle inequality, integrating over $x\in (0,R)^2$, and using (2.58) on the r. h. s. we obtain

$$\begin{aligned} \mathbb {E}\int _{(0,R)^2}|j|^2 \lesssim \sum _{Q,R \ge r_Q\ge 1}\mathbb {E}\int _Q|\nabla \varphi _Q|^2. \end{aligned}$$

Using (2.64) on the l. h. s. and (2.68) on the r. h. s. yields (2.63). $\square$

Remark 2.9

The same argument in $d>2$ yields the bound $\mathbb {E}W_{(0,R)^d}\left( \mu ,n \right) \lesssim 1$. However, the interesting (well known) information from the proof is that in $d>2$ the main contribution comes from the term $W_{(0,R)^d}^2(\mu ,\lambda )$ which collects the contributions on the small scales.

Proof of Lemma 2.6

W.l.o.g. it suffices to prove that for the Poisson point process $\mu$ there exists a random radius $r_*$ such that for any dyadic radii $R \ge r_*$

$$\begin{aligned} \frac{1}{R^d} W^2_{(-R,R)^d} \left( \mu , n \right) + \frac{R^2}{n} \left( n-1 \right) ^2 \lesssim \ln R. \end{aligned}$$

(2.69)

The statement will follow by choosing the maximum of this random radius and the one pertaining to $\nu$.

Step 1. We claim that there exists a constant C and a random radius $r_* < \infty$ a. s. such that for any dyadic radii $R \ge r_*$

$$\begin{aligned} \frac{1}{R^2} W_{(-R,R)^2}^2(\mu ,n)\le C \ln R. \end{aligned}$$

(2.70)

By Lemma 2.8 we may assume that (2.55) holds with $(0,R)^2$ replaced by $(0, 2R)^2$. Furthermore by stationarity of the Poisson point process we may assume that (2.55) holds in the form

$$\begin{aligned} \frac{1}{R^2} \mathbb {E}W_{(-R,R)^2}^2(\mu ,n)\lesssim \ln R, \end{aligned}$$

(2.71)

provided that $R \gg 1$. By [9, Proposition 2.7] it follows that for any $\varepsilon >0$,

$$\begin{aligned} \mathbb {P} \left( \frac{1}{R^2 \ln R}\left| W_{(-R,R)^2}^2 \left( \mu , n \right) - \mathbb {E} W_{(-R,R)^2}^2 \left( \mu , n \right) \right| > \varepsilon \right) \lesssim \exp \left( - C \varepsilon \ln R \right) . \end{aligned}$$

Then (2.70) follows by arbitrarity of $\varepsilon$ together with a Borel-Cantelli argument.

Step 2. We show that there exists a constant C and random radius $r_* < \infty$ a. s. such that for any dyadic radii $R \ge r_*$

$$\begin{aligned} \frac{R^2}{n} \left( n-1 \right) ^2 \le C \ln R. \end{aligned}$$

(2.72)

Since for large $R \gg 1$ we have $\frac{\ln R}{R^2} \ll 1$ (2.72) is equivalent to

$$\begin{aligned} {R^2} \left( n-1 \right) ^2 \lesssim \ln R. \end{aligned}$$

Since $n 4 R^2$ is Poisson distributed with parameter $4 R^2$ by Cramér-Chernoff’s bounds [6, Theorem 1]

$$\begin{aligned} \begin{aligned} \mathbb {P}\left( R^2 \left( n-1 \right) ^2> \ln R \right)&= \mathbb {P}\left( \left| n 4 R^2- 4 R^2\right| > C R \ln ^\frac{1}{2} R \right) \lesssim \exp \left( - C \ln R \right) . \end{aligned} \end{aligned}$$

Finally, by a Borel-Cantelli argument (2.72) holds for any dyadic radii $R \ge r_*$. $\square$