Abstract
We consider the Allen–Cahn equation \({\partial _t}{u}-\Delta u=u-u^3\) with a rapidly mixing Gaussian field as initial condition. We show that provided that the amplitude of the initial condition is not too large, the equation generates fronts described by nodal sets of the Bargmann–Fock Gaussian field, which then evolve according to mean curvature flow.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The aim of the present article is to prove that nodal sets of a smooth Gaussian field, known as the Bargmann–Fock field, arise naturally as a random initial condition to evolution by mean curvature flow.
This problem is related to understanding the long-time behaviour of mean curvature flow: for a sufficiently generic initial datum composed of clusters with typical lengthscale of order 1, one expects that at time \( t \gg 1 \) the clusters have coarsened in such a way that the typical lengthscale is of order \( \sqrt{t} \). In fact, one would even expect that upon rescaling by \( \sqrt{t} \), the clusters become self-similar/stationary at large times [3].
An understanding of such a behaviour remains currently beyond the reach of rigorous analysis although upper bounds on the coarsening rate can be proven via deterministic arguments, see e.g. [9] for the related Cahn–Hilliard dynamics. On the other hand, lower bounds on the rate of coarsening can only be expected to hold for sufficiently generic initial conditions, since for degenerate initial conditions one may not see any coarsening at all.
This motivates the question, addressed in the present work, of what such generic initial condition should look like. Notably, the correlation structure we obtain is the same as the first order approximation of the longtime two-point correlation predicted by Ohta, Jasnow and Kawasaki [10].
A natural way to construct random initial conditions to mean curvature flow is to consider the fronts formed by the dynamics of the Allen–Cahn equation with white noise initial data. Unfortunately this is not feasible, since the scaling exponent \(-\frac{d}{2}\) of white noise on \( \textbf{R}^{d} \), with \(d \geqslant 2\), lies below or at the critical exponent \(-1\) (or \(-\frac{2}{3}\) depending on what one really means by “critical” in this context), under which one does not expect any form of local well-posedness result for the equation.
Instead, we consider the following setting. Let \( \eta \) be a white noise on \({{\textbf {R}}}^d\) with \(d \ge 2\) and let \(\varphi \) be a Schwartz test function integrating to 1. Fix an exponent \(\alpha \in (0,1)\), and for each \(\varepsilon \in (0, 1)\) and \(x\in {{\textbf {R}}}^d\) define
Here, the exponents are chosen in such a way that \(\varphi _x^\varepsilon \) converges to a Dirac distribution and typical values of \(\eta _\varepsilon \) are of order \(\varepsilon ^{-\alpha }\). Our aim is to describe the limit as \( \varepsilon \rightarrow 0 \) of the solutions to the Allen–Cahn equation with initial datum \( \eta _{\varepsilon } \)
The reason for restricting ourselves to \(\alpha < 1\) is that 1 is precisely the critical exponent for which \(\Delta \eta _\varepsilon \) and \(\eta _\varepsilon ^3\) are both of the same order of magnitude, i.e. when \(\alpha +2 = 3\alpha \).
For a fixed terminal time t, the behaviour of (1.2) is not very interesting since one has \(\eta _\varepsilon \rightarrow 0\) weakly, so one would expect to also have \(u_\varepsilon \rightarrow 0\). This is trivially the case for \(\alpha < \frac{2}{3}\) since one has \(\eta _\varepsilon \rightarrow 0\) in \({\mathcal {C}}^\beta \) for every \(\beta < -\alpha \) and the Allen–Cahn equation is well-posed for arbitrary initial data in \({\mathcal {C}}^\beta \) if (and actually only if) \(\beta > -\frac{2}{3}\). As a consequence of Proposition 3.15 below, we will see that it is still the case that \(u_\varepsilon (t)\rightarrow 0\) at fixed t for any exponent \(\alpha < 1\), but this is a consequence of more subtle stochastic cancellations.
It turns out that the natural time and length scales at which one does see non-trivial behaviour are given by
The main result of this article is that for \( \sigma > 1 \), \( u ( \sigma T_{\varepsilon }, x L_{\varepsilon }) \rightarrow \pm 1 \) on sets \( \Omega _{\sigma }^{\pm 1} \), which evolve under mean curvature flow. The initial data (at time \(\sigma = 1\)) for that flow is given by the nodal domains of a centred Gaussian field \(\{\Psi _{1}(x):x\in {{\textbf {R}}}^d \}\) with Gaussian correlation function, also known as the Bargmann–Fock field:
In what follows we will write \( \Psi \) short for \( \Psi _{1}.\) This Gaussian field emerges from the linearisation near zero of (1.2), within a time interval of order 1 (in the original variables) around \(t_{\star } (\varepsilon ) \) with
where \( \mathfrak {c} \) is chosen to make certain expressions look nicer. In fact, roughly up to time \(t_{\star } (\varepsilon ) \) the dynamics of \( u_{\varepsilon } \) is governed by the linearisation of (1.2) around the origin, but at that time the solution becomes of order 1 and starts to follow the flow \( \Phi :\textbf{R}\times \textbf{R}\rightarrow [-1, 1] \) of the nonlinear ODE
which is given by
We will show that a good approximation of \( u_{\varepsilon }(t_{\star }(\varepsilon ), x L_{\varepsilon })\) is given by \( \Phi (0, \Psi (x)) \).
Then, after an additional time of order \( T_{\varepsilon } \), \( u_{\varepsilon } \) is finally governed by the large scale behaviour of the Allen–Cahn equation with random initial condition \( \Phi (0, \Psi ) \), namely by the mean curvature flow evolution of the set \( \{ \Psi =0 \} \). To capture the different time scales we introduce the process
and we summarise our results in the theorem below.
Theorem 1.1
The process \( U_{\varepsilon } \) converges in law as follows for \( \varepsilon \rightarrow 0 \)
The convergences hold for fixed t or \(\sigma \) and locally uniformly over the variable x.
Denote furthermore by \( \Omega ^{+}_{\sigma }, \Omega ^{-}_{\sigma }\) respectively the mean curvature flow evolutions of the sets \( \Omega ^{+}_{1} = \{ x \ :\ \Psi (x) > 0 \}, \ \Omega ^{-}_{1} = \{ x \ :\ \Psi (x) < 0 \}\). Then, there exist a coupling between \(\{U_\varepsilon \}_{\varepsilon \in (0, 1)}\) and \(\Psi \) such that, for every \(\sigma > 1\), one has \(\lim _{\varepsilon \rightarrow 0} U_{\varepsilon }(\sigma , x) = \pm 1\) locally uniformly for \(x \in \Omega ^{\pm }_{\sigma }\), in probability.
Remark 1.2
Although level set solutions to mean curvature flow with continuous initial datum are unique, they might exhibit fattening, meaning that the evolution of the zero level set \( \Gamma _{\sigma } = \textbf{R}^d {\setminus } (\Omega ^{+}_{\sigma } \cup \Omega ^{-}_{\sigma }) \) might have a non-empty interior for some \(\sigma > 1\). In dimension \( d=2 \) this does not happen, as the initial interface is composed of disjoint smooth curves which evolve under classical mean curvature flow, c.f. Corollary 5.7. In dimension \( d \geqslant 3 \) this picture is less clear, and in addition the initial nodal set was recently proven to contain unbounded connected components [5].
1.1 Structure of the paper
The rest of this article is divided as follows. In Sect. 2, we reformulate Theorem 1.1 more precisely and we provide its proof, taking for granted the more technical results given in subsequent sections. In Sect. 3 we study a Wild expansion of the solution to (1.2) which allows us to take advantage of stochastic cancellations to control the solutions on a relatively short initial time interval of length smaller than \((1 - \alpha ) \log {\varepsilon ^{-1}}\). In Sect. 4 we then show how the Bargmann–Fock field arises from this expansion and we track solutions up to timescales of order \(t_\star \). In Sect. 5, we finally conclude by showing that our estimates are sufficiently tight to allows us to patch into existing results on the convergence to mean curvature flow on large scales.
1.2 Notations
For a set \( \mathcal {X} \) and two functions \( f, g :\mathcal {X}\rightarrow \textbf{R}\), we write \( f \lesssim g \) if there exists a constant \( c > 0 \) such that \( f(x) \leqslant c g(x) \) for all \( x \in \mathcal {X}\). If \( \mathcal {X}\) is a locally compact metric space we define \(C_\text {loc}(\mathcal {X}) \) as the space of continuous and locally bounded functions, equipped with the topology of uniform convergence on compact sets. We will write \( P_{t}, P^{1}_{t} \) for the following semigroups on \(\textbf{R}^{d}\):
We denote with \( {{\,\textrm{sgn}\,}}:\textbf{R}\rightarrow \{ -1, 0, 1 \} \) the sign function, with the convention that \( {{\,\textrm{sgn}\,}}(0) = 0\).
2 Main results
In what follows we consider \( (t, x) \mapsto u_{\varepsilon } (t, x) \) as a process on \( \textbf{R}\times \textbf{R}^{d} \) by defining \( u_{\varepsilon }(t, x) = u_{\varepsilon }(0, x) \) for \( t < 0 \). We then show the first part of Theorem 1.1, namely
Theorem 2.1
Let \( u_{\varepsilon } \) solve (1.2) and \(\Psi _{\sigma }, \Phi , U_{\varepsilon }\) be given respectively by (1.3), (1.5) and (1.6). Then
-
1.
For any \( \sigma \in (0, 1) \) the process \( \{ U_{\varepsilon } (\sigma , x) \ :\ x \in \textbf{R}^{d} \} \) converges locally uniformly in law to \( \{ \Psi _{\sigma } (x) \ :\ x \in \textbf{R}^{d} \} \).
-
2.
The process \(\{u_\varepsilon (t_\star (\varepsilon )+t, x L_{\varepsilon }):(t,x) \in {{\textbf {R}}}\times {{\textbf {R}}}^d \}\) converges locally uniformly in law to \(\left\rbrace \Phi \left( t, \Psi (x) \right) :(t,x) \in {{\textbf {R}}}\times {{\textbf {R}}}^d \right\lbrace \).
Proof
The first statement follows, for \(\sigma \in \big (0, \frac{1 -\alpha }{ d/2 - \alpha } \big )\), from similar calculations as in Lemma 4.4 in combination with Proposition 3.15. For \(\sigma \in \big [\frac{1 -\alpha }{ d/2 - \alpha }, 1 \big ) \) it follows again by similar calculations as in Lemma 4.4, this time in combination with Lemma 4.3. Let us pass to the second statement. For some \( {\overline{\alpha }} \in (\alpha , 1) \) consider
It is shown in Proposition 4.6 that the limit as \(\varepsilon \rightarrow 0\) of the process \((t,x)\mapsto u_\varepsilon (t_\star +t,L_\varepsilon x) \) is identical, in probability, to that of \((t,x)\mapsto w^N_\varepsilon (t_\star +t,L_\varepsilon x)\) for some fixed N sufficiently large. From the definition of \( w^{N}_{\varepsilon } \), we have
where \( u^{N}_{\varepsilon } \) is the Wild expansion truncated at level N given by (3.5). Applying Lemma 4.4, we see that the process \((t,x)\mapsto P^1_{t_\star +t-t_1}u^N_\varepsilon (t_1,L_\varepsilon x) \) converges to \((t,x)\mapsto e^t \Psi (x)\) in \({C_\text {loc}({{\textbf {R}}}\times {{\textbf {R}}}^d)}\) in distribution. Since furthermore \(t_\star \gg t_1\), it follows that the process \((t,x)\mapsto w^N_\varepsilon (t_\star +t,L_\varepsilon x)\) converges in \({C_\text {loc}({{\textbf {R}}}\times {{\textbf {R}}}^d)}\) in distribution to the process
thus concluding the proof. \(\square \)
We now turn to the proof of the second part of Theorem 1.1. This is trickier to formulate due to the potential fattening of level sets already alluded to in Remark 1.2. In particular, let us denote by \( (\sigma , x) \mapsto v(f; \sigma , x) \in \{ -1, 0, 1 \}\) the sign of the level set solution to mean curvature flow associated to the initial interface \( \{ f = 0 \} \) in the sense of Definition 5.5, with the difference that the initial condition is given at time \( \sigma =1 \) in the present scale. We will then write \( \Gamma \) for the random interface \( \Gamma = \{ (\sigma , x) \in [1, \infty ) \times \textbf{R}^{d} \ :\ v(\Psi ; \sigma , x) = 0 \} \subseteq \textbf{R}^{d+1} \) and \( \Gamma _{\sigma } = \{ x \in \textbf{R}^{d} \; :\; (\sigma , x) \in \Gamma \}\). In addition, in order to define locally uniform convergence in the complement of \( \Gamma \), let us introduce for any \( \delta \in (0, 1) \) the random sets
Here d(p, X) is the usual point-to-set distance. Furthermore, we can define the (random) norms
and analogously for \( K_{\delta }^{1} \). With these definitions at hand, the next result describes the formation of the initial interface, which appears if we wait an additional time of order \( \log { \log { \varepsilon ^{-1}}} \). Hence we define, for \( \kappa > 0\):
Proposition 2.2
Consider any sequence of times \( \{ t(\varepsilon ) \}_{\varepsilon \in (0, 1)} \subseteq (0, \infty ) \) such that for some \( \kappa >0 \)
Then there exists a coupling between \( u_{\varepsilon } \) and \( \Psi \) such that for any \( \delta , \zeta \in (0, 1) \)
Proof
Up to taking subsequences, it suffices to prove the result in either of the following two cases:
In the first case, the result is a consequence of Proposition 5.4 while in the second case it follows from Lemma 5.3. In both cases the choice of the coupling is provided by Lemma 5.2. \(\square \)
In the case \( t(\varepsilon ) = t_{\star }^{\kappa }(\varepsilon ) \) for some \( \kappa \in (0, \frac{1}{4} ) \) one can also obtain the above result as a consequence of Proposition 4.6. Finally, we show that if we wait for an additional time of order \( T_{\varepsilon } \), the interface moves under mean curvature flow. This result is a consequence of Proposition 5.6.
Theorem 2.3
Consider \( U_{\varepsilon }(\sigma , x)\) as in (1.6) for \( \sigma > 1, x \in \textbf{R}^{d} \). There exists a coupling between \( u_{\varepsilon } \) and \( \Psi \) such that for any \( \delta , \zeta \in (0, 1) \)
3 Wild expansion
The next two sections are devoted to tracking \( u_{\varepsilon } \) for times up to and around \( t_{\star } (\varepsilon ) \). In order to complete this study we divide the interval \( [0, t_{\star }(\varepsilon )] \) into different regions. Let \({\bar{\alpha }}\in (\alpha ,1)\) be fixed and define
We observe that for \( \varepsilon \) small one has
The specific forms of these times are chosen such that in complement to the moment estimates, the error terms in various estimates which appear below remain small when \(\varepsilon \rightarrow 0\). The constant \(-1/2\) which appears in \(t_2(\varepsilon )\) can be replaced by any negative number, and in spatial dimensions 3 or higher can be replaced by 0. The separation of time scales is due to that fact that the linear and nonlinear terms in (1.2) have different effects on the solution over each period.
During the time period \([0,t_1(\varepsilon )]\), the Laplacian dominates and (1.2) can be treated as a perturbed heat equation. One expects that a truncated Wild expansion \( u_{\varepsilon }^{N} \) (where N is the level of the truncation) provides a good approximation for \(u_\varepsilon \) during this initial time period, see Proposition 3.15 at the end of this section. During the time period \([t_1(\varepsilon ),t_2(\varepsilon )]\), the linear term increases the size of the solution from \(\mathcal{O}(\varepsilon ^{\theta })\) for any \( 0< \theta < \frac{d}{2} - {\overline{\alpha }} \) to almost a size of order 1. During this period, the estimate (3.27) in Proposition 3.15 does not reflect the actual size of the solution \(u_\varepsilon \). However, the leading order term \(X^\bullet _{\varepsilon }\) in \(u^N_{\varepsilon }\) (which is the solution to the linearisation near 0 of (1.2)) at time \(t_2(\varepsilon )\) is of order \((\log \varepsilon ^{-1}) ^{-d/4}\). Hence the solution \(u_\varepsilon \) still remains small, and we expect that the non-linear term \(u_\varepsilon ^3\) in (1.2) is negligible: see Lemma 4.3. Eventually one starts to see the classical dynamic of the Allen–Cahn equation during \([t_2(\varepsilon ),t_\star (\varepsilon )]\), as explained in Proposition 4.6.
To establish the aforementioned results, we will frequently make use of the following formulation of the maximum principle.
Lemma 3.1
Let \((a,b) \subset {{\textbf {R}}}\) be a finite interval and let G, R be measurable functions on \((a,b)\times {{\textbf {R}}}^d\) such that G is non-negative. Suppose that v is a function in \(C^2([a,b]\times {{\textbf {R}}}^d) \) satisfying
Then,
3.1 Moment estimates
Let \(\mathcal {T}_3\) be the set of rooted ternary ordered trees defined inductively by postulating that \(\bullet \in \mathcal {T}_3\) and, for any \(\tau _i\in \mathcal {T}_3\), one has \(\tau =[\tau _1,\tau _2,\tau _3] \in \mathcal {T}_3\). In general, for a finite collection of trees \(\tau _1,\dots , \tau _n\) we denote by \(\tau = [\tau _1,\dots ,\tau _n]\) the tree obtained by connecting the roots of the \(\tau _i\) with a new node, which in turn becomes the root of the tree \(\tau \):

These trees are ordered in the sense that \( [\tau _{1}, \tau _{2}, \tau _{3}] \ne [\tau _{1}, \tau _{3}, \tau _{2}] \) unless \( \tau _{2} = \tau _{3} \), and similarly for all other permutations. For example we distinguish the following two trees:

For \(\tau \in \mathcal {T}_3\), we write \(i(\tau )\) for the number of inner nodes of \([\tau ]\) (i.e. nodes which are not leaves, but including the root) and \(\ell (\tau )\) be the number of leaves of \([\tau ]\). Then \(\ell \) and i are related by
For each positive integer n, \(\pi _n= (2n-1)!!\) is the number of pairings of 2n objects so that each object is paired with exactly one other object. For \(\tau =[\tau _{1}, \tau _{2}, \tau _{3}]\in \mathcal {T}_3\), we define \(X^\tau _\varepsilon \) inductively by solving
For \(N \ge 1\), we write \(\mathcal {T}_3^N \subset \mathcal {T}_3\) for the trees with \(i(\tau )\le N\) and we define
which is a truncated Wild expansion of \( u_{\varepsilon } \). Then \(u^N_\varepsilon \) satisfies the following equation
where
Indeed, using (3.4) and (3.3), we have
Let us now introduce some graphical notations to represent conveniently \(X^\tau _{\varepsilon }\) and the integrals that will be associated to them. In what follows the negative heat kernel \(-P^1(t-s,x-y)\) (here the negative sign appears to keep track of the sign of the polynomial term in (3.4)) will be represented by a directed edge

Each endpoint of an edge represents a space-time variable and the kernel is evaluated at their difference. Three different nodes  can be attached to an end of an edge, which represent respectively a fixed space-time variable, integration with respect to Lebesgue measure \( \text { d}s \text { d}y\), and integration with respect to the (random) measure \( - \delta (s) \eta _{\varepsilon }(y) \text { d}s \text { d}y\). Here, \(\delta \) is the Dirac mass at 0 and the minus sign is again just a matter of convention. For example, we have
can be attached to an end of an edge, which represent respectively a fixed space-time variable, integration with respect to Lebesgue measure \( \text { d}s \text { d}y\), and integration with respect to the (random) measure \( - \delta (s) \eta _{\varepsilon }(y) \text { d}s \text { d}y\). Here, \(\delta \) is the Dirac mass at 0 and the minus sign is again just a matter of convention. For example, we have

as well as  .
.
Since all the edges follow the natural direction toward the root, we may drop the arrows altogether and just write  and
and  . For a general tree
. For a general tree  , \(X^{\tau }_\varepsilon \) is represented by the tree \([\tau ]\) with its root coloured red and leaves coloured green.
, \(X^{\tau }_\varepsilon \) is represented by the tree \([\tau ]\) with its root coloured red and leaves coloured green.
Given a tree \(\tau \in \mathcal {T}_3\), we would like to estimate the moment \({{\textbf {E}}}[X^\tau _\varepsilon (t,x)]^2\). The contracting kernel (see (1.1))

which appears when one contracts two noise nodes (i.e. two green nodes), is represented as a green edge. Note that since these kernels are symmetric, green edges are naturally undirected. Moreover, since we are only interested in upper bound and up to replacing \( \varphi ^{\varepsilon } \) with \( | \varphi ^{\varepsilon } | \), we may assume that
Then for each \(\varepsilon \), we define the positive kernel
From Young’s inequality, we see that
for some constant \(c>0\). Another elementary observation is the bound

Here we did not use any green nodes because the distinction between green and black nodes is captured by the difference between the kernels  and
and  , and as per assumption every black node indicates integration over both space and time variables.
, and as per assumption every black node indicates integration over both space and time variables.
We begin with an estimate for  . The second moment is obtained by contracting two leaves,
. The second moment is obtained by contracting two leaves,

For a general tree \(\tau \), the second moment \({{\textbf {E}}}|X^\tau _{\varepsilon }(t,x)|^2\) is obtained by summing over all pairwise contractions between the leaves of \([\tau ,{\bar{\tau }}]\), where \(\bar{\tau }\) is an identical copy of the tree \(\tau \). For instance,

Let us take a closer look at each term. In particular, we can extend our graphical notation in order to obtain efficient estimates for such trees.
More tree spaces. First, we observe that each of the graphs above comes with a specific structure: it consists of a tree with an even number of leaves, together with a pairing among the leaves. In addition the root is coloured red and every node that is not a leaf is the root of up to three planted trees in \( [\mathcal {T}_{3}] \). This suggest the introduction of the following space of paired forests \( \mathcal {F}\) (later on it will be convenient to work with forests and not only trees).
Let \( \mathcal {T}\) be the set of all finite rooted trees and for \( \{ \tau _{i} \}_{i=1}^{k} \subseteq \mathcal {T}\) define \( \ell (\tau _{1} \sqcup \cdots \sqcup \tau _{k} ) = \ell (\tau _{1}) + \cdots \ell (\tau _{k}) \) the total number of leaves of a forest. Then define \( \mathcal {F}\) as
where \( \mathcal {P}_{\ell } \) is the set of possible pairings among the union of all the leaves of the trees \( \tau _{1}, \dots , \tau _{k} \).
We naturally think of elements of \( \mathcal {F}\) as coloured graphs \( \mathcal {G}= (\mathcal {V}, \mathcal {E})\), with the pairing \( \gamma \) giving rise to green edges. Observe that the forest structure of \( \tau _{1} \sqcup \cdots \sqcup \tau _{k} \) induces a partial order on the set \( \mathcal {V}\) of all vertices by defining \( v > v^{\prime } \) if \( v^{\prime } \ne v \) lies on the unique (directed) path joining v to its relative root. As we mentioned, we will be especially interested in elements of \( \mathcal {F}\) where each tree \( \tau _{i} \) is an element of \( [\mathcal {T}_{3}] \), with the twist that up to two such trees can be planted on the same root:
We then set
Finally, we want to introduce a colouring for \( \mathcal {G}\in \mathcal {F}\). We already mentioned that \( \gamma \) is represented by green edges among the leaves and that all the roots are coloured red, but we will also introduce yellow vertices.
Colourings. To simplify the upcoming constructions, let us now write  and
and  for the colour of edges and vertices of some graph \( \mathcal {G}\in \mathcal {F}\) and let \(K_c\) denote the kernel associated to each edge colour. As we will see later on, colours will appear only in certain locations and will be valuated in specific ways. To clarify these points we compile the following tables for the nodes
for the colour of edges and vertices of some graph \( \mathcal {G}\in \mathcal {F}\) and let \(K_c\) denote the kernel associated to each edge colour. As we will see later on, colours will appear only in certain locations and will be valuated in specific ways. To clarify these points we compile the following tables for the nodes
Colour | Where? | Valuation |
|---|---|---|
| Roots | Suprema over spatial variables |
| Inner nodes of paths | Disappear under spatial integration |
| Leaves or untouched inner nodes | Integrate |
and define kernels

Now, if \({\mathcal {G}}=({\mathcal {V}},{\mathcal {E}})\), we write \({\mathcal {V}}_c\) for the set of vertices of colour c. Given \(z_{\mathcal {V}} \in ({{\textbf {R}}}^{d+1})^{{\mathcal {V}}}\) and \(A \subset {\mathcal {V}}\), we write \(z_A \in ({{\textbf {R}}}^{d+1})^{A}\) for the corresponding projection, as well as \(t_A \in {{\textbf {R}}}^{A}\) and \(x_A \in ({{\textbf {R}}}^{d})^{A}\) for its temporal and spatial components. In the particular case when \(A = {\mathcal {V}}_c\) for some colour c we will sometimes simply write \(z_c\) instead of \(z_{{\mathcal {V}}_c}\). Finally, given an oriented edge \(e \in {\mathcal {E}}\), we write \(e = (e_-,e_+)\).
Structure of the estimates. With these notations at hand, for any subgraph \( \mathcal {G}^{\prime } = (\mathcal {V}^{\prime }, \mathcal {E}^{\prime } ) \subseteq \mathcal {G}\in \mathcal {F}\), we set
We can then evaluate the graph at its red roots by

where  . Now, the crux of our bounds is to pick certain spatial variables and use estimates of the following two kinds, for some \( F, G \geqslant 0 \)
. Now, the crux of our bounds is to pick certain spatial variables and use estimates of the following two kinds, for some \( F, G \geqslant 0 \)
In our setting F, G will be two components of \( K_{\mathcal {G}} \), linked to two subgraphs \( \mathcal {G}^{(1)}, \mathcal {G}^{(2)} \subseteq \mathcal {G}\), which, appropriately glued together, form \( \mathcal {G}\).
Glueing. In pictures, we describe such a glueing as follows:

When glueing red nodes onto yellow nodes we will be in a setting in which we use (3.12). As the notation suggests, we also glue red nodes together, and in this case we will use the estimate (3.13). Glueing red nodes is necessary, say in our running example, to decompose

The glueing procedure we just informally suggested is formalised like this.
Definition 3.2
Let \( \mathcal {G}^{(1)}, \mathcal {G}^{(2)} \in \mathcal {F}\) and consider  ,
,  . Given a bijection
. Given a bijection  , we define
, we define

the latter being the equivalence relation generated by  for all \(v \in A^{(1)}\). In this way we also obtain two emebddings \(\mathfrak {e}^{(1)}, \mathfrak {e}^{(2)} \) with
for all \(v \in A^{(1)}\). In this way we also obtain two emebddings \(\mathfrak {e}^{(1)}, \mathfrak {e}^{(2)} \) with  , which we can combine to a map (which is no longer injective)
, which we can combine to a map (which is no longer injective)

Finally, the colour assigned to an identified node \(v \in \mathcal {V}\), i.e. some v belonging to \( \mathfrak {e} A^{(1)} \), is

Here and in what follows we write \( \mathfrak {e} A \) short for \( \mathfrak {e}(A) \). In general, via this procedure the new graph \( \mathcal {G}\) may not belong to the space of forests \( \mathcal {F}\). We therefore introduce the following notion of compatibility between the colours and the structure of \(\mathcal {F}\).
Definition 3.3
A graph \( \mathcal {G}\in \mathcal {F}\) has compatible colouring if for any \( v \in \mathcal {V}\)

Remark 3.4
Note that the rooted forest structure of \({\mathcal {G}}\) is uniquely determined by its colouring of edges (black or green) and vertices (black, red, or yellow).
From here on we always work with compatible graphs. In particular, we have the following result.
Lemma 3.5
Given compatible graphs \( \mathcal {G}^{(1)}, \mathcal {G}^{(2)} \in \mathcal {F}\) and  as in Definition 3.2,
as in Definition 3.2,  is a compatible element of \( \mathcal {F}\), with the same pairing as \( \mathcal {G}^{(1)} \sqcup \mathcal {G}^{(2)} \).
is a compatible element of \( \mathcal {F}\), with the same pairing as \( \mathcal {G}^{(1)} \sqcup \mathcal {G}^{(2)} \).
Proof
Since  consists of roots and since these are always glued onto either roots or inner nodes by Definition 3.3,
consists of roots and since these are always glued onto either roots or inner nodes by Definition 3.3,  again has a natural forest structure. The rule (3.15) furthermore guarantees that the compatibility property is preserved. (Note also that no new yellow nodes are created.) \(\square \)
again has a natural forest structure. The rule (3.15) furthermore guarantees that the compatibility property is preserved. (Note also that no new yellow nodes are created.) \(\square \)
Valuation. Now we define a valuation \( | \mathcal {G}| \) of a compatible graph \( \mathcal {G}\in \mathcal {F}\) as follows:
-
Consider the kernel \( K_{\mathcal {G}} \) defined by the edges of \({\mathcal {G}}\) and integrate it over all the black variables (i.e. variables associated to black vertices), with all remaining variables fixed.
-
Second, integrate over all the spatial components of the yellow variables.
-
Third, take the supremum over the temporal components of the yellow variables.
-
Finally, take the supremum over the spatial components of red variables.
Clearly, the result of such a valuation will depend only on the red temporal variables  . In formulae
. In formulae

Remark 3.6
This definition is consistent with our evaluation of the graph at a given point in the sense that  if all nodes of \( \mathcal {G}\) apart from the red roots are coloured black.
if all nodes of \( \mathcal {G}\) apart from the red roots are coloured black.
Now, our aim will be to combine the valuation with the glueing of two graphs and obtain an estimate of the sort  . Of course, in this form the estimate cannot be true, since the right-hand side has more free (red) variables than the left-hand side; these additional free variables will be integrated over. In addition, in order to obtain a useful bound we have to also take care of the time supremum over
. Of course, in this form the estimate cannot be true, since the right-hand side has more free (red) variables than the left-hand side; these additional free variables will be integrated over. In addition, in order to obtain a useful bound we have to also take care of the time supremum over  : here it will be natural to assume that all yellow nodes are covered by the glueing procedure, and we call such a glueing onto. We capture this in the following notation.
: here it will be natural to assume that all yellow nodes are covered by the glueing procedure, and we call such a glueing onto. We capture this in the following notation.
Definition 3.7
Consider two compatible graphs \( \mathcal {G}^{(1)}, \mathcal {G}^{(2)} \in \mathcal {F}\) and  , together with a bijection
, together with a bijection  . If
. If

then we say that  defines an onto glueing of \( \mathcal {G}^{(2)} \) onto \( \mathcal {G}^{(1)} \). In particular, for
defines an onto glueing of \( \mathcal {G}^{(2)} \) onto \( \mathcal {G}^{(1)} \). In particular, for  it holds that
it holds that  .
.
Now the key result for our bounds is the following lemma. Here we introduce the temporal integration bound  .
.
Lemma 3.8
Consider two compatible \( \mathcal {G}^{(1)}, \mathcal {G}^{(2)} \in \mathcal {F}\) and an onto glueing  . Then for
. Then for  we have
we have

Remark 3.9
We observe that the temporal variables on which the valuation depends are inherited from the glued graph \( \mathcal {G}\), thus determining a pairing among variables of \( \mathcal {G}^{(1)} \) and \( \mathcal {G}^{(2)} \). This is captured by the map \( \mathfrak {e} \). We note in particular that  since the glueing is onto, as well as
since the glueing is onto, as well as  . In fact, we can write
. In fact, we can write  as the disjoint union
as the disjoint union

Remark 3.10
A special case is given by  in which case one has
in which case one has  and \(|{\mathcal {G}}| \le |{\mathcal {G}}^{(1)}|\cdot |{\mathcal {G}}^{(2)}|\).
and \(|{\mathcal {G}}| \le |{\mathcal {G}}^{(1)}|\cdot |{\mathcal {G}}^{(2)}|\).
Proof
Since by assumption  is onto, we have
is onto, we have  and thus
and thus

Note first that we can write

by the assumptions on the colouring of \( \mathcal {G}^{(1)}, \mathcal {G}^{(2)} \) (in particular, recall that  because we colour nodes black after glueing). As a consequence, we have
because we colour nodes black after glueing). As a consequence, we have

where we used that  and
and  do not intersect. It then follows from (3.12) that
do not intersect. It then follows from (3.12) that

Next, observe that  , and that from the definition of the kernel the time variables are ordered so that \( t_{v} \in [0, \mathfrak {t}] \) for any \( v \in \mathcal {V}\). In particular the previous estimate is bounded by
, and that from the definition of the kernel the time variables are ordered so that \( t_{v} \in [0, \mathfrak {t}] \) for any \( v \in \mathcal {V}\). In particular the previous estimate is bounded by

as required. \(\square \)
Running example. Finally, we can use Lemma 3.8 to conclude the estimates for (3.10). It is important to remark that in all cases of our interest the supremum over  in the valuation of \( \mathcal {G}^{(1)} \) will be superfluous, by an application of the semigroup property. This can be swiftly seen by proceeding in the calculation for our running example. Since no confusion can occur, we now write t instead of \(\mathfrak {t}\), observing that the latter does indeed coincide in our case of interest with the temporal variable of the only red node present in the original graph. By (3.14) and Lemma 3.8, we obtain
in the valuation of \( \mathcal {G}^{(1)} \) will be superfluous, by an application of the semigroup property. This can be swiftly seen by proceeding in the calculation for our running example. Since no confusion can occur, we now write t instead of \(\mathfrak {t}\), observing that the latter does indeed coincide in our case of interest with the temporal variable of the only red node present in the original graph. By (3.14) and Lemma 3.8, we obtain

Regarding the first factor, it follows from the semigroup property and the fact that we integrate over all yellow spatial variables that

for some \( c > 0 \). Hence, using Remark 3.10, we have

The second graph on the right-hand side of (3.10) can be bounded by \(B_\varepsilon (t)\) in an analogous way. We recall that every smaller tree is evaluated at the temporal variable it has inherited from the original large tree (so the last two trees have the same contribution, but they are evaluated at different time variables). We omit writing the dependence on such variables for convenience. We conclude that

Here, the number \(15=6+9\) is the total number of ways of pairing 6 green nodes. In addition, we observe that \( B_{\varepsilon }(t) \) can be rewritten, by a change of variables, as
where \( 4 = 2 (\ell (\tau ) -1) \), for the trees \( \tau \) that we took under consideration. We now claim that an analogous bound holds for every tree \(\tau \). More precisely, we have the following result.
Proposition 3.11
For every \(\tau \) in \(\mathcal {T}_3\) and \( q \in [2, \infty ) \),
and
where for each \(a>0\), \(\Gamma _a(t)=\int _0^t(s\vee 1)^{-a} \text { d}s\).
Remark 3.12
We observe that for \( t \geqslant \varepsilon ^{2}\) we have
which leads to the time scale \( t_{1}(\varepsilon )\) (in particular to the constraint \({\bar{\alpha }} < 1\)), since the estimates in Proposition 3.11 improve as \( \ell (\tau ) \) increases only for times \( t \leqslant t_{1}(\varepsilon ) \).
Proof
By hypercontractivity, it suffices to show (3.18) for \(q=2\) since each \(X^\tau _{\varepsilon }\) belongs to a finite Wiener chaos. Let \(\tau \) be a tree in \(\mathcal {T}_3\) and \({\bar{\tau }}\) be an identical copy of \(\tau \). Let \(\gamma \) be a way of pairing the leaves of \([\tau ,{\bar{\tau }}]\) such that each leaf is paired with exactly one other leaf. The coloured graph \([\tau ,{\bar{\tau }}]_\gamma \) is obtained by connecting the leaves of \([\tau ,{\bar{\tau }}]\) with green edges according to the pairing rule \(\gamma \) and connecting the two roots to a red node, so that

As usual, the value associated to the single red node is fixed to (t, x) and since no confusion can occur we write t instead of  . Hence, the estimate (3.18) for \(q=2\) is obtained once we show that for any pairing rule \(\gamma \),
. Hence, the estimate (3.18) for \(q=2\) is obtained once we show that for any pairing rule \(\gamma \),
where \( | \cdot | \) is the valuation introduced above. Let us write \( \mathcal {G}= ( \mathcal {V}, \mathcal {E}) \in \mathcal {F}\) for the compatible tree \( [ \tau , {\overline{\tau }}]_{\gamma } \).
To prove (3.20) we introduce an algorithm that allows us to iterate the type of bounds we described previously. We start by constructing a succession \( \{ p_{i} \}_{i=0}^{N-1} \) of self-avoiding paths \( p_{i} = (\mathcal {V}_{p_{i}}, \mathcal {E}_{p_{i}}) \subseteq (\mathcal {V}, \mathcal {E})\) that cover the entire tree \( \mathcal {G}\).
By self-avoiding path we mean a path with endpoints \({p_{-}}, {p_{+}} \in \mathcal {V}\) (with possibly \({p_{-}} ={p_{+}} \)) such that all points, apart from possibly \({p_{-}}, {p_{+}}\) appear exactly once in an edge (in particular, all edges are distinct). In addition we ask that the endpoints are minimal points with respect to the ordering inherited by the forest structure of \( \mathcal {G}\).
The paths \( \{ p_{i} \}_{i = 0}^{N-1} \) will cover the entire tree \( \mathcal {G}\) in the sense that we will iteratively define compatible graphs \( \mathcal {G}^{(i)} \in \mathcal {F}_{3} \) for \( i \in \{ 0, \dots , N \} \) by onto glueings, satisfying

In particular it is useful to note that we obtain the following chain of embeddings

where each \( \mathfrak {e}_{i} \) is the map of Definition 3.2. Thus we obtain an overall map
defined by composing \( \mathfrak {e} = \mathfrak {e}_{0} \circ \cdots \circ \mathfrak {e}_{i} \) on \( p_{i} \). The way the paths \( p_{i} \) are chosen is described by the following procedure, starting from the graph \( \mathcal {G}^{(0)}= \mathcal {G}\) introduced above.
-
1.
Construction of the path. Assume that for some \( i \in \textbf{N}\cup \{ 0 \} \) we are given a compatible graph \( \mathcal {G}^{(i)} = (\mathcal {V}^{(i)}, \mathcal {E}^{(i)}) \in \mathcal {F}_{3}\), with
 for all \( v \in \mathcal {V}^{(i)} \) (note that this is the case for \( \mathcal {G}^{(0)} \), since we have one red root and no node is coloured yellow). We define \( p_{i} \) by choosing as a starting point any \( v \in \mathcal {V}^{(i)} \) such that
for all \( v \in \mathcal {V}^{(i)} \) (note that this is the case for \( \mathcal {G}^{(0)} \), since we have one red root and no node is coloured yellow). We define \( p_{i} \) by choosing as a starting point any \( v \in \mathcal {V}^{(i)} \) such that  , namely any root of \( \mathcal {G}^{(i)}\).
, namely any root of \( \mathcal {G}^{(i)}\).By assumption, since \( \mathcal {G}^{(i)} \) is an element of \( \mathcal {F}_{3} \), we can follow a path up through any one of the two maximal trees rooted at v and let us call the sub-tree we choose \( \tau (v) \). Then, because of oddity, we can choose to arrive at a leaf such that the pairing \( \gamma \) leads to another leaf, belonging to some \( {\overline{\tau }}(v) \ne \tau (v) \). We then continue the path by descending the maximal subtree this leaf belongs to, until we reach its red root (this may be again v, since v can be the root of up to two trees). We colour all the nodes of \( p_{i} \) yellow, apart from its endpoints and leaves, which are left red and black respectively.
-
2.
Removal. We then define the compatible graph \( \mathcal {G}^{(i+1)} = (\mathcal {V}^{(i+1)}, \mathcal {E}^{(i)} {\setminus } \mathcal {E}_{p_{i}}) \in \mathcal {F}\) with the colourings inherited by \( \mathcal {G}^{(i)} \). Here \( \mathcal {V}^{(i+1)} \) is obtained from \( \mathcal {V}^{(i)} \) by removing all singletons (meaning the two leafs connected by the only green edge \( p_{i} \) has crossed and possibly the endpoints of \( p_{i} \), if any of them was the root of just one tree, or \( p_{i} \) was a cycle). We finally colour
 for \( v \in \mathcal {V}^{(i+1)} \cap \mathcal {V}_{p_{i}} \). In particular (3.11) still holds true for \( \mathcal {G}^{(i+1)} \), so that \( \mathcal {G}^{(i+1)} \) lies in \( \mathcal {F}_{3} \). Moreover, we obtain that \( \mathcal {G}^{(i)} \) is the onto glueing of \( \mathcal {G}^{(i+1)} \) onto \( p_{i} \)
for \( v \in \mathcal {V}^{(i+1)} \cap \mathcal {V}_{p_{i}} \). In particular (3.11) still holds true for \( \mathcal {G}^{(i+1)} \), so that \( \mathcal {G}^{(i+1)} \) lies in \( \mathcal {F}_{3} \). Moreover, we obtain that \( \mathcal {G}^{(i)} \) is the onto glueing of \( \mathcal {G}^{(i+1)} \) onto \( p_{i} \)
with the map
 defined by inverting the removal we just described.
defined by inverting the removal we just described. -
3.
Conclusion. We can now repeat steps 1 and 2 for N times until \( \mathcal {G}^{(N)} = \emptyset \) (if not, there must still be a red root available and we can still follow the previous algorithm). Since at every step we are removing exactly one green edge, we see that this algorithm terminates in \( N = \ell (\tau ) \) steps.
We are left with a collection of N paths \( \{ p_{i} \}_{i = 0}^{\ell (\tau ) -1} \) such that
-
1.
\( \mathcal {E}\) is the disjoint union \( \mathcal {E}= \bigsqcup _{i =1}^{\ell (\tau )-1} \mathcal {E}_{p_{i}} \).
-
2.
Every \( v \in \mathcal {V}\) which is not a leaf appears in exactly thee paths, twice as a root (coloured red) and once as an inner node (coloured yellow). Instead, every leaf appears in exactly one path, coloured black.
We observe that by the semigroup property, every path \( p_{i} \) yields a contribution

where \( \mathfrak {s}_{\varepsilon } \) is defined in (3.16). To conclude, we may now use Lemma 3.8 to obtain

where the map \( \mathfrak {e} \) is defined in (3.21). And similarly, for \( i \in \{ 1, \dots , N-1 \} \), using the definition of the map \( \mathfrak {e} \), we find

so that overall

where  is the set of inner nodes that are not leaves, in view of the considerations above. Since in addition by our observations every node in \( {\overline{\mathcal {I}}} \) appears exactly twice as a root of some path (either a cycle or two different paths), by (3.22) we finally obtain
is the set of inner nodes that are not leaves, in view of the considerations above. Since in addition by our observations every node in \( {\overline{\mathcal {I}}} \) appears exactly twice as a root of some path (either a cycle or two different paths), by (3.22) we finally obtain
which is (3.20). Here we have used that \( | {\overline{\mathcal {I}}} | = 2 i (\tau ) \) since we have two copies of the same tree, and \( 2i(\tau ) = \ell (\tau ) -1 \).
As for (3.19), we can follow the same argument as above, to write:
where \( \nabla \tau \) indicates the same convolution integral associated to the tree \(\tau \) as above, only with the kernel \( - e^{t} \nabla p_{t}(x) \) used in the edge connecting to the root. Graphically, if \( \tau \) is built starting from the trees \( \tau _{1}, \tau _{2}, \tau _{3} \) we have

where the dotted line indicates convolution against the kernel \( - e^{t} \nabla p_{t}(x)\). In particular, we can decompose the graph \( [ \nabla \tau , \nabla {\overline{\tau }}]_{\gamma } \) into the same set of paths \( \{ p_{i} \}_{i =0}^{N-1} \) as for \( [\tau , {\overline{\tau }}]_{\gamma } \). The only difference is that now the path \( p_{0} \) contains two dotted lines coming into the root: all other paths remain unchanged. By the semigroup property the contribution of the path \( p_{0} \) is the same as that of

Hence, using the bound (for some \( c > 0 \))
we find that the contribution of \( p_{0} \) is bounded from above by
which together with the previous calculations yields (3.19). \(\square \)
We can extend the previous result to longer timescales as follows.
Proposition 3.13
For every \( q \in [2, \infty ) \), \(\tau \) in \(\mathcal {T}_3\) and every \(t>t_1(\varepsilon )\), the following estimates hold true
Proof
By hypercontractivity it suffices to prove the result for \( q =2 \). We can change the graphical notation we introduced previously by adding blue inner nodes  associated to a time \( t_{1}>0 \) to indicate integration against the measure \( - \delta _{t_{1}}(s) \text { d}s \text { d}y \): once more, the minus sign is a matter of convention. It is natural though since our lines represent integration against \( - P^{1} \) as a consequence of the minus sign appearing in (3.4). With this notation we have
associated to a time \( t_{1}>0 \) to indicate integration against the measure \( - \delta _{t_{1}}(s) \text { d}s \text { d}y \): once more, the minus sign is a matter of convention. It is natural though since our lines represent integration against \( - P^{1} \) as a consequence of the minus sign appearing in (3.4). With this notation we have

for \( \tau = [\tau _{1}, \tau _{2}, \tau _{3}]. \) For convenience we denote by \( P_{t - t_{1}}^1 \tau _{t_{1}} \) the trees obtained in this manner. Now we can follow the proof of Proposition 3.11 to write
where \( {\overline{\tau }} \) is an identical copy of \( \tau \). The possible paring rules \( \gamma \) for the tree \( P_{t - t_{1}}^{1} \tau _{t_{1}} \) (with an identical copy of itself) are the same as for the tree \( \tau \) (since we only added a node to the edge entering the root), and also the set of paths \( \{ p_{i} \}_{i=0}^{N-1} \) in which the tree is decomposed remains unchanged, up to adding the two nodes corresponding to \( t_{1} \) to the path \( p_{0} \). By the semigroup property, the contribution of the path \( p_{0} \) is then given by
while the contribution of all other paths remains unchanged, with the additional constraint that all temporal variables (apart from the red root) are constrained to the interval \( [0, t_{1}] \).
Hence, following the calculations of the proof of Proposition 3.11 we can bound
This completes the proof of (3.23). For (3.24) one can follow the same arguments in combination with the estimates in the proof of Proposition 3.11. \(\square \)
Next we can compare the Wild expansion and the original solution via a comparison principle.
Lemma 3.14
For every \(\varepsilon \in (0, 1), N\ge 1\) and \((t,x)\in {{\textbf {R}}}_+\times {{\textbf {R}}}^d\), let \( u^{N}_{\varepsilon } \) and \( R^{N} \) be as in (3.6), (3.7). Then
Proof
From (1.2) and (3.6), it follows that the remainder \(v_\varepsilon =u_\varepsilon -u^N_\varepsilon \) satisfies the following equation
The estimate (3.25) is a direct consequence of Lemma 3.1 and the fact that \(v_\varepsilon ^2+3u^N_\varepsilon v_\varepsilon +3(u^N_\varepsilon )^2 \) is non-negative. \(\square \)
Eventually, if we combine all the results we have obtained so far, we obtain an estimate on the distance of the Wild expansion from the original solution until times of order \( (1 - \alpha ) \log {\varepsilon ^{-1}}.\)
Proposition 3.15
For every \(t\le (1- \alpha )\log \varepsilon ^{-1}\), \( q \in [2, \infty ) \) and \( N \in \textbf{N}\)
and
In addition, for every \(c>1\), uniformly over \(t_1(\varepsilon )<t< c\log \varepsilon ^{-1}\)
Proof
From the definition of \(R^N_\varepsilon \) and the moment estimate in Proposition 3.11, we see that for every \(q\ge 2\),
where the sum is taken over all trees \(\tau _1,\tau _2,\tau _3\) in \(\mathcal {T}_3^N\) such that \(\tau =[\tau _1,\tau _2,\tau _3]\notin \mathcal {T}_3^N\). Since \(\ell (\tau )=\ell (\tau _1)+\ell (\tau _2)+\ell (\tau _3)\in [N+2,3N]\) and t satisfies \(e^t \varepsilon ^{1- \alpha }\le 1\), each term in the above sum is at most \((e^t \varepsilon ^{1- \alpha })^{N-1}\Gamma _{d/2}(t \varepsilon ^{-2})^{\frac{3}{2}(N-1)}\). This yields
which, when combined with Lemma 3.14 gives
To derive (3.27), we observe that \(\int _0^t(s\vee \varepsilon ^2)^{-\frac{3d}{4}} \text { d}s\lesssim \varepsilon ^{2-\frac{3d}{2}}\) for \(d\ge 2\). The estimate (3.28) is a direct consequence of (3.27) and Proposition 3.11.
Let us now show (3.29). By the triangle inequality, we have
The first term is estimated using (3.27),
Writing the second term as \(\sum _{\tau \in \mathcal {T}^N_3} P^1_{t-t_1}X^\tau _{\varepsilon }(t_1,x)\) and applying Proposition 3.13, we obtain
In the previous estimate, we have used the fact that \(e^{t_1}\varepsilon ^{1- \alpha }\Gamma _{d/2}^{1/2}(t_1 \varepsilon ^{-2})\le 1 \) for sufficiently small \(\varepsilon \). Combining these estimates yields
for every \(t\ge t_1\). By choosing N sufficiently large, the previous inequality implies (3.29). \(\square \)
4 Front formation
4.1 Tightness criteria
In this subsection we recall a tightness criterion that is useful in the upcoming discussion. Observe that a subset \(\mathcal {F}\) of \(C_\text {loc}({{\textbf {R}}}^d)\) is compact if and only if for every compact set \(K\subset {{\textbf {R}}}^d\), the projection \(\mathcal {F}_K\) of \(\mathcal {F}\) onto C(K) is compact. In particular the following is a consequence of the Arzelà–Ascoli theorem and of the Morrey–Sobolev inequality.
Lemma 4.1
Let \(\{X_\varepsilon \}_{\varepsilon \in (0, 1)}\) be a family of stochastic processes with sample paths in \(C_\text {loc}({{\textbf {R}}}^d)\). Suppose that for every integer \(n\ge 1\), there exists \(q>d\) such that
Then the family of the laws of \(X_\varepsilon \) on \(C_\text {loc}({{\textbf {R}}}^d)\) is tight. In addition, if for every \(n\ge 1\), there exists a \(q>d\) such that
then \(X_\varepsilon \) converges to 0 in probability with respect to the topology of \(C_\text {loc}({{\textbf {R}}}^d)\).
In particular, we deduce the following criterion.
Lemma 4.2
Let \(\{g_\varepsilon \}_{\varepsilon \in (0, 1)}\) be a family of random fields on \({{\textbf {R}}}^d\). Let \(t(\varepsilon )\) and \(L(\varepsilon )\) be positive numbers such that \( \lim _{\varepsilon \rightarrow 0}t(\varepsilon )=\infty \). Assume that there exists a \(q>d+1\) such that
Then the family \(\{P^1_{t(\varepsilon )+t}g_\varepsilon (L(\varepsilon )x):(t,x)\in {{\textbf {R}}}\times {{\textbf {R}}}^d \}_\varepsilon \) is tight on \({C_\text {loc}({{\textbf {R}}}\times {{\textbf {R}}}^d)}\). In addition, if
then \(\{P^1_{t(\varepsilon )+t}g_\varepsilon (L(\varepsilon )x):(t,x)\in {{\textbf {R}}}\times {{\textbf {R}}}^d \}\) converges in probability to 0 in \({C_\text {loc}({{\textbf {R}}}\times {{\textbf {R}}}^d)}\).
Proof
This is a consequence of the following estimates:
in conjunction with Lemma 4.1. \(\square \)
4.2 Weak convergence
Now recall \( t_{2}(\varepsilon ) \) from (3.1) and define
Then we can use the tightness criteria above to describe the behaviour of \( u_{\varepsilon } \) up to times of order \( t_{2}^{\kappa }(\varepsilon ) \).
Lemma 4.3
For every \(N>d/(2-2{\bar{\alpha }})-1\) and every \(\kappa \ge 0\) the process
converges to 0 in probability on \({C_\text {loc}({{\textbf {R}}}\times {{\textbf {R}}}^d)}\).
Proof
For each \(t\ge t_1\), we define
Since \(h_\varepsilon (t,x) {\mathop {=}\limits ^{{\tiny \mathrm def}}}P^1_{t-t_1}u^N_\varepsilon (t_1,x)\) solves \((\partial _t- \Delta -1)h=0\) with initial condition (at time \(t_1\)) \(h(t_1,x)=u^N_\varepsilon (t_1,x)\), the difference \(S^N_\varepsilon =u_\varepsilon -h_\varepsilon \) satisfies
with initial condition \(S^N_\varepsilon (t_1,x)=u_\varepsilon (t_1,x)-u^N_\varepsilon (t_1,x) \). An application of Lemma 3.1 gives
Let \(q>d+1\) be fixed. Applying Proposition 3.15, we have
and hence
From the definitions it is evident that
We observe that at this point we used that \( t_{2}(\varepsilon ) \) contains an additional negative term \( - \frac{1}{2} \log {\log {\varepsilon ^{-1}}} \), at least in dimension \( d =2 \), to obtain an upper bound that vanishes as \( \varepsilon \rightarrow 0 \). As for the second term, we have
which also vanishes as \(\varepsilon \rightarrow 0\) by our choice of N. It follows that
Applying the second part of Lemma 4.2, the above estimates imply that the process \((t,x)\mapsto P^1_{t_\star ^\kappa -t_2^\kappa +t}S^N_\varepsilon (t_2^\kappa ,L_\varepsilon x)\) converges to 0 in probability in \(C_\text {loc}({{\textbf {R}}}\times {{\textbf {R}}}^d)\). \(\square \)
Next, we observe that the truncated Wild expansion converges to the Bargmann–Fock field around time \( t_{\star } (\varepsilon ) \).
Lemma 4.4
For every \(\kappa \ge 0\), as \(\varepsilon \rightarrow 0\), we have:
-
(i)
The process \(\{e^{-\kappa \log \log \varepsilon ^{-1}} P^1_{t_\star ^\kappa -t_1+t}X^\bullet _{\varepsilon }(t_1,L_\varepsilon x):(t,x)\in {{\textbf {R}}}\times {{\textbf {R}}}^d \}\) converges in law in \(C_{\text {loc}}({{\textbf {R}}}\times {{\textbf {R}}}^d)\) to \(\{e^t \Psi (x):(t,x)\in {{\textbf {R}}}\times {{\textbf {R}}}^d \} \) with \( \Psi \) as in (1.3).
-
(ii)
For each \(\tau \in \mathcal {T}_3\setminus \{\bullet \}\), the process \(\{e^{-\kappa \log \log \varepsilon ^{-1}}P^1_{t_\star ^\kappa -t_1+t}X^\tau _{\varepsilon }(t_1,L_\varepsilon x):(t,x)\in {{\textbf {R}}}\times {{\textbf {R}}}^d \}\) converges in probability to 0 in \(C_{\text {loc}}({{\textbf {R}}}\times {{\textbf {R}}}^d)\).
Proof
We first show that the family \(\{e^{-\kappa \log \log \varepsilon ^{-1}}P^1_{t_\star ^\kappa -t_1+t}X^\tau _{\varepsilon }(t_1,L_\varepsilon x):(t,x)\in {{\textbf {R}}}\times {{\textbf {R}}}^d \}_\varepsilon \) is tight in \({C_\text {loc}({{\textbf {R}}}\times {{\textbf {R}}}^d)}\) for every \(\tau \in \mathcal {T}_3\). Hence, let us fix \(q>d+1\). From Proposition 3.15, we have
In addition, we observe that
so that an application of Lemma 4.2 implies tightness for the sequence.
Let us now prove the first point. By construction, the process
is a centered Gaussian random field with covariance
Now, it is straightforward to verify that
with \( \mathfrak {c} \) as in (1.4) and
so that (i) is verified.
As for the second point, let \(\tau \in \mathcal {T}_3\setminus \{\bullet \}\) and q be fixed such that \(q>d+1\). From Proposition 3.13, we have
Since \({\bar{\alpha }}<1\) and \(\ell (\tau )>1\), the right-hand side above vanishes as \(\varepsilon \rightarrow 0\). By Lemma 4.2, this implies (ii). \(\square \)
Remark 4.5
It is possible to show that the process \(\{P^1_{t_\star -t_1+t}u_\varepsilon (t_1,L_\varepsilon x):(t,x)\in {{\textbf {R}}}\times {{\textbf {R}}}^d \}\) converges in law to \(\{e^t \Psi (x):( t,x)\in {{\textbf {R}}}\times {{\textbf {R}}}^d \} \) in \(C_{\text {loc}}({{\textbf {R}}}\times {{\textbf {R}}}^d)\). However, this fact is not needed in what follows, so its proof is omitted.
In the upcoming result we will work with the flow \( {\overline{\Phi }}(t,u) \) given by
which solves (1.5) with initial condition \( {\overline{\Phi }}(0, u) = u \) (the feature that distinguishes \( \Phi \) from \( {\overline{\Phi }} \) is the initial condition). With this definition we have for \( t > 0 \)
To obtain the last bound we observe that
Then for \( |u| \leqslant e^{- t} \) we have \(| \partial _{u}^{2} {\overline{\Phi }}(t, u)| \lesssim e^{2t} -1 \lesssim e^{2 t},\) since in the denominator \(1 + u^{2}(e^{2 t} -1) \geqslant 1\). Instead for \( |u| > e^{-t} \) the leading term in the denominator is \( u^{2}e^{2 t},\) so we find
Next, let us define for every \(t>t_2^\kappa \)
When \(\kappa =0\), we simply write \(w^{N}_{\varepsilon }\) for \(w^{N,0}_{\varepsilon }\). Now we can prove the main result of this section, which states that \( w^{N, \kappa }_{\varepsilon } \) is a good approximation of \( u_{\varepsilon } \) in a time window of order one about time \(t_{\star }^{\kappa }(\varepsilon )\), and at spatial scales of order \(L_{\varepsilon }\).
Proposition 4.6
For every \(\kappa \in [0,\frac{1}{4})\), the process
converges to 0 in probability in \({C_\text {loc}({{\textbf {R}}}\times {{\textbf {R}}}^d)}\) as \(\varepsilon \rightarrow 0\).
Proof
From its definition, we see that \(w^{N,\kappa }_\varepsilon \) satisfies for \( t > t_{2}^{\kappa }(\varepsilon ) \)
where
It follows that the difference \(v^N_\varepsilon =w^{N,\kappa }_\varepsilon -u_\varepsilon \) satisfies the equation
with initial condition at \(t_2^\kappa \) given by \(v^N_\varepsilon (t_2^\kappa ,\cdot )=P^1_{t_2^\kappa -t_1}u^N_\varepsilon (t_1,\cdot )-u_\varepsilon (t_2^\kappa ,\cdot )\). Applying Lemma 3.1, we see that
for every \((t,x)\in [t_2^\kappa ,\infty )\times {{\textbf {R}}}^d\). By Lemma 4.3, the process
converges to 0 in probability in \({C_\text {loc}({{\textbf {R}}}\times {{\textbf {R}}}^d)}\). We also note that in view of (4.3), \(|f^N_\varepsilon (t,x)|\lesssim |\nabla P^1_{t-t_1}u^N_\varepsilon (t_1,x)|^2\). Hence it remains to show that the process
converges to 0 in probability in \({C_\text {loc}({{\textbf {R}}}\times {{\textbf {R}}}^d)}\).
For every \(z_1=(\sigma _1,x_1),z_1=(\sigma _2,x_2)\) in \({{\textbf {R}}}\times {{\textbf {R}}}^d\), define the distance \(d(z_1,z_2)=|\sigma _1- \sigma _2|^{\frac{1}{2}}+|z_1-z_2|\). Let K be a compact set in \({{\textbf {R}}}^{d+1}\) and \(q=d+2\). It suffices to show that
In fact, by the Morrey–Sobolev inequality, the above estimate implies that \(\sup _{z\in K}|H_\varepsilon (z)|\) has vanishing q-th moment as \(\varepsilon \rightarrow 0\), which in turn, implies the convergence of \(H_\varepsilon \) to 0 in \(C_\text {loc}({{\textbf {R}}}\times {{\textbf {R}}}^d)\) in probability. From Proposition 3.13, we have
which implies that
for every \(s\in (t_2^\kappa ,t_\star ^\kappa +{{\,\textrm{dist}\,}}(0,K))\). It follows that for every \(z=(\sigma ,x)\) in K
From the definitions of \(t_2\) and \(t_\star \), the right-hand side above vanishes as \(\varepsilon \rightarrow 0\).
For every \(z_1=(\sigma _1,x_1),z_2=(\sigma _2,x_2)\in K\), we now estimate the increment \(H_\varepsilon (z_2)-H_\varepsilon (z_1) \). The increment in the spatial variables \(\Vert H_\varepsilon (\sigma _1,x_1)-H_\varepsilon (\sigma _1,x_2)\Vert _q\) can be estimated uniformly by a constant multiple of
Taking into account the fact that \(L_\varepsilon \Vert \nabla p^1_{t_\star +\sigma _1-s}\Vert _{L^1({{\textbf {R}}}^d)}\lesssim L_\varepsilon (t_\star +\sigma _1-s)^{-\frac{1}{2}} e^{t_\star -s} \) uniformly for every \(z_1\in K\), this gives the estimate
Simplifying the integration on the right-hand side, using the estimate (4.5), we obtain
To estimate the increment in the time variables, we assume without lost of generality that \(\sigma _1<\sigma _2\) and write
The first term is estimated easily
For the second term, we use the elementary estimates
and
to obtain
Using the estimate (4.5), it is straightforward to verify that
Combining these estimates yields
Since \(\kappa <\frac{1}{4}\), the right-hand side above vanishes as \(\varepsilon \rightarrow 0\), which implies (4.4) and completes the proof. \(\square \)
5 Front propagation
In this section we prove Proposition 2.2 regarding the formation of the initial front and Theorem 2.3 regarding its evolution via mean curvature flow. We start by recalling an a-priori bound on solutions to the Allen–Cahn equation.
Lemma 5.1
For every \( u_{0} \in C_{\textrm{loc}}(\textbf{R}^{d}) \) satisfying \( \sup _{x \in \textbf{R}^{d}} | u_{0}(x) e^{- |x|} | < \infty \), let u be the solution to the Allen–Cahn equation (1.2) with initial condition \( u_{0} \). Then
Proof
We observe that with the definition of \( {\overline{\Phi }} \) as in (4.2) we have \( \Xi (t) = e^{t}/ \sqrt{e^{2t} -1} = \lim _{u \rightarrow \infty } {\overline{\Phi }} (t, u)\), so that \( \Xi (t) \) is a space-independent solution to the Allen–Cahn equation on \( (0, \infty ) \). By comparison, since \( \lim _{t \rightarrow 0} \Xi (t) = \infty \), and approximating \( u_{0} \) with uniformly bounded initial conditions, we obtain \( u(t) \leqslant \Xi (t) \) for all \( t > 0 \). Similarly one derives the upper bound. The growth condition on \( u_{0} \) is used to justify the approximation procedure, as well as the well-posedness of the heat flow started in \( u_{0} \). \(\square \)
Since our results are concerned with convergence in law of the process \( u_{\varepsilon } \), the choice of underlying probability space is not relevant. In the next lemma we build a probability space on which our family of processes converges in probability. We note that the Skorokhod representation theorem is usually stated for discrete families of random variables, rather than continuous ones hence, for completeness, we include a proof of our statement.
Lemma 5.2
There exists a probability space \( (\Omega , \mathcal {F}, \textbf{P}) \) supporting a sequence of processes \( \{u_{\varepsilon }(t,x) \ :\ (t,x) \in [t_{\star }(\varepsilon ), \infty ) \times \textbf{R}^{d} \} \) with the same law as the solutions to (1.2), and a Gaussian process \( \{ \Psi (x) \ :\ x \in \textbf{R}^{d} \} \) satisfying (1.3), such that \( \{ u_{\varepsilon }(t_{\star }(\varepsilon ), x L_{\varepsilon }) \ :\ x \in \textbf{R}^{d} \} \) converges, as \( \varepsilon \rightarrow 0 \), to \( \{ \Phi (0, \Psi (x)) \ :\ x \in \textbf{R}^{d} \} \) in probability in \( C_{\textrm{loc}}(\textbf{R}^{d})\).
Proof
Let us consider a probability space \( (\Omega , \mathcal {F}, \textbf{P}) \) supporting a white noise \( \eta \) on \( \textbf{R}^{d} \). Then define, for \( \varepsilon \in (0, 1) \), the random fields \( x \mapsto X_{\varepsilon }^{\bullet }(t_\star (\varepsilon ), x L_{\varepsilon }) \) by
Here \( \varphi ^{\varepsilon } \) is as in (1.1), \( \mathfrak {c} \) as in (1.4) and we observe that in so far \( x \mapsto X_{\varepsilon }^{\bullet } (t_{\star }(\varepsilon ), x L_{\varepsilon }) \) is a time-independent Gaussian process constructed to have the same law as the solution to (3.3) at time \( t_{\star }(\varepsilon ) \). From the definition of \( t_{\star }(\varepsilon ) \) we obtain the convergence of \( K_{\varepsilon }(x) \rightarrow K(x) \), with
from which we obtain that \( X_{\varepsilon }^{\bullet } (t_{\star }(\varepsilon ), x L_{\varepsilon }) \rightarrow \Psi (x) \) uniformly over x, almost surely (with \( \Psi \) having the required covariance structure), as \( \varepsilon \rightarrow 0 \). In addition, starting from the process \( X_{\varepsilon }^{\bullet } (t_{\star }(\varepsilon ), \cdot ) \) we can construct a sequence of noises \( \eta _{\varepsilon } \) with the same law as (but not identical to) the initial conditions \( \varepsilon ^{\frac{d}{2} - \alpha } \eta * \varphi ^{\varepsilon } \) appearing in (1.2), and such that \( X_{\varepsilon }^{\bullet }(t_{\star }(\varepsilon ), x) = P^{1}_{t_{\star }(\varepsilon )} \eta _{\varepsilon } \).
Now we can follow step by step the proof of Theorem 2.1, to find that if we consider \( u_{\varepsilon } \) the solution to (1.2) with the initial condition \( \eta _{\varepsilon } \) we just constructed, then \( u_{\varepsilon }(t_{\star }(\varepsilon ), x L_{\varepsilon }) \rightarrow \Phi (0, \Psi (x)) \) in probability in \( C_{\textrm{loc}}(\textbf{R}^{d}) \) as \( \varepsilon \rightarrow 0 \). \(\square \)
The next lemma establishes the formation of the fronts by time \( t_{\star }^{\kappa }(\varepsilon ) \) for some \( \kappa \in (0, \frac{1}{2}]\). We write \(C^{k}_{b}(\textbf{R}^{d}; \textbf{R})\) for the space of k times differentiable functions with all derivatives continuous and bounded. Recall further that
We then define the random nodal set
and recall the definition of \( K^{1}_{\delta } \) from (2.1). The proof of the following lemma and of the subsequent proposition follow roughly the approach of [4, Theorem 4.1].
Lemma 5.3
Consider \( (\Omega , \mathcal {F}, \textbf{P}) \) as in Lemma 5.2. For any \( 0 < \kappa \leqslant \frac{1}{2} \) and any sequence \( \{t(\varepsilon )\}_{\varepsilon \in (0, 1)} \) with \( t(\varepsilon ) \geqslant t_{\star }(\varepsilon ) \) such that
it holds that for all \( \delta , \zeta \in (0, 1) \)
Proof
Suppose that along a subsequence \( \{ \varepsilon _{n} \}_{n \in \textbf{N}} \), with \( \varepsilon _{n} \in (0, 1), \lim _{n \rightarrow \infty } \varepsilon _{n} =0 \), it holds that for some \( \delta , \zeta , \zeta ^{\prime } \in (0, 1) \)
By our choice of probability space, up to further refining the subsequence, we can assume that \( u_{\varepsilon _{n}}(t_{\star } (\varepsilon _{n}), \cdot L_{\varepsilon _{n}}) \rightarrow \Phi (0, \Psi (\cdot )) \) almost surely in \( C_{\textrm{loc}}(\textbf{R}^{d}) \). We will then show that our assumption is absurd, by proving that almost surely
In particular, it will suffice to show that for any \( x_{0} \in \Gamma _{1}^{c} \) there exist (random) \( \lambda (x_{0}), \varrho (x_{0}), \varepsilon (x_{0}) > 0 \) such that for all \( \varepsilon _{n} \in (0, \varepsilon (x_{0})) \):
For the sake of clarity, let us refrain from writing the subindex n and fix \( x_{0} \) such that \( \Psi (x_{0}) > 0 \) (the opposite case follows analogously). For the upper bound we use Lemma 5.1 to find for some \( \lambda > 0 \)
To establish the lower bound, consider for any constant \( K >0 \) and any \( \psi \in C^{2}_{b}\) the following function (here \( {\overline{\Phi }} \) is as in (4.2)),
We see that, since \( \partial _{u} {\overline{\Phi }} \geqslant 0 \)
Now we observe that for \( t > 0 \), similarly to (4.3) distinguishing the cases \( |u| \leqslant e^{- t} \) and \( |u| \geqslant e^{- t}\), we can bound
Hence there exists a \( K (\psi ) > 0 \) such that \( v_{\varepsilon } \) is a subsolution to \( \partial _{t} u = L_{\varepsilon }^{-2} \Delta u + u(1 - u^{2}) \) on the time interval \( [0, t(\varepsilon )- t_{\star }(\varepsilon ) ] \) with initial condition \( \psi \). Here we use that \( \limsup _{\varepsilon \rightarrow 0} \{t(\varepsilon )- t^{\frac{1}{2}}_{\star }(\varepsilon ) \} \leqslant 0\), so that for a constant \( C>0 \) independent of \( \varepsilon \) we have \( \exp ( t(\varepsilon )- t_{\star }(\varepsilon )) \leqslant C L_{\varepsilon } \). In particular, by our assumptions and by the upper bound of (5.1), we can choose \( \psi \in C^{2}_{b} \) so that \( \psi (x) >0 \) for x in a closed ball \( {\overline{B}}_{\varrho }(x_{0}) \) about \( x_{0} \) and such that for some \( \varepsilon (\psi ) >0 \)
Now, using that \( u =1 \) is an exponentially stable fixed point for \( {\overline{\Phi }} \), we have that for every \( u > 0 \) there exists a \( \lambda (u) \) that can be chosen locally uniformly over u, such that
for all \( \varepsilon \) sufficiently small, and for \( C>0 \) such that \( t (\varepsilon ) \geqslant t^{\kappa }_{\star }(\varepsilon ) - C\) for all \( \varepsilon \). Then by comparison, using that \( \frac{t (\varepsilon ) - t_{\star }(\varepsilon )}{L_{\varepsilon }} \lesssim \frac{\log {L_{\varepsilon }}}{L_{\varepsilon }} \rightarrow 0 \), for \( \varepsilon \) sufficiently small:
This completes the proof of (5.1) and of the lemma. \(\square \)
The following proposition treats slightly longer time scales. Recall the definition of \( K_{\delta }^{1} \) given in (2.1), for \( \delta \in (0, 1) \).
Proposition 5.4
Consider \( (\Omega , \mathcal {F}, \textbf{P}) \) as in Lemma 5.2 and fix any sequence \( \{ t (\varepsilon ) \}_{\varepsilon \in (0,1)} \), with \( t(\varepsilon ) \geqslant t_\star (\varepsilon ) \), and such that
Then for any \( \delta , \zeta \in (0, 1) \)
Proof
As in the proof of the previous lemma, it suffices to prove that for any subsequence \( \{ \varepsilon _{n} \}_{n \in \textbf{N}}\) with \( \varepsilon _{n} \in (0, 1), \lim _{n \rightarrow \infty } \varepsilon _{n} = 0 \) for which almost surely
it holds that for all \( \delta \in (0, 1) \)
Hence we will work with a fixed realization of all random variables and for the sake of clarity we will refrain from writing the subindex n. In addition, since the case \( \Psi < 0 \) is identical to the case \( \Psi >0 \), let us choose an \( x_{0} \in \textbf{R}^{d}\) such that \( \Psi (x_{0}) > 0 \) and define \( s(\varepsilon ) = t(\varepsilon ) - t_{\star }^{\frac{1}{2}} (\varepsilon ) \). We can also assume that \( s(\varepsilon ) \geqslant 0 \) for all \( \varepsilon \). Our aim is to prove the convergence \(\lim _{\varepsilon \rightarrow 0} u_{\varepsilon }(t_{\star }^{\frac{1}{2} }(\varepsilon ) + s(\varepsilon ),x L_{\varepsilon } ) =1 \) holds true for all x in a ball \( B_{\varrho }(x_{0}) \) about \( x_{0} \) of radius \( \varrho >0 \).
By Lemma 5.3 we already know that there exist \( {\overline{\lambda }} (x_{0}), \varrho (x_{0}) >0\) and \(\varepsilon (x_{0}) \in (0, 1) \) such that:
Here the second bound is a consequence of Lemma 5.1 (in fact in the second statement \( {\overline{\lambda }} \) can be chosen deterministic and independent of \( x_{0} \)). Our aim is to show that this front does not move after an additional time \( s(\varepsilon ) \). Let us define \( {\widetilde{u}}_{\varepsilon }(\sigma , x) = u_{\varepsilon }(t_{\star }^{\frac{1}{2}}(\varepsilon ) + \sigma s(\varepsilon ), x L_{\varepsilon } ) \), which solves
with an initial condition \( {\widetilde{u}}_{\varepsilon , 0}(x) = u_{\varepsilon }(t^{\frac{1}{2}}_{\star }(\varepsilon ), x L_{\varepsilon }). \) Our purpose is to construct an explicit subsolution \( {\underline{u}}_{\varepsilon } \) to (5.3) with initial condition “close” to \( 1_{B_{\frac{\varrho }{2}}(x_{0})} \), such that \( \lim _{\varepsilon \rightarrow 0} {\underline{u}}_{\varepsilon }(1, x) = 1\) for all x in a neighbourhood of \( x_{0} \). Our ansatz is that close to the interface the subsolution is of the following form, for \( \zeta (\varepsilon ) = \frac{s(\varepsilon )}{L_{\varepsilon }^{2}} \):
Here \( d(\sigma , x) \) is the signed distance function associated to the mean curvature flow evolution at time \( \sigma \geqslant 0 \) of the ball \( B_{\frac{\varrho }{2}}(x_{0}) \) with the sign convention \( d(0, x)> 0 \) if \( x \in B_{\frac{\varrho }{2}} (x_{0}) \), and \( d(0, x) \leqslant 0 \) if \( x \in B_{\frac{\varrho }{2}}^{c}(x_{0})\) and \( \mathfrak {q}(u) = \tanh (u) \) is the traveling wave solution to the Allen–Cahn equation:
Our first step is to construct precisely the subsolution near the interface. Define \( {\overline{d}}(\sigma , x) = e^{- \mu \sigma } d (\sigma , x) \), for some \( \mu >0 \) that will be chosen later on. We observe that there are \( \sigma ^{\prime }> 0, \varrho ^{\prime } \in (0, \varrho /2) \) such that \( d(\sigma ,x) \) is smooth in the set
and (see for example [6, Equation (6.4), p. 663]) there exists a constant \( C>0 \), depending on \( \varrho , \varrho ^{\prime }, \sigma ^{\prime } \), such that
In particular, fixing \( \mu \geqslant C \) we have \( (\partial _{\sigma } - \Delta ) {\overline{d}} \leqslant 0 \) on \( Q_{\varrho } \). Then consider, for some \( K_{1} > 0 \)
We claim that for \(K_{1} \) sufficiently large \( w_{\varepsilon } \) is a subsolution to
where
In fact, since \( \dot{\mathfrak {q}} \geqslant 0 \), we can compute
where we used that \( | \nabla d |^{2} =1 \) in a neighborhood of the boundary of \( B_{\frac{\varrho }{2}}\). Now we use the definition of \( \mathfrak {q} \) to rewrite the last term as
At this point we would like to replace \( \mathfrak {q} \) with \( w_{\varepsilon } = \mathfrak {q} - \frac{\lambda }{L_{\varepsilon }} \) in the nonlinearity. We observe that since \( u \mapsto u(1-u^{2}) \) is decreasing near \( u=1 \) and \( u = -1 \) there exists a \( \gamma \in (0, 1) \) such that if \( | \mathfrak {q} | \in ( \gamma , 1) \) and \( \varepsilon \) is sufficiently small, then \( \mathfrak {q}(1 - \mathfrak {q}^{2}) \leqslant w_{\varepsilon }(1 - w_{\varepsilon }^{2}) \). On the other hand, on the set \( |\mathfrak {q}| \leqslant \gamma \) there exists a constant \( c(\gamma ) >0 \) such that \( \dot{\mathfrak {q}} \geqslant c(\gamma )>0 \). Hence in this last case:
where the last inequality holds for all \( \varepsilon \) sufficiently small, and provided \( K_{1} \) is chosen large enough. Hence we have proven (5.4).
The next step is to extend this subsolution \(w_{\varepsilon }\) to all \( x \in \textbf{R}^{d} \) (at the moment it is defined only for \( | x - x_{0} | \in [\varrho /2 - \varrho ^{\prime }, \varrho /2+ \varrho ^{\prime }] \)). Here we follow two different arguments in the interior and the exterior of the ball \( B_{\frac{\varrho }{2}} \). Let us start with the exterior. We observe that for any fixed \( \varrho ^{\prime \prime } \in (0, \varrho ^{\prime }) \) it holds that for all \( \varepsilon \) sufficiently small and some \( \lambda ^{\prime } >0 \):
Here we use that asymptotically, for \( x \rightarrow - \infty \), we have \( \mathfrak {q}(x) \leqslant -1 + 2 e^{- 2 x},\) so that by definition, for some \( c(x_{0}) > 0 \)
where the last inequality holds for \( \varepsilon \) sufficiently small. Now consider \( {\overline{\lambda }} \) as in (5.2) and \( {\overline{\Phi }} \) as in (4.2). Then let \( S^{\varepsilon } \) be the set
Since \( \sigma \mapsto {\overline{\Phi }} (s(\varepsilon ) \sigma , -1 - {\overline{\lambda }} \varepsilon ^{\frac{d}{2} - \alpha }) {\mathop {=}\limits ^{{\tiny \mathrm def}}}{\overline{\Phi }}_{\varepsilon }(\sigma )\) is a spatially homogeneous solution to (5.3) we find that for small \( \varepsilon \),
is a subsolution to (5.3) in the viscosity sense (cf. the proof of Lemma 3.1) on the set
Here we use that asymptotically \( \lambda ^{\prime } L_{\varepsilon }^{-1} \gg \varepsilon ^{\frac{d}{2} - \alpha } \), so that \( {\underline{w}}_{\varepsilon }(\sigma , x) = {\overline{\Phi }}_{\varepsilon } (\sigma ) \) for all \( x \in S^{\varepsilon } \).
Finally, we want to extend the subsolution to the interior of the ball \( B_{\frac{\varrho }{2}}(x_{0}) \). To complete this extension we consider a convex combination between \( {\underline{w}}_{\varepsilon } \) and the constant \( 1 - \frac{\lambda }{L_{\varepsilon }}.\) Let us fix a decreasing smooth function \( \Upsilon :\textbf{R}\rightarrow [0,1] \) such that \( \Upsilon (x) = 1 \) if \( x \leqslant \big ( \frac{\varrho - \varrho ^{\prime }}{2} \big )^{2} \), and \( \Upsilon (x) = 0 \) if \( x \geqslant \big ( \frac{\varrho - \varrho ^{\prime }/2 }{2} \big )^{2}. \) Then define, for some constant \( K_{2} > 0 \)
Note that by considerations on the support of \( \Upsilon \) and the domain of definition of \( {\underline{w}}_{\varepsilon } \), \( {\underline{u}}_{\varepsilon } \) is well defined. We claim that if \( K_{2} \) is sufficiently large the function \( {\underline{u}}_{\varepsilon } \) is a viscosity subsolution to (5.3) on \( [0, \zeta (\varepsilon )^{-1}\sigma ^{\prime }] \times \textbf{R}^{d} \). In fact, by our previous calculations we find
assuming \( K_{2} \geqslant 2 \), and using that \( {\underline{w}}_{\varepsilon } \leqslant 1 - \frac{\lambda }{L_{\varepsilon }}\) and \( {\dot{\Upsilon }} \leqslant 0 \), as \( \Upsilon \) is decreasing. Now on the set \( \{ \Upsilon >0 \} \), we have \( {\underline{w}}_{\varepsilon } \geqslant 0\), provided \( \varepsilon \) is sufficiently small. So using the concavity of \( [0, 1] \ni u \mapsto u (1- u^{2}) \):
Furthermore, we can find a constant \( \nu \in (0, 1) \) such that
Hence we see that on the set \( \{ \Upsilon \leqslant \nu \}\)
On the other hand, on the set \( \{ \Upsilon > \nu \}\) we have for some \( C>0 \):
where the last inequality holds for \( \varepsilon \) sufficiently small.
To conclude, for \( \varepsilon \) sufficiently small, we have constructed a subsolution to (5.3) such that, by (5.2) and up to choosing \( \lambda \) sufficiently large, the initial condition satisfies
By comparison, since \( \lim _{\varepsilon \rightarrow 0} {\underline{u}}_{\varepsilon }(1, x) = 1\), for all x in a neighborhood of \( x_{0} \) and through the upper bound of Lemma 5.1 our proof is complete. \(\square \)
The next result establishes convergence to level set solutions of mean curvature flow. Recall that we have defined
In these variables the initial condition for the mean curvature flow appears at time \( \sigma = 1 \). The level set formulation of mean curvature flow is then given by viscosity solutions to the following equation for \( (t, x) \in [1, \infty ) \times \textbf{R}^{d} \)
Here \( (\nabla w)^{\otimes 2}: \nabla ^{2}w = \sum _{i,j=1}^{d} \partial _{i} w \partial _{j}w \partial _{ij}w \). If \( w_{1} \) is uniformly continuous on \( \textbf{R}^{d} \) there exists a unique viscosity solution to the above equation, see e.g. [8, Theorem 1.8]. Furthermore, we will be only interested in the evolution of the sets \( \{ w > 0 \}, \{ w < 0 \} \) and \( \{ w = 0 \} \), which motivates the following definition.
Definition 5.5
For any \( f \in C_{\textrm{loc}}(\textbf{R}^{d}; \textbf{R}) \) we define \( v(f; \cdot , \cdot ) :[1, \infty ) \times \textbf{R}^{d} \rightarrow \{ -1, 0, 1 \} \) by
with w the viscosity solution to (5.5) with an arbitrary initial condition \( w_{1} \in C^{2}_{b}(\textbf{R}^{d}; \textbf{R}) \) satisfying:
The function \( v(f; \cdot , \cdot ) \) does not depend on the particular choice of \( w_{1} \) by [6, Theorem 5.1].
We recall the definition of the sets \( K_{\delta } \) as in (2.1) for \( \delta \in (0, 1) \):
Now we can state our concluding result.
Proposition 5.6
Consider \( (\Omega , \mathcal {F}, \textbf{P}) \) as in Lemma 5.2 and let \( v(\Psi ; \cdot , \cdot ) :[1, \infty ) \times \textbf{R}^{d} \rightarrow \{ -1, 0, 1 \} \) be as in Definition 5.5. Then for any \( \delta , \zeta \in (0, 1) \)
Proof
In analogy to the previous results, up to considering suitable subsequences we can assume that \( U_{\varepsilon }(1, \cdot ) \rightarrow {\overline{\Phi }}(0, \Psi (\cdot )) \) almost surely in \( C_{\textrm{loc}}(\textbf{R}^{d}) \) as \( \varepsilon \rightarrow 0 \). Then it suffices to prove that almost surely, for any \( \delta \in (0, 1) \)
In the setting just introduced, our aim is to construct suitable super- and sub-solutions to \( u_{\varepsilon }(t_{\star }(\varepsilon ) + (\sigma -1) T_{\varepsilon }, x L_{\varepsilon }) \) with initial conditions that are independent of \( \varepsilon \) and constant outside of a compact set. After establishing convergence to mean curvature flow for these super- and sub-solutions we will use comparison to obtain the convergence of the original sequence. For convenience we will restrict ourselves to the construction of subsolutions, which will guarantee convergence on the set \( \{ v( \Psi ; \cdot , \cdot ) > 0 \} \). The construction of supersolutions is analogous.
Consider a smooth function \( \varphi :\textbf{R}^{d} \rightarrow [-1, 0] \) such that \( \varphi (x) =0\), for all \(| x | \leqslant \frac{1}{2} \) and \( \varphi (x) = -1,\) for all \( | x | \geqslant 1\). Then for any \( R \geqslant 1 \) define \( \varphi _{R}(x) = \varphi (x/R) \) and consider
In particular by our assumptions for any \( R \geqslant 1\) there exists a \( \varepsilon (R) \in (0, 1) \) such that
Here we use the convergence \( U_{\varepsilon }(1, \cdot ) \rightarrow {\overline{\Phi }}(0, \Psi (\cdot )) \) in \( C_{\textrm{loc}} (\textbf{R}^{d}) \) together with the a-priori bound from Lemma 5.1, which guarantees that \( U_{\varepsilon }(\sigma , \cdot ) \geqslant -1 - R^{-1}\) for \( \sigma \geqslant 1 \) and \( \varepsilon \) sufficiently small. Moreover, locally uniformly over \( x \in \textbf{R}^{d} \): \(\lim _{R \rightarrow \infty } {\underline{u}}_{R}(x) = {\overline{\Phi }}(0, \Psi (x))\). Now, let \({\underline{u}}_{R, \varepsilon } (\sigma ,x) \) be the solution to the rescaled Allen–Cahn equation
Then by [4, Theorem 4.1] \(\lim _{\varepsilon \rightarrow 0} {\underline{u}}_{R, \varepsilon } = {{\,\textrm{sgn}\,}}( {\underline{w}}_{R}),\) in \(C_{\textrm{loc}}((1, \infty ) \times \textbf{R}^{d} {\setminus } \{ {\underline{w}}_{R} = 0 \})\), where \( {\underline{w}}_{R} \) is the unique level set solution to (5.5) with initial condition \( {\underline{u}}_{R} \). By comparison, using the ordering (5.6) and the fact that \( U_{\varepsilon } \) also solves (5.7) with a different initial condition, we obtain that for any \( R \geqslant 1\)
where \( {\underline{\mathcal {P}}}^{R} = \{ {\underline{w}}_{R}( \cdot , \cdot ) > 0\} \subseteq (1, \infty ) \times \textbf{R}^{d} \).
Now we would like to pass similarly to the limit \( R \rightarrow \infty \), but we have to take care of the fact that the limiting initial condition \( \lim _{R \rightarrow \infty } {\underline{u}}_{R} = \Psi / \sqrt{1 + \Psi ^{2}} \) may not be uniformly continuous on \( \textbf{R}^{d} \), which complicates the construction of solutions. Of course, this problem is not significant, since we can rescale the initial condition arbitrarily by multiplying with a positive function without modifying the mean curvature flow evolution.
Hence consider a partition of the unity \( \{ \varphi _{k} \}_{k \in \textbf{N}}\) of \( \textbf{R}^{d} \). Namely, for every \( k \in \textbf{N}\), let \( \varphi _{k} :\textbf{R}^{d} \rightarrow [0, \infty ) \) be a smooth function with compact support, such that \( \sum _{k \in \textbf{N}} \varphi _{k}(x) = 1.\) We will assume that the partition is locally finite, in the sense that there exists an \( M \in \textbf{N}\) such that for every \( k_{1}, \ldots , k_{M} \in \textbf{N}\) with \( k_{i} \ne k_{j} \) for all \( i \ne j \) we have \( \cap _{k =1}^{M} \mathop {\textrm{supp}}\limits (\varphi _{k}) = \emptyset \). In addition we assume that \( \sup _{k \in \textbf{N}} \Vert \varphi _{k} \Vert _{C^{2}} < \infty \). Then let
and define
Now we can consider the solution \( {\underline{v}}_{R}\) to (5.5) with initial condition \( {\underline{v}}_{R, 1}(x) = g (x) \cdot {\underline{u}}_{R} (1, x)\), so that from the definition of g we obtain:
By [6, Theorem 5.1] the evolution of the interface does not depend on the particular choice of the initial condition, as long as they share the same initial interface. In particular, since g is strictly positive we find that
The bound (5.8) now guarantees a uniform bound on the solutions (this is the consequence of the comparison principle in [6, Theorem 4.1]) for any \( \alpha \in (0, 1) \):
Since in addition
with \( w_{1} \in C^{2}_{b}(\textbf{R}^{d}; \textbf{R}) \), using compactness as well as stability of viscosity solutions we find that \(\lim _{R \rightarrow \infty } {\underline{v}}_{R}(\cdot , \cdot ) = w(\cdot , \cdot )\) in \(C([1, \infty ) \times \textbf{R}^{d}; \textbf{R})\), where the latter is the unique viscosity solution to (5.5) with initial condition \( w_{1} \). This completes the proof. \(\square \)
The following corollary relates level set solutions to mean curvature flow to classical solutions in the case \( d=2 \). Consider the unit torus \( \textbf{T}= \textbf{R}/\textbf{Z}\). A continuous (resp. smooth) closed curve is any continuous (resp. smooth) map \( \gamma :\textbf{T}\rightarrow \textbf{R}^{2} \). We say that the curve is non self-intersecting if the map \( \gamma \) is injective.
Corollary 5.7
If \( d=2 \), the set \( \Gamma _{1} = \{ \Psi = 0 \} \) consists of a countable collection of disjoint smooth, closed, non self-intersecting curves: \( \Gamma _{1} = \bigcup _{i \in \textbf{N}} \gamma _{i}(\textbf{T}). \) Then, for any \( \sigma \geqslant 1 \) the set \( \Gamma _{\sigma } = \{ v( \Psi ; \sigma , \cdot ) = 0 \}\), with \( v( \Psi ) \) as in Proposition 5.6, is the disjoint union \( \Gamma _{\sigma } = \bigcup _{i \in \textbf{N}} \gamma _{i, \sigma }(\textbf{T}) \) of continuous curves \( \gamma _{i, \sigma } \) which are the mean curvature flow evolution of the curves \( \gamma _{i} \), in the sense of [7].
Proof
The fact that \( \Gamma _{1} \) is the disjoint union of smooth closed curves is proven in Lemma 5.8. Each of these curves evolves according to the level set notion of mean curvature flow, which for concreteness we denote by \( \mathcal {M}_{\sigma } \gamma _{i}(\textbf{T}) \), for \( i \in \textbf{N}\) and \( \sigma \geqslant 1 \). We observe that [6, Theorem 7.3] implies that the sets \( \mathcal {M}_{\sigma } \gamma _{i}(\textbf{T}) \) are pairwise disjoint over \( i \in \textbf{N}\), for any \( \sigma >1 \). In addition the level set mean curvature flow evolution of a smooth closed curve coincides with the classical evolution by [6, Theorem 6.1], as long as the latter is defined. Since by Lemma 5.8 our curves are non self-intersecting, [7] proves that the classical evolution is defined for all times, and our result follows. \(\square \)
Lemma 5.8
Let \( \Psi \) be as in (1.3), in dimension \( d=2 \), and consider the random set \(\Gamma _{1} = \{ x \ :\ \Psi (x) = 0 \} \subseteq \textbf{R}^{2}.\) Then \( \textbf{P}- \)almost surely the set \( \Gamma _{1} \) is a countable union of smooth, non self-intersecting and disjoint closed curves: \(\Gamma _{1} = \bigcup _{i \in \textbf{N}} \gamma _{i}(\textbf{T}),\) with \( \gamma _{i} :\textbf{T}\rightarrow \textbf{R}^{2} \) smooth.
Proof
By [2, Corollary 1.4] there exists a null set \( \mathfrak {N}_{1} \) such that for all \( \omega \in \mathfrak {N}_{1}^{c} \) every connected component of \( \Gamma _{1}(\omega ), \ \mathcal {P}_{1}(\omega ) \) and \( \mathcal {N}_{1}(\omega ) \) is bounded.
Hence the proof is complete if we show that the boundary of every region is given by a smooth closed curve. Let us first show that there exists a null set \( \mathfrak {N}_{2} \) such that for all \( \omega \in \mathfrak {N}_{2}^{c} \) it holds that
This follows from Bulinskaya’s lemma, see for example [1, Lemma 11.2.10], as long as we can prove the following nondegeneracy condition, namely that the map
satisfies that for any \( x \in \textbf{R}^{2} \) the probability measure
has a density \( p_{x}(y) \) with respect to Lebesgue measure on \( \textbf{R}^{3} \) such that for some \( C>0\): \(| p_{x}(y) | \leqslant C, \ \forall x \in \textbf{R}^{2}, \ y \in \textbf{R}^{3}.\) In our case this condition is trivially satisfied as for every \( x \in \textbf{R}^{2} \), h(x) is distributed as a Gaussian vector in \( \textbf{R}^{3}\) with diagonal covariance matrix (here \( \lambda = \frac{d - 2 \alpha }{2} \) and \( C(\lambda )>0 \) is a constant):
It follows that (5.9) holds true. An application of the implicit function theorem allows us to deduce our result. \(\square \)
References
Adler, R.J., Taylor, J.E.: Random Fields and Geometry. Springer Monographs in Mathematics. Springer, New York, xviii+448 (2007)
Beffara, V., Gayet, D.: Percolation of random nodal lines. Publ. Math. Inst. Hautes Études Sci. 126, 131–176 (2017). https://doi.org/10.1007/s10240-017-0093-0. arxiv:1605.08605
Bray, A.: Theory of phase-ordering kinetics. Adv. Phys. 43(3), 357–459 (1994). https://doi.org/10.1080/00018739400101505. arXiv:cond-mat/9501089
Barles, G., Souganidis, P.E.: A new approach to front propagation problems: theory and applications. Arch. Ration. Mech. Anal. 141(3), 237–296 (1998). https://doi.org/10.1007/s002050050077
Duminil-Copin, H., Rivera, A., Rodriguez, P.-F., Vanneuville, H.: Existence of an unbounded nodal hypersurface for smooth Gaussian fields in dimension d \(\ge \) 3, (2021). arXiv:2108.08008
Evans, L.C., Spruck, J.: Motion of level sets by mean curvature. I. J. Differ. Geom. 33(3), 635–681 (1991)
Grayson, M.A.: The heat equation shrinks embedded plane curves to round points. J. Differ. Geom. 26(2), 285–314 (1987)
Ishii, H., Souganidis, P.: Generalized motion of noncompact hypersurfaces with velocity having arbitrary growth on the curvature tensor. Tohoku Math. J. (2) 47(2), 227–250 (1995). https://doi.org/10.2748/tmj/1178225593
Kohn, R.V., Otto, F.: Upper bounds on coarsening rates. Commun. Math. Phys. 229(3), 375–395 (2002). https://doi.org/10.1007/s00220-002-0693-4
Ohta, T., Jasnow, D., Kawasaki, K.: Universal scaling in the motion of random interfaces. Phys. Rev. Lett. 49, 1223–1226 (1982). https://doi.org/10.1103/PhysRevLett.49.1223
Acknowledgements
MH gratefully acknowledges support from the Royal Society through a research professorship, Grant No. RP\R1\191065.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hairer, M., Lê, K. & Rosati, T. The Allen–Cahn equation with generic initial datum. Probab. Theory Relat. Fields 186, 957–998 (2023). https://doi.org/10.1007/s00440-023-01198-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00440-023-01198-5






 for all
for all 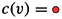 , namely any root of
, namely any root of  for
for 
 defined by inverting the removal we just described.
defined by inverting the removal we just described.