Analytical and numerical analysis on local and global buckling of sandwich panels with strut-based lattice cores

Abstract

Additive manufacturing (AM) offers new possibilities to fabricate and design lightweight lattice materials. Due to the superior mechanical properties of these lattice structures, they have the potential to replace honeycombs as cores in sandwich panels. In addition to the advantage of the integral fabrication thanks to AM, additively manufactured lattice core sandwich panels may be also used as heat exchangers, enabling a multifunctional use of the core. To ensure a reliable and safe structure, the mechanical response of lattice core sandwich panels under given load conditions must be predictable. In conventional sandwich panels subjected to compressive loads, the sandwich’s global buckling and the face sheets’ local buckling are the dominant failure modes. In constrast, core strut buckling may be the critical failure mode in lattice core sandwich panels. Therefore, an analytical 2D model to predict the local buckling of lattice core struts is considered in this study. Furthermore, the critical load for global buckling is obtained based on the first-order shear deformation theory. Thus, the transition from local buckling to global buckling depending on the length-to-thickness ratio is captured by the presented model. The comparison with finite element modeling of the sandwich model with truss cores has proved the accuracy of the derived model.

1 Introduction

The demand for cost reduction and improved structural integrity has increased the need for lightweight structures in engineering applications [1]. Composite structures consisting of two stiff skin layers enclosing a low-density core, known as sandwich panels, exhibit excellent specific mechanical properties and offer opportunities to meet lightweight requirements and enhance the efficiency of the structures. Considering the mechanical performance of sandwich panels, the core properties significantly affect the strength of the sandwich structure [2, 3]. In general, hexagonal honeycombs are the most commonly used cores in sandwich panels due to their superior specific mechanical properties [4, 5]. Further cellular structures may compete with honeycombs in applications where heat exchange and high energy absorption are required [6,7,8]. Since additive manufacturing provides high flexibility in structural design, novel cellular materials can be fabricated and applied as cores in sandwich panels [9,10,11,12]. The design freedom, provided by additive manufacturing technologies, results from the layerwise manufacturing process. In powder bed-based processes, a powder layer is applied first to a bed plate. A laser beam is used to melt the powder layer so that it can bond with the subsequent layer. Repeating the process for all layers of the manufactured part leads to the desired geometry and design. The quality of the additively manufactured structure depends mainly on the exposure strategy and the scanning parameters of the fabrication process [13]. Furthermore, these parameters significantly affect the manufacturing time [14]. Kumar et al. [15] presented a method to combine additive manufacturing with conventional manufacturing processes to provide high-performance sandwich composites. Using selective laser melting and selective laser sintering, lattice core sandwich panels were fabricated in a single manufacturing step [16,17,18,19]. The integral fabrication helped to eliminate the weak adhesive layer between the face sheet and the core, resulting in a higher strength structure [20]. Moreover, manufacturing costs can be reduced by eliminating adhesives and joining steps. Additive manufacturing enables tailoring the core properties to meet local requirements, resulting in customized lightweight core design for aerospace applications [21, 22].

Numerous studies have already analyzed sandwich panels with strut-based lattice materials. Pavano et al. [23] and Monteiro et al. [24] observed that lattice core sandwich panels have comparable strength to honeycomb sandwich panels under 3-point bending load. In sandwich panels under impulsive loading, lattice cores may outperform honeycomb cores [25]. However, using novel cellular materials introduces uncertainties in the design of these structures, as their mechanical behavior under different loading conditions may deviate from that of conventional honeycomb and foam cores [26, 27]. When considering sandwich panels subjected to uniaxial compressive loads, two main failure modes can be identified [28]. Slender sandwich panels can buckle like Euler columns, exhibiting a long half-sinusoidal wave, known as global buckling [29]. The thin face sheets may buckle with decreasing slenderness, deforming as short sinusoidal waves, known as local buckling [30, 31]. The critical buckling load can be predicted by finite element analysis, analytical modeling, or during laboratory experiments [32,33,34,35]. Kardomateas [36] compared several analytical approaches to determine the critical load for global buckling of wide sandwich panels. It was observed that the buckling formulas available in [37,38,39] do not provide a sufficient prediction of the critical buckling load for thick sandwich panels. Saoud and Le Grognec [40] presented an analytical model to predict the critical buckling load merely for isotropic sandwich panels. Nordstrand [41] demonstrated that considering the shear deformation of sandwich panels may increase the accuracy of the buckling load prediction. The buckling behavior of sandwich panels with cellular cores was analyzed using first-order shear deformation theory and numerical analysis in [42,43,44]. The results proved that using the effective properties of the core in analytical models is sufficient to predict the critical buckling load. Furthermore, experimental outcomes on additively manufactured sandwich panels with pyramidal lattice cores were in good agreement with results provided by analytical methods for clamped sandwich panels [45]. However, a new buckling mode may occur in strut-based lattice core sandwich panels. The struts of the lattice core may buckle before the face sheets fail [46, 47]. A common approach to analyze the buckling behavior of strut-based lattices is Euler buckling approximation [48]. Alghamdi et al. [49] investigated the buckling behavior of additively manufactured struts and reported that linear buckling prediction shows good agreement with experimental outcomes for slender beams. Since the Euler critical buckling load depends on the constraint of the lattice joints, many studies assumed simply supported joints that underestimate the buckling load [46, 50, 51].

Since analytical models use effective properties of the lattice material and ignore the local buckling of the lattice struts [52], in this work we intend to introduce an analytical model to predict the local buckling of the struts in lattice core sandwich panels. First, the properties and the topology of the lattice material used as a core are presented. Based on the first-order shear deformation theory and Euler buckling, the critical load for global buckling and local strut buckling of simply supported lattice core sandwich panels are derived. The analysis is conducted for thick and thin sandwich panels to determine the effect of the slenderness ratio on the buckling response of sandwich panels with lattice cores. Thus, the limitation of each approach is given depending on the length-to-thickness ratio of the sandwich panel.

2 Theory and modeling approach

This section presents the methods used in this study to determine the critical buckling load in sandwich panels subjected to uniaxial loads. First, the sandwich model with the corresponding core is introduced. Moreover, the critical load for global buckling based on the first-order shear deformation theory and the local buckling load of the lattice core based on Euler buckling are derived. Finally, the finite element model is described in detail.

2.1 Sandwich model

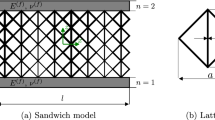
The core is assumed to be made of a periodic strut-based lattice material. Figure 1 illustrates the unit cell of the lattice consisting of four $45^{\circ }$ inclined struts and a single vertical strut. All struts have the strut diameter d. The quantity a describes the size of the quadratic unit cell. An analytical model to determine the effective properties of the considered unit cell was derived in [53]. Based on this model, the effective properties of the unit cell can be given as

$$\begin{aligned}&\frac{E^{(c)}_{xx}}{E_{\textrm{s}}}=\frac{(\sqrt{2}-1)\pi }{4}\, \left( \frac{a}{d}\right) ^{-2},{} & {} \frac{E^{(c)}_{zz}}{E_{\textrm{s}}}=\frac{\pi }{4}\, \left( \frac{a}{d}\right) ^{-2}, \,\text {and }{} & {} \frac{G^{(c)}_{xz}}{E_{\textrm{s}}}=\frac{\pi }{4\sqrt{2}} \,\left( \frac{a}{d}\right) ^{-2} , \end{aligned}$$

(1)

where $E_{\textrm{s}}$ is the elastic modulus of the strut solid material. The effective Poisson’s ratio is $\nu ^{(c)}_{xz}=(\sqrt{2}-1)$, independent of the aspect ratio a/d.

Fig. 1

Lattice unit cell

In this work, a simply supported sandwich panel with a periodic strut-based lattice core exposed to uniaxial compressive load is analyzed. Figure 2a shows the 2D sandwich model consisting of two isotropic face sheets and a strut-based lattice core. The number of lattice unit cells along the sandwich length l and through the core thickness $h^{(c)}$ is described by the quantities $N_x$ and $N_z$, respectively. The isotropic material behavior of the face sheets is described by the elastic modulus $E^{(f)}$ and Poisson’s ratio $\nu ^{(f)}$. The uniaxial load F is distributed over the sandwich thickness as a function of the stiffness and thickness ratio of the sandwich layers. As the effective behavior of the lattice at the macroscale is known, the lattice core can be represented by an orthotropic homogeneous material using the effective properties according to Eq. (1). The sandwich model with the homogenized lattice core is shown in Fig. 2b, where a Cartesian coordinate system at the center of the left edge is introduced.

Fig. 2

Simply supported sandwich models with lattice core and homogenized core exposed to uniaxial compressive load

2.2 Global buckling

As the sandwich model considered in this study consists of a shear deformable core, the shear deformation of the sandwich must be considered to obtain accurate results. The shear deformation is addressed using the first-order shear deformation theory (FSDT) [54, 55]. In FSDT, three degrees of freedom describe the deformation of the sandwich in the considered xz-plane: the horizontal displacement of the sandwich mid-plane $u_0(x)$, the vertical displacement of the sandwich mid-plane $w_0(x)$, and the rotation with respect to the sandwich mid-plane $\psi (x)$. Thus, the displacement field can be given as

$$\begin{aligned}&u(x,z) = u_{0}(x) + z\psi (x), \mathrm {\quad and} \end{aligned}$$

(2)

$$\begin{aligned}&w(x,z) = w_{0}(x). \end{aligned}$$

(3)

Differentiating the displacement functions u(x, z) and w(x, z) yields the following strains

$$\begin{aligned}&\varepsilon _{xx} = \frac{\partial u_{0}}{\partial x} + z \frac{\partial \psi }{\partial x}, \end{aligned}$$

(4)

$$\begin{aligned}&\varepsilon _{zz} = \frac{\partial w}{\partial z}=0, \mathrm {\quad and} \end{aligned}$$

(5)

$$\begin{aligned}&\gamma _{xz} = \frac{\partial w_{0}}{\partial x} + \psi . \end{aligned}$$

(6)

For buckling problems, it is common to neglect the horizontal displacement of the midplane $u_0(x)$, as this term is negligible compared to $z\psi (x)$. Assuming a plane-stress state, stresses can be given as follows

$$\begin{aligned}&\sigma ^{(g)}_{xx} = E^{(g)} \varepsilon _{xx}, \mathrm {\quad and} \end{aligned}$$

(7)

$$\begin{aligned}&\tau ^{(g)}_{xz} = k{G^{(g)}}{\gamma _{xz}}, \end{aligned}$$

(8)

where the quantity g indicates the number of the sandwich layer, with $g=1$ and $g=3$ being the bottom and top face sheet, and $g=2$ being the core layer. Furthermore, the quantity k denotes the shear correction factor that can be determined according to [56] by

$$\begin{aligned}&k=\frac{G_r}{G_v}, \,\, \text {with} \end{aligned}$$

(9)

$$\begin{aligned}&G_v=\frac{2G^{(f)}h^{(f)}}{2h^{(f)}+h^{(c)}}+ \frac{G^{(c)}h^{(c)}}{2h^{(f)}+h^{(c)}}, \,\, \text {and} \end{aligned}$$

(10)

$$\begin{aligned}&\frac{1}{G_r}=\frac{2h^{(f)}}{G^{(f)}(2h^{(f)}+h^{(c)})}+ \frac{h^{(c)}}{G^{(c)}(2h^{(f)}+h^{(c)})}, \end{aligned}$$

(11)

where the quantity $1/G_r$ represents the sum of the weighted shear compliances of the sandwich layers. The shear compliances are weighted with the proportion of the layer thickness in the total thickness of the sandwich $h=2h^{(f)}+h^{(c)}$. The value $G_v$ is the effective shear stiffness of the sandwich according to the laminate theories. It is $G_v=A_{55}/h$. With the assumptions made, the inner potential energy of the sandwich can be expressed as

$$\begin{aligned} \Pi _{\text {i}} = \sum _{g=1}^{3} \Pi ^{(g)}_{\text {i}}, \end{aligned}$$

(12)

where

$$\begin{aligned}&\Pi ^{(1)}_{\text {i}} = \frac{1}{2} \int _{0}^{l} \int _{-h/2}^{-h/2+h^{(f)}} \left( \sigma ^{(1)}_{xx} \varepsilon _{xx} + \tau ^{(1)}_{xz} \gamma _{xz} \right) \, \textrm{d}z \, \textrm{d}x, \end{aligned}$$

(13)

$$\begin{aligned}&\Pi ^{(2)}_{\text {i}} = \frac{1}{2} \int _{0}^{l} \int _{-h/2+h^{(f)}}^{-h/2+h^{(f)}+h^{(c)}} \left( \sigma ^{(2)}_{xx} \varepsilon _{xx} + \tau ^{(2)}_{xz} \gamma _{xz} \right) \, \textrm{d}z \, \textrm{d}x, \end{aligned}$$

(14)

$$\begin{aligned}&\Pi ^{(3)}_{\text {i}} = \frac{1}{2} \int _{0}^{l} \int _{-h/2+h^{(f)}+h^{(c)}}^{-h/2+h^{(c)}+2h^{(f)}} \left( \sigma ^{(3)}_{xx} \varepsilon _{xx} + \tau ^{(3)}_{xz} \gamma _{xz} \right) \, \textrm{d}z \, \textrm{d}x. \end{aligned}$$

(15)

With the external potential energy $\Pi _{\text {e}}$, resulting from the applied load F

$$\begin{aligned} \Pi _{\text {e}}= -\int _{0}^{l}\frac{F}{2}\left( \frac{\partial w}{\partial x}\right) ^2\,\textrm{d}x, \end{aligned}$$

(16)

the total potential energy results as

$$\begin{aligned}&{\Pi }=\Pi _{\text {e}}+\Pi _{\text {i}}. \end{aligned}$$

(17)

As the sandwich model is simply supported at the center of the left and right edge, the following deformation ansatzes

$$\begin{aligned}&w_0(x)= A_m \, \text {sin}\left( \frac{m\,\pi \, x}{l}\right) , \mathrm {\, and} \end{aligned}$$

(18)

$$\begin{aligned}&\psi (x)= B_m \, \text {cos}\left( \frac{m\,\pi \,x}{l}\right) \end{aligned}$$

(19)

satisfy the boundary conditions

$$\begin{aligned} w_0(x=0)=w_0(x=l)=M_y(x=0)=M_y(x=l)=0. \end{aligned}$$

(20)

The quantities $A_m$ and $B_m$ are unknown constants, and m denotes the number of the sinusoidal half waves. Calculus of variation ($\delta \Pi =0$) yields the equilibrium equations of the sandwich model as follows

$$\begin{aligned}&\left( F-k(2G^{(f)}h^{(f)}+G_{xz}^{(c)}h^{(c)})\right) \frac{\partial ^2 w}{\partial x^2}-k\left( 2G^{(f)}h^{(f)}+G_{xz}^{(c)}h^{(c)}\right) \frac{\partial \psi }{\partial x}=0, \mathrm {\,\,and} \end{aligned}$$

(21)

$$\begin{aligned}&k\left( 2G^{(f)}h^{(f)}+G_{xz}^{(c)}h^{(c)}\right) \psi +k\left( 2G^{(f)}h^{(f)}+G_{xz}^{(c)}h^{(c)}\right) \frac{\partial w}{\partial x} \nonumber \\&-\frac{1}{12}\left( E_{xx}^{(c)}h^{(c)^3}+2E^{(f)}h^{(f)}(4h^{(f)^2}+6h^{(f)}h^{(c)}+3h^{(c)^2})\right) \frac{\partial ^2 \psi }{\partial x^2}=0. \end{aligned}$$

(22)

Substituting Eqs. (18) and (19) into Eqs. (21) and 22 leads to the following equation system

$$\begin{aligned} \underbrace{ \begin{bmatrix} F\pi ^2m^2-t_{11} &{} T_{12} \\ T_{21} &{} T_{22}\end{bmatrix}}_{\underline{\underline{T}}} \begin{bmatrix} A_m \\ B_m \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}, \end{aligned}$$

(23)

with

$$\begin{aligned} t_{11}=&\frac{(2kG^{(f)}h^{(f)}+kG_{xz}^{(c)}h^{(c)})\pi ^2m^2}{l^2}, \end{aligned}$$

(24)

$$\begin{aligned} T_{12}=&T_{21}=-\frac{(2kG^{(f)}h^{(f)}+kG_{xz}^{(c)}h^{(c)})\pi m}{l}, \text { and} \end{aligned}$$

(25)

$$\begin{aligned} T_{22}=&-2kG^{(f)}h^{(f)}-kG_{xz}^{(c)}h^{(c)}\nonumber \\&-\frac{(E_{xx}^{(c)}h^{(c)^3}+2E^{(f)}h^{(f)}(4h^{(f)^2}+6h^{(f)}h^{(c)}+3h^{(c)^2}))\pi ^2m^2}{12l^2}. \end{aligned}$$

(26)

The critical buckling load $F_{\textrm{cr}}$ is obtained from the condition det$(\underline{\underline{T}})=0$ and can be given as

$$\begin{aligned} F_{cr}=\frac{T_{12}^2+t_{11}T_{22}}{m^2\pi ^2T_{22}} \end{aligned}$$

(27)

2.3 Local buckling

In addition to the global buckling mode, the struts of the lattice core may buckle. Therefore, the stress in the lattice struts is analyzed in the pre-buckling stage. Due to the uniaxial compressive load, the sandwich structure undergoes a change in length in the load direction, as illustrated in Fig. 3. The change in length $\Delta l$ can be determined by

$$\begin{aligned} \Delta l=\frac{Fl}{E_{xx}^{(c)}h^{(c)}+2E^{(f)}h^{(f)}}. \end{aligned}$$

(28)

Fig. 3

Sandwich model undeformed (solid line) and deformed as result of the uniaxial compressive load (dashed line)

As a result of the total change in length $\Delta l$, each unit cell in the core will be subjected to the following displacement (see Fig. 4)

$$\begin{aligned} \Delta l_{\text {cell}}=\frac{\Delta l}{N_x}= \frac{Fa}{E_{xx}^{(c)}h^{(c)}+2E^{(f)}h^{(f)}}. \end{aligned}$$

(29)

It can be observed that the cell compression resulting from the total sandwich load does not depend on the sandwich length l, but on the unit cell length a. The resulting load of the unit cell can be obtained by

$$\begin{aligned} F_{\text {cell}}=\,\frac{Fa}{h^{(c)}+2\frac{E^{(f)}}{E_{xx}^{(c)}}h^{(f)}}. \end{aligned}$$

(30)

Fig. 4

Core unit cell undeformed (solid line) and deformed as result of the uniaxial compressive load (dashed line)

Induced by the load $F_{\text {cell}}$ the inclined struts within the unit cell are subjected to the compressive load $F_{\text {cell,i}}=-F_{\text {cell}}/\sqrt{2}$, and the vertical strut is tensioned by the load $F_{\text {cell,v}}=F_{\text {cell}}$. The buckling mode of the lattice struts is illustrated in Fig. 5. To assess the buckling load in the inclined struts, the Euler buckling formula is used

$$\begin{aligned} F_{\text {buckling}}=n^2\pi ^2\frac{E_{\textrm{s}}I_{\textrm{s}}}{l_{\textrm{s}}^2}, \end{aligned}$$

(31)

where the quantity n denotes the end constraint factor, $l_{\textrm{s}}$ indicates the strut’s length, and $I_{\textrm{s}}$ describes the second moment of inertia of the lattice strut. A distinction is made between the vertical strut’s length $l_{\textrm{s,v}}=a$, and the inclined strut’s length $l_{\textrm{s,i}}=a/\sqrt{2}$. As the lattice struts are neither simply supported nor clamped at the nodes, n is determined by the rotational support of the nodes. To determine n, the lattice cell’s upper half is considered due to symmetry, as shown in Fig. 6. The rotational support of the vertical strut can be approximated by the rotational support of a simply supported beam subjected to a unit moment $M_1=1$ Nmm at one of the ends. The rotation of this beam at the loaded end can be given as

$$\begin{aligned} \frac{\partial w}{\partial x}=\frac{a}{6E_sI_s} M_1. \end{aligned}$$

(32)

The rotational spring stiffness $k_{\textrm{spring}}$ results as the inverse of the rotation

$$\begin{aligned} k_{\textrm{spring}}=\frac{1}{\frac{\partial w}{\partial x}}=\frac{6E_sI_s}{a}. \end{aligned}$$

(33)

Fig. 5

Buckling mode of the lattice struts induced by the compressive load

Fig. 6

Half of the unit cell to determine the rotational support of the vertical strut

Now, each inclined strut in the unit cell can be approximated by a simply supported beam with a rotational spring at one end, as illustrated in Fig. 7. The critical buckling load can be obtained from the general differential equation for beam buckling

$$\begin{aligned} \frac{\partial ^4 w}{\partial \chi ^4}+\lambda ^2\frac{\partial ^2 w}{\partial \chi ^2}=0, \end{aligned}$$

(34)

where $\lambda ^2=F_{\text {cell,i}}/E_{\textrm{s}}I_{\textrm{s}}$. The general solution for this equation can be given by

$$\begin{aligned} w(\chi )=A_1\textrm{sin}(\lambda \chi )+A_2\textrm{cos}(\lambda \chi )+A_3\chi +A_4, \end{aligned}$$

(35)

where $A_1$, $A_2$, $A_3$, and $A_4$ are unknown constants. The boundary conditions for the simply supported beam with the rotational spring can be given as

$$\begin{aligned} w(\chi =0)=w(\chi =l_{\textrm{s,i}})=M(\chi =0)=0,\, M(\chi =l_{\textrm{s,i}})=-\frac{k_{\textrm{spring}}}{2}\frac{\partial w}{\partial \chi }(\chi =l_{\textrm{s,i}}), \end{aligned}$$

(36)

that results in the following equation system

$$\begin{aligned} \underbrace{ \begin{bmatrix} 0 &{} 1 &{}0&{}1 \\ \frac{3E_{\textrm{s}}I_{\textrm{s}}\lambda }{l_{\textrm{s,v}}} &{}E_{\textrm{s}}I_{\textrm{s}}\lambda ^2 &{}\frac{3E_{\textrm{s}}I_{\textrm{s}}\lambda }{l_{\textrm{s,v}}}&{}0\\ \textrm{sin}(l_{\textrm{s,i}} \lambda )&{}\textrm{cos}(l_{\textrm{s,i}} \lambda )&{}l_{\textrm{s,i}} \lambda &{}1\\ E_{\textrm{s}}I_{\textrm{s}}\lambda ^2 \textrm{sin}(l_{\textrm{s,i}} \lambda )&{}E_{\textrm{s}}I_{\textrm{s}}\lambda ^2 \textrm{cos}(l_{\textrm{s,i}} \lambda )&{}0&{}0 \end{bmatrix}}_{\underline{\underline{Q}}} \begin{bmatrix} A_1 \\ A_2 \\ A_3\\ A_4 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0\\ 0 \end{bmatrix}, \end{aligned}$$

(37)

The determinant of the matrix $\underline{\underline{Q}}$ must vanish to avoid the trivial solution

$$\begin{aligned} \textrm{det}(\underline{\underline{Q}})=E_{\textrm{s}}^2I_{\textrm{s}}^2\lambda ^3\left( (3+\lambda ^2 l_{\textrm{s,i}}l_{\textrm{s,v}})\,\textrm{sin}(l_{\textrm{s,i}} \lambda )-3\lambda l_{\textrm{s,i}}\,\textrm{cos}(l_{\textrm{s,i}} \lambda )\right) =0. \end{aligned}$$

(38)

Equation 38 can be solved numerically and yields the smallest $l_{\textrm{s,i}} \lambda =3.61$, as illustrated in Fig. 8. The end constraint factor results as $n=1.15$ in this case.

Fig. 7

Simply supported beam with a rotational spring support at one end

Fig. 8

Numerical solution of the end constraint factor

A more precise determination of the end constraint factor n was presented in [38]. This method based on beam theory was used by Fan et al. [57] as well as by Omidio and St-Pierre [58] to determine the end constraint factor for periodic lattice materials. Thus, the end constraint factor can be determined using the following stiffness matrix

$$\begin{aligned} \begin{bmatrix}M_1 \\ M_2 \\ V \end{bmatrix}=\frac{E_sI_s}{l_s} \begin{bmatrix} s &{} sc &{} \bar{s}/l_s \\ sc &{} s &{} \bar{s}/l_s \\ \bar{s}/l_s &{} \bar{s}/l_s &{} s^*/l^2_s\end{bmatrix} \begin{bmatrix} \phi _1 \\ \phi _2 \\ \Delta \end{bmatrix}, \end{aligned}$$

(39)

where

$$\begin{aligned} \bar{s}=s(1+c), \quad s^*=2\bar{s}-\pi ^2\frac{F}{F_\textrm{E}}. \end{aligned}$$

(40)

The quantity V denotes the shear force, and $M_1$, $M_2$, $\phi _1$, and $\phi _2$ are the bending moments and rotations at the nodes of the beam element (Fig. 5). The lateral displacement $\Delta$ vanishes for the buckling mode shown in Fig. 5. For the struts subjected to compressive loads, s and c can be given as

$$\begin{aligned} s=\frac{\delta (\textrm{sin}\delta -\delta \textrm{cos}\delta )}{2-2\textrm{cos}\delta -\delta \textrm{sin}\delta }, \qquad c=\frac{\delta -\delta \textrm{sin}\delta }{\textrm{sin}\delta -\delta \textrm{cos}\delta }, \end{aligned}$$

(41)

with

$$\begin{aligned} \delta =\sqrt{\frac{F}{E_sI_s}}l_s=\pi \sqrt{\frac{F}{F_\textrm{E}}}=\pi n,\qquad F_{\textrm{E}}=n^2\pi ^2\frac{E_sI_s}{l_s^2}. \end{aligned}$$

(42)

The following applies to struts under tension

$$\begin{aligned} s=s_1=\frac{\delta _1(\delta _1\textrm{cosh}\delta _1-\textrm{sinh}\delta _1)}{2-2\textrm{cosh}\delta _1+\delta _1\textrm{sinh}\delta }, \qquad c=c_1=\frac{\textrm{sinh}\delta _1-\delta _1}{\delta _1\textrm{cosh}\delta _1-\textrm{sinh}\delta _1}, \end{aligned}$$

(43)

with

$$\begin{aligned} \delta _1=\sqrt{-\frac{F}{E_sI_s}}l_s=\pi \sqrt{-\frac{F}{F_\textrm{E}}}. \end{aligned}$$

(44)

The equilibrium equations at the nodes 1 and 2 result as

$$\begin{aligned}&\left( \frac{s_1}{\sqrt{2}}+\frac{s_1c_1}{\sqrt{2}}+s+s\right) \phi _1-2sc\phi 2=0, \end{aligned}$$

(45)

$$\begin{aligned}&(sc+sc)\phi _1-(s+s)\phi _2=0 \qquad \rightarrow \, c\phi _1=\phi _2. \end{aligned}$$

(46)

Substituting Eq. (46) in Eq. (45) yields the nontrivial solution

$$\begin{aligned} -2sc^2+2s+\frac{s_1}{\sqrt{2}}+\frac{s_1c_1}{\sqrt{2}}=0. \end{aligned}$$

(47)

The only unknown quantity in this equation is n. The numerical solution of Eq. (47) leads to $n=1.17$.

2.4 Finite element model

A linear perturbation analysis in ABAQUS CAE Software is conducted for a 2D sandwich model to verify the results obtained by the analytical model. The Lancoz solver is used to obtain the results. The face sheet layers are modeled using 2D plane stress continuum solid elements. A convergence study revealed that seven elements through the face sheet thickness are required to eliminate inaccuracy induced by the mesh size. Linear beam elements are used to model the lattice core. Six beam elements were used to mesh the lattice struts to avoid mesh size dependence. The sandwich beam is simply supported at the center of the left and right edges. To suppress rigid body motions, the horizontal displacement at the center of the sandwich is constrained. Due to the stiffness ratio and thickness ratio of the core and face sheets, the load F is distributed over the core and the surface layers as follows

$$\begin{aligned}&F^{(f)}=\frac{E^{(f)}h^{(f)}}{E_{xx}^{(c)}h^{(c)}+2E^{(f)}h^{(f)}}\,F, \end{aligned}$$

(48)

$$\begin{aligned}&F^{(c)}=1-2F^{(f)}, \end{aligned}$$

(49)

where the core is subjected to the load $F^{(c)}$, and the face sheets are subjected to the load $F^{(f)}$. In the finite element model, the load $F^{(f)}$ is applied as a pressure load to the face sheets. Using concentrated loads, the load $F^{(c)}$ is applied to the nodes of the lattice cores at the edges. Equations (49) and 48 were obtained by elementary equilibrium conditions. Figure 9 illustrates the boundary conditions and the load application used in the finite element model.

Fig. 9

Load application and boundary conditions in the 2D FE model of the sandwich with the lattice core

3 Results and discussion

This section presents the results of the 2D analysis of lattice core sandwich panels exposed to uniaxial compressive loads. The critical buckling load determined by the presented model is compared to that obtained by finite element analysis. The analysis is performed for three stiffness ratios $E^{(f)}/E^{(c)}_{xx}=600,800,$ and 1000, three layer thickness ratios $h^{(c)}/h^{(f)}=14,21,$ and 28, two lattice configurations with $N_z=5$ and 7, and slenderness ratios $l/h^{(c)}$ between 2 and 60. While varying the slenderness ratios, the length of the sandwich changes, and the core thickness is kept constant ($h^{(c)}=21$ mm). The same applies to the variation of the thickness ratio $h^{(c)}/h^{(f)}$. Thus, the unit cell size a changes only when the number of cells through the core thickness $N_z$ varies. The elastic properties of the material used for the analysis are assumed to be those of an aluminum alloy $E^{(f)}=E_{\textrm{s}}=70$ GPa and $\nu ^{(f)}=\nu _{\textrm{s}}=0.35$. Thus, the stiffness of the face sheets remains constant during the analysis, and the core stiffness is varied.

Figure 10 shows the critical buckling load over the slenderness ratio of the sandwich panel for several layer thickness ratios, the stiffness ratio $E^{(f)}/E^{(c)}_{xx}=1000$, and the core consisting of 7 layers with unit cell size $a=3$ mm. For thick sandwich panels, local strut buckling dominates the stability failure. A critical buckling load plateau is observed for the local buckling region, as the strut load (Eq. 30) here depends on the unit cell size that remains constant with increasing slenderness ratio. The transition from local to global buckling differs slightly for different layer thickness ratios. Starting from slenderness ratio of approx. 20, the global buckling mode dominates. The critical buckling load decreases with increasing sandwich length in the global buckling region. Figures 11 and 12 show the results for the critical buckling of sandwich panels with stiffer cores. It can be seen that the range for the local buckling plateau becomes shorter with increasing core stiffness since the strut diameter of the unit cell increases. The transition from local to global buckling is also captured well by the present model. It is worth noting that the deviation of the local strut buckling prediction from the finite element analysis does not increase with varied layer thickness ratios, or stiffness ratios in the analysis performed. The relative deviation remains approx. 3%, exhibiting a constant behavior for all analyses performed. The buckling response obtained by the FE model is shown in Fig. 13 for both local and global buckling.

Fig. 10

Critical buckling load for a sandwich panel with 7-layer lattice core over the slenderness ratio of the sandwich

Fig. 11

Critical buckling load for a sandwich panel with 7-layer lattice core over the slenderness ratio of the sandwich

Fig. 12

Critical buckling load for a sandwich panel with 7-layer lattice core over the slenderness ratio of the sandwich

Fig. 13

Buckling response obtained in the FE model

The results for the 5-layer core with unit cell size $a=4.2$ mm are illustrated in Figs. 14, 15, and 16. Comparing two cores with the same stiffness ratio but different cell sizes reveals that the critical load for local buckling decreases with increasing cell size. When the sandwich slenderness ratio reaches a particular value where both sandwich configurations show a global buckling behavior, no difference in the critical buckling load is observed, as both sandwich configurations have the same mechanical properties at the macroscale.

Fig. 14

Comparison of the critical buckling load for a sandwich panel with 7-layer lattice core and a sandwich panel with 5-layer lattice core over the slenderness ratio of the sandwich

Fig. 15

Comparison of the critical buckling load for a sandwich panel with 7-layer lattice core and a sandwich panel with 5-layer lattice core over the slenderness ratio of the sandwich

Fig. 16

Comparison of the critical buckling load for a sandwich panel with 7-layer lattice core and a sandwich panel with 5-layer lattice core over the slenderness ratio of the sandwich

Generally, it can be concluded that the present model is able to capture local strut buckling and global buckling of lattice core sandwich panels. The results obtained by the derived model show a satisfying agreement with the results determined by the finite element model. Regarding the computational effort, the present model requires less than one second to determine the critical buckling load. In contrast, the finite element model requires time-consuming modeling and size-dependent computational effort. For instance, sandwich panels with higher slenderness ratios and a significant number of unit cells are more time-consuming than thick sandwich panels with fewer unit cells. Therefore, the presented model provides advantages regarding computational efficiency and can be used advantageously at the initial design stage of lattice core sandwich panels.

4 Conclusion and summary

This study introduced an analytical 2D model to determine the critical buckling load of simply supported lattice core sandwich panels subjected to uniaxial compressive loads. The analytical model considers the global buckling of the sandwich panel and the local buckling of the lattice core struts. For the global buckling analysis, the lattice core is represented by the effective elastic properties of the lattice unit cell. The prediction of the global buckling load is based on the first-order shear deformation theory and considers the shear deformation in all sandwich layers. The local strut buckling load is obtained from the Euler buckling approximation. The end constraint factor of the lattice joints is determined to avoid underestimating the critical buckling load. Compared to detailed finite element analysis, the presented model can reasonably determine the buckling load of lattice core sandwich panels. Furthermore, the derived model captures the transition from local to global buckling region depending on the length-to-thickness ratio. The analysis was performed for several face sheets thicknesses and sandwich slenderness ratios. Unit cell size effects on the buckling response of lattice core sandwich panels were observed. The method presented in this study is applicable to 3D models. For the global buckling analysis, the effective properties of the 3D lattice are required. If the effective properties are known, the analysis can be performed based on the FSDT approach, similar to the one presented in this study. For the local buckling analysis, the 3D lattice unit cell has to be analyzed in the same manner as the 2D unit cell. Depending on the unit cell’s topology, the number of struts within the unit cell, and the unit cell behavior under compressive load, the node constraint factor for Euler buckling can be determined so that the local buckling analysis can be conducted for the 3D case. The presented model cannot predict the local buckling of the face sheets, known as wrinkling. Moreover, the intracell buckling of the face sheets between the lattice nodes is not taken either into account. An extension of this model to consider wrinkling in lattice core sandwich panels should be done in future works.