1 Introduction

Many countries are facing the aging of their population [1]. Problems that are commonly related to the groups on the top of the age pyramid are rising, such as bone deterioration diseases that increase the fracture risk and, in addition to the worsening of the quality of life and mortality of individuals, are financially expensive for the society [2,3,4]. Bone is a living tissue that is strong, tough, and lightweight. Macroscopically, it can be divided into two structures: the highly mineralized cortical bone and the porous structure cancellous bone [5].

The cortical bone is responsible for bearing the main compression and bending loads, and its high toughness and hierarchical architecture lead to efficient energy dissipation [6,7,8,9] through intrinsic damage mechanisms at the sub-microscale (e.g., microcracking) that prevent crack initiation and extrinsic crack-tip shielding mechanisms (e.g., crack bridging) that reduce crack propagation [10,11,12,13]. In this context, numerical methods have been a valuable tool to study the failure of the cortical bone, assessing the mechanical behavior at different scales while considering its heterogeneity, complex geometry, and boundary conditions [14,15,16,17,18,19,20,21].

At the microscale, the cortical bone is considered a four-phase composite material constituted by the interstitial matrix, cement line, secondary osteons, and Haversian canals [22]. The osteons can be interpreted as stiff fibers embedded within a stiff matrix separated by a thin cement line. This interface is known as the constituent with the highest probability to develop a crack [23,24,25], inducing the crack path, and thus, it works as a protective barrier for the osteons as cracks are deflected at it. This phenomenon is consistently observed in experimental data and is deeply related to structure toughness [26, 27]. In addition, it is also important to highlight that its mechanical properties are not consensus due to the difficulty in characterizing a material that is less than \(5~\mu \)m wide [28,29,30,31]. Hence, it is considered a stiff material by some researchers [31,32,33], or as a much less stiff constituent by others [26, 34, 35].

Different methodologies have been employed to capture the damage mechanisms at the microscale of cortical bone. According to Gustafsson et al. [11], the main numerical techniques used in this context are: element deletion where the constitutive equation is modified by damage mechanics degradation, i.e., the damaged element stiffness is decreased to simulate a crack [36, 37]; cohesive elements [38, 39] where cohesive interfaces are degraded through a damage evolution law; and extended finite element method (X-FEM), which uses elements with enriched degrees of freedom to describe cracks without the necessity to predetermine the crack path [40,41,42]. Recently, there has been an effort to describe the behavior of the cortical bone microstructure using the phase field method [43, 44]. However, the modeling of the interfaces (cement lines) in bones has not been addressed so far [45].

The works by Gustafsson et al. [11] and Marco et al. [34] have promising results regarding the microcracking simulation of the cortical bone. Gustafsson et al. [11] use the X-FEM to simulate the crack propagation and a strategy by combining the maximum principal strain criterion with an additional interface damage formulation to capture the influence of the cement line. The features and capabilities of the proposed model are demonstrated through the numerical analyses of a single osteon under three distinct orientations in 2D. For all the analyses, the failure process is described by the propagation of a single crack. Marco et al. [34] propose a criterion for crack propagation in heterogeneous media in combination with the Phantom Node Method (similarly to the X-FEM, the crack is not mesh dependent) that is tested on simplified and realistic geometries. This methodology depicts a single crack developing through the models following the known behavior of the structure. Although these results correlate well with experimental data, these analyses consistently depict a single or a couple of cracks per model. Thus, they do not present situations with a significant number of discontinuities. A collection of microcracks (with less than \(10~\mu \)m in length) are called "diffuse damage" and, even though their role is not entirely understood, are mechanisms that affect the mechanical performance of the structure [46,47,48,49,50].

This work proposes an alternative approach for modeling the cracking phenomenon in bone microstructure based on the mesh fragmentation technique (MFT) [51]. Recently, this discrete crack model has been successfully applied for modeling the failure process of quasi-brittle materials in different contexts [52,53,54,55,56,57]. The MFT allows the representation of the cortical bone as a four-phase material at the microscale. A composed damage model is proposed to simulate the behavior of the interface elements and, consequently, to describe the failure process considering the crack opening, closure, and sliding. This constitutive model is integrated using an implicit and explicit (Impl-Ex) scheme [58] to avoid numerical convergence problems usually found when multiple cracks are expected. Moreover, the initiation and propagation of complex and arbitrary cracks can be simulated without the need for tracking algorithms and totally conducted in the context of the continuum mechanics.

The remainder of this paper is organized as follows: The mesh fragmentation technique applied to represent the cortical bone as a four-phase material and the constitutive model used to describe the failure process considering the properties of the distinct phases of the material are presented in Sect. 2. Also, this section describes the numerical examples performed to validate the proposed approach. In Sect. 3, the results are presented and discussed. Finally, a summary and the main conclusions are drawn in Sect. 4.

2 Methods

2.1 Mesh fragmentation technique

The mesh fragmentation technique (MFT) [51] is employed to simulate the mechanical behavior of the cortical bone and explicitly represent the crack propagation process through the different phases of its microstructure.

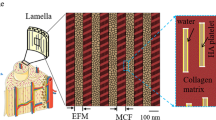
Figure 1 illustrates an overview of the proposed methodology for two-dimensional analysis of the microstructure of the cortical bone. From a given bone structure, as illustrated in Fig. 1a, a conceptual (simplified geometry) model can be defined (Fig. 1b), which is the base for the definition of two-dimensional models, as shown in Figs. 1c (cross-section plane) and 1d (longitudinal plane). In this work, the two-dimensional models are initially discretized in finite elements using standard three-noded triangular finite elements. Then, the mesh fragmentation technique is employed to consider the cortical bone as a four-phase material (interstitial matrix, cement line, secondary osteons, and Haversian canals) and to define the possible crack paths during the failure process (Fig. 1e).

Fig. 1
figure 1

Stages of the proposed methodology for the generation of the two-dimensional geometry: a bone structure (femur); b conceptual representation of the femur diaphysis; c transversal plane of the diaphysis; d longitudinal plane of the diaphysis; e fragmentation of the finite element mesh: e.1 regular mesh, e.2 separation of the standard finite elements, and e.3 insertion of interface elements

Full size image

The MFT is based on the use of triangular finite elements with high aspect ratios (HAR elements). These elements are strategically inserted between the regular three-noded triangular finite elements. Therefore, first, the regular elements (Fig. 1e.1) are separated by duplicating the common nodes, and subsequently, their sizes are reduced. The small gaps formed between adjacent elements (Fig. 1e.2) are filled by pairs of HAR elements (Fig. 1e.3), i.e., pairs of three-noded triangular finite elements, in such a way that the HAR elements inserted between two different phases of the material are defined with mechanical properties appropriated to describe the failure process. In other words, the interfaces matrix–matrix, osteon–osteon and cement line (osteon–matrix) are represented by pairs of HAR elements combined with an appropriate damage model to describe the crack opening, closure, and sliding.

2.2 HAR elements

The high aspect ratio (HAR) elements play a critical role in the failure process as they concentrate all the nonlinear behavior of the material, which allows simulation of the crack propagation process on the matrix, osteon, and between osteon and matrix (cement line).

Figure 2 illustrates a HAR element with its geometric components, base b, defined by the distance between nodes 2 and 3, and height h, by the distance between node 1 and its projection \(1'\) on the element base.

Fig. 2
figure 2

Finite element with high aspect ratio

Full size image

Considering the local coordinate system (n, s), oriented such that axis s coincides with the orientation of the HAR element base (see Fig. 2), the displacement vector of the node i can be defined as:

$$\begin{aligned} {\varvec{u}}^{{\varvec{i}}}=\left\{ \begin{array}{c} {u}_{s}^{i}\\ {u}_{n}^{i}\\ \end{array}\right\} . \end{aligned}$$
(1)

Similarly, a displacement vector at the material point \(1'\) can be written as:

$$\begin{aligned} {\varvec{u}}^{\varvec{1'}}=\left\{ \begin{array}{c} {u}_{s}^{1'}\\ {u}_{n}^{1'}\\ \end{array}\right\} =\left\{ \begin{array}{c} \frac{(u_{s}^{2}b_{2}+u_{s}^{3}b_{1})}{b}\\ \frac{(u_{n}^{2}b_{2}+u_{n}^{3}b_{1})}{b}\\ \end{array}\right\} . \end{aligned}$$
(2)

Therefore, the relative displacement between the node 1 and its projection \(1'\) is given by:

$$\begin{aligned} \hat{{\varvec{u}}}={{\varvec{u}}}^{{\varvec{1}}'}-{{\varvec{u}}}^{{\varvec{1}}}=\left\{ \begin{array}{c} {\hat{u}}_{s}\\ {\hat{u}}_{n}\\ \end{array}\right\} =\left\{ \begin{array}{c} u_{s}^{1'}-u_{s}^{1}\\ u_{n}^{1'}-u_{n}^{1}\\ \end{array}\right\} . \end{aligned}$$
(3)

By the standard finite element (FE) approximation and using Voigt vector notation, the strain tensor at any point within the element can be approximated as follows:

$$\begin{aligned} {\varvec{\varepsilon }}=\left\{ \begin{array}{c} \varepsilon _{ss}\\ \varepsilon _{nn}\\ \gamma _{sn} \end{array}\right\} =\left\{ \begin{array}{c} \frac{h(u_{s}^{3}-u_{s}^{2})}{bh}\\ \frac{-bu_{n}^{1}+(s^{1}-s^{3})u_{n}^{2}+(s^{2}-s^{1})u_{n}^{3}}{bh}\\ \frac{-bu_{s}^{1}+(s^{1}-s^{3})u_{s}^{2}-hu_{n}^{2}+(s^{2}-s^{1})u_{s}^{3}+hu_{n}^{3}}{bh} \end{array}\right\} =\left\{ \begin{array}{c} \frac{u_{s}^{3}-u_{s}^{2}}{b}\\ \frac{{\hat{u}}_{n}^{1}}{h}\\ \frac{{\hat{u}}_{s}^{1}}{h}+\frac{u_{n}^{3}-u_{n}^{2}}{b} \end{array}\right\} . \end{aligned}$$
(4)

Note that Eq. 4 can be split into two vectors, one that is a function of the height h and another that is a function of the base b:

$$\begin{aligned} {\varvec{\varepsilon }}=\underset{{\hat{\varvec{\varepsilon }}}}{\underbrace{h^{-1}\left\{ \begin{array}{c} 0\\ {\hat{u}}_{n}^{1}\\ {\hat{u}}_{s}^{1} \end{array}\right\} }}+\underset{\tilde{{\varvec{\varepsilon }}}}{\underbrace{b^{-1}\left\{ \begin{array}{c} u_{s}^{3}-u_{s}^{2}\\ 0\\ u_{n}^{3}-u_{n}^{2} \end{array}\right\} }}. \end{aligned}$$
(5)

For a general coordinate system, it is possible to rewrite Eq. 4 as:

$$\begin{aligned} {\varvec{\varepsilon }}=h^{-1}\left( {\varvec{n}}\otimes \hat{{\varvec{u}}}\right) ^{s} +\tilde{{\varvec{\varepsilon }}}, \end{aligned}$$
(6)

where \(\left( \bullet \right) ^{s}\) is the symmetrical part of \(\left( \bullet \right) \), \(\otimes \) is the dyadic operator, \({\varvec{n}}\) is the unit vector normal to the element base, and \({\hat{\varvec{u}}}\) is the relative displacement defined in Eq. 3.

As the height h approaches zero (\(h\rightarrow 0\)), the strain component \(\tilde{{\varvec{\varepsilon }}}\) remains bounded, while the component \(\hat{\varvec{\varepsilon }}\) becomes unbounded. Therefore, in the limit, as h tends to zero, node 1 and its projection \(1'\) converge toward the same material point, and the relative displacement \({\hat{\varvec{u}}}\) predominantly influences the element strains. As depicted by Manzoli et al. [51], in this limit situation, Eq. 6 corresponds to the typical kinematics of the Continuum Strong Discontinuity Approach (CSDA) [59, 60] since the relative displacement vector becomes a jump in the displacement field (\([\![{\hat{\varvec{u}}}]\!]\)). Consequently, the analyses can be performed integrally in the context of the continuum mechanics, representing a clear advantage of the proposed approach.

2.3 Material model description

2.3.1 Composed damage model

A composed damage model describes the initiation and propagation crack processes with two independent scalar damage variables that simulate the opening, closure, and sliding via the HAR elements. First, the effective stress tensor, written in local coordinates (see Fig. 2), is defined as the elastic stress tensor \(\bar{\varvec{\sigma }}={\varvec{C}}\varvec{\varepsilon }\). Then, it is split into two tensors, \(\bar{\varvec{\sigma }}^{t}\) and \(\bar{\varvec{\sigma }}^{\tau }\), that contain the normal and tangential stress components, respectively:

$$\begin{aligned} \bar{\varvec{\sigma }}=\underbrace{{\left[ \begin{array}{ll} {\bar{\sigma }}_{ss} &{}\quad 0\\ 0 &{}\quad {\bar{\sigma }}_{nn} \end{array}\right] }}_{\bar{\varvec{\sigma }}^{t}}+\underset{\bar{\varvec{\sigma }}^{\tau }}{\underbrace{\left[ \begin{array}{ll} 0 &{}\quad {\bar{\tau }}_{sn}\\ {\bar{\tau }}_{ns} &{}\quad 0 \end{array}\right] }}, \end{aligned}$$
(7)

and the shear damage \(d^{\tau }\) is applied only to the tangential stress components, as follows:

$$\begin{aligned} \varvec{\sigma }^{\tau }=\bar{\varvec{\sigma }}^{t}+(1-d^{\tau }) \bar{\varvec{\sigma }}^{\tau }\qquad {{\textrm{with}}\quad d^{\tau }({\bar{\tau }}_{ns})}\in [0,1]. \end{aligned}$$
(8)

Hereafter, the effective stress tensor for the implementation of the tension damage \(d^{t}\) is defined as \(\bar{\varvec{\sigma }}^{t_{\textrm{eff}}}=\varvec{\sigma }^{\tau }\), and the nominal stress tensor is given by:

$$\begin{aligned} \varvec{\sigma }^{t}=(1-d^{t})\bar{\varvec{\sigma }}^{t_{\textrm{eff}}}\qquad {{\textrm{with}}\quad d^{t}({\bar{\sigma }}_{nn})}\in [0,1]. \end{aligned}$$
(9)

An updated version of the damage model equations from Rodrigues et al. [52] for a load step \(t+1\) is detailed in Table 1. It is important to highlight that the shear damage (Table 1) does not consider the confinement (friction).

Table 1 Equations for the damage model at the load step \(t+1\)
Full size table

2.3.2 Implicit–explicit integration scheme (Impl-Ex)

The constitutive model presented in the previous section is integrated using an implicit-explicit integration scheme (Impl-Ex) [58, 61] to avoid numerical convergence problems, usually found in problems where multiple cracks are expected.

The Impl-Ex can be divided into two parts for a load step \(t+1\):

  1. 1.

    Implicit stage, in which the standard backward-Euler scheme is used to calculate the effective stress tensor \(\bar{\varvec{\sigma }}_{t+1}\) and the strain-like variable \(r_{t+1}\) is defined;

  2. 2.

    Explicit stage, where the strain-like variable \({\tilde{r}}_{t+1}^{\tau }\) is defined as a function of the implicit value calculated in the previous step. The damage evolution variable \({\tilde{d}}_{t+1}\) is evaluated as a function of the extrapolated internal strain and stress-like variable. Then, the nominal stress tensor \(\varvec{\sigma }_{t+1}^{t}\) is computed.

The tangent operator depicts the condition of the interface element and shall be able to account for the interface’s opening, closure and sliding. Thus, the effective tangent operator is defined as:

$$\begin{aligned} \frac{\partial \varvec{\sigma }_{t+1}}{\partial \varvec{\varepsilon }_{t+1}}=\tilde{{\varvec{C}}}_{t+1}^{tan} \end{aligned}$$
(10)

Table 1 summarizes the equations of the proposed model, and Fig. 3 details the algorithm of the Impl-Ex scheme.

Fig. 3
figure 3

Flowchart of the Impl-Ex integration scheme for the composed damage model

Full size image

2.3.3 Material parameters

The mechanical properties associated with the finite elements are depicted in Table 2. These values are based on Marco et al. [34], except for the shear variables and Young’s modulus of the cement line. It is noteworthy that the shear damage is considered only at the cement line (if present).

Table 2 Mechanical properties of the constituents in cortical bone: Young’s modulus E; tensile strength \(f^{t}\); critical shear stress \(f^{\tau }\); opening fracture energy \(G_{f}^{I}\); sliding fracture energy \(G_{f}^{II}\)
Full size table

2.4 Numerical examples

The analyses describe the mechanical behavior of the cortical bone in two-dimensional and quasi-static simulations. They are based on the boundary conditions and geometry of models that aim to capture the influence of the cement line on the crack pattern. A total of five examples with different configurations are performed: four conceptual representations and one based on a digital image from an experimental test.

The geometries are designed, the finite element mesh is generated, mechanical properties are associated, and boundary conditions are applied using the GiD software (pre- and post-processor) [68]. A routine in MATLAB [69] is responsible for the mesh fragmentation and insertion of the interface elements. The height of the interface elements is defined as \(0.01~\mu \)m, which is enough to minimize the intrinsic errors, according to [51]. Table 3 summarizes the material parameters adopted for each test. The identification of the models is based on the following rule:

  • first character: B for three-point bending test or T for uniaxial tension test;

  • second character: number of osteons in the model, e.g., 1 osteons, 2 osteons or M for multiple osteons;

  • third character: R for the realistic representation of the cortical bone microstructure.

The discontinuities (notches) have been implemented in the geometries to force the crack initiation where the original authors had defined the initial crack.

Table 3 Information of the numerical examples. Size: finite element size, Dof: degrees of freedom, PStrain: plane strain, and Pstress: plane stress
Full size table

Models B1 (Fig. 4) and B2 (Fig. 5) represent the microstructure of the cortical bone in the cross-sectional plane in a three-point bending test. The displacements are applied at the top of the models, and the discontinuities are implemented at the bottom to force the crack evolution to cross the model.

Fig. 4
figure 4

Model B1 is set as a three-point bending test with an osteon (diameter of \(200~\mu \)m) and Haversian canal (diameter of \(50~\mu \)m). The figure is not to scale

Full size image
Fig. 5
figure 5

Model B2 is set as a three-point bending test with a large osteon (diameter of \(200~\mu \)m) with a Haversian canal (diameter of \(50~\mu \)m) and small osteon (diameter of \(120~\mu \)m) with a Haversian canal (diameter of \(60~\mu \)m). The figure is not to scale

Full size image

The model TM (Fig. 6) displays a uniaxial tension test with multiple osteons with different diameters. The discontinuities are placed at the structure’s top and bottom to force the model’s division throughout the analysis. The geometry of the model was extracted from [70] via WebPlotDigitizer [71].

Fig. 6
figure 6

Model TM is set as a uniaxial tension test with multiple osteons distributed in the central part of the geometry. The figure is not to scale

Full size image

The unit models displayed in Fig. 7 present the same osteon embedded in the interstitial matrix on different planes, the osteon is tilted by \(10^{\circ }\) on model T1 (from the vertical axis). The discontinuity is placed at mid-depth with times the length proposed by Gustafsson et al. [11] to impose that the crack will reach the osteon before the cement line is in advanced damage condition.

Fig. 7
figure 7

Models T1 is set in a uniaxial tension test configuration with a single osteon displayed on the longitudinal plane (length of \(750~\mu \)m, and diameter of \(150~\mu \)m) and Havesian canal with a diameter of \(50~\mu \)m. The figure is not to scale

Full size image

The BMR model is based on the geometry of the w06003 specimen tested by Budyn and Hoc [32]. The WebPlotDigitizer [71] was used to capture the test’s geometry using both the original image and the example performed by Marco et al. [34]. Figure 8 compares the image from the experimental test with the numerical representation and details the model’s geometry components and boundary condition. The gray area of the model is not the focus of this work. Therefore, it is discretized with a coarse mesh of CST elements with no interface elements between them, which are associated with the material parameters of the interstitial matrix (see Table 3).

Fig. 8
figure 8

Comparison of the geometry between the experimental and numerical models: a image of the w06003 specimen from [32]; b experimental and numerical overlapped models; c numerical representation of the w06003

Full size image

3 Results and discussions

3.1 Crack pattern

3.1.1 Model B1

Figure 9 illustrates the crack pattern obtained for model B1. When the prescribed displacement is \(0.9~\mu \)m, the main crack starts to develop at the notch (Fig. 9a.3), while the interface between osteon and matrix presents large parallel displacements (Fig. 9a.2). The main crack reaches the cement line at \(1.2~\mu \)m as seen in Fig. 9b. At the end of the analysis, the main crack merges with the cracks at the cement line and presents the bifurcation (Fig. 9c). The osteon is attached to the matrix by a small portion of the interface and does not present any cracking.

Fig. 9
figure 9

Crack pattern of the Model B1 for the following prescribed displacements: a \(0.9~\mu \)m; b \(1.2~\mu \)m; and c \(3~\mu \)m. Displacements are magnified 10 times. Model B1 is depicted with the interface elements (c.1) and without them (c.2)

Full size image

3.1.2 Model B2

Figure 10 details the crack pattern at four different stages of the analysis. When the applied displacement is \(1.2~\mu \)m, there is minimum damage at the notch, but both osteons present parallel displacement relative to the matrix. At \(4~\mu \)m, the crack from the notch (main crack) connects with the cement line and a large portion of the osteon detaches from the matrix. Then, the main crack courses to the smaller osteon, whose cement line is already damaged. Finally, the cracks coalesce into a large discontinuity that crosses the model vertically through the matrix and cement line without crossing the osteons.

Fig. 10
figure 10

Crack pattern of the Model B2 for the following prescribed displacements: a \(1.2~\mu \)m (magnified 10 times); b \(4~\mu \)m (magnified 5 times); c \(6~\mu \)m (magnified 5 times); and d \(10~\mu \)m (not magnified)

Full size image

3.1.3 Model TM

The crack pattern of the model TM is depicted in Fig. 11. The cement lines of the osteons located at the central part of the model present damage, while cracks develop at the notches with the applied displacement of \(1~\mu \)m. At \(2~\mu \)m, the cement line of the larger osteons presents a large displacement, instigating the cracking of the interstitial matrix. The cracks from the notches are influenced by the damaged cement lines and are directed to the nearest osteons. At the end of the analysis, the model presents multiple cracks in the matrix and cement lines, while the osteons do not have discontinuities.

Fig. 11
figure 11

Crack pattern of the Model TM for the following prescribed displacements: a \(1~\mu \)m (magnified 10 times); b \(2~\mu \)m (magnified 10 times); and c \(10~\mu \)m (not magnified)

Full size image

3.1.4 Model T1

The crack pattern is shown at three stages of the analysis in Fig. 12. When the applied displacement is almost \(1.2~\mu \)m, a crack starts to develop at the notch, and the cement line presents large displacements at both ends of the osteon. Then, with \(2.9~\mu \)m the matrix presents cracks at critical points near the ends of the osteons where the cement line is damaged while the crack from the notch develops horizontally toward the osteon. Finally, as the osteon slides in the model, another crack appears in the matrix near the osteon and courses toward the notch on the left (Fig. 12c.3), while the crack on the interface at the top of the osteon progress toward the right edge of the model (Fig. 12c.2).

Fig. 12
figure 12

Crack pattern of the Model T1 for the following prescribed displacements: a \(1.2~\mu \)m (magnified 10 times); b \(2.9~\mu \)m (magnified 5 times); and c \(7.3~\mu \)m (not magnified)

Full size image

3.1.5 Model BMR

The crack pattern obtained in the analysis of the model BMR is shown in Fig. 13. The damage of the cement line before the main crack (originating at the notch) is a recurring phenomenon in this analysis. When the prescribed displacement is \(6.5~\mu \)m, the main crack starts to develop while the cement line of the nearby osteons presents large displacements. At \(19.5~\mu \)m, the large osteon with two Haversian canals is crossed by a crack. Then, as the main crack travels upward, the cracks on the cement lines of the osteons propagate in the interstitial matrix (Fig. 13d). In the end, the model presents multiple cracks that tend to coalesce into one large crack, as can be seen in Fig. 13e.

Fig. 13
figure 13

Crack pattern of the Model BMR for the following prescribed displacements: a \(6.5~\mu \)m (magnified 10 times); b \(13~\mu \)m (magnified 5 times); c \(19.5~\mu \)m (magnified 3 times); d \(26~\mu \)m (not magnified); and e \(29.3~\mu \)m (not magnified)

Full size image

3.2 Constituents role in crack propagation

The different phases of cortical bone at the microscale have an important role in the complex mechanical behavior of the structure. Therefore, to study how sensitive the adopted methodology is to the parameters on the final crack pattern, the numerical examples (using the same boundary conditions and finite element meshes) are reanalyzed with different mechanical properties associated with the cement lines and the osteons.

In this section, the models are carried out three times with different parameters associated with the interface and regular CST elements:

  • (a) with the values listed in Table 2;

  • (b) with the values listed in Table 2, but associating the cement line with the parameters of the interstitial matrix. Thus, only tension damage is considered;

  • (c) homogenized model in which all the elements are associated with the parameters of the interstitial matrix.

The crack patterns are depicted and discussed at the end of the analyses.

The model B1 shows distinct crack patterns when the parameters are tweaked. The coalescence of the crack from the notch with the cracking of the cement line causes the large bifurcated crack seen in 14a. The absence of this interface makes the osteon vulnerable to cracking. In Fig. 14b, it is possible to see that the crack is arrested at the interface of the osteon, but still, the osteon presents minor damage signs. When all the constituents have the matrix properties in Fig. 14c, the main crack propagates directly to the Haversian canal without being arrested.

Fig. 14
figure 14

Comparison of the crack patterns of the model B1 when a all the constituents are considered; b the cement line is associated with the interstitial matrix properties; and c osteons and cement line are associated with the interstitial matrix properties. Displacements are magnified 10 times. The models are shown with prescribed displacement of \(3~\mu \)m

Full size image

Model B2 is designed to force the crack deflection at the cement line, as illustrated in Fig. 15a. This phenomenon is replicated, at least at the beginning of the analysis of Fig. 15b, where the different mechanical parameters of the osteon and matrix influence the crack path at the interface of the large osteon but are not effective in avoiding the cracking of the small osteon. With homogenized parameters (Fig. 15c), the crack formed at the notch is directed to the nearest void, and the cracks that appear at the Haversian canal propagates upward to the small Haversian canal and downward to the notch.

Fig. 15
figure 15

Comparison of the crack patterns of the model B2 when a all the constituents are considered; b the cement lines are associated with the interstitial matrix properties; and c osteons and cement lines are associated with the interstitial matrix properties. Displacements are not magnified. The models are shown with prescribed displacement of \(10~\mu \)m

Full size image

Figure 6 depicts the influence of the cortical bone constituents on the crack pattern of the model TM. In Fig. 6b, the osteons do not show any damage signs and act as barriers to crack growth. Nevertheless, the cracks appear at the Haversian canals and develop through the model, aiming at other voids in Fig. 6c. Although there are two notches in the model, small cracks appear independently within the structure in all situations, and they tend to be influenced by nearby discontinuities, whether Haversian canals or linear cracks.

Fig. 16
figure 16

Comparison of the crack patterns of the model TM when a all the constituents are considered; b the cement lines are associated with the interstitial matrix properties; and c osteons and cement lines are associated with the interstitial matrix properties. Displacements are not magnified. The models are shown when the prescribed displacement is \(10~\mu \)m

Full size image

The cement line allows the sliding of the interstitial matrix to avoid damaging the osteon in model T1 (Fig. 17a). When the shear damage is not considered, the osteon presents stress concentration at its inner vertex, leading to crack initiation in both Fig. 17b, c. Moreover, the main crack is not stopped at the interface and develops inside the osteon.

Fig. 17
figure 17

Comparison of the crack patterns of the model T1 when a all the constituents are considered; b the cement line is associated with the interstitial matrix properties and c osteons; and cement lines are associated with the interstitial matrix properties. Displacements are magnified 2 times. The models are shown with prescribed displacement of \(7.3~\mu \)m

Full size image

The cement lines greatly influence the crack propagation of the model BMR, as can be seen in Fig. 18a. They are the first cracking locations of the model and modify the main crack path. Furthermore, the final crack pattern resembles the experimental result depicted in Fig. 18d. Once the cement line parameters are dismissed, the cracking displayed in Fig. 18b shows that the osteon distinct parameters influence the crack trajectory but stray from the expected behavior. When the homogenized model is analyzed, the cracks seek the Haversian canals since they act as stress concentration mechanisms. Thus, they present a crack pattern that disagrees with what was observed in the test.

Fig. 18
figure 18

Comparison of the crack patterns of the model BMR when a all the constituents are considered, b the cement lines are associated with the interstitial matrix properties and c osteons and cement lines are associated with the interstitial matrix properties. The cracking is marked in red on the experimental test image taken from [32] in d. Displacements are not magnified. The models a–c are shown with prescribed displacement of \(29.3~\mu \)m

Full size image

4 Summary and Conclusions

In this work, the mesh fragmentation technique is used with a composed continuum damage model capable of describing the crack initiation and propagation phenomena on the cortical bone microstructure. It is known that cracks travel in the interstitial matrix and have a high probability of developing through the cement line, as discussed in Boyce et al. [72]. Furthermore, the appearance of multiple small cracks (diffuse damage) is a phenomenon that is observed in situ but not entirely understood [46, 47]. Thus, the proposed numerical model is used with the main objective of reproducing the cracking behavior of the material in the numerical examples. The resulting crack patterns prove that the numerical model is sensitive to the geometry and mechanical properties of the cortical bone constituents providing crack patterns (with multiple discontinuities) that agree with the behavior of this material.

The analyses herein capture the protagonism of the cement line in the overall behavior of the structure. In addition to acting as a crack amplifier, it also originated discontinuities in all examples. Even prior to the main crack (the one that originated at a notch) arrival, the cement line shows large displacements both parallel and orthogonal, this is mainly due to the ultimate properties associated with the interface. The shear strength is easily reached when the interface is sliding, provoking evident changes on the crack path of the models (e.g., model T1 and BMR). Additionally, the methodology is able to present multiple cracks that tend to coalesce (e.g., model B1 and B2) or delay the coalescence process (e.g., model TM) during the analyses, a phenomenon which is also observed experimentally [46, 73].

The numerical examples are also tested using different sets of material parameters: considering all the constituents, neglecting the cement line and homogenizing all constituents with the parameters of the interstitial matrix (with the exception of the Haversian canals) to study their influence on the crack patterns. When the cement line is considered, the osteons do not present cracking inside them as they are protected by this thin interface. The absence of the cement line allows the cracking of the osteons and changes the crack pattern of each model. The osteon parameters influence the crack trajectory when the crack orientation is close to a straight angle (e.g., Model B2 in Fig. 15b and Model TM in Fig. 16b); otherwise, they tend to cross osteons toward the Haversian canal (Fig. 17c). In the homogenized examples, the cracking is orchestrated by the stress concentrations at Haversian canals and notches. Cracks connect these discontinuities and tend to coalesce into a single large crack (e.g., Model BMR in Fig. 18c) or multiple cracks appear in the interstitial matrix and move toward the nearest Haversian canals (e.g., Model T1 in Fig. 17c).

The results demonstrated that the MFT is sensitive to the mechanical parameters of the constituents and can present multiple cracks. When the cement line is taken into account, the obtained results agree with the known behavior of the structure in experimental tests and can be used to further study the phenomena and aspects not fully comprehended e.g., cement line properties and the role of diffuse damage in the overall cortical bone mechanical behavior.

Finally, when compared to other methods, such as the extended finite element method (X-FEM) and embedded finite element method (E-FEM), the MFT demonstrated to be a very promising alternative for modeling multiple cracks when a reasonable unstructured mesh and refinement are adopted. The Impl-Ex algorithm used to integrate the constitutive model ensures numerical convergence, and the methodology does not require tracking algorithms. In addition, combining the HAR element and continuum model does not require a penalty parameter to avoid mesh interpenetration, as typically required in the formulation of zero-thickness elements or a particular integration procedure, as seen in X-FEM formulations.