1 Introduction

In a constantly growing industrial society, technical noise is an indispensable burden. The influence of acoustic noise and vibrations on the human body can certainly cause harmful consequences. The increasing demand for sound and vibration absorbers and noise control devices reflects this problem [1, 2]. To minimise this, solutions have been found primarily in the higher-frequency range above 1500 Hz [3]. The lower-frequency range has limited solutions up to now [4]. Structures which cause the disturbing vibrations also have eigenmodes, which is a phenomenon already known in ancient times [5]. The eigenmodes are forming when the structure is excited at its eigenfrequencies. One common way of vibration attenuation, in this case, is to simply prevent such an excitation. The damping of vibrations can take place actively, semi-actively or passively [6]. If the frequency range of interest is fixed then passive vibration dampers can achieve advantageous results [6, 7] without the need for an active control concept [7, 8]. During recent years, metastructures and metamaterials have gained increasing attention due to their versatile design potential [9]. Such materials or structures are designed for achieving a specific dynamic behaviour which cannot be achieved by standard structures.

Fig. 1
figure 1

Different wedge-shaped ABH based on [10]

Full size image

Metastructures exploiting acoustic black holes are an efficient way for achieving vibration attenuation and noise regulation [11, 12]. An acoustic black hole (ABH) is a geometrical structure from which theoretically no bending wave can escape above a certain frequency [10, 11]. Figure 1 visualises different wedge-shaped ABH investigated in [10]. Their difference lies in the steepness of the wedge. The present contribution outlines the simulation process to reach the maximum vibration attenuation and a decrease of sound radiation in a frequency range of interest. Stacking a certain number of wedges provides a degree of freedom in the design of a metastructure that allows for a simple tunability of the frequency range of attenuation, especially at low frequencies that are difficult to reach without increasing the length of an ABH [13]. Systematic studies are performed for comparing stacked wedges of equal or different lengths with focus on low-frequency vibration mitigation. The methodology developed allows for a theoretical interpretation of the experiments performed on stacked wedge-shaped ABH manufactured by additive manufacturing. Finally, stacked wedges at different lengths are presented that allow broadband attenuation at low frequencies.

2 Wedge-shaped acoustic black hole

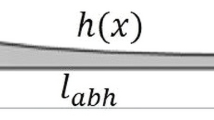
The first idea of a simple 1D wedge-shaped acoustic black hole was stated by Mironov in 1988 [10], allowing the bending wave velocity to become theoretically zero if the thickness decreases according to the power-law curve \(h(x)=\varepsilon x^m\). Herein, x is the distance from the tip, h(x) the corresponding thickness, the parameter \(\varepsilon \) represents the scaling constant and m is a positive rational exponent of the ideal power-law curve with \(m \ge 2\). When manufacturing such a geometry then the thickness cannot vanish and a residual thickness \(h_{\text {tip}}\) remains at the free end of the beam. The attachment of such a wedge to a host beam structure of the length \(l_{\text {beam}}\) and width b results is sketched in Fig. 2 and motivated by [10, 12].

Fig. 2
figure 2

Parameterised beam with a single wedge-shaped ABH motivated by [10, 12], adapted from [22]

Full size image

The power-law curve of a single wedge-shaped ABH suggested in [14] follows the thickness profile

$$\begin{aligned} h(x)=\frac{h_{\text {tot}}-h_{\text {tip}}}{l_{\text {abh}}^m}x^m+h_{\text {tip}}, \end{aligned}$$
(1)

where \(h_{\text {tot}}\) describes the thickness of the beam and hence the overall thickness of the wedge, \(h_{\text {tip}}\) is the remaining thickness at the tip and \(l_{\text {abh}}\) represents the overall length. From [15] the wave number k(x) along the wedge is

$$\begin{aligned} k(x)=\root 4 \of {12}\sqrt{\frac{\rho (1-\nu ^2)\omega ^2}{\text {Eh}(x)}} \end{aligned}$$
(2)

and the corresponding reflection coefficient of the whole edge becomes [15]

$$\begin{aligned} R=\exp \left( -2\int _{x_{\text {tip}}}^{x}\Im \{k(x)\}\text {d}x\right) . \end{aligned}$$
(3)

For \(x_{\text {tip}}\rightarrow \infty \) and \(h_{\text {tip}}=0\), the local wave number tends towards infinity, while the reflection coefficient tends towards zero ([16]), which means that wave energy escaping the wedge is negligible. The wave equations for flexural waves in elastic tapered wedges can be solved with the Wentzel-, Kramers-, and Brillouin-approximation (WKB-method). The WKB-method provides analytical solutions of different orders of approximation to differential equations, which is shown in [17].

The main contribution of the present work is the suggestion of stacked multi-wedge ABH for achieving a low-frequency vibration attenuation and acoustic emission with a compact design. Two different geometrical variants are sketched in Fig. 3. Herein, the thickness \(h_{\text {tot}}\) in Fig. 1 becomes the thickness \(h_0\) of each individual wedge. For a number n of stacked wedges, the overall thickness \(h_{\text {tot}}\) of the beam obeys the relation \(h_{\text {tot}} = nh_0\). Consequently, an increasing number of wedges decreases the thickness \(h_0\) of each wedge as well as the corresponding \(h_{\text {tip}}\). Introducing a variable length of each wedge \(l_{\text {abh}_i}\) results in the geometrical variant in Fig. 3b. This results in a length difference \(l_{\text {abh}_{\text {diff}}}\). The initial thickness \(h_0\) stays the same.

Fig. 3
figure 3

Geometrical variants of a two stacked wedges: (left) equal length [22] and (right) different length

Full size image
Fig. 4
figure 4

Workflow for ABH simulation with different analysis software according to [18]

Full size image

3 Numerical calculation of a multi-wedge

A parametric design for the numerical analysis was chosen in order to be able to determine dispersion curves and to perform a geometrical optimisation. A flexible beam possessing a single- or multi-stack wedge in a CAD-software is the base structure for the subsequent analysis and discussion. The structure is not supported in this simulation, i.e. the degrees of freedom at the boundaries are not fixed. The workflow and interaction are visualised in Fig. 4. The CAD-software SOLIDWORKS was chosen. This software enables a parametric design of the stacked multi-wedge which can be directly linked to the finite element software COMSOL Multiphysics. The numeric computing software MATLAB was used to define dynamically the geometry, physical boundary conditions, material properties, proper mesh settings. This process allows for performing parametric studies.

Table 1 Material properties of steel AISI4340 and 1.2709
Full size table

The main motivation for the multi-stack wedges is the achievement of a low-frequency vibration attenuation for the main beam. Two types of stacked wedges are examined, wedges with equal as well as different lengths. Table 1 shows the material properties chosen for the present study: beam steel AISI4340 and steel 1.2709 for the wedges. The choice is based on the availability of materials for conventional and additive manufacturing within the project. An isotropic loss factor \(\eta \) of 10\(^{-3}\) is assumed for structural damping of the material, a value that is commonly observed for steel structures.

Table 2 Parameters for equal length multi-wedge ABH given in mm
Full size table
Fig. 5
figure 5

Multi-stacked wedges with parameters according to Table 2: (left) simple wedge, (middle) two wedges and (right) ten wedges, adapted from [22]

Full size image

Starting with the multi-wedge with equal lengths according to Fig. 3a, models of a simple wedge, two, three, four and ten stacked wedges are built with the parameters listed in Table 2. Individual ABH-wedge designs of size 30 x 5 x 50 mm are attached to a steel beam of dimensions 30 x 5 x 250 mm. Samples of the simple wedge and two and ten wedges are shown in Fig. 5.

Fig. 6
figure 6

First four natural frequencies and modeshapes for two, three, four and ten wedges with energy indicator calculated with eq. 4

Full size image

Parametric studies are performed for the eigenfrequencies and modeshapes of the overall structure including the beam. An indicator is introduced for determining whether a specific wedge design performs well and localises and subsequently absorbs the vibration energy in the wedge. The indicator is defined as the ratio between the kinetic energy of the ABH compared to the kinetic energy in the beam. This energy is readily available in the finite element calculations by evaluating the indicator of the energy density \(r_E\) [19]

$$\begin{aligned} r_E = \frac{E_{\text {ABH}}^{\text {kin}}}{E_{\text {beam}}^{\text {kin}}} = \frac{\int _{V_{ABH}} w_{\text {ABH}}\,\text {d}V}{\int _{V_{\text {beam}}} w_{\text {beam}}\,\text {d}V}. \end{aligned}$$
(4)

The higher this indicator, the stronger the localisation of energy in the wedge and the better the performance of the ABH design. Figure 6 shows a set of results of the natural frequencies and modeshapes for a specific length of \(l_{\text {abh}}=50\) mm and \(l_{\text {beam}}=250\) mm for different numbers stacked wedges. All the first modal displacements correspond to a bending mode. A dark blue colour represents a small vibration magnitude, whereas a dark red colour highlights large displacements. A properly designed ABH for a frequency range of interest shows large displacements at the wedge and negligible displacements of the main beam. For such a configuration the introduced energy ratio shows values much larger than 1.0.

For the two-wedge configuration, the first natural frequencies and the corresponding energy indicators yield (330 Hz, 5.7), (457 Hz, 58.1), (251 Hz, 65.0) and (1040 Hz, 3.9). Obviously, the second and third modeshape performs much better than the other two. Compared to a single wedge not shown in Fig. 6, the energy indicators for the first four modeshapes read (343 Hz, 3.2), (830 Hz, 25.2), (1234 Hz, 31.2) and (1782 Hz, 10.8). The three-wedge configuration performs similarly with but with strongly reduced natural frequencies. Again, modeshapes two and three outperform modeshapes one and four. However, the absolute performance of modeshapes one and four improves noticeably.

Fig. 7
figure 7

Average transfer functions of a beam with two wedges

Full size image
Fig. 8
figure 8

Average transfer functions of a beam with three wedges

Full size image
Fig. 9
figure 9

Average transfer functions of a beam with four wedges

Full size image
Fig. 10
figure 10

Average transfer functions of a beam with ten wedges

Full size image

The four-wedge configuration shows a significant improvement in performance for all four modeshapes. The smallest energy indicator grew with the number of wedges starting from the single wedge at 3.0, to the two-wedge configuration at 3.9, the three-wedge configuration at 26.4, up to four wedges at 123.5. Increasing the number of stacked wedges did not only increase the energy indicator of each modeshape but also reduced the natural frequencies considerably. The highest value of the energy indicator for the first ten modeshapes achieves 239.1 at 772 Hz. For the ten-wedge configuration, the first natural frequencies are reduced to a range of 117 to 121 Hz with an energy indicator of 96.2 or lower. While the natural frequencies reduce with the number of stacked wedges, the energy indicator first increases and then decreases again, but always performs better than the simple wedge.

Averaged transfer functions are calculated for an in-depth understanding of the dynamic behaviour of the beam configurations discussed in Fig. 6. For this purpose, the displacements for a harmonic excitation at the beam end are calculated along a centre line within the beam and the ABH, respectively, and averaged linearly. The excitation was reached by applying a harmonic force of 10 N at the end of the beam in z-direction. These averaged transfer functions are shown in Figs. 7, 8, 9, 10 for frequency range up to 5 kHz. Its peaks correspond to the natural frequencies of the system. The first four modeshapes are shown already in Fig. 6. Overall, the peaks of the averaged wedge displacement are always higher than the averaged beam displacement. Some modeshapes are only visible in the wedge transfer function, like the second natural frequency at 457 Hz for the two-wedge configuration in Fig. 7. Furthermore, increasing the number of wedges leads to lower natural frequencies and a higher modal density. Both facts are important for achieving a vibration mitigation at low-frequencies.

Parametric studies are performed by varying the geometrical properties of the wedge. Processing the natural frequencies and transfer functions result in dispersion curves shown in Fig. 11. For each wedge configuration, the first ten natural frequencies are plotted. The overall thickness \(h_{\text {tot}}\) is kept constant for each configuration, only \(h_0\) and \(h_{\text {tip}}\) decrease by following the power-law curve h(x). The decrease of the point cloud towards lower natural frequencies confirms the increase of the modal density as pointed out during the discussion of the averaged transfer functions. For the two-wedge configuration the first ten natural frequencies range up to almost 2500 Hz. This range decreases to approximately 250 Hz for ten wedges.

Fig. 11
figure 11

First ten dispersion curves for stacked wedges

Full size image
Fig. 12
figure 12

Dispersion curves of the first ten natural frequencies for a simple-, two-, four- and ten-wedge configuration in dependency of (left) the wedge length \(l_{\text {abh}}\), (middle) the width b and (right) the beam width \(h_{\text {tot}}\) or the beam length \(l_{\text {beam}}\)

Full size image

Varying the wedge length \(l_{\text {abh}}\), the width b and the beam length \(l_{\text {beam}}\) leads to the dispersion curves shown in Fig. 12 for different number of stacked wedges. Each diagram shows the lowest 10 dispersion curves. On top of that, the curves are coloured in dependency of the energy ratio between the wedge and the original beam. A low ratio is coloured in blue and a high ratio in red. A high deflection ratio corresponds to a well-performing configuration at which the wedge vibrates dominantly while the beam remains almost at rest. These dispersion curves enable clear indications of which and how a geometrical parameter of a wedge needs to be adapted for achieving good performance for a frequency range of interest, especially at low-frequency where structural vibrations are dominant.

The top row shows the dispersion curves of a simple wedge which is well-discussed in the literature. For this configuration, an increasing wedge length \(l_{\text {abh}}\) leads to lower natural frequencies and therefore better performance at low frequencies. Increasing the beam height \(h_{\text {tot}}\) increases the natural frequencies. When varying b five natural frequencies remain the same. The first four lines of these correspond to bending modeshapes. The second row represents the dispersion curves for a two-wedge configuration. Again, a long wedge is necessary in order to achieve a successful low-frequency performance. However, the necessary length is reduced from \(>80\) mm for a simple wedge to \(>60\) mm for a two-wedge configuration and to \(>40\) mm for a four-wedge configuration. Finally, a ten-wedge configuration has a very high modal density in the low-frequency range demanding a wedge length of just 30 mm.

The second column shows the dispersion curves in dependency of the beam width b. While the simple and two-wedge configurations show poor performance for the first natural frequency at 343 Hz and 330 Hz, respectively, the four- and ten-wedge configurations have superior performance at 243 Hz and 130 Hz. The third column shows the variation of the beam length \(l_{\text {beam}}\). For a small number of stacked wedges. The beam length does not help shift the natural frequencies towards low frequencies. Only for the ten-wedge configuration a reduction of the beam length leads to a reduction of the lowest natural frequency.

The dispersion curves in Fig. 11 show the first ten natural frequencies in the specific range of a specific system parameter. To achieve a highly performing ABH in the low frequency of about 100 Hz, ten wedges are showing the most promising results. Choosing the number of wedges as 10, the dispersion curves in the last row in Fig. 12 in combination with the energy ratio help to tune the performance of the multi-stacked wedge to a frequency range of interest. Increasing the length \(l_{\text {abh}}\) of the ten-wedge configuration results in lower natural frequencies and a high-performing ABH. Changing the width b shows only a small influence.

This methodology can be taken a step further, by introducing the well-known terminology of cut-on frequency in the context of ABH. Physically, the cut-on frequency marks the frequency above which the localisation of kinetic energy within the ABH is possible. Figure 13 displays the energy for a simple-, two-, three-, four- and ten-wedge configuration with highlighted cut-on frequencies. For the energy calculation, the total kinetic energy of the ABH wedges was used. These results agree nicely with the analytically predicted cut-on frequency derived in [20, 21]. For a varying exponent m, the cut-on frequencies can be calculated according to

$$\begin{aligned} f_{\text {cut}-\text {on}}(m)=\frac{h_{\text {tot}}^{1/m}}{2\pi l_{\text {abh}}^2}\root m \of {\frac{E(40-24\nu )}{12\rho (1-\nu ^2)}}. \end{aligned}$$
(5)

The figure implies that a ten-wedge configuration possesses the lowest cut-on frequency at 117 Hz, followed by the four-wedge ABH with 243 Hz. The three-wedge ABH and two-wedge ABH have their cut-on frequencies at 289 Hz and 330 Hz, respectively. The highest cut-on frequency can be seen for a simple-wedge ABH. This underlines the known fact that an ABH acting at low frequencies needs a long wedge. By introducing a multi-stacked wedge, this limitation can be overcome. The more wedges are stacked, the lower the cut-on frequency becomes.

Fig. 13
figure 13

Total kinetic energy of simple-, two-, three-, four- and ten-wedge ABH with marked cut-on frequencies

Full size image
Fig. 14
figure 14

Sound radiation and displacement of beam without and with a simple-wedge, a four-wedge and ten-wedge configuration, based on [18, 22]

Full size image

Finally, the acoustic radiation of a vibrating beam without and with ABH was calculated as shown in Fig. 14. The structure is simulated inside an air cuboid surrounded by perfectly matching layers which mimic an infinite air space. The sound pressure level is displaced for a base reference of 20 \(\mu \)Pa and a natural frequency below 1500 Hz. For each configuration the resonant frequency is shown. The displayed resonant frequencies where chosen in a very narrow frequency band of 20 Hz to give comparable results. The top picture shows a straight beam with 300 mm length. The displacements result in a clearly vibrating beam and high acoustic radiation in all directions. For a beam with a length of 250 mm and a simple wedge with 50 mm, the displacement within the beam section decreases while the wedge vibrates dominantly and the sound pressure level reduces significantly. Now, for a four-wedge configuration is attached to the beam, the acoustic radiation localised within the wedge increases further and the beam almost remains a rest. Finally, for the ten-wedge configuration, here, the overall acoustic radiation is reduced strongly, showing clearly the benefit of a multi-stacked ABH.

4 Stacked wedges of different length

The individual lengths of multi-stacked wedges are varied for achieving broadband attenuation according to the three configurations sketched in Fig. 15. The geometrical parameters are listed in Table 3.

Fig. 15
figure 15

Ten-wedge configurations for broadband vibration mitigation at low-frequency damping for (left) small and (right) large difference in wedge length

Full size image
Table 3 Parameters for the ten-wedge configurations (\(n=10\)) in Fig. 15 given in mm
Full size table

The aim is to achieve a performance in the low-frequency range between 80 and 120 Hz. For this case, two different variations were used. One with bigger length differences \(l_{\text {abh}_{\text {diff}}}\) of 2.5 mm and with smaller \(l_{\text {abh}_{\text {diff}}}\) of 1 mm. The ABH is attached to a steel beam of dimensions 30 x 5 x 100 mm. For both configurations, the vibration energy is calculated for a harmonic force of 10 N acting at the end of the original beam. Figure 16 displays the calculated energy for the two stacked configurations. The multi-wedge with smaller \(l_{\text {abh}_{\text {diff}}}\) results in more high energy peaks within the frequency range of interest. Each peak corresponds to a natural frequency at which the ABH localises the vibration energy of the beam, and minimises the vibration of the original beam. The maxima are found at the natural frequencies from the corresponding dispersion curves. The highest energy is achieved at 101 Hz with 49.8 J. In comparison, the multi-stacked wedges with \(l_{\text {abh}_{\text {diff}}}=2,5\) mm results in an energy peak of 5.0 J.

Fig. 16
figure 16

Energy for a stacked, ten-wedge configuration at different wedge lengths at low-frequency excitation at the beam end

Full size image

Finally, the energy flow through the cross-sectional area between the wedge and the beam is determined. Exciting the ten-wedge configuration with \(l_{\text {abh}_{\text {diff}}}=2,5\) mm with a force of 10 N at the end of the beam in the vertical direction results in Fig. 17. The peaks in the energy flow correspond to the peaks shown in the kinetic energy in Fig. 16. Figure 17 shows also the ratio between the kinetic energy of the wedge section and the beam section resulting from Eq. (4). A high ratio corresponds to a high energy density in the beam in relation to the beam, resulting in an efficiently working ABH. Similarly, the peaks of this energy indicator fit with the peaks of energy flow. For the presented ten-wedge configuration, energy localised in the ABH is more than 8000 times higher compared to the beam. This underlines the high performance of the proposed multi-stacked wedges.

Fig. 17
figure 17

Energy evaluations for the ten-wedge configuration at an excitation at the beam end with 10 N: (top) transmission of the energy flow through the cross section connecting the beam and the wedge, (bottom) energy density ratio between wedge and beam

Full size image

In Fig. 18, the energy flow after excitation in a stacked-wedge configuration of different wedge lengths (\(l_{\text {abh}_{\text {diff}}}=2,5\) mm) is separated in x-, y- and z-components at low-frequency excitations 80, 100 and 120 Hz. The red arrows symbolise the direction of the energy flow. The highest energy flux can be seen at the tips of the stacked wedges for the z-component. This specific configuration shows for almost all wedges a big amount of energy localisation. The x-and y-components possess at 80 Hz a higher energy flux in the longer wedges. At 100 Hz, the tips of the medium-length wedges show the highest energy flux. The wedges with the shortest length (\(l_{\text {abh}}\)) have the highest energy flux in x-and y-direction at an excitation of 120 Hz. This underlines the broadband low-frequency performance of the multi-stacked wedges at different lengths. Each wedge length contributes at a different frequency.

Fig. 18
figure 18

Energy flow in a ten-wedge configuration of different wedge lengths (\(l_{\text {abh}_{\text {diff}}}=2.5\) mm) separated in x-, y- and z-components at low-frequency excitation

Full size image

5 Comparison between wedges of equal and different lengths

The multi-wedge configuration of equal and different lengths in the low-frequency range between 80 Hz and 120 Hz is compared by evaluating the energy. The total kinetic energy is calculated for the ABH volume. The results for a ten-wedge configuration with an equal length of 50.75 mm and varying wedge length between 43.5 mm and 42.5 mm (\(l_{\text {abh}_{\text {diff}}}\)=1 mm) are shown in Fig. 19. Both multi-stacked wedges were connected to a beam of 100 mm length. The configuration with constant length shows only a single peak of 780 J at 101 Hz in the frequency range of interest. The configuration with varying lengths shows nine peaks with a maximum energy of 50 J. This confirms the broadband performance at low frequency. However, only a smaller part of the energy is channelled to the individual wedge.

Fig. 19
figure 19

Comparison of energy for a ten-wedge configuration for constant and different wedge lengths

Full size image

6 Conclusions

Finite element calculations confirm and explain the capability of multi-stacked wedges for broadband vibration localisation at low-frequency. The numerical scheme was tested for a single wedge which is discussed in detail in the literature. Introducing multiple wedges of equal and different lengths but a uniform total thickness enables the tuning to a frequency range of interest. Multi-stacked wedges with equal length were analysed in terms of natural frequencies, transfer functions and energy indicators that resulted in dispersion curves that can be easily interpreted. This formal procedure allows for quick identification of the geometrical parameters necessary for a specific frequency range of interest. In general, increasing the number of stacked wedges decreases the frequency at which vibration localisation by ABH is achieved. The energy flow between the main beam structure and the multi-wedge shows clearly the energy localisation and its strength and allows for fine-tuning of the design. An ABH with a different number of wedges reduces the acoustic radiation greatly. By varying the length of the stacked wedges, a broadband low frequency was achieved. A ten-wedge configuration is proposed that performs effectively in the frequency range between 80 and 120 Hz. At low-frequency excitation, multi-stacked wedges of equal lengths work nicely at a specific frequency range while wedges of different lengths achieve a broadband vibration localisation.