Skip to main content
SpringerLink
Log in

Effective mass and effective stiffness of finite and infinite metamaterial lattices

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

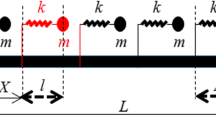
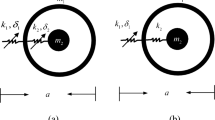
In this paper, we explore the dynamic behaviour of a metamaterial lattice which is composed of elastically connected concentrated masses coupled with local resonators (mass-in-mass lattice also referred to as the Kelvin lattice). This kind of metamaterial lattice is known to be associated with interesting phenomena such as a mass reduction effect, as compared to an equivalent Lagrange lattice composed of elastically connected effective masses. The effective mass of this metamaterial lattice is exactly calculated for finite and infinite metamaterial structures. For finite systems, the effective mass is identified from the eigenfrequencies spectrum of the metamaterial lattice. These eigenfrequencies are obtained for various boundary conditions of the metamaterial lattice, by solving a linear difference eigenvalue problem. For infinite systems, the wave dispersion of the metamaterial lattice is compared to the effective Born–Karman dispersion relation. It is shown for both the finite and the infinite systems, that the effective mass related to each branch (acoustical and optical branches) is proportional to the square of frequency associated with the complementary branch. An asymptotic expansion confirms that the effective mass tends towards the sum of each mass (the primary mass and the mass of the resonator) for the long-wave approximation of the acoustical branch. The effective mass is greater than the sum of each mass for the acoustical branch and is significantly reduced for the optical branch (with eventually a negligible reduced mass). An asymptotic analysis confirms the parametric study for each branch of the lattice spectrum. The effective stiffness is also calculated for both the finite and the infinite systems. A nonlocal continuous approach is developed to approximate the metamaterial lattice response in terms of frequency spectrum or effective mass variation. This study is concluded by a design-oriented methodology for the calibration of the effective mass from the metamaterial lattice properties.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Al Ba’ba’a, H., Nouh, M., Singh, T.: Formation of local resonance band gaps in finite acoustic metamaterials: a closed-form transfer function model. J Sound Vibration 410, 429–446 (2017)

    Article  Google Scholar 

  2. Andrianov, I.V., Awrejcewicz, J., Ivankov, O.: On an elastic dissipation model as continuous approximation for discrete media. Math Problems in Engng (2006). https://doi.org/10.1155/MPE/2006/27373

    Article  MATH  Google Scholar 

  3. Andrianov, I.V., Awrejcewicz, J., Weichert, D.: Improved continuous models for discrete media. Math. Probl. Eng. 986242, 1–35 (2010)

    Article  MATH  Google Scholar 

  4. Born, M., von Kármán, T.: On fluctuations in spatial grids. Physikalishe Zeitschrift 13, 297–309 (1912)

    MATH  Google Scholar 

  5. Born, M.: Lattice dynamics and X-ray scattering. Proc. Physics Soc. 54(4), 362–376 (1942)

    Article  Google Scholar 

  6. Borovnitskii, Y.I.: Impedance theory of wave propagation on infinite periodic structures. J. Sound Vibrat 525, 116801 (2022)

    Article  Google Scholar 

  7. Brillouin, L.: Wave propagation in periodic structures–Electric filters and crystal lattices. Mc Graw-Hill Company, New York (1946)

    MATH  Google Scholar 

  8. Brillouin, L., Parodi, M.: Propagation des ondes dans les milieux périodiques. Masson et cie, Paris (1956)

    MATH  Google Scholar 

  9. Cauchy A.: Sur les différences finies et les intégrales aux différences des fonctions entières d’une on de plusieurs variables, Exercices de mathématiques, page 155- 159, (1828)

  10. Challamel, N., Wang, C.M., Elishakoff, I.: Nonlocal or gradient elasticity macroscopic models: a question of concentrated or distributed microstructure. Mech. Res. Commun. 71, 25–31 (2016)

    Article  Google Scholar 

  11. Challamel, N., Aydogdu, M., Elishakoff, I.: Statics and dynamics of nanorods embedded in an elastic medium: Nonlocal elasticity and lattice formulations. Eur. J. Mech. A/Solids 67, 1–18 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  12. Challamel, N., Wang, C.M., Zhang, H., Kitipornchai, S.: Exact and nonlocal solutions for vibration of axial lattices with direct and indirect neighbouring interactions. J. Eng. Mech (2018). https://doi.org/10.1061/(ASCE)EM.1943-7889.0001441

    Article  Google Scholar 

  13. Chan, C.T., Li, J., Fung, K.H.: On extending the concept of double negativity to acoustic waves. J. Zhejiang Univ Sc. A 7, 24–28 (2006)

    Article  MATH  Google Scholar 

  14. Chang, I.L., Liang, Z.X., Kao, H.W., Chang, S.H., Yang, C.Y.: The wave attenuation mechanism of the periodic local resonant metamaterial. J. Sound Vibration 412, 349–359 (2018)

    Article  Google Scholar 

  15. Cui, T.J., Smith, D.R., Liu, R.: Metamaterials – Theory, Design and Applications. Springer, Berlin (2010)

    Google Scholar 

  16. Dell’Isola F. and Steigmann D.J. (Eds), Discrete and continuum models for complex metamaterials, Cambridge University Press, (2020)

  17. Elaydi, S.: An introduction to difference equations, 3rd edn. Springer, New-York, NY (2005)

    MATH  Google Scholar 

  18. Ghavanloo, E., Fazelzadeh, S.A.: Wave propagation in one-dimensional infinite acoustic metamaterials with long-range interactions. Acta Mech. 230(12), 4453–4461 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  19. Ghavanloo, E., Fazelzadeh, S.A., Rafii-Tabar, H.: Formulation of an efficient continuum mechanics-based model to study wave propagation in one-dimensional diatomic lattices. Mech. Res. Comm. 103, 103467 (2020)

    Article  Google Scholar 

  20. Ghavanloo, E., Fazelzadeh, S.A.: An analytical approach for calculating natural frequencies of finite one-dimensional acoustic metametarials. Meccanica 56, 1819–1829 (2021)

    Article  MathSciNet  Google Scholar 

  21. Goldberg, S.: Introduction to difference equations with illustrative examples from economics, psychology and sociology. Dover Publications, New-York (1958)

    MATH  Google Scholar 

  22. He, C., Lim, K.M., Liang, X., Zhang, F., Jiang, J.: Tunable band structures design for elastic wave transmission in tension metamaterial chain. Eur. J. Mech. A/Solids 92, 104481 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  23. Huang, H.H., Sun, C.T., Huang, G.L.: On the negative effective mass density in acoustic metamaterials. Int. J. Eng. Sc. 47, 610–617 (2009)

    Article  Google Scholar 

  24. Kivshar, Y.S., Zhang, F., Takeno, S.: Nonlinear surface modes in monoatomic and diatomic lattices. Phys. D. 113, 248–260 (1998)

    Article  MATH  Google Scholar 

  25. Lagrange J.L.: Recherches sur la nature et la propagation du son, Miscellanea Philosophico-Mathematica Societatis Privatae Taurinensis I, 2rd Pagination, i-112, 1759 (see also Œuvres, Tome 1, 39–148).

  26. LeVeque, R.J.: Finite difference methods for ordinary and partial differential equations: steady-state and time-dependent problems. Society for Industrial and Applied Mathematics, SIAM (2007)

    Book  MATH  Google Scholar 

  27. Li, J., Chan, C.T.: Double-negative acoustic metamaterial. Phys. Rev. E 70, 055602 (2004)

    Article  Google Scholar 

  28. Liu, Y., Shen, X., Su, X., Sun, C.T.: Elastic metamaterials with low-frequency passbands based on lattice system with on-site potential. J. Vib. Acoust 138(021011), 1–10 (2016)

    Google Scholar 

  29. Marques, R., Martin, F., Sorolla, M.: Metamaterials with negative parameters. Wiley, Hoborken (2007)

    Book  Google Scholar 

  30. Milton, G.W., Willis, J.R.: On modifications of Newton’s second law and linear continuum elastodynamics. Proc. Royal Soc. A/London 463, 855–880 (2007)

    MathSciNet  MATH  Google Scholar 

  31. Mostacelli, M., Comi, C., Marigo, J.J.: On the dynamic behavior of discrete metamaterials: From attenuation to energy localization. Wave Motion 104, 102733 (2021)

    Article  MATH  Google Scholar 

  32. Pendry, J.B.: Fundamentals and Applications of Negative Refraction in Metamaterials. Princeton University Press, Princeton (2007)

    Google Scholar 

  33. Rosenau, P.: Dynamics of nonlinear mass-spring chains near the continuum limit. Phys. Lett. A 118(5), 222–227 (1986)

    Article  MathSciNet  Google Scholar 

  34. Shen, X.H., Sun, C.T., Barnhart, M.V., Huang, G.L.: Analysis of dynamic behaviour of the finite elastic metamaterial-based structure with frequency-dependent properties. J. Vibration Acoustics, ASME 140(031012), 1–11 (2018)

    Google Scholar 

  35. Stein, A., Nouh, M., Singh, T.: Widening, transition and coalescence of local resonance band gaps in multi-resonator acoustic metamaterials: From unit cells to finite chains. J. Sound Vibration 523, 116716 (2022)

    Article  Google Scholar 

  36. Thomson W. (Lord Kelvin): Popular lectures and addresses, Constitution of matter, McMillan and Co, (1889)

  37. Veselago, V.G.: Properties of materials having simultaneously negative values of the dielectric and magnetic susceptibilities. Soviet Phys Solid State USSR 8, 2854–2856 (1967)

    Google Scholar 

  38. Vo, N.H., Pham, T.M., Hao, H., Bi, K., Chen, W.: A reinvestigation of the spring-mass model for metamaterial bandgap prediction. Int. J. Mech. Sc. 221(107219), 1–19 (2022)

    Google Scholar 

  39. Wallis, R.F.: Effect of free ends on the vibration frequencies of one-dimensional lattices. Phys. Rev. 105(2), 540–545 (1957)

    Article  MATH  Google Scholar 

  40. Wattis, J.A.D.: Quasi-continuum approximations to lattice equations arising from the discrete non-linear telegraph equation. J. Phys. A: Math. Gen. 33, 5925–5944 (2000)

    Article  MATH  Google Scholar 

  41. Zhang, H., Wang, C.M., Challamel, N., Gao, R.P.: Modelling vibrating nano-strings by lattice, finite difference and Eringen’s nonlocal models. J. Sound Vib. 425, 41–52 (2018)

    Article  Google Scholar 

  42. Zhou, Y., Wei, P., Tang, Q.: Continuum model of a one-dimensional lattice of metamaterials. Acta Mech. 227(8), 2361–2376 (2016)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Lorient, Institut de Recherche Dupuy de Lôme UMR CNRS 6027, Centre de Recherche, Univ. Bretagne Sud, Rue de Saint Maudé, BP 92116, 56321, Lorient cedex, France

    Yuchen Li & Noël Challamel

  2. Department of Ocean and Mechanical Engineering, Florida Atlantic University, Boca Raton, FL, 33431-0991, USA

    Yuchen Li & Isaac Elishakoff

Authors
  1. Yuchen Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Noël Challamel
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Isaac Elishakoff
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Noël Challamel.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, Y., Challamel, N. & Elishakoff, I. Effective mass and effective stiffness of finite and infinite metamaterial lattices. Arch Appl Mech 93, 301–321 (2023). https://doi.org/10.1007/s00419-022-02250-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-022-02250-x

Keywords

Search

Navigation