Abstract
Owing to anisotropy in the phonon and phason fields, the analysis of the elastic problems in quasicrystals is more difficult than conventional crystals. A rotating cubic quasicrystal disk is considered. Due to the nature of cubic quasicrystals, the associated problem is not axisymmetric. The semi-inverse solution method is applied to derive the closed-form solution. Explicit expressions for the phonon and phason displacements and stresses are obtained. With reference to polar coordinates, the shear stress components of the phonon and phason fields vanish everywhere in the disk, and the radial and hoop stress components of the phonon and phason fields are independent of the angular coordinate \(\theta \). However, the radial and hoop displacements of the phonon and phason fields are related to the angular coordinate. The influence of the material properties on the distribution of the elastic fields is discussed.








Similar content being viewed by others
References
Shechtman, D., Blech, I., Gratias, D., Cahn, J.W.: Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 53(20), 1951–1953 (1984)
Bindi, L., Steinhardt, P.J., Yao, N., Lu, P.J.: Natural quasicrystals. Science 324(5932), 1306–1309 (2009)
Feng, Y.C., Lu, G., Withers, R.L.: An incommensurate structure with cubic point group symmetry in rapidly solidified V-Ni-Si alloy. J. Phys. Condens. Matter 1(23), 3695–3700 (1989)
Wang, R., Qin, C., Lu, G., Feng, Y., Xu, S.: Projection description of cubic quasiperiodic crystals with phason strains. Acta Crystallogr. A 50(3), 366–375 (1994)
Donnadieu, P.: Organization of defects in the first cubic approximant of the quasicrystal Al6Li3Cu. Philos. Mag. A 64(1), 97–110 (1991)
Yang, W., Wang, R., Ding, D.H., Hu, C.: Linear elasticity theory of cubic quasicrystals. Phys. Rev. B 48(10), 6999–7002 (1993)
Gao, Y.: Governing equations and general solutions of plane elasticity of cubic quasicrystals. Phys. Lett. A 373(8–9), 885–889 (2009)
Zhou, W.M., Fan, T.Y.: Axisymmetric elasticity problem of cubic quasicrystal. Chin. Phys. 9(4), 294–303 (2000)
Gao, Y., Ricoeur, A., Zhang, L.: Plane problems of cubic quasicrystal media with an elliptic hole or a crack. Phys. Lett. A 375(28), 2775–2781 (2011)
Yang, L.Z., He, F.M., Gao, Y.: Finite element method for static problems of cubic quasicrystals. Acta Phys. Pol., A 126(2), 471–473 (2014)
Yaslan, H.Ç.: Deriving fundamental solutions for equations of elastodynamics in three-dimensional cubic quasicrystals. Acta Phys. Pol., A 136(3), 474–478 (2019)
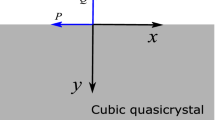
Long, F., Li, X.-F.: Flamant problem of a cubic quasicrystal half-plane. Z. Angew. Math. Phys. 73, 110 (2022)
Genta, G., Gola, M.: The stress distribution in orthotropic rotating disks. J. Appl. Mech. 48(3), 559–562 (1981)
Yeh, K.Y., Han, R.P.S.: Analysis of high-speed rotating disks with variable thickness and inhomogeneity. J. Appl. Mech. 61, 186–191 (1994)
Durodola, J., Attia, O.: Deformation and stresses in functionally graded rotating disks. Compos. Sci. Technol. 60(7), 987–995 (2000)
Zhou, F., Ogawa, A.: Elastic solutions for a solid rotating disk with cubic anisotropy. J. Appl. Mech. 69(1), 81–83 (2002)
Peng, X.L., Li, X.F.: Elastic analysis of rotating functionally graded polar orthotropic disks. Int. J. Mech. Sci. 60(1), 84–91 (2012)
Yadav, T.P., Mukhopadhyay, N.K.: Quasicrystal: a low-frictional novel material. Cur. Opin. Chem. Eng. 19, 163–169 (2018)
Fan, T.: Mathematical Theory of Elasticity of Quasicrystals and Its Applications (2011)
Rochal, S.B., Lorman, V.L.: Anisotropy of acoustic-phonon properties of an icosahedral quasicrystal at high temperature due to phonon-phason coupling. Phys. Rev. B 62(2), 874–879 (2000)
Li, X.F.: A general solution of elasto-hydrodynamics of two-dimensional quasicrystals. Philos. Mag. Lett. 91(4), 313–320 (2011)
Li, X.F.: Elastohydrodynamic problems in quasicrystal elasticity theory and wave propagation. Philos. Mag. 93(13), 1500–1519 (2013)
Bak, P.: Phenomenological theory of icosahedral incommensurate (“quasiperiodic’’) order in Mn–Al alloys. Phys. Rev. Lett. 54(14), 1517–1519 (1985)
Lubensky, T.C., Ramaswamy, S., Toner, J.: Hydrodynamics of icosahedral quasicrystals. Phys. Rev. B 32, 7444–7452 (1985)
Chernikov, M.A., Ott, H.R., Bianchi, A., Migliori, A., Darling, T.W.: Elastic moduli of a single quasicrystal of decagonal Al–Ni–Co: Evidence for transverse elastic isotropy. Phys. Rev. Lett. 80(2), 321–324 (1998)
Rochal, S.B., Lorman, V.L.: Minimal model of the phonon-phason dynamics in icosahedral quasicrystals and its application to the problem of internal friction in the i-AlPdMn alloy. Phys. Rev. B 66, 144204 (2002)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
Here, the relationships between the stiffness constants in plane stress state and in a three-dimensional space are given below. For the former case, \(\sigma _{zz}\) and \(\tau _{zz}\) are equal to 0. By virtue of Eqs. (1) and (2), we can obtain
From the above, we can get the expressions for \(\varepsilon _{zz}\) and \(w_{zz}\) as follows by solving Eqs. (A.1) and (A.2).
Then one substitutes the expressions for \(\varepsilon _{zz}\) and \(w_{zz}\) above into Eqs. (1) and (2) to derive Eqs. (4) and (5). In addition, \(\sigma _{yz},\sigma _{xz},\tau _{yz}\) and \(\tau _{xz}\) are equal to 0 in plane stress state. So the relationships between the stiffness constants in plane stress state and those in a three-dimensional space can be given as follows:
In other words, for plane stress state, the material constants with superscript asterisk can be determined by those for plane strain state. The results for plane strain state can be directly transformed to those for plane stress state through a direct substitution of their relationships. Due to this reason, we omit the asterisk.
Appendix B
The material constants in polar coordinates can be expressed in terms of those in Cartesian coordinates below
where
The specific expressions for\(\ \bar{h}_{1},\) \(\bar{\kappa }_{1},\) \(\bar{\eta }_{1}\) are as follows
where \(C_{11},\) \(C_{12},\) \(C_{44}\) represent three basic elastic parameters of cubic anisotropic materials.
The constants \(\bar{a}_{1},\) \(\bar{b}_{1},\) \(\bar{c}_{1}\) can be obtained by the following matrix equation
Rights and permissions
About this article
Cite this article
Long, F., Li, XF. Elastic field of a rotating cubic quasicrystal disk. Arch Appl Mech 92, 2191–2205 (2022). https://doi.org/10.1007/s00419-022-02169-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00419-022-02169-3