Skip to main content
SpringerLink
Log in

Crack identification in laminated composites based on modal responses using metaheuristics, artificial neural networks and response surface method: a comparative study

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

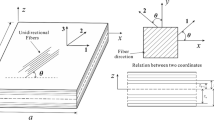
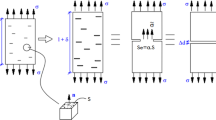
Structures that are difficult to maintain and access need to have an efficient and robust process for continuous monitoring. Such monitoring through damage detection and identification studies is present in several engineering applications as it allows that corrective measures be applied in order to guarantee the structural safety of a given structure, machine or equipment. In particular, laminated composite materials, often used in aeronautical structures, have a complex failure mechanism where delamination or cracks in these materials are often not visible on the surface. Thus, the use of optimization methods for the characterization of damages in these materials becomes relevant. In this study, both the metaheuristic sunflower optimization, the artificial neural networks and the response surface method were used to solve an inverse crack identification problem. The crack was modeled as a thin elliptical hole in a rectangular laminated plate numerically modeled using the finite element method. As a result of the methods used, different approaches to the problem were obtained that present reliable shape, size and position identification of a crack sized between 3 and 30 mm. The results showed substantial and promising results in the uses of both metaheuristic techniques and artificial neural networks. However, neural networks have a certain competitive advantage over optimization techniques as long as the data that feeds the model present a certain level of quantity and quality. Results obtained were able to identify all damage parameters (location, extension and orientation), with errors less than 1%.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Abbreviations

K :

Stiffness matrix

\(\omega _{j}\) :

jth natural frequency of interest

M :

Mass matrix

\(\phi _{{\left( {i,j} \right)}}\) :

Modal shift of the ith node in the jth mode of interest

\(\hat{\phi }_{{\left( {i,j} \right)}}\) :

Modal shift of the ith node in the jth normalized mode of interest

\(Q_{i}\) :

Amount of heat received by the ith plant

P :

Source power

\(r_{i}\) :

Distance between the sun and the ith plant

\(\vec{s}_{i}\) :

Plant direction toward the sun

X* :

Best individual parameter vector

\(X_{i}\) :

Parameter vector of the ith plant

\(d_{i}\) :

Step of the ith plant

λ :

Constant value that defines an “inertial” displacement of the plants

\(P_{i}\) :

Probability of reproduction of the ith plant

\(X_{{\max }}\) :

Upper limit of the parameter vector

\(X_{{\min }}\) :

Lower limit of the parameter vector

\(N_{{{\text{pop}}}}\) :

Number of plants

\(\vec{X}_{{\left( {i,j} \right)}}\) :

ITh plant in the jth generation

\(v_{k}\) :

K Neuron linear combination factor

\(w_{{kj}}\) :

Synapse weight between k and j neurons

ϕ :

Activation function

\(b_{k}\) :

Neuron k trend

\(Y_{i}\) :

ITh response predicted by the artificial neural network

\(\hat{Y}_{i}\) :

ITh response expected by the artificial neural network

γ :

Regularization factor

\(E_{x}\) :

Young's modulus in the x direction

\(E_{y}\) :

Young's modulus in the y direction

\(\nu _{{xy}}\) :

Poisson's ratio in the xy plane

\(G_{{xy}}\) :

Shear modulus in the xy plane

\(x_{{\text{o}}}\) :

Position of the center of the ellipse at x

\(y_{{\text{o}}}\) :

Y Ellipse center position

a :

Larger radius of the ellipse

b :

Minor radius of the ellipse

θ :

Inclination angle of the ellipse's largest radius in relation to the x axis

\(f_{i}\) :

Ith natural frequency of interest (in Hz)

t :

Parameter independent of the parametric equation of the ellipse

\(x_{{\text{e}}}\) :

X rectangular enclosure size

\(y_{{\text{e}}}\) :

Y rectangular enclosure size

\(\phi _{{{\text{h}}(i,j)}}\) :

Modal shift of the ith plate node without damage in the jth mode

\(\phi _{{{\text{d}}(i,j)}}\) :

Modal shift of the ith node of the damaged plate in the jth mode

\(\Delta \hat{\phi }_{{\left( {i,j} \right)}}\) :

Difference between modal shift of the ith node of the real structure in the jth mode of interest and the undamaged structure

\(\Delta \phi _{{\left( {i,j} \right)}}\) :

Difference between modal shift of the ith node in the jth mode

ϕ h(i,j) :

Modal shift of the ith plate node without damage in the jth mode

ϕ d(i, j):

Modal shift of the ith plate node with damage to the jth mode of interest

J :

Objective function

References

  1. Agathos, K., Chatzi, E., Bordas, S.P.A.: Multiple crack detection in 3D using a stable XFEM and global optimization. Comput. Mech. 62(4), 835–852 (2018)

    Article  MathSciNet  Google Scholar 

  2. Alexandrino, P.D.S.L., Gomes, G.F., Cunha, S.S., Jr.: A robust optimization for damage detection using multiobjective genetic algorithm, neural network and fuzzy decision making. Inverse Probl. Sci. Eng. 28(1), 21–46 (2020)

    Article  MathSciNet  Google Scholar 

  3. Budipriyanto, A., Haddara, M.R., Swamidas, A.S.J.: Identification of damage on ship’s cross stiffened plate panels using vibration response. Ocean Eng. 34(5–6), 709–716 (2007)

    Article  Google Scholar 

  4. Chatzi, E.N., et al.: Experimental application and enhancement of the XFEM–GA algorithm for the detection of flaws in structures. Comput. Struct. 89(7–8), 556–570 (2011)

    Article  Google Scholar 

  5. Doebling, S.W., et al.: A summary review of vibration-based damage identification methods. Shock Vib. Digest 30(2), 91–105 (1998)

    Article  Google Scholar 

  6. Fathi, H., Vaez, S.H., Zhang, Q., Alavi, A.H.: A new approach for crack detection in plate structures using an integrated extended finite element and enhanced vibrating particles system optimization methods. In: Structures, vol. 29, pp. 638–651. Elsevier (2021, February)

  7. Gomes, G.F., de Almeida, F.A.: Tuning metaheuristic algorithms using mixture design: application of sunflower optimization for structural damage identification. Adv. Eng. Softw. 149, 102877 (2020)

    Article  Google Scholar 

  8. Gomes, G.F., & Giovani, R.S.: An efficient two-step damage identification method using sunflower optimization algorithm and mode shape curvature (MSDBI–SFO). Eng. Comput. 1–20 (2020). https://doi.org/10.1007/s00366-020-01128-2

  9. Gomes, G.F., da Cunha, S.S., Ancelotti, A.C.: A sunflower optimization (SFO) algorithm applied to damage identification on laminated composite plates. Eng. Comput. 35(2), 619–626 (2019)

    Article  Google Scholar 

  10. Gomes, G.F., da Cunha, S.S., Alexandrino, P.D.S.L., de Sousa, B.S., Ancelotti, A.C.: Sensor placement optimization applied to laminated composite plates under vibration. Struct. Multidiscip. Optim. 58(5), 2099–2118 (2018)

    Article  MathSciNet  Google Scholar 

  11. Gomes, G.F., Mendez, Y.A.D., Alexandrino, P.D.S.L., da Cunha, S.S., Ancelotti, A.C.: A review of vibration based inverse methods for damage detection and identification in mechanical structures using optimization algorithms and ANN. Arch. Comput. Methods Eng. 26(4), 883–897 (2019)

    Article  MathSciNet  Google Scholar 

  12. Hassiotis, S., Jeong, G.D.: Identification of stiffness reductions using natural frequencies. J. Eng. Mech. 121(10), 1106–1113 (1995)

    Article  Google Scholar 

  13. Hossain, M.S., et al.: Artificial neural networks for vibration based inverse parametric identifications: a review. Appl. Soft. Comput. 52, 203–219 (2017)

    Article  Google Scholar 

  14. Hu, H., Wang, J.: Damage detection of a woven fabric composite laminate using a modal strain energy method. Eng. Struct. 31(5), 1042–1055 (2009)

    Article  Google Scholar 

  15. Karsh, P.K., Mukhopadhyay, T., Dey, S.: Spatial vulnerability analysis for the first ply failure strength of composite laminates including effect of delamination. Compos. Struct. 184, 554–567 (2018)

    Article  Google Scholar 

  16. Kaveh, A., Mahdavi, V.R.: Colliding bodies optimization: a novel meta-heuristic method. Comput. Struct. 139, 18–27 (2014)

    Article  Google Scholar 

  17. Khatir, S., Wahab, M.A., Benaissa, B., Köppen, M.: Crack identification using eXtended IsoGeometric analysis and particle swarm optimization. In: Fracture, Fatigue and Wear (pp. 210–222). Springer, Singapore (2018).

  18. Liang, Y.C., Hwu, C.: On-line identification of holes/cracks in composite structures. Smart Mater. Struct. 10(4), 599 (2001)

    Article  Google Scholar 

  19. Lu, Y., Ye, L., Su, Z., Zhou, L., Cheng, L.: Artificial neural network (ANN)-based crack identification in aluminum plates with Lamb wave signals. J. Intell. Mater. Syst. Struct. 20(1), 39–49 (2009)

    Article  Google Scholar 

  20. Mukhopadhyay, T., et al.: Structural damage identification using response surface-based multi-objective optimization: a comparative study. Arab. J. Sci. Eng. 40(4), 1027–1044 (2015)

    Article  MathSciNet  Google Scholar 

  21. Oliver, G.A., Ancelotti, A.C., Gomes, G.F.: Neural network-based damage identification in composite laminated plates using frequency shifts. Neural Comput. Appl. 33(8), 3183–3194 (2021)

    Article  Google Scholar 

  22. Owolabi, G.M., Swamidas, A.S.J., Seshadri, R.: Crack detection in beams using changes in frequencies and amplitudes of frequency response functions. J. Sound Vib. 265(1), 1–22 (2003)

    Article  Google Scholar 

  23. Pereira, J.L.J., Francisco, M.B., da Cunha Jr, S.S., Gomes, G.F.: A powerful Lichtenberg Optimization Algorithm: a damage identification case study. Eng. Appl. Artif. Intell. 97, 104055 (2021)

    Article  Google Scholar 

  24. Pereira, J.L.J., Chuman, M., Cunha Jr, S.S. and Gomes, G.F. (2021), "Lichtenberg optimization algorithm applied to crack tip identification in thin plate-like structures", Engineering Computations, Vol. 38 No. 1, pp. 151–166. https://doi.org/10.1108/EC-12-2019-0564 

  25. Rashedi, E., Nezamabadi-Pour, H., Saryazdi, S.: GSA: a gravitational search algorithm. Inf. Sci 179(13), 2232–2248 (2009)

    Article  Google Scholar 

  26. Saeed, R.A., Galybin, A.N., Popov, V.: Crack identification in curvilinear beams by using ANN and ANFIS based on natural frequencies and frequency response functions. Neural Comput. Appl. 21(7), 1629–1645 (2012)

    Article  Google Scholar 

  27. Sankar, P.A., Machavaram, R., Shankar, K.: System identification of a composite plate using hybrid response surface methodology and particle swarm optimization in time domain. Measurement 55, 499–511 (2014)

    Article  Google Scholar 

  28. Stinchcomb, W., Reifsnider, K.: Fatigue damage mechanisms in composite materials: A review. In Fatigue Mechanisms, ed. J. Fong (West Conshohocken, PA: ASTM International, 1979), 762–787. https://doi.org/10.1520/STP35914S

  29. Sun, H., Waisman, H., Betti, R.: Nondestructive identification of multiple flaws using XFEM and a topologically adapting artificial bee colony algorithm. Int. J. Numer. Methods Eng. 95(10), 871–900 (2013)

    Article  MathSciNet  Google Scholar 

  30. Varna, J., et al.: Damage in composite laminates with off-axis plies. Compos. Sci. Technol. 59(14), 2139–2147 (1999)

    Article  Google Scholar 

  31. Waisman, H., Berger-Vergiat, L.: An adaptive domain decomposition preconditioner for crack propagation problems modeled by XFEM. Int. J. Multiscale Comput Eng 11(6) (2013)

  32. Wei, Z., Liu, J., Lu, Z.: Structural damage detection using improved particle swarm optimization. Inverse Probl. Sci. Eng. 26(6), 792–810 (2018)

    Article  MathSciNet  Google Scholar 

  33. Yang, Xin-She.: Flower pollination algorithm for global optimization. In International conference on unconventional computing and natural computation. Springer, Berlin, Heidelberg, (2012)

    Book  Google Scholar 

Download references

Acknowledgements

The authors would like to acknowledge the financial support from the Brazilian agency CNPq and FAPEMIG (Fundação de Amparo à Pesquisa do Estado de Minas Gerais – Grant APQ-00385-18).

Author information

Authors and Affiliations

  1. Mechanical Engineering Institute, Federal University of Itajubá (UNIFEI), Itajubá, Brazil

    Felipe Mouallem de Assis & Guilherme Ferreira Gomes

Authors
  1. Felipe Mouallem de Assis
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guilherme Ferreira Gomes
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guilherme Ferreira Gomes.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Replication of results

This manuscript is self-contained, in that it contains all necessary theory to reproduce the results, including the preliminaries, i.e., the inverse crack identification in laminate composite plates. The formulation of the inverse problem is described in detail, and all parameters for the numerical examples are provided.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

de Assis, F.M., Gomes, G.F. Crack identification in laminated composites based on modal responses using metaheuristics, artificial neural networks and response surface method: a comparative study. Arch Appl Mech 91, 4389–4408 (2021). https://doi.org/10.1007/s00419-021-02015-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-021-02015-y

Keywords

Search

Navigation