Enhanced numerical integration scheme based on image compression techniques: Application to rational polygonal interpolants

Abstract

Polygonal finite elements offer an increased freedom in terms of mesh generation at the price of more complex, often rational, shape functions. Thus, the numerical integration of rational interpolants over polygonal domains is one of the challenges that needs to be solved. If, additionally, strong discontinuities are present in the integrand, e.g., when employing fictitious domain methods, special integration procedures must be developed. Therefore, we propose to extend the conventional quadtree-decomposition-based integration approach by image compression techniques. In this context, our focus is on unfitted polygonal elements using Wachspress shape functions. In order to assess the performance of the novel integration scheme, we investigate the integration error and the compression rate being related to the reduction in integration points. To this end, the area and the stiffness matrix of a single element are computed using different formulations of the shape functions, i.e., global and local, and partitioning schemes. Finally, the performance of the proposed integration scheme is evaluated by investigating two problems of linear elasticity.

1 Introduction

The traditional finite element method (FEM) offers a robust and well-studied approach for simulating a large variety of physical phenomena governed by partial differential equations [1, 2]. Nonetheless, throughout the years, several extensions have been developed in order to increase the accuracy, widen the field of application and decrease the computation time. In this contribution, we focus on the combination of two such extensions, namely the fictitious domain approach and polygonal elements employing shape functions based on generalized barycentric coordinates. In this context, we propose an efficient solution for computing piece-wise rational integrals arising in the expressions for the element matrices.

1.1 Fictitious domain methods

In the conventional FEM, the computational mesh has to conform to the boundary of the domain of interest. As this is one particular bottleneck in the simulation pipeline, extensive research has been devoted to extending the FEM to unfitted discretizations that do not necessarily conform to geometric features of the given problem. One possibility to exploit this idea is utilized in the extended finite element (XFEM) [3, 4] and the generalized finite element methods (GFEM) [4, 5], where, e.g., an accurate modeling of crack propagation can be achieved. On the other hand, in the context of fictitious domain methods, geometrically highly complex domains are embedded into a larger computational domain of simple shape to achieve a straightforward mesh generation process [6,7,8]. Representatives of this class of methods are the cut finite element method (cutFEM) [9,10,11,12], the Cartesian grid finite element method (cgFEM) [13], the fixed grid finite element method (Fg-FEM) [14, 15] and the finite cell method (FCM) [16,17,18,19]. All of these approaches generally lead to elements intersected by geometric features, and therefore, the application of unfitted meshes inherently involves the computation of discontinuous integrals. Thus, an accurate computation of the element matrices of intersected elements is one of the key factors determining the success of this class of methods.

1.2 Polytopal finite element method

The conventional FEM is based on finite elements of simple shapes, such as triangles and quadrilaterals in 2D and tetrahedrons and hexagons (less often pyramids and wedges) in 3D. The usage of polygonal and polyhedral finite elements offers additional advantages when it comes to enhanced mesh generation procedures, such as transition elements for avoiding hanging nodes [20, 21] and the derivation of conformal polygonal elements in an originally non-conformal mesh [22,23,24]. Furthermore, polygonal elements enable a straightforward discretization and modeling of polycrystalline [25] and rock materials [26]. In the remainder, we follow the theory of conformal polygonal finite element methods based on generalized barycentric coordinates [27, 28]. However, we have to keep in mind that other polygonal/polyhedral element formulations based on, e.g., the Voronoi cell finite element method (VCFEM) [25, 29], the virtual element method (VEM) [30, 31] and the scaled boundary finite element method (SBFEM) [32,33,34], are also possible. An extensive description of these and other related approaches can be found in the review article by Perumal [35]. The main challenges of the polytopal FEM can be seen in the lack of commercial and free mesh generation software, construction of appropriate (high-order) interpolants and in the need for accurate numerical integration schemes.

1.3 Motivation

The investigation of polygonal elements in the context of fictitious domain concept is an exotic combination which further widens the application fields of these methods. A useful feature of such a combination is, e.g., the flexible insertion and modification of voids and inclusions in already existing FE-meshes, consisting completely or partially of polygonal elements. Non-conformal polygonal meshes were already investigated by Duczek and Gabbert [36] in the context of the polygonal finite cell method (poly-FCM). In this case, multiple challenges have to be tackled regarding the numerical integration due to (i) the polygonal shape of the integration domain, (ii) the strong discontinuity within the element and (iii) the generally non-polynomial integrand over the element domain, computed by the linear combination of polygonal basis functions. In the remainder of this article, we especially consider rational shape functions, such as the Wachspress interpolant [37]. Consequently, the computation of the element matrices in unfitted polygonal meshes involves integrals of the following form

$$\begin{aligned} \int _{\varOmega ^{\mathrm {poly}}} \alpha \mathcal {R}\,\mathrm {d}\varOmega , \end{aligned}$$

(1)

where $\varOmega ^{\mathrm {poly}}$ is a polygonal region, $\mathcal {R}$ a rational function and $\alpha$ a step function making the integrand discontinuous. In this contribution, we follow the poly-FCM approach by Duczek and Gabbert [36] which uses a quadtree-decomposition-based integration scheme for computing Eq. (1) over the intersected elements. As an extension to their approach, we implement and investigate the novel numerical integration scheme proposed by Petö et al. [38] that compresses the integration sub-cells resulting from the quadtree-decomposition (QTD) to achieve reduced computational times. Since this latter approach leads to a lower integration point density in the polygonal elements, a special focus is placed on the integration accuracy when computing Eq. (1). Furthermore, note that similar discontinuous rational integrands arise also in case of traditional finite elements when they are (i) distorted and (ii) intersected by domain interfaces. Therefore, the findings regarding the effect of the compressed QTD-based integration scheme have ramifications beyond the scope of polygonal elements.

The remainder of this article is structured in the following way: First, in Sect. 2, the fictitious domain approach and the discretization of the weak form via an unfitted polygonal mesh is outlined in the context of linear elasticity. Then, in Sect. 3, the polygonal shape functions are discussed briefly, while in Sect. 4 the different integration schemes over polygonal elements are elaborated with special attention to discontinuous integrands (see Ref. [38]). Finally, in Sects. 5, 6 and 7, the influence of the proposed integration scheme on (i) the resulting number of integration points, (ii) the reduction in computational time and (iii) the integration accuracy is investigated by means of various examples.

2 Fictitious domain approach for polygonal elements

Consider the weak form of a second-order boundary value problem over the domain $\varOmega$ with its corresponding boundary $\partial \varOmega$ [2, 39]

$$\begin{aligned} \mathcal {B}(\varvec{u},\varvec{v}) = \mathcal {F}(\varvec{v}), \end{aligned}$$

(2)

where in case of linear elasticity, $\varvec{u}$ is the displacement field and $\varvec{v}$ is a test function. Denoting the elasticity matrix in Voigt notation by $\varvec{C}$, the standard strain-displacement operator by $\varvec{L}$, the body forces in $\varOmega$ by $\varvec{b}$ and the surface tractions on the Neumann boundary $\varGamma _{\mathrm {N}} \subset \partial \varOmega$ by $\hat{\varvec{t}}$, the bilinear $\mathcal {B}$ and linear $\mathcal {F}$ functionals are expressed as

$$\begin{aligned} \mathcal {B}(\varvec{u},\varvec{v})= & {} \int _{\varOmega } (\varvec{L} \varvec{v})^T \cdot \varvec{C} \cdot \varvec{L}\varvec{u}\,\mathrm {d}\varOmega \quad \mathrm{and}\end{aligned}$$

(3)

$$\begin{aligned} \mathcal {F}(\varvec{u},\varvec{v})= & {} \int _{\varOmega } \varvec{v}^T \cdot \varvec{b}\,\mathrm {d}\varOmega +\int _{\varGamma _{\mathrm {N}}} \varvec{v}^T \cdot \varvec{\hat{t}}\,\mathrm {d}\varGamma . \end{aligned}$$

(4)

Note that the Neumann boundary conditions are already incorporated in Eq. (4), while the Dirichlet boundary conditions, i.e., the prescribed displacements $\hat{\varvec{u}}$, are realized by an additional condition $\varvec{u}(\varvec{x}) = \hat{\varvec{u}}(\varvec{x})\,\forall \varvec{x} \in \varGamma _{\mathrm {D}}$.

2.1 Fundamentals

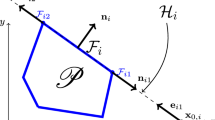
In fictitious domain methods, the original problem stated in Eq. (2) is not solved over the domain $\varOmega$, but over an extended domain $\varOmega _{\mathrm {e}} \supset \varOmega$. In the following, we refer to the original domain as the physical domain $\varOmega _{\mathrm {phys}}$, while the domain extending $\varOmega _{\mathrm {phys}}$ to $\varOmega _{\mathrm {e}}$ we call fictitious domain $\varOmega _{\mathrm {fict}} = \varOmega _{\mathrm {e}} {\setminus } \varOmega _{\mathrm {phys}}$ (see Fig. 1). There are numerous methods that are based on this approach. Here, we follow the general description used in the finite cell method (FCM) [16,17,18,19], for which a first extension to polygonal meshes (poly-FCM) was already outlined by Duczek and Gabbert [36]. Assuming that $\varOmega _{\mathrm {fict}}$ provides zero stiffness and that it is not subjected to any body forces and surface tractions, the weak form over the extended domain reads [16, 40]

$$\begin{aligned} \mathcal {B}_{\mathrm {e}}(\varvec{u},\varvec{v}) = \mathcal {F}_{\mathrm {e}}(\varvec{v}) , \end{aligned}$$

(5)

where the bilinear and linear functionals

$$\begin{aligned} \mathcal {B}_{\mathrm {e}}(\varvec{u},\varvec{v})= & {} \int _{\varOmega _{\mathrm {e}}} (\varvec{L}\varvec{v})^T \cdot \alpha \varvec{C} \cdot \varvec{L}\varvec{u}\, \mathrm {d}\varOmega \quad \mathrm{and}\end{aligned}$$

(6)

$$\begin{aligned} \mathcal {F}_{\mathrm {e}}(\varvec{v})= & {} \int _{\varOmega _{\mathrm {e}}} \varvec{v}^T \cdot \alpha \varvec{b}\,\mathrm {d}\varOmega +\int _{\varGamma _{\mathrm {N}}} \varvec{v}^T \cdot \varvec{\hat{t}}\,\mathrm {d}\varGamma \end{aligned}$$

(7)

are formulated with the help of the indicator function $\alpha$ given in Eq. (8). In order to avoid severe ill-conditioning of the system matrices, a small value $\alpha \ll 1$ is assigned to the integration points in $\varOmega _{\mathrm {fict}}$ [41]. According to Fries and Belytschko [4], such a possible ill-conditioning is expected only for cut elements that exhibit a large difference between the areas of $\varOmega _{\mathrm {phys}}$ and $\varOmega _{\mathrm {fict}}$.

$$\begin{aligned} \alpha (\varvec{x})= {\left\{ \begin{array}{ll} 1.0, &{} \forall \varvec{x} \in \varOmega _{\mathrm {phys}}\\ 0.0\,(\text {in practice}:\,\alpha \ll 1), &{} \forall \varvec{x} \in \varOmega _{\mathrm {fict}} \end{array}\right. } \end{aligned}$$

(8)

Fig. 1

Fictitious domain concept

2.2 Discretization of the weak form

The discretization of the weak form over the extended domain $\varOmega _{\mathrm {e}}$ generally results in an unfitted mesh where the elements are located either completely inside the physical or fictitious domains, or they are intersected by the boundary $\partial \varOmega$. While fictitious elements can be discarded, physical elements are treated as standard polygonal finite elements. The bottleneck of the unfitted discretization is seen in the cut elements (Fig. 2), where (i) the implementation of the boundary conditions and (ii) the computation of element matrices require special care. For more information regarding the first issue, we refer to Refs. [7, 8, 42, 43]. The computation of the cut element matrices—constituting the main focus of this article—will be discussed in greater detail in Sect. 4.2.

Fig. 2

Unfitted polygonal mesh over the extended domain $\varOmega _{\mathrm {e}}$

Similar to the standard FEM [1, 2], the fields $\varvec{u}(\varvec{x})$ and $\varvec{v}(\varvec{x})$ are approximated by a linear combination of the shape functions $\{ N_i^{\mathrm {polys}}(\varvec{\xi }) \}_{i=1}^{n_{\mathrm {v}}}$ (see Sect. 3) and nodal values $\{ \varvec{u}_i \}_{i=1}^{n_{\mathrm {v}}}$ and $\{ \varvec{v}_i \}_{i=1}^{n_{\mathrm {v}}}$ over each polygonal element

$$\begin{aligned} \varvec{u}(\varvec{x}) = \sum _{i=1}^{n_{\mathrm {v}}}\varvec{N}_i^{\mathrm {poly}}(\varvec{\xi }) u_i\quad \mathrm{and}\quad \varvec{v}(\varvec{x}) = \sum _{i=1}^{n_{\mathrm {v}}}\varvec{N}_i^{\mathrm {poly}}(\varvec{\xi }) v_i. \end{aligned}$$

(9)

Then, following the Bubnov–Galerkin approach, the global system of equations is assembled based on the individual element contributions. The system of equations given in Eq. (10), where $\varvec{K}$, $\varvec{U}$ and $\varvec{F}$ are the global stiffness matrix, nodal displacement vector and nodal force vector, respectively, is solved by standard approaches

$$\begin{aligned} \varvec{K} \varvec{U} = \varvec{F}. \end{aligned}$$

(10)

3 Polygonal shape functions

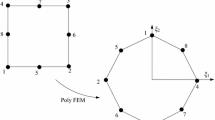
Let us consider a two-dimensional polygonal element with $n_{\mathrm {v}}$ vertices $\{ \varvec{x}_i \}_{i=1}^{n_{\mathrm {v}}}$ given in the global $\varOmega _x^{\mathrm {poly}}$ space. Each global polygonal element $\varOmega _x^{\mathrm {poly}}$ has its corresponding reference space, the so-called canonical polygonal element $\varOmega _{\xi }^{\mathrm {poly}}$ defined in the local coordinate system $\varvec{\xi } = [\xi _1,\,\xi _2]^\mathrm{T}$, as depicted in Fig. 3. The domain $\varOmega _{\xi }^{\mathrm {poly}}$ is a regular polygon, where the coordinates of the $i^{\mathrm {th}}$ vertex are defined on a unit circle by

$$\begin{aligned} \xi _{1i} = \cos (2\pi \cdot i / n_{\mathrm {v}})\quad \mathrm{and}\quad \xi _{2i} = \sin (2\pi \cdot i / n_{\mathrm {v}}). \end{aligned}$$

(11)

Fig. 3

A polygonal element in its local $\varOmega _{\xi }^{\mathrm {poly}}$ and global $\varOmega _x^{\mathrm {poly}}$ configurations transformed by the geometry mapping $\varvec{Q}_{\xi \rightarrow x}$ given in Eq. (17)

Numerous efforts have been made in order to derive interpolants that can be used as shape functions for polygonal elements. These approaches differ in the dimension (polygon or polyhedron) and in the assumptions on their shapes (regular, irregular-convex or irregular-concave) as well as in their computational complexities. In this paper, only a short introduction is given to the available shape functions; for detailed information see Refs. [36, 44]. In order to apply the shape functions in a finite element computation, they must fulfil the requirements for a Galerkin approximant, i.e.,

$$\begin{aligned} \text {non-negativeness}&:&0 \le \phi _i (\varvec{x}) \le 1\end{aligned}$$

(12)

$$\begin{aligned} \text {interpolation nodal data}&:&\phi _i (\varvec{x}_j) = \delta _{ij} \end{aligned}$$

(13)

$$\begin{aligned} \text {partition of unity}&:&\sum _{i=1}^{n_{\mathrm {v}}} \phi _i(\varvec{x}) = 1\end{aligned}$$

(14)

$$\begin{aligned} \text {linear completeness}&:&\sum _{i=1}^{n_{\mathrm {v}}} \phi _i(\varvec{\xi })x_i = \varvec{x} \end{aligned}$$

(15)

where $\phi _i$ denotes the interpolant corresponding to node i. Most approaches use generalized barycentric coordinates

$$\begin{aligned} \phi _i(\varvec{x}) = \dfrac{w_i(\varvec{x})}{\sum _{j=1}^{n_{\mathrm {v}}} w_j(\varvec{x})} , \end{aligned}$$

(16)

as the basis for deriving suitable interpolants, where $w_i$ is a weighting function associated with node i that can be computed in numerous ways. As a first approach, Wachspress proposed a rational basis for convex polygons [45], where $w_i$ is computed based on area computations in the polygonal domain. A MATLAB implementation for this approach can be found in Ref. [46]. The original formulation of the Wachspress shape functions was later simplified by Meyer et al. [47] proposing a method that relies on vector operations only, thus reducing possible round-off errors. Finally, the extension of the Wachspress shape functions to convex polytopes was established by Warren [48]. Computing $w_i$ based on the mean value coordinates (MVC), introduced by Floater [49] enables a formulation for both convex and concave polygonal domains. The MVC was extended to three dimensions as well [50, 51]. Another approach for computing $w_i$ is based on natural element or Laplace coordinates [27, 52], both of which are widely used in the natural element method. Tabarraei and Sukumar [28] provided symbolically pre-computed Laplacian shape functions for regular polygons up to $n_{\mathrm {v}}=8$, over which they are identical to the Wachspress shape function [27]. A polygonal interpolant that is not based on Eq. (16) can be constructed by using the maximum entropy approach proposed by Sukumar [53, 54], which has been also extended to quadratic Serendipity-type shape functions by Rand et al. [55].

In the remainder, we use the rational basis functions proposed by Wachspress as polygonal shape functions $N^{\mathrm {poly}}(\varvec{\xi }) = \phi (\varvec{\xi })$. These functions are defined in the reference space over the canonical element. Based on the isoparametric concept, the geometry mapping from $\varOmega _{\xi }^{\mathrm {poly}}$ to $\varOmega _x^{\mathrm {poly}}$ (Fig. 3) is achieved by a linear combination of basis functions $\{ N_i^{\mathrm {poly}} (\varvec{\xi }) \}_{i=1}^{n_{\mathrm {v}}}$ and nodal positions $\{ \varvec{x}_i = [x_{1i},\,x_{2i}]^\mathrm{T} \}_{i=1}^{n_{\mathrm {v}}}$ in the global space

$$\begin{aligned} \varvec{x} = \varvec{Q}_{\xi \rightarrow x}(\varvec{\xi }) = \sum _{i=1}^{n_{\mathrm {v}}} N_i^{\mathrm {poly}}(\varvec{\xi }) \begin{bmatrix} x_{1i}\\ x_{2i} \end{bmatrix}. \end{aligned}$$

(17)

4 Numerical integration techniques for polygonal elements

Considering standard finite elements, quadrature rules are readily available both in two and three dimensions, while the integration over polytopal elements is more challenging. Note that the need for an accurate integration over polytopal domains does not only arise in FEMs using polygonal/polyhedral elements, but also in immersed boundary methods, where the intersected FEs often contain polytopal sub-domains due to the discontinuity. Numerous contributions have been made for developing accurate integration schemes for polynomial functions over such domains. One may transform the integral over the complicated polytopal domain into surface or line integrals using the divergence theorem [56,57,58,59], or derive special quadrature rules for the polytopal domains via solving the moment fitting equations [60,61,62,63,64, 64]. A third approach, especially used in the polygonal FEM [27, 28, 36, 65, 66], is based on partitioning the polygonal elements into a set of triangular or quadrilateral sub-domains with readily available quadrature rules.¹ This approach is discussed in the next sub-section in greater detail.

4.1 Partitioning scheme

The most common approach regarding the sub-division for integration purposes is to split the polygonal element with $n_{\mathrm {v}}$ vertices into $n_{\mathrm {v}}$ triangular or quadrilateral sub-domains [36]. A third option is to partition the polygonal element into special triangular and quadrilateral regions that are distorted in such a way that only one or two adjacent edges are skewed and use the quadrature formulae derived by Sarada and Nagaraja [67]. In the following, we focus on the first two approaches due to their popularity and the possibility of a straightforward extension by using tetrahedra in 3D. The reference space for the triangular and quadrilateral sub-domains is denoted by $\varOmega _{\eta }^{\mathrm {tri}}$ and $\varOmega _{\eta }^{\mathrm {quad}}$, respectively. In this case, standard quadrature rules can be applied where $\varvec{\eta } = [\eta _1,\,\eta _2]^\mathrm{T}$ refers to the local coordinates. In general, the sub-division of a polygonal element can be executed either in the global or in the local space. If shape functions are easily constructed for the global polygon, e.g., when using Wachspress,² MVC or maximum entropy shape functions, it is a natural choice to perform the integration in the global element. On the other hand, if it is more advantageous to define the shape functions over $\varOmega _{\xi }^{\mathrm {poly}}$, which is the case for the Laplace shape functions [27, 66], the partitioning for integration purposes should be performed in the canonical element [28]. In the following, both the partitioning based on the global $\varOmega _{x}^{\mathrm {poly}}$ and local polygonal (canonical) elements $\varOmega _{\xi }^{\mathrm {poly}}$ are discussed.

4.1.1 Sub-division of the global polygonal element

One approach is to directly sub-divide the global polygonal element $\varOmega _x^{\mathrm {poly}}$ into triangular $\varOmega _x^{\mathrm {tri}}$ or quadrilateral $\varOmega _x^{\mathrm {quad}}$ sub-domains [27, 66]. The relation of these domains to their local spaces, $\varOmega _{\eta }^{\mathrm {tri}}$ and $\varOmega _{\eta }^{\mathrm {quad}}$, is established by means of a simple linear/bilinear geometry mapping $\varvec{x} = \varvec{Q}_{\eta \rightarrow x}(\varvec{\eta })$, as depicted in Fig. 4a. Consequently, the integral of an arbitrary function $\mathcal {F}$ over $\varOmega _x^{\mathrm {poly}}$ is computed for the triangular and quadrilateral decompositions by

$$\begin{aligned} \int _{\varOmega _{x}^{\mathrm {poly}}} \mathcal {F} \mathrm {d} \varOmega= & {} \sum _{i=1}^{n_{\mathrm {v}}}\int _{0}^1 \int _{0}^{1-\eta _1} \mathcal {F}\,|\varvec{J}_{\eta \rightarrow x}^{(i)}|\,\mathrm {d}\eta _1 \mathrm {d}\eta _2\quad \mathrm{and} \end{aligned}$$

(18)

$$\begin{aligned} \int _{\varOmega _{x}^{\mathrm {poly}}} \mathcal {F} \mathrm {d} \varOmega= & {} \sum _{i=1}^{n_{\mathrm {v}}}\int _{-1}^1 \int _{-1}^1 \mathcal {F}\,|\varvec{J}_{\eta \rightarrow x}^{(i)}|\,\mathrm {d}\eta _1 \mathrm {d}\eta _2, \end{aligned}$$

(19)

respectively, where $|\varvec{J}_{\eta \rightarrow x}^{(i)}|$ is the determinant of the Jacobian matrix $\varvec{J}_{\eta \rightarrow x}^{(i)}$ of the geometry mapping $\varvec{Q}_{\eta \rightarrow x}$. Since $\varvec{Q}_{\eta \rightarrow x}$ can be realized via standard linear/bilinear FE shape functions, the determinant of its Jacobian matrix is

$$\begin{aligned} |\varvec{J}_{\eta \rightarrow x}^{(i)}| = {\left\{ \begin{array}{ll} \text {const.} &{}\text{ for } \text{ triangular } \text{ sub-domain }\\ a_0+a_1\eta _1 + a_2\eta _2 &{} \text{ for } \text{ quadrilateral } \text{ sub-domain } \end{array}\right. }, \end{aligned}$$

(20)

where $a_0$, $a_1$ and $a_2$ are constants depending on the coordinates of the corner vertices of the sub-domain $\varOmega _x^{\mathrm {quad}(i)}$.

Fig. 4

Example for the global $\varOmega _x^{\mathrm {poly}}$ and local $\varOmega _{\xi }^{\mathrm {poly}}$ quadrilateral partitioning schemes. The domain with purple colour highlights a single quadrilateral sub-domain in different spaces using the geometry mappings indicated by the arrows. The decomposition into triangular sub-domains follows analogously. a Sub-division of the polygonal element in the global space. The integration over the sub-element requires one mapping. b Sub-division of the polygonal element in its reference space. The integration over the sub-element requires two mappings. (Color figure online)

4.1.2 Sub-division of the local polygonal element

Another approach is to perform the partitioning in the local space of the polygonal element $\varOmega _{\xi }^{\mathrm {poly}}$, resulting in $\varOmega _{\xi }^{\mathrm {tri}}$ and $\varOmega _{\xi }^{\mathrm {quad}}$ [26,27,28, 36, 66]. In this case, the relation between $\varOmega _{\xi }^{\mathrm {poly}}$ an $\varOmega _{x}^{\mathrm {poly}}$ is established based on a geometry mapping $\varvec{x} = \varvec{Q}_{\xi \rightarrow x}(\varvec{\xi })$ using the rational polygonal shape functions according to Eq. (17). Compared to the first approach, an additional second mapping $\varvec{\xi } = \varvec{Q}_{\eta \rightarrow \xi }(\varvec{\eta })$ from $\varOmega _{\eta }^{\mathrm {tri/quad}}$ to $\varOmega _{\xi }^{\mathrm {tri/quad}}$ is needed. Here, standard linear/bilinear shape functions are sufficient. An example for subdividing a polygonal element into quadrilateral sub-elements is depicted in Fig. 4b. Taking both geometry mappings into account, the integral of the function $\mathcal {F}$ over $\varOmega _x^{\mathrm {poly}}$ can be transformed into

$$\begin{aligned} \int _{\varOmega _{x}^{\mathrm {poly}}} \mathcal {F} \mathrm {d} \varOmega= & {} \int _{\varOmega _{\xi }^{\mathrm {poly}}} \!\! \mathcal {F}\,|\varvec{J}_{\xi \rightarrow x}| \mathrm {d}\varOmega = \sum _{i=1}^{n_{\mathrm {v}}}\int _{0}^1 \int _{0}^{1-\eta _1} \mathcal {F}\,|\varvec{J}_{\eta \rightarrow \xi }^{(i)}| |\varvec{J}_{\xi \rightarrow x}|\,\mathrm {d}\eta _1 \mathrm {d}\eta _2 \end{aligned}$$

(21)

$$\begin{aligned} \int _{\varOmega _{x}^{\mathrm {poly}}} \mathcal {F} \mathrm {d} \varOmega= & {} \int _{\varOmega _{\xi }^{\mathrm {poly}}} \!\! \mathcal {F}\,|\varvec{J}_{\xi \rightarrow x}| \mathrm {d}\varOmega = \sum _{i=1}^{n_{\mathrm {v}}}\int _{-1}^1 \int _{-1}^1 \mathcal {F}\,|\varvec{J}_{\eta \rightarrow \xi }^{(i)}| |\varvec{J}_{\xi \rightarrow x}|\,\mathrm {d}\eta _1 \mathrm {d}\eta _2 \end{aligned}$$

(22)

for the triangular and quadrilateral decompositions, respectively. Considering the geometry mapping $\varvec{Q}_{\eta \rightarrow \xi }^{(i)}$ for the sub-domain $i \in [1; n_{\mathrm {v}}]$ with standard linear/bilinear FE shape functions, the determinant of its Jacobian matrix is the form

$$\begin{aligned} |\varvec{J}_{\eta \rightarrow \xi }^{(i)}| = {\left\{ \begin{array}{ll} \mathrm{const.} &{}\text{ for } \text{ triangular } \text{ sub-domain }\\ b_0+b_1\eta _1 + b_2\eta _2 &{} \text{ for } \text{ quadrilateral } \text{ sub-domain } \end{array}\right. }, \end{aligned}$$

(23)

where $b_0$, $b_1$ and $b_2$ are constants depending on the coordinates of the corner vertices of the sub-domain $\varOmega _{\xi }^{\mathrm {quad}(i)}$. Furthermore, due to the use of Wachspress shape functions for the geometry mapping, the determinant $|\varvec{J}_{\xi \rightarrow x}|$ is a rational function regardless of the shape of the sub-domains.

Comparing Eqs. (18) and (19) to Eqs. (22) and (21), it is clear that the sub-division of the global element leads to integrands of lower complexity. Consequently, using the same quadrature rule in $\varOmega _{\eta }^{\mathrm {tri/quad}}$, Eqs. (18) and  (19) can be computed with higher accuracy than Eqs. (22) and  (21). On the other side, since $\varOmega _{\xi }^{\mathrm {poly}}$ is the same for all global polygonal elements, the shape functions can be written and computed more conveniently in the local space of the polygonal element. A comparison of the integration quality for the two partitioning schemes using different polygonal shape functions and number of integration points can be found in the work by Sukumar and Tabarraei [27]. In the context of linear elasticity, Taberraei and Sukumar [28] use the triangular partitioning scheme in the local coordinate system, where in each triangle 25 integration points are used for an accurate computation of the integrals similar to Eq. (21).

4.2 Considering discontinuous integrands

The integration techniques discussed in the previous section allow for a simple and robust computation of continuous integrals over polygonal elements. However, if the integrand is discontinuous, more sophisticated integration techniques are required to guarantee highly accurate results. Discontinuous integrands generally arise in the extended finite element method (XFEM) [4, 68], the generalized finite element method (GFEM) [4, 5, 69], and in the fictitious domains methods [7, 8, 70], such as the cut finite element method (cutFEM) [9,10,11,12], Cartesian grid finite element method (cgFEM) [13], fixed grid finite element method (Fg-FEM) [14, 15] and finite cell method (FCM) [16,17,18,19]. There are numerous techniques that are commonly used in these methods for computing the discontinuous integrals. These techniques are, e.g., based on (i) the derivation of unique quadrature rules using moment fitting techniques [64, 71, 72], (ii) finding an equivalent polynomial that has the same integral value as the discontinuous integral [73, 74], (iii) reducing the dimensionality of the integral by applying the divergence theorem [57], or (iv) the construction of a local integration mesh (LIM) for better capturing the domains $\varOmega _{\mathrm {phys}}$ and $\varOmega _{\mathrm {fict}}$ in the cut element. The construction of an LIM consisting of boundary-conforming sub-regions has obvious benefits in terms of integration accuracy [12, 75,76,77,78,79]; however, we will concentrate on an LIM based on the quadtree-decomposition (QTD) of the intersected domains that does not conform to the boundary [17, 80]. Although this technique results in a poorer convergence, it does not require finding the discontinuity within the elemental domain often involving the solution of a nonlinear system of equations [77]. In our opinion, this approach fits better into the general philosophy of fictitious domain methods. Furthermore, it works robustly regardless of the geometry description that is provided and the dimensionality of the problem.

4.2.1 Quadtree-decomposition

Using the QTD in a two-dimensional setting, each triangular/quadrilateral sub-domain of the polygonal element undergoes a successive decomposition into a set of triangular/quadrilateral sub-domains called sub-cells with decreased size and increased density in the vicinity of the discontinuity $\partial \varOmega$. Similar to the classification of the global elements, the resulting unfitted sub-cells can also be classified as physical, fictitious and cut as depicted in Fig. 5. The QTD algorithm with triangular sub-cells is outlined in Refs. [36, 81]. In the remainder, the focus is kept on the partitioning of the polygonal elements into quadrilateral sub-domains for which the compression algorithms are readily available (Sect. 4.2.2) [38]. The QTD is performed in the local-space of the cut quadrilateral sub-domains $\varOmega _{\eta }^{\mathrm {quad}}$ by repeating the following three steps for each cut sub-cell until the refinement level k of the QTD is reached:

• 1. Split the given sub-cell into four equal-sized quadrants representing four new sub-cells.

• 2. Map the four new sub-cells to the global polygonal element $\varOmega _x^{\mathrm {poly}}$ using:

  • (a) $\varvec{Q}_{\eta \rightarrow x}$ (polygon partitioning was performed in $\varOmega _x^{\mathrm {poly}}$; Sect. 4.1.1),

  • (b) a combination of $\varvec{Q}_{\eta \rightarrow \xi }$ and $\varvec{Q}_{\xi \rightarrow x}$ (polygon partitioning was performed in $\varOmega _{\xi }^{\mathrm {poly}}$; Sect. 4.1.2).

• 3. Determine for each sub-cell whether it is cut by the boundary or not and mark the cut sub-cells for further decomposition. This procedure is executed in the global space.

Fig. 5

Numerical integration in the cut polygonal element based on the quadtree-decomposition $(k=3)$ of the quadrilateral sub-domains in the canonical element

Each created sub-cell is defined in its own local space $\varOmega _{\zeta }^{\mathrm {sc}}$ with the coordinate system $\varvec{\zeta } = [\zeta _1,\,\zeta _2]^\mathrm{T}$. The relation of the reference sub-cell to the corresponding sub-cell in the $\eta$-space $\varOmega _{\eta }^{\mathrm {sc}}$ is achieved by the geometry mapping $\varvec{\eta } = \varvec{Q}_{\zeta \rightarrow \eta } (\varvec{\zeta })$, as depicted in Fig. 5. Considering $n_{\mathrm {v}}$ quadrilateral domains in the polygonal element, each of which containing $n_{\mathrm {sc}}$ sub-cells resulting from the QTD, the integral of the piece-wise rational function $\alpha \mathcal {R}$ over the cut polygonal element $\varOmega _x^{\mathrm {poly}}$ is computed as the sum of integrals over the individual quadrilateral sub-cells by Eqs. (24) and (25) for the local and global partitions of an element, respectively

$$\begin{aligned} \int _{\varOmega _{x}^{\mathrm {poly}}} \alpha \mathcal {R}\,\mathrm {d} \varOmega= & {} \sum _{i=1}^{n_{\mathrm {v}}} \sum _{j=1}^{n_{\mathrm {sc}}} \int _{-1}^1 \int _{-1}^1 \alpha \mathcal {R}\,\underbrace{|\varvec{J}_{\zeta \rightarrow \eta }^{(j)}|}_{\text {const.}} \underbrace{|\varvec{J}_{\eta \rightarrow \xi }^{(i)}|}_{\text {linear}} \underbrace{|\varvec{J}_{\xi \rightarrow x}|}_{\text {rational}}\,\mathrm {d}\zeta _1 \mathrm {d} \zeta _2, \end{aligned}$$

(24)

$$\begin{aligned} \int _{\varOmega _{x}^{\mathrm {poly}}} \alpha \mathcal {R}\,\mathrm {d} \varOmega= & {} \sum _{i=1}^{n_{\mathrm {v}}} \sum _{j=1}^{n_{\mathrm {sc}}} \int _{-1}^1 \int _{-1}^1 \alpha \mathcal {R}\,\underbrace{|\varvec{J}_{\zeta \rightarrow \eta }^{(j)}|}_{\text {const.}} \underbrace{|\varvec{J}_{\eta \rightarrow x}^{(i)}|}_{\text {linear}}\,\mathrm {d}\zeta _1 \mathrm {d} \zeta _2. \end{aligned}$$

(25)

While for each sub-cell $|\varvec{J}_{\zeta \rightarrow \eta }^{(j)}|$ has a constant value due to the simple geometry mapping $\varvec{Q}_{\zeta \rightarrow \eta }$ [17], the non-constant terms are functions of the mapped coordinates. During the numerical integration in each sub-cell, a Gaussian quadrature rule is applied using $n \times n$ integration points as depicted for a single sub-cell in Fig. 5 with $n=3$.

4.2.2 Sub-cell compression schemes

Although the QTD-based integration scheme allows for a robust and fully automatic computation of discontinuous integrals, its main drawback is seen in the exponentially increasing number of sub-cells as the refinement level k increases. This leads to high numerical costs both for performing the QTD itself and for computing the integrals over the sub-cells [82], especially for nonlinear problems [83]. As a solution to this problem, Petö et al. [38] introduced a novel approach based on image compression techniques for reducing the number of integration points and consequently the computational time. In the following, the main idea of this method is briefly discussed; for further information, we refer to the original article [38]. The compression algorithm is inserted directly between the QTD and the numerical integration stages as an intermediate step and requires only minor modification in an already existing code. There are several algorithms that can be used for the compression of two-dimensional sub-cells, such as the run-length encoding (RLE), image block representation (IBR) and minimal rectangular partition (MRP) [84,85,86]. Among these methods, the IBR (see Fig. 6) is the most suitable choice combining high compression rates, a low computational overhead and low implementational effort. If the QTD-based integration is used, the discontinuity in the integrals is captured by agglomerating integration points in the vicinity of the boundary. For the sake of consistency, the cut sub-cells are generally not subjected to the compression step.

Let the compression rate $\lambda =n_{\mathrm {IP}}^{\mathrm {after}}/n_{\mathrm {IP}}^{\mathrm {before}}$ define the ratio of the number of integration points before $n_{\mathrm {IP}}^{\mathrm {before}}$ and after $n_{\mathrm {IP}}^{\mathrm {after}}$ the compression, where a successful compression is indicated by $\lambda$-values below one. Distributing $n \times n$ integration points in the physical, fictitious and cut sub-cells, the compression ratio $\lambda$ for the IBR algorithm is depicted by the black dashed curve in Fig. 7 based on the example shown in Fig. 6. Note that already for smaller refinement levels k, a significant compression can be achieved $(\lambda \approx 0.7$ for $k=3)$ and that $\lambda$ is independent from n. However, according to Abedian et al. [83, 87], the fictitious integration points, whose only purpose is to prevent a possible ill-conditioning of the system matrices, can be replaced by a significantly smaller set of integration points. Following this reduction in fictitious integration points (RFIP) approach and only considering the physical integration points after the compression, even better results can be achieved, requiring only 30–40% of the original integration points, as depicted by the solid lines in Fig. 7.

In Ref. [38], a piece-wise polynomial integrand is assumed for which it was shown, that compressing only the physical sub-cells but not the cut ones, the same accuracy can be obtained as with the standard QTD-based integration scheme; however, with significantly less computational time. If the discontinuous integrand is not a piece-wise polynomial but a piece-wise rational function, the integration accuracy of the Gaussian quadrature depends on the density of the integration points in all integration sub-domains. That is to say, it is not enough to monitor the integration regions where the integrand is discontinuous (cut sub-cells), but it is equally important to guarantee an accurate integration in the physical sub-cells, where the integrand is continuous. Therefore, when compressing the physical sub-cells, a deterioration of the integration accuracy is expected due to the rational nature of the integrand function. The actual effect due to the compression is examined in detail in Sects. 5, 6, and 7.

Fig. 6

Numerical integration in the cut polygonal element based on the IBR compression technique (same example as depicted in Fig. 5)

Fig. 7

Compression rates $\lambda$ for the IBR algorithm when considering either all integration points in the polygonal element after the compression (black dashed line) or only the physical ones (solid lines)

5 Integration error

The integration error introduced when computing the integrals in Eqs. (24) and (25) is caused by the fact, that neither rational nor discontinuous functions can be integrated exactly via standard Gaussian quadrature rules. In the following, the errors in integration accuracy caused by the rational and discontinuous nature of the integrands are denoted by $e_{\mathcal {R}}$ and $e_{\mathcal {D}}$, respectively. Using a QTD-based integration scheme, for the integral over all sub-cells

$$\begin{aligned} I(e_{\mathcal {R}},e_{\mathcal {D}}) = I_{\mathrm {phys}}(e_{\mathcal {R}}) + I_{\mathrm {cut}}(e_{\mathcal {R}},e_{\mathcal {D}}) \end{aligned}$$

(26)

holds, where $I_{\mathrm {phys}}$ and $I_{\mathrm {cut}}$ denote the integrals over the physical and cut sub-cells, respectively. Note that while $I_{\mathrm {phys}}$ only depends on $e_{\mathcal {R}}$, for $I_{\mathrm {cut}}$ both $e_{\mathcal {R}}$ and $e_{\mathcal {D}}$ are relevant. Since the compressed sub-cells generally have a decreased integration point density compared to the uncompressed ones (see Figs. 5 and 6), using the same integration order results in an increased error $e_{\mathcal {R}}$ when compression is used. However, following the approach by Petö et al. [38] and only compressing the physical sub-cells, this affects $I_{\mathrm {phys}}$ only while $I_{\mathrm {cut}}$ is unchanged. In order to investigate the influence of the compression (particularly based on the IBR algorithm) on the integration accuracy, in Sects. 5.1 and 5.2 the area and stiffness matrix of the cut polygonal element depicted in Figs. 5 and 6 are computed.³ The vertices V of the distorted polygonal element in the global space as well as the center $\varvec{x}_c$ of the unit circle $(r=1)$ introducing the discontinuity are given as:

$$\begin{aligned} V = \left\{ \begin{bmatrix} 2.7\\ 2.0 \end{bmatrix}, \begin{bmatrix} 2.0\\ 3.0 \end{bmatrix}, \begin{bmatrix} 0.5\\ 1.0 \end{bmatrix}, \begin{bmatrix} 1.8\\ 0.5 \end{bmatrix}, \begin{bmatrix} 2.5\\ 1.0 \end{bmatrix} \right\} ,\,\varvec{x}_c = \begin{bmatrix} 3\\ 2 \end{bmatrix}. \end{aligned}$$

(27)

Furthermore, since partitioning the polygonal element in the global and local spaces (see Sects. 4.1.1 and 4.1.2) generally leads to different integral formulations, the effect of the IBR compression is examined for both settings using quadrilateral sub-domains. Throughout the simulations in this article rational Wachspress shape functions [27] are used, which can be also formulated directly over the convex global element enabling a simpler and less error-prone numerical integration.

5.1 Numerical example: Error in the area approximation

The approximate solution for the area A is obtained via Eqs. (24) and  (25), where for the current example $\mathcal {R}=1$ applies. Based on the model of the single polygonal element given in Eq. (27), a reference solution for the area can be computed analytically resulting in $A_{\mathrm {ref}} = 2.286616571808802$ which can be used for computing the error $e_A$ by Eq. (28), where in case of a QTD-based integration $A = A_{\mathrm {phys}} + A_{\mathrm {cut}}$ holds

$$\begin{aligned} e_A = \left| \frac{A_{\mathrm {ref}}-A}{A_{\mathrm {ref}}}\right| \times 100\% = \left| 1-\frac{A_{\mathrm {phys}}}{A_{\mathrm {ref}}} -\frac{A_{\mathrm {cut}}}{A_{\mathrm {ref}}}\right| \times 100\%. \end{aligned}$$

(28)

5.1.1 Local sub-division scheme

The approximation quality when using a local partitioning scheme is depicted in Fig. 8 for various refinement levels $k=1,2,\ldots ,15$ and integration orders with $n=1,2,5$ and 10 integration points per direction. Based on Eq. (28), the ratios

$$\begin{aligned} \rho _{\mathrm {phys}}= & {} (1-A_{\mathrm {phys}}/A_{\mathrm {ref}})\times 100\% \end{aligned}$$

(29)

$$\begin{aligned} \rho _{\mathrm {cut}}= & {} A_{\mathrm {cut}}/A_{\mathrm {ref}}\times 100\%, \end{aligned}$$

(30)

depicted in Fig. 8a and b are introduced. Both values show an exponential convergence as the number of refinement levels k is increased. In case of $\rho _{\mathrm {cut}}$, the number of integration points per direction n plays a role for small values of k only, while for $\rho _{\mathrm {phys}}$ its effect is only significant for rather large values of k. Using $n=1$ results in such a poor integration over the large physical sub-cells that the ratio $\rho _{\mathrm {phys}}$ cannot be further improved after a certain refinement level $(k=4)$, resulting in a poor convergence of the entire error $e_A$ as depicted in Fig. 8c. Since $\rho _{\mathrm {cut}}$ is not affected by the compression, the increased error in $e_{A}$ when a compression is used is directly correlated to $\rho _{\mathrm {phys}}$. Nonetheless, not only that increasing n results in an improved convergence of $\rho _{\mathrm {phys}}$ and consequently of $e_A$ in general, but also the small differences between the results obtained with and without compression vanish, even for slightly increased n, as depicted in Fig. 8d.

Fig. 8

Effect of the compression on the integration accuracy when computing the area of the physical domain in a cut polygonal element. The sub-division is performed in the local space. a Ratio $\rho _{\mathrm {phys}}$ based on Eq. (29). b Ratio $\rho _{\mathrm {cut}}$ based on Eq. (30). c $e_A$, $\rho _{\mathrm {phys}}$ and $\rho _{\mathrm {cut}}$ for $n=1$. d Error $e_A$ based on Eq. (28)

5.1.2 Global sub-division scheme

As a comparison, we perform the same computations for the second case, where the polygonal element $\varOmega _{x}^{\mathrm {poly}}$ is subdivided in the global space; see a Eq. (25). In this case, no rational mapping from $\varOmega _{\xi }^{\mathrm {poly}}$ to $\varOmega _{x}^{\mathrm {poly}}$ has to be considered. Therefore, when computing the area $(\mathcal {R}=1)$, the chosen rational polygonal shape function does not play any role. The accuracy of the computation of the area depends solely on how well $|\varvec{J}_{\eta \rightarrow x}|$ in Eq. (19) can be integrated. Since $|\varvec{J}_{\eta \rightarrow x}|$ is a linear function as given in Eq. 20, the accuracy of the Gaussian quadrature over the physical sub-cells is recovered already for a single integration point $(n=1)$ per sub-cell. Consequently, the same accuracy is obtained regardless of the number of integration points and whether a compression was performed or not. This can be seen in Fig. 9a where all curves for $n=1$, 2, 5 and 10 are overlapping for the uncompressed and compressed sub-cells. Nonetheless, due to the discontinuous integrals over the cut sub-cells, the influence of n is still present as observed in Fig. 9b. Here, the relative error in the area approximation $e_A$ improves for increased values of n.

Fig. 9

Ratio $\rho _{\mathrm {phys}}$ and error $e_A$ for the global sub-division scheme. a Ratio $\rho _{\mathrm {phys}}$ based on Eq. (29). b Error $e_A$ based on Eq. (28)

5.2 Numerical example: Error in the stiffness matrix

In this sub-section, the integration accuracy for computing the stiffness matrix is investigated using the same cut polygonal element and integration approaches as in the previous section. For this computation, a homogeneous material with a Young’s modulus of $E=209.9$ MPa and a Poisson’s ratio of $\nu = 0.29$ is chosen and a plane-stress state is assumed. In the following, we denote the polygonal shape functions defined over $\varOmega _x^{\mathrm {poly}}$ by $\hat{N}_i^{(\mathrm {poly})}(\varvec{x})$ while for the shape functions over $\varOmega _{\xi }^{\mathrm {poly}}$ the notation $N_i^{(\mathrm {poly})}(\varvec{\xi })$ is used. Applying the same notation to the stiffness matrices in the global and local formulations, the variables $\hat{\varvec{K}}$ and $\varvec{K}$ are introduced, respectively. The components of $\hat{\varvec{K}}$ typically contain integrals of the form

$$\begin{aligned} \hat{k} = \int _{\varOmega _x^{\mathrm {poly}}} \frac{\partial \hat{N}_i^{(\mathrm {poly})} (\varvec{x}) }{\partial x_m} \frac{\partial \hat{N}_j^{(\mathrm {poly})} (\varvec{x}) }{\partial x_n}\,\mathrm {d} \varOmega , \end{aligned}$$

(31)

while the components of $\varvec{K}$ are expressed by more complex integrals due to the change in variables:

$$\begin{aligned} k&= \int _{\varOmega _{\xi }^{\mathrm {poly}}} \left( \dfrac{\partial \xi _1 }{\partial x_m}\dfrac{\partial N_i^{(\mathrm {poly})}(\varvec{\xi })}{\partial \xi _1} + \dfrac{\partial \xi _2 }{\partial x_m} \dfrac{\partial N_i^{(\mathrm {poly})}(\varvec{\xi })}{\partial \xi _2} \right) \nonumber \\&\quad \times \left( \dfrac{\partial \xi _1 }{\partial x_m}\dfrac{\partial N_j^{(\mathrm {poly})}(\varvec{\xi })}{\partial \xi _1} + \dfrac{\partial \xi _2 }{\partial x_m} \dfrac{\partial N_j^{(\mathrm {poly})}(\varvec{\xi })}{\partial \xi _2} \right) |\varvec{J}_{\xi \rightarrow x}|\,\mathrm {d} \varOmega . \end{aligned}$$

(32)

In both cases, $i,j = 1,2,\ldots ,n_{\mathrm {v}}$ and $m,n = 1,2$. The rational derivatives of the Wachspress shape functions can be found in Ref. [46], where the given formulae also apply to the global shape functions. In the following, for computing $\hat{\varvec{K}}$ the global partition-based approach given in Eq. (25) is used, while for $\varvec{K}$ the integrals are solved via the local approach in Eq. (24). For evaluating the convergence in the stiffness matrices, we use the formula [2]

$$\begin{aligned} e_K = \frac{||\varvec{K}_{\mathrm {ref}}-\varvec{K}||_{L_2}}{||\varvec{K}_{\mathrm {ref}}||_{L_2}} \times 100 \% , \end{aligned}$$

(33)

where for the $2n_{\mathrm {v}}\times 2n_{\mathrm {v}}$-dimensional stiffness matrix of a two-dimensional polygonal element with $n_{\mathrm {v}}$ vertices, the standard $L_2$-norm $||\cdot ||_{L_2}$ is defined as

$$\begin{aligned} ||\varvec{K}||_{L_2} = \left( \sum _{i=1}^{2n_{\mathrm {v}}} \sum _{j=1}^{2n_{\mathrm {v}}} |K_{ij}|^2 \right) ^{1/2}. \end{aligned}$$

(34)

The reference values for the global and local approaches are obtained by using a highly accurate integration with $k=15$ and $n=50$ resulting in the norms

$$\begin{aligned} ||\hat{\varvec{K}}_{\mathrm {ref}}||_{L_2}= & {} 2.587287053379724 \times 10^5\quad \text {and}\end{aligned}$$

(35)

$$\begin{aligned} ||\varvec{K}_{\mathrm {ref}}||_{L_2}= & {} 2.582566542956506 \times 10^5. \end{aligned}$$

(36)

The results obtained with and without compression are depicted for the global and local formulations in Fig. 10a and b, respectively. Note that since for the two plots two different reference values were used, $\hat{\varvec{K}}_{\mathrm {ref}}$ and $\varvec{K}_{\mathrm {ref}}$, the errors cannot be directly compared. However, it can be observed that due to the significantly simpler integral formulations of the global approach, the integration accuracy is affected only marginally by the compression. In contrast, the integrand in case of the local formulation contains extra mappings and inverse Jacobian terms, resulting in a more complex rational expression. Consequently, the deterioration of the integration accuracy can be clearly observed when the compression is used.

Fig. 10

Error in the $L_2$-norm of the stiffness matrix for various refinement levels k and integration points n per direction and sub-cell. a Error $e_K$ in the global formulation. b Error $e_K$ in the local formulation

Fig. 11

Problem of a statically loaded perforated plate and its exemplary discretization by an unfitted mesh consisting of quadrilateral, pentagonal, hexagonal and heptagonal polygonal elements. a Problem definition. b Unfitted polygonal mesh

6 Numerical example: Perforated plate

So far, the integration error with and without the compression of sub-cells was investigated only on the element level. In this section, the effect of the integration error is investigated in the context of finite element analysis by solving a linear elastic problem (see Fig. 11a), using unfitted polygonal meshes with different element sizes, such as the one depicted in Fig. 11b. The assumed material properties are the same as the ones given in Sect. 5.2. For the decomposition, the QTD-approach is used without and with the IBR compression. In both cases, a possible ill-conditioning of the system matrices is avoided by using the RFIP approach [38, 83, 87], requiring only a negligible number of fictitious integration points. For the approximation of the displacement field, rational Wachspress shape functions are used. In the remainder of the article, the polygonal shape functions are defined in the local space of the elements $\varOmega _{\xi }^{\mathrm {poly}}$ due to the following reasons:

• 1. According to Sect. 5, the integration quality in polygonal elements is visibly affected by the compression of sub-cells, while this influence is not observed in polygonal elements employing global shape functions. Since the effect of reducing the number of integration points is the main focus of this article, locally defined shape functions allow for a more stringent investigation of the compressed QTD.

• 2. Not all polygonal shape function can be defined over arbitrarily distorted polygonal elements in the global space. The rational Wachspress interpolant is a suitable representative, which can be defined in the global space; however, it requires the element to be convex.

• 3. In most FE softwares, the shape functions are commonly generated in the local space of the implemented elements.

Considering the reasons mentioned above, we employ a local partitioning scheme, which is aligned with the definition of the shape functions in $\varOmega _{\xi }^{\mathrm {poly}}$. Consequently, integrals of the form given in Eq. (24) have to be solved.

6.1 Convergence in the energy norm

The quality of the results is measured by the relative error $e_{\mathrm {E}}$ in the energy norm $|| \cdot ||_{\mathrm {E}}$ according to [2]

$$\begin{aligned} e_{\mathrm {E}} = \frac{||\varvec{u}_{\mathrm {ref}} - \varvec{u} ||_{\mathrm {E}}}{|| \varvec{u}_{\mathrm {ref}} ||_{\mathrm {E}}} = \sqrt{\left| \dfrac{\mathcal {B}_e(\varvec{u}_{\mathrm {ref}},\varvec{u}_{\mathrm {ref}})-\mathcal {B}_e(\varvec{u},\varvec{u})}{\mathcal {B}_e(\varvec{u}_{\mathrm {ref}},\varvec{u}_{\mathrm {ref}})} \right| } \times 100 [\%], \end{aligned}$$

(37)

for which the reference value $1/2\,\, \mathcal {B}_e(\varvec{u}_{\mathrm {ref}},\varvec{u}_{\mathrm {ref}})=0.7021812127$ from Ref. [16] is used. The corresponding results are depicted in Fig. 12 for various settings, also including the case $k=0$ where no integration sub-cells are used (Fig. 12a). Considering a uniform h-refinement of the given problem with linear elements, the theoretical optimal convergence rate in the energy norm is algebraic with the factor $\beta = 1/2$ [2, 16]. In the following, the effect of the integration accuracy of the piece-wise rational integrands on the convergence rate is discussed, while focusing on the terms piece-wise (Sect. 6.1.1) and rational (Sect. 6.1.2), separately.

Fig. 12

Error in the energy norm $e_{\mathrm {E}}$ during h-refinement using different refinement levels k of the QTD and number of integration points per direction n. In each plot, the theoretical convergence rate for linear shape functions is depicted. For $n=5$ and 10 in sub-figure (b), the theoretical convergence rate is already obtained in the depicted DOF-range, and therefore, these curves are overlapping. a $k=0$ (no QTD). b $k=3$. (Color figure online)

6.1.1 Effect of the discontinuity

Using $k=0$ with low-order quadrature rules results in a poor convergence; however, increasing the value of n quickly leads to an improved solution quality as both the rational and discontinuous parts of the piece-wise rational integrands are integrated more accurately, leading to decreased errors $e_{\mathcal {D}}$ and $e_{\mathcal {R}}$ (cf. Sect. 5). For $n=10$ the theoretical convergence rate is basically obtained (magenta curve in Fig. 12a). Although in case of $k=0$, no QTD is performed both the physical and cut polygonal elements are partitioned once for integration purposes (to facilitate the use of standard Gaussian quadrature rules) as depicted in Fig. 4b. Despite the optimal convergence rate, using $k=0$ with a globally increased quadrature order is extremely inefficient. As an example, the discretization by 40,000 elements is investigated for the settings $k=0,\,n=10$ (magenta curve Fig. 12a) and $k=3,\,n=2$ (red curve in Fig. 12b). While in both cases an optimal convergence and an error $e_{\mathrm {E}} < 1\%$ is reached, the first settings results in 230,700 integration points in total and 9 times more computational time for generating the stiffness matrices than the second setting.

Performing a QTD with $k=3$ (Fig. 12b) does not only lead to better results due to the more accurate resolution of the boundary, but the results are obtained much more efficiently as the number of integration points is not increased everywhere, but only in the vicinity of the discontinuity. With the reduced error $e_{\mathcal {D}}$ in case of $k=3$, the optimal convergence rate is already obtained for $n=2$ basically in the entire investigated DOF-range. The fast recovery of the theoretical convergence rate with increasing n is explained by the fact that only low-order elements are used. That is to say, due to the relatively poor approximation of the displacement field by low-order elements the integration error caused by the discontinuous integrand in cut elements is balanced with the discretization error. Since the optimal convergence rate is already obtained for $k=3$, using higher refinement levels $k>3$ enabling an even better resolution of the boundary is not meaningful and results in the same curves as depicted in Fig. 12b.

6.1.2 Effect of the rational integrand

The stationary value of the curve $n=1$ (blue) in Fig. 12b is caused by the inaccurate integration of the rational functions present in the whole computational domain, i.e., both in the physical and cut elements, which leads to an error $e_{\mathcal {R}}$ dominating the entire solution quality. This phenomenon has been already discussed with respect to Figs. 8 and 10, revealing the higher importance of $e_{\mathcal {R}}$ over $e_{\mathcal {D}}$ for small values of n. Although the stationary state is not yet reached, but essentially the start of this effect can be observed also for the curve $n=2$ (red) in Fig. 12b due to the same reason. Furthermore, since the depicted curves in Fig. 12b are identical to the ones obtained with higher refinement levels k, the conjecture that the deterioration of the convergence rates for $n=1$ and 2 are not caused by $e_{\mathcal {D}}$ is confirmed. On the contrary, for the curves when $k=0$ (Fig. 12a), where the discontinuity is approximated very poorly, the sub-optimal convergence is caused not only by $e_{\mathcal {R}}$, but also by $e_{\mathcal {D}}$, resulting in the difference between Fig. 12a and b.

6.2 Efficiency of the compression

Although on the element level in Sect. 5 the effect of the compression was clearly detected for the local definition of the shape functions and partitioning of the element, for the current example, basically no loss in accuracy resulting from the compression can be observed in the wide range of investigated discretizations. What is even more, for achieving the same accuracy, only 55–38% of the original integration points are required by the compressed QTD, depending on the chosen integration settings (see Fig. 13). Note that while in case of Fig. 7 the compression was compared to a QTD where all sub-cells and integration points are considered, in the current case, the comparison is made to a QTD where the fictitious integration points are already considerably reduced by the RFIP approach [38, 83, 87]. Nonetheless, still a remarkable compression is achieved, even when $k=3$ and $n=2$ is used.

Moreover, the overall reduction in the computational time is not only influenced by the number of resulting integration points after the compression, but also by the time invested for performing the compression itself. The spent time depends on the complexity of the algorithm for detecting cut sub-cells and on the implementation quality of the QTD procedure. In the ideal case, the additional time should be always smaller than the time saved during the integration over the compressed QTD [38]. The time savings for computing the element matrices are depicted in Fig. 14 for three different settings. In all three cases, a discretization by 40,000 elements is used, representing the first stage where an error $e_{\mathrm {E}} \le 1 \%$ is obtained (Fig. 12). Already for the simplest meaningful setting a reduction in computational time is possible, which can be even further increased once a higher refinement level k and quadrature rule by $n\times n$ integration points are used (Fig. 14).

Fig. 13

Compression ratio $\lambda$ for various mesh sizes, refinement levels k and integration points per direction n. a $k=3$. b $k=5$. c $k=7$

Fig. 14

Time requirements for the computation of the element matrices (physical and cut) for a compressed compared to an uncompressed QTD. For all three cases, a discretization by 40,000 elements is used. The colours in the bars indicate the time proportions spent on the computation of the physical and cut element matrices. (Color figure online)

Remark 1

In this example, Wachspress’ shape function defined in the canonical element was investigated in particular, for which a clear deterioration in the integration accuracy due to the IBR compression was shown on the element level (see Sect. 5). Nonetheless, when embedded into an FE analysis, the compression had marginal effects on the solution quality and already when $n \ge 2$ was used, optimal convergence rates were obtained (see Fig. 12b). As such results cannot be further improved, the same performance of the globally defined shape functions is very likely, which were only tested on the element level in Sect. 5 and no negative effects resulting from the compression were shown.

Remark 2

Note that regarding the quality of the results and the success of the compression, the fact that only low-order polygonal shape functions are used plays a significant role. If high-order shape functions are utilized, the optimal convergence rates would not be achieved already for $k=3$ and especially not for $k=0$. Also, from Sect. 5 it is known that the effect on the integration accuracy of the compression is present on the element level. In our opinion, the fact that it is hardly detectable in the results of the simulation is due to the reason that the introduced integration error is dominated by the discretization error due to the low-order shape functions; however, this statement requires further research. Furthermore, it has already been shown in Ref. [38] that the computational time can be significantly reduced for higher refinement levels k and polynomial degrees p. Regarding high-order elements also high-order quadrature rules have to be used which correlates with an increase in n (investigated in this contribution). Due to the low-order polygonal shape functions, lower values of k and n already suffice for obtaining an optimal algebraic convergence rate. While a reduction in computational time is possible even for $k=3$ with $n=2$, as it is shown in Fig. 14, the full potential of the compression scheme is expected to emerge for unfitted polygonal meshes once high-order polygonal interpolants are available, where an accurate numerical integration is of utmost importance.

7 Numerical example: Porous multicrystalline domain

In this section, a porous multicrystalline domain depicted in Fig. 15a is investigated, where the Young’s modulus varies linearly for each grain depending on the grain size from 50.000 (smallest) to 250.000 MPa (largest), as indicated by the greyscale coloring. While setting up an FE-mesh for such domain is cumbersome, a Cartesian FC-mesh would lead to oscillatory stress fields and reduced convergence properties due to the inaccurate capturing of the material interfaces [88, 89]. Hence, the computational mesh is obtained by assigning for each grain a single polygonal element. The magnitude of the displacement field of such a domain is depicted in Fig. 15c. The void regions are introduced through the fictitious domain concept, leading to cut polygonal elements indicated by yellow color in Fig. 15a. The corresponding displacement field of the porous material is shown in Fig. 15d.

Fig. 15

Numerical example of a porous multicrystalline domain with a computational mesh and b solution characteristics when the IBR compression scheme is used. The magnitude of the displacement fields is depicted for a computational domain c without and d with the ellipsoidal cavities. In both cases, a scaling factor of 59.48 is used, while the dashed lines indicate the contours of the undeformed bodies. a Multicrystalline domain with void regions. The same boundary conditions apply as in the problem depicted in Fig. 11. b Error in the strain energy according to Eq. (38) (blue), reduction in integration points (red) and computational time (purple). c Displacements without void regions $(u_{\min }=0$ mm, $u_{\min }=3.83 \cdot 10^{-3}$ mm). d Displacements with void regions $(u_{\min }=0$ mm, $u_{\min }=6.75 \cdot 10^{-3}$ mm). (Color figure online)

For studying the effect of the IBR compression, a constant discretization is used in conjunction with various refinement levels k and $n \times n$ integration points per sub-cell. The corresponding results are depicted in Fig. 15b, where the IBR compression using only the physical integration points is compared to the standard QTD utilizing all the integration points (both physical and fictitious, cf. Fig. 7). A possible ill-conditioning during the simulation with compression is avoided by using the approach introduced by Abedian et al. [83, 87]. Note that for the current example no reference solution exists. Therefore, instead of using Eq. (37), the relative deviation in the strain energy due the reduction in integration points is measured by

$$\begin{aligned} \varDelta _{\mathrm {SE}} = \left| \dfrac{\mathcal {B}_e(\varvec{u}_{\mathrm {QTD}},\varvec{u}_{\mathrm {QTD}})-\mathcal {B}_e(\varvec{u}_{\mathrm {IBR}},\varvec{u}_{\mathrm {IBR}})}{\mathcal {B}_e(\varvec{u}_{\mathrm {QTD}},\varvec{u}_{\mathrm {QTD}})} \right| \times 100 [\%], \end{aligned}$$

(38)

where $\varvec{u}_{\mathrm {QTD}}$ and $\varvec{u}_{\mathrm {IBR}}$ are the approximated displacement fields (for a given k and n) without compression and with the IBR compression scheme, respectively. There are two important facts to be noted regarding $\varDelta _{\mathrm {SE}}$ in Fig. 15b: First, the differences are growing with increasing k until they reach a stationary value. This is in perfect agreement with the general behavior of the compression which has a higher compression rate $\lambda$ for increasing values of k (see Fig. 7 and red curves in Fig. 15b). It is clear that a better compression leads to less integration points and therefore, to higher differences in the integral values. Once the compression ratio $\lambda$ reaches a stationary value, the deviations $\varDelta _{\mathrm {SE}}$ also converge to a finite maximum value. Second, despite the growing nature of $\varDelta _{\mathrm {SE}}$ in Fig. 15b, the maximum deviation is marginal already for $n=2$ $(\varDelta _{\mathrm {SE}} = 0.0057\%)$. It is crucial to emphasize that due to the lack of a reference solution, $\varDelta _{\mathrm {SE}}$ in Eq. (38) expresses only a relative difference between the two approximate solutions $\varvec{u}_{\mathrm {QTD}}$ and $\varvec{u}_{\mathrm {IBR}}$. Although $\varDelta _{\mathrm {SE}}$ may increase for higher values of k, the error compared to the real solution (see $e_{\mathrm {E}}$ in Sect. 6) is not increasing and generally, both $\varvec{u}_{\mathrm {QTD}}$ and $\varvec{u}_{\mathrm {IBR}}$ are more accurate when a higher refinement level k is used. In terms of efficiency of the compression, a significant compression ratio $\lambda$ could be obtained requiring only 25.75% of the integration points in its converged state (red curves in Fig. 15b). However, the time savings during the numerical integration are reduced by the time investment for performing the compression, and therefore, the saving in computation time $\tau$ (purple curves in Fig. 15b) cannot reach the same rates as $\lambda$. In the current example for $n=2$, this means about $10\%$ time saving during the computation of the element matrices. While $\tau$ can be even more significant, i.e., even smaller when more integration points are used [38], such settings are not required for low-order polygonal shape functions, as also concluded at the end of the previous numerical example.

8 Conclusion

Following the poly-FCM approach proposed by Duczek and Gabbert [36] and the fundamental concept of polygonal elements based on generalized barycentric coordinates [27, 28], the enhanced numerical integration scheme based on compressed quadtree-decompositions introduced by Petö et al. [38] was investigated in the context of unfitted polygonal meshes. The straightforward implementation of this novel approach for polygonal meshes was clearly demonstrated and the resulting integral formulations over the compressed local integration mesh were discussed both for local and global sub-divisions of polygonal elements. Since the compression procedure leads to a decreased integration point density for integrating discontinuous non-polynomial functions, the effect of the compression on the integration quality was investigated, with a particular focus on the rational shape functions proposed by Wachspress. The influence of the compression on the integration quality was clearly detectable on the element level based on a local definition of the shape functions and a local decomposition of the polygonal element. On the contrary, for globally defined shape functions and partitioning schemes, the area approximation and the computation of the stiffness matrix are written in a much simpler form, for which the compression resulted basically in no errors. When embedded into an entire simulation of a linear elasticity problem, the compression had a negligible effect on the quality of the results, while requiring 26–55% of the original integration points. In conclusion, the compression is compatible with unfitted polygonal meshes with piece-wise rational integrands and it is able to achieve similar results as described in Ref. [38] in the context of the standard FCM with Cartesian meshes and polynomial shape functions. However, the lack of proper high-order polygonal shape functions constitutes a significant limitation, both with respect to the achievable convergence rates and the exploitation of the full potential of the compressed QTD-based integration scheme.