Abstract
Numerical simulations are used to study the dynamics of a developing suspension Poiseuille flow with monodispersed and bidispersed neutrally buoyant particles in a planar channel, and machine learning is applied to learn the evolving stresses of the developing suspension. The particle stresses and pressure develop on a slower time scale than the volume fraction, indicating that once the particles reach a steady volume fraction profile, they rearrange to minimize the contact pressure on each particle. We consider the timescale for stress development and how the stress development connects to particle migration. For developing monodisperse suspensions, we present a new physics-informed Galerkin neural network that allows for learning the particle stresses when direct measurements are not possible. We show that when a training set of stress measurements is available, the MOR-physics operator learning method can also capture the particle stresses accurately.






























Similar content being viewed by others
Data availability
Data is available from the authors upon reasonable request
References
Abbas M, Climent E, Simonin O, Maxey MR (2006) Dynamics of bidisperse suspensions under Stokes flows: linear shear flow and sedimentation. Phys Fluids 18:1–20. https://doi.org/10.1063/1.2396916
Adams RA, Fournier JJ (2003) Sobolev spaces. Elsevier
Ainsworth M, Dong J (2021) Galerkin neural networks: a framework for approximating variational equations with error control. SIAM J Sci Comput 43(4):A2474–A2501
Antolik JT, Howard A, Vereda F, Ionkin N, Maxey M, Harris DM (2023) Shear-induced migration of a suspension under quasi-planar confinement. arXiv:2302.10380
Barros de Moraes EA, D’Elia M, Zayernouri M (2023) Machine learning of nonlocal micro-structural defect evolutions in crystalline materials. Comput Methods Appl Mech Eng 403:115743
Batchelor GK, Van Rensburg J (1986) Structure formation in bidisperse sedimentation. J Fluid Mech 166:379–407. https://doi.org/10.1017/S0022112086000204
Boodaghidizaji M, Khan M, Ardekani AM (2022) Multi-fidelity modeling to predict the rheological properties of a suspension of fibers using neural networks and gaussian processes. Phys Fluids 34(5):053101
Boyer F, Pouliquen O, Guazzelli É (2011) Dense suspensions in rotating-rod flows: normal stresses and particle migration. J Fluid Mech 686:5–25. https://doi.org/10.1017/jfm.2011.272
Butler JE, Majors PD, Bonnecaze RT (1999) Observations of shear-induced particle migration for oscillatory flow of a suspension within a tube. Phys Fluids 11(10):2865–2877. https://doi.org/10.1063/1.870145
Chang C (1994) Effect of particle size distributions on the rheology of concentrated bimodal suspensions. J Rheol 38(1):85. https://doi.org/10.1122/1.550497
Chun B, Kwon I, Jung HW, Hyun HC (2017) Lattice Boltzmann simulation of shear-induced particle migration in plane Couette- Poiseuille flow: local ordering of suspension. Phys Fluids 29(29):121605–121605. https://doi.org/10.1063/1.4991428
Chun B, Park JS, Jung HW, Won YY (2019) Shear-induced particle migration and segregation in non-brownian bidisperse suspensions under planar poiseuille flow. J Rheol 63(3):437–453
Clevert DA, Unterthiner T, Hochreiter S (2015) Fast and accurate deep network learning by exponential linear units (elus). arXiv:1511.07289
Coussot P (1994) Steady, laminar, flow of concentrated mud suspensions in open channel. J Hydraul Res 32(4):535–559
Cui FR, Howard AA, Maxey MR, Tripathi A (2017) Dispersion of a suspension plug in oscillatory pressure-driven flow. Phys Rev Fluids 2(9):094303. https://doi.org/10.1103/PhysRevFluids.2.094303
Da Cunha FR, Hinch EJ (1996) Shear-induced dispersion in a dilute suspension of rough spheres. J Fluid Mech 309:211–223
Dance SL, Maxey MR (2003) Incorporation of lubrication effects into the force-coupling method for particulate two-phase flow. J Comput Phys 189:212–238. https://doi.org/10.1016/S0021-9991(03)00209-2
Davis PJ, Rabinowitz P (2007) Methods of numerical integration. Courier Corporation
Davis RH, Gecol H (1994) Hindered settling function with no empirical parameters for polydisperse suspensions. AIChE J 40(3):570–575
Dbouk T, Lobry L, Lemaire E (2013) Normal stresses in concentrated non-brownian suspensions. J Fluid Mech 715:239–272
Di Carlo D (2009) Inertial microfluidics. Lab Chip 9:3038–3046. https://doi.org/10.1039/b912547g
Drew DA (1983) Mathematical modeling of two-phase flow. Annu Rev Fluid Mech 15:261–291. https://doi.org/10.1146/annurev.fl.15.010183.001401
Drew DA, Lahey RT (1993) Analytical modeling of multiphase flow. In: Roco M, Butterworth-Heinemann (eds) Particulate two-phase flows
Duraisamy K, Iaccarino G, Xiao H (2019) Turbulence modeling in the age of data. Annual Rev Fluid Mech 51(1):357–377
Gadala-Maria F, Acrivos A (1980) Shear-induced structure in a concentrated suspension of solid spheres. J Rheol 24(6):799–814
Gallier S, Lemaire E, Peters F, Lobry L (2015) Percolation in suspensions and De Gennes conjectures. Phys Rev E 92:020301
Gao C, Xu B, Gilchrist JF (2009) Mixing and segregation of microspheres in microchannel flows of mono- and bidispersed suspensions. Phys Rev E 79(3):036311. https://doi.org/10.1103/PhysRevE.79.036311
Graham AL, Altobelli SA, Fukushima E, Mondy LA, Stephens TS (1991) Note: NMR imaging of shear induced diffusion and structure in concentrated suspensions undergoing Couette flow. J Rheol 35(1):191–201. https://doi.org/10.1122/1.550227
Hampton RE, Mammoli AA, Graham AL, Tetlow N, Altobelli SA (1998) Migration of particles undergoing pressure-driven flow in a circular conduit. J Rheol 41(3):621. https://doi.org/10.1122/1.550863
Harris CR, Millman KJ, van der Walt SJ, Gommers R, Virtanen P, Cournapeau D, Wieser E, Taylor J, Berg S, Smith NJ, Kern R, Picus M, Hoyer S, van Kerkwijk MH, Brett M, Haldane A, del Río JF, Wiebe M, Peterson P, Gérard-Marchant P, Sheppard K, Reddy T, Weckesser W, Abbasi H, Gohlke C, Oliphant TE (2020) September. Array programming with NumPy. Nature 585(7825):357–362. https://doi.org/10.1038/s41586-020-2649-2
He L, Tafti DK (2019) A supervised machine learning approach for predicting variable drag forces on spherical particles in suspension. Powder Technol 345:379–389
Howard A, Maxey M, Yeo K (2018) Settling of heavy particles in concentrated suspensions of neutrally buoyant particles under uniform shear. Fluid Dyn Res. https://doi.org/10.1088/1873-7005/aabfa6
Howard AA, Maxey MR (2018) Simulation study of particle clouds in oscillating shear flow. J Fluid Mech 852:484–506
Howard AA, Maxey MR, Gallier S (2022) Bidisperse suspension balance model. Phys Rev Fluids 7(12):124301
Husband DM, Mondy LA, Ganani E, Graham AL (1994) Direct measurements of shear-induced particle migration in suspensions of bimodal spheres. Rheol Acta 33(3):185–192. https://doi.org/10.1007/BF00437303
Jin H, Kang K, Ahn K, Briels W, Dhont J (2018) Non-local stresses in highly non-uniformly flowing suspensions: the shear-curvature viscosity. J Chem Phys 149(1)
Jin H, Kang K, Ahn KH, Dhont JK (2014) Flow instability due to coupling of shear-gradients with concentration: non-uniform flow of (hard-sphere) glasses. Soft Matter 10(47):9470–9485
Kanehl P, Stark H (2015) Hydrodynamic segregation in a bidisperse colloidal suspension in microchannel flow: a theoretical study. J Chem Phys 142(21). https://doi.org/10.1063/1.4921800
Karniadakis GE, Kevrekidis IG, Lu L, Perdikaris P, Wang S, Yang L (2021) Physics-informed machine learning. Nat Rev Phys 3(6):422–440
Karnis A, Goldsmith H, Mason S (1966) The kinetics of flowing dispersions: I. Concentrated suspensions of rigid particles. J Colloid Interface Sci 22(6):531–553. https://doi.org/10.1016/0021-9797(66)90048-8
Kingma DP, Ba J (2015) Adam: a method for stochastic optimization. arXiv:1412.6980
Koh CJ, Hookham P, Leal LG (1994) An experimental investigation of concentrated suspension flows in a rectangular channel. J Fluid Mech 266
Leighton D, Acrivos A (1987) The shear-induced migration of particles in concentrated suspensions. J Fluid Mech 181:415–439
Lhuillier D (2009) Migration of rigid particles in non-Brownian viscous suspensions. Phys Fluids 21(2):023302. https://doi.org/10.1063/1.3079672
Li Y, Perlman E, Wan M, Yang Y, Meneveau C, Burns R, Chen S, Szalay A, Eyink G (2008) A public turbulence database cluster and applications to study lagrangian evolution of velocity increments in turbulence. J Turbul 9:N31
Li Z, Kovachki NB, Azizzadenesheli K, Liu B, Bhattacharya K, Stuart A, Anandkumar A (2021) Fourier neural operator for parametric partial differential equations. In: International conference on learning representations
Lomholt S, Maxey MR (2003) Force-coupling method for particulate two-phase flow: Stokes flow. J Comput Phys 184(2):381–405. https://doi.org/10.1016/S0021-9991(02)00021-9
Lu L, Jin P, Pang G, Zhang Z, Karniadakis GE (2021) Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat Mach Intell 3(3):218–229
Lyon MK, . Leal LG (1998a) An experimental study of the motion of concentrated suspensions in two-dimensional channel flow. Part 1. Monodisperse systems. J Fluid Mech 363. https://doi.org/10.1017/S0022112098008817
Lyon MK, Leal LG (1998b) An experimental study of the motion of concentrated suspensions in two-dimensional channel flow. Part 2. Bidisperse systems. J Fluid Mech 363. https://doi.org/10.1017/S0022112098008829
Maxey MR, Patel BK (2001) Localized force representations for particles sedimenting in Stokes Flow. Int J Muliphase Flow 27:1603–1626
Metzger B, Butler JE (2010) Irreversibility and chaos: role of long-range hydrodynamic interactions in sheared suspensions. Phys Rev E 82(5):51406
Metzger B, Butler JE (2012) Clouds of particles in a periodic shear flow. Phys Fluids 24(2):021703. https://doi.org/10.1063/1.3685537
Metzger B, Pham P, Butler JE (2013) Irreversibility and chaos: role of lubrication interactions in sheared suspensions. Phys Rev E 87(5). https://doi.org/10.1103/PhysRevE.87.052304
Miller RM, Morris JF (2006) Normal stress-driven migration and axial development in pressure-driven flow of concentrated suspensions. J Nonnewton Fluid Mech 135(2–3):149–165. https://doi.org/10.1016/j.jnnfm.2005.11.009
Monsorno D, Varsakelis C, Papalexandris M (2017) Poiseuille flow of dense non-colloidal suspensions: the role of intergranular and nonlocal stresses in particle migration. J Nonnewton Fluid Mech 247:229–238
Morris JF (2009) A review of microstructure in concentrated suspensions and its implications for rheology and bulk flow. Rheol Acta 48(8):909–923. https://doi.org/10.1007/s00397-009-0352-1
Morris JF, Boulay F (1999) Curvilinear flows of noncolloidal suspensions: the role of normal stresses. J Rheol 43:1213–1237
Nott PR, Brady JF (1994) Pressure-driven flow of suspensions: simulation and theory. J Fluid Mech 275:157. https://doi.org/10.1017/S0022112094002326
Nott PR, Guazzelli É, Pouliquen O (2011) The suspension balance model revisited. Phys Fluids 23(4):043304. https://doi.org/10.1063/1.3570921
Pang G, D’Elia M, Parks M, Karniadakis GE (2020) npinns: nonlocal physics-informed neural networks for a parametrized nonlocal universal laplacian operator. algorithms and applications. J Computat Phys 422:109760
Patel RG, Desjardins O (2018) Nonlinear integro-differential operator regression with neural networks. arXiv:1810.08552
Patel RG, Trask NA, Wood MA, Cyr EC (2021) A physics-informed operator regression framework for extracting data-driven continuum models. Comput Methods Appl Mech Eng 373:113500
Peherstorfer B, Willcox K (2016) Data-driven operator inference for nonintrusive projection-based model reduction. Comput Methods Appl Mech Eng 306:196–215
Pesche R (1998) Etude par simulation numerique de la ségrégation de particules dans une suspension bidisperse. Ph. D. thesis, Université de Nice-Sophia Antipolis, France
Pesche R, Bossis G, Meunier A (1998) Numerical simulation of particle segregation in a bidisperse suspension. HAL preprint:hal-00694958
Pham P, Butler JE, Metzger B (2016) Origin of critical strain amplitude in periodically sheared suspensions. Phys Rev Fluids 1(2):022201. https://doi.org/10.1103/PhysRevFluids.1.022201
Pham P, Metzger B, Butler JE (2015) Particle dispersion in sheared suspensions: crucial role of solid-solid contacts. Phys Fluids 27(5). https://doi.org/10.1063/1.4919728
Phillips RJ, Armstrong RC, Brown RA, Graham AL, Abbott JR (1992) A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration. Phys Fluids 4(1):30–40. https://doi.org/10.1063/1.858498
Pivkin IV, Richardson PD, Karniadakis G (2006) Blood flow velocity effects and role of activation delay time on growth and form of platelet thrombi. Proc Natl Acad Sci USA 103(46):17164–9. https://doi.org/10.1073/pnas.0608546103
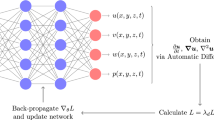
Raissi M, Perdikaris P, Karniadakis GE (2019) Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comp Phys 378:686–707
Reyes B, Howard AA, Perdikaris P, Tartakovsky AM (2021) Learning unknown physics of non-newtonian fluids. Phys Rev Fluids 6(7):073301
Richardson JF, Zaki WN (1954) The sedimentation of a suspension of uniform spheres under conditions of viscous flow. Chem Eng Sci 3(2):65–73. https://doi.org/10.1016/0009-2509(54)85015-9
Sarabian M, Firouznia M, Metzger B, Hormozi S (2019) Fully developed and transient concentration profiles of particulate suspensions sheared in a cylindrical couette cell. J Fluid Mech 862:659–671
Schroen K, van Dinther A, Stockmann R (2017) Particle migration in laminar shear fields: a new basis for large scale separation technology? Separation and Purification Technology 174:372–388
Semwogerere D, Morris JF, Weeks ER (2007) Development of particle migration in pressure-driven flow of a Brownian suspension. J Fluid Mech 581:437. https://doi.org/10.1017/S0022112007006088
Semwogerere D, Weeks ER (2008) Shear-induced particle migration in binary colloidal suspensions. Phys Fluids 20(4):043306. https://doi.org/10.1063/1.2907378
Servais C, Jones R, Roberts I (2002) The influence of particle size distribution on the processing of food. J Food Eng 51(3):201–208
Shauly A, Wachs A, Nir A (2000) Shear-induced particle resuspension in settling polydisperse concentrated suspension. Int J Multiphase Flow 26(1):1–15
Sirignano J, Spiliopoulos K (2018) Dgm: a deep learning algorithm for solving partial differential equations. J Comp Phys 375:1339–1364
Snook B, Butler JE, Guazzelli É (2016) Dynamics of shear-induced migration of spherical particles in oscillatory pipe flow. J Fluid Mech 786(5):128–153. https://doi.org/10.1017/jfm.2015.645
Wang Y, Ouyang J, Wang X (2021) Machine learning of lubrication correction based on gpr for the coupled dpd-dem simulation of colloidal suspensions. Soft Matter 17(23):5682–5699
Yeo K (2011) Some aspects of suspension flows: Stokes to turbulent flows. Ph. D. thesis, Brown University
Yeo K, Maxey MR (2010) Dynamics of concentrated suspensions of non-colloidal particles in Couette flow. J Fluid Mech 649:205. https://doi.org/10.1017/S0022112009993454
Yeo K, Maxey MR (2010) Simulation of concentrated suspensions using the force-coupling method. J Comput Phys 229(6):2401–2421. https://doi.org/10.1016/j.jcp.2009.11.041
Yeo K, Maxey MR (2011) Numerical simulations of concentrated suspensions of monodisperse particles in a Poiseuille flow. J Fluid Mech 682:491–518
You H, Yu Y, Silling S, D’Elia M (2020) Data-driven learning of nonlocal models: from high-fidelity simulations to constitutive laws. arXiv:2012.04157
You H, Yu Y, Trask N, Gulian M, D’Elia M (2021) Data-driven learning of nonlocal physics from high-fidelity synthetic data. Comput Methods Appl Mech Eng 374:113553
Yu B et al (2018) The deep ritz method: a deep learning-based numerical algorithm for solving variational problems. Commun Math Stat 6(1):1–12
Zarraga IE, Leighton DT (2002) Measurement of an unexpectedly large shear-induced self-diffusivity in a dilute suspension of spheres. Phys Fluids 14(7):2194. https://doi.org/10.1063/1.1483304
Acknowledgements
The authors thank Dr. Kyongmin Yeo for his contributions to the monodisperse FCM code and helpful discussions.
A.A.H. acknowledges support from the National Science Foundation Graduate Research Fellowship under Grant No. DGE 1058262 and support from the U.S. Department of Energy, Advanced Scientific Computing Research program, under the Scalable, Efficient and Accelerated Causal Reasoning Operators, Graphs and Spikes for Earth and Embedded Systems (SEA-CROGS) project (Project No. 80278), and the Physics-Informed Learning Machines for Multiscale and Multiphysics Problems (PhILMs) project (Project No. 72627). J.D. acknowledges support from the National Science Foundation Mathematical Sciences Graduate Internship Program. The computational work was performed using PNNL Institutional Computing at Pacific Northwest National Laboratory and computational resources and services at the Center for Computation and Visualization, Brown University. R.G.P also acknowledges support from the PhILMs project for this work.
Pacific Northwest National Laboratory (PNNL) is a multi-program national laboratory operated for the U.S. Department of Energy (DOE) by Battelle Memorial Institute under Contract No. DE-AC05-76RL01830.
Sandia National Laboratories is a multimission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International, Inc., for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
A.1 Additional bidisperse suspension plots
In this section, we provide figures analogous to Figs. 7–11 for bidisperse suspensions with \(\phi _B = 0.4\), \(\lambda = 0.6\), and \(\beta = 0.5\) (Figs. 28–30) and \(\beta = 0.25\) (Figs. 33–35).
Volume fraction profiles at accumulated strain \(\gamma = 0-260\) for \(\phi _B = 0.4\), \(\lambda =0.6\), and \(\beta = 0.25\). The volume fraction is averaged of the channel center line at \(y/a = 20.0\). The \((\cdot )^*\) notation denotes the profile is averaged over four reseeded simulations, as discussed in “Reseeding procedure” section
Particle contact pressure profiles as defined by Eq. 4 at accumulated strain \(\gamma = 0-260\) for \(\phi _B = 0.4\), \(\lambda =0.6\), and \(\beta = 0.25\)
A.2 Galerkin neural network implementation
In order to apply Galerkin Neural Networks to the SBM formulation in “Learning the stress in monodisperse suspensions” section, we must first formulate it as a variational problem whose operator is symmetric and positive-definite. To accomplish this, we use a simple least squares variational approach:
The space \(L^{2}(\Omega _{\gamma }; H^{1}(\Omega _{y}))\) is the Sobolev space (Adams and Fournier 2003) of all functions u such that
is finite, where
For ease of notation, we define
Here, \(C>0\) is a constant that determines how strongly the boundary condition is enforced. We take \(C=0.1\) in all examples.
The basis function \(\Sigma _{i}^{NN}\) is obtained by solving the following optimization problem:
where \(\mathcal{N}\mathcal{N}\) denotes the set of all realizations of a feedforward neural network of fixed width and depth. We denote by \(\sigma _{22,i}\) the ith approximation to \(\sigma _{22}\) using the first i basis functions \(\{\Sigma _{j}^{NN}\}_{j=1}^{i}\); \(\sigma _{22,i}\) is obtained by solving the discrete variational problem
where \(S_{i} = \text {span}\{\Sigma _{0}^{NN},..., \Sigma _{i}^{NN}\}\). We take \(\sigma _{22,0}\) to be the initial approximation to the PDE and set \(\Sigma _{0}^{NN}:= \sigma _{22,0}\). For all of the simulations in “Physics-informed machine learning with the suspension balance model” section, we take \(\sigma _{22,0} = 0\). This choice of initial approximation means that we do not assume any prior knowledge of the solution. One can of course use a more informed initial approximation if it exists, e.g. coarse result from another numerical method.
To evaluate the loss functional in Eq. 23, we approximate the integrals using high-order Gaussian quadrature rules such as the ones described in Davis and Rabinowitz (2007). In particular, for a given function \(g: \Omega \rightarrow \mathbb {R}\), we use the quadrature rule given by the weights \(\{w_{i}\}_{i=1}^{m}\) and nodes \(\{(y_{i}, \gamma _{i})\}_{i=1}^{m}\) as follows:
The key idea behind Galerkin Neural Networks is the approximation \(\Sigma _{i}^{NN} \approx \sigma _{22} - \sigma _{22,i-1}\) – that is, the ith basis function is an estimate of the error in the approximate solution \(\sigma _{22,i-1}\). As the error \(\sigma _{22}-\sigma _{22,i-1}\) decreases, its structure grows increasingly complex and contains high frequency modes. Thus, the first basis functions may be viewed as approximating low frequency error components while later basis functions approximate high frequency error components. A discussion and demonstration of the hierarchical nature of Galerkin Neural Networks alongside theoretical properties may be found in Ainsworth and Dong (2021).
A.3 MOR-Physics parameters
In this section, we provide additional details for the MOR-Physics operator parameterization used in “Data based machine learning for particle stresses” section. To perform training, we first partition the FCM simulations into 60% training data, 20% validation data, and 20% test data. Over the course of training, we track the validation loss and select the operator with the lowest validation loss as our learned operator. Below we list the hyperparameters we used in the studies,
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Howard, A.A., Dong, J., Patel, R. et al. Machine learning methods for particle stress development in suspension Poiseuille flows. Rheol Acta 62, 507–534 (2023). https://doi.org/10.1007/s00397-023-01413-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00397-023-01413-z