Bulk rheometry at high frequencies: a review of experimental approaches

Abstract

High-frequency rheology is a form of mechanical spectroscopy which provides access to fast dynamics in soft materials and hence can give valuable information about the local scale microstructure. It is particularly useful for systems where time-temperature superposition cannot be used, when there is a need to extend the frequency range beyond what is possible with conventional rotational devices. This review gives an overview of different approaches to high-frequency bulk rheometry, i.e. mechanical rheometers that can operate at acoustic (20 Hz–20 kHz) or ultrasound (> 20 kHz) frequencies. As with all rheometers, precise control and know-how of the kinematic conditions are of prime importance. The inherent effects of shear wave propagation that occur in oscillatory measurements will hence be addressed first, identifying the gap and surface loading limits. Different high-frequency techniques are then classified based on their mode of operation. They are reviewed critically, contrasting ease of operation with the dynamic frequency range obtained. A comparative overview of the different types of techniques in terms of their operating window aims to provide a practical guide for selecting the right approach for a given problem. The review ends with a more forward looking discussion of selected material classes for which the use of high-frequency rheometry has proven particularly valuable or holds promise for bringing physical insights.

Introduction

Small amplitude oscillatory measurements probe the response of an equilibrium structure of a material and deliver its rheological fingerprint in the frequency domain. Changing the frequency also infers a variation in the length scale that is probed. Low-frequency moduli depend on slow processes which are typically reflecting collective, large-scale phenomena, whereas measurements at high frequencies will reveal the more local-scale dynamics. In fact, in order to obtain an integrated picture of many complex fluids or soft solids, oscillatory measurements over an extended frequency range are typically required. The exact location of the “high-frequency region” on an absolute frequency scale depends on the characteristic time scales of the material under investigation (Ferry 1980; Willenbacher and Oelschlaeger 2007). For thermorheologically simple materials with relaxation times governed by the same physical mechanism, time-temperature superposition can be applied to cover ranges outside of the instrumentation limits and rotational devices suffice (Ferry 1980). However, for many complex materials, this principle does not hold and the high-frequency region has to be reached physically by means of different measurement instruments. We will therefore need special “high-frequency rheometers” to extend the frequency domain of classical rotational devices.

Theoretical frameworks for using and interpreting specifically the high-frequency response have been developed for different material classes, including simple fluids (Zwanzig and Mountain 1965), colloidal dispersions (Brady 1993; Lionberger and Russel 2000; Swan et al. 2014; Varga and Swan 2015; Palierne 1990), or polymeric systems, either monophasic (Rouse 1953; Zimm 1956; MacKintosh et al. 1995; Morse 1998; Harmandaris et al. 2003; Gardel et al. 2004) or multiphasic (Roland and Ngai 1992; Grizzuti et al. 2000; Colby and Lipson 2005). The scaling behaviour as well as the limiting high-frequency response are of interest and can be interpreted quantitatively, e.g. to:

• Characterise local stress contributions (Schroyen et al. 2019) or determine interaction strengths in colloidal suspensions (Bergenholtz et al. 1998b; Fritz et al. 2002b);

• Investigate local dynamics in emulsions (Liu et al. 1996; Romoscanu et al. 2003a);

• Obtain detailed insights in the dynamics of glasses (Hecksher et al. 2017), hydrogels (Jamburidze et al. 2017), and wormlike micellar solutions (Willenbacher et al. 2007);

• Identify fast relaxation processes in polymers and the effects of monomer friction (Kirschenmann 2003; Szántó et al. 2017) or bond characteristics in associative polymer systems (Goldansaz et al. 2016; Zhang et al. 2018).

Furthermore, the high-frequency response directly mimics the time scales of several practical applications and is relevant for instance for the characterisation of printing inks in light of their performance (Vadillo et al. 2010), or for studying biological materials (Kudryashov et al. 2001; Singh et al. 2006; Nassar et al. 2010; Johannsmann et al. 2013). Another practical application for colloidal dispersions, which can often be unstable, lies in the use of the high-frequency limiting hydrodynamic scalings to directly evaluate the dispersion quality (Schroyen et al. 2017).

Conventional rotational rheometers typically operate at maximal frequencies below f = 10 − 50 Hz, the limit being set by inertial effects of both instrument and sample. These inertial effects scale with ∝ f² and despite software corrections they will eventually dominate. The exact limit depends on the properties of the measurement system and sample: the torque generated by instrument inertia is ∝ I ⋅ f², with I the inertial moment of the instrument, and is particularly problematic when measuring from the oscillating surface, while sample inertia generates a torque $\propto \left (\frac {\rho f}{\eta } \right )^{2}$, with ρ and η the fluid density and viscosity (Ewoldt et al. 2015). A vast array of techniques has been developed since the middle of the previous century to access higher frequencies. In this review, we focus mainly on techniques that directly probe bulk material properties using well-defined kinematic conditions. Other useful methods include for instance surface fluctuation reflection spectroscopy until the intermediate kHz range (Tay et al. 2008; Pottier et al. 2013), Brillouin spectroscopy in the GHz range (Mather et al. 2012; Still et al. 2013; Hecksher et al. 2017), shear wave speed measurements (Joseph et al. 1986), or microrheological methods that span a large frequency region until the large kHz domain. Different microrheological techniques, e.g. using differential dynamic microscopy (Cerbino and Trappe 2008; Edera et al. 2017), diffusive wave spectroscopy (Pine et al. 1988; Scheffold et al. 2004), passive particle tracking (Mason et al. 1997), or active microrheology (Keller et al. 2001; Wintzenrieth et al. 2014), have been developed and successfully applied. However, they are indirect and therefore require the extrapolation of bulk properties, which can be an issue for instance for heterogeneous systems. Moreover, the local flow field generated in these systems is often a disturbance velocity field around a probe particle, which is non-viscometric and dependent on the probe material shape and its interaction with the sample (Cai et al. 2011). For an extensive review on microrheology which addresses these issues and gives an excellent overview of both fundamental and experimental issues, the reader is redirected to the recent monograph by Furst and Squires (2017).

High-frequency (HF) rheometrical techniques span a range between 1 and 10⁸ Hz, starting from methods that directly extend the accessible frequencies of conventional rotational rheometers to setups operating in the MHz range, where fluid inertia and the limits of the continuum world become important. This review is structured as follows: wave propagation effects are discussed first as it plays a key role in instrument design considerations. Different techniques are then introduced and discussed based on their mode of operation, the complexity of the device, and the analysis method used. The review concludes with a few practical applications that illustrate the value of high-frequency rheometry for different complex material classes, which is hopefully motivating to select and use an adequate HF technique.

Shear wave propagation

Drag flow rheometers operating in oscillatory mode mostly probe material properties by means of a shear deformation generated by one oscillating surface. The sample’s response can be determined either from the force or torque on that moving surface or from a second, stationary surface. Oscillatory displacements in a bulk fluid lead to waves which propagate through the sample. For most classical rheometrical devices, a transverse wave is generated and assumed to be reflected immediately back. As a consequence, the magnitude of the velocity varies linearly over the gap, resulting in a constant shear rate. This is referred to as the gap loading limit in a landmark paper by Schrag (1977). However, this linear shear profile is not the general solution.

Consider an oscillatory in-plane movement of a surface with velocity u₀(t) = U₀ ⋅ e^j2πft, which induces a shear wave (Adler et al. 1949; Thurston 1959) travelling in a direction normal to the plane of motion. The velocity profile in this normal (z) direction can be obtained by solving the one-dimensional wave equation (Adler et al. 1949; Schrag et al. 1965), or from the Navier-Stokes equations for irrotational flow (Deen 1998), as follows:

$$ u(z,t) = \left[ A_{1} e^{j \gamma_{w} z} + A_{2} e^{-j \gamma_{w} z} \right] \cdot e^{j 2 \pi f t}. $$

(1)

The sample properties enter through the complex wave propagation coefficient $\gamma _{w} = \sqrt { \frac {-j 2 \pi f \rho }{\eta ^{*}}}$, with ρ the density and η^∗ the linear viscoelastic complex viscosity. η^∗ can contain both in- and out-of-phase components and relates to the complex modulus of the material $G^{*} = G^{\prime } + jG^{\prime \prime } = j 2 \pi f \eta ^{*}$, with magnitude $|G^{*}|= \sqrt {(G^{\prime })^{2} + (G^{\prime \prime })^{2}}$ and phase $\delta = \tan ^{-1} \left (\frac {G^{\prime \prime }}{G^{\prime }} \right )$. Constants A₁ and A₂ depend on the boundary conditions. Equation 1 illustrates that propagation effects inherently influence the signal detection, since both amplitude and phase vary along the direction of propagation. Furthermore, the wave created at the surface of the excitation unit is gradually attenuated with increasing distance due to the dissipation of energy inherent to a viscoelastic material. This is depicted schematically in Fig. 1. It must be realised that such an irreversible process for the attenuating wave is technically a solution for a diffusion equation.

Fig. 1

Schematic of a shear wave propagating from a surface. The wave is gradually attenuated in the propagation direction; λ_s is the wavelength and d_s the penetration depth, illustrated for δ = 45^∘ (3–4). For a material with ρ = 1000 kg/m³ and |η^∗| = 1 Pa⋅s measured at 1 kHz, λ_s ≈ 2.6 mm and d_s ≈ 1.5 mm

In case of a sample confined between two surfaces, with the oscillating surface at z = −H, the resulting velocity profile of the shear wave is as follows:

$$ u(z,t) = - u_{0}(t) \cdot \frac{\sin(\gamma_{w} z)}{\sin(\gamma_{w} H)}. $$

(2)

Figure 2 shows the normalized amplitude of the velocity (U/U₀) and the phase angle between the velocity of the plate and the fluid in the gap of the rheometer as a function of frequency for a typical gap H = 1 mm and a viscoelastic fluid with δ = 45^∘. The velocity field gradually varies between two limiting cases. At low frequencies, we find the gap loading limit: the wave travels through a fluid that is confined between two surfaces and is reflected before it becomes attenuated. The wavelength of the shear wave is long compared with the gap so that no phase shift occurs. A second limit is encountered at very high frequencies where the surface loading limit is reached. The wavelength and penetration depth of the shear wave are now much smaller than the gap and the wave is completely damped inside the fluid. As a consequence, the shear rate at the plate is increased.

Fig. 2

2D plots of the relative amplitude U/U₀ of the velocity vector (left) and the phase angle difference between the motion of the plate and the sample Δδ_u (right) of a shear wave travelling between two surfaces as a function of frequency, for a 1-mm gap. The bottom surface (z = − 0.001 m) oscillates while the top surface (z = 0 m) is fixed. The fluid properties are as follows: ρ = 1000 kg/m³, |η^∗| = 1 Pa⋅s, δ = 45^∘. The dashed line indicates the typical upper limit of a commercial instrument

Gap or surface loading limitations

Rheological measurements are mostly performed within either of the two limiting cases. Schrag (1977) determined the effect of wave propagation on shear rheological measurements when operating outside of these limits, i.e. when the measurement gap H is similar in magnitude compared with the wavelength λ_s:

$$ \lambda_{s} = \frac{1}{\sqrt{\frac{\rho \cdot f}{2 \pi |\eta^{*}|}} \cos\left( \frac{\delta}{2}\right)}, $$

(3)

and penetration depth d_s:

$$ d_{s} = \frac{1}{\sqrt{\frac{\rho \cdot 2 \pi f}{|\eta^{*}|}} \sin\left( \frac{\delta}{2}\right)}. $$

(4)

Figure 3 shows d_s and λ_s as a function of frequency f and phase angle δ for a material with properties ρ = 1000 kg/m³ and |η^∗| = 1 Pa⋅s. Both variables scale with $\propto \sqrt {|\eta ^{*}|}$, and the curves shift up or down for different fluid properties. The penetration depth decreases with increasing phase angle δ due to enhanced damping, which is in contrast with the wavelength. Only at small phase angles (δ ≤ 18^∘), λ_s becomes smaller than d_s. Two important conclusions can be drawn. First, operation in the gap loading limit becomes increasingly difficult at higher frequencies (> 1 kHz), as measurement gaps need to be below 0.1 mm. The limit is critical mainly for materials with phase angles close to 90^∘ and small values of |η^∗|, and hence poses an issue for low-viscous fluids. Second, the limit of surface loading conditions is always set by the penetration depth since the wave must be fully damped. This requires large gaps (> 1 mm) for frequencies < 10 kHz and is a limiting factor in particular when measuring quasi-elastic materials.

Fig. 3

Penetration depth d_s (surface plot) and wavelength λ_s (mesh plot) of the shear wave as a function of frequency f and phase angle δ for a material with ρ = 1000 kg /m³ and |η^∗| = 1 Pa⋅s

For the intermediate case, the non-homogeneous deformation profile needs to be accounted for Läuger and Stettin (2016), which given the fact that in rheological measurements, fluid properties are unknown and requires an iterative solver. Schrag (1977) provided expressions for correcting the measured viscoelastic properties in case of a shear wave travelling between two walls. For measurements at the stationary wall, the expressions for correcting the measured modulus $\vert {G}^{*}_{m} \vert$ and phase δ_m reduce to:

$$ \begin{array}{@{}rcl@{}} \frac{\left| G^{*}_{m} \right|}{\left| G^{*} \right|} &=& \beta H \cdot \left[ \tan^{2}(\delta/2) + 1 \right]^{1/2}\\ && \cdot \left[ \frac{2}{\cosh \left( \tan(\delta/2) \cdot 2 \beta H \right) - \cos(2 \beta H)} \right]^{1/2}, \end{array} $$

(5)

$$ \begin{array}{@{}rcl@{}} \delta_{m} - \delta &=& -(\delta/2) + \tan^{-1} \left( \frac{{\tanh}(\alpha H)}{\tan(\beta H)} \right), \end{array} $$

(6)

with factors $\alpha = 2 \pi f \left (\frac {\rho }{\vert G^{*} \vert } \right )^{1/2} \sin \limits (\delta /2)$ and $\beta = 2 \pi f \left (\frac {\rho }{\vert G^{*} \vert } \right )^{1/2} \cos \limits (\delta /2)$. The corrected modulus |G^∗| and phase δ are equal to $\vert G^{*}_{m} \vert$ and δ_m only in the gap loading limit. Both functions are coupled and need to be solved together. Shear wave propagation effects on the measured amplitude ratio |AR|, the ratio of measured force over displacement, and phase are compared in Fig. 4 for different phase angles at a measurement gap of 100 μ m (|η^∗| = 1 Pa⋅s). The effect strongly depends on the phase angle of the material: with decreasing phase angle, the effect on the amplitude increases whereas that on the phase becomes less important. Furthermore, while the phase shift is always negative, the shift in |AR| changes sign with decreasing phase angle, eventually leading even to an overestimation of the modulus.

Fig. 4

Deviations from the gap loading limit: measured amplitude $\left (\varDelta (\vert AR \vert )_{rel} = 100 \cdot \frac {\vert AR \vert _{meas} - \vert AR \vert }{\vert AR \vert } \right )$ (left) and phase shift $\left (\varDelta \delta = \delta _{meas} - \delta \right )$ (right) as a function of frequency. Calculations are executed at the stationary wall (H = 100μ m) on a Newtonian sample with ρ = 1000 kg/m³ and |η^∗| = 1 Pa⋅s

The wavelength and penetration depth are key design factors and will, for a certain material and frequency range, define the required gap for operation within either of the two limits. The penetration depth is of particular importance at very high frequencies since it defines the maximal distance over which the sample can be probed. Therefore, as a rule of thumb, it should be at least a factor 10 larger than the characteristic length scale of the microstructure.

Techniques

Figure 5 shows a schematic overview of the typical frequency ranges of the different types of techniques that will be discussed. Subresonant rheometers have an accessible frequency range < 10 kHz and are typically designed to operate in the gap loading limit. In the kHz region, the wavelength decreases below 1 mm for many materials (Eq. 3, depending on the exact sample properties) and gap loading operation is only reached for very small gaps. Rheometers operating at or near resonance frequencies in the kHz range mostly function within the surface loading limit. At large ultrasonic frequencies (> 1 MHz), the penetration depth becomes so small that surface properties rather than bulk properties are probed (4). Cantilevers will be briefly discussed separately; so far it has proven challenging to accurately extract rheological properties due to the complex deformation profiles and related setups have mainly been used as viscosity sensors. The working principles of the different types of high-frequency techniques are discussed in more detail below. Table 1 provides a comparative overview of their operating limits. Note that the measurable ranges of modulus and/or viscosity are used as indicators for sensitivity from a materials perspective. While true, geometry-independent measures are the detectable forces and displacements, these do not allow a straightforward comparison owing to the wide range of measurement principles.

Fig. 5

High-frequency rheometrical techniques compared based on their accessible frequency ranges. Commercial rotational rheometers are given as a reference. The transition between the acoustic (20 Hz–20 kHz) and the ultrasound (> 20 kHz) range is indicated as well. Discrete resonance frequencies accessible using bulk resonance or ultrasound methods are indicated by thin vertical bars, while marked areas delineate continuous regions

Table 1 Comparison of dynamic ranges (min–max) in frequency, reported temperature ranges, complex viscosity/modulus, strain amplitude, and required sample volume for different techniques

Subresonant drag flow rheometers

Subresonant rheometers working in the acoustic frequency range can be used to determine complex material properties at frequencies that directly extend the accessible frequency range of commercial rotational devices, starting from mid-range values of the latter (Fig. 5). The majority of such techniques makes use of piezotechnology, where a coupling is obtained between an electric field and mechanical response. Their measurement principle is similar to those of conventional rheometers, i.e. the material is confined in between 2 parallel surfaces with one being used to drag the material along. Gap loading operation can typically be assumed at least if the flow profile is homogeneous, which can be an issue for compressional instruments. Excitation of the plate is carried out by small piezoelectric elements instead of a heavy motor, which reduces the inertia of the measurement system drastically and allows for small strain amplitudes. The upper limit in frequency range is given by mechanical resonances of the system, which constitute an important design criterion. Below, different methods are discussed and compared based on their method of deformation and resulting flow field.

Piezo shear rheometers (PSR-1)

The motion of a piezoactuator depends on the polarisation direction of the material, and transverse waves can either be created directly or via a translation. A first design, introduced by Cagnon and Durand (1980) and shown in Fig. 6a, contained 2 sets of piezoceramic shear elements attached to glass surfaces. Excitation elements, driven by an AC voltage, directly create a linear shear deformation, while the elements on the opposite side were used for detection. The design was both simple and robust and facilitated a large operating range in terms of frequency (Table 1 (A.1)). Extensions were made to the original design, including optical paths for microscopy and light scattering studies or external magnets for magnetorheological studies (Yamamoto et al. 1986; Gallani et al. 1994; Martinoty and Collin 2010; Auernhammer et al. 2006). In order to ensure gap loading conditions, measurement gaps are typically small (order $\sim 100 \mu$m) and require accurate alignment. Roth et al. (2010) proposed a design which used piezoelectric shear stacks rather than single elements (Fig. 6b), which increase the sensitivity and reduce both electric cross-talk and the possible occurrence of parasitic displacements. The maximum temperature limit is reduced because of the decomposition temperature of the glue used for the stacks from $\sim 150$ to < 100 ^∘C (Table 1 (A.2)). Calibration is relatively simple for linear shear rheometers with decoupled excitation and detection units. Without important electromechanical contributions from the system, material properties can be derived in a straightforward manner by comparing the excitation (V_o) and detected (V_i) signals:

$$ {{|AR|}_{s}} = \left|{\frac{F}{x_{s}}}\right| = A_{p} \cdot \frac{V_{i}}{V_{o}}. $$

(7)

|AR|_s is the shear amplitude ratio, while A_p represents a system constant. Both the complex modulus and phase angle can be derived easily from the detected signal. Furthermore, measurements can be carried out at small strain amplitudes and required sample volumes are small (Table 1). The linear shear motion generally favoured rectangular substrates: surface tension effects can therefore be an issue for smaller volumes, in particular for fluids with low bulk viscosities (Johnston and Ewoldt 2013).

Fig. 6

Overview of different subresonant piezo rheometers (Table 1 (A)): linear shear rheometers with a monolithic shear elements (A.1) (Reprinted figure with permission from Cagnon and Durand (1980), Copyright (1980) by the American Physical Society) or b shear stacks (A.2) (Roth et al. (2010) and Schroyen et al. (2017) - Reproduced by permission of The Royal Society of Chemistry), c rotational shear flow (A.3) (Reprinted by permission from the Licensor: Springer Nature, Kirschenmann and Pechhold (2002), Copyright (2002)), and d squeeze flow rheometers (A.4) (Reprinted with permission from Crassous et al. (2005), Copyright (2005), The Society of Rheology)

A different type of design was developed by Kirschenmann and Pechhold (2002) and is shown in Fig. 6c. The setup consists of a piezo-wheel with 6 spokes, used to translate the linear motion of the piezo elements into a rotation. Driving elements are attached to 3 spokes and create a rotational shear deformation, while elements on the other spokes are used for detection. The coupling of the excitation and detection reduces the sensitivity and complicates the analysis: fluid properties need to be determined by subtracting the response of the empty cell from the measured complex torque (Table 1 (A.3)). Furthermore, the complete measurement system had significant inertia, reducing the accuracy near or above only 1 kHz. Nonetheless, important advantages are the rotational symmetry and the possibility for decoupling the measurement cell from the piezoelements, hence facilitating the temperature control and allowing for a temperature range exceeding that of the piezoelectric material.

The resolution of these piezo shear rheometers (PSR-1) is largely determined by the accurate detection and analysis of the response signal. The most accurate results were obtained with linear shear rheometers using piezoelectric stacks and applying an extensive calibration step, with measurable complex viscosities as small as 0.05 Pa⋅s and a phase accuracy within 2^∘ (Schroyen et al. 2017). A discussion on different sources of error can be found in Athanasiou et al. (2019). For coupled designs such as the piezo rotational rheometer (Kirschenmann and Pechhold 2002), the sensitivity decreases by a factor of 10. The upper limit is set by the mechanical compliance—or deformability—of the piezoelements or stacks and is typically high. A second important criterion is the maximum frequency limit, which depends on the successful suppression of inertial effects and is favoured by simple, robust designs. The accessible frequency range is typically limited below 5 kHz.

Piezo compressional rheometers (PSR-2)

It is easier to generate and detect a compressional deformation with a piezo crystal. Oscillatory squeeze flow rheometers make use of longitudinal waves to determine complex material properties. Early designs of PSR-2 consisted of two substrates that are directly attached to piezoelectric elements which confine the sample, similar in mechanical construction to original linear shear setups (Fig. 6a) (Bartolino and Durand 1977; Hébraud et al. 2000). In the case of a no-slip boundary condition, the compressional deformation induces a Poiseuille flow that moves radially outwards through the gap. For an axisymmetric cell operated within the lubrication approximation (gap H ≪ substrate radius R) and in the absence of inertia, slip, surface tension, or compressibility effects, the complex modulus can be derived via the measured normal amplitude ratio (|AR|_n = |F/x_z|) (7):

$$ |G^{*}| = \frac{2}{3 \pi} \frac{H^{3}}{R^{4}} \cdot {|AR|}_{n}. $$

(8)

Similar to PSR-1, |AR|_n is obtained directly via the response of the piezoelements. First-order correction factors for inertia, slip coefficients, and compressibility have been derived (Hébraud et al. 2000; Wingstrand et al. 2016; Laun et al. 1999; Kirschenmann 2003; Meeten 2004). Surface tension effects are difficult to correct for a priori and were specifically investigated by Cheneler et al. (2011). Due to the compressional motion, both the strain amplitude and force exerted by the sample are amplified compared with a setup which exerts a linear shear motion: the displacement in the radial direction x_r/x_z ∝ R/H, while |F/x_r|∝ R³/H² (Hébraud et al. 2000). The actual displacement amplitudes of the piezoelements can hence be much smaller, facilitating integrated devices, or for a given set of piezos, the sensitivity of the device can be enhanced. Pechhold et al. (2008) developed for instance a squeeze flow setup with excitation and detection elements positioned at the bottom (Fig. 6d) (Crassous et al. 2005). Both the linear viscoelastic moduli and compressibility could be determined by measuring at different gap heights. The setup was eventually combined with a rotational piezo rheometer (Fig. 6c) for simultaneous shear and squeeze flow measurements (Pechhold et al. 2011).

Interest in integrated lab-on-a-chip devices has promoted the development of miniaturised setups as well. Sánchez et al. (2008) designed and empirically modelled a mini squeeze flow setup with decoupled excitation and detection elements for measurements on highly viscous samples with volumes < 10μ l. However, only the complex viscosity was reported and displayed considerable scatter. Alternatively, Cheneler et al. (2011) developed a microsqueeze flow rheometer for nanoliter volumes.

The sensitivity of PSR-2 is significantly higher compared with PSR-1 as a result of the compressional rather than shear motion (8) (Table 1 (A.4)). By playing with and optimising the gap height between 20 and 200 μ m, Crassous et al. (2005) succeeded in accurately measuring complex viscosities as low as 10^− 3 Pa⋅s. The force amplification also reduces the upper limit for the measurable modulus, which is set by the measurement system’s compliance. Squeeze flow rheometers are easy to construct and frequencies until the low kHz region can readily be obtained, similar to linear shear flow devices. Furthermore, longitudinal piezoelements have a higher temperature resistance compared with shear stacks. The main disadvantage stems from the nature of the applied flow field: compressional flow inherently induces pressure gradients and can create non-homogeneous flow profiles and apparent, system-dependent properties (Hébraud et al. 2000). This can be worrisome in particular for more complex microstructures which are unknown a priori.

Other shear rheometers

Shear rheometers with different methods of excitation/detection have been developed as well, although their practical use has yet been limited. For instance, Chen and Lakes (1989) performed broadband measurements on viscoelastic solids by means of an electromagnetically driven torsional apparatus (Table 1 (A.5)). Effects of resonances were reduced by decoupling the detection of the displacement via interferometry and by numerically correcting for the resonance behaviour. Recently, Koganezawa et al. (2017) developed an electromagnetically driven planar shear setup for the characterisation of viscoelastic materials. The displacement is detected independently with a laser Doppler vibrometer. A first attempt was made at modelling the first resonance modes of the setup to extend the measurable frequency range ≥ 10 kHz, but needs refinement. Verbaan et al. (2015) suggested a more direct approach for extending the upper limit of subresonant techniques by introducing a high-viscous damper into the design. In addition, double-leaf springs were implemented to guide the sliding of a plate and prevent out-of-plane displacements. The damper effectively alters the behaviour around the resonance frequency, but adaptations to the setup are required to improve the sensitivity for fluids with lower viscosities (Table 1 (A.6)).

Recent years have also seen a growing interest for materials characterisation using only small sample volumes or in confined environments. Christopher et al. (2010) designed a MEMS-based nanopositioner stage for in-plane oscillations (Table 1 (A.7)). The sample is confined at gaps < 20μ m, which reduces the required sample volume but requires very careful alignment. Excitation of the oscillation is carried out by a thermal actuator, which is connected to the stage via parallel dual lever nanopositioners. The displacement is detected optically. While several MEMS-based viscosity probes have been developed recently, the setup developed by Christopher et al. (2010) seems to be the only subresonant shear probe able to measure both amplitude and phase (at least to some extent).

Bulk resonators and immersed rheometers

A second main category involves devices which operate at high acoustic or low ultrasonic frequencies (Fig. 5). Besides a few exceptions, setups in this range make use of resonating structures that undergo well-defined deformations. Their measurement principle is based on the effect of the viscoelastic fluid on a shift in the resonance frequency. The resonance can usually be detected precisely, but has a disadvantage that only discrete frequencies can be probed. Because of the reduced penetration depth and wavelength at kHz frequencies, operation of such devices will be mostly in the surface loading limit, so that the distance between the resonating structure and stationary wall or sample surface needs to be large (3). The penetration depth d_s is still sufficiently large so that bulk properties are being probed (4). Similar to the previously discussed subresonant rheometers, different designs have been considered (Table 1 (B)).

Torsional resonators

Torsional resonators consist of cylindrical elements that are immersed in the fluid and undergo a purely torsional deformation. The motion creates a propagating shear wave that is attenuated by the viscoelastic fluid. The deformation profile of the shear wave in the surface loading limit is well understood and rheological properties can readily be derived, but may be coupled with inertial effects. Inertia becomes even more important for resonators operating at high ultrasonic frequencies, such as the quartz crystal microbalance, which are described below (ultrasound rheometers). Resonance modes of torsional setups can either be driven piezoelectrically, magnetostrictively, or electromagnetically.

Piezoelectric resonators were introduced first by Mason (1947) and are generally driven by a quartz crystal deformed in torsional mode, resonating at one or more discrete frequencies depending on the dimensions of the structure. The resonance modes are very temperature-dependent: precise temperature control is crucial, and the temperature range of most devices is close to room temperature (Table 1 (B.1)). Figure 7a shows a schematic of a piezoelectrically driven torsional resonator and sketches the penetration of the torsional wave into the sample (Bergenholtz et al. 1998b). In order to obtain both amplitude and phase of a complex material, two independent measures of the sample’s contribution are analysed: the shift in resonance frequency f_r and a damping factor. The latter is generally derived via the broadening of the resonance curve Δf (Stokich et al. 1994; Bergenholtz et al. 1998b). The Q-factor

$$ Q = \frac{f_{r}}{\varDelta f} $$

(9)

quantifies the extent of damping and needs to be large (≫ 1/2) for sufficient measurement accuracy. In case of piezoelectrically driven resonators, excitation and detection are straightforward. The impedance of the material Z_f = X_f + jY_f, or its complex resistance against flow, depends on the measured properties via:

$$ {X}_{f} = {A}_{1} \cdot (\Delta{f} - \Delta {f}{~}_{air}), $$

(10)

$$ Y_{f} = A_{2} \cdot (f_{r} - f_{r,\text{air}}). $$

(11)

If the radius of curvature of the resonator is sufficiently large compared with the wavelength and penetration depth, Z_f can be related directly to the linear viscoelastic moduli:

$$ G^{\prime} = \frac{{X_{f}^{2}} - {Y_{f}^{2}}}{\rho}, $$

(12)

$$ G^{\prime\prime} = \frac{2 \cdot X_{f} Y_{f}}{\rho}. $$

(13)

The material’s impedance hence contains both inertial and viscoelastic contributions. Constants A₁ and A₂ must be determined through calibration (Bergenholtz et al. 1998b; Fritz et al. 2003). Required sample volumes are large, typically > 10 ml, to ensure operation in the surface loading limit (Table 1). Note that the influence of inertia on the resonance behaviour can be of interest as well, for instance for the determination of film thicknesses (Bücking et al. 2007).

Fig. 7

Overview of different resonator methods (Table 1 (B)). a Schematic of a piezoelectrically driven torsional resonator (B.1) and illustration of the wave penetration from the surface of the resonator into the sample (Reprinted from Bergenholtz et al. (1998b), Copyright (1998), with permission from Elsevier). b Drawing of a planar shear resonator (B.5): d is the gap between both substrates ((3),(4)); the bottom substrate is driven electromagnetically ((5),(6)) (Reprinted by permission from the Licensor: Springer Nature, Romoscanu et al. (2003b), Copyright (2002))

Electromagnetic or magnetostrictive torsional resonators oscillate in an electric or magnetic field. Specific examples include the multiple lumped resonator (Schrag and Johnson 1971) or the torsional pendulum (Blom and Mellema 1984). Contrary to piezo-driven resonators, detection of the oscillatory displacement is generally performed independently, i.e. either optically or electromagnetically via separate detection coils. Larger strain amplitudes are typically required to obtain sufficient signal-to-noise ratios (Table 1 (B.2)). Romoscanu et al. (2003c) succeeded in performing calibration-free measurements by measuring the phase shift digitally, via a single excitation/detection coil, and by accurately modeling the system’s response. In order to optimise the Q-factor as a function of the material properties, the resonating structure can be adapted, for instance by introducing coaxial segments (Nakken et al. 1995). More recently, Brack et al. (2018) made use of such coaxial resonators to implement a method for simultaneous measurements at multiple discrete frequencies. Alternatively, rather than using a fully immersed structure, Poulikakos et al. (2003) developed a torsional resonator loaded only at the free end for characterising soft solids (Valtorta et al. 2007). Torsional resonators were combined with rotational devices as well for simultaneous steady shear flow and high-frequency measurements (van den Ende et al. 1992; Dinser et al. 2008), which enable probing materials under non-equilibrium conditions.

Resonators that analyse the frequency shift f_r and bandwidth Δf typically have excellent resolution, making them suitable for low-viscous materials (> 10^− 4 Pa⋅s). Although the design of the resonating structure can be optimised, the limit set by the Q-factor reduces the accuracy in case of excessive damping (Table 1 (B.1–B.2)). The measurable complex viscosity range is therefore limited < 1 Pa⋅s. The operation frequency depends on the natural frequency of the resonator and typically varies between 0.1 and 100 kHz; by combining different resonating structures multiple discrete frequencies can be sampled.

Wang et al. (2008) adapted an electromagnetically driven pendulum apparatus for measurements on more viscous materials. It was observed that analysing the maximum angular velocity $\omega _{\max \limits }$ rather than the bandwidth Δf increases the accuracy for materials with |η^∗| > 0.2 Pa⋅s and can extend the accessible viscosity range > 1 Pa⋅s (Table 1 (B.3)). In a follow-up paper, Wang et al. (2010) derived an analysis of the entire resonance curve for operation in a continuous frequency window around f_r rather than at a single discrete value. Important drawbacks were the presence of parasitic in-plane displacements, a rather limited frequency range ($f_{r} \sim 10^{2}$ Hz), and severe design limitations due to the gap loading assumption at such low frequencies (4). In spite of these drawbacks, the proposed method can be of interest for extending the measurement range of resonators.

Traveling torsional waves

In addition to resonator methods, McSkimin (1952) introduced a method for determining bulk viscoelastic properties in the kHz region by means of guided waves transmitted along an immersed cylindrical rod. The fluid impedance Z_f (12−13) could be derived semi-empirically from the measured attenuation and phase shift of the wave after reflection from the free end. Excitation and detection are carried out either using piezoelectric or magnetostrictive materials (McSkimin 1952; Nakajima and Wada 1970; Glover et al. 1968; Poddar et al. 1978). While most setups make use of immersed rods, hollow tube instruments with increased sensitivity and reduced sample volume were developed as well (Glover et al. 1968). These instruments however require a full analysis of the viscoelastic wave propagation since surface loading conditions cannot be assumed for the fluid inside the tube. Generally, reflected wave methods show an increased applicability towards more viscous fluids ($\eta ^{*} \sim 10^{-3} - 10$ Pa⋅s) compared with torsional resonators with freely damped waves (Table 1 (B.4)). Operation outside of discrete resonance frequencies allows continuous operation and facilitates measurements at elevated temperatures. However, a major drawback was found to be the existence of non-linearities in the torsional motion, which causes systematic errors (Glover et al. 1968; Gaglione et al. 1993).

Planar resonators

In-plane oscillations of platelike structures create well-defined planar shear waves. Romoscanu et al. (2003b) developed an electromagnetically driven parallel plate resonator (Fig. 7b). Fluids are confined between the two plates with an adjustable gap thickness of order $\sim 100 \mu$m. At such gaps, wave propagation effects cannot be ignored (3), and wave propagation and fluid-structure interactions need to be accounted for. Viscoelastic properties are obtained from the frequency and phase shift of a damped reflected wave around discrete resonance frequencies, hence interpolating between different methods (Mason 1947; McSkimin 1952). The instrument performed well in terms of accessible viscosity range compared with other resonator methods (Table 1 (B.5)), although a correction factor was required for viscosities > 0.1 Pa⋅s. Since surface loading is not a requirement, the setup uses much smaller sample volumes. However, it could only be operated at a single frequency and below 1 kHz, which limits its advantages as a resonator technique.

Other deformations

Resonators with other types of deformation modes have been constructed as well. Determining viscoelastic properties from resonating structures with more complex deformation modes requires an often non-trivial determination of the fluid-structure interaction. One example is the vibrating wire rheometer, which makes use of an immersed wire in a magnetic field (Retsina et al. 1987; Hopkins and de Bruyn 2016). The exact resonance mode ($\sim 1$ kHz, Table 1 (B.6)) can be altered via the amount of pretension on the wire and needs to be modelled for deriving material properties. Although the setup showed good accuracy as a viscometer, a critical evaluation of the measured phase is still missing. In a recent follow-up study, strain-sensitive optical sensors were implemented for enhancing the accuracy on the measured displacement (Malara et al. 2017).

Resonators that undergo more ill-defined deformation modes may generate non-viscometric flow fields. They have mainly been applied as viscometers and are therefore not included here; some examples are briefly discussed below (cantilevers and resonating viscometers).

Ultrasound rheometers

High-frequency ultrasound rheometers employ resonance modes in the MHz range (Fig. 5). At such high frequencies, the penetration depth d_s (4) reduces to the order of μ m or smaller, depending on the fluid properties and exact frequency range. Consequently, only the microstructure near the wall of the resonator is probed and care must be taken that bulk properties are still being measured. Required sample volumes for surface loading operation on the other hand are much smaller, typically < 0.1 ml.

Shear waves

Most ultrasound rheometers operate in shear mode and employ resonating thickness-shear quartz crystals. The resonance frequencies of these crystals are much higher than those used for torsional resonators. Thickness-shear mode resonators, or quartz crystal microbalances, were originally used for mass detection of thin films due to the strong sensitivity of the resonance curve to the inertia of a loaded sample at very high frequencies (Sauerbrey 1959; Johannsmann 2008). However, the resonance behaviour is influenced by viscous damping as well and detection of both frequency shift and bandwidth, e.g. from impedance measurements, enabled the derivation of viscoelastic properties (10–11) (Reed et al. 1990). For instance, Fig. 8a sketches a thickness-shear mode resonator and illustrates the change in resonance behaviour due to a load. A factor complicating the analysis is the strong coupling between inertia and viscoelasticity (Johannsmann 2008). Decoupling these contributions is possible using wave interference at small gaps but is difficult to carry out experimentally. Viscoelastic properties for different types of complex fluids could only be determined by accurate modelling of the behaviour of the thickness-shear mode resonator and fluid-structure interaction. For instance, Bandey et al. (1999) described various loading conditions, including semi-infinite (surface loading) and finite (reflection effects) viscoelastic fluids, Newtonian fluids, and ideal inertial layers. Furthermore, although the crystals primarily exert a shear deformation, it was found that parasitic longitudinal waves are present and need to be taken into account as well (White and Schrag 1999). In order to derive viscoelastic moduli, careful calibration with Newtonian standards of varying density and/or viscosity is hence required (Buckin and Kudryashov 2001).

Fig. 8

Examples of ultrasound rheometers (Table 1 (C)):.a Illustration of a thickness-shear mode resonator (C.1) and of the shift in the measured resonance behaviour due to a load placed on top of the quartz plate (Reproduced from Johannsmann (2008) with permission from the PCCP Owner Societies). b Schematics of reflectometer setups (C.3) with normal (top) or inclined incident waves (bottom) (Reprinted from Yoneda and Ichihara (2005), with the permission of AIP Publishing)

Despite the experimental difficulties, thickness-shear mode rheometers are relevant to obtain rheological information of viscoelastic fluids and films in the MHz range. Similar to torsional resonators, they are sensitive towards low-viscous materials (${|\eta ^{*}|}_{\min \limits } \sim 10^{-4}$ Pa⋅s) but require much less sample (Table 1 (C.1)). More advanced configurations were developed as well, such as a high temperature- and pressure-resistant setup (< 1 GPa, Table 1 (C.2)) (Theobald et al. 1994), or more recently a resonator with interdigitated electrodes for simultaneous measurements of mass, viscosity and conductivity (Muramatsu et al. 2016).

Reflectometry

Reflectometry, introduced by Mason et al. (1949), is based on the analysis of the reflection coefficient of a planar shear wave at the interface of an elastic solid and the fluid under investigation (O’Neil 1949). Quartz crystals are used to create a planar shear wave and detect the reflected wave. Alig et al. (1997) adapted the original single-frequency pulse technique to a quasi-broadband acoustic system for simultaneous measurements over a wider frequency span. Figure 8b illustrates different modes of operation depending on the angle of the incident/reflected wave to the surface. The fluid impedance Z_f (12–13) can be derived from the measured complex reflection coefficient ${R}_{f} = |{R}_{f}| {e}^{-j {\delta }_{f}}$:

$$ Z_{f} = Z_{e} \cos(\theta) \cdot \frac{1 - {R_{f}^{2}} + 2jR_{f} \sin(\delta_{f})}{1 + {R_{f}^{2}} + 2jR_{f} \sin(\delta_{f})}, $$

(14)

with Z_e the impedance of the elastic solid, 𝜃 the incident wave angle (Fig. 8b), and |R_f| and δ_f respectively the measured amplitude and phase of the reflection coefficient. Inclined wave measurements are more sensitive due to an amplification of the signal (14) (Yoneda and Ichihara 2005), but are more difficult to conduct and were found to be prone to diffraction effects. In general, reflectometer setups are less sensitive and accurate than thickness-shear mode resonators, but the continuous frequency range can be of interest (Table 1 (C.3)). Integrated reflectometry setups for measurements at elevated temperatures were constructed as well (McSkimin 1956). While longitudinal ultrasonic transducers allow for a larger temperature range, devices based on shear waves are typically more sensitive; (Ono et al. 2007) aimed at combining both benefits by using shear waves converted from a longitudinal transducer for a high-temperature reflectometer setup with a potential range until 400 ^∘C.

Cantilevers and resonating viscometers

Immersed resonating structures can be used to determine bulk rheological properties at frequencies > 100 Hz (Table 1). However, they generally require a large sample volume to fulfil surface loading conditions. Recent years have seen an increased interest for fluid characterisation at small scales, e.g. to reduce sample volumes or perform in situ measurements. In combination with advances in fabrication methods, this has pushed the development of miniature fluid sensors.

Cantilevers

AFM microcantilevers have been used for various applications where high sensitivities are required, including force measurements or spectroscopy (Berger et al. 1997). Furthermore, experimental investigations have shown that cantilevers operated at their resonance frequency can be used for deriving fluid viscosities based on the oscillation displacement, which is used as a feedback parameter (Bergaud and Nicu 2000; Ahmed et al. 2001). Such derivations generally incorporate a theoretical analysis based on the work of Sader (1998) on the frequency response of an immersed beam cantilever, driven by a thermal driving force and undergoing flexural vibration modes. The size of the oscillating structure is typically much smaller than the wavelength of motion. As a result, hydrodynamic length scales were found to be very small ($\sim 10 \mu$m), reducing the required sample volume (≤ 1 nl) but limiting the structural length scale that can be studied. Smaller cantilever dimensions showed an enhanced sensitivity for the fluid viscosity (Boskovic et al. 2002).

Deriving rheological properties from the frequency response of a cantilever is less trivial due to the complex flow field around the tip, and modelling the complex hydrodynamic force exerted by the fluid remains challenging (Belmiloud et al. 2008). Dufour et al. (2012) determined linear viscoelastic moduli over a substantial frequency range around multiple discrete resonances (1 − 100 kHz) with a cantilever on a chip (Fig. 9a, Table 1 (D)). However, the resulting accuracy on the rheological properties was limited and improvements to both the experimental setup and modelling approaches are still required (Lemaire et al. 2013). Similar to torsional resonators, the quality factor of the oscillation in the fluid must be sufficiently high for accurate detection of the frequency response. Larger ‘mesoscale’ cantilevers with reduced sensitivity but larger Q-factors were constructed for probing fluids with larger moduli (Mather et al. 2012).

Fig. 9

a Schematic of a microcantilever on a silicon chip with integrated excitation and detection (Table 1 (D)) (Dufour et al. 2012). b A MEMS metallic suspended plate resonator for viscosity sensing of complex fluids (Reprinted from Reichel et al. (2010), Copyright (2010), with permission from Elsevier)

Resonating viscometers

In addition to flexural cantilevers, other types of complex resonating structures have been developed for measuring fluid properties at elevated frequencies. For instance, Fig. 9b shows a MEMS metallic suspended plate resonator for viscosity sensing of complex low-viscous fluids (Reichel et al. 2010, 2011). Different membrane and immersed resonators, using either Lorentz force or piezo actuation, have been developed for viscosity and density measurements on low-viscous fluids (Reichel et al. 2009; Clara et al. 2016; Lu et al. 2017; Lucklum et al. 2011). Other examples include parallel plate and waveguide techniques for probing viscosities > 1 Pa⋅s (Abdallah et al. 2016; Kazys et al. 2013). Miniaturised probes in particular offer substantial potential for in situ measurements in confined environments (Ruiz-Díez et al. 2015), and novel fabrication methods have enabled the creation of elegant three-dimensional mesostructures (Ning et al. 2018). Nonetheless, a major drawback compared with more traditional resonance methods remains the often ill-defined flow field surrounding these devices. The fluid-structure interaction is hence non-trivial, especially for viscoelastic materials, and their applicability has been limited to detecting density and viscosity. A complete description of viscosity probes lies outside of the scope of this review.

Applications

This section discusses some of the applications for high-frequency rheometry. Note that it is not exhaustive, but aims to highlight some questions for material classes for which high-frequency rheometry has proven useful and has further potential. As already mentioned above, the exact location of the “high-frequency region” on an absolute frequency scale depends on the characteristics of the material, and we focus on examples for which homebuilt high-frequency setups rather than conventional rheometers need to be used. Only applications related to bulk viscoelastic properties are described here. High-frequency rheometry, and ultrasound rheometry in particular, can also be used to derive properties of viscoelastic films and even interfaces (Wolff and Johannsmann 2000; DeNolf et al. 2011; Zhao et al. 2015). Furthermore, high-frequency methods often display a high resolution towards the detectable viscosity (Table 1) and are therefore suitable as viscometers for low-viscous and/or biological fluids as well (Reichel et al. 2015). Figure 10 compares typical measurable ranges in frequency and modulus of high-frequency methods applied to different material classes.

Fig. 10

Applicability of high-frequency methods for different material classes. Coloured regions delineate the measurement range of different methods: subresonant piezo rheometers operating in shear (PSR-1, light red) or compression (PSR-2 extension, dark red), bulk resonators (light green), guided wave techniques (dark green), thickness shear mode resonators (light blue), and reflectometers (dark blue). Marked regions indicate the measurement range of interest for specific material classes: a colloidal dispersions/gels and b polymers (black; full) and macromolecular solutions (grey; dashed)

Colloidal dispersions/gels

Early work on colloidal dispersions dates back half a century, e.g. Hellinckx and Mewis (1969) applied a guided wave method (McSkimin 1952) to characterise pigment dispersions at high processing shear rates. In general, the complex rheological behaviour of concentrated colloidal dispersions is set by the interplay between different interaction forces, either thermodynamic or hydrodynamic in origin, and the (shear rate dependent) microstructure (Mewis and Wagner 2012). These different contributions act on time and length scales which depend on the specific relaxation processes. Being able to vary the frequency above 10 Hz using bulk high-frequency rheometry is a powerful tool to directly probe local properties. Dispersions can be studied irrespective of the size, properties, or volume fraction of the dispersed phase. Figure 10a shows the applicability of different techniques to determine the high-frequency response of colloidal dispersions and gels. Subresonant piezorheometers offer the highest versatility since they allow to scan the frequency-dependent stress contributions in a continuous manner. When relaxation frequencies are > 1 kHz, or for studying low-viscous dispersions, resonator methods can be applied. Ultrasound rheometers are of lesser interest; the penetration depth will decrease to the order of the structural length scales of the material at higher ultrasonic frequencies (4).

The high-frequency response can be used to obtain quantitative information for various applications. Knowledge on the relaxation behaviour is important for the design, handling and understanding of complex materials. In case of a dilute Brownian suspension, the characteristic relaxation time can be predicted through the diffusional motion of a particle inside the medium. Relaxation frequencies typically decrease with volume fraction due to a reduced self-diffusion coefficient (Brady 1993; Bergenholtz et al. 1998a) and are influenced by colloidal interactions, particle shape, and structural effects, necessitating experimental characterisation (Bergenholtz et al. 1998b; Kirkwood and Auer 1951; Schroyen et al. 2017). At volume fractions above the glass transition, colloidal dispersions display multiple relaxation mechanisms: high-frequency measurements are highly useful to directly determine the fast ‘beta’ relaxation processes related to local in-cage rearrangements (Hecksher et al. 2017; Athanasiou et al. 2019). In emulsions, interfacial contributions resulting from surface tension give rise to additional relaxation times as well. High-frequency rheology has been employed to study the fast, local scale relaxation dynamics (Liu et al. 1996; Mason 1999; Romoscanu et al. 2003a, 2003c). In general, for soft systems, these techniques have a lot of potential for elucidating the interplay between the ‘softness’ of the dispersed phase and, for example, hydrodynamic effects.

High-frequency rheometry enables a fine analysis of the interplay between local scale hydrodynamic and interparticle forces (steric, electrostatic, direct hard contacts) (Brady 1993; Swan et al. 2014; van der Werff et al. 1989; Shikata and Pearson 1994; Woutersen et al. 1994). Information on this length scale is relevant for understanding phenomena that occur when particles come close together, such as at high shear stresses or rates, leading to shear thickening (Wagner and Brady 2009; Hsiao et al. 2017), or for flow phenomena in colloidal aggregates and gels (Colombo and Del Gado 2014; Wang et al. 2019). The dissipative part of the response has proven particularly valuable to identify contributions for suspensions as well as for emulsions and foams (Schroyen et al. 2019; Liu et al. 1996; Gopal and Durian 2003). For instance, this allowed a direct investigation of the influence of complex surface topographies on the local stress contributions in colloidal suspensions (Comtet et al. 2017; Schroyen et al. 2019), as illustrated in Fig. 11. The reduced stresses were calculated via substraction of and subsequent non-dimensionalisation by the bulk hydrodynamic stresses, and directly reveal the interplay between lubrication and colloidal forces. The HF scalings deviate substantially for varying surface topographies, indicating different dominant stress mechanisms or interactions at small length scales. Open questions are the influence of shape anisotropy, the role of roughness and non-central interactions in the viscosity and rigidity of colloidal aggregates and gels (Pantina and Furst 2005; Wang et al. 2019), or the importance of short-range interactions and hydrodynamics in concentrated colloidal gels or glasses. Alternatively, the elastic response in the high-frequency limit can be used to derive the average interparticle pair-potential (Zwanzig and Mountain 1965), which has been applied for instance to sterically (Zwanzig and Mountain 1965; Elliott and Russel 1998; Weiss et al. 1999; Nommensen et al. 2000; Duits et al. 2001) or electrostatically stabilised dispersions (Bergenholtz et al. 1998b; Fritz et al. 2002a).

Fig. 11

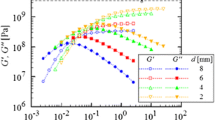
Reduced viscous (top) and elastic (bottom) stress amplitudes as a function of the dimensionless frequency, compared with the Brownian timescale, for particles with different surface characteristics (Schroyen et al. 2019). Measurements on a commercial instrument are combined with piezo shear rheometry. The lines present the theoretical limits for hydrodynamic lubrication (dashed) and repulsive hard-sphere (dotted) interactions and delineate the HF scaling regimes

Colloidal interactions alter the rheological response directly via the interaction potential and indirectly through the microstructure (Mewis and Wagner 2012). The latter can be applied to obtain direct, quantitative information on the microstructure of the dispersion. At frequencies that are very high compared with the characteristic relaxation frequency, the viscous response is dominated by bulk hydrodynamic stresses depending only on the effective volume fraction taken up by the fillers (Sierou and Brady 2001). The limiting hydrodynamic high-frequency response can therefore be used to quantify the local microstructure and dispersion state in attractive, partially dispersed suspensions (Bossis et al. 1991; Vermant et al. 2007; Schroyen et al. 2017). This is of large practical interest, e.g. for product evaluation or for scanning the efficiency of dispersion methods (Potanin 1993; Schroyen et al. 2017). Furthermore, the ability of separating microstructural contributions would be of large interest for studying non-equilibrium structures and thixotropy in attractive systems, but requires an integrated high-frequency and large-shear instrument.

Polymers and supramolecular materials

For polymeric and macromolecular solutions as well as melts, the high-frequency response can be used to investigate the microstructure on a local scale, such as the Rouse dynamics, monomeric friction effects, associative interactions, and transient forces. In case of dilute solutions, the fluid viscosity is generally low, rendering torsional resonator methods highly suitable for probing bulk properties (Fig. 10b). The Birnboim-Schrag multiple-lumped resonator (Schrag and Johnson 1971) was used extensively for determining the viscoelastic behaviour of various dilute polymer solutions, such as star or comb-polymers (Mitsuda et al. 1973a, 1973b), and was applied for instance for estimating small degrees of long-chain branching based on the measured relaxation times (Mitsuda et al. 1974). Furthermore, both torsional resonators and oscillatory squeeze flow instruments have proven useful to study the short-time dynamics and structure of wormlike micellar solutions (Buchanan et al. 2005; Willenbacher and Oelschlaeger 2007; Oelschlaeger et al. 2009) or polysaccharide solutions (Oelschlaeger et al. 2013). By combining different rheometrical techniques together with DWS microrheology, Willenbacher and Oelschlaeger (2007) provided an integrated picture of the viscoelastic response of a micellar solution, spanning a frequency range of 8 decades. The different techniques showed good agreement and proved that, through the high-frequency response, characteristic features of the wormlike micelles such as the persistence length can be derived accurately.

Although polymers often display a complex relaxation spectrum, as do macromolecular solutions, moduli are orders of magnitude higher and different measurement approaches are required (Fig. 10b). Subresonant piezo rheometers have been implemented for decades to study the properties of side-chain liquid-crystal polymers and/or composite materials (Gallani et al. 1994; Pozo et al. 2009; Roth et al. 2010). For instance, Zanna et al. (2002) investigated the influence of different molecular parameters on the rheological properties of cross-linked polysiloxane. Piezo rheometry was combined with time-temperature superposition to extend the accessible range even more, and the high-frequency region could be used to determine the onset of and scaling in the Rouse regime. Polymer gels display a power law regime at low frequencies governed by the overall network properties. Similar to colloidal gels, the high-frequency response can be used to investigate local scale properties and has been applied to assess the flexibility of the chains comprising the network based on scaling laws (Gittes et al. 1997). For homogeneous polymers with structural length scales that are sufficiently small (4), faster processes at or above the intermediate regime can be probed by performing measurements at even higher frequencies. Szántó et al. (2017) measured the entanglement relaxation time of polyethylene melts by means of quartz resonators operating in the MHz range, which was recently extended for copolymers of poly-1-butene and polyethylene (Liu et al. 2019).

In general, high-frequency rheometry is particularly useful for materials to which time-temperature superposition does not apply. It will therefore be very relevant for further work on the local dynamics of complex macromolecular systems. For instance, for semi-crystalline polymers, the rubbery plateau modulus can only be determined using high-frequency rheology (Struik 1987; Tajvidi et al. 2005; Szántó et al. 2017). In addition to obtaining this important information, the role of solvents as well as the challenging question of entanglement dilution can be addressed properly (Gold et al. 2019). In this regard, revisiting the linear viscoelasticity of block copolymers, where failure of time-temperature superposition was used by Rosedale and Bates (1990) to determine the disorder-to-order transition temperature, is of interest. Along the same lines, solutions of associating systems such as organogels or hydrogels are not amenable to time-temperature superposition, unless the solvent is athermal (Rubinstein and Colby 2003). This renders the utilisation of high-frequency rheometric methods necessary (Rodriguez Vilches et al. 2011; Collin et al. 2013). The obtained information on local dynamics may provide insights into the microscopic mechanisms governing the viscoelastic response of the investigated systems. Importantly, for associative systems, or even for concentrated solutions in complex solvents such as ionic liquids, it is unclear whether application of time-temperature superposition is appropriate even if a master curve can be obtained, since interpretation of the shift factors is complicated (Gold et al. 2017; Zhang et al. 2018). Independent high-frequency measurements can be very valuable in this regard.

High-frequency rheology can provide important insight in biomaterials as well. For instance, cells are active soft materials, and the protein filaments that compose the cytoskeleton display fast dynamics unique to semiflexible polymers (Koenderink et al. 2006; Kollmannsberger and Fabry 2011). Atakhorrami et al. (2014) studied the scale-dependent mechanics of semiflexible polymer networks and compared bulk rheological properties with the local response obtained from microrheology. Important discrepancies were observed between both techniques in the intermediate regime (> 100 Hz), owing to local non-continuum effects. More recently, Rigato et al. (2017) investigated the properties of different cell types under cytoskeletal drug treatments directly and over a large frequency range by means of AFM. While structural elements of the cytoskeleton dominated the response at low frequencies, the high-frequency response (> 1 kHz) could be described by relaxation modes of single filaments, as illustrated in Fig. 12, where the viscoelastic moduli are fitted with a double power law. These results offer new therapeutic routes as well, e.g. for the detection of malign tumor cells, which showed distinct mechanical characteristics owing to the filaments that become more tense (Rigato et al. 2017; Mohammadi and Sahai 2018). In order to improve the quantification of such analyses, further developments in the field of high-frequency rheometry will be essential (Schächtele et al. 2018).

Fig. 12

High-frequency rheology of living fibroblasts, measured by AFM (Reprinted by permission from the Licensor: Springer Nature, Rigato et al. (2017), Copyright (2017)). The moduli were fitted with a double power law model (full line), accounting for a low-frequency regime governed by the mesoscale network and a high-frequency regime dominated by single filament dynamics

Conclusion

The current review provided an overview of different high-frequency bulk rheometrical techniques that have been developed, spanning a frequency range from 0.1 to 10⁸ Hz. Table 1 presented a comparative summary of different device types. Although a multitude of techniques has been developed, not all are as practically useful. Wave propagation effects play an important role in high-frequency rheology and influence not only the experimental design parameters but also the structural length scales that can be probed. Subresonant piezorheometers can operate in a continuous manner until the low kHz range. Shear mode rheometers operate under a simple flow profile and are hence more accurate, but the resolution is limited and can be extended by using compressional instruments. Bulk resonators extend the frequency range further in a discrete manner. They are highly sensitive but excessive damping can be an issue. Guided wave methods on the other hand are less accurate but provide access to higher moduli. Ultimately, in the MHz range, both thickness shear mode resonators and reflectometers have been used. The penetration depth of the wave decreases < 10μ m and measured values do not necessarily represent bulk properties. When scanning for an applicable technique, different parameters have to be taken into account: the frequency range associated with the length/time scale at interest, the range in moduli, sample volume, and environmental parameters. In Fig. 10, practical instrument ranges were compared with the measurement ranges at interest for different materials. These ranges are a crucial design criterion.

Different techniques target specific material classes and frequencies, and identifying a suitable high-frequency method depends on the exact application that is addressed. For many complex materials such as colloidal dispersions, micellar solutions, or some polymer solutions and melts, access to low-to-intermediate kHz frequencies is highly relevant for probing interactions and specific features of the local scale microstructure. Examining the ultrasound MHz range can be useful for detecting very fast processes and relaxation times of homogeneous materials, i.e. polymer glasses, or to determine rheological properties of viscoelastic films. Furthermore, high-frequency rheology should be seen as complementary to conventional shear rheology. Combining high-frequency measurements with conventional rotational tests can offer an integrated view over the microstructure, ranging from collective properties at low frequencies to local scale properties at high frequencies.