Introduction

In 1985, Howard Barnes and Ken Walters published a provocative paper entitled “The yield stress myth?” (Barnes and Walters 1985), in which they asserted that the yield stress is an experimental artifact, and notably that all fluids will show viscous (indeed, Newtonian) behavior at sufficiently small stresses. They stated that “the yield stress hypothesis, which has hitherto been a useful empiricism, is no longer necessary, and … fluids which flow at high stresses will flow at all lower stresses, i.e., the viscosity, although large, is always finite and there is no yield stress.”Footnote 1 This assertion by two very prominent rheologists caused a flurry of discussion and publication, with substantial parsing of the meaning of the words “yield stress;” i.e., is the yield stress a material property or a useful approximation for materials that exhibit a large reduction in viscosity over a narrow shear stress range? Barnes and Walters supported their assertion with data obtained using a constant-stress rheometer that showed a Newtonian regime at stresses lower than the apparent yield stress, and Barnes subsequently showed similar data on a number of different materials (Barnes 1999; Roberts and Barnes 2001), including Carbopol.

The concept of a yield-stress fluid was popularized by Bingham, who included such fluids in the context of yielding in many classes of materials in his 1922 book Fluidity and Plasticity (Bingham 1922). Barnes (1999) has written a comprehensive review of the history of the study of yielding, in which he places the common yield-stress fluids currently being studied in the context of phenomena like creep in metals and plastics. Modern interest in yield-stress fluids largely dates from work by Oldroyd (1947) and Prager (Hohenemser and Prager 1932; Prager 1961) that put the description of such materials into an invariant continuum formulation that can be applied to flows in complex geometries. Both Oldroyd and Prager assumed that there is a transition between a solid and a fluid at a critical value of a stress invariant, typically taken to be a yield surface defined by the von Mises criterion (Prager 1961). Prager assumed that no deformation was possible on the “solid” side of the yield surface. Oldroyd assumed that the material is an incompressible elastic (Hookean) solid before yielding, with a stress proportional to the strain, and a viscous material thereafter, with a stress that is linear in the rate of deformation. Most subsequent investigators have assumed that the solid has an infinite modulus, in which case no deformation is possible prior to yielding, and the assumption of linearity after yielding has been generalized to include power-law behavior and even viscoelasticity. The Oldroyd–Prager formulation, with a discontinuous transition between solid and liquid, is at the heart of the yield-stress controversy initiated by Barnes and Walters.

Møller et al. (2009a) showed that the apparent Newtonian viscosity observed by Barnes at stresses below the apparent yield stress was not a true viscosity but was in fact an experimental artifact whose value depends on the waiting time prior to measurement (i.e., the elapsed time between initiating the deformation and recording the measurement), increasing with a power-law dependence on the waiting time; the exponents were between ½ and 1, depending on the material. What is in fact being observed is a response of the unyielded material that gives a ratio of stress to shear rate that is independent of the imposed stress, hence appearing to be a constant viscosity.

The schematic in Fig. 1, from Barnes and Nguyen (2001), illustrates a typical startup experiment at constant shear rate, showing an initial region of apparent linear elastic behavior followed by a transition region that appears to be non-linearly elastic prior to yielding, with some ambiguity regarding the location of the transition to viscous flow. The figure also illustrates a variety of definitions of the yield stress deduced from such a startup experiment that are clearly different and depend on the understanding of the material response in the neighborhood of the transition. The nature of the deformation of the pre-yielded material has received attention only relatively recently, as summarized in Bonn et al. (2015), but there were early indications of the significance of the pre-yielding mechanics and the fact that a simple elastic (or rigid) treatment was inadequate. More than 30 years ago, Nguyen and Boger (1983) found that the yield stress was a strongly increasing function of rotor RPM in their classic vane measurements on “red mud,” which Denn and Bonn (2011) showed was consistent with the behavior of a viscoelastic Kelvin–Voigt solid that yielded at a critical strain. It is this pre-yielding behavior that we address here.

Fig. 1
figure 1

Sketch of the stress response in a startup experiment at a constant shear rate, with various definitions that have been used to define the yield stress. After Barnes and Nguyen (2001)

Full size image

We focus here on the most basic of yield-stress fluids, an aqueous Carbopol that is a simple (i.e., non-thixotropic) yield-stress fluid for which the yield stress is the same whether increasing or decreasing the shear rate in a cyclic manner (Bonn and Denn 2009; Møller et al. 2009b; Ovarlez et al. 2013; Balmforth et al. 2014; Coussot 2014). We use a modern rheometer to examine the response of the Carbopol to a variety of deformations in order to elucidate how the mechanics of the unyielded material manifest themselves in some standard rheological tests. Perhaps the main issues that have been discussed over the past decades and that we address here are:

  • Is the yield stress a flow to no-flow transition? i.e., as per Barnes and Walters (1985), is there viscous flow below the yield stress?

  • Can the yield stress be inferred by extrapolation of the flow curve to zero shear rate?

  • Can the yield stress be inferred from startup experiments?

  • Are non-linear oscillatory shear measurements a better way to infer the yield stress?

Materials

Our model yield-stress fluid is a 0.6 wt. % solution of Carbopol Ultrez U10 in ultra-pure water (Milli-Q) that has been stirred for 1 h and adjusted to a pH of approximately 7 by adding drops of 20 wt. % sodium hydroxide (Sigma-Aldrich) solution. The Carbopol gel is homogenized by shaking and stirring manually. All rheological measurements were carried out using an Anton Paar MCR302 rheometer equipped with a 50-mm-diameter cone-and-plate geometry with a 1° cone and roughened surfaces to avoid wall slip. To characterize the system, we first consider the response of the Carbopol gel to small-amplitude oscillatory shear. The storage (G′) and loss (G″) moduli at a strain of 0.05 are shown in Fig. 2. G′ is much larger than G″, more than an order of magnitude so at frequencies below 1 Hz. The unyielded material is thus clearly a viscoelastic solid, with a nearly constant storage modulus (G′ ∼ ω 0.05), but the frequency dependence of the loss modulus (G″ ∼ ω 0.32 for ω ≥ 0.8 Hz) is weaker than that of a single Kelvin–Voigt element. We return to oscillatory forcing subsequently.

Fig. 2
figure 2

Linear viscoelastic response at a strain of 0.05

Full size image

Rheology experiments

Extrapolation to zero shear rate: flow curves

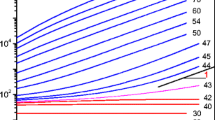
We now turn to the measurement of flow curves. As noted by Barnes (1999), the yield stress obtained by extrapolation of the steady-state flow curve to zero shear rate depends on the shear rate range chosen. We therefore performed experiments over different shear rate ranges, both increasing and decreasing the shear rate in a shear rate ramp. Figure 3 shows the result of twelve independent runs with a maximum shear rate of 100 s−1, six with increasing shear rate, and six with decreasing shear rate, all with different minimum shear rates ranging from 10 to 10−4 s−1. All of the data overlap for shear rates slightly above 10−3 s−1 and are well fitted by a Herschel–Bulkley model with a yield stress of 53.7 ± 2.7 Pa and a power-law exponent n = 0.4. Extrapolation of the flow curves obtained starting from high rates appears to give a reliable value of the yield stress. Initial data from the two lowest increasing runs, with starting shear rates of 10−4 and 10−3, respectively, lie below the curve and apparently reflect insufficient accumulated strain to reach a steady flow. This is consequently a residual effect of the elasticity of the unyielded material seen in Fig. 2 and should not be taken into account; it is not a steady-state behavior.

Fig. 3
figure 3

Flow curves for increasing (red symbols) and decreasing (black symbols) imposed shear rates. Measuring time per point is 10 s. The yield stresses are extrapolated from the flow curves of the decreasing imposed rates by fitting with the Herschel–Bulkley model, giving a mean yield stress of τ y= 53.7 ± 2.7

Full size image

Flow to no-flow transition

As already mentioned, Barnes and Walters (1985) showed data obtained using a constant-stress rheometer that exhibited a Newtonian regime at stresses lower than the apparent yield stress, and they inferred from this that the yield-stress material flows with a very high viscosity below the yield stress. Møller et al. (2009a) subsequently showed that these high viscosities do not correspond to a steady state, and thus should be discarded. For the system studied here, the apparent viscosity is shown in Fig. 4 as a function of shear stress for measurements taken at imposed constant stresses with different waiting times, plotted together with stress-controlled data at decreasing stresses and the decreasing rate data. The decreasing stress data lie on the same Herschel–Bulkley curve as the decreasing rate data. The increasing stress data show the phenomenon observed by Barnes, namely an apparent viscosity at low stresses that is nearly constant and five or more orders of magnitude larger than the high-rate viscosity of the fully yielded material. The data also show the phenomenon observed by Møller et al. (2009a) wherein the apparent viscosity plateau increases with increasing measuring time, in this case, diverging with a power-law exponent of 0.4.

Fig. 4
figure 4

Apparent viscosity versus stress for increasing imposed stresses (filled red symbols), together with data at decreasing stress (blue stars) and decreasing imposed shear rates (open black symbols)

Full size image

Startup: experiments at a constant shear rate

Figure 3 raises the question of how to understand startup flows. The buildup of the apparent viscosity as a function of time at constant imposed shear rate is shown for our Carbopol sample in Fig. 5a. The steady-state values are the same as those shown in Fig. 3 at the same shear rates. It is more instructive to consider the same data replotted in Fig. 5b as stress versus strain. Here, there is overlap up to a strain of about 0.1, then a small rate-dependent separation until all curves exhibit a sharp break to a constant stress at a strain between 0.2 and 0.3. The yield stress that is inferred from the break in slope at the lowest shear rate is about 54 Pa, which is in agreement with the value found from the flow curves in Fig. 3. The flow curve obtained at decreasing rates contains the same information as the startup measurement, but the extrapolation of the flow curve minimizes the effect of finite rate on the determination of the yield stress. Stress overshoot, which is not observed in our material, could be a complicating factor in the use of a startup measurement, since the sharp transition observed in Fig. 5a would be absent. Observations and discussions of stress overshoot may be found, for example, in Bonnecaze and Brady (1992) and Liddell and Boger (1996).

Fig. 5
figure 5

a Buildup of apparent viscosity as a function of time for four imposed shear rates. b The same measurements but with the data plotted as shear stress as a function of strain

Full size image

Oscillatory measurements

We now return to oscillatory measurements, this time carried out at finite strains. G′ and G″ are shown in Fig. 6 as functions of strain for different frequencies. The material is linear up to a strain of about 0.1, after which a strain dependence is observed. The strain dependence of G′ and G″ becomes significant at strains of about 0.3, with increasing dissipation and ultimately with G′ becoming smaller than G″ at strains of order unity. (G′ and G″ are the fundamental terms in a harmonic representation of the oscillatory stress response. Higher harmonics are negligible for this material in the strain range studied.)

Fig. 6
figure 6

G′ and G′′ as functions of strain at different frequencies

Full size image

The same data are plotted as total stress versus strain for different frequencies in Fig. 7. This is a revealing way to visualize the data, as shown by Christopoulou et al. (2009) for a colloidal glass and by Dinkgreve et al. (2016) for non-thixotropic yield-stress fluids including emulsions, foam, and Carbopol. There is a linear stress-strain relation with a modulus of 235 Pa at all frequencies up to a strain of about 0.1, after which there is a small frequency dependence that is followed by transition to a softer material. The transition strain is equal to 0.22 for all frequencies up to 1 Hz, with a small increase thereafter. The transition stress increases with increasing frequency above 1 Hz, from about 50 to 72 Pa. This behavior is reminiscent of the startup at constant shear rate data shown in Fig. 5. The increase in the transition stress with frequency mirrors the increase in G″, and it is likely that the transition is determined by the strain, with the small increase in stress a consequence of the fact that an increasing portion of the stress is from dissipative non-recoverable strain. An ideal Oldroyd–Prager yield-stress fluid would exhibit no frequency dependence.

Fig. 7
figure 7

Total stress in oscillatory shear as a function of strain at different frequencies

Full size image

The effect of viscoelasticity: pre-yielding mechanics

Perhaps the main question from the above observations is how to understand the effect(s) of elasticity that become important at small deformations. We can gain some insight by considering the simplest viscoelastic models for small strains, the Kelvin–Voigt solid and the Maxwell fluid:

$$\begin{array}{@{}rcl@{}} &&\text{Kelvin--Voigt solid: }\quad \tau =G\gamma +\eta \dot{\gamma} \end{array} $$
(1a)
$$\begin{array}{@{}rcl@{}} &&\text{Maxwell fluid: }\qquad\quad \tau +\lambda \dot{\tau} =\eta \dot{\gamma} \end{array} $$
(1b)

The Maxwell fluid asymptotically approaches a stress equal to \(\eta \dot {\gamma }\) in a constant shear rate deformation, while the response for t < < λ is τ = γ t; this is qualitatively the behavior seen in Fig. 5, except that experimental viscosity is a (strongly) decreasing function of the shear rate. The stress for the Kelvin–Voigt model for this deformation is proportional to strain, but with an offset equal to \(\eta \dot {\gamma }\), so there is no superposition in the elastic regime as seen in Fig. 5b.

The Maxwell fluid simply exhibits a Newtonian behavior in a constant stress deformation, with no time dependence. The strain in the Kelvin–Voigt solid evolves exponentially as

$$ \gamma =\frac{\tau} {G}\left( 1-e^{-Gt/\eta} \right), $$
(2)

which can be manipulated into the form

$$ \frac{\tau} {\dot{\gamma} }=\eta_{\text{app}}=\eta e^{Gt/\eta} . $$
(3)

That is, the Kelvin–Voigt solid appears to have a shear viscosity in a constant stress deformation that is independent of stress and deformation rate but increases with waiting time. This is qualitatively the behavior seen for the increasing controlled stress data in Fig. 3 and is a qualitative explanation of the observation of a Newtonian regime below the yield stress by Barnes and Walters. The single Kelvin–Voigt element model is instructive, but it is too elementary to be of quantitative use, however.

Of course, a material cannot be roughly a Maxwell fluid in one class of deformations and roughly a Kelvin–Voigt solid in another unless there is a hidden variable in a more general formulation that interpolates between the behaviors. This is the case in the kinematic hardening model used by Dimitriou et al. (2013), for example, in which the “back stress” evolves dynamically and affects the mechanics. The back stress can be viewed as a “lambda parameter” (e.g., Denn and Bonn (2011)) in simple shear flow and causes the location of the yield surface to adjust, depending on the deformation state, as in the general framework of the evolution of the yield stress surface for elastoviscoplastic solids that was developed by Naghdi and Srinivasa (1992). The kinematic hardening model can be shown to be roughly Maxwellian for small deformations at a constant shear rate and to be Maxwellian for the difference τ − τ y close to yielding, so it reflects the behavior seen in Fig. 5. Dimitriou et al. (2013) have shown via a numerical simulation at constant stress that the model predicts behavior qualitatively like that shown in Fig. 4.

Concluding remarks

This short article is intended to highlight the significance of the description of the pre-yielded material in considering the mechanics of yield-stress fluids. For the simple yield-stress fluid considered here, the transition appears to be based on a critical strain, with the possibility of dissipative deformations in a viscoelastic solid that make the critical stress under transient conditions deformation dependent. It is clear experimentally that the appearance of a Newtonian fluid regime at stresses below the yield stress is an artifact that would be observed with the simplest viscoelastic solid representation, namely a Kelvin–Voigt solid. We have not addressed the likely failure of the Oldroyd–Prager formalism following yielding, but there is convincing evidence that a viscoelastic fluid description is necessary for materials like the Carbopol studied here. Indeed, Fraggedakis et al. (2016) have employed both kinematic hardening and a viscoelastic model by Saramito (2007) to describe the kinematics and settling dynamics of a spherical particle through a Carbopol gel.

Finally, we note that for the ideal (non-thixotropic) yield-stress fluid studied here, the transition in a plot of total stress versus strain in finite-amplitude oscillatory shear gives a value of the yield stress that is consistent with the yield stress obtained by extrapolation of the flow curve and the value obtained in a startup experiment, with the added information of the yield strain. This method has the advantage of eliminating artifacts associated with startup flows or extrapolation of the flow curve. Any of these methods properly used, however, can give a reliable value of the yield stress.