Numerical simulations of linear viscoelasticity of monodisperse emulsions of Newtonian drops in a Newtonian fluid from dilute to concentrated regime

Abstract

The bulk viscoelastic properties of monodisperse emulsions of Newtonian drops in a Newtonian matrix subjected to small amplitude oscillatory shear (SAOS) flow are investigated by means of arbitrary Lagrangian Eulerian finite element method 3D numerical simulations. Volume fractions of the suspended phase from the dilute to the concentrated regime (up to 30 %), and a range of several orders of magnitude of the drops-to-matrix viscosity ratio and of the frequency of the oscillatory flow are examined; the eventual presence of slip between the two fluids is also considered. The computational results are compared with theory, yielding a quantitative agreement with Oldroyd (Proc R Soc Lond A 218:122–132, 1953) predictions in a wide range of values of the considered parameters, even well beyond the dilute regime, and also in the cases with slip.

Appendices

Appendix A: Details on the computational approach

In this Appendix, we explain in detail two main aspects of our simulations, both of them already mentioned in the main text: (i) how we guarantee that wall effects are negligible; (ii) how we succeed in reducing the computational cost of our simulations by building up suitable simulation domains (the “bulky” subdomains alluded to in the main text) containing relatively few drops with respect to the number of drops that would pertain to the complete simulation domain at a given volume fraction. To illustrate those issues, for the sake of simplicity in the exposition, we perform our discussion in 2D. The proposed methodology is general, however, and all the 3D results reported in the paper are obtained in the way described in this Appendix.

Let us consider a 2D square cell filled with a Newtonian fluid with monodisperse Newtonian drops with volume fraction ϕ=0.27. The viscosity ratio between the drops and the matrix is λ=2.0, no slip acts between the drops and the matrix. The side of the cell is 36 times the initial radius of the drops, and the system is subjected to small amplitude oscillatory shear flow with frequency ω=0.4 (made dimensionless as explained in “Results and discussion”). In Fig. 14, a scheme of such domain in its initial configuration is reported, where the distribution of the drops is random. The upper and lower sides of the square are solid walls that move according to Eq. 14. Due to computational reasons, in the generation of the random initial positions of the drops, the constraint is added that they cannot cross the vertical boundaries of the flowcell.

Fig. 14

Geometry of the 2D computational domain. ϕ=0.27

If we look at a series of concentric square subcells characterized by a progressively smaller side (the red squares in Fig. 14), the initial volume fraction of the drops in those changes with the side of the subdomain we take into account, since the overall initial distribution of the drops is random. Moreover, whereas ϕ is constant in time in the “big” domain (the drops cannot cross the vertical boundaries of the flowcell), it can vary in the “red” subdomains, since the drops can cross the red sides during oscillations. In Fig. 15, the time-averaged volume fraction of the drops is reported versus the side of the subdomain in which it is computed, made dimensionless by the radius of the drops R _d, for an overall volume fraction ϕ=0.27, λ=2.0, ω=0.4. Each point in the diagram is in turn the average of the results obtained for ten different random initial distributions of the drops.

Fig. 15

Average volume fraction of the drops ϕ in a subdomain of the 2D computational domain as a function of the dimensionless side of the subdomain $\frac {L}{R_{\mathrm {d}}}$

By looking at Fig. 15, it can be seen that by progressively decreasing the side of the subdomain (i.e., by going left along the $\frac {L}{R_{\text {d}}}$-axis), ϕ initially increases: this is due to the fact that not all the room in the very external region of the original computational domain is really available to the drops, since, as hinted above, the drops must not cross the vertical boundaries of the flowcell; then, for $\frac {L}{R_{\text {d}}}$ in the range 18−24, the average volume fraction in the red box recovers the imposed value, as highlighted by the dashed horizontal line.

For each configuration of the drops, the average shear rate and shear stress are computed in all the considered subdomains. From those data, the viscoelastic moduli of the system are obtained and can be plotted as a function of the side of the red box. This is done for the elastic modulus G ^′ in Fig. 16 (G ^′ having been made dimensionless as written in “Mathematical model”). It is evident from Fig. 16 that G ^′ changes with the side of the subdomain in which it is computed. If one looks at the range $\frac {L}{R_{\text {d}}}=18-24$, where ϕ does not change with $\frac {L}{R_{\text {d}}}$ and is equal to the imposed one (as we have seen in Fig. 15), it can be noticed that G ^′ is also constant with $\frac {L}{R_{\text {d}}}$ in there. The same behavior is also noticed for the loss modulus G ^″ (not shown). From such observations, it can be deduced that a subdomain with a side in the range 18–24 is in fact representative of the bulk of the emulsion. In addition, it can be observed that the G ^′-value computed for $\frac {L}{R_{\text {d}}}=36$ (the whole domain, including the solid walls) also overlaps the values computed in the boxes with $\frac {L}{R_{\text {d}}}\in [18,24]$, thus letting us conclude that for the considered overall volume fraction, the size of the whole computational domain is large enough to make wall effects irrelevant in the calculation of the elastic modulus. For G ^″ similar results are obtained, and analogous conclusions can be drawn.

Fig. 16

Elastic modulus G ^′ in a subdomain of the 2D computational domain as a function of the dimensionless side of the subdomain $\frac {L}{R_{\text {d}}}$. Overall volume fraction ϕ=0.27

In view of developing a procedure for computational saving, let us now take the same ten random distributions of the drops from which the results in Figs. 15 and 16 are computed, and, from each one, remove all the drops whose centers initially lie outside a square with side $\frac {L}{R_{\text {d}}}=24$, and replace them with pure matrix. With reference to the configuration shown in Fig. 14, the result of such procedure is displayed in Fig. 17.

Fig. 17

Geometry of the 2D computational domain with an empty frame. ϕ=0.27

If we consider a sequence of concentric square subcells of decreasing side with $18\leq \frac {L}{R_{\text {d}}} \leq 24$ (e.g., the green squares in Fig. 17), the volume fraction of the drops in each of those (averaged over time and different initial configurations) is of course the same as in the subdomains characterized by the same side with the system fully filled with drops. The choice of considering such interval stems from the result that in a box whose side belongs to that range the volume fraction of the system is the imposed one, and the moduli are the “bulky” ones.

For such “peculiar” emulsions, the moduli can be computed at varying $\frac {L}{R_{\text {d}}}$ between 18 and 24, as done above. If we compute, then, the percent distance between the G ^′ values in the full and the “framed” system for the same side of the subdomain, as $\epsilon =100|\frac {G'_{\text {full}}-G'_{\text {frame}}}{G'_{\text {full}}}|$, we find that such discrepancy is always below 2.5 %. This lets us argue that removing the drops in the space between the boundaries of the box with $\frac {L}{R_{\text {d}}}=24$ (where the “bulky” conditions are verified), and the boundaries of the whole domain makes us commit a small error, but lets us “save” about 55 % of the drops.

We consider now a 2D square domain filled with a dilute emulsion of Newtonian drops in a Newtonian fluid (volume fraction ϕ=0.07), with viscosity ratio λ=2.0, and subjected to SAOS flow with ω=0.4. The side of the cell is 60 times the initial radius of the drops. In Fig. 18, a scheme of such domain in its initial configuration is reported, where the distribution of the drops is random. As in the case with ϕ=0.27 shown in Fig. 14, in the generation of the random initial positions of the drops, the constraint is added that they cannot cross the vertical boundaries of the flowcell.

Fig. 18

Geometry of the 2D computational domain. ϕ=0.07

As we did above, we take into account several concentric square subcells with a progressively decreasing side (the red squares in Fig. 18), and compute the average over ten random initial configurations of the time-averaged volume fraction of the drops in those subdomains. The results of such calculations are shown in Fig. 19.

Fig. 19

Average volume fraction of the drops ϕ in a subdomain of the 2D computational domain as a function of the dimensionless side of the subdomain $\frac {L}{R_{\text {d}}}$

As the side of the subdomain is progressively decreased from $\frac {L}{R_{\text {d}}}=60$, ϕ initially increases due to the fact that not all the room in the very external region of the computational domain is really available to the drops because of the constraint that the drops cannot cross the vertical boundaries of the flowcell; then, for $\frac {L}{R_{\text {d}}}$ between 24 and 30, the average volume fraction is constant and equal to the imposed value ϕ=0.07, as highlighted by the dashed horizontal line.

The average shear rate and shear stress are computed in all the considered boxes, from which the viscoelastic moduli of the system are obtained as a function of the side of the box. The plot of G ^′ versus $\frac {L}{R_{\text {d}}}$ for ϕ=0.07 is displayed in Fig. 20. As for ϕ=0.27 (Fig. 16), the elastic modulus changes with the side of the subdomain in which it is computed. Where ϕ does not change and is equal to the imposed one ($\frac {L}{R_{\text {d}}}\in [24,30]$), G ^′ does not change as well, thus letting us deduce that a subdomain with dimensionless side in the range 24–30 is representative of the bulk of the emulsion. In addition, in analogy to what happens for ϕ=0.27, the G ^′ value computed when taking the whole domain, including the solid walls, also overlaps the values computed in the boxes with $\frac {L}{R_{\text {d}}}\in [24,30]$, so also for ϕ=0.07 the size of the whole computational domain we have chosen is large enough to make wall effects irrelevant in the calculation of the viscoelastic properties.

Fig. 20

Elastic modulus G ^′ in a subdomain of the 2D computational domain as a function of the dimensionless side of the subdomain $\frac {L}{R_{\text {d}}}$. Overall volume fraction ϕ=0.07

In analogy to what we did for ϕ=0.27, we take the ten random distributions of the drops we generated with an overall volume fraction ϕ=0.07, and we remove from each of them all the drops whose centers initially lie outside a square with side $\frac {L}{R_{\text {d}}}=30$, replacing them with pure matrix. Then, we compute the moduli of the system with an empty frame at varying $\frac {L}{R_{\text {d}}}$ between 24 and 30. In that range, the percent distance between the G ^′ values in the full and the framed system is between 3.5 and 7 %. This makes us conclude that, if we want to compute the viscoelastic moduli in the box with $\frac {L}{R_{\text {d}}}=30$, where we have found that the “bulky” conditions are verified, removing the drops in the space between the boundaries of such subcell and the boundaries of the domain would let us realize a computational saving, but make us commit a nonnegligible error.

By comparing the results at ϕ=0.27 and ϕ=0.07 presented in this Appendix, we can infer that there is a screening effect among the drops. Indeed, we see that at low volume fractions (e.g., ϕ=0.07), the absence of drops outside the subdomain where we compute the viscoelastic properties of the system has a considerable influence on the calculated values, whereas, at high volume fractions (e.g., ϕ=0.27), the difference between the results calculated in the full and the framed system is almost negligible. From such observation, we can conclude that, in 2D, at low ϕ-values the complete system must be simulated, whereas, at high volume fractions, it is allowed to simulate a system where only the region in which the moduli are computed is filled with drops, without losing the representativity of the real system.

In 3D, however, the situation is even more favorable, since the hydrodynamic interactions among the suspended objects decay much faster (in space) than in 2D. Indeed, we find that, for ϕ=0.05, the percent discrepancy between the G ^′ values computed in a “bulky” subdomain of a cell fully filled with drops, and the corresponding value computed in a subdomain surrounded by pure matrix is less than 3 %. In the present paper, then, full systems are simulated for volume fractions below 0.05; above such value, the frame approach is used.

Appendix B: Oldroyd formulas in the no-slip case

From Oldroyd (1953), in the absence of interfacial slip between the drops and the matrix, the following expressions for the moduli of a monodisperse emulsion of Newtonian drops in a Newtonian fluid subjected to small amplitude oscillatory shear flow can be derived as follows:

$$ G^{\prime}=\frac{(\eta\tau-\xi)\omega^{2}}{1+\tau^{2}\omega^{2}} $$

(20)

$$ G^{\prime\prime}=\frac{\eta\omega+\xi\tau\omega^{3}}{1+\tau^{2}\omega^{2}} $$

(21)

where η is the overall viscosity of the emulsion, τ is its relaxation time, and ξ is a further parameter “naturally” arising in Oldroyd deduction. Such quantities can be in turn expressed as follows:

$$ \eta=\eta_{\text{m}}\frac{10(\lambda+1)+3(5\lambda+2)\phi}{10(\lambda+1)-2(5\lambda+2)\phi} $$

(22)

$$ \tau=\frac{1}{4}\tau_{\text{em}}\frac{(19\lambda+16)[2\lambda+3-2(\lambda-1)\phi]}{10(\lambda+1)-2(5\lambda+2)\phi} $$

(23)

$$ \xi=\frac{1}{4}\eta_{\text{m}}\tau_{\text{em}}\frac{(19\lambda+16)[2\lambda+3+3(\lambda-1)\phi]}{10(\lambda+1)-2(5\lambda+2)\phi} $$

(24)

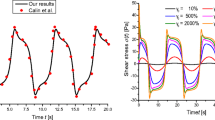
with η _m the viscosity of the matrix, λ the ratio between the viscosities of the drops and the suspending phase, ϕ the volume fraction of the suspended phase, and $\tau _{\text {em}}=\frac {\eta _{\text {m}}R_{\text {d}}}{\Gamma }$ the emulsion time (where R _d is the initial radius of the monodisperse drops, and Γ is the interfacial tension between the two liquids). The blue curves displayed in Figs. 4, 5, 6, 7, 8, 9, 10, and 11 are built according to these laws.

Appendix C: Oldroyd formulas in the case with interfacial slip

Even in the case where interfacial slip acts between the suspended drops and the suspending matrix, Eqs. 20 and 21 still hold true. Instead, the expressions of η, τ, and ξ become:

$$ \eta=\eta_{\text{m}}\frac{10(\lambda+1)+3(5\lambda+2)\phi+10\alpha\lambda(3\phi+5)}{10(\lambda+1)-2(5\lambda+2)\phi+10\alpha\lambda(5-2\phi)} $$

(25)

$$ \begin{array}{rcl} \tau=\frac{1}{4}\tau_{\text{em}}\frac{(19\lambda+16)[2\lambda+3-2(\lambda-1)\phi]}{10(\lambda+1)-2(5\lambda+2)\phi+10\alpha\lambda(5-2\phi)}+\\ \frac{1}{4}\tau_{\text{em}}\frac{2\alpha\lambda[2(19\lambda-40)\phi-5(19\lambda+24)]}{10(\lambda+1)-2(5\lambda+2)\phi+10\alpha\lambda(5-2\phi)} \end{array} $$

(26)

$$ \begin{array}{rcl} \xi=\frac{1}{4}\eta_{\text{m}}\tau_{\text{em}}\frac{(19\lambda+16)[2\lambda+3+3(\lambda-1)\phi]}{10(\lambda+1)-2(5\lambda+2)\phi+10\alpha\lambda(5-2\phi)}+\\ \frac{1}{4}\eta_{\text{m}}\tau_{\text{em}}\frac{2\alpha\lambda[3(19\lambda-40)\phi+5(19\lambda-24)]}{10(\lambda+1)-2(5\lambda+2)\phi+10\alpha\lambda(5-2\phi)} \end{array} $$

(27)

with η _m the viscosity of the matrix, λ the ratio between the viscosities of the drops and the suspending phase, ϕ the volume fraction of the suspended phase, $\tau _{\text {em}}=\frac {\eta _{\text {m}}R_{\text {d}}}{\Gamma }$ the emulsion time (where R _d is the initial radius of the monodisperse drops, and Γ is the interfacial tension between the two liquids), and α the dimensionless slip parameter (see “Results and discussion”). The black and red curves displayed in Figs. 12 and 13 are built according to these laws.