Analytical ultracentrifugation in colloid and polymer science: new possibilities and perspectives after 100 years

Abstract

Analytical ultracentrifugation (AUC) is a classical polymer and colloid analysis technique invented by Theodor Svedberg 100 years ago. Modern hard- and software and powerful computers make it now possible to develop the methodology beyond what was possible with this technique before. This perspective aims to describe new possibilities, which extend the possibilities of AUC beyond the classical repertoire of the determination of distributions of sedimentation coefficient, particle size, and molar mass as well as stoichiometries and interaction constants of interacting systems. High-resolution simultaneous characterization of particle size and optical property distributions, investigation of nucleation by reaction in the AUC cell, characterization of particle interactions at a very high concentration, and characterization of complex fluids or osmotic pressures over large concentration ranges even crossing phase boundaries are among the discussed topics. They show that even after 100 years of successful application, AUC still has much yet unexplored potential in colloid and polymer science.

Graphical Abstract

This perspective paper spans from the days of invention of analytical ultracentrifugation to now including nonmainstream methodology and instrumentation, which has a huge potential for the future. This includes multiwavelength detectors, high-resolution particle size distributions, chemical reactions in the ultracentrifuge, high-concentration work, osmotic pressure distributions, and characterization of complex fluids.

Introduction

Analytical ultracentrifugation (AUC) is a classical technique of colloid and polymer science and was invented 100 years ago by Theodor Svedberg at the University of Uppsala in Sweden for the determination of nanoparticle sizes [1, 2]. Although the first centrifuge was only spinning up to 20,000 rpm, he reported particle sizes of gold, barium sulfate, clay, and arsenic trisulfide sols in the range of 20–150 nm [1], a size range, which was at these days only available by Zsigmondy’s ultramicroscope [3]. With the shortly later reported ultracentrifuge, even particle sizes became observable that cannot be observed in the ultramicroscope anymore due to insufficient light scattering [2]. Svedberg reported gold particle sizes as well as particle size distributions below 10 nm. He was even able to determine the thickness of a protective gelatin layer around the gold colloids yielding unprecedented information about colloidal systems at this time [2]. In 1926, he was awarded the Nobel prize “for his work on disperse systems,” which includes his pioneering AUC investigations [4]. In 1925, Svedberg published a first paper on the determination of the molecular weight of macromolecules in a sedimentation equilibrium study on hemoglobin proving its macromolecular character [5]. This was a very important contribution given the fact that at that time, it was debated if such molecules are macromolecules as proposed by Hermann Staudinger or colloidal aggregates of smaller molecules. It is interesting to note in this respect that Svedberg did not point out the support of his results for Staudinger’s debated concept of macromolecules [6]. Staudinger himself tried to raise funds for his own AUC but was not successful [6].

The fact that especially biomacromolecules could be well characterized by AUC sedimentation equilibrium [5, 7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] and sedimentation velocity [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25] by means of important physicochemical parameters like molar mass, sedimentation, diffusion, and frictional coefficients as well as shape historically proved to be a game changer because since then the interest in AUC focused on the investigation of biomacromolecules rather than nanoparticles. Consequently, after commercialization of AUC in the 1950s, most AUCs were found in biophysics—rather than in colloid laboratories. In the following decades, the AUC yielded a wealth of important information on biological macromolecules [26,27,28] but was applied by far less for synthetic polymers [29] or nanoparticles [29,30,31]. Historically, besides the proof of the macromolecular character, the density gradient experiment by Meselson and Stahl was important in proving the semiconservative mechanism of DNA replication [32] in agreement with the expectations from the Watson and Crick model.

However, in the 1970s, the interest in AUC started to decrease due to the advent of faster and cheaper techniques for macromolecular characterization like light scattering, gel permeation chromatography, or sodium dodecyl sulfate poly(acrylamide) gel electrophoresis (SDS page). Until 1990, only a few old AUCs with an instrument design from the 1960s were still in operation and the successful application of AUCs for decades appeared to have come to an end. However, at the beginning of the 1990s, Beckman Instruments introduced the Optima XL-A AUC, which was a modern generation AUC controlled by a computer with digital data output [33]. This led to a renaissance of AUC [34] since the digital data output allowed for the application of powerful computer programs for the evaluation of the experiments. The most used and popular programs for the evaluation of AUC experiments are Sedfit [35, 36], UltraScan [37, 38], and Sedanal [39], which can all be used for free. These programs allow fitting hundreds of experimental scans to the Lamm equation or models for interacting systems, revealing unprecedented details in the experiments, which was not possible with the classical instruments without digital data acquisition. Information, which can now be routinely obtained are distributions of molar mass, sedimentation, diffusion, and frictional coefficients as also information about shape as well as interaction constants and stoichiometry for interacting systems. These advanced new possibilities led to the broad application of AUC in several research fields of current importance like adenovirus gene therapy [40, 41] or particle sizing of nanoparticle-based medicinal products [42] just as two examples.

In addition to the data evaluation capabilities, the detection optics of the AUC were extended from the initial UV–Vis absorption optics by interference optics on the commercial AUC platform (Beckman Optima XL-I [43]). Also, a fluorescence optics became available for the Beckman Optima XL-I as an add-on [44] but this optics is not available anymore for the most modern commercial instrument, the Beckman-Coulter Optima. Besides these commercial optics, users also developed powerful optical systems, which were typically installed on preparative ultracentrifuges transforming them into AUCs. These range from Schlieren optics [45] and single wavelength turbidity optics for the determination of particle size distributions [46, 47] via multiwavelength UV–Vis optics [48,49,50,51,52] or the related multiwavelength turbidity detection [53] to multiwavelength fluorescence detection [54]. The multiwavelength UV–Vis detector was made open source within the open AUC project [55], and the design drawings can be downloaded by everybody interested [56]. Its alignment is literature described [57]. This detector is also commercially available from Nanolytics.

In particular, the multiwavelength detectors have unlocked a new quality of information being available from AUC experiments since they open up a new wavelength axis in the AUC data, which have so far been 2D plots of a concentration-dependent quantity like the UV–Vis absorption at a certain wavelength or the fluorescence in dependence of the radial position in the AUC cell. They can certainly be considered the most important AUC hardware development since the introduction of the Optima XL-A AUC and will play an important role in future AUC methodology due to the much higher information content, which can be obtained with these detectors. Due to their importance, the two multiwavelength detectors are briefly introduced here. Figure 1 shows the optical input and the data output from the multiwavelength absorption and fluorescence detectors. Although the optical input of the two detectors is different, their data output is the same providing a sedimentation coefficient distribution with a whole UV–Vis/fluorescence spectrum for each sedimentation coefficient in the distribution. Both detectors are selective to detect certain chromophores in the UV–Vis spectrum resp. fluorescent labels with a given emission wavelength so that they have the potential to also play an important role in biophysics. Here, it is often of interest to observe a given labeled component in a mixture of other components like blood serum. Also, the high sensitivity of fluorescence optics is of interest allowing for the detection down to picomolar concentrations.

Fig. 1

Overview of optical input to the MWL- and MWE-AUC setups and data output from the analysis of an experiment with fluorescently labelled silica particles using HDR-MULTIFIT [53]. Figure reproduced from Ref. [54] with permission of the Royal Society of Chemistry

Fig. 2

a Schematic setup of 3^rd generation UV–Vis multiwavelength optics based on mirror optics free of chromatic aberration. b Photo of 2^nd generation UV–Vis multiwavelength optics still using lens-based optics. c Schematic setup of multiwavelength fluorescence optics and d photo of the multiwavelength fluorescence optics. Images reproduced from a Ref. [51] with permission of the American Chemical Society, b Refs. [58, 59] with permission of Springer Verlag, and c, d Ref. [54] with permission of the Royal Society of Chemistry

Both optics shown in Fig. 2 were designed as add-on for preparative ultracentrifuges and apply CCD array-based spectrometers. They are not yet commercially available despite their obvious high potential besides multiwavelength UV–Vis absorption optics as add-on for preparative ultracentrifuges developed by Nanolytics. Beckman-Coulter has released a new AUC, the Optima, allowing for fast detection of radial scans (a few s) at a given wavelength so that several wavelengths can be scanned within a reasonable time interval before the sample moved already too much, but this is no real multiwavelength optics since the wavelengths are not detected simultaneously as in the here discussed CCD-array spectrometer-based optics. Further technical improvements of the multiwavelength detectors are developed like extension of detection to the near-infrared for gold colloids [52] and detection with ultrafast cameras under constant illumination [60].

The described multiwavelength detectors now allow for the determination of spectral properties for all species, which are separated and detectable in the AUC even for most complex mixtures. Figure 3 shows such an example of a mixture of 24 different CdTe nanoparticles, which were separated with Angström resolution in particle size, revealing the spectral properties of each individual species besides their size and shape [61].

Fig. 3

a UltraScan 2-dimensional spectrum analysis [62] for a CdTe nanoparticle mixture, integrated over all analyzed wavelengths. Darker color indicates a higher relative concentration. A frictional ratio of 1.0 indicates a spherical structure. b Concentration histogram transformation of the sedimentation coefficient to particle core diameter (without ligand/solvation shell) for the data shown in a together with the results of the core distribution evaluated by deconvolution of the mixture absorption data with excellent agreement [61]. Each peak represents the integrated concentrations from all wavelengths. Each species is labeled with a number; the zeroth species denotes a magic cluster. c The 1 s-1 s transition maxima from the absorbance spectra of the first 7 species isolated during the AUC experiment with the corresponding CdTe core diameters (legend on right). d The partial concentration of each species in optical density units plotted over sedimentation coefficient and absorption wavelength. 2DSA analysis resulted in a clear baseline separation of 24 individual species, consistently reproduced for all wavelengths. Reproduced from Ref. [61] with permission of Wiley–VCH

In this perspective, not only the possibilities using the new multiwavelength detectors will be discussed, but also the capabilities of the powerful AUC evaluation software leading to particle size distributions with almost atomic resolution as the one shown in Fig. 3b, as well as the methodology to investigate chemical reactions in the AUC, determination of the equation of state of colloids, interaction analysis in highly concentrated dispersions or the analysis of complex fluids. Some of these methods are not new but can profit a lot from the new hard and software developments in modern AUC. These new possibilities and perspectives after 100 years of AUC will be presented here.

High-resolution characterization of particle/polymer size and optical properties

The example in Fig. 3 has already impressively demonstrated that particle size distributions of small colloids have Angström resolution [61], which was, however, already known for a while [63]. This is possible since AUC detects all particles, and therefore, the particle size distributions are statistically relevant. 10¹⁰–10¹⁸ particles are detected in a typical 350 ml volume of 1 mg/ml concentration for particle sizes of 1 nm and 100 nm with densities of 1 g/ml resp. 20 g/ml. This is in contrast to electron microscopy, which detects only a few particles and also might suffer from drying artifacts but has the advantage to show an image of the particles at high resolution. However, multiwavelength (MWL) AUC now offers also the detection of optical properties on top of the hydrodynamic separation by the AUC. This has been exploited in several studies as will be discussed in the following. It is remarkable that the MWL detector already allows a good insight into the sample without any evaluation. This has been shown for a food pigment β-carotene stabilized by gelatin (Fig. 4, upper image) [64].

Fig. 4

Reproduced from Ref. [64] with permission of Springer

Upper image: left side: assumed structure of the β-carotene microparticle system, right side: color change of β-carotene/gelatin microparticles due to particle size and structure. Lower image: three-dimensional plots of the raw data from a band sedimentation experiment with β-carotene detected with the MWL detector. The axes are wavelength, absorbance, and radial position. i Scan 1 (1.5 min); ii scan 10 (15 min); iii scan 18 (27 min); iv scan 40 (60 min).

The color of the nanoparticles gradually changes from yellow to red depending on the relative amount of H and J aggregates (Fig. 4, upper image). Multiwavelength AUC of this sample in a sedimentation velocity experiment allows capturing the sedimentation process as a video as experimental raw data. Snapshots at different times give an insight into the different spectrally resolved components (Fig. 4, lower image).

Already from the raw data of the experiment, it can be seen that big β-carotene particles (460 nm) with a low amount of gelatin (280 nm) sediment first. These are possibly aggregates. Then, the main fraction follows where β-carotene shows a much higher gelatin content. Finally, free unbound gelatin sediments. This already shows the main components of this experiment and these can be further characterized. However, often, the above raw data information is already sufficient.

MWL detection also proved useful for the characterization of the smallest silver clusters between 1 and 5 atoms [65], carbon nanotube–intercalant-surfactant complexes [66], gold nanorods, different species of single-wall carbon nanotubes and CdTe nanoparticles [67], yield, mass, and structure of silver patches on colloidal silica [68], as well as West Nile Virus RNA–protein interactions where the protein and nucleic acid signals could be separated by spectral decomposition such that sedimentation information from each individual species, including any complexes, could be dearly identified based on their spectral signatures [69]. The UltraScan as well as the SEDANAL and HDR-MULTIFIT software packages are the currently available evaluation programs, which can directly work with multiwavelength datasets [38, 70, 71].

In the following, the special virtue of the spectral information will be illustrated in more detail for the example of a mixture of DNA of different sizes (absorption maximum at 258 nm) and bovine serum albumin (BSA) with protein absorption at 230 and 280 nm [72]. The UltraScan evaluation software has a module for spectral deconvolution, which can deconvolute a sum spectrum of two spectrally different components if the UV–Vis spectra of the two components are known and can be used as the reference for deconvolution by the matrix shown in Fig. 5.

Fig. 5

Deconvolution of the spectral information of a BSA-DNA mixture. The detected MWL-AUC signal can be deconvoluted with the extinction spectrum L of DNA (red) and L of BSA (blue) in the matrix shown in the upper left. That way, the data only belonging to each of the two components can be extracted from the MWL sedimentation profiles, and the sedimentation profile for each component can be calculated. Examples are shown for various mixing ratios of DNA and BSA. Reprinted from Ref. [72] with permission of Elsevier

The spectral deconvolution works very well leading to the possibility to treat each of the components individually if desired. If the interaction between the molecules leads to a complex, this species can also clearly be identified [69].

If we now take the evaluation of the sedimentation coefficient distribution with the wavelength as an additional axis, we already obtain a lot of information about the BSA-DNA mixture, as we can see in Fig. 6 left image. The upper plot shows different species with different spectra and the two yellow peaks show the BSA. In the top view (lower image in Fig. 6), more details can be seen. Remarkably, the protein absorbance spectrum at a sedimentation coefficient of 4.3 S (S = Svedberg = 10⁻¹³ s, two yellow peaks) can be clearly distinguished from the adjacent DNA peak with an absorbance maximum around 258 nm, despite the proximity of the peaks (4.5 S vs. 5.2 S). Minor species can be identified based on their spectra. The straight lines attest to the high resolution and robustness of this approach to fit multiwavelength data. Each wavelength is separately analyzed.

Fig. 6

Reproduced from Ref. [72] with permission of Elsevier

Left image: upper image: 3D view of the sedimentation profile as a function of wavelength for the 50:50 DNA–BSA mixture after 2DSA-Monte Carlo analysis. The protein absorbance spectrum at 4.3 S (two yellow peaks) can be clearly distinguished from the DNA peak with an absorbance maximum around 258 nm. Minor species can be identified based on their spectrum. Lower image: projection view of the 2DSA-Monte Carlo sedimentation profile as a function of wavelength for a 50:50 DNA–BSA mixture. Right image: global genetic algorithm Monte Carlo analysis of decomposition results obtained from six different DNA and BSA mixtures analyzed on the open AUC MWL instrument (top left) and the dual-wavelength results obtained from the Beckman-Coulter XL-A (right panel). The separate decomposition results for DNA (red) and BSA (blue) are combined in the left panel pseudo-3D plot to illustrate the exceptional separation achieved by spectral decomposition which even separates species with nearly identical sedimentation coefficients (the two major species sedimenting near 5 S). This approach demonstrates the superior resolution obtained from MWL analysis compared to the global two-wavelength analysis performed on the Beckman-Coulter XL-A (right panel, green). Lower panel: differential distributions from the same data shown above (red): decomposition for DNA, blue: decomposition for BSA, green: nonseparated XL-A data for DNA–BSA mixtures globally fitted to the genetic algorithm–Monte Carlo analysis. A color representation of this figure is provided in the color plate section to allow the reader to distinguish the DNA and BSA contributions based on color.

If the spectrally deconvoluted data obtained from this six different DNA and BSA mixtures in Fig. 5 are evaluated with a global genetic algorithm Monte Carlo analysis, results with the unsurpassed resolution are obtained (Fig. 6 right image).

One can clearly identify the different DNA species (red) as well as the BSA species (blue) and not only their diffusion-corrected sedimentation coefficient distributions can be determined but also their frictional ratio distribution, which is proportional to the shape/hydration (Fig. 6 right image). The values of the well-known BSA molecule and its oligomers agree very well with literature-known data.

If these data are compared to the analysis of the same samples run on a commercial Beckman XL-I instrument using two wavelengths (green datasets in Fig. 6), one can see two differences: (a) the clear assignment of all individual species in the MWL dataset and (b) the higher resolution of the MWL data. These examples are transferable to any other kind of samples, and it can be imagined how advantageous such spectral separation could be if a nanoparticle has a different spectral signature from its polymeric stabilizer. Then, all different scenarios could be detected since the AUC signals are quantitative, and thus, the concentration of each species can be evaluated. Therefore, free stabilizer, the amount of stabilizer on the nanoparticles, aggregated nanoparticles with too little or no stabilizer, etc. could be easily detected, which is essential information to characterize a colloidal sample.

However, in most cases, colloids are stabilized by (electro)steric stabilization with organic (macro)molecules on their surface. In that case, it is not easy to determine the density of these particles, because the particles have a dispersity in core size (unless they are magic size clusters) as well as in the number of ligand molecules on their surface. Since the density of the typically inorganic cores and the organic ligands is largely different, this then leads to a density distribution superimposed with the particle size distribution as was shown for ferritin, which is composed of different oligomers, which can contain different amounts of ferrihydrite in their cores [73]. If the densities of the core–shell particles are in the range of 0.7–2 g/ml, density variation is a powerful method to determine particle size and density distributions simultaneously by sedimenting the particles in water and heavy water resp. protonated and deuterated solvent and their mixtures. For hard bodies, the density of the particle can be assumed to be constant and the correlation of the sedimentation coefficients in the two solvents leads to the density and size distributions if the densities and viscosities of the two solvents are known. This was especially applied in industry for the determination of particle size and density distributions of latex formulations [74, 75]. Recently, Demeler et al. used a density variation approach together with a multiwavelength analysis for the determination of drug loading of lipid nanoparticle formulations, which are of great medical importance [76]. In this case, the ca. 50 nm lipid nanoparticles entrapped short interfering RNA (siRNA) as a drug. Since the siRNA and lipids have much different densities and also UV–Vis absorption, multiwavelength AUC is particularly well suited to determine the drug loading of different lipid nanoparticle formulations. By measuring in 4 different H₂O/D2O-based mixed solvents, the density distributions of the loaded lipid nanoparticle formulations could be evaluated, which contain information about the loading, but additionally, the optical separation of lipid and siRNA signal opened another way to determine the degree of loading [76]. On top of that, the sedimentation coefficient, diffusion coefficient, and molar mass distributions which belong to the standard information from sedimentation velocity experiments were available. This study demonstrates the information content, which is available by multiwavelength experiments on organic hybrid nanoparticles, many of which are of huge scientific and industrial importance. A special recent example with a system design like the above-described RNA-loaded lipid nanoparticles is the famous mRNA COVID-19 vaccines.

For inorganic core–shell nanoparticles, however, the situation is different due to the high core densities so density variation techniques do not work since the variations in the solvent density only have a very minor effect on the sedimentation of high-density nanoparticles. As a consequence, the densities of inorganic nanoparticles are usually not easy to access and can also not be determined in a density oscillation tube, because typically the density distribution is quite pronounced even for monomodal particle size distributions and only an average density would be measured leading to erroneous calculations of derived parameters like particle size and density from AUC.

Carney et al. suggested a method to overcome this problem by making a hard sphere assumption for the sample, which allows to calculate the particle density with the experimentally accessible sedimentation and diffusion coefficient for the species under consideration [77]. Knowing the density, the sample molar mass and particle size can be calculated. If the densities and molar masses for the core and ligand shell material are known, which is usually the case, it is possible to calculate the number of atoms in the particle core as well as the number of ligands on the particle [77]. This was tested for several defined gold nanoparticles as well as their mixtures, and the results agreed very well with those from mass spectrometry [77]. Since these experiments were carried out in toluene, the hard sphere assumption can be justified because the organic molecules do not physically attach solvent molecules as is the case in water (hydration).

The custom grid method implemented in UltraScan allows calculating the determination of distributions of two parameters out of three if the third one is held constant [78]. These three hydrodynamic parameters are molar mass, particle density, and particle anisotropy resp. frictional ratio f/f₀. This was demonstrated to obtain density distributions of CdSe in octadecene and PbS in octane [78]. This methodology implemented into UltraScan was used by Demeler and colleagues for the determination of the densities of ZnO and CuInS₂ core–shell particles in ethanol resp. toluene [79]. Here, the application of parametrically constrained spectrum analysis (PCSA) allowing to address polydispersity in more than one dimension was used under the assumption of a constant f/f₀ resp. shape to determine the nanoparticle density from which parameters like core and shell thicknesses can be calculated if their bulk material densities are known.

For water as a solvent, however, the situation is different since water molecules attach to the ligands and as the density of this hydration water is ca. 10% higher than that of the surrounding water [80]; the hard sphere approach is not easily adaptable to aqueous systems, where hydration plays an important role [81], and therefore, the ligand shell density cannot be easily calculated from the known density of the ligand molecule.

A solution to this problem was suggested by Gonzalez-Rubio et al. who eliminated the density of the ligand shell in sedimentation velocity experiments by ligand density matching by the solvent [82]. That way, the core size distribution of the nanoparticles is directly accessible under these isobuoyant ligand shell conditions. While the hydrodynamic size of the entire particle is available via the diffusion coefficient, the size and molar mass of the core can be calculated from the sedimentation coefficient with the knowledge of the core material density and atom molar mass, which is the beauty of this approach. Very often, not the entire particle size of nanoparticles is of interest but that of the particle core like for semiconductor or metal nanoparticles with their core size-dependent optical properties. This is directly available if the particle core material density is known, which is usually the case. With the known particle and core size distributions, the shell thickness distribution is also available. In addition, frictional coefficients referenced to a spherical particle core could be obtained, which reflect the influence of particle shape, ligand shell, and hydration on the nanoparticle friction. Therefore, this approach appears to be versatile for aqueous systems since the densities of many typical nanoparticle stabilizer systems for water are not too different from those of water. Thus, density matching of the ligand shell appears to be feasible for many nanoparticles. However, cases may also occur, where the density of a given ligand is not matchable by the solvent, which is a limitation of this method.

Since the particle size resolution of the AUC is in the Angström range, the technique is especially well suited for the observation of very small particles. If a multiwavelength detector is used, the spectral properties are available in addition, which is especially attractive for metal and semiconductor nanoparticles with their size-dependent properties as demonstrated in Fig. 3. Besides the high size resolution, even information about the atomic composition of the samples can be obtained, if a model of the particle structure is available. This was recently demonstrated by Boldt et al. [83]. They investigated CdSe magic size clusters (MSCs) by AUC for which a structural model was proposed by Beecher et al. (see Fig. 7a) [84]. The MSCs were synthesized at elevated temperatures according to Zanella et al. [85], and the MSC growth with time could be followed by simple UV–Vis spectroscopy. This is shown in Fig. 5c by the spectral changes with time by the development of the characteristic MSC peak maxima at 350 nm, 380 nm, 406 nm, and 434 nm. These correspond to the structures shown in Fig. 7a.

Fig. 7

Reproduced from Ref. [83] and Ref. [84] with permission of the American Chemical Society

A Structure and size of three CdSe MSCs with their characteristic UV–Vis absorption. B UV/Vis absorption spectra of samples taken at specific intervals from the MSC batch and C van Holde-Weischet plots of corresponding samples of MSC batch 1 (filled symbols) and batch 2 (open symbols), showing monodisperse samples at the absorption edges of the different clusters and continuous growth (polydisperse particles) after 120 min

Analysis of sedimentation velocity experiments with the van Holde-Weischet method yields a diffusion-corrected sedimentation coefficient distribution without any assumptions about the sample shows extremely monodisperse MSCs Cd₅₆Se₃₅ (380 nm), Cd₈₄Se₅₆ (406 nm), and Cd₁₂₀Se₈₄ (434 nm) evident as almost vertical integral distributions (Fig. 7d). A vertical line would correspond to a monodisperse sample. Only for the largest clusters detected at 434 nm, a broader distribution was evident showing the transition of the strictly monodisperse MSCs to CdSe nanoparticles. The reproducibility of the results for 2 different batches was good with the exception of the species detected at 434 nm.

Further evaluation of the sedimentation coefficient distributions applying the methods of Carney [77] and Gonzalez-Rubio et al. [82] for the determination of the particle core and shell densities, which is essential for hybrid particles, even allowed for the precise determination of particle density and size as well as the molar mass of core and shell for each of the detected species. If a proposed structure of the particles exists as in the case of the CdSe MSCs [84] (Fig. 7a), it is possible to convert the determined molar mass into the atom numbers of Cd and Se in the core as well as the number of ligand molecules on the particle surface as shown in Table 1. For such quantitative analysis, it is essential that the species are very small and therefore show no light scattering and they have defined specific absorption bands.

Table 1 Stoichiometry of batch 3 (Mule et al. [86]) and batch 2 (Zanella et al. [85]) averaged over all data corresponding to the same MSC fractions, as calculated from the methods by Carney and González-Rubio reproduced from Ref. [83] with permission of the American Chemical Society

It can be seen from Table 1 that the ion numbers of Cd²⁺ and Se²⁻ in the different MSCs of the Beecher model [84] can be very well reproduced and the deviation from the model is typically well below 10%. This shows that ion numbers can be determined by AUC even in species with 2 different ions after Carney et al. have already successfully demonstrated the value to correctly determine atom and stabilizer molecule numbers in small stabilized gold nanoparticles [77]. However, while the ligand number determination worked well in the work of Carney et al., the deviations seen by Boldt et al. between the model and experiment in Table 1 were large and could even extend 50% in the case of the oleic acid (OA), which shows that, in this case, the experimentally found ligand coverage is significantly lower as assumed in the model. The reason for this discrepancy is that, in the geometric model calculations, the length of the linear carbon chain has been used, an assumption that will hold better for a densely packed ligand shell, as opposed to one in which the alkyl chains have a larger degree of freedom or are even bent as in case of oleic acid resulting in much fewer ligands in the experiments as compared to the model.

Overall, the above example demonstrates that it is possible to determine the ionic composition and the ligand number even of particles with two different ions directly in solution from the crude reaction mixture without any cleaning step, which could influence the experimental results. This atomic/molecular resolution in the determination of nanoparticle compositions well shows the development the technique has made from the determination of particle size distributions in the days of Svedberg 100 years ago and now. This extremely high resolution and the possibility to determine complete nanoparticle compositions even in multimodal mixtures is certainly of interest for many nanoparticle systems since it is desired to synthesize nanoparticles with targeted sizes, compositions, and thus properties.

The multiwavelength UV–Vis detector can not only be applied for the detection of the absorbance spectra of samples but in the case of particles also to detect their wavelength-dependent turbidity. Since the wavelength-dependent scattering intensity is I $\sim$ λ⁻⁴ (λ = wavelength), the sensitivity of turbidity detection is high at small wavelengths and lower at higher ones. Traditional turbidity detectors work with a single wavelength [46, 87, 88] and detect at a fixed radial position in dependence on time. This is also true for analytical centrifuges operating at speeds <  5500 rpm [89].

If broad particle size distributions needed to be characterized, the particle size distributions were determined at two different concentrations. Using the coupling particle size distribution technique [90], the combination of the size distribution part determined at a high concentration for the small particles with that determined at a low concentration for large particles allowed to partly compensate the large variation in turbidity since I $\sim$ r⁶ (r = particle radius). The problem of the large turbidity variation with particle size could be overcome using multiwavelength turbidity detection [53]. Employing the full range of available wavelengths in the CCD array spectrometer-based multiwavelength detection systems, the dynamic range of the turbidity measurements is maximized due to I $\sim$ λ^-4. Figure 8 shows how these experiments work. To allow for the investigation of even very broad particle size distribution, a rotational speed ramp is applied (gravitational sweep technique [47]) as already well established in single wavelength turbidity detection experiments [90].

Fig. 8

Reproduced from Ref. [53] with permission of the Royal Society of Chemistry

Strategy for the multiwavelength speed ramp experiment and data evaluation using HDR-MULTIFIT including the determination of optical properties as well as high dynamic range particle size analysis

Then, the UV–Vis spectra are determined at a fixed position in dependence on time (steps 1 and 2 in Fig. 8). The size-dependent turbidity of the particles is corrected using Mie’s theory and a wavelength selection algorithm selects, which wavelength range is taken into account for each transmission range and range of sedimentation coefficients. This sophisticated analysis algorithm guarantees to evaluate as many wavelengths as possible for each data range to achieve the best signal-to-noise ratio, while at the same time the linearity of the detector signal to sample concentration is maintained (OD < 1). Finally, the particle size distribution is calculated. This procedure is a significant improvement for the quantitative determination of particle size distributions over the entire colloidal range utilizing the high resolution of AUC and at the same time the highest possible dynamic range as well as the maximum possible amount of data for averaging to maximize the signal quality. The only limitation of this technique is that the particles scatter light.

Despite using the Mie scattering theory to evaluate quantitative particle size distributions even of light-absorbing particles, particle size and wavelength-dependent light scattering in the data can be separated from particle size-independent light absorption. This could be desired if not all quantities for the Mie evaluation are known for the sample of interest. One possibility is the refractive index matching of the nanoparticles with solvent, which is, however, limited to particles with a low enough refractive index to be matched by the solvent. By refractive index matching, all light scattering effects can be removed (see also Fig. 15 and corresponding discussion). The other potential possibility would be to utilize the 1/λ⁴ dependence of light scattering and construct a baseline to correct the data for light scattering effects. This requires MWL data and with modern computing power, such separations appear feasible even for large datasets.

While the above methodology applies a hard sphere approach and calculates the size of the hydrodynamically equivalent sphere d_h, many nanoparticles are anisotropic so the knowledge of d_h is only of limited use. Walter et al. showed for graphene oxide nanosheets that their lateral dimensions can be determined by AUC as a distribution from the sedimentation coefficient distribution [91].

Fig. 9

a Relative deviation of AFM sheet analysis and AUC model for varying hydrodynamic density. Error bars give the standard deviations for 90 mass% of the distribution. The best fitted parameter is marked by the intersection with the dotted line. b Comparison of the graphene oxide nanosheet diameter distributions based on the AFM statistics and the AUC modeling with best fit for the hydrodynamic density

For this, the following steps are necessary:

• 1. Determination of the lateral size distribution of the sheets by AFM

• 2. Determination of the sedimentation coefficient distribution by AUC

• 3. Comparison of both distributions for varying hydrodynamic density to determine the density for the best fit, assuming a constant height of a sheet as determined by AFM

The results of his evaluation are shown in Fig. 9. Once the optimum hydrodynamic density is determined, which gives the best fit with the AFM data, a sedimentation coefficient distribution of graphene oxide nanosheets can be converted to the sheet diameter distribution. This assumes spherical sheets, but overall, the agreement with the AFM data was found to be good justifying this assumption. This elegant approach then allows avoiding tedious AFM investigations including counting to determine the distribution of the sheet dimensions [91]. Since in AUC all sheets are measured, the statistical significance is also much higher than it can be in the AFM investigation with a limited number of particles. Such methodology should be adaptable to other anisotropic particles like carbon nanotubes [92], which were already very successfully characterized by AUC including their surfactants and associated ions [93,94,95,96], noble metal nanorods, and layered double hydroxide nanosheets. This opens up the fast characterization of dimension distributions of anisotropic particles with high statistical significance and should be especially advantageous if repeated analyses of samples of the same identity are necessary.

In addition, it is possible to characterize aggregates and agglomerates, which can have complex shapes and are often loosely packed, by AUC. Here, a hard sphere approach would certainly lead to too small determined particle sizes and since aggregates are a common problem in colloid science, their size determination is important. Wohlleben reported a solution to this problem with a derivation, which relates the hydrodynamic radius R_h,N of a fractal aggregate to the sedimentation coefficient of the fractal aggregate s_N provided that the radius r_p and sedimentation coefficient s_P of the primary particles as well as the fractal dimension D_f > 1 and < 3 of the aggregate are known (see Eq. 1) [97].

$${R}_{h,N}={r}_{P} {s}_{P}^{\frac{1}{1-{D}_{f}}} {s}_{N}^{\frac{1}{{D}_{f}-1}}$$

(1)

Combining the optical and hydrodynamic properties accessible via a multiwavelength sedimentation velocity experiment in a single analysis proved to be highly advantageous for colloids with anisotropic shapes as demonstrated for gold nanorods [98]. By the introduction of an optical back coupling (OBC) method for multiwavelength AUC, Peukert et al. were able to couple the embedded geometrical information about diameter and length in the UV–Vis spectra of gold nanorods with the corresponding sedimentation coefficient distribution. This allows to access multidimensional information if the optical properties of the plasmonic nanoparticles can be correctly modeled. In their work, three different approaches were compared, the classical Gans model [99, 100], an analytical longitudinal polarization model (LP), which considers only the polarization along the long axis of the nanorods [101] and an orientationally averaged FEM model of nanoparticles in water. They yielded the length and width distribution of the gold nanorods according to the three different models, and this information could be obtained with TEM width and length distribution results. This information is shown for two example nanoparticles in Fig. 10. The length and width distributions evaluated according to the different models agree well with each other and the reference evaluation of the TEM micrographs. This shows that multiwavelength AUC is a powerful and accurate tool for the determination of length and width distributions of gold nanorods.

Fig. 10

Reproduced from Ref. [98] with permission of Springer Nature

Size distributions for two citrate-stabilized gold nanorod samples. Comparison of a 2D length and diameter distribution (Gans), b the corresponding two one-dimensional size distributions for citrate sample 1 for the different optical models, c the two-dimensional size distribution (Gans), and d the corresponding two one-dimensional size distributions for citrate sample 2 in comparison with results from TEM analysis. The insets show the size distribution of nanorods obtained by TEM. One hundred particles were TEM-counted for each sample.

If the different optical signatures of nanospheres and nanorods can be used, the described method can also measure the relative concentrations of different species and estimate the thickness of different ligand shells on the particles from the diffusion coefficient because the dimensions of the nanoparticle core are known. This powerful methodology can be also transferred to the investigation of other plasmonic metal nanoparticles, provided that they have optical signatures in the UV–Vis range, which can be accessed by multiwavelength AUC and the required information of the size, shape, or composition can be obtained by analyzing the extracted spectra.

The OBC method can also be used, to determine the composition distributions of nanoparticle alloys of plasmonic metals [102]. Silver and gold as well as their alloys have significantly different UV–Vis spectra. These can be used as the optical signature for the composition of metal alloy nanoparticles, which can be coupled with the hydrodynamic information available from the sedimentation coefficient distribution. As in the case of the above-discussed determination of gold nanorod dimension distributions, a correct optical model is essential to relate the optical information in the UV–Vis spectrum to the composition information in the investigated nanoparticle alloy. An empirical fitting parameter C was used to best approximate simulated spectra to the experimental ones for gold and silver and the alloys; a linear relationship of C between that for gold and silver was assumed. These optical data could then be coupled with the sedimentation coefficient distributions to yield the particle size distribution vs. the molar fraction of gold in the alloy nanoparticles (Fig. 11). The agreement between simulated and experimental data was found to be good. Also, the particle size distributions of the spherical nanoparticles agreed very well with those from electron microscopy (Fig. 11). In addition, the average gold content in the alloys agreed well with that determined by ICP-OES [102]. Therefore, multiwavelength AUC with OBC evaluation is capable to determine 2D particle size–composition distributions for plasmonic metal nanoparticle alloys with excellent statistics and without any purification steps, which is not yet possible by any other method.

Fig. 11

Reproduced from Ref. [102] with permission of the Royal Society of Chemistry

Size and composition distributions for experimental data obtained by multiwavelength AUC and OBC analysis. Output distribution of OBC method for a 30 nm alloy NPs with 25% gold molar fraction, b 35 nm alloy NPs with 50% gold molar fraction, and c 40 nm and 42 nm Au and 50% gold molar fraction alloy NPs. Marginalized number weighted cumulative distribution as a function of diameter (green) and a gold molar fraction (blue) for d 30 nm alloy NPs with 25% gold molar fraction, e 35 nm alloy NPs with 50% gold molar fraction, and f 40 nm Au and 42 nm 50% gold molar fraction alloy NPs.

The above examples have shown impressively what is possible if the optical information of the multiwavelength detector can be coupled with the hydrodynamic information of the AUC. Although the two examples above are restricted to plasmonic metal nanoparticles, there is no reason why no other approaches will be developed to couple other optical information in the UV–Vis spectra with the sedimentation coefficient distribution of the AUC as long as an optical model for the description of the UV–Vis spectra is available.

Since the quality, resolution, and statistical significance of particle size distributions from AUC are very high, they can be used to characterize and define particle standards [103]. It is remarkable in this context that AUC became included as a characterization technique in the OECD Test No. 125 about nanomaterial particle size and size distribution of nanomaterials [104]. This makes AUC a globally acceptable technique for the characterization of particles in a regulatory context [105].

Chemical reactions in the AUC

The excellent particle size resolution of AUC in the Angström range even for multicomponent mixtures and the possibility to even determine atom and ligand numbers in core–shell particles makes AUC an excellent tool for the investigation of particle nucleation reactions. Nucleation is a phenomenon of significant scientific and technological importance and was already first addressed by Gibbs in 1876 [106]. Until today, it is not yet fully understood and debated [107]. One of the reasons is that the time and spatial scales for nucleation and growth are extremely broad, so it is still an analytical as well as a theoretical challenge to investigate nucleation phenomena [108]. Since nucleation can occur on very fast time scales, it is no phenomenon, which is investigated by slow AUC techniques but rather fast synchrotron-based scattering techniques like coupled small and wide-angle X-ray scattering. Nevertheless, classical techniques like active enzyme centrifugation [109] allow to perform chemical reactions inside the AUC cell with the subsequent observation of the reaction products. This was first exploited in the so-called synthetic boundary crystallization approach with a focus on the determination of stabilizer efficiencies to stabilize certain particle sizes [110, 111]. In these experiments, band sedimentation cells are used (Fig. 12a), which have an additional compartment for the addition of a second reactant, which then flows into the sample sector of the AUC cell through a thin capillary upon hydrostatic pressure generated by the acceleration of the ultracentrifuge. This generates a thin band of the reactant on the solution in the sector with a very sharp interface. To avoid mixing upon layering of the band, the density of the solution in the sample sector must be higher than that of the overlaid reactant.

Fig. 12

a Band sedimentation AUC centerpiece showing the additional compartment for a second solution, which is connected to the sample sector by thin capillaries. b Schematic representation of the sedimentation and diffusion of a nonreacting band (red) in the solution (yellow). c Experimentally observed band sedimentation profiles with UV–Vis absorption optics and d schematic representation of the overlay of a reactant (yellow zone) onto a second reactant solution (black). For further explanation see the text. a, b, and c are reproduced from Ref. [112] with permission of the American Chemical Society and d is reproduced from Ref. [111] with permission of Elsevier

Figure 12b schematically shows the overlay of a solution onto a solvent, which is the normal band sedimentation experiment. The sample band (red) starts to sediment in the solvent (yellow) and the band broadens by diffusion. The observed experimental concentration profiles are shown in Fig. 12c for the example of absorption optics. Band sedimentation has significant advantages over conventional sedimentation velocity experiments. It needs only a minimal sample amount (a few μg rather than a few hundred). Also, the bands which are formed in the case of multimodal distributions correspond to pure species rather than the sum of all species sedimenting slower than the faster sedimenting component visible as a step in the concentration profile. Despite these obvious advantages, band sedimentation is only very rarely applied in AUC. The reason is that the conventional software for evaluation does not properly account for the boundary conditions of the experiment. These are layering an aqueous solution onto a heavy water-based one or more generally a protonated solvent over a deuterated one. This is necessary to meet the requirement that the overlaid solution needs to have a smaller density than the solution in the sample sector to avoid mixing during the overlay process. However, it is known that water and heavy water form a dynamic density gradient, which can even be exploited for the fast separation of particles according to their density [113]. In the case of band sedimentation, the interdiffusion of water and heavy water causes strong gradients in solvent density and viscosity, which are not yet taken into account in the evaluation algorithms but have a significant influence on band sedimentation and diffusion [112, 114].

In the case of a chemical reaction, the situation is different from conventional band sedimentation as schematically shown in Fig. 12c. The chemical reaction initially starts at the interface between the two reactants, but due to significant reactant interdiffusion as a result of the high concentration gradients, the overlaid reactant quickly mixes with the other reactant forming the shown yellow reaction zone (Fig. 12d). This leads to the formation of the first reaction product (1 generation). This can sediment and diffuse out of the reaction zone, where further reaction/growth is quenched or move back into the reaction zone to continue the reaction/growth forming the next larger species (generation 2). This again has the same possibilities as the first formed species, and so, further reaction/growth species form because diffusion is the dominating effect over sedimentation due to the small size of the species. While the term generations implies defined species, which we indeed only have seen so far in our limited investigations on Au, Ag, and CdS nucleation, a continuous distribution of sizes is also possible.

Since the reaction zone is only a few μm thick and also the amount of overlaid reactant is low, it is used up within the first seconds of the experiment. This means that no further reaction can occur and the sample consists of a thin band on top of the solvent containing various particle sizes. These are then separated as is known from band sedimentation experiments (see Fig. 12b, c) and the sedimentation coefficient resp. particle size distributions can be evaluated.

Reduction of Ag⁺ in the presence of polyacrylic acid (PAA) according to a recipe of Henglein [115] yielded long-lived silver clusters, which are ideal to test the chemical reaction directly inside the AUC as described above since the UV–Vis spectra of the different silver clusters were reported in the literature. Figure 13a, b shows the experimental raw data at the beginning and a later stage of the experiment. In the beginning, one dominating peak is visible but with time and sample separation; more peaks show up at different radial positions in the AUC cell. This example again shows that already the raw data from a multiwavelength experiment contain valuable information. Evaluation of the dataset with the UltraScan multiwavelength module allowed us to determine the sedimentation coefficient distribution as well as the corresponding spectral axis clearly showing different cluster species (Fig. 13c). Since their UV–Vis spectra are literature known, the clusters could be assigned on basis of their UV–Vis spectra (Fig. 13c, d). This validates the experiment to perform chemical reactions directly in the ultracentrifuge since the literature reported silver clusters were found.

Fig. 13

Formation and sedimentation of silver clusters. a, b Snapshots from a video showing the formation of the band and its sedimentation from two different angles and two different times. a is at the early stage of the experiment, while b is at a later stage. c Sedimentation coefficient distribution with additional wavelength axis showing the UV–Vis spectra of each separated cluster species. d The UV–Vis spectra of each separated species

However, it is difficult to assign the silver clusters alone from the sedimentation coefficient distributions, because (a) the dynamic density gradient forming upon the overlay process which starts the reaction is not yet taken into account in the evaluation software and (b) the density of the silver clusters is unknown, which prevents their size and molar mass calculation from the sedimentation coefficient. If the same silver cluster sample is investigated by conventional sedimentation velocity experiments [65], it is not possible to separate individual spectra for the different separated species and thus they cannot directly be assigned. The cluster sizes could only be evaluated using different models, which left an uncertainty in the size of the detected species. This clearly shows the advantage of the band-forming experiment.

When sodium borohydride was used as the reductant of Ag⁺ and was overlaid on a silver salt solution with CTAB as a surfactant, also different very small silver species were formed [116]. Eight different silver species were detected in the sedimentation coefficient distribution, and with the assumption of a model, the particle size distribution could be calculated with Angström resolution yielding species in the range of 400–1200 pm resp. 1–41 silver atoms, again showing the very high resolution of AUC. When the spectral information was accessed, spectral changes in the different species could be detected for the different species but the most obvious change was that a peak at 400 nm vanished with increasing particle size [116].

The reaction in the AUC method was also reported for the formation of gold colloids stabilized with thioglycerol by their reduction with borohydride [117]. Again, sedimentation coefficient distributions could be determined together with the corresponding wavelength data. However, unlike in the case of silver clusters formed in presence of PAA, the UV–Vis spectra showed multiple peaks and appeared erroneous. 20 different species could be revealed in the range from 4 to 911 gold atoms and core sizes from 0.5 to 3.8 nm including 4 of the known magic size clusters using a core–shell model based on the known densities of core and shell material and the known shell thickness [117].

Another chemical reaction which can advantageously be studied in the AUC is the formation of membranes composed of polyelectrolyte complexes of countercharged polyelectrolytes [118,119,120]. This is shown in Fig. 14. The principle of the experiment is simple. In the example in Fig. 14, negatively charged alginate which is not absorbing light is overlaid with light-absorbing oligochitosan, and the different stages of the experiment are schematically shown in Fig. 14A. In the beginning of the experiment (a) the detected absorption is negative because the light absorbing oligochitosan is in the solvent sector where its signal is subtracted from the nonabsorbing sample. Upon overlay of the chitosan solution (b) a membrane shown in black starts to form immediately. The membrane grows in thickness with time even after the overlay has finished (c) until no further polyelectrolyte complex formation takes place anymore.

Fig. 14

Reproduced from Ref. [118] with permission from Elsevier

A Principle of the membrane formation experiments in a synthetic boundary cell. Component positions and absorption scans (a) before layering, (b) during layering, and (c) after layering is finished, though chitosan is not yet completely complexed. □, air; ▩, chitosan I; ▨ chitosan II; ■, membrane; ▨, alginate, …, capillary. B Membrane location (red arrow) in the right centerpiece sector of a synthetic boundary cell after completing the experiment and C Membrane equilibration after the complete polycation consumption at 5000 rpm, 370 nm, and 20 °C.

The membrane can be observed after the experiments (Fig. 14B) and its formation and growth in thickness with time can be easily observed using the UV–Vis absorption optics of the AUC (Fig. 14C). Such experiments offer valuable information about membrane formation processes.

All the above-reported experiments clearly show that chemical reactions in the AUC can yield the earliest species in a chemical reaction because the reaction is quenched already after a short time. Multiple species could be revealed for the investigated noble metals and showed almost atomic resolution for the detected species, and in some cases, it was even possible to derive spectral information for each particle. This is so far unsurpassed possibility for the high-resolution investigation of nucleation phenomena in the AUC with the advantages of high statistical relevance, high resolution, and the possibility to directly work in the solution phase. Other chemical reactions like the formation of membranes can also be investigated. However, a current weakness of the approach is that only the selective UV–Vis absorption optics is used. Although the nonselective Rayleigh interference optics is potentially also useable, its application is currently restricted by the fact that it detects the local refractive index changes as the sum of all components, which are involved in the chemical reaction. This includes spectator ions as counterions of the educts as well as stabilizer molecules and even the dynamic H₂O/D₂O gradient making the signal interpretation complex.

Another issue is the sample/solvent compatibility with the cell material. The typical band sedimentation cells are made of charcoal-filled Epon or similar material, which is not compatible with many organic solvents so the studies reported above were limited to aqueous solvents. Metal centerpieces with suitable resistance against organic solvents are not self-sealing and therefore not useable. However, meanwhile, it is possible to 3D print centerpieces from various materials [121, 122]. A part of the currently tested materials is already resistant against several organic solvents, but if a chemically inert polymer like poly(etheretherketon) can be printed into a self-sealing AUC centerpiece, essentially all solvents would become available for performing chemical reactions in the AUC using band forming centerpieces. The only limitations would then be solvents, which chemically attack the window materials like for example the dissolution of quartz windows in very alkaline solutions. But here, the choice between sapphire and quartz windows can minimize these problems, and silane-based coating of the windows for example with a hydrophobic or fluorine-based surface layer could greatly minimize the chemical attack of the window materials.

Interactions in highly concentrated dispersions

Interactions in highly concentrated dispersions are of great scientific and technical importance since technical dispersions are usually highly concentrated, and the high concentration range is also passed when a dispersion is dried to form ordered structures like colloidal crystals or mesocrystals. Nevertheless, if one considers the latter process more closely, the question arises of how colloidally stable nanoparticles, which repel each other in diluted dispersions become attractive when they are dried. Therefore, highly concentrated dispersions are important to investigate in terms of the particle interactions in the high-concentration regime. Unfortunately, this is experimentally very challenging, since all optical methods cannot be used due to the high turbidity, and electron microscopy is also not suited due to the requirement to dry the sample and thus change the state, which shall be investigated.

This problem can be solved if the refractive index of the particles can be matched to eliminate light scattering and turbidity. However, in such a case, the Rayleigh interference optics cannot be used anymore because of the lack of a refractive index difference between the sample and solvent. Therefore, the sample needs to have a chromophore to be detected with the UV–Vis absorption optics. Xu et al. used fluorescently labeled silica nanoparticles with their refractive index matched by a glycerol water mixture and were able to detect concentrations up to. ca. 65 vol.-%, very close to the maximum 74 vol.-% in the densest sphere packing in a single sedimentation equilibrium experiment (Fig. 15) [123]. Therefore, this single AUC experiment is able to characterize the interactions from 0 to 65 vol.-%.

Fig. 15

A typical experimental sedimentation–diffusion equilibrium concentration profile (dotted line), corresponding fitting profiles (solid line), and the residual difference (top figure) for a silica nanoparticle dispersion at an initial concentration of 15 vol% at 1100 rpm. Three regions, marked as I, II, and III, are divided by dashed lines. Radial position refers to the radial distance from the center of rotation. Equilibrium is reached, as indicated by an unchanged concentration gradient for at least 10 h. Figure reproduced from Ref. [123] with permission of the Royal Society of Chemistry

As can be seen in Fig. 15, three concentration ranges with clearly different behavior can be identified in the sedimentation equilibrium concentration profile detected by MWL UV–Vis absorption optics and converted to vol.-% via a calibration curve: I (0–12 vol-%) with an exponential profile typical for solutions and diluted dispersions, which can be described by the classical sedimentation equilibrium Eq. (2). In the intermediate concentration region II (12–22 vol.-%), the effect of the surface charge z comes into play and the surface charge can be calculated using Eq. 3, which describes this concentration region. In the high concentration region III (> 22 vol.-%), the particle interactions can be accessed by the second osmotic virial coefficient B₂ and the molar mass of the particles is also available from Eq. 4 [123].

$$c\left(r\right)=c\left({r}_{1}\right) \mathrm{exp}\left(\frac{{r}^{2}-{r}_{1}^{2}}{2{L}_{\omega }^{2}}\right)$$

(2)

$$c\left(r\right)=c\left({r}_{2}\right)+\frac{V\left({r}^{2}-{r}_{2}^{2}\right){c}_{s}}{{z}^{2}{L}_{\omega }^{2}}$$

(3)

$$c\left(r\right)=c\left({r}_{3}\right) \mathrm{exp}\left(\frac{{\omega }^{2}\left(1-\overline{v}{\rho }_{s}\right)}{2RT}{M}_{\mathrm{app}}\left({r}^{2}-{r}_{3}^{2}\right)-{B}_{2}M\left(c\left(r\right)-c\left({r}_{3}\right)\right)\right)+E$$

(4)

In these equations, r is the position indicating the radial distance from the center of rotation; r₁, r_2, and r₃ radial reference points; L_ω = kT/V(ρ_p − ρ_s)ω² the centrifugal length with kT the thermal energy, ρ_p the colloidal particle density, ρ_s the solvent density, ω = angular velocity, and V the volume of one particle; z the particle surface charge number; c_s the half total ion concentration; RT the product of the molar gas constant R and the temperature T; M_app = M/(z + 1) the apparent molar mass with the real molecular mass M; B₂ the second virial coefficient and E the baseline offset.

The particle size and charge z were calculated in good agreement with the values obtained by SEM resp. electrophoretic mobility measurements. B₂ was calculated to be negative in the high-concentration region pointing to an attractive particle interaction at high concentrations. These attractive interactions were manifested in the formation of a gel phase as shown in Fig. 16.

Fig. 16

a A typical absorbance profile showing the presence of a phase boundary at ca. 6.94 cm using an arbitrary wavelength of 700 nm after the sedimentation–diffusion equilibrium was reached for silica nanoparticles of an initial concentration of 15 vol% at 1100 rpm. Such a phase boundary is also observed using other wavelengths; b pH gradient along the radial position, characterized by a pH indicator at the sedimentation–diffusion equilibrium for silica nanoparticles of an initial concentration of 15 vol% at 5000 rpm. A phase boundary is located at about 7.06 cm and therefore an artificial bump appears; c pictures of the gel phase (yellowish color due to fluorescence) obtained after sedimentation–diffusion equilibrium is reached and the silica nanoparticles packing inside the freeze-dried gel. Figure reproduced from Ref. [123] with permission of the Royal Society of Chemistry

One can see the phase boundary to the gel phase in Fig. 16a and a very strong pH gradient detected via an indicator dye in Fig. 16b ranging from pH 7 to pH > 13 due to a Donnan equilibrium. The gel phase is formed in the region of high pH due to crosslinking of the deprotonated silanol groups on the silica surface via protons [123]. Since the swelling degree of a gel depends on the rotational speed [124], it should be possible to unswell the gel by an increase of the rotational speed and vice versa if no new crosslinks are formed.

Fig. 17

a Experimental sedimentation–diffusion equilibrium concentration profile for silica nanoparticles of an initial concentration of 15 vol% at 40,000 rpm (black) and at 1100 rpm (red) after having been subjected to 40,000 rpm. b Experimental sedimentation–diffusion equilibrium profile for silica nanoparticles of an initial concentration of 15 vol% at 5000 rpm (black) and at 1100 rpm (red) after having been subjected to 5000 rpm. c Gel directly after the experiment, d overnight, e after one month, and f when taken out of the AUC cell. a and b reproduced from Ref. [123] with permission of the Royal Society of Chemistry

When the gel was subjected to 40 000 rpm, it was deswelling considerably visible by its boundary at ca. 7.08 cm (Fig. 17a black curve). Decreasing the speed to 1100 rpm only led to partial reswelling of the gel, while the major part remained unswollen (red curve Fig. 17a) and the further movement of this gel boundary towards the cell bottom even indicated further crosslinking. However, repeating this experiment by changing the speed from 5000 to 1100 rpm and back showed complete reversibility of the gel. The gel remained intact over long times as shown in Fig. 17c–e and can be isolated from the AUC cell as a separate gel phase (Fig. 17f).

Subjecting the gel to water led to its dissolution and adding NaCl led to shrinkage of the gel phase due to additional crosslinking [123]. Both results are consistent with the crosslinking of the silica particles by countercations. What the above-discussed experiment clearly shows is that AUC sedimentation equilibrium with refractive index matched nanoparticles can be used to investigate almost the entire concentration range from ideal dilution to almost the concentration of a solid body. No other technique can generate such a big concentration range in a single experiment introducing AUC as the method of choice to experimentally study particles in the high concentration regime but at the same time also at lower concentrations yielding such important information like particle size, charge, molar mass, and the virial coefficient for their interaction. Nevertheless, the refractive index matching causes the attractive van der Waals forces to vanish. This may be desired as in the above-described case, which identified crosslinking by counterions as attractive interaction. However, other cases may exist, where van der Waals forces are of interest in the high-concentration analysis, and in such cases, refractive index matching cannot be applied.

Osmotic pressure and phase boundary determination of multiphase systems

AUC can be applied to derive full equations of state of colloids in a simple sedimentation equilibrium experiment [125]. Since sedimentation equilibrium is a thermodynamic equilibrium between sedimentation and diffusion, rigorous thermodynamics can be applied to determine the radially dependent osmotic pressure even across phase boundaries in multiphase systems since AUC is a first principle method. This is a very advantageous situation since the whole concentration dependence of the osmotic pressure is determined over a larger concentration range (up to 2000 data points possible per measurement) rather than single data points determined by time-consuming osmotic pressure measurements. Furthermore, different pressure regimes are accessible by simple variations of the rotational speed.

The osmotic pressure difference between a point in a sample of distance r_i from the center of rotation and the meniscus of the sample r_m is given by Eq. 5 [126].

$$\mathrm{\Delta \Pi }=\Pi \left({r}_{i}\right)-\Pi \left({r}_{m}\right)={\omega }^{2}{\left(\frac{\partial \rho }{\partial c}\right)}_{\mu }{\int }_{{r}_{m}}^{{r}_{i}}c\left(r\right) r dr$$

(5)

where c is the concentration in w/w of the solute species, ω the angular velocity, and ${\left(\frac{\partial \rho }{\partial c}\right)}_{\mu }$ the density increment of the sample, at the constant chemical potential of water and salt, concerning concentration. ${\left(\frac{\partial \rho }{\partial c}\right)}_{\mu }$ can be obtained from density measurements of a concentration series in an oscillation tube.

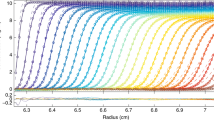
Page et al. reported on using this methodology to determine the equation of the state of laponite clay with initial concentrations of 0.4 and 1.5 wt.-% [125]. Application of Eq. 5 to the sedimentation equilibrium profile yielded a continuous dependence of the osmotic pressure, over orders of magnitude between ~ 10¹ Pa and 10⁴ Pa, and a wide concentration range, in agreement with standard theoretical considerations. Calculating the water layer thickness l_w on laponite from the measured volume fractions yielded the data shown in Fig. 18.

Fig. 18

Osmotic pressure (log scale) plotted against a water layer thickness, l_w, and b log(l_w) for disc-like laponite RD particles of thickness 1 nm and diameter 25 nm. Open squares represent AUC experimental data and open spheres represent literature experimental data [127]. The solid line in the high-concentration regime represents the theoretical osmotic pressure calculated using Eq. 4, and the gray line in the low-concentration regime represents the theoretical osmotic pressure. Vertical lines delineate the literature-determined phase boundaries at l_w = 67 and 230 nm, and in a the Debye length for 10³ M salt, of ~ 10 nm. Inset: the experimental data in the low-concentration regime, and the calculated osmotic pressure, for average particle diameters of 20 nm (black solid line), 25 nm (gray solid line), and 30 nm (black dashed line), shown on a linear scale. c The experimental setup as well as the approach to equilibrium leading to 3 different laponite phases: dilute, 2-phase, and gel. Figure reproduced from Ref. [125] with permission of Wiley–VCH

It can be seen that the osmotic pressure can be determined continuously from the dilute via the 2-phase to the gel regime (Fig. 18a–c). In the dilute regime, the centrifuge data agree rather well with the ideal gas case. At interparticle distances a little longer than at the two-phase boundary, deviation from the ideal gas case is observed continuing through the two-phase region into the region of long-range interactions. From distances at or below the gel phase limit, the data follows the theoretical curve for this regime [128]. Thus, the osmotic pressure was measured continuously across the 3 regimes agreeing well with theoretical predictions demonstrating that the AUC can substitute hundreds of tedious and time-consuming osmotic pressure measurements by a single sedimentation equilibrium experiment.

The case of osmotic pressure determination for dissolved resp. dispersed phases is very similar to the determination of the swelling pressure–concentration curves in gels [129]. From these curves, molecular parameters like the chain length between two crosslinks and the shear modulus of the gel can be determined via a modified Flory–Huggins equation [130]. The methodology of the experiments for the determination of swelling pressure-concentration curves as well as further AUC experiments with gels and microgels has been comprehensively described [124].

In a recent mini-review, such AUC studies on the determination of the osmotic pressure equation of state for ferrofluids, colloidal systems (clays, polystyrene, photonic material self-assembly), determination of solid–liquid equilibria of mass transfer limited (high viscosity) chemical systems such as deep eutectic solvents, ionic liquids, and process intensification devices such as centrifugal contactor separators were treated [131].

Investigation of complex fluids by AUC

A further interesting field of AUC with significant future potential, which is also not yet well known, is the application of AUC to investigate complex liquids like surfactant-free microemulsions and/or systems showing the Ouzo effect [132]. These systems are ternary mixtures consisting of water, a hydrophobic substance like octanol, and a hydrotrope like ethanol, which can act as a surfactant leading to various superstructures. Here, the ability of the AUC is utilized to generate concentration gradients, which can be well adjusted via the rotational speed and thus cover a larger range in the phase diagram. That way, AUC can generate gradients in the

• Concentration

• Composition

• Osmotic pressure

• Chemical potential

• Molar mass/size

All of which are experimentally accessible making AUC a very powerful method for the characterization of these complex fluids.

Already for a simple binary system like ethanol/dodecane, giant critical fluctuations can be observed above the miscibility gap using low centrifugal fields (2000 g) [133]. Investigating the temperature and centrifugal field effects for this system, strong gradients of ethanol concentration were found several degrees above the phase transition. An increase in the rotation speed or decrease in temperature led to steeper gradients in composition. Evaluation of these gradients by the standard sedimentation equilibrium methodology yields an apparent molar mass of ethanol three orders of magnitude higher than the real value (55–540 molecules). These composition gradients do not influence the distribution gradient of solutes such as dyes like Nile red. In addition, often within the concentration gradients, a turbid zone was observed, similar to critical coalescence. This layer is a few millimeters thick and separates two fluids with low compositional gradients. These effects were qualitatively explained using the Flory–Huggins solution model coupled with classical density functional theory (DFT). The theoretical work showed that hetero-phase fluctuations can be triggered by gravity even far from the critical point [133].

This work has important implications and shows that near the critical point, even in a low centrifugal field, a concentration gradient for a small molecule like ethanol can be reached, which would not be possible to reach even applying the best available ultracentrifuges. This shows that low-speed or so-called soft centrifugation is possible near in temperature but even far in composition from the upper critical solution temperature [133]. Such effects would be very beneficial to exploit for large-scale separations in continuous centrifuges, which only have limited centrifugal fields but due to the formation of the detected large structures can easily separate desired molecules.

In the system ethyl acetate–ethanol–water, two types of centrifuge-induced phase separation were identified by AUC studies and predictions based on a phenomenological theory of mixing, which generally agreed well with the experimental results [134]. The phase diagram of this system is well known (Fig. 19) [135].

Fig. 19

Reproduced from Ref. [134] under CC BY 4.0. For more background on the mentioned compositions, the reader is referred to Ref. [134] and references cited therein

Ternary phase diagram of ethyl acetate/ethanol/water by mole (left) and weight (right) fraction, showing the miscibility gap and the tie lines determined by Robles et al. [135] (black cubes). Experimental points obtained in this work without Nile red (blue cubes) and with Nile red (red spheres) at 25 °C and atmospheric pressure are shown. The red arrows point at compositions of special interest: pre-Ouzo 20 (PO20), critical point (CP), concentrated living network (CLN), and living network (LN).

Four mixture compositions all being close to the phase boundary of the system were of special interest to this study as indicated by red arrows in Fig. 19 right: PO20, CP, CLN, and LN. It was found that centrifugation could induce two different types of phase separation: centrifuge-induced emulsification (CIE) and centrifuge-induced criticality (CIC) [135].

Fig. 20

a, b Raw data of sedimentation equilibria as a number of fringes ∆J(r) versus radius and different experimental speeds for four studied ternary compositions. No Nile red as the dye is present, and the temperature is 25 °C. c Sample of PO20 + Nile red dye showing macroscopic droplets after centrifugation at 17,000 g (15,000 rpm), which can be easily separated by low centrifugal fields as shown in d by preparative ultracentrifugation at 10,000 rpm and 25 °C. a and b are reproduced from Ref. [134] under CC BY 4.0

Centrifuge-induced emulsification is a true phase transition, and the concentration gradients already get very high for PO20 at low centrifugal speeds as 10,000 rpm (Fig. 20a). At slightly higher speeds, already a turbid zone appears as indicated by the red arrow. Theoretical simulations predicted a terminal velocity increase of up to 10⁶ for the solute in this system [134]. This has a huge potential for fast separations using low centrifugal fields as a present in continuous high-capacity centrifuges. Indeed, the AUC of PO20 revealed aggregates with an average of 330 molecules and high aggregate sizes of up to 5000 molecules, which explains why even low centrifugal fields can lead to phase separation (Fig. 20c). These macroscopic droplets can then be easily separated as two separate phases at low centrifugal fields as shown in Fig. 20d. This demonstrates that it is possible to extract a solute in a centrifugal field away from the proximity of a critical point (CP).

For CLN, the effect is smaller and although at high speeds, also high concentration gradients are observed, the turbid demixed zone only starts to form at the bottom at the highest applied speed of 50,000 rpm (red arrow). Therefore, the PO20 composition is much better suited for soft centrifugation separation of solutes as demonstrated in Fig. 20c, d for Nile red as a model for a low molecular solute.

The other type of observed phase separation is centrifuge-induced criticality (Fig. 20b), which is characterized by gradual composition changes. As can be seen in Fig. 19b, the centrifuge-induced concentration changes are much smaller than those induced by centrifuge-induced emulsification. In the case of the living network (LN) composition, the concentration gradients are negligible even at 50,000 rpm as one would expect for a mixture of simple liquids. At the critical point (CP), the concentration gradients are expectedly higher similar to those observed for CLN, but with the important difference that no demixing was observed and the concentration gradient remained continuous. This shows that the well-studied separations starting from the solvent-rich corner (CLN) towards the critical point (CP) inducing sedimentation and coalescence are much less effective even above 40,000 rpm than centrifuge-induced emulsification.

Overall, these AUC experiments on complex fluids demonstrate that AUC is well suited to characterize aggregates in such fluids, create large concentration gradients, and also induce phase separation all controllable by temperature and the applied centrifugal field. What would be very desirable is a dye that can monitor the composition of the ternary fluid by changes in its UV–Vis spectrum as a result of the changing dielectric constant of the solvent mixture. That way, the compositional changes in the phase diagram crossed by the AUC-induced gradients would be quantitatively accessible via the AUC UV–Vis absorption optics, and therefore, the best conditions for separations could be quantitatively evaluated.

Conclusions and outlook

100 years after its invention, analytical ultracentrifugation turned out to be even more powerful than ever. It was a long way from the determination of average sedimentation, diffusion, and frictional coefficients as well as average molar masses in the days of Svedberg 100 years ago to the nowadays routine determination of whole distributions of these quantities. In addition, several further physicochemical properties are nowadays available. The main reason for this quantum leap in AUC performance is digital data acquisition, which allows evaluation by computers, which rapidly get more powerful. This led to the development of several very powerful software packages for the evaluation of AUC data. But also, hardware improvements like the multiwavelength UV–Vis absorption and fluorescence detectors have a very high potential because they open an additional spectral axis in AUC experiments, which allows for obtaining much more information, than was possible by all traditional AUC experiments before. Coupling the optical data and the hydrodynamic AUC data yields whole distributions of gold nanorod dimensions or compositions of gold-silver alloys—information that was impossible to obtain by AUC before. Spectral properties of all separated species even in multicomponent mixtures are now available, and it is even possible to perform chemical reactions directly in the AUC cell. This methodology is very promising to investigate nucleation processes due to the high resolution and statistical significance of AUC experiments. The new detectors have sparked several new applications, and AUC methodology has been developed to solve important scientific problems like the investigation of highly concentrated dispersions. But also in the field of complex fluids or for the determination of the equation of state by using AUC as an osmometer replacing up to thousands of osmometer experiments with a single sedimentation equilibrium experiment, AUC shows its potential. It appears very likely that several further new methods will be developed for AUC, allowing for a further increase in the amount of physicochemical information available via AUC experiments. AUC will continue to play an important role in colloid and polymer science in the next 100 years to come. It will be a pleasure to see the further development of this classical but also modern technique in the coming years.