Uncertainties in the Arctic Ocean response to CO$_2$: a process-based analysis

Abstract

Using an ensemble of atmosphere–ocean general circulation models (AOGCMs) in an idealized climate change experiment, this study evaluates the contribution of different ocean processes to Arctic Ocean warming. On the AOGCM-mean, the Arctic Ocean warming is greater than the global ocean warming, both in the volume-weighted mean, and at most depths within the upper 2000 m. However, the uncertainty of Arctic Ocean warming is much larger than the uncertainty of global ocean warming. The Arctic warming is greatest a few 100 m below the surface and is dominated by the import of extra heat, which is added to the ocean at lower latitudes and is conveyed to the Arctic mostly by the large-scale barotropic ocean circulation. The change in strength of this circulation in the North Atlantic is relatively small and not correlated with the Arctic Ocean warming. The Arctic Ocean warming is opposed and substantially mitigated by the weakening of the Atlantic meridional overturning circulation (AMOC), though the magnitude of this effect has a large model spread. By reducing the northward transport of heat, the AMOC weakening causes a redistribution of heat from high latitudes to low latitudes. Within the Arctic Ocean, the propagation of heat anomalies is influenced by broadening of cyclonic circulation in the east and weakening of anticyclonic circulation in the west. On the model-mean, the Arctic Ocean warming is most pronounced in the Eurasian Basin, with large spread across the AOGCMs, and accompanied by subsurface cooling by diapycnal mixing and heat redistribution by mesoscale eddies.

1 Introduction

Atmosphere–ocean general circulation models (AOGCMs) are widely used for projections of future changes in ocean circulation, heat transport and uptake, including in the subpolar and polar regions of the Northern Hemisphere (e.g., Vavrus et al. 2012; Koenigk and Brodeau 2014; Burgard and Notz 2017; Nummelin et al. 2017; Oldenburg et al. 2018; Årthun et al. 2019; Khosravi et al. 2022). One of the more intriguing findings from some of these studies is that, even though the Atlantic meridional overturning circulation (AMOC) weakens with increasing atmospheric $\hbox {CO}_2$ concentration, the ocean heat transport to the Arctic increases (e.g., Koenigk and Brodeau 2014; Nummelin et al. 2017; Burgard and Notz 2017; Oldenburg et al. 2018; Årthun et al. 2019; Yang and Saenko 2012). The associated increase in the Arctic ocean heat content (OHC) can have major implications for surface climate (e.g., Holland and Bitz 2003; Nummelin et al. 2017), sea ice cover (e.g., Koenigk and Brodeau 2014; Årthun et al. 2019) and sea level rise in the region (e.g., Gregory et al. 2016; Couldrey et al. 2021). It has been shown that one of the main causes of the increased heat transport to the Arctic Ocean under increasing $\hbox {CO}_2$ is related to warmer temperatures of the northward flowing Atlantic waters (Koenigk and Brodeau 2014; Oldenburg et al. 2018). In the subpolar North Atlantic, the warming of these waters is enhanced by decreased heat loss to the atmosphere (Nummelin et al. 2017). The latter is due, at least in part, to the cooling of sea surface temperature due to the AMOC weakening. The reduction of heat loss from the North Atlantic further weakens the AMOC (Garuba and Klinger 2016; Gregory et al. 2016; Couldrey et al. 2021). The gyre circulation in the northern North Atlantic and the associated heat transport have also been noted as important contributors to the Arctic Ocean warming (e.g., Jungclaus et al. 2014; Oldenburg et al. 2018; van der Linden et al. 2019).

Several approaches have been used to explore the mechanisms of Arctic Ocean warming under increasing $\hbox {CO}_2$ in the atmosphere. In some studies, the advective component of ocean heat transport is separated into contributions from changes in ocean velocity, temperature, and combinations thereof (e.g., Koenigk and Brodeau 2014; Oldenburg et al. 2018). The advective ocean heat transport is also sometimes decomposed into overturning and gyre components (e.g., Yang and Saenko 2012; Jungclaus et al. 2014; Oldenburg et al. 2018; van der Linden et al. 2019).Gregory et al. (2016) and Couldrey et al. (2021) use an ensemble of AOGCMs from the Flux-Anomaly-Forced Model Intercomparison Project (FAFMIP; Gregory et al. 2016) to separate the contributions of added heat and redistributed heat to the OHC change, including in the Arctic Ocean. Nummelin et al. (2017) estimate heat convergence in the Arctic Ocean from the difference between the ocean heat content tendency and surface heat flux in an ensemble of models from the Coupled Model Intercomparison Project phase 5 (CMIP5); a similar approach is applied by Burgard and Notz (2017).

In this study, we aim to investigate several aspects of the Arctic Ocean warming in response to increasing $\hbox {CO}_2$ using the methods described in Sect. 2. In Sect. 3 we present a further separation of the processes contributing to the warming. Unlike in previous CMIPs, the diagnostics representing ocean heat convergences due to different dynamical and physical processes have been officially requested for the CMIP6 models (Griffies et al. 2016). We also take advantage of the fact that such a request was made for the CMIP5 models participating in FAFMIP (Gregory et al. 2016; see also Sect. 2). The availability of detailed heat budget diagnostics makes it possible to estimate the net oceanic heat convergence without the need to compute it as a residual between the surface heat flux and temperature tendency (as in Nummelin et al. 2017, and Burgard and Notz 2017). It also provides us with an opportunity to further separate the net oceanic heat convergence into contributions from different-scale ocean processes (large-scale ocean circulation, mesoscale eddy effects and small-scale mixing) and estimate the associated uncertainties. As far as we know, this has never been done before for the Arctic Ocean. It is shown, in particular, that while the large-scale ocean circulation dominates the increased heat convergence in the Arctic Ocean, mesoscale eddy effects and small-scale mixing contribute substantially to the horizontal and vertical structure of warming in the basin’s interior.

In Sect. 4, we investigate the influence of ocean dynamics outside of the Arctic Ocean on the region’s warming under increasing atmospheric $\hbox {CO}_2$. Motivated by previous studies (e.g., Yang and Saenko 2012; Jungclaus et al. 2014; Oldenburg et al. 2018; van der Linden et al. 2019; Årthun et al. 2019), the focus is on the baroclinic overturning and barotropic gyre components of ocean circulation and heat transport in the North Atlantic. Some of these previous studies, while investigating the role of gyre and overturning ocean circulations on the Arctic Ocean warming, are based on individual models. Here, instead, we use an ensemble of AOGCMs and address the following questions: (1) which component (overturning or gyre) dominates the increased heat transport to the Arctic Ocean under $\hbox {CO}_2$ forcing and, importantly, what are the associated spreads across AOGCMs? (2) are there relationships between changes in the ocean overturning and gyre circulations in the North Atlantic and GIN Sea (Greenland, Iceland and Norwegian Seas) and the Arctic OHC change?

In Sect. 5 we address the contributions to the Arctic Ocean warming from heat addition and redistribution, using a tracer-based approach similar to that employed in Banks and Gregory (2006), Xie and Vallis (2012), Garuba and Klinger (2016), Gregory et al. (2016) and Garuba et al. (2020). Some potential sources of uncertainties are discussed in Sect. 6, while our main conclusions and possible future research directions are presented in Sect. 7.

2 Methods

We analyze a climate change experiment where atmospheric $\hbox {CO}_2$ concentration increases at 1$\%$ $\hbox {year}^{-1}$ (1pctCO2), along with the corresponding output from a preindustrial control experiment (piControl). Unless stated otherwise, the analysis is based on the AOGCMs in Table 1.

Table 1 The AOGCMs employed in this study for heat budget analysis, with the corresponding climate model intercomparison project (CMIP)

To evaluate the contribution of different-scale ocean processes to the Arctic OHC change, we utilize the process-based heat budget diagnostics (Gregory et al. 2016; Griffies et al. 2016). The net change in local ocean temperature (All scales) is partitioned into contributions from the large-scale (or resolved) circulation (Large), mesoscale eddy effects (Meso; this also includes submesoscale eddy effects if they are represented in a model) and small-scale diapycnal mixing processes (Small). For Boussinesq models with fixed cell thickness, this can be written as follows:

$$\begin{aligned} \underbrace{c \ \partial _{t} \theta }_{\text {All scales}} = \underbrace{ - c \ \textbf{u} \cdot \nabla \theta }_{\text {Large}} \underbrace{ \ - c \ (\textbf{u}^{*} \cdot \nabla \theta + \nabla \cdot \textbf{J}^{\textrm{iso}}_{\theta }) }_{\text {Meso}} \underbrace{ \ - c \ \nabla \cdot \textbf{J}^{\textrm{dia}}_{\theta }}_{\text {Small}} \ + \ F \ \delta (z), \end{aligned}$$

(1)

where $\theta$ is the potential temperature (some models use conservative temperature), $\textbf{u}$ represents the resolved ocean currents in the analyzed models, $\textbf{u}^{*}$ is the parameterized eddy-induced velocity (Gent and McWilliams 1990; Griffies 1998), $-\nabla \cdot \textbf{J}^{\textrm{iso}}_{\theta }$ represents temperature convergence due to isopycnal or isoneutral mixing (Redi 1982; Griffies et al. 1998; Griffies 1998), and $-\nabla \cdot \textbf{J}^{\textrm{dia}}_{\theta }$ is temperature convergence due to diapycnal (or vertical) mixing processes and all other effects represented in the models (see Griffies et al. 2016); F is the surface heat flux, with $\delta (z)$ (in $\hbox {m}^{-1}$) being the Dirac delta function (assuming ocean surface at $z = 0$), and c is the constant volumetric heat capacity. Combining Large and Meso gives the super-residual transport (SRT; Kuhlbrodt et al. 2015; Saenko et al. 2021)—a useful quantity which facilitates comparison between models that parameterize ocean mesoscale eddy effects, such as in the employed AOGCMs, and models where these effects are explicitly resolved. The corresponding CMIP6 variable names are as follows (Griffies et al. 2016; Gregory et al. 2016): All scales$\rightarrow$temptend; SRT $\rightarrow$temprmadvect; Large$\rightarrow$temprmadvect−temppadvect; Meso$\rightarrow$temppadvect$+$temppmdiff; Small$\rightarrow$tempdiff$+$other, prefixed by “opot" or “ocon" for, respectively, potential or conservative temperature. Note: while the terms in Eq. 1 have units of W $\hbox {m}^{-3}$, the corresponding CMIP6 variables are in W $\hbox {m}^{-2}$. More details on the ocean heat budget diagnostics can be found in Griffies et al. (2016) and Gregory et al. (2016) (see also Sect. 6).

The evolution of the net rate of heat content change in the Arctic Ocean (i.e., the vertically integrated All scales in Eq. 1) and the processes contributing to it are presented in Fig. 1. The warming rate of the region typically increases with time. It is mostly given by the difference between changes in the large-scale heat convergence and surface heat loss. The contribution from the mesoscale eddy processes is relatively minor but, as we shall see, these processes play an important role in redistribution of heat inside of the Arctic Ocean. The area with the largest surface heat loss anomalies will be shown to be in the eastern Arctic Ocean. It what follows, the analysis of the Arctic Ocean heat budget is focused on the mean ocean-climate state corresponding to years 61–80 of 1pctCO2; i.e., the 20-year period centred at the time of atmospheric $\hbox {CO}_2$ doubling.

Fig. 1

Evolution of the net vertically integrated rate of heat content change in the Arctic Ocean in 1pctCO2 (relative to piControl) north of 78$^\circ$ N (All scales; decadal and ensemble mean), with vertical lines representing ± 1 intermodel standard deviation. Also presented are contributions to All scales due to the resolved large-scale ocean circulation (Large), all mesoscale and submesoscale eddy-related processes (Meso) and surface heat flux (i.e., change in F). Positive values indicate heat gain by the ocean. Note: the vertical mixing processes (Small) do not contribute to the heat budget integrated vertically through the whole water column. Uncertainties in Large, Meso and Small are discussed in Sect. 3 (Fig. 6c)

The relative role of addition and redistribution of heat for the OHC change is explored using one of the AOGCMs, HadCM3. The approach is similar to those employed in e.g. Banks and Gregory (2006), Xie and Vallis (2012), Garuba et al. (2020) and Garuba and Klinger (2016). In both 1pctCO2 and piControl, we introduce passive tracers representing added heat ($T_a$) and redistributed heat ($T_r$). In the ocean interior, $T_a$ and $T_r$ are transported in the same way as $\theta$ in Eq. 1; $T_a$ is initialized with a zero field, while $T_r$ has the same initial distribution as $\theta$. The surface boundary condition for $T_r$ is $F_{clim}$, both in 1pctCO2 and piControl, where $F_{clim}$ is the climatological surface heat flux calculated from piControl. For $T_a$, the surface boundary condition is $F^{'}=F-F_{clim}$, where F is the surface heat flux either in 1pctCO2 or in piControl. Under this framework, $\theta = T_a+T_r$ is a very good approximation in HadCM3, although not exact due to non-linearities and some other effects.

Fig. 2

Ensemble mean a rate of change of Arctic Ocean heat content (OHC) in 1pctCO2 (relative to piControl) below 100 m depth, b its standard deviation (STD) and c the ratio of the OHC change in (a) to its STD in (b). The black contour in (a) indicates the Arctic Ocean interior region (with depths typically exceeding 500 m) which is used for a more detailed analysis in the text. An approximate position of the Lomonosov Ridge, separating the Arctic Ocean into the Eurasian Basin and Amerasian Basin, is indicated in (a) with dashed line

3 Physics and dynamics of Arctic Ocean warming

The Arctic Ocean warming is spatially nonuniform (Fig. 2a). In the eastern part of the Arctic Ocean (Eurasian Basin), which is directly influenced by inflow of warm Atlantic Ocean waters, the OHC increases more than in the western part (Amerasian Basin, which includes the Canada Basin, the Makarov Basin and some other basins). Similar patterns of Arctic Ocean warming can be seen in Nummelin et al. (2017) and Khosravi et al. (2022). However, the spread in the Arctic Ocean warming across the AOGCMs is also larger in the Eurasian Basin (Fig. 2b). The ratio of the OHC change to the corresponding intermodel standard deviation (STD) (Fig. 2c) is within the 1–2 range in most regions, which illustrates the large uncertainty in the Arctic Ocean warming in response to $\hbox {CO}_2$ (also noted by Khosravi et al. 2022).

Fig. 3

Ensemble mean barotropic ocean circulation (Sv; 1 Sv $=$ 10$^{6}$ $\hbox {m}^{3}$ $\hbox {s}^{-1}$) in the Arctic Ocean in a piControl and b 1pctCO2, with positive values indicating anticyclonic circulation. The corresponding fields of intermodel standard deviations (STDs) are presented in panels (c, d). In panels (a, b), also shown are 1000-m (dashed red) and 3500-m (solid red) bathymetric contours

Before discussing the contribution of individual processes to the Arctic Ocean warming in Fig. 2a, it is useful to consider some major features of the large-scale ocean circulation in the region and their changes in 1pctCO2. The depth-integrated flow is characterized by a cyclonic circulation in the eastern Arctic and anticyclonic gyre in the western Arctic (Fig. 3a). The cyclonic circulation consists of about 5 Sv of Atlantic inflow. (Woodgate et al. (2001) estimate the transport of the boundary current in the Eurasian Basin to be 5±1 Sv; 1 Sv $=$ 10$^{6}$ $\hbox {m}^{3}$ $\hbox {s}^{-1}$.) It penetrates to the Arctic Ocean mostly through the Barents Sea and also along the east side of Fram Strait, and leaves the Arctic along the western side of Fram Strait. The strength of the anticyclonic circulation in the western Arctic, the upper part of which constitutes the Beaufort Gyre, is also about 5 Sv in piControl (Fig. 3a), with quite large spread across the models (Fig. 3c). In 1pctCO2, the cyclonic circulation in the east broadens, deviates from the boundary and penetrates to the Amerasian Basin (Fig. 3b). In contrast, the anticyclonic depth-integrated circulation in the west weakens and its area decreases. The corresponding spread across the models is presented in Fig. 3d.

The pattern of wind-stress curl in piControl is characterized by mostly negative values in the Arctic Ocean interior (Fig. 4a).(Note: here and in what follows, “wind-stress" refers to the net surface stress applied at the liquid ocean surface due to wind-ocean stress and ice-ocean stress; Griffies et al. 2016). This is consistent with Timmermans and Marshall (2020; their Fig. 2c). Large negative wind-stress curl values in the western Arctic Ocean favour anticyclonic circulation in the region. The area of negative wind-stress curl values somewhat decreases in 1pctCO2, but not the magnitude (Fig. 4b). In fact, the magnitude of negative wind-stress curl somewhat increases in the western Arctic Ocean interior in 1pctCO2, possibly due to decreased sea-ice thickness and cover. The spread across the AOGCMs in the wind-stress curl is large in the GIN Sea, Barents Sea and near the Bering Strait, but not in the Arctic Ocean interior (Fig. 4c, b). It therefore appears that the changes in the depth-integrated circulation in the Arctic Ocean (Fig. 3b) are more due to changes in the ocean’s thermohaline structure in 1pctCO2, including due to the (non-uniform) Arctic Ocean warming (Fig. 2a), than due to changes in the winds.¹

Fig. 4

Ensemble mean wind-stress curl (10$^{-7}$ Pa $\hbox {m}^{-1}$) in the Arctic Ocean in a piControl and b 1pctCO2. The dashed contour corresponds to zero wind-stress curl. The corresponding fields of intermodel standard deviations (STDs) are presented in panels (c, d). The curl is calculated from the boundary fluxes of momentum that quantify the net momentum imparted to the liquid ocean surface arising from the overlying atmosphere, sea ice, icebergs, ice shelf, etc. (see Griffies et al. 2016, for more details)

The spatial structures of individual processes contributing to the Arctic Ocean heat balance below 100 m depth (i.e., mostly outside of the shelf regions) in piControl and its change in 1pctCO2 are presented in Fig. 5. It is evident that the intensity of these processes is typically weaker in the Arctic Ocean than in the GIN Sea. This is expected, since the GIN Sea is a region of strong vertical mixing associated with a large heat loss to the atmosphere, which in a steady state must be balanced by an equally large ocean heat convergence.

Focusing on the Arctic Ocean, it can be seen that, in piControl, cooling of the subsurface interior through small-scale vertical mixing tends to be concentrated along the shelf break regions (Fig. 5a). (Interestingly, Rippeth and Fine 2022, discuss some observational evidence for enhanced mixing-driven cooling of the Atlantic waters along the Arctic Ocean shelf break.) This cooling is closely balanced by warming from SRT; i.e., the combined effect of large-scale and mesoscale processes (Fig. 5b), as expected in a steady state and follows from Eq. 1 below the surface when $\partial _{t} \theta \rightarrow 0$. The general structure of the net heat transport, which is concentrated along the continental slope and also above the Lomonosov Ridge (Fig. 5b), is broadly consistent with the schemes of Arctic Ocean heat advection based on observational data (e.g., Woodgate et al. 2001; Dmitrenko et al. 2008).

Further partitioning SRT into contributions from large-scale advection and mesoscale effects is presented in Fig. 5c,d. It shows positive heat advection by Large in the Barents Sea, along the eastern side of Fram Strait and further into the Arctic Ocean along the continental slope (Fig. 5c). Meso, through slumping of isopycnals, removes some of this heat from the continental slope regions and deposits it towards the interior, mostly just off continental slope (Fig. 5d). The latter process is offset by Large, implying that the large-scale flow deviates from isotherms (i.e. $\int \textbf{u} \cdot \nabla \theta \ dz \ne 0$) under different angles along the shelf break and in the Arctic Ocean interior. In piControl, this Large–Meso near compensation in the boundary–interior heat exchange tends to be confined to the upper 500 m layer. Overall, the main mechanism of the Arctic Ocean heat budget in piControl involves heat transport to the basin by Large, mostly along the continental slope, heat redistribution by Meso and heat flux to the surface by Small, followed by its loss to the atmosphere.

Fig. 5

Partitioning of the model ensemble-mean rate of change of Arctic Ocean heat content (W $\hbox {m}^{-2}$) below 100 m depth, in a–d piControl and e–h 1pctCO2 relative to piControl, into contributions due to (a, e) small-scale diapycnal mixing (Small), b, f the super-residual transport (SRT = Large + Meso), c, g the resolved large-scale ocean circulation (Large) and d, h all mesoscale and submesoscale eddy-related processes (Meso). The colour scale is limited to ± 10 W $\hbox {m}^{-2}$ for plotting purposes. Positive values correspond to heat being added to the region deeper than 100 m, whereas a negative number indicates cooling below 100 m. The thin black contour in (a) indicates the 100 m isobath, roughly corresponding to the shelf break region, while the thick green contour in (e) indicates the region where the ensemble mean surface heat loss by the ocean in 1pctCO2 (relative to piControl) increases by more than 10 W $\hbox {m}^{-2}$. Note: the net warming in 1pctCO2 (relative to piControl) represents the sum of large positive/negative signals in panels (e, f), and so it is shown on a different colour scale in Fig. 2a

In 1pctCO2, the Arctic Ocean is warmed by the joint influence of large-scale heat advection and mesoscale eddy effects; i.e., by SRT =Large+Meso (Fig. 5f). Large warms the Arctic Ocean interior, mostly in Eurasian Basin (Fig. 5g). Some of the warming associated with Large penetrates to the Amerasian Basin through the central Arctic, deviating from the continental slope. This appears to be related, at least in part, to the changes in the Arctic Ocean large-scale circulation, in particular to the broadening of cyclonic circulation in the east and its deviation from the boundary (Fig. 3b). Khosravi et al. (2022) also note (based on their analysis of ocean temperature structure in the CMIP6 models under two climate change scenarios) that the warming signal propagates from the Eurasian Basin to the Canadian Basin cyclonically, but more through the central Arctic rather than along the boundary current. Meso mostly acts to redistribute the extra heat inside the basin, offsetting some of the warming due to Large in the Arctic Ocean interior. The removal of heat from the boundary regions by Meso weakens (Fig. 5d,h), possibly due to increased stratification which tends to decrease the slope of isopycnals.

Changes in diapycnal mixing (Small) act to cool the eastern Arctic Ocean (Fig. 5e). This subsurface cooling is favoured by the locally enhanced surface heat loss, the area of which is indicated by the green contour in Fig. 5e. The persistence of surface and subsurface cooling in the eastern Arctic Ocean enhances heat convergence in the region, mostly due to large-scale heat advection (Fig. 5f, g). This is consistent with Koenigk and Brodeau (2014) who show that the Barents Sea plays an important role in transporting heat to the Arctic Ocean, with some of the heat being lost locally to the atmosphere. Rippeth and Fine (2022) discuss some observational evidence of changing mixing patterns in the eastern Arctic Ocean. They note that the decline of sea ice cover during the past couple of decades has led to increased ocean–atmosphere coupling, with potential for enhancement of turbulent mixing in the eastern Eurasian basin. In contrast, in the GIN Sea there are vast areas where the weakened small-scale mixing, including due to partly suppressed convection (Saenko et al. 2021), leads to subsurface warming by Small (Fig. 5e), which tends to be compensated by cooling due to changes in Large and Meso (or SRT; Fig. 5f). In this regard, it is interesting to note that Stouffer et al. (2006), in their North Atlantic freshwater hosing experiments, find a northward shift of the sites of surface heat loss and ocean deep convection from the GIN Sea to the Barents Sea, and the resulting increase in the northward heat transport in the high latitudes of the North Atlantic (their Fig. 8).

The vertical structure of heat balance in the Arctic Ocean region deeper than 500 m (see Fig. 2a) is presented in Fig. 6 (the 500-m depth criteria was selected to exclude the Barents Sea and parts of the Kara Sea and to focus on the Arctic Ocean interior). In piControl, the heat convergence due to SRT is mostly confined to the upper $\sim$ 1000 m layer and is closely balanced by cooling due to Small (Fig. 6a). In most of the upper 1500 m layer, SRT is dominated by Large. Within the 100–500 m layer there is a sizable contribution from Meso to the warming. However, Meso mostly acts to redistribute the heat in the Arctic Ocean interior, with its depth-averaged value being small. Partitioning Meso further into contributions from the eddy-induced advection and isopycnal diffusion indicates that the former tends to warm the Arctic Ocean interior, while the latter tends to make it colder (not shown).

It should be noted that ocean mesoscale eddies are known to play an important role in setting water column properties, including in the changing Arctic Ocean (e.g., Armitage et al. 2020). AOGCMs, such as those examined in this study, rely on sophisticated parameterizations to represent some mesoscale and submesoscale eddy effects in the ocean. This also applies to the Arctic Ocean where the Rossby radius in the basin’s interior is $\sim$ 10–15 km (Nurser and Bacon 2014; Timmermans and Marshall 2020). For example, all AOGCMs employed here for heat budget analysis use variable eddy transfer coefficients to represent eddy-induced advection in the ocean (Gent and McWilliams 1990) (Table 3). Some AOGCMs also include the Fox-Kemper et al. (2011) parameterization of ocean mixed layer eddies (or submesoscale eddies). Still, the accuracy of these eddy parameterizations in the Arctic Ocean remains to be assessed, especially given the large spread across the models (see also Sect. 6).

Fig. 6

a–c Ensemble mean profiles of a heat convergences in piControl, b their changes in 1pctCO2 (relative to piControl) and c the intermodel standard deviations for the Arctic Ocean interior region (within the black contour in Fig. 2a). The profiles correspond to the net heating rate (All scales, black) and its partitioning into contributions from the resolved large-scale circulation (Large, green), all mesoscale and submesoscale eddy-related processes (Meso, red) and small-scale diapycnal mixing and all other effects (Small, blue); also presented is the superresidual transport (SRT = Large + Meso, dashed gray). d The ensemble mean profiles of (solid) net heating rates in 1pctCO2 (relative to piControl) and (dashed) intermodel STDs for (magenta) the global ocean and (black) Arctic Ocean

In 1pctCO2, the vertical structure of the Arctic Ocean heat balance is strongly disrupted (Fig. 6b), with the heat convergence changes being often greater than the corresponding piControl values (Fig. 6a). The net heat anomaly penetrates to 1500 m depth, being largest around 400 m depth, consistent with Vavrus et al. (2012) and Khosravi et al. (2022). Koenigk and Brodeau (2014) also note that most of the heat which is not passed to the atmosphere in the Barents Sea is stored in the Arctic intermediate layer of Atlantic waters. The net warming (All scales) is dominated by heat convergence due to Large (Fig. 6b), as expected from the corresponding horizontal field (Fig. 5g). The warming is enhanced by Meso and opposed by Small in the upper $\sim$ 500 m layer and vice versa below this depth; Meso mostly acts to redistribute the heat. However, the corresponding uncertainties are large (Fig. 6c). The cooling effect of Small in the upper 500 m layer (Fig. 6b) is mostly confined to the eastern part of the Arctic Ocean (Fig. 5e). The spread of the Arctic Ocean warming across the models typically increases toward the surface (Fig. 6c). This applies to the net warming rate as well as to the warming rates associated with the individual processes. An exception is the 400–700 m layer where the warming uncertainties in Large and Meso increase locally. However, the uncertainty in SRT does not have this local maximum, indicating that the intermodel warming variations due to changes in Large and Meso tend to anticorrelate. Also, the spread in All scales is smaller than in Large and Meso above 700 m, and smaller than Small above 500 m, implying anticorrelation.

To put the Arctic Ocean warming and its spread across the AOGCMs into context, Fig. 6d compares the profiles of Arctic Ocean warming rate and its intermodel STD with the corresponding profiles for the global ocean. This shows that in the layer below the upper several hundred meters and above 1500 m depth, the rate of the Arctic Ocean warming is about two times larger than that of the global ocean, which is in line with Khosravi et al. (2022). However, the uncertainty of Arctic Ocean warming below the upper layer is much larger than the uncertainty of global ocean warming (Fig. 6d).

4 Link to ocean circulation and its changes outside of the Arctic

Bryan's (1982) decomposition of advective ocean heat and freshwater transports into contributions from the overturning and gyre components is part of the CMIP data request, as described in Griffies et al. (2016; see their section I10). For the heat transport, the corresponding CMIP6 variable names are htovovrt (overturning component) and htovgyre (gyre component). While such a geometric decomposition may not always reflect the roles of the corresponding ocean dynamics in transporting heat and freshwater (Saenko et al. 2002), it can provide useful insight into processes acting in the North Atlantic and their links to the Arctic Ocean. Indeed, the decomposition is widely employed in discussions of the mechanisms of heat transport changes in the Arctic Ocean in response to $\hbox {CO}_2$ forcing, most often based on individual models (e.g., Yang and Saenko 2012; Jungclaus et al. 2014; Oldenburg et al. 2018; van der Linden et al. 2019). We build on these earlier studies to examine both multimodel-mean changes and intermodel spread in the overturning and gyre components of heat transport to the Arctic Ocean. This decomposition also sets the stage for our subsequent analysis of the baroclinic overturning and barotropic gyre circulations in the North Atlantic under increasing $\hbox {CO}_2$ and their relationships with the Arctic OHC change.

Fig. 7

(Solid) Ensemble mean a northward heat transport in the North Atlantic Ocean in piControl (PW; 1 PW $=$ 10$^{15}$ W) and its overturning and gyre components and b change in the northward heat transport in the North Atlantic Ocean in 1pctCO2 (relative to piControl) and contribution to the change from the overturning and gyre components. (Dotted) the corresponding intermodel STDs. Also shown in panel (a) is an observational estimate of heat transport at 47$^\circ$ N in the Atlantic Ocean from Ganachaud and Wunsch (2003), with vertical bar indicating its uncertainty. The model data used in constructing this figure is from the following AOGCMs: FGOALS-s2, GISS-E2-1-G, HadGEM3-GC31-LL, HadGEM3-GC31-MM, IPSL-CM6A-LR, MRI-ESM2-0, UKESM1-0-LL, EC-Earth3-CC (see Acknowledgments)

In piControl, the net heat transport in the low-latitude Atlantic Ocean, which is mostly due to heat advection, is dominated by the overturning component. This is because both the vertical temperature contrast and the AMOC strength are strong at these latitudes. Around 45$^\circ$ N, the net northward heat transport is about 0.6 PW, both simulated and observed (Fig. 7a). At these latitudes, the Atlantic Ocean advective heat transport is roughly equally partitioned between the overturning and gyre components, although the corresponding spreads across the models are quite large. North of 50$^\circ$ N, the heat transport is dominated by the gyre component, which is consistent with previous studies (e.g., Grist et al. 2010; Yang and Saenko 2012; van der Linden et al. 2019). This is because the strong subpolar gyre circulation acts on a relatively strong zonal temperature contrast in the region. For example, it requires some 5 K of temperature contrast to maintain 0.5 PW of heat transport, given a 25-Sv strong subpolar gyre circulation (see Fig. 10a). On the other hand, the vertical temperature contrast decreases north of 50$^\circ$ N and, as we discuss in Sect. 4.1, the vertical flow (deep water formation) begins to play an increasingly large role in the AMOC structure. Closer to the Arctic, as the ocean’s thermal structure becomes more homogeneous, the heat transport weakens, being only about 0.1±0.03 PW at 75$^\circ$ N (where the uncertainty corresponds to ±1 intermodel STD). The intermodel spread in the heat transport and its overturning and gyre components also tend to decrease with latitude, although not with the same rate as the transports themselves (Fig. 7a).

In 1pctCO2, the heat transport decreases south of about 60$^\circ$ N, but increases north of this latitude (Fig. 7b), implying increased heat convergence in the Arctic Ocean, in agreement with previous studies (e.g., Nummelin et al. 2017). The increased heat convergence in the Arctic Ocean is favoured by increased heat divergence through vertical mixing in the eastern part of the Arctic Ocean; i.e., in the region where heat loss from the ocean to the atmosphere strongly increases in response to increasing $\hbox {CO}_2$ (as noted in Sect. 3). At 75$^\circ$ N, the heat transport increase is about 0.07±0.04 PW (where the uncertainty corresponds to ±1 intermodel STD), which is comparable to the heat transport in piControl at this latitude. The increase is dominated by the gyre component (Fig. 7b). The contribution from the overturning component to the heat transport increase is also positive north of 60$^\circ$ N. Both the gyre and overturning heat transport changes have large spreads across the models (Fig. 7b). Interestingly, in their historical climate simulation, Jungclaus et al. (2014) also find that the gyre component dominates ocean heat transport increase at 60–65$^\circ$ N toward the end of the 20th century, with positive contribution from the overturning component.

It should be noted that Oldenburg et al. (2018) find that in their model, the overturning component contributes approximately 0.04 PW to the heat transport increase north of 75$^\circ$ N, while the gyre heat transport change is approximately − 0.02 PW at these latitudes (their Fig. 2d–f). These values are comparable to the spread across the models at these latitudes, as given by the corresponding ±1 intermodel STDs (Fig. 7b). This also suggests that such results, obtained based on a single climate model, should be interpreted with caution. Another possible source of some discrepancy with our results could arise from the fact that Oldenburg et al. (2018) investigate the heat transport response to abrupt $\hbox {CO}_2$ quadrupling, while we consider a gradual $\hbox {CO}_2$ increase scenario (i.e., 1pctCO2) and focus on $\hbox {CO}_2$ doubling.

4.1 Link to overturning circulation

The AMOC has a major influence on climate, including through its role in the northward transport of heat. However, its relationship with the Arctic Ocean warming in response to $\hbox {CO}_2$ forcing remains unclear (e.g., see discussions in Nummelin et al. 2017; van der Linden et al. 2019). Nummelin et al. (2017) show that it is a reduction in the subpolar North Atlantic heat loss which enhances ocean heat transport to the Arctic Ocean under increasing $\hbox {CO}_2$ forcing. A substantial fraction of this heat input to the northern North Atlantic could be due to a feedback wherein some initial $\hbox {CO}_2$-induced AMOC weakening tends to cool the region, thereby reinforcing surface heat flux to the northern North Atlantic (or reducing heat loss from it), as was concluded based on some specifically designed model experiments by Gregory et al. (2016), Garuba and Klinger (2016) and Couldrey et al. (2021). For example, in the four AOGCMs employed by Gregory et al. (2016), this feedback nearly doubles the heat input to the subpolar North Atlantic associated with the doubling of $\hbox {CO}_2$; in Garuba and Klinger (2016), it is about 70$\%$ of the heat added to the region. In addition, it was found that the $\hbox {CO}_2$-induced changes in ocean circulation, mainly associated with the AMOC weakening, lead to a strong redistributive cooling in the North Atlantic and Arctic Ocean (Gregory et al. 2016; Couldrey et al. 2021; see also Sect. 5). Therefore, the net effect from the AMOC weakening on the Arctic Ocean warming is not easy to foresee.

Fig. 8

Ensemble mean Atlantic meridional overturning circulation (AMOC; Sv; 1 Sv $=$ 10$^{6}$ $\hbox {m}^{3}$ $\hbox {s}^{-1}$) in the North Atlantic in a piControl and b 1pctCO2. The corresponding fields of the AMOC intermodel standard deviations (AMOC STDs; Sv) are presented in panels (c, d). The blue boxes in panel (a) indicate the regions of AMOC maximum strength (the mid-latitude AMOC cell) and AMOC extension into the GIN Sea (the GIN Sea overturning cell); these regions are used to calculate the corresponding AMOC strength indexes in Fig. 9

In piControl, the ensemble mean AMOC strength at 26$^\circ$ N is 16.0±3.2 Sv (the uncertainty corresponds to ±1 intermodel STD). This is comparable to 17.8 Sv, which is an observational estimate of the mean AMOC strength at 26$^\circ$ N for the 2004–2018 period with interannual STD of about 1.8 Sv (Moat et al. 2020; their Table 1). The ensemble mean AMOC pattern indicates that most of the deep water formation in the Atlantic occurs between about 50$^\circ$ and 65$^\circ$ N, with some deep water forming further north in the GIN Sea (Fig. 8a). The AMOC intermodel spread tends to be larger over the latitudes where the AMOC strength is also large (Fig. 8c).

In 1pctCO2, the ensemble mean AMOC strength at 26$^\circ$ N decreases to 12.4 ± 2.5 Sv. This is mostly due to a reduction of deep water formation between 50$^\circ$ and 65$^\circ$ N, whereas the strength of the AMOC extension north of 65$^\circ$ N remains essentially unaffected (Fig. 8b). Interestingly, the AMOC spread across the models is smaller in 1pctCO2 than in piControl almost everywhere in the North Atlantic (Fig. 8c, d). However, the fractional spread remains roughly the same: the ratio of the piControl AMOC, averaged over the large blue box in Fig. 8a, to its STD in Fig. 8c averaged over the same region is 3.1; the corresponding ratio for the 1pctCO2 AMOC is 3.0.

Fig. 9

Scatter plots of change in the Arctic Ocean heat content in the 100–500 m layer (TW; 1 TW $=$ 10$^{12}$ W) in 1pctCO2 (relative to piControl), plotted against a change in the strength of the mid-latitude AMOC cell in 1pctCO2 (relative to piControl) and b the strength of the midlatitude AMOC cell in piControl (Sv; 1 Sv $=$ 10$^{6}$ $\hbox {m}^{3}$ $\hbox {s}^{-1}$). c, d The same as (a, b), except for the GIN Sea overturning cell. The two AMOC overturning cells are indicated with blue boxes in Fig. 8a. As the measure of the overturning strength in each cell we use the maximum value of the baroclinic (overturning) streamfunction in the Atlantic basin. The correlation coefficients (corr. coef.) are also indicated. The dashed lines in panels (a, b) correspond to linear regression (see Table 2 for the values of the AMOC strength and its change in each AOGCM)

In models with a larger weakening of the AMOC, the warming of the Arctic Ocean is smaller (Fig. 9a). This relationship between the AMOC change and the Arctic Ocean OHC change appears to arise from the basin-scale heat redistribution, identified in the specifically designed model experiments (Garuba and Klinger 2016; Gregory et al. 2016; Garuba et al. 2020; Couldrey et al. 2021; see also Sect. 5): as the AMOC weakens, more heat accumulates in the ocean at the lower latitudes and less heat is redistributed to the higher northern latitudes. As a result, the northern North Atlantic and Arctic Ocean tend to become colder. This redistributive cooling in the north is opposed by heat input at the surface, amplified by a feedback wherein, as the sea surface temperature cools, the heat flux from the atmosphere to the ocean increases locally (e.g., Gregory et al. 2016). However, this extra surface heat input to the northern North Atlantic also acts to weaken the AMOC even further, thereby enhancing the redistributive cooling in the north. The net effect of these, and perhaps some other processes, is that the more AMOC weakens, the less heat accumulates in the Arctic Ocean (Fig. 9a).

Interestingly, there is also anticorrelation between the AMOC maximum in piControl and the Arctic Ocean warming in 1pctCO2 (Fig. 9b); i.e., models with larger AMOC maximum in piControl tend to simulate smaller Arctic OHC change in 1pctCO2. However, this anticorrelation seems to arise due to anticorrelation between the AMOC maximum in piControl and the AMOC maximum change in 1pctCO2 (not shown; the corresponding correlation coefficient is −0.65), which is consistent with previous studies (e.g., Gregory et al. 2005; Weaver et al. 2007; Winton et al. 2014). That is, models with a stronger AMOC tend to produce stronger AMOC weakening. This implies that the spread across the AOGCMs in the piControl AMOC strength indirectly contributes to the spread in the Arctic Ocean warming. Therefore, it is essential to understand better the causes of the AMOC spread, as discussed in Sect. 6.

There are no similar relationships between the AMOC extension into the GIN Sea and the Arctic Ocean warming (Fig. 9c, d). Moreover, the models do not show a consistent change in the AMOC extension to the GIN Sea, with the ensemble mean GIN Sea overturning being essentially unaffected (see also Fig. 8). This suggests that at high northern latitudes the contribution of the overturning heat transport to the Arctic Ocean warming arises mostly due to the warmed waters being advected by the (largely unaffected) piControl overturning circulation, consistent with Oldenburg et al. (2018).

Fig. 10

Ensemble mean barotropic ocean circulation (Sv; 1 Sv $=$ 10$^{6}$ $\hbox {m}^{3}$ $\hbox {s}^{-1}$) in the northern North Atlantic in a piControl and b 1pctCO2. The corresponding fields of intermodel standard deviations (STDs) are presented in panels (c, d). Red boxes in panel (a) indicate the subpolar Atlantic and GIN Sea gyres discussed in the text. In models that use free surface methods, the quasi-barotropic streamfunction fields are diagnosed as described in Griffies et al. (2016; Eq. H46). These streamfunctions were adjusted here to be equal to zero along the eastern boundary of the Atlantic Ocean

4.2 Link to gyre circulation

The barotropic circulation in the northern North Atlantic is characterized by cyclonic gyres centred in the Labrador Sea (subpolar gyre) and in the GIN Sea (Fig. 10a). On the considered time-space scales, the strength of this circulation is mainly determined by wind-stress curl and bottom pressure torque (e.g., Mellor 1999). The ensemble mean barotropic circulation is not strongly affected in 1pctCO2 (Fig. 10b). The gyre circulation spread across the models in piControl is similar to that in 1pctCO2 (Fig. 10c,d), except in the Labrador Sea where the spread is larger in piControl. This is because some models simulate a strong barotropic recirculation cell in the north-west Labrador Sea in piControl, while others do not. (This is also why in Fig. 11 we use the barotropic streamfunction averaged over large areas, rather than its minimum, to characterize the gyre strength.)

Fig. 11

Scatter plots of change in the Arctic Ocean heat content in the 100–500 m layer (TW; 1 TW $=$ 10$^{12}$ W) in 1pctCO2 (relative to piControl) plotted against a change in the subpolar Atlantic gyre strength in 1pctCO2 (relative to piControl) and b the subpolar Atlantic gyre strength in piControl (Sv; 1 Sv $=$ 10$^{6}$ $\hbox {m}^{3}$ $\hbox {s}^{-1}$). c, d The same as (a, b), except for the GIN Sea gyre. The two gyres are indicated with red boxes in Fig. 10a. As the measure of the gyres strength we use the mean value of the barotropic streamfunction averaged over the regions where the streamfunction is less than −10 Sv for the subpolar North Atlantic gyre and less than −2 Sv for the GIN Sea gyre. The correlation coefficients (corr. coef.) are also indicated (see Table 2 for the values of the subpolar North Atlantic gyre (SG) strength and its change in each AOGCM)

There is no relationship between the barotropic gyre circulation change in the subpolar North Atlantic and the Arctic OHC change (Fig. 11a). Moreover, the models do not simulate a consistent weakening or strengthening of this gyre in 1pctCO2. The gyre changes do not correlate with the wind-stress curl averaged over the subpolar North Atlantic (not shown), suggesting that bottom pressure torques contribute to the gyre changes. Similarly, the relationship between the GIN Sea gyre change and Arctic OHC change is not strong (Fig. 11c), with the AOGCMs being inconsistent in simulating this gyre strength response to the doubling of $\hbox {CO}_2$ in 1pctCO2. Also, there is essentially no relationship between the subpolar gyre strength in piControl and the Arctic Ocean warming (Fig. 11b); the same applies to the GIN Sea gyre strength in piControl (Fig. 11d). This suggests that the increase in the gyre heat transport to the Arctic Ocean at high northern latitudes is more due to warmer ocean temperatures than due to changes in the gyre circulation. The importance of warmer ocean temperatures for the heat transport increase to the Arctic Ocean under different climate change scenarios have been emphasized before (Koenigk and Brodeau 2014; Nummelin et al. 2017; Oldenburg et al. 2018; van der Linden et al. 2019).

Table 2 The strengths of AMOC and subpolar North Atlantic gyre (SG) (Sv; 1 Sv $=$ 10$^{6}$ $\hbox {m}^{3}$ $\hbox {s}^{-1}$) in piControl and their changes in 1pctCO2 relative to piControl ($\varDelta$AMOC and $\varDelta$SG) in the employed AOGCMs

It should also be noted that van der Linden et al. (2019) find that in their model, the barotropic gyre circulation in the GIN Sea strengthens (becomes more cyclonic; their Fig. 9c) in response to abrupt $\hbox {CO}_2$ quadrupling, thereby contributing to the Arctic Ocean warming. Oldenburg et al. (2018) also note that at 70$^\circ$ N, a strengthened gyre circulation advects warmed surface waters to the Arctic in response to abrupt $\hbox {CO}_2$ quadrupling in their model. Unlike in these studies, we consider a gradual $\hbox {CO}_2$ increase scenario (i.e., 1pctCO2) and focus on the $\hbox {CO}_2$ doubling (rather than quadrupling). Therefore, it is possible that under a stronger $\hbox {CO}_2$ forcing than considered here, or under an abrupt $\hbox {CO}_2$ increase scenario, AOGCMs become more consistent in simulating the GIN Sea gyre response.

5 Role of heat addition and redistribution

To obtain further insight on the causes of the Arctic OHC changes under increasing $\hbox {CO}_2$, in particular on the role of AMOC weakening, we analyze the 1pctCO2 and piControl experiments where the OHC change is partitioned into contributions from heat addition and redistribution (see Sect. 2). The experiments were conducted using one of the analysed AOGCMs, HadCM3. While the choice of this model was dictated primarily by its availability to us, we note that it produces heat transport in the Atlantic Ocean and AMOC strength which are reasonably close to observational estimates. In particular, at 47$^\circ$ N in the Atlantic the time-mean ocean heat transport simulated by HadCM3 is 0.57 PW, which is close to the Ganachaud and Wunsch (2003) observational estimate of 0.6$\pm$0.09 PW at this latitude. The time-mean AMOC strength at 26$^\circ$ N in HadCM3 is 15.8$\pm$1.1 Sv, where the uncertainty corresponds to 1 interannual standard deviation. This is comparable to the AMOC observational estimate at this latitude discussed in Sect. 4.1.

Fig. 12

Change in (a, c) ocean heat content (OHC; ZJ per degree of latitude; $1~\textrm{ZJ} = 10^{21}$ J) and b, d vertical temperature profiles in 1pctCO2 at $2 \times CO2$ (years 61–80) relative to piControl for a, b Atlantic and/or Arctic oceans and c, d global ocean. Also shown are the contributions to the OHC (or temperature) change from heat addition and redistribution. The figure is based on output from HadCM3 simulations

In the northern North Atlantic and Arctic, the ocean warming is due to addition of heat, which is opposed by a comparable in magnitude cooling from heat redistribution (Fig. 12a); the contributions from heat addition and redistribution to the meridional structure of thermosteric sea level change are also comparable (not shown). The sum of OHC changes due to heat addition and redistribution (dashed green) closely follows the net OHC change (black), as expected. These results are consistent with the results from the FAFMIP experiments (Gregory et al. 2016; Couldrey et al. 2021). There is a strong relationship between the redistributive cooling in the Arctic Ocean and the AMOC weakening (Fig. 13); the correlation coefficient between the decadal-mean AMOC strength in 1pctCO2 and $\varDelta T_r$ north of 75$^\circ$ N is 0.94 (with $\varDelta$ denoting the difference between $T_r$ in 1pctCO2 and piControl). There is also a relationship, although less strong, between the AMOC weakening and redistributive warming south of 30$^\circ$ N in the Atlantic Ocean, with the latter confined mostly to the upper ocean. The correlation coefficient between the decadal-mean AMOC strength in 1pctCO2 and $\varDelta T_r$ in the 0–500 layer of the Atlantic Ocean within 30$^\circ$ S–30$^\circ$ N is − 0.69. These relationships suggest that the AMOC weakening, through limiting the northward transport of heat, acts to mitigate the Arctic Ocean warming (and increase warming in the low-latitude ocean). This supports one of the results in Sect. 4.1, that with the AMOC weakening the Arctic Ocean warming tends to decrease (Fig. 9a). Similarly, Garuba et al. (2020) conclude that AMOC weakening mitigates Arctic sea ice loss through the advection of the redistributive temperature anomalies into the Arctic Ocean.

Comparing the Atlantic and Arctic OHC change (Fig. 12a) with the global OHC change (Fig. 12c; cf. Fig. 10 in Gregory et al. 2016) shows that much of the redistributive warming in the global ocean is linked, directly or indirectly, to the redistributive cooling in the northern North Atlantic and Arctic oceans (blue curve in Fig. 12a, c). That is, since heat redistribution must integrate close to zero globally (by the experimental design), then the AMOC-driven weakening of the northward transport of heat and cooling in the North Atlantic (negative values in the blue curve in Fig. 12a) must be compensated by redistributive warming elsewhere (positive values in the blue curve in Fig. 12c).

Fig. 13

The AMOC maximum strength (Sv; $1~\textrm{Sv} = 10^{6}~\textrm{m}^{3}~\textrm{s}^{-1}$) in 1pctCO2 plotted against volume-weighted mean redistributive temperature change ($\varDelta T_r$) in 1pctCO2 (relative to piControl) in the Arctic Ocean north of 75$^\circ$ N. The cross symbols correspond to the decadal-mean values of these quantities from the first 150 years of 1pctCO2 (i.e., from the preindustrial $\hbox {CO}_2$ level until it exceeds $4 \times CO$ $_2$), while the dashed line is the linear regression. The correlation coefficient (corr. coef.) is also indicated. The figure is based on output from HadCM3 simulations

The vertical structure of $\varDelta \theta$ in the Arctic Ocean has comparable in magnitude and opposite in sign contributions from $\varDelta T_a$ and $\varDelta T_r$ (Fig. 12b). Negative $\varDelta T_r$ nearly compensates for positive $\varDelta T_a$ in the uppermost Arctic Ocean. This creates a layer of warmest $\varDelta \theta$ between about 100 and 1000 m. This contrasts with the global ocean where the influence on the vertical profile of $\varDelta \theta$ from $\varDelta T_r$ is small (Fig. 12d); only a small fraction of heat is redistributed from the 0 to 500 layer into the deeper ocean globally. The net warming in the upper 1500 m layer in the Arctic Ocean simulated by HadCM3 is comparable to that in the global ocean (Fig. 12b, d). In contrast, we had previously shown that the multimodel-mean warming in this layer is larger in the Arctic Ocean than in the global ocean (Fig. 6d). However, it should be kept in mind that the vertical warming profile in the Arctic Ocean has a large spread across the AOGCMs.

6 Discussion: sources of uncertainties

Our analysis has revealed large uncertainties in the Arctic Ocean response to increasing $\hbox {CO}_2$ in AOGCMs. These uncertainties could have originated from a number of sources. We have identified one such source: the spread across the AOGCMs in the AMOC strength in piControl (Fig. 9b). Indeed, it has been shown in e.g. Gregory et al. (2005), Weaver et al. (2007), Winton et al. (2014), Couldrey et al. (2023), and confirmed here (Sect. 4.1), that climate models with a stronger AMOC tend to produce stronger AMOC weakening in response to $\hbox {CO}_2$, thereby mitigating the Arctic Ocean warming (Fig. 9a). It has also been demonstrated that differences in mean climate states can impact the response of AMOC to increasing $\hbox {CO}_2$ (Weaver et al. 2007; Saenko et al. 2004). It therefore seems essential to identify, among other factors, the causes of the AMOC spread across AOGCMs. While addressing this topic comprehensively may require a series of studies, it seems useful to briefly discuss it here.

In an AOGCM, ocean circulation can be influenced by external (as seen by the ocean) and internal factors. The external influence comes from boundary fluxes, mostly at the surface, whereas the internal factors may include ocean physical parameterizations and parameters. We therefore partition the associated uncertainties accordingly. While in a coupled system, given its many feedbacks, it may not be possible to fully distinguish between these two sources of uncertainties, such a partitioning can be a useful initial step towards addressing the problem.

6.1 External

Differences in surface fluxes of water, heat and momentum can result in differences in the simulated ocean circulation even when all other aspects of an ocean model are identical. Here we present the ensemble mean fluxes of water and heat in the employed AOGCMs, along with the corresponding intermodel STDs. These components of surface buoyancy flux are known to have direct influence on the AMOC (e.g., Gregory et al. 2005; Stouffer et al. 2006; Weaver et al. 2007; Gregory et al. 2016; Couldrey et al. 2023; Jackson et al. 2023) and on the production of Labrador Sea Water (e.g., Yashayaev and Loder 2009). In addition, we present the pattern of wind-stress curl and the corresponding intermodel STD. While wind-stress curl is more related to the gyre circulation than to the overturning circulation, it is directly related to the vertical Ekman velocity. The latter contributes to the subduction/obduction rates (e.g., Marshall et al. 1993) and, through its impact on the density structure, can be an important factor in preconditioning deep convective mixing (e.g., Killworth 1983).

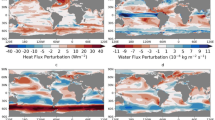
Water flux The spread in the surface water flux across the AOGCMs is particularly large near Greenland and in the Labrador Sea, where it is comparable to the ensemble mean water flux (Fig. 14a, b). A representative value for the spread in the whole subpolar North Atlantic is $15 \times 10^{-6}$ kg $\hbox {m}^{-2}$ $\hbox {s}^{-1}$. A positive anomaly of this size would result in a freshwater input of more than 0.1 Sv, using $7 \times 10^{12}$ $\hbox {m}^{2}$ as the area of the Atlantic Ocean between 50$^\circ$–70$^\circ$ N and 60$^\circ$ W–0$^\circ$. The largest spread across the AOGCMs in the freshwater input to the region ranges from 0.15 Sv in MPI-ESM1.2-LR to 0.46 Sv in MRI-ESM2.0, or 0.31 Sv. Jackson et al. (2023) show that a freshwater perturbation of 0.3 Sv, if applied continuously over the northern North Atlantic, can lead to a more than 50$\%$ weakening of the AMOC strength in a set of CMIP6 AOGCMs. Since the difference in the AMOC strength between MPI-ESM1.2-LR and MRI-ESM2.0 is only about 10$\%$ (Table 2), there are likely other factors affecting the AMOC spread. This further follows from the fact that there is essentially no relationship between the net freshwater input to the subpolar North Atlantic (between 50$^\circ$–70$^\circ$ N and 60$^\circ$ W–0$^\circ$) and AMOC strength in piControl (the corresponding correlation coefficient is 0.14).

Heat flux The spread in the surface heat flux is also particularly large in the northern North Atlantic and in the region of western boundary current in the subtropical North Atlantic (Fig. 14c,d). It has been shown, using specifically designed experiments, that the AMOC strength is particularly sensitive to anomalies in surface heat flux (e.g., Gregory et al. 2005; Weaver et al. 2007; Garuba and Klinger 2016; Gregory et al. 2016; Couldrey et al. 2023). For example, using the FAFMIP heat flux experiments with an ensemble of AOGCMs,Couldrey et al. (2023) found a strong anticorrelation between the net heat input to the North Atlantic (i.e., perturbation and feedback) and AMOC change.

For the employed AOGCMs, the spread in the surface heat loss by the subpolar North Atlantic ocean (between 50$^\circ$–70$^\circ$ N and 60$^\circ$ W–0$^\circ$), as given by 1 STD in piControl (Fig. 14d), is 11.6 W $\hbox {m}^{-2}$. A positive heat flux of this magnitude to the North Atlantic can be associated with a negative AMOC anomaly of about 5 Sv (Couldrey et al. 2023). The piControl heat loss by the ocean in the subpolar North Atlantic strongly correlates with the in piControl AMOC strength (correlation coefficient is 0.86), consistent with Couldrey et al. (2023), and anticorrelates with the Arctic Ocean warming by Large in 1pctCO2 (correlation coefficient is −0.64, significant at the 5$\%$ level). Thus, the spread across the AOGCMs in the North Atlantic heat flux in piControl contributes, although indirectly, to the spread in the Arctic Ocean warming in 1pctCO2. However, it should be kept in mind that uncertainties in the North Atlantic heat flux may be caused, in part, by uncertainties in some ocean physical parameterizations and parameters, through their impact on the AMOC strength (see next subsection).

Wind-stress curl In the subtropical North Atlantic, the spread in the wind-stress curl is relatively small (compared to the magnitude of the ensemble mean wind-stress curl). However, it is not small in the subpolar North Atlantic (Fig. 14e, f). This spread would lead to differences in the vertical Ekman velocity, $w_{Ek} = \rho ^{-1} \nabla \times ({\varvec{\tau }}/f)$, and could affect the subduction/obduction rates in the region. Taking $\nabla \times {\varvec{\tau }} =$0.5$\times$10$^{-7}$ Pa m$^{-1}$ as a representative value for the wind-stress curl uncertainty in the subpolar North Atlantic (Fig. 14f), and setting $\rho =$10$^3$ kg m$^{-3}$ and $f=$10$^{-4}$ s$^{-1}$, we obtain $w_{Ek} =$0.5$\times$10$^{-6}$ m s$^{-1}$ or about 15 m year$^{-1}$. This is a rather large value, given the estimated contribution of $w_{Ek}$ to the net subduction (obduction) rates in the North Atlantic (e.g., Marshall et al. 1993). However, there is essentially no relationship between $\nabla \times {\varvec{\tau }}$, averaged between 50$^\circ$–70$^\circ$ N and 60$^\circ$W–0$^\circ$, and AMOC strength in piControl; the corresponding correlation coefficient is −0.20.

We also note that the spread in $\nabla \times {\varvec{\tau }}$ is consistent with the spread in the barotropic gyre circulation in the subpolar North Atlantic in piControl (Fig. 10c). In particular, given $\beta \psi _x=\nabla \times {\varvec{\tau }}+BT$, where $\beta \equiv {df / dy}$ (e.g., Mellor 1999), and setting $\beta =$ $2 \times 10$ $^{-11}$ $\hbox {m}^{-1}$ $\hbox {s}^{-1}$ and $L=$2$\times$10$^{6}$ m (which is a typical width of the ocean in the region), a wind-stress curl anomaly of $\nabla \times {\varvec{\tau }} =$0.5$\times$10$^{-7}$ Pa $\hbox {m}^{-1}$ can lead to an anomaly in the vertically integrated flow of $\psi \simeq L \ \beta ^{-1} \ \nabla \times {\varvec{\tau }}$= 0.5$\times$10$^{10}$ kg $\hbox {s}^{-1}$ or $\approx$ 5 Sv (unless compensated by an anomaly in the bottom pressure torque, BT). This value is comparable to the spread in the barotropic gyre circulation in the subpolar North Atlantic (Fig. 10c).

Fig. 14

Time-mean and model-mean patterns of a surface water flux, c surface heat flux heat (both positive downward) and e wind-stress curl in the Northern Atlantic in piControl and b, d, f their intermodel standard deviations (STD)

6.2 Internal

We next consider some internal factors and the associated uncertainties in the AOGCMs that could have affected the AMOC strength in piControl. Given the links between the ocean general circulation, mesoscale eddies and small-scale vertical mixing (e.g., Wunsch and Ferrari 2004), our discussion focuses on the processes contributing to the 2nd and 3rd terms on the right-hand side of Eq. 1.

Table 3 Information on the ocean physical parameterizations in the employed AOGCMs

Meso This term combines the time tendencies of heat due to the convergence of three-dimensional fluxes from the parameterized eddy-induced velocity (Gent and McWilliams 1990; Griffies 1998) and parameterized diffusive eddy fluxes directed along neutral or isopycnal surfaces (Redi 1982; Griffies et al. 1998). The corresponding eddy transfer and diffusivity coefficients are not measured directly. However, there are some observational constrains on them. For example, it seems reasonable to think that the global rate with which the parameterized mesoscale eddies extract potential energy from the mean ocean state should not exceed the energy supplied from external sources, such as winds (Wunsch and Ferrari 2004). Taking this into consideration, Saenko et al. (2018) used an OGCM to show that reducing the eddy transfer coefficient (or layer thickness diffusivity coefficient) in the Gent and McWilliams (1990) scheme ($K_{GM}$) can increase the AMOC strength by several Sv, in line with the scaling arguments of Marshall et al. (2017). Saenko et al. (2018) also showed that with all other factors being the same, differences in $K_{GM}$ can lead to differences in the surface-to-subsurface penetration of passive heat anomalies. In some employed AOGCMs, $K_{GM}$ is capped at quite low values (Table 3). In addition to affecting the AMOC strength in piControl (Marshall et al. 2017; Saenko et al. 2018), such a capping of $K_{GM}$ can influence the AMOC response to a strengthening of zonal winds in the Southern Ocean (Farneti and Gent 2011), expected under increasing $\hbox {CO}_2$ (e.g., Gregory et al. 2016; their Fig.2a). In turn, a strengthening of the Southern Ocean winds, uncertain on its own, can influence an interhemispheric component of the AMOC (e.g., Wolfe and Cessi 2011).

Furthermore, while in all of the employed AOGCMs the $K_{GM}$ coefficient varies in space and time (Table 3), the adopted formulations for $K_{GM}(x,y,z,t)$ may differ. In particular, most models use the Visbeck et al. (1997) formulation or some modifications of it. In Visbeck et al. (1997), the eddy transfer coefficient is proportional to the neutral slope, resulting in enhanced $K_{GM}$ values in the regions of strong mesoscale eddy activity in the ocean (e.g., western boundary currents). In some AOGCMs, for example in CESM2, HadCM3, MRI-ESM2.0, $K_{GM}$ also depends on the local stratification; in CESM2 and MRI-ESM2.0, this dependence follows Danabasoglu and Marshall (2007). This may lead to large values of $K_{GM}$ not only in the eddy-active ocean regions, but also inside of the subtropical gyres (see Fig.1d in Danabasoglu and Marshall 2007). It is not clear how this would affect the dependence of the AMOC strength on $K_{GM}$; in their ocean model sensitivity experiments, Marshall et al. (2017) used horizontally-constant values of $K_{GM}$.

For diffusive fluxes directed along neutral (or isopycnal) surfaces (Redi 1982; Griffies 1998), the employed AOGCMs use either variable or fixed values for the corresponding mesoscale eddy diffusivity, $K_{I}$ (Table 3). Imposing different values for $K_{I}$ can substantially affect the sensitivity of AMOC to surface freshwater perturbations in climate models (Sijp and England 2009). Also, the diffusion of heat along isopycnals has been shown to be a major term regulating heat uptake by the ocean in response to increasing atmospheric $\hbox {CO}_2$ (Gregory 2000).

In some models the Meso term may also include the time tendency of heat due to the convergence of three-dimensional fluxes from the submesoscale eddy parameterization (see Table 3). This parameterization aims at better representing the effect of mixed layer eddies in ocean models (Fox-Kemper et al. 2011). These submesoscale eddies typically have much smaller size than mesoscale eddies, because of small Rossby radius within weakly stratified mixed layers. As noted by Fox-Kemper et al. (2011), the primary impact of this parameterization is a shoaling of the mixed layer, with the largest effect in polar winter regions. Because this was still a rather novel parameterization at the time of CMIP6, its presence in some AOGCMs and absence in others (Table 3) may have introduced an additional uncertainty to the Arctic Ocean heat budget, given the important role of deep mixing in the northern North Atlantic for local heat uptake by the ocean (Messias and Mercier 2022). The submesoscale eddy parameterization has two adjustable parameters that are not yet well constrained by observations or theory: frontal width and mixing timescale (Fox-Kemper et al. 2011).

Small This term represents the time tendency from the convergence of parameterized fluxes associated with dianeutral (or diapycnal) processes as well as vertical boundary layer processes. This includes the shear-driven and boundary layer mixing (Pacanowski and Philander 1981; Gaspar et al. 1990; Large et al. 1994; Umlauf and Burchard 2003), tidally driven mixing (Simmons et al. 2004), convective adjustment, small background diffusion and some other vertical mixing processes. These parameterizations have a number of adjustable parameters, sensitivity to which are often explored in ocean-only models rather than in AOGCMs. For example, in the parameterization of tidally driven mixing above rough topography (Simmons et al. 2004), employed in some of the AOGCMs (Table 3), the vertical decay scale and local dissipation efficiency are two of the more uncertain parameters. Varying the former, within its uncertainty ranges, can substantially affect stratification and overturning circulation in the deep ocean (Saenko et al. 2012).

It should be noted that the processes associated with Small, their link to Meso and mechanical energy input to the ocean, and their impact on the global ocean overturning circulation is an active area of research (e.g., Stanley and Saenko 2014). Many of them have not been fully understood or perhaps even established (see review in Wunsch and Ferrari 2004); some are represented in AOGCMs in a rather simplified way, if at all (Table 3). However, what has been established, based on microstructure measurements (e.g., Gregg 1987) and tracer release experiments (e.g., Ledwell et al. 1993), is that vast ocean regions, away from rough topography and below the mixed layer, are characterized by a rather weak “background” diapycnal diffusivity level of about 10$^{-5}$ $\hbox {m}^2$ $\hbox {s}^{-1}$. This is reflected in the employed AOGCMs. However, even the background vertical diffusion coefficient varies considerably across them (Table 3), introducing an additional level of uncertainty to the ocean heat budget.

In summary, differences in ocean physical parameterizations and parameters are a plausible explanation for the AMOC spread across the AOGCMs, along with variations in the surface heat flux to the subpolar North Atlantic. A contribution from variations in the surface fluxes of water and momentum also cannot be ruled out. While separating the influence from all these factors may not be trivial, given many feedbacks operating in an AOGCM, the problem certainly needs to be explored further.

7 Conclusions

We use heat budget diagnostics from an ensemble of AOGCMs, run in preindustrial control (piControl) and an idealized (1pctCO2) climate change experiment, to investigate the contribution of different ocean processes to the warming in the Arctic Ocean interior. In addition, we investigate the links between the Arctic OHC change in 1pctCO2 (relative to piControl) and the baroclinic overturning and barotropic gyre components of the ocean circulation in the North Atlantic. We also address the question of contributions to the Atlantic and Arctic OHC changes from the addition and redistribution of heat. Our main conclusions are as follows:

• In all models, the Arctic Ocean warms under the 1pctCO2 scenario. At doubled $\hbox {CO}_2$, the Arctic Ocean warming is greater than the global ocean warming in the volume-weighted mean, and at most depths within the upper 2000 m. The Arctic warming is greatest a few 100 m below the surface.

• The Arctic Ocean warming is dominated by the import of extra heat which is added to the ocean at lower latitudes due to climatic warming. This added heat is conveyed to the Arctic via the subpolar gyre and GIN Sea mostly by the large-scale barotropic ocean circulation. The change in strength of this circulation in the North Atlantic is relatively small and not correlated with the Arctic Ocean warming.

• The Arctic Ocean warming is opposed and substantially mitigated by the weakening of the AMOC, though the magnitude of this effect has a large intermodel spread. By reducing the northward transport of heat, the AMOC weakening causes a redistribution of heat from high latitudes to low latitudes.

• In the multimodel mean, the Arctic Ocean warming is most pronounced in the Eurasian Basin, with large spread across the AOGCMs, and it is accompanied by subsurface cooling by diapycnal mixing (i.e. upwards, towards the cold sea surface) and heat redistribution by mesoscale eddies (vertically and horizontally).

• The propagation of heat anomalies across the Arctic Ocean is affected by broadening of the depth-integrated circulation in the east and weakening of anticyclonic circulation in the west.

  In future studies, it would be helpful to undertake a similar process-based analysis of Arctic Ocean warming based on a multimodel ensemble of AOGCMs where some of the mesoscale eddy effects are explicitly resolved. This may also decrease the AMOC spread, given AMOC’s sensitivity to the eddy transfer coefficient in the Gent and McWilliams (1990) scheme. However, this would require using ocean model components with rather high resolution, given that the first baroclinic Rossby radius in the Arctic Ocean is $\sim$ 10–15 km in the basin’s interior and even smaller in the vast Arctic shelf regions (Nurser and Bacon 2014; Timmermans and Marshall 2020); Heuzé et al. (2023) report on some improvements in water properties and circulation at eddy-permitting resolution in the Arctic Ocean. It would also be helpful to investigate heat addition and redistribution in other models, using the tracer-based approach applied here.