Application of gene expression programming for seasonal rainfall forecasting in Western Australia using potential climate indices

Abstract

This study presents the development of rainfall forecast models using potential climate indices for the Kimberley region of Western Australia, using 100 years of rainfall and climate indices data for four rainfall stations. Three different modeling techniques: multiple linear regression (MLR), autoregressive moving average with exogenous input (ARIMAX), and gene-expression programming (GEP) were applied to develop prediction models. Preliminary analysis suggests that Western Tropical Indian Ocean (WTIO) and Southern Oscillation Index (SOI) have significant impacts on summer rainfall generation for the region. Developed models’ performances were evaluated using Pearson correlation coefficient ($r$), root mean square error ($RMSE$), mean absolute error $(MAE)$, Nash–Sutcliffe efficiency $(NSE)$, and refined Willmot index of agreement (${d}_{r}$). It is found that the GEP model exclusively outperforms the other two alternatives. In the calibration period, the GEP model resulted in a Pearson correlation coefficient (r) values ranging from 0.76 to 0.85, which are significantly higher than that achieved from MLR (0.32 to 0.44) and ARIMAX (0.53 to 0.83) models, while for the validation period, the correlation values for the models ranged from 0.74 to 0.87 for GEP, 0.35 to 0.51 for MLR and 0.59 to 0.77 for ARIMAX models. Considering other statistical error statistics it can be concluded that the GEP model is the best representative seasonal rainfall forecasting model for the region.

1 Introduction

Reliable forecasting of rainfall variability has always been a kind of special interest in meteorology, engineering hydrology as well as in agricultural economy. Rainfall forecasting could play an important role in making investment and management decisions and risk management policies in many sectors including agriculture, water management infrastructures, coastal and disaster management, and their preparedness plans. Such forecasting has always been challenging as too many factors are involved in the generation of rainfall, therefore it is understood that the prediction outcome may not be of optimum accuracy. However, having a forecast several months in advance can be a privilege, which may offer a certain scale of flexibility to the stakeholders to take timely decisions as well as mitigate associated risks of damage.

At present, two methods namely: dynamic method and statistical method are widely used to predict future rainfalls (Goddard et al. 2001). Dynamic models are encoded with the physics of the ocean, the interaction of the land and its atmosphere, which requires the most recent data of the present scenario and supercomputer resources to run the ensemble model and perform a computationally intensive calculation. Thus, all these intrinsic and sophisticated requirements made the dynamic method comparatively complex, expensive, and operationally time-consuming (Evans et al. 2020; Schepen et al. 2012). On the other hand, the statistical model requires long-term uninterrupted data to evaluate the relationship between the response variable and significantly contributing predictor variables. Therefore, the statistical model is relatively simple that requires less development time and supercomputer resources. While compared with dynamic models, statistical models are found to be widely preferred over their counterparts, due to the simplicity of the formation and easy-to-use application. Furthermore, dynamic models have not shown significant prediction performance over simple statistical models despite using high-tech resources (Abbot and Marohasy 2014; Mekanik et al. 2016).

To date, several statistical techniques have widely been used to develop rainfall prediction models. These techniques include both linear and non-linear approaches. Seasonal rainfall events being a complex phenomenon, requires analyzing both linear and non-linear relationships for its prediction. Among the linear techniques, multiple linear regression (MLR) is the most popular approach that was widely used by many researchers, hydrologists, and climatologists (Hossain et al. 2018b; Islam and Imteaz 2019; Mekanik et al. 2013; Rasel et al. 2016). Among non-linear techniques, artificial intelligence (AI) based models such as an artificial neural network (ANN), adaptive neuro-fuzzy interference system (ANFIS), support vector machine (SVM), genetic programming (GP), and gene expression programming (GEP) have drawn immense attention and been successfully applied in rainfall, streamflow, and rainfall-runoff forecasting. It is understood that non-linear techniques have superior capability of explaining the underlying non-linear relationships among the variables which are found as unexplained via linear regression.

By far, ANN is the most used nonlinear statistical approach which reveals the presence of existing nonlinear relationships (either visible or hidden) among the variables. ANN has been used to model and simulate complicated time series, weather forecasting, rainfall-runoff modeling, and other hydrological and meteorological prediction models (Akhtar et al. 2009; Chiang and Chang 2009; Esha and Imteaz 2020; Hossain et al. 2020; Thirumalaiah and Deo 2000; Yilmaz et al. 2011). Despite the successful application of ANN in capturing non-linear mechanisms, researchers are often reluctant to use ANN on broad scales due to its consequential fundamental disadvantages. ANN is labeled as a black-box model as it is not capable to provide the function structure and any definite function or equation on how to calculate the output. Moreover, ANN models are deemed as complex and the outcomes are not easily interpretable (Gandomi and Alavi 2013; Hashmi et al. 2011). In parallel, GP has emerged as the most popular alternative technique to overcome the drawbacks of the ANN (Koza 1994). The main advantages of GP over ANN are its capability of capturing knowledge from the experimental data without making assumptions and finally providing a prediction equation (Alavi and Gandomi 2011). The structure of the equation is simple, which facilitates its further use for hand calculation for daily design practices (Gandomi and Alavi 2013). An extended version of GP has also received global attention in the field of structural engineering, water resources, and hydrology, known as gene expression programming (GEP) (Ferreira 2001).

The use of GP and GEP has received great exposure in many hydrological and meteorological analyses around the world. The application of these techniques had a wide variety spanning from scouring prediction for hydraulic structures (Azamathulla 2012; Azamathulla and Ghani 2010; Azamathulla et al. 2010; Guven et al. 2008), water demand forecasting (Shabani et al. 2018), estimating evapotranspiration (Shiri et al. 2013, 2014a, 2014b), rainfall-runoff modeling (Drecourt 1999; Fernando et al. 2012a, 2012b; Khu et al. 2001; Savic et al. 1999), and spatial interpolation of data (Adhikary et al. 2016b, 2016a). A recent study showed that the GEP model offered higher efficiency in predicting specific return period events compared to the Regional Flood Estimation (RFE) method for Auckland, New Zealand (Zorn and Shamseldin 2015). In that study, the authors reported a relative error of the GEP model in flood estimation for 10 and 100 years period are 29% and 18% respectively, whereas the RFE model resulted in an error of 48% and 44% respectively. Another study used the GEP technique to model a stage-discharge relationship, where the GEP model was recommended as it outperformed traditional methods such as regression analysis and stage-discharge rating curve (Guven and Aytek 2009). Prior to that, genetic programming was applied to forecast El Nino3.4 time series that illustrated a prediction up to 12 months in advance (De Falco et al. 2005).

Several previous studies were conducted on explaining Australian rainfall variability that revealed a strong teleconnection between climate drivers and Australian rainfalls in different regions (Cai et al. 2011; Chowdhury and Beecham 2013; Feng et al. 2010; Fierro and Leslie 2013; Ghamariadyan and Imteaz 2020, 2021a, b; Hossain et al. 2018a; Islam and Imteaz 2019, 2020; Kirono et al. 2010; Marshall and Hendon 2014; McBride and Nicholls 1983; Mekanik et al. 2013; Risbey et al. 2009; Taschetto and England 2009; Tularam 2010). However, these teleconnections often depend on the geographical location of the site and varies with different seasons (Risbey et al. 2009). Therefore, sound knowledge of the climate drivers and their influence on localized rainfall events can facilitate predicting the trend of the seasonal rainfall. For Australia, Pacific Ocean SST anomalies have shown a high influence on rainfall generation in tropical and eastern regions, whereas, Indian Ocean SST anomalies play a key role in rainfall generation in southern and western regions. To be precise, Indian Ocean Dipole (IOD) and Southern Annular Mode (SAM) have been found as influential drivers for rainfall generation in south-eastern and western parts, Blocking highs for southern parts, and ENSO Modoki and Madden Julian Oscillation (MJO) for north-western and northern parts (Ashok et al. 2003a, 2003b; Marshall and Hendon 2014; Rasel et al. 2016; Risbey et al. 2009; Schepen et al. 2012; Taschetto and England 2009; Tibaldi et al. 1994; Ummenhofer et al. 2008). Among all these drivers, in general ENSO grouped indices were found as the major contributor to rainfall generation all over Australia (Montazerolghaem et al. 2016).

To evaluate the teleconnection between climate drivers and Australian rainfall variability, some of the studies considered the entire Australian seasonal rainfalls (Cai et al. 2011; Drosdowsky and Chambers 2001; Forootan et al. 2016; Kirono et al. 2010; McBride and Nicholls 1983; Risbey et al. 2009; Schepen et al. 2012), where the rest kept their studies restricted within a zone such as Queensland (Abbot and Marohasy 2012, 2014; Tularam 2010), South Australia (Chowdhury and Beecham 2013; Kamruzzaman et al. 2017; Nicholls 2010; Rasel et al. 2016; Tozer 2014), South West Western Australia (England et al. 2006; Evans et al. 2020; Feng et al. 2010; Islam and Imteaz 2020; Ummenhofer et al. 2008), and South East and East Australia (Mekanik et al. 2013; Murphy and Timbal 2008; Verdon et al. 2004). Rainfall in different locations can be generated via the interaction among different climate drivers within the region. Under such circumstances, localized prediction can be made with maximum precision and accuracy, therefore, a localized prediction is preferred as it considers the engagement of local dominant factors, resulting in reliable model development that depicts efficient prediction performance.

Current literature suggests that most of the attempts related to seasonal rainfall forecasting in Western Australia (WA) were region-based, with a majority of them were developed for South West Western Australia (Cai and Cowan 2006; England et al. 2006; Feng et al. 2015; Smith et al. 2000; Ummenhofer et al. 2008). Apart from these, a limited number of investigations were made on Central West Western Australian (CWWA) rainfall and North West Australian (NWA) rainfall variability (Feng et al. 2013; Fierro and Leslie 2013; Lin and Li 2012; Rotstayn et al. 2012). Among the studies performed in NWA, Rotstayn et al. (2012) evaluated and confirmed the influence of aerosol and greenhouse gas for an increase in summer rainfall. This was further consolidated by Shi et al. (2008), where they investigated the dynamics of the observed trend towards increased rainfall and compared the observed trend with model forced with increasing aerosol. Their study also reported an increment in NWA rainfall due to high and low sea level pressure (SLP) anomalies. In conjunction with this, an increase in NWA summer rainfall (December to February) was found to be relative to tropical Atlantic atmospheric vertical motion and southern Indian ocean climate indices (Feng et al. 2013; Lin and Li 2012). Surprisingly to date, none of the studies considered both SST and SLP-based ENSO indices and Western Tropical Indian Ocean (WTIO) index as contributors for NWA rainfall events. This study aimed to cover that gap and investigated the influence of lagged relationships among the climate indices on seasonal summer rainfall (December-January–February) variability in the Kimberley region of North West Western Australia (NWWA) using three different techniques, MLR, ARIMAX, and GEP. It should be emphasized that this is the first time such a GEP technique has been used to forecast long-term seasonal rainfall in Australia. Used GEP tool will provide some equations for forecasting summer rainfall in the region several months in advance, which can be easily used by the stakeholders without having expert knowledge for different agro-economic decision-making, as well as formulating polocies for the mitigation of damage due to flooding/drought.

2 Data and study area

The Kimberley region of Western Australia has been selected for this study due to its tropical positioning of the land in the north and diversified contribution in agriculture production, fishing and mining industry, construction, tourism, and retail trade for both the state of WA and the country. The main agricultural area in Kimberly is around 14,000 hectares around the Ord River Irrigation Area (ORIA) which makes an annual economic contribution worth 87 million Australian Dollars (AUD) in the Australian economy. Additionally, this region is popular for pastoral leases that create employment in remote areas mostly for the aboriginal community.

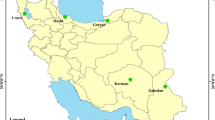
At present, the Kimberley region holds approximately 80% of freshwater resources in Western Australia, where most of the towns are getting their water being supplied from bore fields. Due to the pastoral nature of the inland and being dependent on limited freshwater resources, the region is vulnerable to saltwater intrusion and flooding due to sea-level rise associated with extreme weather events such as tropical cyclones during the summer season (December-January–February). This has created a demanding necessity of developing reliable rainfall prediction models for the region so that the associated adverse effects can be tackled down to save lives with minimal social and economic loss. This study considered the NWWA’s Kimberley region’s main rainfall season (summer rainfall events) to develop prediction models. Figure 1 and Table1 illustrate the study area and geographical location of selected rainfall stations. Four rainfall stations from the Kimberley region were selected considering uninterrupted data availability with fewer missing values.

Fig. 1

The geographical location of the study area and selected rainfall stations

Table 1 Overview of the selected rainfall stations in the Kimberley region

For preliminary analysis and model development purposes, 100 years of monthly rainfall data were collected from the Australian Bureau of Meteorology website (http://www.bom.gov.au/climate/data/). Also, 100 years (1916 to 2015) of climate indices data was collected from the climate explorer website (http://climexp.knmi.nl/). Climate drivers namely Southern Oscillation Index (SOI) (SLP based), ENSO indices Nino3.4, Nino4, Nino3 (SST based), El Nino Modoki index (EMI), Dipole Mode Index (DMI), and Western Tropical Indian Ocean (WTIO) have been selected, extracted, and utilized to determine the significance of the correlations between rainfall and individual climate indices. A brief description of SOI and WTIO has been presented in Table 2 as these two climate indices showed a significant correlation with NWWA summer rainfall. A detailed description of the rest of the climate indices can also be found in the previous study of Islam and Imteaz (2019). For model development, the entire dataset was partitioned into two sets: calibration or training set (1916–1985) and validation or testing set (1986–2015), as using a partitioning ratio of 70:30 for calibration and validation data set is recommended for such model development (Ferranti 2012; Vaze et al. 2012).

Table 2 Brief description of influential climate indices in this study

Australian Bureau of Meteorology being a federal government authority, collects and maintains rainfall and other weather data with very high integrity and accuracy. Several weather data including the rainfall data used in this study have been used by numerous reseearchers for many climate related researches. Out of more than 8000 active rainfall stations, some stations experienced some missing data. However, the selections selected in this study was having no missing data as well as longer coverage of data period (> 100 years). Climate indices data is managed by the World Meteorological Organization (WMO) with highest level of accuracy.

The selection of variables for model development was followed by the selection of analytical methodology that involved a stepwise selection of analytical approach beginning with linear technique, followed by time series analysis and then, gene-expression programming.

3 Methodology

3.1 Multiple linear regression

Multiple linear regression (MLR) is a statistical measure that evaluates the strength of the linear relationship between the dependent and two or more independent variables. The dependent variable is known as the response variable while the independent variable is known as the predictor. The mathematical expression of MLR is presented below in Eq. (1):

$$Y = c + \beta_1 X_1 + \beta_2 X_2 + e$$

(1)

where, Y is the dependent variable (i.e. rainfall), ${X}_{1}$ and ${X}_{2}$ are the independent variables (i.e., lagged WTIO and lagged SOI); ${\beta }_{1}$ and ${\beta }_{2}$ are the regression model coefficients; $c$ is constant, and $e$ is an error.

The prediction efficiency of an MLR model is often tested with the goodness of fit and multicollinearity checks. A goodness of fit value is usually tested with statistical parameters namely Pearson correlation coefficient (r), root mean square error (RMSE), mean absolute error (MAE), and refined Willmott index of agreement $({d}_{r})$. For all these parameters, a value close to 1 represents a good fit. Multicollinearity is the association of the residuals (autocorrelation) derived from the predictors during the regression process, thus, can undermine the prediction efficiency. Tolerance $(T)$ and variance inflation factor $\left(VIF\right)$ values are good indicators of multicollinearity among the predictors and can be utilized to avoid exaggerated predictive performance of a model. In addition to that, Durbin-Watson (DW) test can also be used to detect the multicollinearity present among the predictors. A detailed description of the MLR methodology and associated testing techniques for the model performance can be found in Islam and Imteaz (2019).

3.2 Univariate autoregressive integrated moving average with exogenous input (ARIMAX)

ARIMA model is used to predict future value considering the influence of their past, current value, and past errors. It is the combination of ‘AR’, ‘I’, and ‘MA’, where ‘AR’ stands for Auto-Regressive, ‘I’ stands for Integrated, a time series which needs to be differenced to make a non-stationary series to stationery, ‘MA’ stands for Moving Average. This model can be used to analyze and forecast univariate time series data. The expression of the model function consists of two segments, one is seasonal and the other one is non-seasonal. Generally, it is expressed as (p,d,q)*(P, D, Q). Where ‘p’ represents the non-seasonal auto-regressive, ‘d’ represents non-seasonal differencing, and ‘q’ represents the non-seasonal moving average. P, D, and Q represent the same for the seasonal segment (Corporation 2013; Adamowski et al. 2012). This study used the non-seasonal segment only as no seasonality was found in the time series.

An ARIMA model is termed as ARIMAX, whenever any exogenous input or predictors are included in a conventional ARIMA model (Kamruzzaman et al. 2013). In the ARIMAX model development for this study, two kinds of input orders were necessary: ARIMA order (dependent variable: summer rainfall) and Transfer function order (predictors or exogenous input: lagged climate indices). A detailed description of these two orders can be found in the previous study of Islam and Imteaz (2020). The mathematical expression for the ARIMAX model is presented below in Eq. (2):

$$\Delta {Y}_{t}={\upvarepsilon }_{t}+\sum_{i=1}^{p}{\mathrm{\varphi }}_{i}{\Delta Y}_{t-i}\sum_{j=1}^{q}{\uptheta }_{j}{\upvarepsilon }_{t-j}+\sum_{m=1}^{M}{\upbeta }_{m }{X}_{t-\mathrm{m}}$$

(2)

where, ${\varphi }_{1}\dots , {\varphi }_{p}$ and ${\theta }_{1}\dots , {\theta }_{q}$ are the parameters; ${\varepsilon }_{1}, {\varepsilon }_{t-1}$ are white noise errors and ${\beta }_{1}\dots , {\beta }_{m}$ are the parameters of independent variables input ${X}_{1}$ and $t$ is the time.

ARIMAX model development follows three steps (Box and Jenkins 1976; Cryer and Chan 2008):

Step1: Identification: In this step, the raw data is checked to verify whether the data is stationary or not. If the data set is found as non-stationary, differencing is performed to make it stationary.

Step 2: Parameter Estimation and Selection: In this step correlograms of the autocorrelation function (ACF) and partial autocorrelation function (PACF) are explored to choose the accurate ‘AR’ and ‘MA’ order. The ‘AR’ order relay on the lag of PACF cut and the ‘MA’ order relay on the lag of ACF cut. However, decision-making on their order is not that simple as several trials and errors are required to select the appropriate order. Some general guidelines can be followed in the selection of AR and MA orders as discussed in the previous study of Islam and Imteaz (2020).

Step 3: Diagnostic Check: Model adequacy is validated using diagnostic checks where the residual of the ARIMAX model should satisfy the requirement of being white noise. This requirement can be verified in two ways, one is drawing a residual ACF and PACF plot and checking on the spikes. If the spikes stay between the boundary lines (by at least 95%), it indicates the residual is white noise. Another way of such a check is to carry out a Ljung-Box test, in which if the p-value is more than 0.05, the null hypothesis gets verified as being white noise (Ljung and Box 1978). A successful deployment of all these three steps and subsequent verification can provide sufficient evidence of the model’s forecasting capability.

3.3 Gene expression programming

GEP is a combination of the principles of genetic algorithms (GA) and genetic programming (GP). The basic disagreement between these three algorithms (GA, GP, and GEP) is their nature or the way of representing chromosomes. GA utilizes a linear string of fixed length of chromosomes and GP utilizes non-linear entities of tree-based chromosomes with different sizes and shapes (parse tree) and GEP is encoded as a simple linear string of fixed length chromosomes and expressed as nonlinear entities of different sizes and shapes (Ferreira 2001).

In GEP, genotype and phenotype are the two vital types of entities that are structurally and functionally different from each other. In genotype, chromosomes are simple small linear entities composed of one or more genes, where replication, mutation, recombination, and transposition can be performed easily. In phenotype, Expression Trees (ETs) are the algebraic or mathematical expression of the genetic information encoded in respective chromosomes. Genetic code is incorporated with the symbol of the chromosome and the terminal functions. This genetic code decides the structural organization of the function and terminals in expression trees. Moreover, GEP genes are combined with two elements one is the head and another one is the tail. The head encoded the functions for expression. It represents both the function set (F) and the terminal set (T). On the other hand, the tail represents the only terminal set (T). This terminal set from the tail acts as a reservoir for an argument required by the function that can be used in the head while there is a shortage of terminals. Therefore, the head contains functions, variables, and constants but the tail contains only variables and constants. For any problem, head (h) length can be selected manually, and tail length (t) needs to be calculated using the following Eq. (3):

$$t=h\left(n-1\right)$$

(3)

where, n is the number of variables/arguments required by the functions, h is the head length, t is the tail length. For example, any gene consists of function [Q, *, /, −, + , a, b], head length is selected as 10 and the number of arguments is 2, in that scenario, the tail length is t = 10*(2–1) + 1 = 11. Therefore, the length of the genes is 10 + 11 = 21. GEP represented two types of languages: one is related to genes and the other one is the language of ETs. The system that decides the structure of ETs and their interactions and provides the sequence of genes is called the Karva language.

3.3.1 An overview of gene expression programming algorithms

The process of GEP begins with the random origination of chromosomes of the primary population. These chromosomes are decoded into computer programs and their fitness is evaluated by the appropriate fitness function. From the outcome of the fitness test, individuals are selected to reproduce with a further modification that leaves progeny with new offspring. In the reproduction phase, genomes or chromosomes are improved by several genetic operators namely replication, mutation, inversion sequence (IS) transposition, root insertion sequence (RIS) transposition, gene transposition, one-point and two-point recombination, and gene recombination. Elaborative details about the functionality of these genetic operators can be found in Ferreira (2001). The reproduced individuals then go through the same development procedure such as genomes expression, engagement of the chosen environment, and reproduction with further modification. The procedure is repeated until an adequate result has been obtained. An overview of the gene expression programming (GEP) algorithm has been presented in Fig. 2. Further to this, an explanation of the GEP genes formation framework or structure has been presented in the following subsections.

Fig. 2

An overview of Genetic Expression Programming (GEP)

3.3.1.1 Open reading frames (ORFs) and genes

Open reading frames (ORFs) are a coding order of the gene, in terms of biology: begins with a start codon, continues with amino acid codons, and finishes with termination codons. ORFs are the sequences upstream from the start codon and sequences downstream from the stop codon, thus presents the framework/structure of GEP genes. In GEP, the beginning site is the first spot of a gene however, the termination/stop may not necessarily be the last spot. Therefore, for some instances, the GEP genes may have a noncoding downstream region from the termination or stop point. This noncoding downstream region permits the modification of genomes through genetic operators for producing accurate programs. For example, if an equation as given below in Eq. (4) is considered:

$$\sqrt[3]{{\left( {a + b} \right)*\left[ {c*\left( \frac{d}{e} \right)} \right]}}$$

(4)

The following ORF diagram should be the structure of the formation and chromosome of the equation in terms of ETs as presented in Fig. 3.

Fig. 3

Example of an ORFs: a expression tree; b chromosome (genotype)

In Fig. 3 (a), “Q” is the cube root function, a, b, c d, and e are the terminals, and + , − and * are the addition, subtraction, and multiplication function. The expression presented in Fig. 3 (b) is called ORFs Karma expression, which started at “Q” (position 0) and terminating at “e” (position 9). The way of reading the expression tree is: left to right, then from top to bottom. The starting point of the ORFs is related to the root of the ETs that creates the first line of the ET. Considering the number of arguments of each element, the next line continues by generating the requisite number of nodes. For example, the root of the ET presented in Fig. 3 will start with “Q” at position 0. As the cube root function has only one argument, the next line continues with one node at position 1, which is “*”. This multiplication factor required two arguments thus the next line continued with “ + ” and “*” at node positions 2 and 3, respectively. For node position 2, the next line got filled up with terminal/ leaf nodes “a” and “b” at positions 4 and 5. On the other hand, for node position 3, the next line got one terminal/ leaf node “c” at position 6 and one argument node “/” at position 7. At this stage, the argument node at position 7 required two more branches which are terminal/ leaf nodes “d” and “e” at positions 8 and 9, respectively. This terminates the growth of the ET as no further offspring are grown.

3.3.1.2 Multigenic Chromosomes

Chromosomes in GEP usually contain more than one gene of equal length. As the entity of a complex individual requires complex genes, it is necessary to have multigenic genomes to develop complex entities. For any problem in GEP, the gene number and the head number are selected by the user. Each gene encoded the sub-expression tree (sub-ET), and these sub-ETs are interconnected to create a more complex entity.

Figure 4 presents a scenario where the total gene length is 29, comprised of three genes, each terminating at different position (with tails denoted as bold) based on the fitness to derive the output eqution of a complex problem. In this scenario, a multigenic chromosome consists of three genes, forming three open reading frames for sub-ETs as each ORF constructed a particular sub-ET. While the first element of each gene is in position 0, the position also indicates the end of each ORF. In Fig. 4, the first ORF terminates at position 5 in sub-ET₁, the second ORF ends at position 5 in sub-ET₂, and the final one terminates at position 7 in ET₃.

Fig. 4

Expression of multigenic chromosomes a three genes and b sub-ETs encoded by three genes

3.4 GEP model development for rainfall forecasting

GEP methodology has been applied to develop models to represent relationships between climate indices and rainfall. The GEP form of the prediction model can be presented as in Eq. (5):

$$Y= f ({X}_{1}, {X}_{2}, \dots {X}_{n})$$

(5)

where, $Y$ is the dependent or response variable (seasonal summer rainfall), ${X}_{1, } {X}_{2, \dots .}{X}_{n}$ are the predictors or independent variables (large-scale climate indices).

The methodology for generating the GEP model can be presented in the following flowchart presented in Fig. 5.

Fig. 5

Flow chart of the methodology used in this study

The major steps that followed to predict seasonal summer rainfall using GEP are given below:

• a. Random generation of the initial population of the chromosome (genotype) where the length of the chromosome is fixed.

• b. Individual chromosome in the initial population is translated into phenotypes that are expressed by an Expression Tree (ET).

• c. Selection of a best-suited fitness function namely correlation coefficient, mean absolute error, and relative error to evaluate the performance of the developed program.

• d. Selection of the terminal (T) set, and function (F) set to generate chromosome. The selection of these two functions entirely depends on the nature of the problem, users' understanding, and the trial-and-error process.

• e. Selection of the structural organization of the chromosome, which is the combination of head length (h), gene number, and genetic operators. The reproduction of the chromosome is performed by utilizing best-performing individuals’ programs through a genetic operator such as replication, mutation, transposition, and recombination.

• f. Selection of linking functions such as addition, multiplication, subtraction, or division, respectively. It must be selected before the program runs to obtain the equation by connecting all the subtrees.

• g. The development of a new generation program through reproduction is the last step.

• h. Re-application of steps 2 and 7 until the selected termination benchmark is reached.

This study considered root mean square error (RMSE) with parsimony pressure as a fitness function to evaluate the model fitness. Parsimony pressure in the model ensures that the developed model is not overfitted and is in the best-fit conditions. The predictability in the parsimonious model is more accurate compared to the generally developed model. Besides, the selection of the terminal and function set is also of great importance for better prediction model development. The terminal set contains independent variables that get selected from the correlation analysis. The selection of a functional set is usually performed considering the nature of the problem, simplicity to use, and past evidence of the function as an efficient and effective tool. For this study, the climate indices that showed the highest significant correlation with seasonal rainfall were selected as a terminal set, where the selected functional set has been presented in Table 3. Table 3 also presents the genetic operators used to create genetic variation in the chromosome population. As required for the problem encountered, random models were generated with a combination of the function set and terminal set until they reached a valid solution. As suggested in Ferreira (2001) and Guven and Aytek (2009), the chromosome gene number was set as a minimum of 3 to a maximum of 6, the head length was set from 6 to10, and “addition” was considered as the linking function.

Table 3 Initial setting of the GEP model

3.5 Performance metrics

Development of prediction models require evaluating the model performances; thus, several statistical metrics were used such as root mean square error (RMSE), mean absolute error (MAE), Nash–Sutcliffe efficiency (NSE), and refined Willmot index of agreement (${d}_{r}$). Among them, $RMSE$ and $MAE$ are the most prominent method of error measurement in hydro-informatics, where a lower value of $RMSE$, and $MAE$ indicates a better predictability performance of the model (Saigal and Mehrotra 2012; Singh et al. 2005; Shabani et al. 2018).

Nash–Sutcliffe Efficiency (NSE) was measured to evaluate the predictability skill of a developed hydrological model as it assesses its goodness of fit (Nash and Sutcliffe 1970). NSE is calculated using the following Eq. (6):

$$NSE=1-\frac{{\sum }_{i=1}^{n}{({P}_{i}-{O}_{i})}^{2}}{{\sum }_{i=1}^{n}{({O}_{i}-\overline{O })}^{2}}$$

(6)

where, ${P}_{i}$ is the predicted value of the ith observation, ${O}_{i}$ is the observed value of the ith observation; $\overline{O }$ observed mean value and $n$ is the number of observations. The $NSE$ value ranges from 0 to 1, where a value of 1 means the developed model is a perfect fit and it has a perfect predictive skill. On the other hand, $NSE$ value equal to 0 indicates the modeled values are as accurate as of the observed mean value; where a value of NSE < 0 indicates there is a severe error in the data and the observed mean is a better predictor compared to the developed model. Thus, $NSE$ value close to 1 ensures the predictive skill of a model (Gupta and Kling 2011; McCuen et al. 2006).

Refined Willmot Index of Agreement (${d}_{r}$) is another new statistical parameter introduced by Willmott et al. (2012) to evaluate the skillfulness of the developed model. It specifies the sum of the magnitudes of the differences between the predicted and observed deviations from the observed mean relative to the sum of the magnitudes of the perfect model (${P}_{i}={O}_{i}$, for all$i$) and observed deviations from the observed mean. The refined index of agreement (${d}_{r}$) can be calculated using the following Eq. (7):

$$d_r = \left\{ \begin{gathered} 1 - \frac{{\sum_{i = 1}^n \left( {P_i - O_i } \right)}}{{c\sum_{i = 1}^n \left( {O_i - \overline{O}} \right)}}, when \hfill \\ \sum_{i = 1}^n \left( {P_i - O_i } \right) \le c\sum_{i = 1}^n \left( {O_i - \overline{O}} \right) \hfill \\ \frac{{c\sum_{i = 1}^n \left( {O_i - \overline{O}} \right)}}{{\sum_{i - 1}^n \left( {P_i - \overline{O}} \right)}} - 1, when \hfill \\ \sum_{i = 1}^n \left( {P_i - O_i } \right) \ge c\sum_{i = 1}^n \left( {O_i - \overline{O}} \right) \hfill \\ \end{gathered} \right\}$$

(7)

where, ${P}_{i}$ is the predicted value of the ith observation, ${O}_{i}$ is the observed value of the ith observation,

$\overline{O }$ is the observed mean value and $n$ is the sample size. A “$c$” value equal to 2 is suggested in the equation. The “${d}_{r}$” value ranges from –1 to + 1, where a positive value indicates a good fit, while a negative value indicates the opposite.

4 Results and discussion

4.1 Preliminary analysis

In this study, a single correlation or Pearson correlation $(r)$ was used to evaluate the lagged relationship between climate indices and seasonal rainfalls of Western Australia. Four rainfall stations from the Kimberley region of NWWA were selected to conduct this study. At first, single correlation analyses were performed between climate indices and seasonal rainfall to identify potential predictors. It was observed that for Kimberley, maximum rainfall occurred in the summer season. This study evaluates the influences of selected climate indices on summer rainfall for the Kimberley region. Climate indices with statistical significance (at 1% and 5% levels) were considered for further analysis. All these analyses were performed using the IBM SPSS Statistics 26 software package.

4.1.1 Single correlation analysis

Once the rainfall data and climate data were extracted from the database, bivariate correlation or single correlation analysis was performed to evaluate the lagged relationship between the climate indices and the rainfall events. Seasonal summer rainfall and monthly values of climate indices namely SOI, WTIO, DMI, Nino3.4, Nino3, Nino4, and EMI were considered for the analysis. For the climate indices, lagged monthly values (March_(n-1) to November_n) was used, where ‘n’ is the year for which the seasonal summer rainfall is to be predicted, and (n-1) is the immediately previous year. The outcome of the single correlation analysis is presented in Table 4.

Table 4 Pearson correlation $(r)$ of lagged climate indices with summer rainfall

From the correlation analysis, it was observed that SLP based ENSO index (i.e., SOI) showed great influence on NWWA summer rainfall for the selected rainfall stations. This outcome has been found consistent with the findings of Fierro and Leslie (2013), as they mentioned that SOI has the most robust relationship with November to April rainfall. On the other hand, SST-based climate indices (i.e., Nino3.4, Nino3, Nino4, and EMI) showed very little influence on summer rainfall. Moreover, DMI which is the indicator of IOD did not show any influence at all (except for the station- Quanbun Downs). This finding is aligned with the available literature, where the researchers demonstrated that SLP based climate index (SOI) has influence on NWWA summer rainfall and SST based ENSO, ENSO Modoki (EMI) index, and IOD has no significant impact on it. However, tropical Indian ocean indices may have a positive impact (Lin and Li 2012; Shi et al. 2008). Furthermore, the data presented in Table 4 also confirmed that WTIO has a significant correlation with summer rainfall for all the selected stations in NWWA.

4.2 MLR model development

4.2.1 Multiple linear regression analysis

From this outcome of single correlation analyses, various MLR model sets with a different combination of lagged indices (WTIO-SOI, WTIO-Nino4, WTIO-Nino3, and DMI-SOI) were developed. The description of the model sets has been presented in Table 5.

Table 5 Multiple regression model sets for selected rainfall stations in the Kimberley region

The outcome of the MLR model sets has been presented in Table 6. The multiple linear regression model output showed that Pearson correlation $(r)$ has increased compared to the single correlation analyses. From Table 6, it is observed that the WTIO-SOI model showed the highest correlation compare to the other combination model. Therefore, the lagged WTIO-SOI model has been considered as the best model for the selected rainfall stations. The best model for each of the rainfall stations with associated regression coefficient, Pearson correlation $\left(r\right),$ Durbin-Watson (D-W), Tolerance (T), and VIF values are presented in Table 7. It can be observed that all these models have satisfied the requirements of having no autocorrelations among the residuals and the predictors.

Table 6 Pearson Correlation (r) results with the different model sets in MLR

Table 7 Summary of the regression model

A validation test was carried out to evaluate the appropriateness of the model selection in the calibration period. Statistical parameters such as Pearson correlation $(r)$, $RMSE, MAE$, and refined Willmot index of agreement (${d}_{r}$) were calculated. A Comparative demonstration of the statistical parameters for the MLR model in both calibration and validation period has been presented in Table 8. From Table 8, it is noticeable that comparatively high Pearson correlation $\left(r\right)$ and refined Willmot index of agreement (${d}_{r}$) values are evident in the validation period, where $RMSE$ and $MAE$ values were relatively low if compared to the calibration period.

Table 8 Model description of the selected MLR model both in calibration and validation period

4.3 ARIMAX model development

4.3.1 Exogenous input/ predictors, ARIMA order, and transfer function input selection

In ARIMAX model development, climate indices that exhibit significant correlation in single correlation analysis were selected as exogenous input. Several ARIMAX model sets were developed with different lagged climate indices combinations (WTIO-SOI, WTIO-Nino4, WTIO-Nino3, and DMI-SOI) to evaluate their predictability performance. The IBM SPSS Statistics 26 software package was used for all of these analyses.

In the identification stage, summer rainfall and climate indices data were analyzed. Rainfall and climate indices were found as non-stationery and rainfall patterns as non-seasonal. However, in the ARIMAX model, data sets are needed to be stationary, therefore differencing (d) of the data was performed. Figure 6 depicts the data condition before and after differencing was performed for the station—Anna Plains. A similar approach has also been applied for the rest of the rainfall stations and selected climate indices.

Fig. 6

Rainfall data for Anna Plains: a before differencing, b after differencing

To select the AR and MA order in the ARIMAX model, ACF and PACF plots were drawn for the selected rainfall stations. AR order is selected from the PACF plot and MA order is selected from the ACF plot, considering the spike outside of the boundary lines and some other guidelines to select the appropriate order. Figure 7 presents the ACF and PACF plots with respective lag numbers for rainfall station—Anna Plains. ARIMAX (0,1,1) order was found as appropriate for Anna Plains and a similar approach has been applied for the rest of the rainfall stations. Table 9 presents the selected ARIMA orders and transfer function orders for all the rainfall stations considered in this study.

Fig. 7

Rainfall data for Anna Plains: a ACF plot and b PACF plot

Table 9 ARIMA and transfer function orders

4.3.2 ARIMAX model development and selection of best forecast model

Once all the requirements of the ARIMAX model set up were satisfied, several ARIMAX models with the combination of influential indices namely WTIO-SOI, WTIO-Nino4, WTIO-Nino3, and DMI-SOI were developed. Table 10 presents a different combination of ARIMAX model sets with respective Pearson correlation $(r)$ values.

Table 10 Pearson correlation (r) results with the different model sets in ARIMAX

From Table 10, it is eminent that the WTIO-SOI model combination depicted the highest correlation statistics compare to the other combination sets except for Anna Plains. For Anna Plains, both WTIO-SOI and WTIO-Nino4 showed a good correlation, however, to keep the model set simple and consistent with other rainfall stations, WTIO-SOI model set was selected for further model development.

The statistical performance of the best models during the calibration period has been presented in Table 11. For Anna Plains, Bidyadanga, Gogo Station, and Quanbun Downs, the model sets with the highest correlation values are WTIO_Aug-SOI_Mar, WTIO_Aug-SOI_May, WTIO_Aug-SOI_Mar, and WTIO_Oct-SOI_Nov with correlation ($r$) values of 0.83, 0.68, 0.65, and 0.53. Except for Quanbun Downs, all the remaining rainfall stations showed good predictability for at least four months lead time. This confirms the selected models’ prediction capability at least four months in advance. Many other models were also found with longer lead times but having lower correlation values, or higher errors for these selected stations, hence they were not chosen as the best model.

Table 11 Model description of the selected ARIMAX models in the calibration period

Once the best model got selected, a diagnostic check was carried out to verify the accuracy of the developed model. To check the autocorrelation of the residuals, a Ljung-Box test was performed. From this test, it was found that the residuals are being white noise for all the rainfall stations as the $p$-values for all the selected models were found as greater than 0.05 (Ljung and Box 1978). Another approach for such a check was to draw a residual ACF and PACF plot and check for the spikes. If the spikes are found to stay between the boundary lines (at least by 95%), it indicates the residual is white noise. Figure 8 presents the evidence that all the spikes are within the boundary lines, thus, no autocorrelation is present among the residuals.

Fig. 8

Residual ACF and PACF plots for a Anna Plains, b Bidyadanga, c Gogo Station and d Quanbun Downs

Once the ARIMAX model got developed, a validation test was performed for the selected model set. Table 12 presents the model description for the developed ARIMAX models in both calibration and validation periods. In the validation tests, the Pearson correlation $(r)$ increased significantly for all the rainfall stations except Anna Plains. An increase in refined Willmott index of agreement (${d}_{r}$) was also observed for the same. Similarly, a reduction in error values is also an indicator of the models’ prediction performance as observed, in particular for Bidyadanga.

Table 12 Model description of the selected ARIMAX model both in calibration and validation period

4.4 GEP model

For GEP model development, the most influential predictors were selected from the correlation analyses between summer rainfall and climate indices. Among four rainfall stations, Bidyadanga and Gogo Station’s summer rainfall exhibited a significant correlation with WTIO and SOI. For Anna Plains, WTIO, SOI, and Nino4, and for Quanbun Downs, WTIO, DMI, SOI, and Nino3 showed a significant correlation. Considering the facts, several model sets having different combinations of climate indices were developed and their performances were evaluated. While preparing the model sets, only one climate index from each Indian and Pacific Ocean was selected. Such selection was necessary so that any autocorrelation effect between Indian Ocean indices (i.e., WTIO, DMI) and Pacific Ocean Indices (i.e., SOI, Nino3, and Nino4) is avoided.

4.4.1 GEP model development and selection of best forecast model

GEP model development is not that straight-forward as several trials and errors are required to obtain optimum output from the developed model. This involves setting up and deciding on appropriate parameters (i.e., head size, gene number, and linking function). Head size and gene numbers are often get modified to achieve optimum results. To keep the model equation simple, head size is usually kept limited to 7–10 and gene number is set between 3 and 6. For this study, in particular, keeping head size 9 and gene number 5 has been found as most suitable. Furthermore, “addition” is found as best suited as the linking function. Several GEP models were developed using different combinations such as DMI-Nino3, DMI-SOI, WTIO-SOI, WTIO-Nino3, and WTIO-Nino4 for the Kimberley region. All these analyses were performed using the ‘GeneXpro-Tools 5’ software. Table 13 presents different model sets prepared with influential climate indices using the GEP method and their respective Pearson correlation $(r)$ values.

Table 13 Pearson correlation (r) results with the different model sets in GEP

As illustrated in Table 13, the WTIO-SOI model showed good prediction performance in all four rainfall stations. Apart from the WTIO-SOI model, WTIO-Nino3 also showed good predictability for Quanbun Downs only. However, to obtain a consistent and user-friendly model set for all these stations, only WTIO-SOI models were analyzed further. Table 14 presents the selected best models for each rainfall station with their statistical performances both in the calibration and validation period.

Table 14 Model description and selection of best GEP model in calibration and validation period

Table 14 shows that the Pearson correlation $(r)$ is increased in the validation period for all the selected rainfall stations except for Quanbun Downs. For all these models, relatively low $RMSE,$ and $MAE$ values also indicate them as good prediction models. Also, the $NSE$ values ranged from 0.57 to 0.72 in the calibration period and from 0.45 to 0.70 in the validation period respectively, suggesting a good fit. Overall, for all the developed models, the $NSE$ value has been found as above 0.50 that indicates a good fit for all the models. The refined Willmott index of agreement (${d}_{r}$) value close to or more than 0.70 in both calibration and validation period also indicates the skillfulness of the developed model. All the developed GEP models showed prediction capability of the seasonal summer rainfall four months in advance except for Quanbun Downs, in which the prediction deemed possible only one month in advance. Many other models were found with longer lead times but having lower correlation values, or higher errors for these selected stations, hence they were not chosen as the best model. During the evaluation procedure, it was discovered that as the number of generations increases, so do the correlation values. The correlation value, however, does not increase after reaching an optimum level. The number of generations got too big for a few stations to discover an optimal solution, and the statistical performance of those models appeared to be poor.

GEP models offer a unique feature of the model expression structure in terms of Expression Trees (ETs). The procedure of obtaining the output equation from ET has already been discussed in earlier Sect. 3.3.1. As an example Fig. 9 shows the ETs of Anna Plains. Furthermore, Table 15 presents the output equation only for the best model from each station considering higher correlation values with lower errors.

Fig. 9

Expression tree of anna plains

Table 15 Output equation of best developed GEP model for the selected rainfall stations

4.5 Comparisons between MLR, ARIMAX, and GEP model

The statistical performance indicators of the best models developed using different forecast methods are presented in Table 16, where indicators like Pearson correlation $(r)$, refined Willmot Index of Agreement (${d}_{r}$), RMSE and MAE values for the selected model sets are presented. A schematic diagram of how the best performing models were selected for each stations are presented in Fig. 10.

Table 16 Comparison of Pearson’s correlation ($r$), refined Willmot index of agreement (${d}_{r}$), RMSE and MAE between MLR, ARIMAX, and GEP model

Fig. 10

A schematic diagram of selection of best performing model

For, Anna Plains, the WTIO_April-SOI_Mar model developed using MLR showed its capability to forecast summer rainfall eight months in advance with a correlation of 0.36 and 0.42 in calibration and validation periods respectively. However, for the ARIMAX model a different model set, WTIO_Aug-SOI_Mar showed its capability of forecasting four months before the event with a correlation of 0.83 and 0.65 in calibration and validation periods, respectively. The same model set, i.e., the WTIO_Aug-SOI_Mar model developed using GEP showed similar forecasting capability as ARIMAX (i.e., four months in advance), with a significant correlation of 0.82 in both calibration and validation period.

For Bidyadanga, the WTIO_Aug-SOI_Nov model set developed using MLR showed a significant correlation of 0.44 and 0.51 in the calibration and validation periods, respectively. It showed a prediction capability of one-month in advance. In both ARIMAX and GEP methods, the WTIO_Aug-SOI_May model set showed promising performance pertaining high correlations in both calibration and validation periods. In calibration and validation periods, the ARIMAX model returned a correlation value of 0.68 and 0.77 respectively, wherein for the GEP model, the correlation values obtained were as high as 0.85 and 0.87 respectively. Both the model sets showed their prediction capability four months in advance.

For Gogo Station, the WTIO_Aug-SOI_Mar model set showed the best correlation in MLR, ARIMAX, and GEP methods, whereas, WTIO_Oct-SOI_Nov model set was outstanding in performance for Quanbun Downs. For Gogo Station, Pearson correlation values for calibration and validation periods were found as 0.36 and 0.35 (MLR), 0.65 and 0.74 (ARIMAX), and 0.76 and 0.78 (GEP). Similarly, for Quanbun Downs, correlation values were reported as 0.32 and 0.36 (MLR), 0.53 and 0.59 (ARIMAX), and 0.76 and 0.74 (GEP) in calibration and validation periods, respectively. For Gogo Station, the selected model has been found as capable to predict four months in advance, where, for Quanbun Downs, the selected model can predict just a month earlier than the actual event.

While the performance of the forecasting methods is compared in terms of Pearson correlation $(r)$ values, it is evident that GEP models have shown impressive performance than the other two methods. In calibration and validation periods, the correlation $(r)$ value in the GEP model ranged from 0.76 to 0.82 and 0.74 to 0.87, respectively. These correlation values are quite outstanding compared to MLR model (0.32 to 0.36 in calibration and 0.35 to 0.51 in validation period) and ARIMAX model (0.53 to 0.83 in calibration and 0.59 to 0.77 in validation period). This is also depicting a greater underlying contribution of the predictors is evident in the developed models, as a Pearson correlation $(r)$ value of more than 0.5 is considered as a large effect (Field 2013).

A similar observation about the GEP model’s superiority over others was made in terms of the refined Willmot index of agreement (${d}_{r}$) values. The refined Willmot index of agreement (${d}_{r}$) value is an indicator of the model fitness, where, a relatively high positive value indicates a good fit (Willmott et al. 2012). In the GEP model, the ‘${d}_{r}$’ value in calibration and validation period ranged from 0.69 to 0.75 and 0.65 to 0.75 respectively. Such positive ‘${d}_{r}$’ values are a good indicator for GEP model’s prediction capability over MLR and ARIMAX models.

The MLR, ARIMAX, and GEP models were further compared considering their error measurement statistics. As presented in Table 16, the developed GEP model returned relatively low RMSE and MAE values in both calibration and validation periods, while compared to the MLR and ARIMAX models. As a lower value of RMSE and MAE indicates a better predictability performance of the developed models, the GEP model can be considered as best compared to the rest of the developed models (Saigal and Mehrotra 2012; Singh et al. 2005).

To understand the predictability performance of the developed models at different rainfall stations, observed versus predicted plots were drawn for selected MLR, ARIMAX, and GEP models. As presented in Fig. 11, it is evident that the GEP model showed prominent prediction performance as almost mimicking the trend of the naturally occurred rainfall events. GEP model’s trend also demonstrated its capability of capturing extreme events such as heavy rainfalls and droughts. As observed, the ARIMAX model showed moderate prediction performance as it successfully captured some of the extreme events while been failed in other instances. In contrast, the MLR model showed relatively poor performance among all the three techniques, capturing none of the extreme events as well as demonstrating instances of underestimation and overestimation of the events. Both MLR and ARIMAX models, being a linear and time-series approach respectively were outperformed by the non-linear GEP model in which the existing non-linear relationship between rainfall and climate indices was considered to better explain the underlying variability.

Fig. 11

Comparison between MLR, ARIMAX, and GEP models’ prediction performances for a Anna plains, b Bidyadanga, c Gogo Stations, and d Quanbun downs

5 Conclusion

In this study, the rainfall forecasting capability of an artificial intelligence method (i.e., GEP) was evaluated against the conventional linear method (i.e. MLR) and time-series technique (i.e., ARIMAX), where lagged climate indices were used as input variables. Monthly summer rainfall events for four stations located in the Kimberley region of NWWA were analyzed, and the investigation resulted in the identification of influential climate indices and their interactions responsible for the region's summer rainfall variability. Climate indices namely WTIO and SOI were found as the most dominant factor contributing to the rainfall events for the NWWA region. Thus, several model sets were developed using the combination of WTIO-SOI at different lagged months and used as the input sets for MLR, ARIMAX, and GEP models. To achieve the best prediction results, a different combination of model sets were analyzed for different techniques that returned different prediction performances for different models at different lead times.

Overall, the prediction model developed using the GEP technique showed good predictability compared to MLR and ARIMAX techniques for all four rainfall stations. The WTIO-SOI model set for the GEP model showed a high correlation ranging from 0.76 to 0.85 in the calibration period and 0.74 to 0.84 in the validation period. For all the stations, the GEP model set showed a prediction capability of up to four months in advance except for Quanbun Downs, where the prediction was made possible just a month earlier of the event. For Anna Plains, the MLR model showed a prediction capacity of up to eight months in advance, however, the correlation coefficient values were comparatively low, depicting poor prediction performance. In conjunction with the correlation coefficient being used as a performance evaluator, other statistical parameters also suggested the superiority of the GEP model over two other alternative methods. These include a substantial increase in the refined Willmott index of agreement (${d}_{r}$) for calibration and validation periods as well as low error measurements in RMSE and MAE values. Apart from these justified indications, GEP models explicitly offered the form of the functions utilized in the system as well as an easy-to-understand mathematical presentation.

Nonetheless, the outstanding performance of the GEP model to predict NWWA’s summer rainfall is quite impressive, however, improvisation of the model’s prediction performance is a never-ending process until the prediction equates to the observation. Thus, further study can be performed to explore the outstanding variability that remained unexplained (i.e., residuals) by the developed model. The best possible approach could be developing a hybrid model as any linear or nonlinear model by itself may not be able to explain all the underlying mechanisms involved in a complex rainfall generation system. Based on the findings obtained in this study, residual analysis of ARIMAX models to feed-in into the GEP models and vice-versa may result in improved forecasting of the rainfall in the region.