1 Introduction

The El Niño-Southern Oscillation (ENSO) is the dominant seasonal to inter-annual climate variation generated through coupled interaction between atmosphere and ocean in the tropical Pacific (Bjerknes 1969). El Niño is the warm phase of ENSO and can exert its influence on large-scale changes in climate regionally as well as remotely through atmospheric teleconnections, affecting extreme weather events worldwide (Diaz et al. 2001; Alexander et al. 2002; McPhaden et al. 2006). There is ample evidence for the close relationship between El Niño and climate anomalies across the globe (Wallace et al. 1998; White et al. 2014; Luo and Lau 2019). As El Niño evolves at a slower rate compared to the weather system and is one of the most predictable climate fluctuation on the earth (on lead times of up to several months) (Goddard et al. 2001; Wang et al. 2020b), it can be used in statistical prediction models to make seasonal forecasts which are unfeasible for dynamical prediction models. One example is the seasonal forecast of tropical cyclones (Wahiduzzaman et al. 2020). Therefore, a long-time lead and skillful prediction of El Niño is crucial and necessary for decision makers when estimating climate anomalies (Capotondi and Sardeshmukh 2015; Wang et al. 2020a). During the past decades, there were numerous efforts to improve El Niño prediction (Latif et al. 1998; Mason and Mimmack 2002; Tang and Hsieh 2002; Luo et al. 2008; Clarke 2014; Tao et al. 2020). The most severe restriction to long-lead time El Niño prediction is the so-called spring prediction barrier (SPB), referring to a rapid decrease in prediction skill in boreal spring (Zheng and Zhu 2010; Duan and Wei 2013; Duan and Hu 2016). Prediction schemes including complex climate models and statistical approaches have relatively limited prediction power for long-lead (over 6 months) forecasting due to the SPB (Collins et al. 2002). In order to solve the SPB problem, statistical El Niño prediction approaches based on complex network analysis have been introduced, which extend El Niño prediction to 1 year in advance (Ludescher et al. 2013, 2014; Meng et al. 2018; Ludescher et al. 2019). Since climate fields such as temperature can be interpreted as a climate network (Yamasaki et al. 2008; Gozolchiani et al. 2011), predictions have benefited from network representations of El Niño-related climate variables. In the established network, different regions of the world are regarded as nodes, which interact with each other by exchanging heat and material, etc., and these interactions are the links of the whole climate network (Steinhaeuser et al. 2010). After the pioneering work of Ludescher (Ludescher et al. 2013), similar approaches were conducted aiming at further improvements of El Niño prediction using climate network (Fan et al. 2017, 2018; Meng et al. 2020). All of these predictions are formed in a similar way: if a prediction index crosses a certain threshold from below, it predicts that during some time interval in the future, there will be an El Niño event. More precisely: based on meteorological input data at many nodes, a scalar predictive index is calculated as an indication of link strength. If this index overcomes a threshold value with other conditions satisfied, the El Niño index is expected to become positive within a certain time window. If so, this is counted as a successful prediction, otherwise, it is a false alarm. If a positive ENSO phase occurs without prior threshold crossing of the predictive index within the given time window, this is regarded as a missed hit. The differences between these methods lie in the choice of input climate variables, area of nodes for establishing network, and how link strength is measured, which one could call “technical details”, but also might be decisive for prediction skill. According to the reported hit rates and false alarm rates, these methods are very promising and seem to have solved the SPB problem.

However, due to the length of the time window during which the positive ENSO phase might occur after the threshold crossing of the predictive index, and the quasi-periodic occurrence of ENSO itself (Gaucherel 2010; Zhang and Zhao 2015), it is not easy to see whether these predictions have real predictive skill or are just a consequence of the rather generous interpretation of success together with the regularity of the ENSO phenomenon. In the original publications, the authors provided performance measures to evaluate prediction skill, for example, by reporting the receiver operating characteristic (ROC) curve or splitting their data into training and test sets (Ludescher et al. 2013). However, there is no common performance measurement to compare these works, and in particular no comparison to a benchmark predictor. Besides, it is not evident how to provide a benchmark prediction in these studies. Therefore, in this paper, we develop a benchmarking method that can estimate and compare prediction skills, aiming at providing a reference for improving El Niño predictions in the future.

2 Existing climate network-based ENSO prediction schemes

In this paper, we take two existing climate network-based El Niño prediction models from separate studies as examples and create benchmarks to estimate and compare their predictability. One scheme is from Ludescher’s pioneering work (Ludescher et al. 2014) and the other one is from Meng’s work (Meng et al. 2018). Both papers develop a prediction index based on climate network analysis and give an El Niño warning for the next year or next 18 months when the index crosses a given threshold from below. However, due to relatively complicated conversion of the generated predictive index series into the forecasts of events, it is not perfectly transparent how much of the performance is due to skill of the predictive index, and how much is due to suppressing spurious forecasts by the conversion into event prediction.

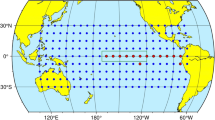
In order to make our paper self-contained, we describe in this section in some detail previous work. Both studies define an index to represent the degree of cooperative resp. disorder between nodes in certain basins. This index is based on the time evolution of the link strength between the nodes i and j. In Ludescher’s work, links are established between nodes of two basins: the “El Niño basin” (i.e.,the equatorial Pacific corridor) and the rest of the Pacific Ocean. In the other study, only nodes from the Niño3.4 area (i.e., \(5^{\circ }\)S–\(5^{\circ }\)N, \(120^{\circ }\)W–\(170^{\circ }\)W) are used (see Fig. 1). The procedures to calculate these finite time-window cross-correlations between different nodes are identical in both studies, as the time-delayed cross-covariance function is defined:

$$\begin{aligned} C^{(t)}_{i,j}(-\tau )=\frac{\left<T_i(t)T_j(t-\tau )\right>-\left<T_i(t)\right>\left<T_j(t-\tau )\right>}{\sqrt{\left<(T_i(t)-\left<T_i(t)\right>)^2\right>}\sqrt{\left<(T_j(t-\tau )-\left<T_j(t-\tau )\right>)^2\right>}} \end{aligned}$$
(1)
$$\begin{aligned} C^{(t)}_{i,j}(\tau )=\frac{\left<T_i(t-\tau )T_j(t)\right>-\left<T_i(t-\tau )\right>\left<T_j(t)\right>}{\sqrt{\left<(T_i(t-\tau )-\left<T_i(t-\tau )\right>)^2\right>}\sqrt{\left<(T_j(t)-\left<T_j(t)\right>)^2\right>}} \end{aligned}$$
(2)

This time-delayed cross-covariance is calculated for each 10th day t during the whole time span in Ludescher’s work. \(T_k(t)\) in the formula (1) and (2) is the daily atmospheric temperature anomaly at node k. In Ludescher’s work, daily surface atmospheric temperatures (1950–2013) are used, which are divided into two parts, i.e. the learning phase (1950.01–1980.12) and the prediction phase (1981.01-2013.12). The data is obtained from the National Centers for Environmental Prediction/National Center for Atmospheric Research Reanalysis I project. They use Niño 3.4 index as the El Niño index. For Meng’s study, they calculate this \(C^{(t)}_{i,j}\) for each month t (the first day where the months starts) in the selected time span (1981.01–2017.12) and the daily mean near surface (1000 hPa) air temperature fields are applied for analyzing the links between nodes in the Niño3.4 basin. In Meng’s work, they used 4 different data-sets separately to establish this link strength. In our paper, we only take the dataset which gives the best result in their paper, i.e. the daily near surface (1000 hPa) air temperature (1979–2018) from the ERA-Interim re-analysis. They use the Oceanic Niño Index (ONI) to represent El Niño’s variation (obtained from https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php). In formula (1) and (2), time lag \(\tau \) is between 0 and 200 days in both models, which can guarantee a reliable estimate of the background noise level (Ludescher et al. 2013; Meng et al. 2018). The brackets denote an average over the past 365 days, according to

$$\begin{aligned} \left<f(t)\right>=\frac{1}{365}\sum _{a=1}^{365}f(t-a) . \end{aligned}$$
(3)

The two studies then convert the set of these \(C^{(t)}_{i,j}(\tau )\) into an index representing the link strength in two different ways. Ludescher et al. define the link strength \(S_{ij}(t)\) as the difference between the maximum and the mean value of the cross-correlations \(C^{(t)}_{i,j}(\tau )\) in the time window, divided by its standard deviation as:

$$\begin{aligned} S_{ij}(t)=\frac{\text {max}(C^{(t)}_{i,j}(\tau ))-\text {mean}(C^{(t)}_{i,j}(\tau ))}{\text {Std}(C^{(t)}_{i,j}(\tau ))}. \end{aligned}$$
(4)

The average of \(S_{ij}(t)\) over all pairs of nodes (i, j) in the whole network forms the index S(t), and its threshold crossing from below is interpreted as a precursor of an El Niño event. The optimal value for this threshold is determined by optimizing the prediction skill on the first half of data (training set, years 1950–1980, as mentioned above). The performance is then tested in the second part of the data (test set, 1981–2013), which is called the prediction phase, and the values of thresholds are further modified to adjust both parts of the data. Prediction skill is evaluated by the hit rate (HR) and false alarm rate (FAR).

In Meng’s study, a forecasting index (FI) is proposed which presents the coherence between the different nodes in the Niño3.4 area. \(C^{(t)}_{i,j}(\theta )\) is the highest peak value of the cross-correlation function, where \(\theta \) indicates the time lag when the function comes to the highest (Meng et al. 2018). The degree of coherence/disorder of the nodes in the Niño 3.4 basin is qualified by the average value of all links at their peak:

$$\begin{aligned} C(t)=\frac{2}{N(N-1)}\sum _{i=1}^{N-1}\sum _{j=i+1}^{N}C^{(t)}_{i,j}(\theta ), \end{aligned}$$
(5)

where N is the number of nodes in the Niño 3.4 basin, \(N=105\). Therefore, higher values of C(t) represent higher coherence in the Niño 3.4 basin. The forecasting index FI is defined as:

$$\begin{aligned} FI(t)=\frac{1}{m+1}\sum _{a=0}^{m}\ln (C(t-a))-\ln (C(t)), \end{aligned}$$
(6)

where m is the total number of months preceding t since the first month of the whole data (i.e. January 1981), so that Eq. (6) denotes the negative anomaly of \(\ln C(t)\). This minus sign was used so that peaks of FI correspond to peaks in the ONI. FI is evaluated from January 1984 for each month (Meng et al. 2018). The threshold set for this model is 0.

Fig. 1
figure 1

The climate network area of the two studies which we compared. The network of Ludescher’s work consists of 14 grid points in the El Niño basin (red symbols,including the NINO1, NINO2,NINO3, and NINO3.4 regions and one grid point south of the NINO3.4 region) and 193 grid points outside of this basin (blue symbols). The network of Meng’s study consists of 105 grid points in the NINO3.4 region (yellow symbols)

Full size image

Actually, the rules for making predictions are slightly more involved than just the threshold crossing from below. In Ludescher’s work, it is defined that when the link strength S(t) crosses the threshold from below and simultaneously the Niño 3.4 index is below 0.5 \(^{\circ }\)C, a warning will be given and an El Niño is expected to start in the following calendar year. In Meng’s work, one needs to track both ONI and FI from the beginning of the previous El Niño. If FI(t) rises from a local minimum for at least two continuous months, the time at which FI(t) crosses 0 (if it is not during El Niño/La Niña period, i.e. − 0.5 \(^{\circ }\)C < ONI < 0.5 \(^{\circ }\)C) is counted as a potential warning of either El Niño or La Niña event within approximately the next 18 months. Additionally, if there occurs a La Niña event within these 18 months, another El Niño is predicted to occur within 18 months after the end of La Niña. Following these, a true hit of El Niño is counted if within 18 months after the potential signal an El Niño occurs or a La Niña followed by an El Niño within the next 18 months occurs, otherwise, it is counted as a false alarm.

3 Benchmarking methodology

Generally, prediction skill can be estimated by comparing the proximity of both the prediction and a benchmark to the observations (Pappenberger et al. 2015). A forecast can only be regarded as skillful if it has more prediction power than benchmark forecasts (Jolliffe and Stephenson 2008). Common benchmarks contain naïve forecasts, namely based on either climatology or on persistence (Cattell 1991). As a benchmark, climatology is useful for phenomena with strong seasonality, while prediction based on persistence works for short range forecast (Harrigan et al. 2018). A forecast scheme based on persistence often shows good predictability for short lead times and the prediction skill breaks down afterwards (Chiera et al. 2009).

El Niño predictions can be roughly divided into 2 types. One is the forecast of SST anomalies or of the index in the Niño basins, spanning the westernmost Niño-4 area to the easternmost Niño1+2 region, in which the Niño indices or results from other models are often used as benchmarks to verify El Niño prediction skill (Jin et al. 2008; Barnston et al. 2015; Tseng et al. 2017). The other one is as what we reported above, namely the two-category outlooks (above or below threshold), acting as a categorical (or binary) forecast for telling whether there will be an El Niño event or not (Fan et al. 2018; Meng et al. 2020). These climate network-based El Niño predictors are data based, which means that they do not use a physical model of the process but instead make use of correlations and dependencies between different data sets. For such type of forecasts, a classical way is to use surrogate data as a benchmark: one would generate artificial random time series of the predicative index, which share essential statistical properties with the true predictive index series. Conventionally, these properties are the auto-correlation function (or power spectrum), and the marginal distribution (Schreiber and Schmitz 2000). These surrogate data are otherwise random, thus their predictive skill will provide a benchmark compared with any truly skillful predictor. However, for short data sets, the generation of appropriate surrogates is error prone, so that this benchmark is hard to obtain. In Ludescher’s work (Ludescher et al. 2013), instead, a randomization of blocks of annual data was used which destroys correlations on time scales of more than one year. We propose here a modification of the method of surrogate data as a quantitative assessment of the predictive skill for statistical data based El Niño prediction.

3.1 Typical patterns in ONI time series

Before introducing our surrogates for benchmarking, we firstly extract typical patterns in the Oceanic Niño Index (ONI) time series from 1950 to 2019 denoted as x in formula (7).

$$\begin{aligned} E(x(\sigma )|\alpha ) = \frac{1}{n}\sum _{t: |x_t-\alpha |<\epsilon } x_{t+\sigma }, \end{aligned}$$
(7)

where \(\alpha \) is the value of the condition, \(\epsilon \) is some tolerance which controls how rarely or how frequently the condition will be satisfied by the data, n is the number of time indices t fulfilling the condition and \(\sigma \) is the lead time for forecasting. Whenever \(x_t \in [\alpha -\epsilon ,\alpha +\epsilon ]\), \(x_{t+\sigma }\) contributes to the corresponding conditional value. Hence, we calculate the climatological future of \(x_t\) fulfilling the condition. One can also interpret those values \(x_{t+\sigma }\) where \(x_t\) satisfies the condition as an empirical ensemble, and \( E(x(\sigma )|\alpha )\) is the ensemble mean.

A simple El Niño forecast can be achieved by applying this conditional average method, with a slightly more complicated condition: in addition to \(x_t \in [\alpha -\epsilon ,\alpha +\epsilon ]\), \(x_t-x_{t-1}>\delta \) should be ensured, i.e., that the signal \(x_t\) is rising with a slope larger than \(\delta \) when crossing the threshold \(\alpha \). One can also interpret this in the sense of the analogues method, see Lorenz (Lorenz 1969). Figure 2 (left) shows the conditional expectations of the ONI index over lead time \(\sigma \) for different threshold values \(\alpha \). Negative \(\sigma \) are also considered, i.e., the average signal before it satisfies the condition. The pattern as a whole shows that before and after an El Niño event, the ONI index has the tendency to be negative, which is in agreement with the fact that successive El Niño events are typically separated by several years.

We choose the tolerance \(\epsilon \)=0.3 in order to find sufficiently many segments of ONI(t) which match the condition. \(\delta \) is set to be 0.3 to ensure that the time series is increasing within the tolerance of certain \(x_{t}\). We take 6 different condition values, \(\alpha =0.6, 0.3, 0, -0.3, -0.6\). According to Fig. 2 (left), the conditional average signals of ONI with different \(\alpha \) all grow and reach a maximum after about 8 months, which indicates that on average an El Niño is expected to reach a peak after these 8 months. For \(x_t=0.6\pm \epsilon \) (i.e. \(\alpha \) = 0.6), it is already during the onset of an El Niño, hence the whole result is not surprising but merely a proof of what we already know. When we lower \(\alpha \) to 0, still the conditional average shows the signature of an El Niño, which actually is so merely because in addition we require the slope of the ONI to be positive. So this threshold crossing with a positive slope can be used as an El Niño forecast, where the onset occurs on average already 1-2 months later (at \(\sigma \) = 1 or 2), and the peak occurs around the month 8. Hence, if we use the analogue forecast to predict El Niño based on the ONI itself, the lead time is much less than 1 year. This simple prediction can be used as a benchmark to the climate network-based El Niño prediction.

Fig. 2
figure 2

Conditional average of ONI (If ONI reaches \(\alpha \) ± \(\epsilon \) at any time t, the conditional ONI calculates the average of all ONI values after a time \(\sigma \) (i.e. conditioned on the value of \(\alpha \)). Trivially, conditional ONI at \(\sigma =0\) is identical to \(\alpha \) (within ± \(\epsilon \)); left: based on ONI index itself with \(\epsilon \) = 0.3, \(\delta \)=0.3; right: based on two climate network-based El Niño prediction models; at \(\sigma =0\) the predictive index crosses its respective threshold)

Full size image

3.2 Conditional average of ONI given by network-based El Niño prediction models

We use the method of conditional averages now to examine the network-based forecasts as well to make a comparison of both models. The statement in Ludescher’s (2014) and Meng’s work (2018) is that if their respective predictive index (built on external inputs) crosses a certain threshold from below and not during certain ENSO period, then there will be an El Niño event in the future (where “future” is slightly different in the two forecast schemes). We therefore calculate the conditional expectation value of real ONI, where the condition is that the predictive index of either forecast method crosses its respective threshold from below.

The result is shown in Fig. 2 (right). According to Fig. 2 (right), for the predictions given by the index S(t) of Ludescher et al., El Niño onset (i.e., ONI\((t)>\)0.5, crossing blue dashed line) occurs around 12 months after the warnings, while from Meng’s index, this prediction lead time is shorter (i.e., the time when the red dashed line crosses the blue dashed line). Additionally, the peak value of the conditional average of ONI obtained from Meng’s prediction index is much smaller than that from Ludescher’s work, indicating that the response of ONI to the threshold crossings of FI is less specific or the prediction lead time is less stable. This difference can be partly explained by Fig. 3, in which we present the temporal distribution (0-24 months after the warning is given) of the real El Niño onsets after a warning is given by these two models. In Ludescher’s work, the prediction period is between 1980–2013, during which 8 warnings are given; while in Meng’s work, the model covers the period between 1984–2017, and 11 warnings are given by Meng’s model (Fig. 4). In Fig. 3, month 0 on the vertical axis indicates again that the corresponding predictive index crosses its threshold from below with extra conditions satisfied, this is the time of the given warning. The color bar represents the value of the observed ONI in the following 24 months, where the color changing to reddish indicates the ONI values > 0.5 (El Niño starts). The x axis indicates each warning given by these two models. For example, the warning 1 in the left panel, real El Niño starts 15 months after this warning (color turns to reddish), while warning 3 is launched 6 months before the El Niño starts. From Fig. 3, we can see that El Niño occurs at least 6 months later when a warning is given by Ludescher’s model (reddish appears after month 6). However, the lead time of Meng’s model is less stable, some is very long to 2 years (for example, warning 1 in the right panel of Fig. 3), while some even smaller than 4 months (for example, warning 7).

Fig. 3
figure 3

Temporal distribution of predicted El Niño onset given by climate network-based El Niño prediction models and the following real ONI (left: Ludescher’s model, the original model covers the period of 1980–2013, during which the model gives 8 warnings; right: Meng’s model, the original model covers the period of 1984–2017, during which the model gives 11 warnings)

Full size image

Figures 2 and 3 suggest that the prediction lead time for El Niño forecast is more stable in Ludescher’s model, because of a more homogeneous El Niño response. The authors of both papers claimed that their climate network-based method would extend El Niño prediction lead time so that the spring barrier problem might be overcome. We verify by Figs. 2 and 3 that the onset of El Niño starts on average more than 6 months after the respective warning. However, the lead time for prediction is not stable, especially in Meng’s model.

Fig. 4
figure 4

Reproduction of the predictive indices from two cited papers and their 2-year shifted version (left: Ludescher’s model; right: Meng’s model. The green shades under the Niño index curve are the El Niño period. True forecasts are marked by the green lines; false alarms are marked in the orange dashed lines)

Full size image

3.3 Compare two prediction models in a relatively fair way

Fig. 5
figure 5

Temporal distribution of predicted El Niño onset at the exact lead time given by climate network-based El Niño prediction model and the following real ONI value during the period of 1984–2013 (left: Ludescher’s model; right: Meng’s model. The number inside the bars indicate the real ONI values.)

Full size image
Fig. 6
figure 6

Comparison of two models during the period of 1984–2013 by HR and FAR at the exact lead time (top: Meng’s model; bottom: Ludescher’s model)

Full size image

In the original papers, the prediction performance was quantified by considering the hit rate HR and false alarms rate FAR under some additional rules, which convert the threshold crossing into a warning. Figure 3 illustrates that we need additional benchmarks in order to fully understand the power of these two forecasts schemes. In Sect. 4.1 we will introduce our benchmark method for comparing these two models in their original spirit, which is the main methodological contribution of this paper. Here, however, we compare these two models by a warning scheme for both of them in order to assess: (1) their accuracy under the same lead time; (2) which model can give longer lead times under the same accuracy. For that we reproduce these two forecast models (see Fig. 4), i.e., we calculate their respective predictive indices as time series. Our reproduction result is very close to the original paper, although there exist some small differences, due to some technical details not mentioned in the original studies.

The lead time for predictions in both studies are different and also not very exact. For example, Ludescher et al. defined that an El Niño will develop in the following calendar year after their prediction model gives an alarm warning; while the lead time for Meng’s prediction model is over 18 months. Here, we study the performance under the same lead times for both models, so that we can compare them under a relatively same standard. Additionally, we select the same period 1984–2013 (in Ludescher’s model, the prediction series is from 1980–2013; in Meng’s model, the prediction series is from 1984–2017; so we take 1984–2013 as the common period) for both models to compare their separate prediction performance. For a warning, we still use the same conditions as defined in the two original studies. During the period of 1984-2013, there are 7 warnings given by Ludescher’s model and 8 warnings given by Meng’s model (in Fig. 5). In Fig. 5, month 0 on the y-axis denotes when the prediction model launches a warning (similar as in Fig. 3), and we only present the lead time 0–12 months here as an illustration. Additionally, we count separately the number of hits in the lead time interval of 0–24 months and get the false alarms at the same time (false alarm = warnings − hits). We calculate the accuracy, namely the hit rate HR (the number of hits / the number of events) and the corresponding false alarm rate FAR (the number of false alarms / the number of non-events), for both models in these lead time intervals during the common period 1984–2013. Specifically, for every month after the warning, we count in how many cases there is an ongoing El Niño event in this month and calculate the HR and FAR at each exact prediction lead time.The top panel of Fig. 6 presents the performance of Meng’s model under different lead time, which performs better at the lead time of 8–12 months (with highest HR and lowest FAR.) The bottom panel of Fig. 6 is Ludescher’s model, which is superior at the longer lead time (13–17 months). From Fig. 6, we can see that during the same time period (1984–2013), Meng’s model performs better at a shorter lead time than Ludescher’s model (for example, at the lead time of 6 months, Meng’s model gives higher HR and lower FAR than Ludescher’s), while Ludescher’s model outperforms at the longer lead time (for example, at 15 months). Ludescher’s prediction shows less spread of the timing of El Niño around its peak and at peak both modes have equally high hit rate, therefore we conclude that these two climate network-based models indeed serve as a predictor on the annual time scale.

4 A benchmarking method for El Niño predictions

4.1 Circular time shifted sequence as benchmark

Our analysis has revealed that both climate network-based prediction models can forecast an El Niño event at larger lead times than the simple prediction scheme based on the analogues of ONI values (our benchmark of Sect. 3.1). Here we apply a circular shift method as a benchmark for phenomena which like ENSO show oscillations on some typical time scales but are not periodic, where data sets are small and the actual prediction is a complicated function of the inputs. For the binary predication of El Niño (i.e., a yes/no prediction), a benchmark would be a random predictor. If the true predictor gives n warnings, we could generate a time series which contains exactly n level crossings at random time instances. One way to achieve this is to cut the time series of S(t) or FI(t) into segments of 12 months and to randomly re-arrange them (shuffling), although this would introduce a large number of jumps in the new sequences at the cuts. However, it will not be surprising if this shuffling predictor is much less skillful than the original one, since, e.g., two warnings might follow each other with a very short time interval in between, or there might be a gap of many years, while the original predictor has a certain regularity. Hence, we need a method which decouples the time series of predictions from the time series of the true signal, but which conserves relevant properties of the predictions such as modes of oscillation, locking with the seasons, or smoothness.

The El Niño prediction to which we refer contains only 19 El Niño events during the period from 1950 to 2013 (the period used in Ludescher’s pioneering work (Ludescher et al. 2013, 2014)). Moreover, these prediction methods use a time window in which the predicted event should occur. A useful benchmark is required to meet some criteria (Cattell 1991): the first one is relevance, which indicates the ability to capture the characteristic of the original problem. Portability and scalability are also included, which means the benchmark can be used for testing different systems and systems of different sizes. Besides, the benchmark needs to be comprehensible and therefore credible (Vihinen 2012). Following these criteria, we here create a benchmark by using a circular shifting method, which is based on the spirit of the circular block-bootstrapping procedure (Politis and Romano 1994; Wilks 2011). It means that part of the series is shifted into the future and the most recent prediction is wrapped around and will cover the initial time window, where due to the time shift no predictive index is available. So in formula, if the original predictive index is I(t) and is given on the time interval \(t\in [t_0,t_1]\), the shifted index reads:

$$\begin{aligned} {\hat{I}}_ (t) = \left\{ \begin{array}{ll} I(t-\delta t) &{}t \in [t_0+\delta t,t_1 ]\\ I(t_1-\delta t+t) &{} t \in [t_0,t_0+\delta t]. \end{array}\right. \end{aligned}$$
(8)

By this procedure, the temporal correspondence between predictive index and the signal is destroyed, while the overall properties of the index, in particular its potential temporal regularity and its marginal distribution are conserved exactly. We will use integer multiples of years for the shift \(\delta t\), because the El Niño phenomenon is tied to the seasons (17 out of 20 El Niño events from 1950 to 2020 started in the first half year covering MAMJJA and only 3 in SONDJF). If we shifted by intervals less than full years, although there will be more samples in the benchmark surrogate, part of the shifting would destroy the seasonality of the El Niño phenomenon, leading to meaningless results. Therefore, from the 34 years in the two studies we compared, 33 additional values of performance are obtained for the 33 possible shifts. If one of the two signals, forecast or verification, has a slowly decaying auto-correlation function, one should exclude shifts of \(|\delta |<\) the correlation time in order to make sure that the shift really destroys the correlation between forecast and verification. In the case of El Niño, a shift by more than 1 year satisfies this condition.

4.2 Evaluation measures

In the case of climate network-based El Niño prediction as introduced before, the forecast is a binary one, i.e., it predicts whether or not in a given time window in the future there will be an El Niño event. For a binary forecast, there are two types of errors, often called the issue of sensitivity versus specificity: either an event might be predicted to follow but it will not—a false alarm; or an event that was not predicted finally occurs—a missed hit (Kaiserman et al. 2005; Fenlon et al. 2018). Since both errors might induce very different costs, a representation called receiver operating characteristic (ROC) is in use (Kharin and Zwiers 2003; Gönen et al. 2006). It reports the fraction of successfully predicted events (hit rate HR) as a function of the false alarm rate FAR, where the latter is tuned by the sensitivity of prediction scheme. In the El Niño predictions which we mentioned above, hit rates and false alarm rates are calculated either for setting the optimal threshold value or as a quantifier of the prediction skill in both two studies (Ludescher et al. 2014; Meng et al. 2018).

In order to derive a benchmark for these predictors, we calculate the false alarm rates (FAR) and hit rates (HR) for every \(\delta t\) shifted predictive series with a fixed threshold. Since we do not adjust the threshold again but use the same one as the original forecast, these can be assumed to be randomized out of sample predictions. These results will be represented as a scatter plot in the plane of hit rate versus false alarm rate. If the hit rate and false alarm rate of the prediction scheme are better than the performances of all the shifted index series, then this is a clear indication that the predictor performs well due to genuine correlations between predictive index and El Niño index. If instead, performance of the true predictor is inside the skill distribution of the shifted versions of the predictive index, we conclude that it is the similarity of statistical properties of these two time series that give rise to the performance, not the specific correlation between them.

Table 1 Analogous-based El Niño prediction model with different predictability
Full size table

4.3 Benchmarking a naïve El Niño prediction scheme

Fig. 7
figure 7

Frequency distributions of hits and false alarms given by shifted naïve El Niño forecast model (from left to right: prediction model using 6, 8, 10 months as the lead time; as the prediction model is based on the ONI from 1950–2019, we shift the model by 1 year each time, therefore the maximum shift length is 69)

Full size image
Fig. 8
figure 8

Comparison of prediction skills of the original models and their shifted versions by fitting bivariate Gaussians: the outermost ellipses denote the 95% quantiles, and the red disks represent the performances of the unshifted predictor. (from top to down: prediction model using 6, 8, 10 months as lead time; (FA_ori,HR_ori) indicates the original FAR and HR before shifting; (FA_shift, HR_shift) denotes the FAR and HR of shifted series)

Full size image

Before applying the circular time shifted benchmark method to the real predication case, we firstly design a categorical El Niño prediction model based on the Oceanic Niño Index (ONI), which is used as an illustration of how circular time shifted benchmark works. We take ONI from 1950 to 2019 (data from https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni). In Sect. 3.1, the conditional average of the ONI under the condition \(\alpha =0\) and \(\delta =0.3\) shows a clear signature of an El Niño event, with a lead time of 2 months on average. We hence use this condition here (i.e. threshold \(\alpha =0\) and \(\delta =0.3\), the predictability is decreasing when the threshold comes to negative, therefore we take the positive threshold. When \(\alpha =0.6\) is already at the El Niño period, therefore we choose \(\alpha =0\) as the threshold as it provides the longer prediction lead time compared to \(\alpha =0.3\), see Fig. 2 (left)) to create a naïve predictor. As mentioned before, this can be interpreted in the spirit of an analogues forecast (Lorenz 1969). Based on this definition, a hit is counted if the ONI is in the positive state of ENSO (i.e., ONI > 0.5 for at least 5 months) at least once within 5 months after lead time, considering that once El Niño starts, it comes to a peak on average after 5 months. Otherwise, it is counted as a false alarm.

Empirically, for a lead time of 6 months, a threshold of value 0 yields optimal predictability, with a hit rate of 0.65 and false alarm rate of 0.24. When we increase the lead time, the predictability decreases, with a smaller hit rate and larger false alarm rate (the threshold remains at 0 for all lead times, since it was not our goal to optimize these forecasts). Therefore, depending on lead time, we have a forecast which we call “good” (lead time 6 months), “mediocre” (lead time 8 months) and “bad” (lead time 10 months), see Table 1.

We then apply the circular shift method to these three forecasts. Indeed, as shown in Fig. 7, the circular shifts affect the performance of the three forecasts in quite different ways: The model with the best prediction skill (lead time = 6 month) loses most of its predictability when the predictions are shifted with respect to the verification, these shifts give less hits and more false alarms compared to the original model. The model with the worst prediction skill (lead time = 10 months) does not lose much of its predictability after shifting, and some shifts can even yield more hits and less false alarms. This indicates that if the model has a good predictability, after time shifting, it will lose its predictability, while for a bad model does not.

Fig. 9
figure 9

Frequency distributions of hits and false alarms given by shifted versions of the two different El Niño prediction models (from left to right: the results of Ludescher’s model and the results of Meng’s model; when the shift length is 0, the corresponding dots indicate the hits and false alarms given by the original series)

Full size image
Fig. 10
figure 10

Comparison of prediction skill of the two models in the FAR-HR-plane (Top: Ludeshcer’s model, bottom: Meng’s model; (FA_ori,HR_ori) indicates the original FAR and HR before shifting; (FA_shift, HR_shift) denotes the FAR and HR of shifted series)

Full size image

In order to further quantify how the prediction skill changes among the original model and its shifted versions, we represent the skill of each individual forecast (original or time shifted) by a vector in the plane of HR versus FAR. In the scatter plot of skills (FAR vs. HR) of the 69 shifted forecasts (as we take ONI from 1950–2019 to create these analogous models, therefore we get 69 shifted series), we fit a bi-variate normal distribution to these data. The lines of equal probability density (contour lines) are ellipses centered around \((\mu _x,\mu _y\)), described by

$$\begin{aligned} \left( \begin{array}{c} x-\mu _x\\ y -\mu _y \end{array}\right) \Sigma ^{-1}(x-\mu _x, y-\mu _y) = c^2, \end{aligned}$$
(9)

where x and y represent the FAR and HR, respectively, \((\mu _x,\mu _y\)) are the mean values over the 69 performances of the shifted predictions, and \(\Sigma ^{-1}\) is the inverse of a co-variance matrix. The outermost ellipses in Figs. 8 and 10 denote the 95% quantile, i.e., 95% of the probability lies inside. We assume a null hypothesis that the original forecast is a member of the shifted forecasts ensemble, which would mean that it has not more skill than a random forecast. This hypothesis is rejected with 95% confidence if the performance of the unshifted predictions is outside this ellipse. In addition, in order to perform better, its HR should be higher and FA should be lower than the mean over the shifted forecasts, i.e., its vector (FA_original model,HR_original model) should be in the second quadrant. In Fig. 8 such scatter plots together with the 95% confidence ellipse are shown for the three naïve predictions. The good predictor doubtlessly outperforms all its shifted versions, with the original vector (FA_original,HR_original) located outside of the outermost ellipse as well as in the second quadrant, indicating the higher HR and lower FA compared to all of the shifted series. The mediocre predictor is closer to the border of the 95% confidence ellipse, and the bad predictor lies well within the ellipses and it is not in the quadrant which indicates a better prediction skill as well. So for the bad prediction model, we cannot reject the null hypothesis that this is a member of these randomly shifted predictions and hence it has no further forecast skill. The advantage over pure randomization of the predictor lies in the fact that all shifted predictors are identical in all statistical properties, but the specific correlations between predictant and shifted predictors are destroyed.

4.4 Circular time shifted benchmarking for climate network-based models

Eventually, we apply our time-shifting method to the two time series of the predictive indices S(t) and FI(t). In both papers, the time period covers 34 years (in (Ludescher et al. 2014): 1980–2013; in (Meng et al. 2018): 1984–2017). The time series in Fig. 4 (upper panels) are our own reproductions of the two predictive indices using the same dataset as mentioned in the original paper. The lower panels show one the same index time series after shift by 2 years as an example. Our reproductions catch the main characteristics of original results which are published as figures in the corresponding papers, with the same correct hits and false alarms, even though there are some small differences in very details. We shift the predictive index time series by multiples of 1 year and totally acquire 33 time series in each case. Correct predictions and false alarms given by these time series are counted following the rules defined in these 2 papers, and the frequency distributions of hit rates and false alarm rates of these shifted series are presented in Fig. 9 together with the performance of the original forecasts.

Figure 9 shows how time shifting of the index series S(t) and of FI(t) reduces the number of correct predictions and increases the number of false alarms compared to its original predictive index before shifting. Figure 10 shows the 95%-quantiles of the fitted bi-variate Gaussian’s in the FAR-HR-plane. While the original (FA_ori,HR_ori) of Meng’s model is rather close to the boundary of the corresponding ellipse and also its FAR is larger than the mean FAR over all shifted versions, this model is at the border of our benchmarking test: Its performance is close to being compatible with the performance of a random FI(t) series which has the same statistical properties as Meng’s FI(t) series. The result is much more favorable for Ludescher’s forecast: While its FAR is close to the mean FAR of all shifted versions, its HR is definitely much better and sticks out from all those of the shifted versions. We conclude that Ludescher‘s model passes our benchmark approach much better than Meng‘s method. This is consistent with the conclusion we obtained in Sect. 3.3. We want to stress that the the performance of the two network-based models is still better than that of the naïve ONI predictor used as another benchmark. When we set certain prediction lead time, either network-based model has its own best performance at certain lead time range (for example, for Meng’s model, it performs best when the prediction lead time is between 8–12 months; Ludescher’s model performs better at longer lead time compared to Meng’s model, as it gives the best performance when the prediction lead time is between 13–17 months. Our naïve ONI predictor is not able to give reasonable prediction at this longer lead time.) Therefore, both of the climate network-based models performs well in some sense, and they will find their applications.

5 Conclusion

We compare two climate network based El Niño prediction models in different ways and construct a method for benchmarking predictions on short data sets which relies on a new type of surrogate data. By shifting the forecast time series with respect to the verification time series, we destroy correlations between forecast and verification while conserving all statistical properties of the forecast. We demonstrate the usefulness of this benchmark to assess and compare different prediction schemes for El Niño forecasts.

We first compare two existing prediction models by their prediction skills on the same prediction lead times; and study how long the lead time can be given at their best accuracy. However, the notion of lead time is used here in a more general way: Normally, one would make a prediction for El niño-onset a certain time ahead, the lead time. If the onset really takes place at this moment, this would be a hit. However, such an accurate forecast is close to impossible on longer lead times. In the fair comparison, Sect. 3.3, we therefore were more generous and counted a hit if at lead time there is an ongoing El Niño event. In the original publications, there was no precise lead time, but a long time interval, during which an El Niño-onset was supposed to take place. For Ludescher’s model, they predict that an El Niño episode will start in the following calendar year when the prediction index crosses the threshold under certain conditions. As for Meng’s model, this is even broader, giving the forecast within next 18 months. For stakeholders, it is not easy to directly use this kind of predictions, not only because of this broad-range prediction lead time, but also the uncertainty behind these predictions. In our Sect. 3.3, we compare both models in a time resolved way, from 1 to 24 months after the warning is given, including all the range of both “next calendar year” and “next 18 months”. It is beneficial to do this for two reasons, firstly, we can solve the existing problem of broad-range prediction lead time; additionally, we can compare both models relying on their performance at shorter or longer lead times, and to estimate their suitable application situations. From this initial comparison based on the observational data, we find that Ludescher’s model is more stable and indeed has skill on longer lead times. We further compare these two models with the naïve prediction model based on analogous method. Even though the performance at different lead times in both network-based models are not very stable, they outperform the naïve prediction model, since they have much better performance at longer prediction lead time. Finally, we compare these two climate network based prediction models by our circular shifting benchmark method. Prediction skills of shifted time series in both models decrease compared to their original time series. However, Ludescher’s model shows a more obvious decrease under shifting compared to Meng’s model, which indicates that the former one performs more robustly than the latter one. The reason for causing this difference may come from the choice in different domains for building climate network and different indices created in these two studies. In Meng’s work, the nodes for establishing network only cover the Niño 3.4 basin, without considering nodes outside the basin as Ludescher’s work does.

In future work on El Niño prediction, we may need to think more about the influence from outside of the El Niño basin. For these kind of climate network-based predictions, it is also better to estimate their performance at certain exact lead times like we did in this research, to decrease the uncertainty and provide more information for stakeholders. Our benchmark method can be used to assess other forecasts and can be easily generalized to multi-categorial forecasts or real values forecasts, by studying the root mean squared prediction error as a function of the time shift. As the prediction for La Niña is not covered by these climate network based forecasts we discussed here, we do not explore our benchmarking on La Niña’s prediction. Besides, La Niña and El Niño events are not symmetric (Wu et al. 2010; Im et al. 2015), El Niño usually decays rapidly by next summer, while La Niña can persist and appear twice or even multiple times over consecutive years (Bonsal and Lawford 1999; Okumura and Deser 2010), the prediction mechanism behind El Niño and La Niña may be very different. However, if there exists binary La Niña forecasts, our benchmarking methods can also be applied to estimate their prediction skills. In this paper, we do not cover this aspect.