Midlatitude unstable air-sea interaction with atmospheric transient eddy dynamical forcing in an analytical coupled model

Abstract

While recent observational studies have shown the critical role of atmospheric transient eddy (TE) activities in midlatitude unstable air-sea interaction, there is still a lack of a theoretical framework characterizing such an interaction. In this study, an analytical coupled air-sea model with inclusion of the TE dynamical forcing is developed to investigate the role of such a forcing in midlatitude unstable air-sea interaction. In this model, the atmosphere is governed by a barotropic quasi-geostrophic potential vorticity equation forced by surface diabatic heating and TE vorticity forcing. The ocean is governed by a baroclinic Rossby wave equation driven by wind stress. Sea surface temperature (SST) is determined by mixing layer physics. Based on detailed observational analyses, a parameterized linear relationship between TE vorticity forcing and meridional second-order derivative of SST is proposed to close the equations. Analytical solutions of the coupled model show that the midlatitude air-sea interaction with atmospheric TE dynamical forcing can destabilize the oceanic Rossby wave within a wide range of wavelengths. For the most unstable growing mode, characteristic atmospheric streamfunction anomalies are nearly in phase with their oceanic counterparts and both have a northeastward phase shift relative to SST anomalies, as the observed. Although both surface diabatic heating and TE vorticity forcing can lead to unstable air-sea interaction, the latter has a dominant contribution to the unstable growth. Sensitivity analyses further show that the growth rate of the unstable coupled mode is also influenced by the background zonal wind and the air–sea coupling strength. Such an unstable air-sea interaction provides a key positive feedback mechanism for midlatitude coupled climate variabilities.

Appendix: Coupled model details

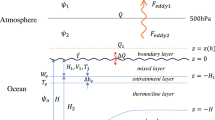
As in Fang and Yang (2011), we assume that the midlatitude coupled air-sea model has a one-layer quasi-geostrophic atmosphere overlying an upper ocean, as illustrated in Fig. 1.

1.1 Atmospheric equations

The seasonal-mean atmospheric quasi-geostrophic potential vorticity (QGPV) equation in $z$-coordinate can be written as

$$\left( {\frac{\partial }{\partial t} + \frac{{\partial \overline{\psi }_{a} \left( z \right)}}{\partial x}\frac{\partial }{\partial y} - \frac{{\partial \overline{\psi }_{a} \left( z \right)}}{\partial y}\frac{\partial }{\partial x}} \right)\overline{q}_{a} + r\nabla^{2} \overline{\psi }_{a} \left( z \right)$$

$$\quad \quad = f_{o} \frac{\partial }{\partial z}\left( {\frac{1}{{N_{a}^{2} }}\frac{{\overline{Q}_{d} }}{{\overline{T} }}} \right) + f_{o} \frac{\partial }{\partial z}\left( {\frac{1}{{N_{a}^{2} g}}\frac{{\overline{Q}_{eddy} }}{{\overline{T} }}} \right) + \overline{F}_{eddy}$$

(A1)

$$\overline{q}_{a} = \nabla^{2} \overline{\psi }_{a} \left( z \right) + f + \frac{\partial }{\partial z}\left( {\frac{{f_{o}^{2} }}{{N_{a}^{2} g}}\frac{\partial }{\partial z}\overline{\psi }_{a} \left( z \right)} \right)$$

(A2)

where the over bar denotes the seasonal mean and the prime represents the synoptic transient flow. $\overline{q}_{a}$ is the seasonal-mean quasi-geostrophic potential vorticity. $\psi_{a} \left( z \right)$ is the atmospheric geostrophic streamfunction at height $z$. $N_{a}$ is the atmospheric Brunt–Väisälä buoyancy frequency. $f_{o}$ is a reference value of the Coriolis parameter. The damping effect is proportional to the vorticity with the characteristic time scale $r^{ - 1} = 5$ days, where $r$ is the diffusive coefficient (Pedlosky 1970). $\overline{Q}_{d}$ is the seasonal-mean diabatic heating. $\overline{F}_{eddy} = - \nabla \cdot \overline{{\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{h}^{'} \zeta^{\prime}}}$ is the seasonal-mean atmospheric transient eddy vorticity forcing and $\overline{Q}_{eddy} = - \overline{{\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{h}^{'} \cdot \nabla_{h} \left( {f_{o} \partial \psi_{a}^{'} \left( z \right)/\partial z} \right)}} - \overline{{w^{\prime}N_{a}^{2} g}}$ is the seasonal-mean transient eddy thermal forcing.

Separate each variable $\overline{x}$ into a basic state $\overline{x}^{c}$ and perturbation $\overline{x}^{a}$ denoted as seasonal-mean anomaly. Since the adjustment time scale of the ocean is longer than that of the atmosphere, the atmosphere is relatively steady and the time-varying term in the equation could be negligible. The seasonal anomaly QGPV equation linearized around a basic state yields

$$\overline{u}^{c} \frac{{\partial \nabla^{2} \overline{\psi }_{a}^{a} \left( z \right)}}{\partial x} + \overline{u}^{c} \frac{\partial }{\partial x}\left[ {\frac{\partial }{\partial z}\left( {\frac{{f_{o}^{2} }}{{N_{a}^{2} g}}\frac{\partial }{\partial z}\overline{\psi }_{a}^{a} \left( z \right)} \right)} \right] + \beta \frac{{\partial \overline{\psi }_{a}^{a} \left( z \right)}}{\partial x} + r\nabla^{2} \overline{\psi }_{a}^{a} \left( z \right) = f_{o} \frac{\partial }{\partial z}\left( {\frac{1}{{N_{a}^{2} }}\frac{{\overline{Q}_{d}^{a} }}{{\overline{T}^{c} }}} \right) + \frac{{f_{o} }}{{N_{a}^{2} g}}\frac{\partial }{\partial z}\overline{Q}_{eddy}^{a} + \overline{F}_{eddy}^{a}$$

(A3)

$$\frac{1}{{H_{a} }}\mathop \int \nolimits_{z\left( h \right)}^{{H_{a} }} \left\{ {\overline{u}^{c} \frac{{\partial \nabla^{2} \overline{\psi }_{a}^{a} \left( z \right)}}{\partial x} + \beta \frac{{\partial \overline{\psi }_{a}^{a} \left( z \right)}}{\partial x} + r\nabla^{2} \overline{\psi }_{a}^{a} \left( z \right)} \right\}dz = \frac{1}{{H_{a} }}\mathop \int \nolimits_{z\left( h \right)}^{{H_{a} }} \left\{ {f_{o} \frac{\partial }{\partial z}\left( {\frac{1}{{N_{a}^{2} }}\frac{{\overline{Q}_{d}^{a} }}{{\overline{T}^{c} }}} \right) + \frac{{f_{o} }}{{N_{a}^{2} g}}\frac{\partial }{\partial z}\overline{Q}_{eddy}^{a} + \overline{F}_{eddy}^{a} } \right\}dz$$

(A4)

$$\overline{\psi }_{a}^{a} = \frac{1}{{H_{a} }}\mathop \int \nolimits_{z\left( h \right)}^{{H_{a} }} \overline{\psi }_{a}^{a} \left( z \right)dz$$

(A5)

$$\overline{u}^{c} \frac{{\partial \nabla^{2} \overline{\psi }_{a}^{a} }}{\partial x} + \beta \frac{{\partial \overline{\psi }_{a}^{a} }}{\partial x} + r\nabla^{2} \overline{\psi }_{a}^{a} = \frac{1}{{H_{a} }}\mathop \int \nolimits_{z\left( h \right)}^{{H_{a} }} \left\{ {f_{o} \frac{\partial }{\partial z}\left( {\frac{1}{{N_{a}^{2} }}\frac{{\overline{Q}_{d}^{a} }}{{\overline{T}^{c} }}} \right) + \overline{F}_{eddy}^{a} } \right\}dz.$$

(A6)

After vertically integrating Eq. (A3) from the top of the boundary layer (denoted by $z\left( h \right)$) to the tropopause, the barotropic component of atmosphere can be obtained and the vortex stretching term in the potential vorticity will disappear since the temperature anomaly proportional to the vertical gradient of atmospheric streamfunction anomaly is zero in the boundaries. $\overline{\psi }_{a}^{a}$ is defined to represent the vertically integrated atmospheric streamfunction anomaly and does not change with height. The vertically integrated transient eddy thermal forcing term is close to zero and can be neglected here since the anomalous transient eddy heating is small both near the top of the tropopause and in the lower troposphere (Fig. 2c). Thus the barotropic component atmospheric equation (A6) is obtained in which diabatic heating and transient eddy vorticity forcing are two PV sources to influence the atmospheric anomaly. After detailed observational analyses, we parameterize the vertically integrated $\overline{F}_{eddy}^{a}$ using the meridional second-order derivative of SST anomaly with a positive linear coefficient $\gamma$. The diabatic heating forcing can be parameterized with SST anomaly as introduced in Sect. 4. Then the atmospheric equation (A6) can be written as

$$\overline{u}^{c} \frac{{\partial \nabla^{2} \overline{\psi }_{a}^{a} }}{\partial x} + \beta \frac{{\partial \overline{\psi }_{a}^{a} }}{\partial x} + r\nabla^{2} \overline{\psi }_{a}^{a} = - \lambda \overline{T}_{1}^{a} + \gamma \frac{{\partial^{2} \overline{T}_{1}^{a} }}{{\partial y^{2} }}$$

(A7)

1.2 Oceanic equations

Besides the constant-depth mixed layer $\left( {H_{1} } \right)$, a thin entrainment layer $\left( {\Delta h_{e} } \right)$ and a thermocline layer $\left( {H_{2} } \right)$ are embedded in the upper ocean, which is governed by the oceanic QGPV equation:

$$\frac{d}{dt}q_{0} = \nabla \times \frac{{\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\tau } }}{{\rho_{r} H}}$$

(A8)

$$q_{0} = \nabla^{2} \psi_{0} - \frac{1}{{L_{o}^{2} }}\psi_{o} + \beta y$$

(A9)

where $\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\tau }$ is the surface wind stress, $\psi_{0}$ the oceanic streamfunction, $q_{0}$ the oceanic QGPV and $L_{0}$ the oceanic baroclinic Rossby radius of deformation. $\rho_{r}$ is the reference density of upper ocean. $H = H_{1} + H_{2}$ is the depth of upper ocean. The oceanic Rossby wave propagates westward under the beta effect. The linearized oceanic QGPV equation driven by the wind stress is

$$\frac{\partial }{\partial t}\left( {\nabla^{2} \overline{\psi }_{o}^{a} - \frac{1}{{L_{0}^{2} }}\overline{\psi }_{o}^{a} } \right) + \beta \frac{{\partial \overline{\psi }_{o}^{a} }}{\partial x} = \frac{1}{{\rho_{r} }}\nabla \times \frac{{\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\tau } }}{H}$$

(A10)

The wind stress can be estimated by $\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\tau } = \rho_{a} c_{D} \left| {\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{a} } \right|\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{a}$, where $\rho_{a}$ is the atmospheric density, $\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{a}$ the surface wind and $c_{D}$ the drag coefficient. The surface wind stress is proportional to the wind at the surface. Suppose that the surface wind speed is in a linear relationship with the wind speed in average layer, then the curl of wind stress can be expressed by $\alpha \nabla^{2} \overline{\psi }_{a}^{a}$, where $\alpha$ is the wind stress coupling coefficient. Neglect the relative vorticity contribution to the PV using longwave approximation, the final form of linearized baroclinic Rossby wave equation is

$$- \frac{1}{{L_{0}^{2} }}\frac{{\partial \overline{\psi }_{o}^{a} }}{\partial t} + \beta \frac{{\partial \overline{\psi }_{o}^{a} }}{\partial x} = \alpha \nabla^{2} \overline{\psi }_{a}^{a}$$

(A11)

To determine the sea surface temperature, the SST evolution equation of the mixed layer (Frankignoul 1985) is considered:

$$\frac{{\partial T_{1} }}{\partial t} + \overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{1} \cdot \nabla T_{1} = - \frac{{W_{e} }}{{H_{1} }}(T_{1} - T_{e}) + \frac{\Delta Q}{{\rho_{r} c_{p} H_{1} }}$$

(A12)

The entrainment, advection and net air-sea heat exchange are the main processes that influence the change of SST. $T_{1}$ represents the temperature of the mixed layer and approximates to the SST since the mixed layer is deep and uniform in winter. $T_{e}$ denotes the temperature at the bottom of the entrainment layer. The vertical temperature gradient of the entrainment layer with a constant depth $\Delta h_{e}$ is assumed to be consistent with that of thermocline layer (Wang et al. 1995), thus

$$T_{1} - T_{e} = \Delta h_{e} \frac{{T_{1} - T_{r} }}{\eta }$$

(A13)

where $T_{r}$ is a constant reference temperature of the motionless deep layer and $\eta$ is the instantaneous depth of the thermocline layer. $H_{1}$ is the depth of the mixed layer. $\Delta Q$ is the net downward heat flux in the mixed layer and $c_{p}$ is the oceanic heat capacity at constant pressure. $\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{1} = k \wedge \nabla \psi_{o} + \left( {1 - H_{1} /H} \right)\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{s}$ denotes the horizontal flow in the mixed-layer which consists of geostrophic and Ekman components. The geostrophic part is determined by the pressure field and the Ekman velocity is set by the vertical shear current $\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{s}$ between the mixed layer and the quasi-geostrophic upper ocean. The vertical shear is governed by surface wind stress (Zebiak and Cane 1987)

$$f\varvec{k} \wedge \overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{s} = \frac{{\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\tau } }}{{\rho_{r} H_{1} }} - r_{s} \overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{s}$$

(A14)

where $r_{s}$ is the Rayleigh damping coefficient. Using the relationship between the surface wind stress and atmospheric streamfunction, $\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{s}$ can be calculated:

$$fv_{s} = \alpha \frac{H}{{H_{1} }}\frac{\partial }{\partial y}\psi_{a} + r_{s} u_{s}; \, \, fu_{s} = \alpha \frac{H}{{H_{1} }}\frac{\partial }{\partial x}\psi_{a} - r_{s} v_{s}$$

(A15)

Thus

$$u_{s} = \alpha \frac{H}{{H_{1} \left( {f^{2} + r_{s}^{2} } \right)}}\left( {f\frac{{\partial \psi_{a} }}{\partial x} - r_{s} \frac{{\partial \psi_{a} }}{\partial y}} \right); \, \, v_{s} = {{\alpha }}\frac{H}{{H_{1} \left( {f^{2} + r_{s}^{2} } \right)}}\left( {f\frac{{\partial \psi_{a} }}{\partial y} + r_{s} \frac{{\partial \psi_{a} }}{\partial x}} \right)$$

(A16)

The entrainment velocity at the base of the mixed layer ($W_{e}$) indicates the pumping effect through the mixed-layer base, which can be written as,

$$W_{e} = H_{1} \nabla \cdot \overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{1} = \frac{{H_{1} \left( {H - H_{1} } \right)}}{H}\nabla \cdot \overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{s} = \frac{{H_{1} \left( {H - H_{1} } \right)}}{H}\left( {\frac{{\partial u_{s} }}{\partial x} + \frac{{\partial v_{s} }}{\partial y}} \right) = \alpha \nabla^{2} \psi_{a} \frac{{f\left( {H - H_{1} } \right)}}{{f^{2} + r_{s}^{2} }}$$

(A17)

Similar to the derivation of the atmospheric equation, each variable can be decomposed into a climatological mean and a seasonal-mean anomaly:

$$T_{1} = \overline{T}_{1}^{c} + \overline{T}_{1}^{a} ;\;\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{1} = \overline{{\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} }}_{1}^{a} ;\;W_{e} = \overline{W}_{e}^{c} + \overline{W}_{e}^{a} ;\;\Delta Q = \Delta \overline{Q}^{c} + \Delta \overline{Q}^{a}$$

(A18)

$$\eta = H_{2} + \overline{\eta }^{a} ;\;\overline{\eta }^{a} = \frac{f}{b}\overline{\psi }_{o}^{a}$$

(A19)

where the anomalous depth of thermocline is expressed by streamfunction of the upper ocean using the quasi-geostrophic linear equilibrium relationship $f\nabla^{2} \overline{\psi }_{o}^{a} = b\nabla^{2} \overline{\eta }^{a}$. $b$ is the buoyancy. The linearized SST evolution equation can be derived as

$$\frac{\partial }{\partial t}\overline{T}_{1}^{a} = - \overline{{\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} }}_{1}^{a} \cdot \nabla \overline{T}_{1}^{c} + c_{1} \overline{\psi }_{o}^{a} - c_{2} \overline{T}_{1}^{a} - c_{3} \overline{W}_{e}^{a} + \frac{{\Delta \overline{Q}^{a} }}{{\rho_{r} c_{p} H_{1} }}$$

(A20)

$$c_{1} = \frac{{f\Delta h_{e} \overline{W}_{e}^{c} }}{{bH_{1} H_{2}^{2} }}\left( {\overline{T}_{1}^{c} - T_{r} } \right);\;c_{2} = \frac{{\Delta h_{e} \overline{W}_{e}^{c} }}{{H_{1} H_{2} }};\;c_{3} = \frac{{\Delta h_{e} }}{{H_{1} H_{2} }}\left( {\overline{T}_{1}^{c} - T_{r} } \right)$$

(A21)

Neglect the mean zonal gradient of SST, the temperature advection by anomalous current can be written as

$$\quad - \overline{{\overset{\lower0.1em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} }}_{1}^{a} \cdot \nabla \overline{T}_{1}^{c} = c_{4} \left( {\frac{{\partial \overline{\psi }_{o}^{a} }}{\partial x} + \frac{{H - H_{1} }}{H}\overline{v}_{s}^{a} } \right);\; c_{4} = - \frac{{\partial \overline{T}_{1}^{c} }}{\partial y}$$

(A22)

where $c_{4}$ is the mean meridional gradient of SST. Since the net surface heat flux generally tends to damp SST anomalies, the net surface heat flux anomaly term can approximate to negative SST anomaly with a positive parameter $\gamma_{0}$. Thus Eq. (A20) can be rewritten as

$$\frac{{\partial \overline{T}_{1}^{a} }}{\partial t} = c_{1} \overline{\psi }_{o}^{a} - c_{2} \overline{T}_{1}^{a} - c_{3} \overline{W}_{e}^{a} + c_{4} \frac{{\partial \overline{\psi }_{o}^{a} }}{\partial x} + c_{4} \frac{{H - H_{1} }}{H}\overline{v}_{s}^{a} - \gamma_{0} \overline{T}_{1}^{a}$$

(A23)