1 Introduction

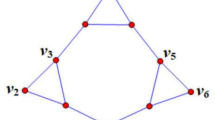
Given is a finite simple connected graph. Initially, all vertices are unburned. One new vertex, called a source, may be burned every round. If a vertex was burned in the previous round, all its unburned neighbours become burned in the current round. Once a vertex is burned, it cannot be unburned. The burning number b(G) of a graph G is the minimum number of rounds required to burn every vertex. See Fig. 1 for examples.

Fig. 1
figure 1

The path on 4 vertices, the Petersen graph, and a HIT. The path has burning number 2 and the other graphs have burning number 3. Sources are highlighted in gray, and numbers on the vertices indicate the round in which they become burned. Note that only one source suffices to achieve the burning number for the Petersen graph, and two sources suffice to achieve the burning number for the HIT

Full size image

Such a problem was studied initially by Alon [2] to solve a communication problem, where they showed that the burning number of an n-dimensional hypercube is \(\lceil n/2\rceil +1\). Independently, the problem was investigated under the name graph burning by Bonato et al. to model the spread of social contagion and influential nodes [6]. The graph burning problem has since garnered much attention, with results focussed on bounds [4], complexity [5], and approximation schemes [18]. The problem has also been investigated for the directed graph variant [16]. For a general summary on the state of the art, we refer the interested reader to the following survey [7].

One particularly interesting family for graph burning is the path graph. It was shown by Bonato et al. that a path on n vertices has burning number exactly \(\lceil \sqrt{n}\rceil \) [9]. As paths are seemingly the most sparse with respect to graph burning, Bonato et al. gave the following conjecture in the same paper.

Conjecture 1

(Burning Number Conjecture [9]) Let G be a connected graph on n vertices. Then \(b(G)\le \lceil \sqrt{n}\rceil \).

In the same paper, they gave a reduction which shows that if Conjecture 1 is true for trees, then it is true for all graphs.

Lemma 1

(Corollary 2.5 of [9]) For a graph G, we have that

$$\begin{aligned} b(G) = \min \{b(T): T \text { is a spanning tree of }~G\}. \end{aligned}$$

While Conjecture 1 has not been proven in full, it has been shown to be true for certain graph classes, such as spider graphs [8] and some p-caterpillar graphs [15]. The conjecture is also known to hold for large enough graphs with minimum degree 3 or 4 [4], and it is known to hold asymptotically [19]. Recently, it was also shown to be true for trees where every internal vertex is of degree 3 [11].

In this paper, we show that Conjecture 1 is true for homeomorphically irreducible trees (HITs)Footnote 1, which are trees without degree-2 vertices (Theorem 1). HITs are counterparts to paths, cycles, and hamiltonicity, as the former minimizes and the latter maximizes the number of degree-2 vertices.

2 Burning number of HITs

Let G be a finite simple connected graph, and let xy be a bridge in G. Let us denote the component that contains x upon deleting xy as \(G_x(xy)\). For vertices x, y in G, let \(d_G(x,y)\) denote the length of a shortest path between x and y, where the length of a path is the number of edges in the path. We shall write |G| to refer to the number of vertices in G. In a tree T, a leaf is a vertex of degree 1 and internal vertices are vertices of degree greater than 1 (non-leaf vertices).

Lemma 2

Let \(n\ge 6\). Any tree T on n vertices contains a vertex x with neighbours \(v_1,\ldots , v_k\) such that \(|T_x(xv_k)|\ge 2\lceil \sqrt{n}\rceil -1\) and \(|T_{v_i}(xv_i)|< 2\lceil \sqrt{n}\rceil -1\) for \(i\in [k-1] = \{1,2,\ldots , k-1\}\).

Proof

Let T be a tree on n vertices. Take a leaf \(\ell \) and its neighbour x. We have that

$$\begin{aligned} |T_x(x\ell )| = n-1 \ge 2\lceil \sqrt{n}\rceil -1, \end{aligned}$$

where the last inequality follows as \(n\ge 6\). Let \(v_1,\ldots , v_k\) denote the neighbours of x where \(v_k=\ell \). If \(|T_{v_i}(xv_i)|< 2\lceil \sqrt{n}\rceil -1\) for \(i\in [k-1]\), then we are done. Otherwise, there exists a neighbour, without loss of generality, \(v_1\), where \(|T_{v_1}(xv_1)| \ge 2\lceil \sqrt{n}\rceil -1\). Let \(u_1,\ldots , u_j\) denote the neighbours of \(v_1\), where \(u_j=x\). If \(|T_{u_i}(v_1u_i)|< 2\lceil \sqrt{n}\rceil -1\) for all \(i\in [j-1]\), then we are done. Otherwise, we continue in the same manner; such a process must terminate as T is finite. \(\square \)

Lemma 3

Let \(n\in {\mathbb {N}}^{>0}\). Let T be a HIT where \(|T|\le 2n-1\). Then T contains at most \(n-2\) internal vertices.

Proof

In a HIT, there are at least two more leaves than internal vertices. Suppose for a contradiction that T contains at least \(n-1\) internal vertices. Then T contains at least \(n+1\) leaves, meaning that \(|T| \ge (n-1) + (n+1) = 2n > 2n-1\). This gives the required contradiction, and therefore T contains at most \(n-2\) internal vertices. \(\square \)

2.1 Graph Burning

We shall formalize the notion of graph burning. Let G be a graph, and let \(S=(x_1,x_2,\ldots ,x_k)\) be a sequence of vertices, called sources. Initially, in round 0, all vertices start as an unburned vertex. In round i, burn the vertex \(x_i\) (if it is not burned already) as well as any unburned vertices that have burned neighbours in round \(i-1\), for \(i\in [k]\). If at the end of round k, all vertices of G are burned, we call S a burning sequence for G. The burning number b(G) of G is the length of a shortest burning sequence for G. Note that burning sequences do not in general have unique lengths.

In the proof of the following results, we require a notion of graph burning where multiple sources can be burned in round 1. Let V(G) denote the vertex set of G. For \(U\subseteq V(G)\) and vertices \(x_i\in V(G)\), let \(M = (U\cup \{x_1\}, x_2, \ldots , x_k)\) be a sequence. In round 1, burn all vertices in the set \(U\cup \{x_1\}\); in round i, proceed as done in the traditional burning sequence. We call M a modified burning sequence for G if all vertices of G are burned after round k. The modified burning number \(b^{U}(G)\) of G is the length of a shortest modified burning sequence for G, with some set \(U\subseteq V(G)\).

Let G be a graph with a degree-2 vertex v, with neighbours u and w. Smoothing v is the process of removing the vertex v and adding an edge uw. Note that if G is a finite simple connected graph, then the resulting graph remains finite, simple, and connected.

Lemma 4

Let T be a tree with one degree-2 vertex v, and let \(T'\) be the HIT obtained from T by smoothing v. Then

$$\begin{aligned} b^{\{v\}}(T) \le b(T'). \end{aligned}$$

Proof

Let \((x_1,\ldots , x_k)\) be a (not necessarily optimal) burning sequence for \(T'\). We claim that \((\{v,x_1\}, x_2,\ldots , x_k)\) is a modified burning sequence for T. This would imply that any burning sequence for \(T'\) yields a modified burning sequence of the same length for T, from which we may conclude that \(b^{\{v\}}(T) \le b(T')\).

Suppose for a contradiction that \((\{v,x_1\}, x_2,\ldots , x_k)\) is not a modified burning sequence for T. This means there exists a vertex w in T that is not burned at the end of round k. Clearly w cannot be one of the sources. Since \((x_1,\ldots , x_k)\) is a burning sequence for \(T'\), w is a burned vertex at the end of round k. Suppose that w becomes burned in \(T'\) in round j for some \(j\le k\). Since w is not a source, there must be a source \(x_i\) with \(i<j\) such that \(d_{T'}(w,x_i) =j-i\).

Because w remains unburned in T, we must have that \(d_{T}(w,x_i) >j-i\). Then the path from w to \(x_i\) in T must contain the vertex v, as this is the only difference between trees T and \(T'\). It follows that \(d_{T}(w,x_i) = j-i+1\). But then \(d_{T}(w,v)\le j-i\). This would mean that w becomes a burned vertex in T no later than round \(1+j-i\), since v is burned in round 1. Since \(1+j-i\le k\), this means that w is burned in T at the end of round k. This gives the required contradiction. \(\square \)

Theorem 1

Let T be a HIT on n vertices. Then \(b(T) \le \lceil \sqrt{n}\rceil \).

Proof

We prove by induction on the number of vertices n. For the base case, we consider the 4 HITs possible for \(n\le 5\). If \(n=1\), the HIT is a tree on a single vertex, which has burning number 1. For \(n=2\), the HIT is a tree with a single edge between two leaves, which has burning number 2. For \(n=4\) and \(n=5\), we have star graphs, which have burning number 2 by choosing the internal vertex to be the first source. We may now assume that T is a HIT on \(n\ge 6\) vertices, and that for all HITs with number of vertices fewer than \(n-1\), the theorem holds.

By Lemma 2, T contains a vertex x with neighbours \(v_1,\ldots , v_k=y\) such that \(|T_x(xy)|\ge 2\lceil \sqrt{n}\rceil -1\) and \(|T_{v_i}(xv_i)|< 2\lceil \sqrt{n}\rceil -1\) for \(i\in [k-1]\). Let \(i\in [k-1]\). We claim that the longest distance from x to any vertex in \(H_i:=V(T_{v_i}(xv_i))\) is at most \(\lceil \sqrt{n}\rceil -1\).

Consider the induced subtree \(T_i:=T[H_i\cup \{x\}]\). Since \(|H_i| <2\lceil \sqrt{n}\rceil -1\), it follows that \(|T_i| \le 2\lceil \sqrt{n}\rceil -1\). By Lemma 3, there can be at most \(\lceil \sqrt{n}\rceil -2\) internal vertices in \(T_i\). Since x is a leaf in \(T_i\), at most \(\lceil \sqrt{n}\rceil -2\) vertices of \(H_i\) are internal vertices in T. It follows immediately that any longest path in T from x to a vertex in \(H_i\) is of distance at most \(\lceil \sqrt{n}\rceil -1\). As this is true for all \(i\in [k-1]\), it follows that the distance from x to every vertex in \(T_x(xy)\) is at most \(\lceil \sqrt{n}\rceil -1\).

We now claim that T can be burned in at most \(\lceil \sqrt{n}\rceil \) rounds, by burning x in round 1. Observe that upon burning x in round 1, with no additional sources in \(T_x(xy)\), all vertices of \(T_x(xy)\) will be burned by the end of round \(\lceil \sqrt{n}\rceil \). Indeed, this occurs since the distance from x to every vertex in \(T_x(xy)\) is at most \(\lceil \sqrt{n}\rceil -1\).

The vertex y will become burned in round 2, as it is a neighbour of x. It remains to show that \(b^{\{y\}}(T_y(xy))\le \lceil \sqrt{n}\rceil -1\). Suppose first that y is a degree-2 vertex in \(T_y(xy)\). Let \(T'\) denote the HIT obtained by smoothing y in \(T_y(xy)\). By Lemma 4, we have that \(b^{\{y\}}(T_y(xy))\le b(T')\). On the other hand, suppose now that y is not a degree-2 vertex. Then \(T_y(xy)\) itself is a HIT and we have the inequality \(b^{\{y\}}(T_y(xy))\le b(T_y(xy))\). Now we also have that

$$\begin{aligned} |T'| < |T_y(xy)| = n - |T_x(xy)| \le n-2\lceil \sqrt{n}\rceil + 1 \le (\lceil \sqrt{n}\rceil -1)^2. \end{aligned}$$

It follows by induction hypothesis that \(b(T') \le \lceil \sqrt{n}\rceil -1\) and \(b(T_y(xy))\le \lceil \sqrt{n}\rceil -1\). Therefore, we obtain \(b^{\{y\}}(T_y(xy))\le \lceil \sqrt{n}\rceil -1\), and we are done. \(\square \)

It follows immediately from Lemma 1 and Theorem 1 that the burning number conjecture is true for all graphs that contain a homeomorphically irreducible spanning tree (HIST) (Corollary 1).

Corollary 1

Let G be a graph on n vertices with a HIST. Then \(b(G)\le \lceil \sqrt{n}\rceil \).

Apart from appearing in the movie ‘Good Will Hunting’, HITs have been studied extensively within graph theory as a fundamental structure, with initial results concerning enumeration of labelled and unlabelled HITs [14]. HITs are counterparts to paths, cycles, and hamiltonicity, which all maximize the number of degree-2 vertices. Naturally, the problem of determining whether a graph contains a HIST has been thoroughly investigated. While this decision problem has been shown to be NP-complete [1], finding conditions for when a graph contains a HIST is an ongoing research area [13, 20]. For example, it is known that every connected and locally connected graph with at least 4 vertices contains a HIST [10].

3 Concluding Remarks

We have shown that HITs (trees without degree-2 vertices) with n vertices satisfy the burning number conjecture, i.e., that they have burning number at most \(\lceil \sqrt{n}\rceil \). Consequently, any graph that contains a HIST also satisfies the burning number conjecture. HITs are antithetical to paths, as the former contains no degree-2 vertices and the latter maximizes them. It is interesting to see that in the extreme cases, with respect to the number of degree-2 vertices, the burning number conjecture holds; to prove the conjecture in full, it remains to show true for the intermediate instances.

The proof of Theorem 1 hinges on Lemma 3, which is not true for trees with degree-2 vertices. We suspect therefore that another proof strategy is necessary for proving the full conjecture. Nevertheless, we show that Theorem 1 can be used to find bounds on the burning number for general graphs by adding leaves.

Corollary 2

Let T be a tree on n vertices. If T has d degree-2 vertices, then

$$\begin{aligned} b(T)\le \lceil \sqrt{n+d}\rceil . \end{aligned}$$

Proof

Add a leaf to every degree-2 vertex and apply Theorem 1. \(\square \)

Unfortunately, this bound underperforms the recent bound presented in [11] for large enough n, which shows that for a tree on n vertices and d degree-2 vertices,

$$\begin{aligned} b(T) \le \lceil \sqrt{n+d+8}\rceil -1. \end{aligned}$$

In future, it may be of interest to find bounds on the burning number of general graphs by looking at spanning trees with the maximum number of leaves (Maximum Leaf Spanning Tree or equivalently, Connected Dominating Set; the problems are known to be NP-complete [17], but some bounds are known [3, 12]). This would give a bound on the number of degree-2 vertices, which can be used in combination with the above burning number bound and Lemma 1.