Loose Edge-Connection of Graphs

Abstract

In the last years, connection concepts such as rainbow connection and proper connection appeared in graph theory and obtained a lot of attention. In this paper, we investigate the loose edge-connection of graphs. A connected edge-coloured graph G is loose edge-connected if between any two of its vertices there is a path of length one, or a bi-coloured path of length two, or a path of length at least three with at least three colours used on its edges. The minimum number of colours, used in a loose edge-colouring of G, is called the loose edge-connection number and denoted ${{\,\textrm{lec}\,}}(G)$. We determine the precise value of this parameter for any simple graph G of diameter at least 3. We show that deciding, whether ${{\,\textrm{lec}\,}}(G) = 2$ for graphs G of diameter 2, is an NP-complete problem. Furthermore, we characterize all complete bipartite graphs $K_{r,s}$ with ${{\,\textrm{lec}\,}}(K_{r,s}) = 2$.

1 Introduction and Motivation

In this paper, we consider simple and undirected graphs only. For notation and graph theoretic terminology, we generally follow the book of West [18]. Aside from that, we denote by $n = |V(G)|$ the order of a graph G and by $m =|E(G)|$ the size of G. The degree of a vertex v of G, denoted by $\deg _G(v)$, is the number of edges of G incident with the vertex v. We will denote by $\Delta (G)$ and by $\delta (G)$ the maximum degree and the minimum degree of the graph G, respectively. Furthermore, for simplicity, we denote by [k, l] the set of integers $\{k,k+1,\ldots ,l\}$ if $k\le l$. Note that $[k, l] = \emptyset$ for $k > l$.

Two edges are adjacent if they share a common vertex. Two edges are semi-adjacent if they are not adjacent but there is a third edge that is adjacent to both of them.

The weight w(e) of an edge $e=uv$ is the sum of degrees of its end-vertices, i.e. $w(e)=deg(u)+deg(v)$. The reduced maximum weight $\textrm{rw}(G)$ of the graph G is defined as $\textrm{rw}(G)=max\{w(e)-1:e \in E(G)\}$.

Let G be a graph. A path L in G is a subgraph of G consisting of a vertex set $\{v_1,v_2,\ldots ,v_k\}$ and edge set $\{v_1v_2,v_2v_3,\ldots , v_{k-1}v_k\}$. For simplicity, we write $L:v_1v_2\ldots v_k$ and, if L contains two vertices u, v, then we denote by uLv the subpath of L between u and v. Two vertices, say $u,v\in V(G)$, are connected by a path L if the end vertices of L are u and v. Such a path is denoted as an u, v-path.

The circumference of a graph G, $\textrm{cir}(G)$, is the length of the longest cycle. We will denote by $C_k$ (resp. $K_k$, resp. $K_{r,s}$) the cycle (resp. the complete graph, resp. complete bipartite graph) on $k \ge 3$ (resp. k, resp. $r \ge 1$ and $s \ge 1$) vertices.

Let ${\mathbb {A}}=\{a,b,c,\ldots \}$ be a finite alphabet, i.e. a set of colours, digits, symbols, ..., whose elements are called letters. A word A of length k over ${\mathbb {A}}$ is a sequence of letters, say $A:a_1a_2a_3\ldots a_k$ where $a_i\in {\mathbb {A}}$ for all $i\in [1,k]$. Let us recall some properties that words can have (see e.g. [10]). A word A is

... proper:

if consecutive letters are not identical,

... rainbow:

if it does not contain two identical letters,

... conflict-free:

if at least one letter occurs exactly once in A,

... monochromatic:

if all letters are identical,

... odd:

if each letter of the alphabet ${\mathbb {A}}$ appears an odd number of times or zero times in A,

... loose:

if either A consists of exactly one letter, of exactly two different letters, or has at least three different letters.

of words over an alphabet ${\mathbb {A}}$, Brause, Jendrol’, and Schiermeyer [3] have introduced a graph theoretic meta-concept as follows.

Consider a graph G. If there is an edge colouring $\phi :E(G)\rightarrow {\mathbb {A}}$, then we can associate to a path $L = v_1v_2\ldots v_{k}$ with $v_i\in V(G)$ for all $i\in [1,k]$, L being a subgraph of G, a word $\phi (v_1v_2)\phi (v_2v_3)\ldots \phi (v_{k-1}v_k)$.

Now, let ${\mathcal {P}}$ be a property of words over the alphabet ${\mathbb {A}}$. Considering an edge colouring $\phi :E(G)\rightarrow {\mathbb {A}}$ we say that L has the property ${\mathcal {P}}$ if the associated word $\phi (v_1v_2)\phi (v_2v_3)\ldots \phi (v_{k-1}v_k)$ has property ${\mathcal {P}}$.

Let G be a connected graph, ${\mathbb {A}}$ be an alphabet with k letters, ${\mathcal {P}}$ be a property of words, and $\phi :E(G)\rightarrow {\mathbb {A}}$ be an edge-colouring. The edge-colouring $\phi$ of G is ${\mathcal {P}}$ edge-connected if any two distinct vertices of G are connected by a path having the property ${\mathcal {P}}$. The minimum integer k, for which there exists an edge colouring $\phi :E(G)\rightarrow {\mathbb {A}}$ with $|{\mathbb {A}}|=k$ that makes G to be ${\mathcal {P}}$ edge-connected, is the ${\mathcal {P}}$ edge-connection number of G.

From a practical point of view, the ${\mathcal {P}}$ edge-connection of graphs plays an important role for security and accessibility in communication networks. While the information which one sends through a network from one node to another has to be protected by passwords, it is of high importance that the password sequences of information transferring paths meet some prescribed requirements. Since managing a whole bunch of passwords, that are assigned to direct information transferring paths between two nodes, is expensive, it is a natural question to ask for a minimum number of passwords securing the information transferring paths. By representing each node as a vertex, each direct information transferring path between two nodes as an edge, each possible password by a different colour, and the prescribed requirements for the password sequences of information transferring paths by a property ${\mathcal {P}}$ for a word over the alphabet of colours, the above problem is translated to finding the ${\mathcal {P}}$ edge-connection number of a path.

Chartrand et al. [8] introduced the concept of rainbow connection; that is, the concept of the ${\mathcal {P}}$ edge-connection where property ${\mathcal {P}}$ is rainbow. Let $\textrm{rc}(G)$ denote the rainbow edge-connection number. Returning to the mathematical problem and its applications, the ${\mathcal {P}}$ edge-connection number of graphs have been intensively studied for some of the mentioned properties, for example if property ${\mathcal {P}}$ is rainbow [7, 8, 12,13,14, 16], proper [1, 2], odd [3], or conflict-free [11]. In this paper, we concentrate on the loose edge-connection, which is a relaxation of the concepts rainbow connection and conflict-free connection. A motivation to study the loose edge-connection comes also from the loose-colouring of embedded graphs, see e.g. [9, 17], or [10]. Note that the loose vertex-connection of simple connected graphs is studied in a more general version in [4].

We say that a path L, which is a subgraph of a graph G with an edge colouring $\phi :E(G)\rightarrow [1, k]$, is loose edge-coloured if the path consists of one edge, or exactly two differently coloured edges, or has at least three edges that are coloured with at least three distinct colours.

A connected graph G, coloured by an edge colouring $\phi :E(G)\rightarrow [1,k]$, is loose edge-connected if any two distinct vertices are connected by a loose coloured path. The least integer k, for which there exists an edge colouring $\phi :E(G)\rightarrow [1, k]$ that makes G loose edge-connected, is called the loose edge-connection number of G is denoted by ${{\,\textrm{lec}\,}}(G)$.

Observe, that any rainbow connected graph is also loose connected. Also, if a graph G is a spanning subgraph of a graph H and ${{\,\textrm{lec}\,}}(G) = k$, then ${{\,\textrm{lec}\,}}(H) \le k$.

In the sequel, a path in an edge coloured graph will be called monochromatic, bi-chromatic, and loose if its edges are coloured with exactly one colour, exactly two colours, and with at least three colours, respectively.

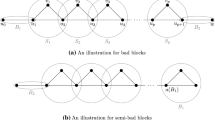
A block B of a connected graph G is an induced subgraph of G of order at least 2 which is 2-connected and, with respect to this condition, maximal; that is, B is 2-connected, but for every $v\in V(G){\setminus } V(B)$, the graph $G[V(B)\cup \{v\}]$ is not 2-connected or contains a cut-vertex. We note that if $n(B) \ge 3$, then we say that B is non-trivial. Otherwise, if $n(B) = 2$ and B is isomorphic to $K_2$, we say that B is trivial.

The block-cutpoint graph of a graph G is a bipartite graph B(G) in which one partite set consists of the cut-vertices of G, and the other has a vertex $b_i$ for each block $B_i$ of G. We include $vb_i$ as an edge of B(G) if and only if $v \in B_i$. When G is connected, its block-cutpoint graph is a tree whose leaves are blocks of G. These blocks are called leaf blocks. If B is a trivial block and $e\in E(B)$ is the edge of B, then e is a cut-edge of G; that is, $G-e$ is disconnected.

Let C(G) be the graph induced on the set $E(C)\subseteq E(G)$ of all cut-edges of G consisting of all vertices of G that are incident to the edges of the set E(C). More precisely,

$$\begin{aligned} V(C(G))=\bigcup _{uv\in E(C)}\{u,v\}\quad \textrm{and}\quad E(C(G)) = E(C). \end{aligned}$$

The graph C(G) is called the cut-edge graph of G. (see [18], p. 156).

Let $F_t$ (resp. ($K_{|V(F)|})_t$) be a graph obtained from a graph F (resp. from the complete graph $K_{|V(F)|}$) by attaching t leaves, $t \ge 0$, to every vertex of F (resp. of $K_{|V(F)|})$.

Let H be a non-trivial connected graph, F be a 2-connected graph, and $t \ge 0$ be an integer. A graph H is of type (t, F) if $F \subseteq H \subseteq (K_{|V(F)|})_t$, and H contains a vertex adjacent to exactly t leaves.

The rest of this paper is organized as follows: Sections 2–7 contain some preliminary statements that are necessary for the proofs of our main results. In Sections 8 the characterization of all complete bipartite graphs with ${{\,\textrm{lec}\,}}(K_{r,s}) = 2$ is given. Section 9 deals with graphs of diameter at most 2. In Section 10, the precise values of the loose edge-connection number for all non-trivial connected graphs of diameter at least 3 are determined.

2 Loose Edge-connection of Trees

Lemma 1

If G is a tree, then ${{\,\textrm{lec}\,}}(G) = \textrm{rw}(G)$.

Proof

Let G be a tree on n vertices. Observe that if G has a loose colouring then for any edge e all edges adjacent to e together with e are colored with mutually distinct colours. This means that ${{\,\textrm{lec}\,}}(G) \ge \textrm{rw}(G)$.

To prove that ${{\,\textrm{lec}\,}}(G) \le \textrm{rw}(G)$ we proceed by induction on the order n of G. The inequality trivially holds for $n \le 3$, Let G be a tree on $n \ge 4$ vertices and the inequality hold for any tree on less than n vertices.

Consider a leaf u of G. Let v be its neighbour in G and let x be the unique neighbour of v which not a leaf if G is not a star. If G is a star then an arbitrary neighbour of v is chosen as x. Then the graph $G - uv$ has a loose colouring with at most $\textrm{rw}(G - uv) \le \textrm{rw}(G)$ colours. This colouring induces a partial loose colouring of G in which all edges, up to uv, are coloured, Let F(xv) be the set of colours in this colouring used on xv and all edges adjacent to xv. As $|F(xv)| \le \textrm{rw}(G) - 1$, we can colour the edge vu with colour $c = \min \{[1, \textrm{rw}(G)] {{\setminus }} F(xv)\}$. $\square$

3 Graphs of Type R

Let $R = C_3 = K_3$. Let $V(R_t) = \{x,y,z,x_i,y_i,z_i; i\in [1,t]\}$, $E(R_t) = \{xy, xz, zy, zz_i, yy_i, xx_i; i\in [1,t]\}$. Observe that $\Delta (C(R_t)) = \textrm{rw}(C(R_t))=t$.

Lemma 2

If H is a graph of type (t, R), then the following hold:

• 1. If $t = 1$ and $|E(C(H))| = 1$, then ${{\,\textrm{lec}\,}}(H) = 2$.

• 2. If $t \le 2$ and $|E(C(H))| \ge 2$, then ${{\,\textrm{lec}\,}}(H) = 3$.

• 3. If $t \ge 3$, then $t \le {{\,\textrm{lec}\,}}(H) \le t + 1$. Moreover, ${{\,\textrm{lec}\,}}(H) = t+1$ if and only if H contains two vertices $b_1$ and $b_2$ such that $\deg _{C(H)}(b_1) + deg_{C(H)}(b_2) \ge 2t - 1$.

Proof

First we consider the graph $R_t$. Observe that ${{\,\textrm{diam}\,}}(R_t) = 3$ with $t \ge 3$ and ${{\,\textrm{lec}\,}}(R_t) \ge \max \{3, t\}$. The following loose edge-colouring with three colours is suitable for $R_1$: $\varphi (xy) = \varphi (zz_1) = 1$, $\varphi (yz) = \varphi (xx_1) = 2$, and $\varphi (xz) = \varphi (yy_1) = 3$.

The colouring $\varphi (xx_i)=\varphi (yy_i)=\varphi (zz_i)=i+1$ for every $i\in [3,t]$, $\varphi (xy) = \varphi (xx_1) = \varphi (yy_1) = 1$, $\varphi (xz) = \varphi (xx_2) = \varphi (zz_1) = 2$, and $\varphi (yz) = \varphi (yy_2) = \varphi (zz_2) = 3$ is a suitable loose edge-colouring of $R_t$ with $t + 1$ colours for all $t \ge 2$.

We need to show that $t + 1$ colours are necessary for $t \ge 3$. We start with the graph $R_3$. Assume that three colours are enough to get a loose connection of $R_3$. Then all three leaves attached to each vertex of $C_3$ of $R_3$ are coloured with three different colours. Consider the vertices x and y. Let, w.l.o.g., $\varphi (xx_i)=\varphi (yy_i)=\varphi (zz_i)=i, i \in [1, 3]$. There is a loose $x_i, y_i$-path in $R_3$ such that $\{\varphi (xz), \varphi (yz)\} = [1, 3] {{\setminus }} \{i\}$. But for any $j, j \ne i$, we also have $\{\varphi (xz), \varphi (yz)\} = [1, 3] {{\setminus }} \{j\}$, a contradiction.

Assume that there is a loose colouring of $R_t$ with t colours for $t \ge 4$, $\varphi (xx_i)=\varphi (yy_i)=\varphi (zz_i)=i, i \in [1, t]$, and let colours 1, 2, and 3 are used on the edges of $C_3$. If we delete from $R_t$ the edges coloured with colour $k \in [4, t]$, we get a loose colouring of $R_3$ with three colours. This contradicts the nonexistence of such a colouring of $R_3$.

Case 1. Let $t\ge 3$. Consider first the graph $G_1 = R_t {{\setminus }} \{xx_t, xx_{t-1}, yy_t, yy_{t-1}\}$. It has the following loose edge-colouring $\varphi$ with t colours: $\varphi (xx_i) = \varphi (yy_i) = \varphi (zz_i) = i$, $i \in [1, t - 3]$, $\varphi (xx_{t-2}) = \varphi (xz) = \varphi (zz_t) = t$, $\varphi (yy_{t-2}) = \varphi (yz) = \varphi (zz_{t-1}) = t - 1$, and $\varphi (xy) = \varphi (zz_{t-2}) = t - 2$. It is easy to see that any graph H of type (t, R) which is a subgraph of $G_1$ has a loose edge-colouring with t colours.

We need to show that $t + 1$ colours are necessary for $t \ge 3$ if H has two vertices, say, x and z, whose degree sum in C(H) is at least $2t - 1$. Assume for the contrary that the graph H has a loose edge-colouring $\varphi$ with t colours. Consider the graph H and its vertices $x, x_i,i \in [1, t - 1]$, z, and $z_j, j \in [1, t]$. Let, w.l.o.g., $\varphi (xx_i) = \varphi (zz_i) = i,i \in [1, t - 1]$, and $\varphi (zz_t) = t$. Let $\varphi (xz) = c$. Then the edges xy and yz have to be coloured with different colours, say a and b. Then there is neither a loose $x_a, z_a$-path nor a loose $x_b, z_b$-path in H. A contradiction.

Case 2. Let $t \le 2$. If H contains at least three leaves, then ${{\,\textrm{diam}\,}}(H) = 3$, $H \subseteq R_2$, and, by Case 1, ${{\,\textrm{lec}\,}}(H) = 3$. If H has exactly two leaves, then one can easily show that ${{\,\textrm{lec}\,}}(H) = 3$ and an edge-colouring of $C_3$ consists of three different colours. If H has one leaf, we colour all the edges of the 3-cycle of $C_3$ with colour 1 and remaining edges of H with colour 2.

This completes the proof of the lemma. $\square$

4 Graphs of Type Q

Let $Q = C_4$, $t \ge 0$, and let $V(Q_t) = \{x, y, v, w, x_i, y_i, v_i, w_i; i \in [1, t]\}$ and $E(Q_t) = \{vx, wx, vy, wy, xx_i, yy_i,$ $vv_i, ww_i; i \in [1, t]\}$.

The diamond D is a graph consisting of the cycle $C_4$ with exactly one diagonal.

Lemma 3

If H is a graph of type (t, Q). then the following hold:

• (i) If $1 \le t \le 2$, then $3 \le {{\,\textrm{lec}\,}}(H) \le 4$. Moreover, ${{\,\textrm{lec}\,}}(H) = 4$ if and only if the cycle $C_4$ of H contains no diagonal and at least three vertices each adjacent to exactly two leaves.

• (ii) If $t = 3$, then $3 \le {{\,\textrm{lec}\,}}(H) \le 4$. Moreover, ${{\,\textrm{lec}\,}}(H) = 4$ if and only if the cycle $C_4$ of H does not contain any diagonal, or $C_4$ contains a diagonal xy, $\deg _{C(H)}(x) = 3$ and $\deg _{C(H)}(y) = 3$, or $\deg _{C(H)}(y) = 2$ and $\deg _{C(H)}(v) = \deg _{C(H)}(w) = 3$.

• (iii) If $t \ge 4$, then ${{\,\textrm{lec}\,}}(H) = t$.

Proof

First we consider the graph $Q_t$. Observe that ${{\,\textrm{diam}\,}}(Q_t) = 4$ and ${{\,\textrm{lec}\,}}(Q_t) \ge \max \{3, t\}$. A suitable loose edge-colouring of $Q_1$ with three colours is: $\varphi (vx) = \varphi (wy) = 1, \varphi (vy) = 3$, $\varphi (wx) = 2$ and $\varphi (xx_1) = \varphi (yy_1) = 3, \varphi (vv_1) = \varphi (ww_1) = 2$. A suitable loose edge-colouring of $Q_t, t \ge 2$, with at least four colours follows: $\varphi (vx) = 1, \varphi (wx) = 2, \varphi (wy) = 3, \varphi (vy) = 4$, and $\varphi (xx_i) = \varphi (yy_i) = \varphi (vv_i) = \varphi (ww_i) = i, i \in [1, t]$. This gives ${{\,\textrm{lec}\,}}(Q_2) \le 4$, ${{\,\textrm{lec}\,}}(Q_3) \le 4$, and ${{\,\textrm{lec}\,}}(Q_t) = t$ for $t \ge 4$.

If $t \ge 4$, then the loose colouring of H with $\max \{3, t\}$ colours follows from the loose colouring of $Q_t$ with t colours.

Next we distinguish four cases:

Case 1. Let $t = 2$.

Subcase 1.1 Let on $C_4$ of H there are at most two vertices each adjacent to exactly two leaves. Then it is a subgraph of one of the following graphs: $H_1 = (V_1, E_1)$ with $V_1 = \{x, x_1, x_2, v, v_1, v_2, y, y_1, w, w_1\}$, $E_1 = \{xv, xx_1, xx_2, vv_1, vv_2, vy, yy_1, yw, ww_1, wx\}$ and a loose edge-colouring $\phi (xx_1) = \phi (vv_1) = \phi (vy) = \phi (yy_1) = 1$, $\phi (xv) = \phi (yw) = 2$, $\phi (xx_2) = \phi (wx) = \phi (vv_2) = \phi (ww_1) = 3$. $H_2 = (V_2, E_2)$ with $V_2 = \{x, x_1, x_2, v, v_1, y, y_1, y_2, w, w_1\}$, $E_2 = \{xv, xx_1, xx_2, vv_1, vy, yy_1, yy_2, yw, ww_1, wx\}$ and a loose edge-colouring $\phi (xx_1) = \phi (vv_1) = \phi (vy) = \phi (yy_1) = 1$, $\phi (xv) = \phi (yw) = 3$, $\phi (xx_2) = \phi (wx) = \phi (yy_2) = \phi (ww_1) = 2$.

It is easy to see that the graph H has a loose edge-colouring with three colours obtained from one of the above colouring of the graph $H_1$ or $H_2$.

Subcase 1.2 Let on $C_4$ of H there are at least three vertices, say x, v, and y, each adjacent to exactly two leaves. Assume that there is a loose edge-colouring $\phi$ with three colours. We can assume, w.l.o.g., that $\phi (xx_1) = \phi (vv_1) = 1$ and $\phi (xx_2) = 2$.

Subcase 1.2.1 Let $\phi (xv) = 1$. Then $\{\phi (xw), \phi (wy)\} = \{2, 3\}$, otherwise there is no loose $x_1, y$-path, and $\{\phi (vy), \phi (wy)\} = \{2, 3\}$, otherwise there is no loose $v_1, w$-path in H. This gives, in order, $\phi (vv_2) = 3$ (because a loose $x_2, v_2$-path), $\phi (xw) = 2$, $\phi (wy) = 3$, $\phi (vy) = 3$ (because a loose $x_2, y$-path) and $\phi (wy) = 2$ (because a loose $v_1, w$-path), a contradiction.

Subcase 1.2.2 Let $\phi (xv) = 2$. Then $\{\phi (xw), \phi (wy)\} = \{1, 3\}$ and $\phi (vy) = 3$ because of a loose $x_2, y$-path and loose $x_1, y$-path. This implies that there is no $x_1, v_1$-path, a contradiction.

Subcase 1.2.3 Let $\phi (xv) = 3$. Then $\{\phi (xw), \phi (vy)\} = \{1, 2\}$, $\phi (wy) = 3$ $\phi (vv_2) = 2$, and, w.l.o.g., $\phi (yy_1) = 1$, $\phi (yy_2) = 2$. This implies the nonexistence a loose $v_i, y_i$-path in H for some $i \in \{1, 2\}$, a contradiction.

Subcase 1.3 Let the cycle $C_4$ of H contains a diagonal xy, that is H contains a block which is the diamond D. Then H is a subgraph of the graph $D_2$. This graph has the following loose edge-colouring $\phi$. $\phi (xx_1) = \phi (vv_1) = \phi (yy_1) = \phi (vy) = 1$, $\phi (xw) = \phi (xx_2) = \phi (yy_2) = \phi (ww_1) = 2$, and $\phi (xv) = \phi (xy) = \phi (vv_2) = \phi (wy) = \phi (ww_2) = 3$. From this colouring we can easily get a required colouring of H.

Case 2. Let $t = 3$ and H does not contain a diagonal xy. Assume, that H has a loose edge-colouring with three colours and $\deg _{C(H)}(x) = 3$. Let the neighbour leaf $x_i$ of x be adjacent to x via edge $xx_i$ coloured with a colour i. Then between x and y there should be three mutually different bi-chromatic x, y-paths but there are exactly two. A contradiction, which shows that at least four colour are necessary for a loose edge-colouring of H. Such a colouring is induced by the above colouring of $Q_3$ because $H \subseteq Q_3$.

Case 3. Let $t = 3$ and H contain a diagonal xy. Denote by D the diamond, that is the subgraph of H. Assume, that H has a loose edge-colouring $\varphi$ with three colours.

Subcase 3.1. Let $\deg _{C(H)}(x) = 3$. Let the neighbour leaf $x_i$ of x be adjacent to x via the edge $xx_i$ coloured with a colour i.

Subcase 3.1.1. Let $\deg _{C(H)}(y) = 3$ and let the neighbour leaf $y_i$ of y is adjacent to y via the edge $yy_i$ coloured with colour $i, i \in \{1, 2, 3\}$. As H has a loose edge-colouring with three colours, there should be three distinct bi-chromatic x, y-paths of length two. But there are exactly two, a contradiction.

Subcase 3.1.2. Let $\deg _{C(H)}(y) = 2$ Let ${\bar{Q}}_3 = (Q_3 {{\setminus }} \{yy_1, ww_3\}) \cup \{xy\}$. The graph ${\bar{Q}}_3$ has the following loose edge-colouring: $\varphi (vx) = \varphi (wx) = 1$, $\varphi (xx_1) = \varphi (vv_1) = \varphi (ww_1) = 1$; $\varphi (yw) = \varphi (yy_2) = 2$, $\varphi (xx_2) = \varphi (vv_2) = \varphi (ww_2) = 2$, and $\varphi (vy) = \varphi (xy) = \varphi (xx_3) = 3$, $\varphi (yy_3) = \varphi (vv_3) = 3$. Observe, that each subgraph $H \subseteq {\bar{Q}}_3$ of type (t, Q) containing the diamond D has a loose edge-colouring with three colours.

To the end of the proof in this case it is enough to show that the graph $Q^* = (Q_3 {\setminus } \{yy_3\}) \cup \{xy\}$ does not have any loose edge-colouring with three colours. Assume the opposite. Let it has such a colouring $\varphi$. Let the neighbour leaf $y_i$ of y be adjacent to y via the edge $yy_i$ coloured with a colour $i \in \{1, 2\}$. Then the following situation, w.l.o.g., appears in $Q^*$: $\{\varphi (xv), \varphi (vy)\} = \{1, 3\}$ and $\{\varphi (xw), \varphi (wy)\} = \{2, 3\}$ because there are loose $x_1, y_1$-path and $x_2, y_2$-path of length al least three. This, w.l.o.g., enforces $\varphi (xy) = 1$ and then no loose $x_3,v_3$-path exists. A contradiction

Subcase 3.1.3. Let $\deg _{C(H)}(y) \le 1$ and let $y_1$ be the neighbour of y. Then $H \subseteq G^1 = (Q_3 {{\setminus }} \{y_2, y_3\}) \cup \{xy\}$. The graph $G^1$ has the following loose edge-colouring with three colours: $\varphi (xv) = \varphi (xw) =$ $\varphi (xx_1) =$ $\varphi (ww_1) = \varphi (vv_1) = 1$, $\varphi (xy) = \varphi (ww_2) =$ $\varphi (xx_2) =$ $\varphi (yw) = \varphi (vv_2) = 2$, and $\varphi (yv) = \varphi (ww_3) =$ $\varphi (xx_3) =$ $\varphi (yy_1) = \varphi (vv_3) = 3$. It is easy to see that colouring $\varphi$ of $G^1$ just described has the required properties of loose edge-coloring. From this colouring of $G^1$ one easily derives a loose edge-colouring with three colours of any subgraph H of $G^1$, which is of of type (t, Q).

Subcase 3.2. Let $\deg _{C(H)}(x) \le 2$ and $\deg _{C(H)}(y) \le 2$. Consider the graph $G^* = Q_3 {{\setminus }} \{xx_2, yy_1\} \cup \{xy\}$. The following edge-colouring $\varphi$ of $G^*$ is a loose one: $\varphi (xv) = \varphi (xw) =\varphi (xx_1) = 1$, $\varphi (vv_1) = \varphi (ww_1) = 1$, $\varphi (vy) = \varphi (wy) = \varphi (vv_2) = 2$, $\varphi (yy_2) = \varphi (ww_2) = 2$, $\varphi (xy) = \varphi (xx_3) = \varphi (vv_3) = 3$, and $\varphi (yy_3) = \varphi (ww_3) = 3$. From this colouring of $G^*$ one easily derives a loose edge-colouring with three colours of any subgraph H of $G^*$, which is of type (t, Q).

Case 4. Let the graph H contain both diagonals xy and vw. Then $H \subseteq G^2 = Q_3 \cup \{xy, vw\}$. It is easy to find a suitable loose edge-colouring of $G^2$ with three colours when we color edges xv and yw with colour 1, the edges xw and yv with colour 2, and the edges xy and vw with colour 3.

This finishes the proof of Lemma 3$\square$

5 Graphs of Type P

Let $P = C_5$. Consider $P_t$ with $t \ge 0$. Let $V(P_t) = \{x, y, z, u, v, x_i, y_i, z_i, u_i, v_i; i \in [1, t]\}$ and $E(P_t) = \{ux, vx, uy, vz, yz, xx_i, yy_i, zz_i, uu_i, vv_i; i \in [1, t]\}$.

Lemma 4

If H is of type (t, P), then the following statements hold:

• (i) If $1 \le t \le 2$, then ${{\,\textrm{lec}\,}}(H) = 3$.

• (ii) If $t = 3$, then $3 \le {{\,\textrm{lec}\,}}(H) \le 4$. Moreover ${{\,\textrm{lec}\,}}(H) = 4$ if and only if the cycle $C_5$ of H does not contain any diagonal and there are, on $C_5$, two vertices each of which is adjacent to three leaves.

• (iii) If $t \ge 4$, then ${{\,\textrm{lec}\,}}(H) = t$.

Proof

First we consider the graph $P_t$. As ${{\,\textrm{diam}\,}}(P_t) \ge 3$, we have ${{\,\textrm{lec}\,}}(P_t) \ge \max \{3, t\}$. A suitable loose colouring of $P_1$ is as follows: $\varphi (xv) = \varphi (yz) = \varphi (xx_1) = \varphi (vv_1) = 2$, $\varphi (xu) = \varphi (vz) = \varphi (zz_1) = 1$, and $\varphi (uy) = \varphi (uu_1) = \varphi (yy_1) = 3$.

To get a suitable loose edge-colouring of $P_2$ we first take a subgraph $P_1$ of $P_2$ and colour its edges as above and then colour the remaining edges of $P_2$ as follows: $\varphi (uu_2) = 1, \varphi (yy_2) = 2$, and $\varphi (xx_2) = \varphi (vv_2) = \varphi (zz_2) = 3$.

There is no loose edge-colouring of $P_3$ with three colours. Assume, for a contrary, that there is one, $\phi$, with colours a, b, and c. Observe, that there must be an edge, say, w.l.o.g., uy, with $\phi (uy) = b$ and $\phi (e) \ne b$ for all $e \in \{ux, vx, vz, yz\}$. As all three colours have to be used on the the edges incident to leaves adjacent to u as well as to y, there are two edges $uu_i$ and $yy_j$ with $\phi (uu_i) = \phi (yy_j) = a \ne b$. Then there is no loose $u_i,y_j$-path, a contradiction.

The following is a suitable loose colouring of $P_t, t \ge 3$: $\varphi (xu) = 1, \varphi (xv) = \varphi (yz) = 3, \varphi (uv) = 2, \varphi (vz) = 4$, and $\varphi (xx_i) = \varphi (yy_i) = \varphi (zz_i) = \varphi (uu_i) = \varphi (vv_i) = i, i \in [1, t]$. This gives ${{\,\textrm{lec}\,}}(P_3) = 4$ and ${{\,\textrm{lec}\,}}(P_t) = t$ for $t \ge 4$. It is easy to see that any graph $H \subseteq P_t$, which is of type (t, P) for $t \ge 4$, has ${{\,\textrm{lec}\,}}(H) = t$.

Next we distinguish three cases:

Case 1. Let $t = 3$, H contain no diagonal on its cycle $C_5$, and have at least two vertices adjacent to exactly three leaves. Assume that H has a loose edge-colouring $\phi$ with three colours 1, 2, and 3. Evidently, all these three colours have to appear on $C_5$ and let, w.l.o.g., colour 3 be unique on $C_5$.

Subcase 1.1. The graph H contains on $C_5$ two adjacent vertices, say u and x, each of which is adjacent to exactly 3 leaves. Let $\phi (xx_i) = \phi (uu_i) = i$. Colour 3 cannot appear on the edge ux because otherwise there is no loose $u_1,x_1$-path and we would have a contradiction. Let $a \in \{1, 2\}$. If $\{\phi (xv), \phi (vz)\} = \{a, 3\}$ then there is no loose $x_a,z$-path in H; a contradiction. The case $\{\phi (xu), \phi (uy)\} = \{a, 3\}$ is analogous. Hence, in this case, H requires four colours for its loose edge-colouring. As $H \subseteq P_3$ we can use the loose edge-colouring of $P_3$ for H.

Subcase 1.2. The graph H contains on $C_5$ two non-adjacent vertices, say x and y, each of which is adjacent to exactly 3 leaves. Let $\phi (xx_i) = \phi (yy_i) = i$. If $\{\phi (ux), \phi (uy)\} = \{a, 3\}$ then there is no loose $x_a,y_a$-path in H; a contradiction. If $\{\phi (xv), \phi (vz)\} = \{a, 3\}$ then there is no loose $x_a,z$-path in H; a contradiction. The case when $\{\phi (yz), \phi (vz)\} = \{a, 3\}$ is symmetric to the latter one. This means that H requires four colours for its loose edge-colouring. Now we use the loose edge-colouring of $P_3$ for H.

Case 1.3. Let H contain on $C_5$ exactly one vertex, say v, adjacent to exactly three leaves. Then H is subgraph of the graph $G^3 = P_2 \cup \{v_3\} \cup \{vv_3\}$, which has a loose edge-colouring obtained from the colouring of $P_2$ extended by $\phi (vv_3) = a$. This colouring of $G^3$ induces a loose edge-colouring of H with three colours.

Case 2. Let H contain the cycle $C_5$ with a diagonal. Then, w.l.o.g., H contains a subgraph $G^4 = (V(G^4), E(G^4))$ with vertex set $V(G^4) = \{x, y, z, u, v\}$ and the edge set $E(G^4) = \{ux, vx, uy, yz, xy, vz\}$. If we colour the edges of $E(G^4)$ as follows $\phi (vx) = \phi (xy) = 1$, $\phi (ux) = \phi (yz) = 2$, and $\phi (uy) = \phi (vz) = 3$, we can easily extend this colouring to a loose edge-colouring of H with three colours.

Case 3. If H contains at least two diagonals on its $C_5$, then we solve first the situation for its subgraph with one diagonal as in Case 3, and then colour arbitrarily the remaining diagonals.

This completes the proof of the lemma. $\square$

For the completeness we mention the following:

Lemma 5

If $G_t$ is a graph obtained from the cycle $C_k, k \ge 6$, by attaching t leaves, $t \ge 1$, to every vertex of $C_k$, then ${{\,\textrm{lec}\,}}(G_t) = \max \{3, t\}$.

Proof

We colour the edges of $C_k$ alternatively by $1, 2, 3, 1, 2, 3, \dots$ and t leaves incident with any vertex v of $C_k$ with t different colours from the set [1, t]. It is easy to see that in such a colouring of the graph $(C_k)_t$ any two vertices are connected by a loose path. $\square$

6 2-connected Graphs with Small Circumference

The smallest size among connected graphs G with $\textrm{cir}(G) = k$ has the cycle $C_k$. The problem of characterization of all (2-connected) graphs G with property $\textrm{cir}(G) = k$ is difficult in general but it is very interesting. As an example of a specific problem of this type is the problem of characterization of Hamiltonian graphs, see e.g. [18], Chapter 7.2 and Appendix B. There are also lot of papers devoted to the study of estimations on bounds of the circumferences of graphs from particular classes. In this section we characterize all 2-connected graphs of small circumference.

Denote by $K_{2,s}, s \ge 2$, the complete bipartite graph with vertex set $V(K_{2,s})=\{x,y, v_i, i \in [1,s]\}$ and edge set $E(K_{2,s})=\{xv_i, yv_i, i \in [1, s]\}$.

The graph $K'_{2, s}$ is obtained from $K_{2,s}$ by inserting the edge xy. ($D = K'_{2, 2}$ is also known as a diamond.) The graph $K^+_{2,s}$, $s \ge 3$, is obtained from $K_{2,s}$ by inserting the edge $v_2v_3$.

Let $P_{r,s}$, $r\ge 1, s\ge 1$, be the graph with vertex set $V(P_{r,s})$ = $\{x,y,z,u_1,...,u_r,v_1,...,v_s\}$ and edge set $E(P_{r,s}) = \{yz, xu_i, yu_i, i\in [1,r], xv_j, zv_j, j \in [1,s]\}$.

The graphs $P'_{r,s}$ and $P''_{r,s}$, $r \ge 1, s \ge 1$, come from the graph $P_{r,s}$ by inserting the edge xy and the edges xy and xz, respectively.

Note that $C_5 = P_{1, 1}, C^1_5 = P'_{1, 1}, C^2_5 = P''_{1, 1}$, ${\bar{C}}^2_5 = P'_{1, 1} + u_1v_1$, $C^3_5 = P''_{1, 1} + yv_1$, ${\bar{C}}^3_5 ={\bar{P}}''_{1, 1} + u_1v_1$, $C^4_5 = C^3_5 +yv_1$, $C^5_5 = K_5$, and all denote the cycle $C_5$ of length 5 with k diagonals, $k \in [1, 5]$.

Theorem 1

Let ${\mathcal {B}}_k$ be the set of all 2-connected graphs G with $\textrm{cir}(G) = k$. Then

• (i) ${\mathcal {B}}_3 = \{K_3 = C_3\}$,

• (ii) ${\mathcal {B}}_4 = \{K_4, K_{2,s}, K'_{2,s}, s \ge 2\}$.

• (iii) ${\mathcal {B}}_5 = \{{\bar{C}}^2_5, C^3_5, {\bar{C}}^3_5, C^4_5, K_5, K^+_{2,l}, l \ge 3, P_{r,s}, P'_{r,s}, P''_{r,s}, r \ge 1, s \ge 1\}$

Proof

Let, for the contrary, there is a 2-connected graph $B \notin {\mathcal {B}}_3 \cup {\mathcal {B}}_4 \cup {\mathcal {B}}_5$ with $\textrm{cir}(B) \le 5$ such that B has the smallest order among all counterexamples.

If B has a vertex v with $\deg _B = 2$, we delete v and add the edge between its two neighbour provided that they are not adjacent in B. The resulting graph $B \star v$ has smaller order than G, hence $B \star v \in {\mathcal {B}}_3 \cup {\mathcal {B}}_4 \cup {\mathcal {B}}_5$. If we return back to G we can see that either $B \in {\mathcal {B}}_3 \cup {\mathcal {B}}_4 \cup {\mathcal {B}}_5$ or B contains a cycle of length at least 6. In both case we have a contradiction.

Let the minimum degree $\delta (B) \ge 3$. Consider a vertex $v \in V(B)$ with $\deg _B(v) = \delta (B)$ and an edge vw of B. Contract the edge vw and simplify all the so obtained multiple edges. The obtained graph $B \star vw$ is connected and each non-trivial block of it is in ${\mathcal {B}}_3 \cup {\mathcal {B}}_4 \cup {\mathcal {B}}_5$. Next we consider two cases.

Case 1. Let $B \star vw$ be 2-connected. Then all its vertices are of degree at least 3 and $B \star vw \in {\mathcal {B}}_3 \cup {\mathcal {B}}_4 \cup {\mathcal {B}}_5$. But then $B \in {\mathcal {B}}_3 \cup {\mathcal {B}}_4 \cup {\mathcal {B}}_5$ or B contains a cycle of length at least 6, a contradiction.

Case 2. Let $B \star vw$ has a cut vertex $v^*$. Then each block of $B \star vw$ has at least three vertices. One can easily see that then B contains a cycle of length at least 6, a contradiction. $\square$

7 Loose Edge-connection of 2-connected Graphs

The complete solution for 2-connected graphs is given in the following.

Theorem 2

If G is a 2-connected graph, then $\textrm{lec}(G) = \min \{3, \textrm{rc}(G)\}.$

For its proof we first show the following lemma.

Lemma 6

If G is a 2-connected graph, then ${{\,\textrm{lec}\,}}(G) \le 3$.

Proof

We have to show how to colour the edges of the graph G with colours from the set $A = \{1, 2, 3\}$ to get a loose edge-connection of G. Our procedure depends on the circumference $\textrm{cir}(G)$ of G.

If $\textrm{cir}(G) = 3$, then we have to colour the graph $K_3$, see Theorem 1, the complete graph on three vertices. It will play an important role later. It is easy to see that ${{\,\textrm{lec}\,}}(K_3)=1$. If $K_3 = C_3$ is a block in a graph of order at least 4, the edges of $K_3$ are colored with three colours.

If $\textrm{cir}(G) = 4$, then we have to color the graphs from the set ${\mathcal {B}}_4$, see Theorem 1.

Let the loose edge-colouring of $K_{2, r}$ be as follows: $\varphi (xv_1) = 1$, $\varphi (xv_2) = 2$, $\varphi (xv_i) = 3, i \in [3, r]$, $\varphi (yv_1) = 2$, $\varphi (yv_2) = 3$ and $\varphi (yv_i) = 1, i \in [3, r]$. Observe, that between any two vertices of $K_{2, r}$, except for the pair x and y, there is a loose (using three colours) path. For the pair x and y, if $r \ge 3$, there are three different bi-chromatic x, y-paths of length three using the same three colours.

A loose edge-colouring of the graph $K'_{2, r}$ is obtained from that of $K_{2, r}$ using $\varphi (xy) = 1$.

If $\textrm{cir}(G) = 5$, then we have to color the graphs from the set ${\mathcal {B}}_5$, see Theorem 1. Let the loose edge colouring of $P_{r,s}$ be defined as follows: $\varphi (xu_1) = 1$, $\varphi (xu_i) = 2$, $i \in [2,r]$, $\varphi (yz) = 3$, $\varphi (xv_1) = 3$, $\varphi (xv_j) = 1, j\in [2,s]$, $\varphi (yu_1) = 2$, $\varphi (yu_i) = 3$, $i \in [2, r]$, $\varphi (zv_1) = 1$, $\varphi (zv_j) = 2$, $j \in [2, s]$.

Note that for $r \ge 2$, $s \ge 1$, and any pair of vertices of $P_{r,s}$, except for the pair x and y, there is, in $P_{r,s}$, a loose path using three colours. For the pair x and y there are three differently bi-colored x, y-paths of length two using the same three colours. The inserted edge in $P'_{r,s}$ is coloured with colour $\varphi (xy) = 2$ (the inserted edges in $P''_{r,s}$ are colored with colours $\varphi (xy) = 3$ and $\varphi (xz) = 2$).

A loose edge-colouring of the graph $K^+_{2,r}$ is obtained from that one of $K_{2,r}$ using colour 1 for the edge $v_2v_3$.

The proof that the loose edge-connectivity of the remaining graphs from ${\mathcal {B}}_5$ is at most 3 is easy and is left to the reader.

If $\textrm{cir}(G) \ge 6$, we proceed as follows. Colour the edges of the longest cycle C alternatively by 1, 2, 3, 1, 2, 3, .. and other edges of G with colour 1. We distinguish three cases.

Case 1. For any two vertices x and y on the cycle C there is a path of length at least three, which is a loose path.

Case 2. If $x\in V(C)$ and $y\notin V(C)$, then there are two paths connecting y with two vertices $z_1,z_2$ on the cycle C. At least one of them is distinct from x, say $z_1$. By Case 1 there is a path L on C of length at least 3 from $z_1$ to x, which is loose (uses three colors). Now, taking the path from $z_1$ to y (which is vertex disjoint with L except of vertex $z_1$) we obtain a loose x, y-path.

Case 3. Let $x, y \notin V(C)$. Similarly as above, there are two vertex disjoint paths from x to $z_1$ and from y to $z_2$ with $z_1, z_2 \in V(C), z_1 \ne z_2$. As in Case 2 there is a loose path from $z_1$ to $z_2$ along the cycle C which leads to a loose path from x to y. $\square$

Corollary 1

For every two vertices x and y of a 2-connected graph G with ${{\,\textrm{cir}\,}}(G) \ge 6$ there is a loose x, y-path.

Proof

of Theorem 2. To prove it first observe the following statements.

• 1. $\textrm{lec}(G) = 1$ if and only if $\textrm{rc}(G) = 1$ if and only if G is complete graph.

• 2. $\textrm{lec}(G) = 2$ if and only if $\textrm{rc}(G) = 2$.

Now for all remaining 2-connected graphs we have

$$\begin{aligned} 3 = \textrm{lec}(G) \le \textrm{rc}(G). \end{aligned}$$

This proves the theorem. $\square$

8 Loose Edge-connection Number of Complete Bipartite Graphs

The complete solution for the complete bipartite graphs is given in the following.

Theorem 3

If $K_{r,s}, r \ge s \ge 1$, is a complete bipartite graph, then the following statements hold:

• (i) $\textrm{lec}(K_{1,s}) = s.$

• (ii) $\textrm{lec}(K_{r,s}) = 2$ if $2 \le s \le r \le 2^s.$

• (iii) $\textrm{lec}(K_{r,s}) = 3$ otherwise.

Proof

Let $K_{r,s}$ be a complete bipartite graph with the vertex set $V(K_{r,s}) = X \cup Y$, where $X = \{x_1, \dots , x_r\}$ and $Y = \{y_1, \dots , y_s\}$. Let $S_i = K_{1,s}$ be the star with the vertex set $V(S_i) = \{x_i\} \cup Y$. First we consider case (ii).

Let $\phi$ be an edge-colouring of $K_{r,s}$ with two colours a and b. Recall that a path in an edge-coloured graph is called bi-chromatic (resp. monochromatic) if on its edges exactly two colors (resp. one) are (is) used.

Let ${\textbf{s}}(i) = (a_{i,1}, \dots , a_{i,s})$ be a vector of colours of the edges of the star $S_i$ such that $\phi (x_iy_j) = a_{i,j}$ for all $i \in [1, r]$ and $j \in [1, s]$.

This colouring has the following obvious two properties:

Claim 1

If ${\textbf{s}}(k) \ne {\textbf{s}}(l)$ then a bi-chromatic $x_k, x_l$-path exists in $K_{r,s}$.

Claim 2

If there is $a_{i,k} \ne a_{i,l}$ in ${\textbf{s}}(i) = (a_{i,1}, \dots , a_{i,s})$, then $K_{r,s}$ contains a bi-chromatic 2-path $y_kx_iy_l$.

Observe, that for $r > 2^s$ there is no loose edge-coloring of $K_{r,s}$ with two colours. The reason is that the number of different binary vectors of dimension s is $2^s$. Then, by the pigeonhole principle, there is a pair of stars, $S_k$ and $S_l$, with the same vector of colours, ${\textbf{s}}(k)$ and ${\textbf{s}}(l)$, respectively, and we have no bi-chromatic path of length two between the pair of vertices $x_k$ and $x_l$.

If $2 \le s \le r \le 2^s$, then there exists a loose edge-colouring of $K_{r,s}$. It is enough to consider the vectors of colours for the stars $S_i, i \in [1, s - 1]$, with the following properties: $\phi (x_iy_j) = a$ for $j \le i$ and $\phi (x_iy_j) = b$ for $i + 1 \le j \le s$. For $i \in [s, r]$ we colour the edges of stars $S_i$ with such vectors of colours that are mutually distinct from already chosen ones.

To see that this edge-colouring is loose, observe that Claim 1 ensures us that for any pair of vertices $x_k$ and $x_l$, $1 \le k < l \le r$, there is a bi-chromatic path of length two between them. The choice of the first $s - 1$ vectors of colour ensures the existence of a bi-chromatic $y_k,y_l$-path of length two for any pair of vertices $y_k$ and $y_l$ for any pair k and l with $1 \le k < l \le s$. See Claim 2.

This completes the proof of the theorem for the case (ii).

The proof of theorem in the cases (i) and (iii) follows from Lemma 1 and from Lemma 6, respectively. $\square$

9 Graphs with Diameter at Most 2

To continue we need some more definitions.

The join of two simple graphs G and H, written $G \vee H$, is the graph obtained from the disjoint union $G + H$ by adding the edges $\{xy: x \in V(G), y \in V(H)\}$, see [18].

A nontrivial block B of a graph G is called $\textit{large}$ if ${{\,\textrm{cir}\,}}(B) \ge 6$ and it is called $\textit{small}$ if $3 \le {{\,\textrm{cir}\,}}(B) \le 5$.

Recall that a block B is called trivial if it consists of a cut-edge e. In this case we sometimes will write $B = e$.

It is easy to see that graphs of ${{\,\textrm{diam}\,}}(G) \ge 3$ have the loose edge-connection number $\textrm{lec}(G) \ge 3$. So the necessary condition for graphs G to have $\textrm{lec}(G) = 2$ is to have ${{\,\textrm{diam}\,}}(G) = 2$. In the previous section we have characterized all complete bipartite graphs B that have $\textrm{lec}(B) = 2$.

Observe, that if a graph H is a spanning subgraph of a non-complete graph G and $\textrm{lec}(H) = 2$, then $\textrm{lec}(G) = 2$.

Let G and H be graphs with loose edge-connection number two. Then it is easy to prove that $\textrm{lec}(G \vee H) = 2$, and $\textrm{lec}(K_1 \vee (G + H)) = 2$.

In Theorem 2 we have mentioned that for a graph G it holds $\textrm{lec}(G) = 2$ if and only if $\textrm{rc}(G) = 2$. Several classes of graphs G with $\textrm{rc}(G) = 2$ are known, see e.g. [5, 15], or [17]. For example, Caro et al. [5] have proved that any non-complete n-vertex graph with minimum degree

$$\begin{aligned} \delta (G) \ge \frac{n}{2} + \log n \end{aligned}$$

has $\textrm{rc}(G) = 2$.

It is known (cf. [6]) that deciding whether $\textrm{rc}(G) = 2$ is an NP-complete problem. Hence, the problem to decide whether $\textrm{lec}(G) = 2$ is also NP-complete.

The following problem seems to be interesting.

Problem 1

Characterize all connected graphs G with

$$\begin{aligned} \textrm{lec}(G) = 2. \end{aligned}$$

Theorem 4

Let G be a graph with ${{\,\textrm{diam}\,}}(G)\le 2$. Then

• (i) ${{\,\textrm{lec}\,}}(G)=1$ if $G = K_n, n \ge 2$, and

• (ii) $2 \le {{\,\textrm{lec}\,}}(G) \le \max \{3, \Delta (C(G))\}$ otherwise. Moreover, all three bounds are tight.

Proof

Since (i) is trivial, we prove (ii). If ${{\,\textrm{diam}\,}}(G)=2$, then G is either 2-connected or has exactly one cut-vertex. If it is 2-connected, then the proof of our theorem follows from Theorem 2.

If G contains a cut-vertex, v, then each block of G is trivial or 2-connected. The vertex v is adjacent to all vertices of $V(B)-v$ because of ${{\,\textrm{diam}\,}}(G)= 2$. Trivial blocks of G form the graph C(G) which is a star $K_{1,\Delta (C(G))}$. Each nontrivial block B is either a large block or contains a small block as a spanning subgraph.

The trivial blocks are coloured with distinct colours from $[1, \Delta (C(G)]$. The specific small blocks from the set $\{D, K_4, C_5^2, C_5^3, {\bar{C}}_5^3, C_5^4, K_5\}$, that are present in G, are coloured with respect to the colouring of the trivial blocks according to the proofs of Lemmas 2, 3, and 4. The block $K_3$ and the remaining blocks are coloured as in Lemma 6 with colours from [1, 3].

Next, we need to show that for any pair of two vertices u and w there is either an edge uw, or a bi-chromatic u, w-path of length two, or a loose u, w-path (using at least three colours).

If the vertices u and w belong to the same block B we are done.

Let $u \in V(B_i)$ and $w \in V(B_j)$, where $B_i$ and $B_j$ are different non-trivial blocks of G and at least one of them is not in $\{K_3, D, K_4, C_5^2, C_5^3, {\bar{C}}_5^3, C_5^4, K_5\}$. If there is either a loose u, v-path in $B_i$ or a loose w, v-path in $B_j$ then these paths together with the edge vu or vw, respectively, give a loose u, w-path. This situation always appears, with exceptions, when both vertices u and v and v and w correspond to the vertices x and y or z of the blocks (graphs) from the families ${\mathcal {B}}_4$, or ${\mathcal {B}}_5$. But in these exceptional cases, as mentioned in the proof of Lemma 6, for the pairs u and v and for the pair v and w there are three mutually differently colored with three colours bi-chromatic u, v-path and v, w-path, respectively. A suitable combination of a bi-chromatic u, v-path with a differently coloured bi-chromatic v, w-path provides a required loose u, w-path.

Let $B_i$ and $B_j$ be both from the set $\{K_3, D, K_4, C_5^2, C_5^3, {\bar{C}}_5^3, C_5^4, K_5\}$. Observe that in any block B from this set there are two distinct paths of length at most three between v and any other vertex $v'$ of B which together use all three colours.

If $u \in B_i$ and $w \in B_j$, one can easily combine such a u, v-paths of $B_i$ with a v, w-path of $B_j$ to get a needed bi-chromatic or a loose u, w-path.

If u is in a trivial block $B_1 = uv$ and w is in a nontrivial block $B_j$, we use the same consideration as above to show the existence of a need v, w-path.

To see, that the bounds 2 and 3 are tight, see Theorem 3. For the tightness of the third bound see the graph $K_{1,s}, s \ge 3$. $\square$

10 Graphs with Diameter at Least 3

A nontrivial block B of a graph G is of type P (or of type Q, or of type R) if it is of type (t, P) (or of type (t, Q), or of type (t, R), respectively) for some $t \ge 0$.

We recall that a block $B \in \{{\mathcal {B}}_3 \cup {\mathcal {B}}_4 \cup {\mathcal {B}}_5\}$ of a graph G is small.

A cut-vertex v of an edge-coloured small block B of a graph G is of $\textit{type}$ (a, b) with respect to B if $deg_B(v)=2$, one edge incident with v is coloured with a and the second one with b, $a \ne b$. Otherwise it is called $\textit{universal}$ with respect to B.

Theorem 5

Let G be a connected graph with ${{\,\textrm{diam}\,}}(G)\ge 3$. The following statements hold:

• (i) If G is 2-connected or $0 \le \Delta (C(G))\le 2$, then $3 \le {{\,\textrm{lec}\,}}(G) \le 4$. Furthermore, ${{\,\textrm{lec}\,}}(G) = 4$ if and only if G contains a block B which is a cycle of length 4 having three distinct vertices $b_1, b_2, b_3 \in V(B)$ with $\deg _{C(G)}(b_1) = \deg _{C(G)}(b_2) = \deg _{C(G)}(b_3) = \textrm{rw}(C(G)) = 2$, or

• (ii) If $\Delta (C(G)) \ge 3$, then $\textrm{rw}(C(G))\le {{\,\textrm{lec}\,}}(G) \le \textrm{rw}(C(G)) + 1$. Furthermore, ${{\,\textrm{lec}\,}}(G) = \textrm{rw}(C(G)) + 1$ if and only if

  • (1) G contains a block B which is a cycle of length 5 having two distinct vertices $b_1, b_2 \in V(B)$ with $\deg _{C(G)}(b_1) = \deg _{C(G)}(b_2) = \textrm{rw}(C(G)) = 3$, or

  • (2) G contains a block B which is a cycle of length 4 and $\deg _{C(G)}(b) = \textrm{rw}(C(G)) = 3$ for a vertex $b \in V(B)$, or

  • (3) G contains a block B which is a cycle of length 3 having two distinct vertices $b_1, b_2 \in V(B)$ with $\deg _{C(G)}(b_1) + \deg _{C(G)}(b_2) \ge 2 \textrm{rw}(C(G)) - 1$, or

  • (4) G contains a block B which is a diamond D, $V(D) = \{x, v, y, w\}$, $\textrm{rw}(C(G)) = 3$, and $\deg _{C(G)}(x) + \deg _{C(G)}(y) = 6$ or $\sum _{b \in V(B)}\deg _{C(G)}(b) \ge 11$.

Proof

Part 1. Colouring. Let ${\mathcal {D}} = \{K_3, C_4, D, K_4, C_5, C_5^1, C_5^2, {\bar{C}}_5^2, C_5^3, {\bar{C}}_5^3, C_5^4, K_5\}$ be a set of specific small blocks. Recall that any large block and any small block, other than that from ${\mathcal {D}}$, has a loose edge-colouring with three colours. Between any two distinct vertices of large blocks and any two vertices of small blocks other than that from ${\mathcal {D}}$, except two specific x and y of small blocks, there exists a loose path (coloured with at least three colours). The vertices x and y are connected with three mutually distinct bi-chromatic x, y-path.

Any small block B from ${\mathcal {D}}$ has a loose edge-colouring with three colours in which any two vertices of B are adjacent or are connected by a bi-chromatic path. See the proof of Lemma 6.

Our colouring follows the properties of the block-cutpoint graph B(G) of G. Choose a vertex of B(G) corresponding to a block B as a root. We colour edges of the blocks from this root to the leaf blocks. First we colour edges of B as described in Lemma 6 if B is 2-connected and with colour 1 if B is trivial. If B is trivial (i.e. $B = \{e\}$, where e is an edge) we colour all edges of the component of C(G) containing the edge e according to the proof of Lemma 1.

General Step: Let v be a cut vertex on B and let $B_1, \dots , B_k, S_1,\dots ,S_l, T_1, \dots ,T_r$ be other blocks containing v as cut-vertex, where $B_i$, for $i \in [1,k]$, is a large block, $S_j$, for $j \in [1,l]$, is a small block, and $T_s$, for $s \in [1,r]$, is a trivial block. First we colour large blocks, next small blocks different from blocks from ${\mathcal {D}}$, then small blocks from ${\mathcal {D}}$, and, finally, trivial blocks.

We distinguish three cases.

Case 1. Let $deg_B(v)=1$ and $\varphi (wv) = a$ be a colour of the unique edge wv in B. Then for every $i \in [1,k]$ the edges of the block $B_i$ are coloured with colours from the color set $\{a, b, c\}$ as stated in the proof of Lemma 6

If $S_j$, $j \in [1,l]$, is a small block from $({\mathcal {B}}_3 \cup {\mathcal {B}}_4 \cup {\mathcal {B}}_5){{\setminus }} {\mathcal {D}}$ and $\deg _{S_j}(v) = 2$, then the edges incident to v in $S_j$ are colored with colours from $\{a, b, c\}$ so that the vertex v becomes of type (b, c), where $b \ne a \ne c$. Next we finish the colouring of edges of $S_j$ as described in the proof of Lemma 6. If $\deg _{S_j}(v) \ge 3$, then we colour $S_j$ directly as in Lemma 6.

If $S_j \in {\mathcal {D}}$, then its edges are coloured together with all trivial blocks (edges) incident to the vertices of the block $S_j$. In this case we colour the subgraph H of type (t, O) for $t \ge 1$ and $O \in \{P, Q, R\}$ as described in Lemmas 4, 3, and 2, respectively, taking into consideration the following three facts: (i) The edges of the longest cycle of H incident with the vertex v have to obtain in H the colours b and c. (ii) Some of edges of H at v can already be coloured (This can happen if the block B is trivial, or there are several blocks of types from $\{P, Q, R\}$ at the considered cut vertex v). (iii) If H is of type (1, R), we colour its edges with three colours as in $R_1$ because $H \subset R_1$.

If $S_j \in {\mathcal {D}}$ and there no trivial blocks incident to vertices of $S_j$, i.e. $S_j$ is a subgraph of type (0, O), we colour its edges as in Lemma 6 except of the case when $S_j = C_3 = K_3$. In the later case the edges of $C_3$ are coloured with three distinct colours.

Let there be trivial blocks at v, i.e., $r \ge 1$. If this block is a part of a subgraph of type (t, O) where $t \ge r$ and $O \in \{P, Q, R\}$ at v, then all trivial blocks are coloured as a part of the colouring of the first considered subgraph of type O. If there is no subgraph of type (t, O) for $t \ge 1$ and $O \in \{P, Q, R\}$ at v, then the edges of all trivial blocks (i.e. edges) are part of a component of C(G). In this case we colour all edges of this component as described in the proof of Lemma 1.

Case 2. Let $deg_B(v)=2$ and the vertex v be of type (a, b). Then the large block $B_i$, for any $i \in [1,k]$ is coloured with colours from the color set $\{a, b, c\}$ as in the proof of Lemma 6.

The block $S_j$, for any $j \in [1,l]$, $S_j \notin {\mathcal {D}}$, is handled as a large block if v has, in it, degree at least three, or such that the vertex v becomes of type (a, b) in the colouring of $S_j$, if v has degree two. If $S_j \in {\mathcal {D}}$ is a subgraph H of type (t, O) for $t \ge 1$ and $O \in \{P, Q, R\}$, then we consider the subgraph H of type O and colour it as described in Case 1.

Trivial blocks $T_s$ are handled in the same way as in Case 1.

Case 3. Let $deg_B(v)\ge 3$. Our colouring in this case continues as in Case 2 keeping in mind that all small blocks $S_j$, $j \in [1,l]$, have to be colored in such a way that the cut-vertex v becomes of type (a, b) if it is of degree two in $S_j$.

If all blocks containing v as a cut-vertex are colored, v is called $\textit{ready}$.

To continue in the colouring of G a next, not ready, cut-vertex from a colored block is chosen.

The procedure of colouring finishes if every cut vertex of G is ready.

Observe, see Lemmas 1, 2, 3, 4 and 6, that our colouring uses colours from the set $M = [1,\textrm{rw}(C(G))]$ except for the cases listed in our Theorem 5. These exceptional cases use the colours from the colour set $M^* = [1, 4]$ if G contains a subgraph H of type Q described in Lemma 3 (i) and from the colour set $M' = [1,\textrm{rw}(C(G)) +1]$ if G contains subgraphs H of type (t, O) for $t \ge 1$ and $O \in \{P, Q, R\}$ described in the Lemmas 4 (ii), 3 (ii), and 2 (iii), respectively.

Part 2. Loose connectivity. To finish the proof of the theorem it is necessary to show that any two distinct vertices $w_1$ and $w_2$ are connected by an edge $w_1w_2$, or bi-chromatic $w_1,w_2$-path of length 2, or a loose (with at least three different colours) $w_1,w_2$-path of length at least 3. Such a path exists if both $w_1$ and $w_2$ belong to the same block, to the same component of C(G), or to the same subgraph H of type (t, O) where $t \ge 1$ and $O \in \{P, Q, R\}$.

If there is an $w_1,w_2$-path going through two vertices, say $u_1$ and $u_2$, of a large block or of a small block, then the part between them can be replaced by a loose $u_1,u_2$-path lying inside the block.

Hence, it is sufficient to show the existence of such a loose $w_1,w_2$-path for any two blocks $B_1$ and $B_2$ with a common cut-vertex z, $w_1\in V(B_1)$ and $w_2\in V(B_2)$, $w_1\ne z\ne w_2$.

If the block $B_1$ is large, then there is a loose $w_1, z$-path in $B_1$, which together with a $z,w_2$-path in $D_2$ gives a needed loose $w_1, w_2$-path.

Let the block $B_1$ be small and $B_2$ be either small or trivial. If the vertex $w_1$ is not corresponding to any of the vertices x and y of $B_1 \in \{K_{2,s}, K'_{2,s}, K^+_{2,s}\}$ or to any of the vertices x, y and z of $B_1 \in \{P_{2,s}, P'_{2,s}, P''_{2,s}\}$, respectively, then there is, in $B_1$, a loose $w_1,z$-path. This path together with a $z, w_2$-path gives a required loose $w_1,w_2$-path.

If the vertex $w_1$ and the vertex $w_2$ are corresponding to some of the above mentioned vertices x, y, or z of $B_1$ and of $B_2$, respectively, then one can easy recognise in G a loose $w_1, w_2$-path of length 3 or 4. $\square$