1 Introduction

Gyárfás [5] obtained the following bound on the size of the largest monochromatic subtree we can find in any r-coloring of the complete graph \(K_n\):

Theorem 1

([5]) If the edges of \(K_n\) are colored with r colors then there is a monochromatic subtree with at least \({n\over r-1}\) vertices.

This estimate is sharp if \(r-1\) is a prime power and \((r-1)^2\) divides n. Füredi [2] improved on this bound for r-s for which there is no affine space of order \(r-1\). The following lemma was a key tool in the proof of Theorem 1 in [5].

Lemma 2

([5]) In every r-coloring of a complete bipartite graph on n vertices there is a monochromatic subtree with at least \({n\over r}\) vertices.

A double star is a special tree obtained by joining the centers of two disjoint stars. Mubayi strengthened Lemma 2 in [9] as follows (proved also independently by Liu, Morris and Prince [8]).

Lemma 3

([8, 9]) In every r-coloring of a complete bipartite graph on n vertices there is a monochromatic double star with at least \({n\over r}\) vertices.

This implies that if the edges of \(K_n\) are r-colored, then either all color classes are connected or there is a monochromatic double star with at least \({n\over r-1}\) vertices. Let us denote by f(n, r) the size of the largest monochromatic double star we can find in any r-coloring of \(K_n\). The previous remark raises the following natural problem.

Problem 4

([4]) Is it true that \(f(n,r)\ge \frac{n}{r-1}\) for all \(r\ge 3\)?

Note that for \(r=2\) this is not true as seen by a random 2-coloring (see [4] for details). In [4] we proved the following weaker lower bound on f(n, r).

Theorem 5

([4]) For \(r\ge 2\) there is a monochromatic double star with at least \({n(r+1)+r-1 \over r^2}\) vertices in any r-coloring of the edges of \(K_n\).

For \(r\ge 3\) this improved a result of Mubayi [9], who proved that there is a monochromatic subgraph of diameter at most three with at least \({n\over r-1+1/r}\) vertices in every r-coloring of \(K_n\).

For \(r=2\) the bound in Theorem 5 is close to best possible (see [4]). However, it is possible that for \(r\ge 3\), f(n, r) is larger, maybe even as large as \(\frac{n}{r-1}\) (Problem  4). Perhaps surprisingly, despite significant research efforts (see e.g. [7, 9, 10])), as far as we know there has been no improvement on the bound in Theorem 5. In this note we give a slight improvement on this bound.

Theorem 6

Let \(\delta = \frac{1}{1500 r^9}\). For \(r\ge 3\) there is a monochromatic double star with at least \({n(r+1)+r-1 \over r^2} + \delta n\) vertices in any r-coloring of the edges of \(K_n\).

No effort is made to optimize the \(\delta\) improvement since it is probably far from optimal, we just wanted to make the point that Theorem 5 does not give the right asymptotics for f(n, r). The original question whether \(f(n,r)\ge {n\over r-1}\) still remains open. Note that Letzter [7] proved that there is a triple star of size at least \({n\over r-1}\) improving a result of Ruszinkó [10] (a triple star is a tree obtained by joining the centers of three disjoint stars by a path of length 2).

2 Proofs

Proof of Theorem 6

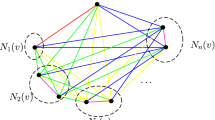
Our starting point is the argument from [4]. Let \(r\ge 3\), \(\delta = \frac{1}{1500 r^9}\) and \(M={n(r+1)+r-1 \over r^2}\). Consider an r-colored \(K_n\). We will show that there is a monochromatic double star with at least \(M+\delta n\) vertices. Consider an arbitrary vertex p of \(K_n\) and we denote by \(A_i\) the set of vertices which are connected to p with an edge of color i. If a vertex \(a\in A_i\) has more than \(M+\delta n-|A_i|-1\) edges of color i going to other \(A_j\)-s, then we have a monochromatic double star (with centers a and p) in color i with \(M+\delta n\) vertices. Thus we may assume that this is not the case. Let us denote by \(H_i\) the graph consisting of the edges of color i going out of \(A_i\). Consider the r-partite graph G with partite classes \(A_i\) obtained by the removal of the edges in \(H_i\) and inside the \(A_i, 1\le i \le r\). Just as in [4] (see (1) in [4]) from the previous remark and from the Cauchy-Schwartz inequality we can get the following lower bound:

$$\begin{aligned}&2|E(G)| > \sum _{i=1}^r |A_i|\left( n-1-|A_i|\right) - 2\sum _{i=1}^r |A_i|\left( M+\delta n-|A_i|-1\right)&\nonumber \\&\qquad =\sum _{i=1}^r |A_i|(n+|A_i|+1-2M-2\delta n)=\sum _{i=1}^r |A_i|^2+(n-1)(n+1-2M-2\delta n)&\nonumber \\&\qquad \ge {(n-1)^2\over r}+(n-1)(n+1-2M - 2\delta n)= (n-1)\left( (r-2)M - 2\delta n\right) . \end{aligned}$$
(1)

\(\square\)

Define G(i, j) as the bipartite subgraph of G spanned by \([A_i,A_j]\). Note that there are no edges of color i or j in G(i, j) by definition. Let d(v, H) denote the degree of v in the graph H and let \(d_k(v,H)\) denote the degree of v in color k in the graph H. For any edge \(e=xy\) of color k, \(x\in A_i,y\in A_j\), we define

$$\begin{aligned} s_{ijk}(x,y)=d_k(x,G)+d_k(y,G(i,j)), \; t_{ijk}(x,y)=d_k(x,G(i,j))+d_k(y,G). \end{aligned}$$

Thus we have two double stars, \(S_{ijk}(x,y)\) of size \(s_{ijk}(x,y)\) and \(T_{ijk}(x,y)\) of size \(t_{ijk}(x,y)\), of color k in G. We will sum \(s_{ijk}(x,y)+t_{ijk}(x,y)\) and estimate this sum. Again just as in [4] (see page 534) using the Cauchy–Schwartz inequality again and (1) we get :

$$\begin{aligned}&\sum _{1\le i<j\le r} \sum _{k\ne i,j} \sum _{xy\in E(G(i,j)) }\left( s_{ijk}(x,y)+t_{ijk}(x,y) \right)&\nonumber \\&\qquad =\sum _{i=1}^r \sum _{x\in A_i}\sum _{k\ne i}d_k^2(x,G)+ \sum _{i=1}^r \sum _{j\ne i}\sum _{k\ne i,j}\sum _{x\in A_i}d_k^2(x,G(i,j))&\end{aligned}$$
(2)
$$\begin{aligned}&\ge {\left( \sum _{i=1}^r\sum _{x\in A_i} \sum _{k\ne i} d_k(x,G)\right) ^2 \over (r-1)\sum _{i=1}^r|A_i|}+ {\left( \sum _{i=1}^r\sum _{j\ne i}\sum _{k\ne i,j}\sum _{x\in A_i}d_k(x,G(i,j))\right) ^2\over (r-1)(r-2)\sum _{i=1}^r|A_i|}&\nonumber \\&\qquad ={(2|E(G)|)^2\over (r-2)(n-1)}> 2|E(G)|\left( M - \frac{2\delta n}{r-2}\right) . \end{aligned}$$
(3)

Since altogether we summed the cardinalities of the vertex sets of 2|E(G)| monochromatic double stars, (3) implies that at least one of them has size at least \(M - \frac{2\delta n}{r-2}\).

To improve on this first note that we must have the following upper bound

$$\begin{aligned} {2|E(G)|\over (r-2)(n-1)} < M + \delta n, \end{aligned}$$
(4)

since otherwise the same argument would lead to a monochromatic double star of size at least \(M+\delta n\).

To get an improvement in (3) we will need to add back some of the removed edges in \(\cup H_i\). We will make use of the “defect form” of the Cauchy-Schwarz inequality (as in [11] or in [6]): if \(1\le l \le m\) and

$$\begin{aligned} \sum _{i=1}^{l} x_i = \frac{l}{m}\sum _{i=1}^m x_i +\Delta , \end{aligned}$$

then

$$\begin{aligned} \sum _{i=1}^m x_i^2\ge \frac{1}{m} \left( \sum _{i=1}^m x_i\right) ^2+\frac{\Delta ^2m}{l(m-l)}\ge \frac{1}{m} \left( \sum _{i=1}^m x_i\right) ^2+\frac{\Delta ^2}{l}. \end{aligned}$$

First we show the following stability result: in G apart from a small number of exceptional vertices all vertices have degrees close to the average degree in every color otherwise we are done again. Let \(\overline{d}(G)\) denote the average degree in graph G and let \(\overline{d}_k(G)\) denote the average degree in graph G in color k. A vertex \(x\in A_i, 1\le i \le r\) is called \(\eta\) -exceptional for some \(\eta > 0\) if (at least) one of the following holds:

  • There exists \(k\not = i\) for which we have

    $$\begin{aligned} \left| d_k(x,G) - \frac{\overline{d}(G)}{r-1}\right| > \eta n, \end{aligned}$$
    (5)

  • There exist \(j\not = i\) and \(k\not = j,i\) for which we have

    $$\begin{aligned} \left| d_k(x,G(i,j)) - \frac{\overline{d}(G)}{(r-1)(r-2)}\right| > \eta n. \end{aligned}$$
    (6)

Then we have the following stability claim:

Claim 7

Let \(\alpha = 12 \delta\). One of the following two cases holds:

  1. (i)

    G has a monochromatic double star of order at least \(M+\delta n\).

  2. (ii)

    The number of \(\alpha ^{1/3}\)-exceptional vertices in G is less than \(\alpha ^{1/3} n\).

Proof of Claim 7

Assume that (ii) does not hold, so we have at least \(\alpha ^{1/3} n\) exceptional vertices for which either (5) or (6) holds (for some k or k, j, respectively). Then there are at least \(l=\frac{\alpha ^{1/3}}{4} n\) (for simplicity assume that this is an integer) exceptional vertices x for which always the same, say (5), holds and always in the same direction, say larger (the proof will be similar in the other cases), so for some k

$$\begin{aligned} d_k(x,G) > \frac{\overline{d}(G)}{r-1} + \alpha ^{1/3} n. \end{aligned}$$
(7)

For each of these l exceptional vertices x we pick a \(k_x\) for which (7) holds. Denote by \(E=\{ (x,k_x)\}\) the set of these l pairs, so \(|E|=l=\frac{\alpha ^{1/3}}{4} n\).

We will lower bound the sum of squares in line (2) a bit differently, namely for the summation

$$\begin{aligned} \sum _{i=1}^r \sum _{x\in A_i}\sum _{k\ne i}d_k^2(x,G) \end{aligned}$$
(8)

we will use the defect form of the Cauchy–Schwarz inequality instead of the original. We rearrange the summation in (8) so that we start with the l terms

$$\begin{aligned} \sum _{(x,k)\in E} d_k^2(x,G). \end{aligned}$$

On one hand by the definition of E we have

$$\begin{aligned} \sum _{(x,k)\in E} d_k(x,G) > l \frac{\overline{d}(G)}{r-1} + l \alpha ^{1/3} n. \end{aligned}$$
(9)

On the other hand \(\Delta\) is defined by

$$\begin{aligned} \sum _{(x,k)\in E} d_k(x,G) = l \left( \frac{\sum _{i=1}^r \sum _{x\in A_i}\sum _{k\ne i}d_k(x,G)}{(n-1)(r-1)} \right) + \Delta = l \frac{\overline{d}(G)}{r-1} + \Delta . \end{aligned}$$
(10)

Hence, by (9) and (10), we get

$$\begin{aligned} \Delta > l \alpha ^{1/3} n. \end{aligned}$$
(11)

Applying the defect form of the Cauchy-Schwarz inequality with \(l=\frac{\alpha ^{1/3}}{4} n\), we get

$$\begin{aligned} \sum _{i=1}^r \sum _{x\in A_i}\sum _{k\ne i}d_k^2(x,G) \ge \frac{\left( \sum _{i=1}^r \sum _{x\in A_i}\sum _{k\ne i}d_k(x,G)\right) ^2 }{(n-1)(r-1)} + \frac{\Delta ^2}{l}. \end{aligned}$$

Thus using (11) we get an extra

$$\begin{aligned} \frac{\Delta ^2}{l} > \frac{l^2 \alpha ^{2/3} n^2}{l} = l \alpha ^{2/3} n^2 = \frac{\alpha }{4} n^3 \end{aligned}$$

term when we lower bound the sum of squares in line (2), which leads to an extra

$$\begin{aligned} \frac{\alpha n^3}{8 |E(G)|}\ge \frac{\alpha n}{4} \end{aligned}$$

(just using \(2|E(G)|\le n^2\)) increment in the size of the double star in (3). Thus we get a monochromatic double star of size at least

$$\begin{aligned} M - \frac{2\delta n}{r-2} + \frac{\alpha n}{4} \ge M + \delta n, \end{aligned}$$

so indeed (i) holds (here we used \(\frac{\alpha }{4} \ge 3 \delta\).)

If (5) holds for l vertices in the other direction (smaller), the proof is almost identical. Finally, assume that (6) holds for l vertices in the larger direction, i.e. for some k, j

$$\begin{aligned} d_k(x,G(i,j)) > \frac{\overline{d}(G)}{(r-1)(r-2)} + \alpha ^{1/3} n. \end{aligned}$$
(12)

We proceed similarly as above. For each of these l exceptional vertices x we pick a pair \((k_x, j_x)\) for which (12) holds. Denote by \(E=\{ (x,k_x,j_x)\}\) the set of these l triples, so \(|E|=l=\frac{\alpha ^{1/3}}{4} n\).

Here we will use the defect form of the Cauchy–Schwarz inequality for the other part of the summation in (2), i.e.

$$\begin{aligned} \sum _{i=1}^r \sum _{j\ne i}\sum _{k\ne i,j}\sum _{x\in A_i}d_k^2(x,G(i,j)). \end{aligned}$$
(13)

We rearrange the summation in (13) so that we start with the l terms

$$\begin{aligned} \sum _{(x,k,j)\in E} d_k^2(x,G(i,j)). \end{aligned}$$

On one hand by the definition of E we have

$$\begin{aligned} \sum _{(x,k,j)\in E} d_k(x,G(i,j)) > l \frac{\overline{d}(G)}{(r-1)(r-2)} + l \alpha ^{1/3} n. \end{aligned}$$
(14)

On the other hand here \(\Delta\) is defined by

$$\begin{aligned} \sum _{(x,k,j)\in E} d_k(x,G(i,j))= & {} l \left( \frac{\sum _{i=1}^r \sum _{j\ne i}\sum _{k\ne i,j}\sum _{x\in A_i}d_k(x,G(i,j))}{(n-1)(r-1)(r-2)} \right) + \Delta \nonumber \\= & {} l \frac{\overline{d}(G)}{(r-1)(r-2)} + \Delta . \end{aligned}$$
(15)

Hence, by (14) and (15), we get

$$\begin{aligned} \Delta > l \alpha ^{1/3} n. \end{aligned}$$
(16)

Applying the defect form of the Cauchy-Schwarz inequality with \(l=\frac{\alpha ^{1/3}}{4} n\), we get

$$\begin{aligned} \sum _{i=1}^r \sum _{j\ne i}\sum _{k\ne i,j}\sum _{x\in A_i}d_k^2(x,G(i,j)) \ge \frac{\left( \sum _{i=1}^r \sum _{j\ne i}\sum _{k\ne i,j}\sum _{x\in A_i}d_k(x,G(i,j))\right) ^2 }{(n-1)(r-1)(r-2)} + \frac{\Delta ^2}{l}. \end{aligned}$$

Thus using (16) again we get an extra

$$\begin{aligned} \frac{\Delta ^2}{l} \ge \frac{l^2 \alpha ^{2/3} n^2}{l} = l \alpha ^{2/3} n^2 = \frac{\alpha }{4} n^3 \end{aligned}$$

term when we lower bound the sum of squares in line (2), which leads to an extra

$$\begin{aligned} \frac{\alpha n^3}{8 |E(G)|}\ge \frac{\alpha n}{4} \end{aligned}$$

increment in the size of the double star in (3) and we can finish as above. Finally, the case when (6) holds for l vertices in the other direction (smaller), the proof is almost identical.□

Let us return to the proof of Theorem 6, and assume that we have no monochromatic double star of order at least \(M+\delta n\). Then we have (ii) in Claim 7. An \(\alpha ^{1/3}\)-exceptional vertex is simply called exceptional, so we have fewer than \(\alpha ^{1/3} n\) exceptional vertices. Let us take a non-exceptional vertex \(x\in A_1\). This exists since we may assume wlog that \(A_1\) is the largest \(A_i\) and then for our choice of \(\alpha\) (\(\alpha = 12 \delta\))

$$\begin{aligned} |A_1|\ge \frac{n-1}{r} > \alpha ^{1/3} n. \end{aligned}$$

Since x is non-exceptional we have

$$\begin{aligned} d(x,G) \le (r-1) \frac{\overline{d}(G)}{r-1} + (r-1) \alpha ^{1/3} n = \frac{2|E(G)|}{n-1} + (r-1) \alpha ^{1/3} n. \end{aligned}$$
(17)

Recall that \(H_1\) is the graph consisting of the removed edges of color 1 going out of \(A_1\) and that

$$\begin{aligned} d_1(x,H_1) < M+\delta n-|A_1| . \end{aligned}$$
(18)

(17) and (18) imply that there exists a \(j\not = 1\) (wlog \(j=2\)) such that

$$\begin{aligned}d_2(x,H_2) &\ge \frac{1}{r-1} \left( (n-1) - |A_1| - d(x,G) - d_1(x,H_1)\right)&\nonumber \\&> \frac{1}{r-1} \left( (n-1) - |A_1| - \frac{2|E(G)|}{n-1} - (r-1) \alpha ^{1/3} n - M - \delta n+|A_1| \right)\nonumber \\& > \frac{1}{r-1} \left( (n-1) - (r-2) M - (r-2)\delta n - (r-1) \alpha ^{1/3} n - M - \delta n \right) \nonumber \\& \ge \frac{1}{r-1} \left( (n-1) - (r-1) M - (r-1) \delta n - (r-1) \alpha ^{1/3} n \right) \nonumber \\& \ge \frac{1}{r-1} \left( \frac{n}{r^2} - 2 (r-1) \alpha ^{1/3} n\right) = \frac{n}{(r-1)r^2} - 2 \alpha ^{1/3} n. \end{aligned}$$
(19)

Here in the third line we used (4), while in (19) the definition of M.

Denote by \(N_k^G(x, U)\) the color-k neighbors of the vertex x in the subset \(U\subseteq V(G)\) in the graph G. Since x is non-exceptional we have

$$\begin{aligned} |N_2^G(x, A_3)| \ge \frac{\overline{d}(G)}{(r-1)(r-2)} - \alpha ^{1/3} n> \frac{n-1}{r(r-1)(r-2)} - \alpha ^{1/3} n > \alpha ^{1/3} n \end{aligned}$$
(20)

for our choice of \(\alpha\). Indeed,

$$\begin{aligned} 2 \alpha ^{1/3}< \frac{1}{r^3} < \frac{1}{r(r-1)(r-2)}. \end{aligned}$$

Let us take a non-exceptional vertex \(y\in N_2^G(x, A_3)\) (this is possible because of (20)). Since y is non-exceptional we have

$$\begin{aligned} d_2(y,G(1,3)) \ge \frac{\overline{d}(G)}{(r-1)(r-2)} - \alpha ^{1/3} n. \end{aligned}$$
(21)

Consider the color-2 double star with centers x and y and leaf-sets \(N_2^{(G\cup H_2)}(x,V(G)\setminus A_1)\) and \(N_2^G(y,A_1)\). Using the fact that x is non-exceptional, (19) and (21), the size of this double star is at least

$$\begin{aligned}&d_2(x,G) + d_2(x,H_2) + d_2(y,G(1,3))&\nonumber \\&\qquad> \frac{\overline{d}(G)}{r-1} - \alpha ^{1/3} n + \frac{n}{(r-1)r^2} - 2 \alpha ^{1/3} n + \frac{\overline{d}(G)}{(r-1)(r-2)} - \alpha ^{1/3} n&\nonumber \\&\qquad> M - \frac{2\delta n}{r-2} + \frac{n}{(r-1)r^2} - 4 \alpha ^{1/3} n > M + \delta n, \end{aligned}$$
(22)

(using the estimate in (3) again), a contradiction (using our choices for \(\delta\) and \(\alpha\)). Indeed,

$$\begin{aligned} 4 \alpha ^{1/3} + 3 \delta< 5 \alpha ^{1/3} \le \frac{1}{r^3} < \frac{1}{(r-1)r^2}. \end{aligned}$$

\(\square\)

3 Conclusion

We gave a slight improvement on the size of a monochromatic double star we can guarantee in every r-coloring of the edges of \(K_n\). Let us summarize where the improvement came from. Stability is used to show that most of the vertices are a part of monochromatic double stars of approximately the same size that was obtained in [4]. This allows us to start with a typical vertex, get the double star as we had before, but also get the extra edges from \(x\in A_1\) to \(A_2\) in color 2 which we didn’t have before.

However, the original question whether there is a double star of size at least \({n\over r-1}\) still remains open. No effort was made to optimize the improvement, we just wanted to make the point that Theorem 5 does not give the right asymptotics for f(n, r). With a more careful analysis one might be able to improve this further; perhaps even to the right order of magnitude, \(\delta = c/r^3\) for some constant c. However, our approach, using only the r-partite graph on the \(A_i\)-s, is not sufficient to prove \(f(n,r)\ge {n\over r-1}\); there is an example demonstrating that. Indeed, consider the following random construction (for simplicity we describe it only for \(r=3\)). We have \(|A_i|=(n-1)/3, 1\le i \le 3\) and we have random bipartite graphs between the \(A_i\)-s with the following densities: in color 1 between \(A_1\) and \(A_2\) and between \(A_1\) and \(A_3\) with density \((1/4 - \epsilon )\) for some small \(\epsilon\) and between \(A_2\) and \(A_3\) with density \((1/2 + 2 \epsilon )\). The other colors are similar. Then it is easy to verify that there is no monochromatic double star of size at least n/2 in the tripartite graph; the point is that any \(x\in A_2\) and \(y\in A_3\) will have a large common neighborhood in \(A_1\) in color 1 with high probability which can only be counted once. Thus in order to prove \(f(n,r)\ge {n\over r-1}\) (if it is true), one needs to use the edges inside the \(A_i\)-s or of course use totally new ideas.