Abstract
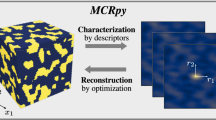
Reconstructing microstructures from statistical descriptors is a key enabler of computer-based inverse materials design. In the Yeong–Torquato algorithm and other common methods, the problem is approached by formulating it as an optimization problem in the space of possible microstructures. In this case, the error between the desired microstructure and the current reconstruction is measured in terms of a descriptor. As an alternative, descriptors can be regarded as constraints defining subspaces or regions in the microstructure space. Given a set of descriptors, a valid microstructure can be obtained by sequentially projecting onto these subspaces. This is done in the Portilla–Simoncelli algorithm, which is well known in the field of texture synthesis. Noting the algorithm’s potential, the present work aims at introducing it to microstructure reconstruction. After exploring its capabilities and limitations in 2D, a dimensionality expansion is developed for reconstructing 3D volumes from 2D reference data. The resulting method is extremely efficient, as it allows for high-resolution reconstructions on conventional laptops. Various numerical experiments are conducted to demonstrate its versatility and scalability. Finally, the method is validated by comparing homogenized mechanical properties of original and reconstructed 3D microstructures.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Generating realizations of random heterogeneous composite materials is a recent field of research. It aims at enabling digital workflows such as numerical simulation and inverse design [1, 2] in order to accelerate materials engineering. Microstructure characterization and reconstruction (MCR) can be used for (i) generating multiple microstructure realizations from a single sample, (ii) reconstructing a small, periodicFootnote 1 structure from a large, aperiodic CT scan, (iii) creating 3D structures from 2D slices and (iv) exploring hypothetic materials by interpolating in the descriptor space. A multitude of approaches has been developed in the last decades that is summarized in different review articles [3,4,5]. A brief introduction is given in the following, whereby a distinction between descriptor and machine learning (ML)-based methods is made.
In ML-based reconstruction algorithms, a generative model is trained on a data set of microstructures. If the data set is sufficiently large, the trained model can be utilized to efficiently generate new realizations of the same structure. A common example for such a generative model is an autoencoder [6, 7]. Similarly, extensive research is dedicated to generative adversarial networks (GANs) [8]. These models, which usually outperform autoencoders in terms of sample quality, have been modified in multiple ways including conditional GANs [9, 10], StyleGAN [11], and gradient penalty [12]. Applications to steels [13] and various other materials [14] show high image quality. To combine the advantage of both models, they have been bundled by employing the decoder simultaneously as a generator. This improves 2D-to-3D reconstruction [15,16,17] and makes the models applicable to extremely small data sets [18]. The disadvantage of ML-based methods is generally the need for a training data set and the difficulty of estimating the model applicability after a distribution shift.
In contrast, descriptor-based methods do not require a training data set but only a single reference. For this purpose, the morphology of the reference structure is quantified using statistical, translation-invariant descriptors like volume fractions or two-point correlations [19]. Microstructure realizations are then generated from given descriptors by solving an optimization problem. The Yeong-Torquato algorithm [19, 20] is potentially the most common method in this regard. It is based on a stochastic, gradient-free optimization algorithm where the search space is restricted to structures of the same volume fractions. The constant volume fractions are ensured by only swapping two different-phase pixel locations in each iteration. Unfortunately, the deficient efficiency and scalability of this stochastic optimization algorithm necessitates subsequent works on efficiency improvements such as multigrid schemes [21,22,23,24], efficient descriptor updates [25, 26] different-phase sampling rules [27], optimized weighting of correlation functions [28], and the swap of multiple interface pixels at the same time [29]. Moreover, efficient reconstructions from Gaussian random field-based methods are used as initialization [30, 31]. Many of these methods and further ideas are discussed in detail in [4]. Successful applications include various materials, e.g., soils [32], sandstone [33], chalk [30] and batteries [26]. As an alternative, gradient-based optimization algorithms can solve the optimization problem in fewer iterations as long as the descriptors are differentiable. This differentiable microstructure characterization and reconstruction (DMCR) idea is presented in [34], extended to 3D in [35] and validated in [36]. An open-source implementation is available in MCRpy [37] and multiple approaches from the literature implement similar ideas [38,39,40]. The drastically reduced number of iterations enables the use of computationally more intensive descriptors like Gram matrices of pre-trained neural networks [41] or descriptors based on a hierarchical wavelet transform [42]. Similarly, the same descriptors can be computed with a higher fidelity [43]. With specific material classes in mind, adapted algorithms have been proposed for certain inclusion, pore or grain geometries. Examples are metallic materials [44, 45], fiber composites [46,47,48] and magnetorheological elastomers [49]. In cases where the morphology is too complex to be described by Voronoi cells, ellipsoids or cylinders, it can still be sensible to simplify the geometry for computational efficiency [50]. Finally, the optimization problem may be solved by a black-box shooting method based on arbitrary descriptors, as long as efficient generators are available [51].
It is worth noting that many microstructure reconstruction algorithms are inspired by the field of texture synthesis [52]. Texture synthesis aims at efficiently generating large images that are perceptually similar to a small reference. For example, in a computer game or an animated movie, it may be used for rendering near-regular or irregular cobblestone images onto a road without directly tiling the same image. As an example from microstructure reconstruction, the Gram matrix-based algorithms [35, 38, 40] are inspired by a well-known texture synthesis algorithm by Gatys et al. [53]. Similarly, the descriptor-based neural cellular automaton method in [54] is inspired by [55]. This is reasonable as the goals of microstructure reconstruction and texture synthesis are very similar. There are, however, some differences. First, texture synthesis results are required to appear similar to humans, whereas microstructure reconstruction results are measured by their effective properties like the stiffness, permeability and fracture resistance. Secondly, reconstructing 3D structures from 2D or 3D data is a very common target in microstructure reconstruction but is never aimed at in texture synthesis. Despite similar algorithms and ideas, these and other differences limit the congruence of the fields.
The present work is motivated by noting the similar goals of texture synthesis and microstructure reconstruction and aims at bridging the gaps between the two fields. In particular, it is noted that the Portilla-Simoncelli algorithm [56], which is very well-known in texture synthesis, shows a very promising potential in microstructure reconstruction. To the authors’ best knowledge, the capabilities of the Portilla-Simoncelli algorithm in the context of microstructure reconstruction have never been explored systematically. To be specific, the contributions of the present work lie in
-
recognizing and explaining that the Portilla-Simoncelli algorithm can be interpreted as a descriptor-based microstructure reconstruction algorithm,
-
discussing the sequential projection-based reconstruction as a fundamental alternative with respect to the classical optimization-based microstructure reconstruction procedures,
-
extending the algorithm to reconstruct 3D microstructures from 2D slices, and
-
validating this expansion by independent descriptor computations as well as the effective elastic and plastic material properties.
The algorithm is introduced in Sect. 2 where the mentioned conceptual differences with respect to typical microstructure reconstruction algorithms are discussed. This comprises a dimensionality expansion for 2D-to-3D reconstruction. Extensive numerical experiments are given in 2D and 3D in Sect. 3. Finally, a conclusion is drawn in Sect. 4.
2 Methods
As a basis, an introduction to common descriptor-based microstructure reconstruction approaches is given in Sect. 2.1. The sequential projection procedure in the Portilla-Simoncelli algorithm is outlined in Sect. 2.2 and contrasted to the minimization-based approach. In Sect. 2.3, different ideas for 2D-to-3D reconstruction are reviewed and a suitable solution for the present algorithm is presented. Finally, the implementation is outlined in Sect. 2.4.
2.1 Descriptor-based microstructure reconstruction
The idea behind descriptor-based microstructure reconstruction is to characterize the morphology of the structure \({\textbf {x}}\) in terms of translation-invariant, statistical descriptors \({\textbf {D}}_i({\textbf {x}})\), where \(i \in \left\{ 1,\ldots ,n_\text {D}\right\}\) enumerates different descriptors, which might themselves be multi-dimensional. Examples for these descriptors are volume fractions, grain size distributions, spatial correlations, etc. Then, microstructure reconstruction is formulated as the inverse process.
In some cases, like Gaussian random fields, a material realization can be directly sampled from given descriptors [57, 58]. In the general case, such a mapping is not known, so microstructure reconstruction is formulated as an optimization problem
where the space of possible microstructures \(\Omega\) is searched for the solution \({\textbf {x}}^\text {rec}\), which minimizes the cost function
The cost function accumulates the error between the desired microstructure and the current reconstruction, which is measured in terms of various descriptor. Descriptor-based microstructure reconstruction algorithms differ in how exactly they parametrize the microstructure \({\textbf {x}}\) and search space \(\Omega\) as well as in how they solve the optimization problem in Eq. 1.
The present work aims at parametrizing structures by general voxel grids. This is given in 2D by
and in 3D by
To solve the optimization problem given in Eq. 1, as discussed in section 1, an error measure is commonly defined in the descriptor space and minimized in an iterative procedure. The global minimum, which may be non-zero especially in the 2D-to-3D case, can in principle be found by the Yeong-Torquato algorithm. However, it requires millions to billions of iterations. Hence, the feasible descriptor fidelity is limited by its computational effort. This restriction is relaxed in DMCR [34], where gradient-based optimization algorithms are used. This method converges significantly faster and requires hundreds to thousands of iterations, although it might converge to a local minimum [43]. In contrast to these algorithms, in the following, a method is presented that reduces the number of iterations even further, leading to a leap forward in resource efficiency.
2.2 Sequential descriptor projection
A radically different approach to microstructure reconstruction lies in regarding the statistical descriptors as constraints
to to be satisfied exactly instead of descriptors to match as well as possible. Intuitively, each descriptor constraint defines a subregion in the space of possible microstructures. As an example, the volume fraction constraint
is a linear constraint. Another example is the normalized total variation, which is defined in 2D as
where \(\tilde{k}\) and \(\tilde{l}\) denote the periodic next neighbors of k and l. Using the modulo operator mod, this is expressed as
The normalized variation can be interpreted as the amount of phase boundary per unit volume. Equation 7 defines multiple hyperplanes because different signs are possible within the absolute operator \(\vert \bullet \vert\). Equivalently, symmetry considerations of pixel permutations show that multiple solutions must be possible. The constraints \(C_\phi\) and \(C_\mathcal {V}\) are shown schematically in Fig. 1 (center) for a structure of two pixels. The intersection of all these spaces defines a subspace of valid microstructures, the feasible region
Herein and in the remainder of this work, it is assumed that the maximum and minimum of the signal are also considered as descriptors with the associated constraints
and
respectively. This is equivalent to restricting the search space in optimization-based reconstruction in Eq. 3. All structures in \(\Omega _\textrm{f}\) exactly fulfil all the prescribed descriptors. If too few descriptors are specified, then the region is too large, indicating that relevant microstructural features are not captured. If too many descriptors are prescribed, then there might be no intersection at all. Thus, a trade off needs to be found. In the seminal work [56], Portilla and Simoncelli (i) introduced this concept in the context of texture synthesis, (ii) proposed a suitable set of descriptors (therein called texture model) and (iii) developed a robust algorithm to solve this constraint satisfaction problem.
Schematic visualizations of the search space, the constraint sets and the loss function for a microstructure with two pixels, \(x_1\) and \(x_2\). Gradient-based descriptor optimization (left) is compared to the projection-based approach (center, right). The volume fraction and variation constraints are denoted by \(C_\phi\) and \(C_\mathcal {V}\), respectively, whereas \(C_g\) denotes a general non-linear constraint. Note that the translation-invariance of the descriptors manifests itself as a symmetry of the constraint sets with respect to certain pixel permutations. The intersection between the constraint sets defines the feasible region \(\Omega _\textrm{f}\), which is visualized by a green dot. It may be disconnected due to symmetry considerations. A random initialization \({\textbf {x}}_0\) is iteratively projected (yellow arrows) onto the constraint sets until convergence is reached. On the right, the arrow tips for the last steps are omitted because they would occlude the intersection
The idea behind the Portilla-Simoncelli algorithm is to project any randomly initialized microstructure to the feasible region. Because multiple complex descriptors are considered, the shape of the feasible region may be too complex to derive a single projection step. The solution is an iterative procedure: For each descriptor \({\textbf {D}}_i\), where \(i \in \{1,\ldots , n_\textrm{D}\}\), a projection is derived that satisfies \({\textbf {D}}_i\) only. The issue of non-uniqueness is handled by choosing the projection that changes the structure as little as possible. These projections are carried out sequentially for all descriptors. This is shown in Fig. 1 (center), where the random initialization \({\textbf {x}}_0\) is first projected to \(C_\mathcal {V}\) and then to \(C_\phi\). In this case, the constraints are orthogonal to each other and therefore the algorithm terminates after one loop through all descriptors. In the general case, however, the projection to enforce a descriptor \({\textbf {D}}_i\) might violate previously satisfied descriptors. This is shown in Fig. 1 (right) for a generic constraint \(C_\textrm{g}\). In this case, the whole procedure is repeated in a loop until it converges to the feasible region \(\Omega _\textrm{f}\), which is defined as the intersection of all descriptor constraints. This stands in contrast to the DMCR method shown in Fig. 1 (left), where all descriptors are jointly considered in a loss function \(\mathcal {L}\), which is minimized iteratively. It is worth noting that the minima of \(\mathcal {L}\) coincide with \(\Omega _\textrm{f}\) and that \(\mathcal {L}\) quantifies the distance to \(\Omega _\textrm{f}\). Portilla and Simoncelli [56] make it very clear that they provide no proof regarding the convergence of their algorithm, but report that all their numerical experiments converged. Furthermore, it can be noted that the choice of descriptors does not only influence the existence of a solution, but also the convergence of the algorithm. The more independent the descriptors are, the fewer steps are required for convergence.
The update rules themselves
are defined by gradient projection. Herein, the gradientFootnote 2 of the descriptor error defines the direction for a line search in the microstructure space. The step width \(\lambda\) is chosen such that it satisfies the constraint \(C_{D_i}(\textrm{x})\). Hence, it is defined explicitly as a function of the current solution and the reference descriptor
This needs to be derived for each descriptor separately and is carried out in the original work by Portilla and Simoncelli [56]. While projections for simple constraints like the volume fraction can be defined easily, other descriptors like the auto-correlation are significantly more challenging to consider. For this reason, the gradient projection for the two point correlation \(\Pi _{S_2}\) and other operators are approximated in [56]. Due to the combination with sufficiently many other descriptors, the algorithm converges in practice.
The descriptors as well as the corresponding projection operators in the Portilla-Simoncelli algorithm are closely linked to the multiscale representation of the signal itself, the steerable pyramid. The steerable pyramid is a multilevel decomposition of an image into P different resolution levels and Q orientations. This is outlined in algorithm 1. A given image \({\textbf {x}}\) is first decomposed into its a high-pass residual
and low-pass content
by convolution with a high-pass and low-pass filter \(f_\textrm{h}\) and \(f_\textrm{l}\), respectively. Therein and in the following, \(\overline{\bullet }\) indicates that the associated quantity is a part of the pyramid. Then, for each pyramid level \(p \in \{1,\ldots ,P\}\), oriented band-pass filters \(f_{\textrm{b}q}\) are applied
where the index b stands for band-pass and q enumerates the orientations. Based on this, a down-sampled low-pass representation
is computed for the next higher pyramid level, where the down-sampling function \(f_\textrm{d}\) reduces the resolution of the image by a factor of two. The resulting representation comprises \(\overline{{\textbf {x}}}^\textrm{h}\), \(\overline{{\textbf {x}}}^{pq} \; \forall \; p \in \{1,\ldots ,P\}, \; q \in \{1,\ldots ,Q\}\) and \(\overline{{\textbf {x}}}^{P}\), but not \(\overline{{\textbf {x}}}^{p} \; \forall p<P\). This makes it a special case of a Laplace pyramid, in contrast to Gaussian pyramids, which are often employed in microstructure reconstruction. More details on the data structure are given in [56, 59].
Based on this representation, the descriptor set comprises marginal statistics like variance, skewness and kurtosis as well as cross-correlations and central crops of the auto-correlations of the residual \(\overline{{\textbf {x}}}^\textrm{h}\), the oriented sub-bands \(\overline{{\textbf {x}}}^{pq} \; \forall \; p,q\) as well as the partially reconstructed images at each scale. The consequence of computing such descriptors on a steerable pyramid is discussed in the following, whereas the reader is referred to [56, 60, 61] for more details on the definitions as well as the associated projection operators. Because the correlations are computed on the residuals as well as the partially reconstructed images, they resemble phase and surface correlations. Hence, the insufficiency of the two-point correlation function \({\textbf {S}}_2\) in describing complex structures, which is very well-known in the field of microstructure reconstruction, is compensated by surface correlations and cross-correlations. Because all correlations are restricted to a central crop, the number of parameters is comparably small. It should be mentioned that the central cut does not discard long-range information because of multi-level pyramid. This is analogous to the multi-scale descriptors in DMCR presented in [34]. Short-range correlations, which lie within the cutoff radius on the fine scales, are computed with high accuracy. On the coarser scales, the same cutoff radius represents a longer correlation, which is therefore not omitted from the descriptor set but merely computed at a lower accuracy and higher speed.
2.3 Dimensionality expansion
Reconstructing 3D structures from 2D slices requires dimensionality expansion. To the authors’ knowledge, such an expansion has not been proposed yet for the Portilla-Simoncelli algorithm. After briefly discussing 2D-to-3D dimensionality expansions in different microstructure reconstruction frameworks, a solution for the Portilla-Simonceli algorithm is proposed.
GANs A 2D discriminator can be provided with 2D training data or 2D slices of a 3D volume. Hence, training a 3D generator from 2D data is possible for GAN-based architectures [62, 63] as well as for models which combine GANs with autoencoders [17], transformers [64] or other models.
Diffusion models Diffusion models as the new state of the art in image generation are known to be more stable than GANs and yield high-quality results, also for microstructures [65, 66]. Unfortunately, the dimensionality of the model must match the training data [67], so the GAN dimensionality extension method is not applicable here. Simply applying a 2D denoising process on slices in alternating directions creates disharmony and does not converge. As a solution, harmonizing steps were proposed very recently by Lee and Yun [68].
Autoencoders Encoder-decoder-models have been trained in the context of microstructure reconstruction and modified for 2D-to-3D applications. An interesting solution lies in regarding the third dimension as time and handling it by a video model in the latent space [69, 70]. Furthermore, a slice mismatch loss is introduced in [71], however, this approach is not truly 2D-to-3D since at least one 3D training sample is required.
MPS In multi-point statistics, dimensionality extension can be achieved by searching for patterns on each slice and plane [72] or on random slices [73].
Descriptor-based optimization If the microstructure is reconstructed by descriptor-based optimization, the dimensionality extension can be achieved by means of the descriptor computation. This is done for the Yeong-Torquato [20, 30, 74], where descriptor information in various directions and planes determines whether or not a pixel swap should be accepted. Similarly, in the DMCR [35] algorithm, descriptors are computed in all possible slices in different directions. This means that the direction of the gradient is averaged over the three dimensions before it is used in the optimization step.
Proposed solution The Portilla-Simoncelli algorithm as a sequential descriptor-based projection approach is conceptually very similar to the gradient-based descriptor optimization idea of the DMCR algorithm. Hence, a similar dimensionality expansion might be feasible. However, gradient-based projections are performed sequentially instead of the minimization of the accumulated descriptor error. In order to avoid complex interference between the sequential projections and the averaged gradient directions, a simpler alternative is presented.
The simple solution is to sequentially update individual slices for each direction, where the slice update consists of a single pass through all projection operators. This is shown in algorithm 2: For each iteration of the 2D-to-3D expansion, the outer-most loop iterates over the three dimensions. In each dimension, a loop iterates over all slices that are orthogonal to that direction. For each slice, the inner-most loop carries out all descriptor projections as if a 2D structure was reconstructed. The result from the loop over the three spatial directions are averaged and represent the 3D result of that single iteration. A stabilization inspired by a viscous regularization in partial differential equation solvers or by a momentum term in stochastic gradient descent algorithms can be introduced at this point. However, the numerical experiments of the authors suggest that no stabilization is needed. In this context, it is noted that no proof exists why this algorithm should converge to a stable state, however, this is the case in practice. Note that the same applies to the sequential projection of individual descriptors itself in the Portilla-Simoncelli algorithm.
2.4 Implementation
An open-source implementation of the 2D Portilla-Simoncelli algorithm is taken from GitHub [60]. This code is a Python port of the original Matlab code [61] and is mainly based on Numpy. A difference with respect to [56] lies in the pyramid-based image representation. In contrast to the Matlab code, the Heeger and Bergen steerable pyramid is implemented [59] as explained in [75]. The main difference between the two is that the former is complex, while the latter is real. Although the former is known to yield superior results, especially for relatively ordered patterns [56], the performance is similar in most cases [75]. The grayscale version of the code is used as-is for the 2D examples and modified for the 2D-to-3D dimensionality expansion. For this purpose, the code is restructured and an additional loop is introduced as given in algorithm 2. Since the individual slice updates for each given dimension are independent of each other, the algorithm is accelerated by multiprocessing. The loop over all slices is parallelized using a Pathos pool [76, 77]. This compensates for the single-core nature of the underlying Numpy code and leads to an approximate ten-fold increased speed of the reconstruction process. The reconstruction is carried out on a conventional laptop with a \(12^\textrm{th}\) Gen Intel(R) Core(TM) i7-12800 H CPU. The memory requirements are negligible and the GPU is not used.
The open-source tool MCRpy is used for evaluating the quality of the reconstructed structures. This package is developed and described in former works of the authors [37]. It provides a number of microstructure descriptors that can be computed on 2D microstructure data or on 2D slices of 3D data. The specific settings are given in Table 1.
MCRpy is also used as a reference in order to compare the Portilla-Simoncelli algorithm to descriptor-based optimization procedures. It allows to reconstruct microstructures from descriptors in an optimization-based manner. Thereby, arbitrary microstructure descriptors can be combined in a loss function to define the optimization problem, which can be solved using a number of algorithms. Therein, the descriptors, loss functions and algorithms can be interchanged in a flexible manner and may also be provided by the user as plug-in modules. In the present work, differentiable descriptors are used, enabling an efficient solution of the optimization problem by gradient-based algorithms, making the reference an example for DMCR [34]. To be specific, the two-point correlation \({\textbf {S}}_2\) [19] and the VGG-19 g matrices \({\textbf {G}}\) [38, 41] are used with a simple mean squared error loss function and the L-BFGS-B algorithm. Similar results could have been achieved with the MCRpy implementation of the Yeong-Torquato algorithm, albeit with a much higher computational cost. The settings are given in Table 2.
3 Numerical experiments
To provide an initial understanding of the capabilities and limitations of the method, the Portilla-Simoncelli algorithm is first applied in 2D to a number of different material classes and compared to algorithms from the literature in Sect. 3.1. Then, the 2D-to-3D reconstruction is investigated in Sect. 3.2 as well as the algorithm’s performance and scalability. Finally, the dimensionality expansion is validated in subsection 3.3 by numerical simulation and homogenization using structures where a 3D reference is available.
3.1 Baseline in 2D
As a first investigation of the capabilities and limitations of the Portilla-Simoncelli algorithm, it is compared to optimization-based microstructure reconstruction from statistical descriptors. For this purpose, Fig. 2 shows a comparison for five different material classes. Therein, the reference structures are taken from [38], where they are released under the Creative Commons license [78]. As a reference reconstruction algorithm, the DMCR implementation in MCRpy [37] is used. Similar results would have been achieved with the Yeong-Torquato algorithm. A visual investigation shows that the results are similarly good as the conventional methods for most materials. This is quantified by microstructure descriptors in Table 3. As expected, optimization-based reconstruction algorithms are best when measured by the descriptors that was used for reconstruction, i.e., reconstructions from \({\textbf {S}}_2\) excel when measured by \({\textbf {S}}_2\) and reconstructions from the Gram matrices \({\textbf {G}}\) excel when measured by \({\textbf {G}}\). The volume fraction \(\phi\) given in Eq. 6 is also listed in Table 3, however it should be mentioned that \(\phi\) is highly correlated to \({\textbf {S}}_2\). Moreover, in practice, the reconstructed, real-valued structure is often binarized with a threshold which is chosen such that the reference volume fraction is matched exactly. Clearly, this and other post-processing methods should be employed in a real-world application. However, the present work is focused on the algorithm itself and therefore presents unprocessed results directly. Comparing the other, independent descriptor in each case confirms that the descriptor errors mostly are in the same order of magnitude for the Portilla-Simoncelli algorithm as for DMCR. The copolymer deserves special attention. It can be seen that the fine, fingerprint-like structure is reproduced by the Portilla-Simoncelli algorithm, whereas it poses a serious challengeFootnote 3 for methods based on \({\textbf {S}}_2\). The quality is inferior to the Gram matrix-based reconstruction, which, however, takes significantly longer than the Portilla-Simoncelli algorithm, especially if executed on CPU. An in-depth analysis of the performance and scalability is carried out in subsection 3.2 in the context of 3D reconstruction.
Pointing out limitations of scientific algorithms is equally important as demonstrating their capabilities. As shown in Fig. 3, the Portilla–Simoncelli algorithm fails to reproduce long-range correlations and higher-order information. In the alloy example, the connectivity information of the grain boundary indicator constitutes high-order information which is often not captured by two-point correlation-based descriptors. However, it should be mentioned that even with higher-order descriptors, the long and thin lines of the alloy structure make it a notoriously challenging case. In contrast, the inability to reconstruct the fiber-reinforced polymer (FRP) might be more surprising to most researchers. The inclusions therein are approximately circular and already a very crude random sequential addition algorithm yields far superior results. The reason again lies in connectivity and long range information. For the PMMA in Fig. 2, the disconnected and approximately convex inclusion shapes pose no challenges to the algorithm. However, at the high resolution and volume fraction of the FRP, this seemingly trivial information becomes high-order and long-range and is therefore beyond the capabilities of the method. In summary, despite the limitations displayed in Fig. 3, a great number of materials is reconstructed accurately as shown in Fig. 2, with a competitive morphological accuracy and a superior performance.
Failure cases of the 2D Portilla-Simoncelli algorithm [56] when applied to microstructure data. Despite seeming unequal and unequally complex, the alloy (a) as well as the fiber-reinforced polymer (FRP) (c) are characterized by connectivity information, which manifests itself in higher-order correlations that are not captured by the method. The alloy is taken from [38], where it is released under the Creative Commons license [78]. The FRP is generously provided by the Institute of Lightweight Engineering and Polymer Technology at the Dresden University of Technology and described in [66]
The competitive results of the 2D Portilla-Simoncelli algorithm in Fig. 2 naturally give rise to the following question: Is the good performance rooted purely in the projection-based approach or is the unique descriptor set of correlations in the steerable pyramid also needed? This question can be simply answered by an ablation study, where only \(\phi\) and \({\textbf {S}}_2\) as well as the signal minimum and maximum are used in a projection-based algorithm. In every iteration, \({\textbf {S}}_2\) is first accounted for and only then followed by a volume fraction correction and a final clipping. Although similar ablations are given in the original work by Portilla and Simoncelli [56], it is worth illustrating this aspect in the context of microstructures specifically. The ceramics microstructure is chosen for this ablation, because it can be reconstructed very well from \({\textbf {S}}_2\) alone as shown in Fig. 2. This requires a projection operator specifically for \({\textbf {S}}_2\). In this case, a closed solution for \(\lambda\) in the gradient projection as formulated in Eq. 12 could not be found and instead, an approximation is made. The lengthy expressions for \(\Pi _{{\textbf {S}}_2}\) are given in [56]Footnote 4 and the results are shown in Fig. 4: Although large-scale features quickly form from the initial random noise, it can be seen that the reconstruction quality is not even remotely acceptable. The plot of the temporal evolution shows that the result is not stable, as features appear and disappear after a single iteration. Moreover, even the volume fractions are strongly violated, making the result resemble the carbonate more than the ceramics, which should have been reconstructed. Because the ceramics can be reconstructed very well with DMCR based on \({\textbf {S}}_2\) only, there is no doubt that the projection-based approach using the approximated projection operators is insufficient here. Instead, the Portilla-Simoncelli descriptor set is essential to the success of the overall algorithm.
Ablation study showing temporal evolution of the microstructure using the projection method with conventional descriptors. The two-point correlation, volume fractions and minimum and maximum are corrected for iteratively in this order. Because the correlation projection is only approximate, the algorithm fails to converge and does not yield an acceptable solution
With this ablation confirming the relevance of the Portilla-Simoncelli descriptor set, a natural question is how well the Yeong-Torquato algorithm or DMCR might work based on this descriptor. Although implementing this exceeds the scope of this work, the authors assume that classical, optimization-based microstructure reconstruction algorithms based on the Portilla-Simoncelli descriptors might work at least equally well as they currently do. However, the number of iterations of these algorithms is much higher than in the projection-based algorithm. Especially in 3D, the Yeong-Torquato algorithm and DMCR require millions to billions and hundreds to thousands of iterations, while the projection method converges after ten iterations.Footnote 5 To the authors’ best knowledge, there exists no gradient-based or gradient-free optimization algorithm for such high-dimensional search spaces which converges to comparable solutions within ten iterations. Hence, similar wallclock times can only be achieved if the cost per iteration is so much lower than with the Portilla-Simoncelli algorithm that it compensates for the increased number of iterations. In the authors’ opinion, this is currently hard to imagine. However, in view of the weaknesses regarding long-range correlations, an advantage of optimization-based reconstruction algorithms with the Portilla-Simoncelli descriptors might be the possibility to add in long-range information. While the present work proceeds to investigate the 2D-to-3D reconstruction as its central topic, this idea is a promising candidate for future research.
3.2 Performance in 3D
Figure 5 shows the results of the 2D-to-3D reconstruction proposed in algorithm 2. Thereby, the reference microstructures are identical to the 2D benchmarks given in Fig. 2. It can be seen that the structures are largely reconstructed very well. Upon a visual inspection, all materials show plausible structures that resemble the 2D references on all faces and naturally blend together at the edges. Only the copolymer constitutes an exception, as the true length of the fingerprint-like lamellar structures is not reached in 3D, although Fig. 2 shows that the 2D algorithm can in principle recover such structures. To complement this visual impression with numerical values, Table 3 shows the descriptor errors. When comparing the results from the 2D Portilla-Simoncelli algorithm to the proposed 2D-to-3D expansion, the descriptor errors are largely in the same order of magnitude. The 3D result is consistently worse by a factor of \(50 \%\) to \(100 \%\), except for the copolymer, where the previously discussed phenomenon can be clearly observed in the descriptors. It is concluded that the proposed 2D-to-3D reconstruction method can cover most, but not all morphologies that the 2D baseline can reconstruct. The reduction in accuracy is acceptable in face of the additional difficulty of matching orthogonal slices to each other.
Results of the proposed 2D-to-3D reconstruction when applied to the references shown in Fig. 2. Although the quality of the copolymer is reduced when compared to the 2D case, the remaining materials are reconstructed very well
To deepen the understanding of the algorithm’s behavior, the temporal evolution of the solution over the iterations is investigated exemplarily by means of the carbonate structure. Figure 6 shows some intermediate solutions as well as the random initialization. It can be seen that the result of the very first iteration can already be identified as the correct material, albeit with considerable noise. The next few iterations (iterations 1 through 3 are shown here) remove this noise and sharpen the microstructural features, while leaving the overall shapes and their positions unchanged. After that, the algorithm quickly reaches a stable state, where the solution varies very little. These visual impressions can easily be quantified by observing the norm of the microstructure updates in each iteration as well as the microstructure descriptors. This is shown in Figs. 7 and 8, respectively.
Temporal evolution of the microstructure solution over the course of iterations (left to right). The result of the first iteration (b) already differs from the random initialization (a) and defines the locations of the main structural features. While the first few iterations notably reduce the noise and increase the result quality (c–d), the solution remains relatively stable after that (e)
Convergence behavior of the 2D-to-3D reconstruction algorithm measured by the microstructure updates. The mean squared error (MSE) between each iteration and the previous result is plotted. Although the value does not decrease to numerical precision within 50 iterations, it can be seen that the changes are relatively small after the first ten iterations
The high performance of the algorithm requires further discussion along with its scalability. As discussed previously, a major advantage of the algorithm is its high performance, which is rooted in the very few iterations: Even in 3D, only 10 iterations are needed for obtaining high-quality solutions. For comparison, the Yeong-Torquato algorithm as the most well-known descriptor-based reconstruction algorithm requires millions or even billions of iterations, because every single iteration merely changes two pixels. The convergence plot in Fig. 7 would look quite differently, as it would randomly jump back and forth between 0 (for unaccepted swaps) and 2/(KLM) (for accepted swaps). As a compensating factor, it should also be mentioned that the computational cost of an individual iteration is significantly lower. This is because descriptors can be updated after pixel swaps instead of recomputing them from scratch, making the number of iterations insufficient for evaluating performance. Despite this factor, to the authors’ best knowledge, reconstructing complex microstructures with \(256^3\) pixels in less than ten minutes on a conventional laptop as in the present work is not feasible with the Yeong-Torquato algorithm. As mentioned in Sect. 2.1, the DMCR algorithm previously proposed by the authors reduced the number of iterations to hundreds or thousands by leveraging differentiable descriptors for efficient, gradient-based optimization algorithms. Although this significantly reduces the wallclock time, the multiple gradients required by quasi-Newton algorithms and the high memory cost of automatic differentiation necessitate expensive hardware.
The scalability of the method with the number of voxels is not trivial to quantify. It is clear that the descriptors are projected on every slice in every direction, leading to \(\mathcal {O}(K)\) evaluations, assuming \(K \approx L \approx M\). The projections in turn are partially applied in Fourier space, adding a further factor of \(\mathcal {O}(K^2 \textrm{log}^2 K)\). However, it is not straightforward to determine theoretically how the application of the projection operators scales, as some of them require iterative approximations to solutions of equation systems. As an example, the first iteration takes notably longer than the subsequent ones. For this reason, the scalability is determined experimentally as shown in Fig. 9. Assuming that caching effects can be neglected for \(K>128\), the method scales super-polynomially as can be seen in the double-logarithmic plot. As a comparison, DMCR theoretically scales polynomially in 2D and 3D as long as the correlation length is kept constant [34]. In practice, the authors could observe the polynomial scaling of DMCR in 2D, but not in 3D. An explanation might be that the slice-based descriptor computation makes the 3D algorithm memory-bound, while the 2D algorithm is compute-bound. For this reason, the comparison is made purely based on numerical experiments in the following For DMCR based on the Gram matrices, reconstruction times between 100 and 110 minutes on NVidia Quadro RTX 8000 GPUs are reported in the literature [40] for \(200^3\) voxels. The MCRpy implementation is slightly slower: On NVidia A100 GPUs, the authors measured 35 minutes, 1:50 h and 20 h for a resolution of \(64^3\), \(128^3\) and \(256^3\) voxels respectively. For the same resolutions, the 3D Portilla-Simoncelli algorithm requires less than 2, 3 and 10 min, respectively, even on significantly inferior hardware. As can be seen in Fig. 9, even microstructures with a resolution of \(512^3\) voxels are reconstructed in 75 min on a conventional laptop. However, as mentioned in Sect. 3.1, the Gram matrix-based DMCR yields superior results, allowing to trade off efficiency for accuracy. Similarly, Gaussian random field-based approaches outperform the presented algorithm in terms of computational efficiency, but are more limited in the types of morphologies they can generate [57, 79]. Thus, the present work complements the Pareto frontier of reconstruction algorithms by an additional method between direct sampling and gradient-based optimization.
Scalability of the presented 2D-to-3D reconstruction method based on the Portilla-Simoncelli algorithm and DMCR based on Gram matrices, where the latter fails in the high-resolution case due to memory limitations. The computations are carried out on a conventional laptop with a \(12^\textrm{th}\) Gen Intel(R) Core(TM) i7-12800 H CPU for the Portilla-Simoncelli algorithm and an Nvidia A100 GPU for DMCR, respectively
3.3 2D-to-3D validation
While the 3D results in subsection 3.2 show the morphological plausibility of the reconstructed structures in terms of microstructure descriptors, a proper evaluation in terms of effective behavior is not possible without a 3D ground truth. For this reason, Fig. 10 shows three validation cases for the 2D-to-3D reconstruction where a true reference is available. The structures are taken from [36, 80], where they are released under the Creative Commons license [78]. Like in that work, the descriptor information for the reconstruction only stems from three orthogonal 2D slices that are extracted from the 3D volume, thus simulating the 2D-to-3D dimensionality expansion workflow while also accounting for anisotropy. A visual inspection shows that the first two examples, the columnar and lamellar spinodoid structures, are reconstructed very well. In contrast, the long-range correlations of the TiFe system poses similar challenges as the 2D structures shown in Fig. 3. This strong difference is not visible in the descriptor errors, which are given in Table 4. This naturally poses the question of what magnitudes of descriptor error are tolerable. Different descriptors have a different sensitivity with respect to different morphological aspects of the structure. For this reason, a very reliable way of deciding if a structure is reconstructed sufficiently well is to compute its effective properties. With a specific application at hand, it is much easier for an engineer to derive a tolerable variation in the effective material properties than a threshold for a number of statistical descriptors. Correlating these two is an important topic for future research, which, however, exceeds the scope of this work.
Microstructure reconstruction results for 2D-to-3D reconstruction using the proposed method based on the Portilla-Simoncelli algorithm. In contrast to Fig. 5, a full 3D reference is available. Three slices are extracted for computing the reference descriptors and no further information is passed to the reconstruction algorithm. Visually good results are achieved for the columnar and lamellar spinodoid structures, whereas the long-range correlations of the TiFe system exceed the capabilities of the method. All reference structures are taken from [36] where they are released under the Creative Commons license [78]
To compare the reconstruction results with the reference solution in terms of effective mechanical properties, numerical simulations are carried out using DAMASK [81]. Using a simple isotropic elasto-plastic constitutive model for the two-phase materials, the elastic surfaceFootnote 6 and the homogenized, directional yield strength \(\overline{\sigma }_\textrm{y}\) and Young’s modulus \(\overline{E}\) are determined as described in Appendix A. The material parameters are chosen to mimic the \(\beta\)-Ti and TiFe phase for the TiFe system as well as to mimic polyvinyl chloride (PVC) and a void-like much softer phase for the spinodoids. They are given in Table 5.
The elastic surfaces [82], i.e., a 3D visualization of the Young’s modulus for each possible direction of load, for the three exemplary structures from Fig. 10 are shown in Fig. 11. The approximately isotropic characteristic of the TiFe’s elastic response (Fig. 11c) are qualitatively and quantitatively well matched in the reconstructed microstructure. The maximum relative deviation of \({0.6\,\mathrm{\%}}\) underlines this conclusion. For both spinodoid structures (Fig. 11a, Fig. 11b) the highly anisotropic behavior is qualitatively well preserved in the reconstructed microstructures. However, the maximum relative difference is with approximately \({10\,\mathrm{\%}}\) and \({8\,\mathrm{\%}}\) for the columnar and lamellar spinodoid, respectively, significantly higher than for the TiFe structures. The deviations are presumably based on slight morphological differences of the reconstructed microstructures. Especially in the case of anisotropic microstructural features, a slightly reduced connectivity or reduced length of one phase in a certain direction might decrease the stiffness perceptibly. Additionally, the reconstruction is performed to match only one slice of the original microstructure for each Cartesian direction. Assuming a statistically not perfectly homogeneous distribution of the descriptors in these directions, the reconstructions cannot perfectly match the original microstructure and so not their properties.
The results shown in Fig. 12, where the relative difference of the directional Young’s modulus and the directional yield strength in all three Cartesian directions are presented, seem to support the conclusions drawn from the elastic surfaces. The reconstructed TiFe structure differs only slightly with less than \({0.5\,\mathrm{\%}}\) in both properties in all three directions. The Young’s modulus of the reconstructed columnar spinoid is found to be approximately 5% to 10% smaller compared to the original one. This is possibly due to a slightly decreased interconnection of the stiffer PVC phase in the respective loading direction. In the case of the lamellar spinodoid, the Young’s modulus is found to be approximately \({5\,\mathrm{\%}}\) smaller in the stiff x- and y-direction, whereas it is found to be quantitatively well matched in z-direction. When interpreting the homogenized yield strength of the spinodoid structures, spurious noise in the reconstructed microstructure has to be considered. This noise, as slightly visible in the reconstructed microstructures in Fig. 10, might act as stress concentrator, resulting in a possible decrease of the effective yield strength. This effect could explain the deviation of more than \({-5\,\mathrm{\%}}\) in z-direction, i.e. the direction of the columnar features, for the columnar spinodoid and the deviations of approximately \({-2\,\mathrm{\%}}\) in the x- and y-direction, i.e. the direction of the lamellar features, in case of the lamellar spinodoid. Further effects, resulting from the aforementioned three slice-based reconstruction approach as well as statistical deviations, contribute to minor difference of the here considered, homogenzied properties.
Comparison of homogenized properties of the original (ori) and reconstructed (rec) microstructures from Fig. 10 in terms of their relative difference
4 Conclusions and outlook
The Portilla-Simoncelli algorithm from the field of texture synthesis is recognized as a potent microstructure reconstruction algorithm and extended for 2D-to-3D expansion. Revisiting the role of descriptors in microstructure reconstruction, it is noted that they usually serve as a basis for an objective function \(\mathcal {L}\). Commonly, microstructure reconstruction is then formulated as an optimization problem with the aim of finding structure realizations that minimize \(\mathcal {L}\). In contrast, in the Portilla-Simoncelli algorithm, descriptors are regarded as constraints that need to be satisfied. In other words, each descriptor defines a subspace or region in the space of possible microstructures, and the intersection defines acceptable solutions to the reconstruction problem. Consequently, projection operators are derived for each descriptor that (approximately) project any given point in the microstructure space to the closest point in the corresponding descriptor subspace. Sequentially applying these projections in a loop yields an efficient and versatile reconstruction algorithm if suitable descriptors are chosen.
Based on this idea of sequential gradient projection, this work
-
1.
identifies the Portilla-Simoncelli algorithm as a viable solution to the 2D microstructure reconstruction problem;
-
2.
shows applications throughout a number of material classes, discussing successes and failures of the method;
-
3.
provides an ablation by projection-based reconstruction from the two-point correlations, confirming the relevance of the Portilla-Simoncelli descriptor set;
-
4.
develops an extension of the method for 2D-to-3D reconstruction;
-
5.
applies the same to various material classes and
-
6.
finally validates the 2D-to-3D reconstruction by numerical simulation and homogenization using data where a fully known 3D ground truth is available.
By requiring only ten iterations, the method is extremely efficient, which is especially relevant in the 3D case. Concretely, on a conventional laptop, volume elements of \(256^3\) and \(512^3\) voxels are reconstructed in 9 min and 1:15 h, respectively. To the authors’ best knowledge, these low memory and CPU requirements are unparalleled in the context of generic and complex material structures. Moreover, like all descriptor-based algorithms, no training phase or data set is required, since the reference descriptor can stem from a single example or from descriptor interpolation.
Naturally, the method is not a panacea and its limitations are discussed equally transparently as its capabilities. This gives clear ideas for future research efforts. As a first example, the inability of the method to reproduce long-range correlations should be addressed, possibly by means of suitable microstructure descriptors. This leads to the second limitation, namely the need for specific projection operators whenever the descriptor set is altered, reducing the algorithm’s flexibility. In view of the success of the lineal path and cluster correlation functions in microstructure reconstruction, it should be investigated if (approximate) projection operators can be defined for these descriptors. Finally, further improvements of classical descriptor-based reconstruction algorithms like the Yeong-Torquato algorithm might be achievable using the unique descriptor set developed by Portilla and Simoncelli [56].
Data availability
No datasets were generated or analysed during the current study.
Code availability
The code is made available upon reasonable request.
Notes
The periodicity is given only within the limits of the discretization.
The gradient projection is conceptually similar to the DMCR approach, but the difference lies in the order of updates and in the determination of \(\lambda\). While the gradient \(\nabla {\textbf {D}}_i\) is weighted and averaged over all descriptors and only then applied to \({\textbf {x}}\) in DMCR, this order is reversed in the Portilla-Simoncelli algorithm. Furthermore, the step width \(\lambda\) is chosen by the optimization algorithm in DMCR, whereas in the Portilla-Simoncelli algorithm, expert knowledge on the microstructure descriptors is used to derive it a priori.
This result is not only obtained in the present work, but also in the work by Li et al. [38].
Specifically, the derivation is given in Appendix A.2 of [56].
This is discussed and analyzed in the context of 3D reconstruction in Sect. 3.2.
The reader is kindly referred to [36] for more details.
References
Olson GB (1997) Computational Design of Hierarchically Structured Materials. Science 277(5330):1237. https://doi.org/10.1126/science.277.5330.1237
W. Chen, A. Iyer, R. Bostanabad, Data-centric design of microstructural materials systems, Engineering p. S209580992200056X (2022). https://doi.org/10.1016/j.eng.2021.05.022. https://linkinghub.elsevier.com/retrieve/pii/S209580992200056X
Bargmann S, Klusemann B, Markmann J, Schnabel JE, Schneider K, Soyarslan C, Wilmers J (2018) Generation of 3D representative volume elements for heterogeneous materials: A review. Progress in Materials Science 96:322 https://doi.org/10.1016/j.pmatsci.2018.02.003. https://linkinghub.elsevier.com/retrieve/pii/S0079642518300161
Bostanabad R, Zhang Y, Li X, Kearney T, Brinson LC, Apley DW, Liu WK, Chen W (2018) Computational microstructure characterization and reconstruction: Review of the state-of-the-art techniques. Progress in Materials Science 95:1. https://doi.org/10.1016/j.pmatsci.2018.01.005
Sahimi M, Tahmasebi P (2021) Reconstruction, optimization, and design of heterogeneous materials and media: Basic principles, computational algorithms, and applications. Physics Reports 939:1 https://doi.org/10.1016/j.physrep.2021.09.003. https://linkinghub.elsevier.com/retrieve/pii/S0370157321003719
R. Cang, Y. Xu, S. Chen, Y. Liu, Y. Jiao, M.Y. Ren, Microstructure Representation and Reconstruction of Heterogeneous Materials via Deep Belief Network for Computational Material Design, arXiv:1612.07401 [cond-mat, stat] pp. 1–29 (2017). ArXiv: 1612.07401
M. Faraji Niri, J. Mafeni Mase, J. Marco, Performance Evaluation of Convolutional Auto Encoders for the Reconstruction of Li-Ion Battery Electrode Microstructure, Energies 15(12), 4489 (2022). https://doi.org/10.3390/en15124489. https://www.mdpi.com/1996-1073/15/12/4489
X. Li, Z. Yang, L.C. Brinson, A. Choudhary, A. Agrawal, W. Chen, A Deep Adversarial Learning Methodology for Designing Microstructural Material Systems, in Volume 2B: 44th Design Automation Conference (American Society of Mechanical Engineers, Quebec City, Quebec, Canada, 2018), pp. 1–14. https://doi.org/10.1115/DETC2018-85633
A. Iyer, B. Dey, A. Dasgupta, W. Chen, A. Chakraborty, A Conditional Generative Model for Predicting Material Microstructures from Processing Methods, arXiv:1910.02133 [cond-mat, stat] (2019). arxiv:1910.02133
J. Feng, X. He, Q. Teng, C. Ren, C. Honggang, Y. Li, Reconstruction of porous media from extremely limited information using conditional generative adversarial networks, Physical Review E 100, 033308 (2019). https://doi.org/10.13140/RG.2.2.32567.98727. Publisher: Unpublished
Fokina D, Muravleva E, Ovchinnikov G, Oseledets I (2020) Microstructure synthesis using style-based generative adversarial networks. Physical Review E 101(4):1. https://doi.org/10.1103/PhysRevE.101.043308
Y. Li, X. He, W. Zhu, H. Kwak, Digital Rock Reconstruction Using Wasserstein GANs with Gradient Penalty, IPTC (2022)
J.W. Lee, N.H. Goo, W.B. Park, M. Pyo, K.S. Sohn, Virtual microstructure design for steels using generative adversarial networks, Engineering Reports 3(1) (2021). https://doi.org/10.1002/eng2.12274. https://onlinelibrary.wiley.com/doi/10.1002/eng2.12274
H. Amiri, I. Vasconcelos, Y. Jiao, P.E. Chen, O. Plümper, Quantifying complex microstructures of earth materials: Reconstructing higher-order spatial correlations using deep generative adversarial networks. preprint, Geology (2022). https://doi.org/10.1002/essoar.10510988.1. http://www.essoar.org/doi/10.1002/essoar.10510988.1
Shams R, Masihi M, Boozarjomehry RB, Blunt MJ (2020) Coupled generative adversarial and auto-encoder neural networks to reconstruct three-dimensional multi-scale porous media. Journal of Petroleum Science and Engineering 186:1. https://doi.org/10.1016/j.petrol.2019.106794
Feng J, Teng Q, Li B, He X, Chen H, Li Y (2020) An end-to-end three-dimensional reconstruction framework of porous media from a single two-dimensional image based on deep learning. Computer Methods in Applied Mechanics and Engineering 368:113043. https://doi.org/10.1016/j.cma.2020.113043
Zhang F, Teng Q, Chen H, He X, Dong X (2021) Slice-to-voxel stochastic reconstructions on porous media with hybrid deep generative model. Computational Materials Science 186:110018. https://doi.org/10.1016/j.commatsci.2020.110018
Y. Zhang, P. Seibert, A. Otto, A. Raßloff, M. Ambati, M. Kastner, DA-VEGAN: Differentiably Augmenting VAE-GAN for microstructure reconstruction from extremely small data sets, arXiv:0904.3664 [cs] (2023)
Torquato S (2002) Statistical Description of Microstructures. Annual Review of Materials Research 32(1):77. https://doi.org/10.1146/annurev.matsci.32.110101.155324
Yeong CLY, Torquato S (1998) Reconstructing random media. Physical Review E 57(1):495. https://doi.org/10.1103/PhysRevE.57.495
Alexander SK, Fieguth P, Ioannidis MA, Vrscay ER (2009) Hierarchical Annealing for Synthesis of Binary Images. Mathematical Geosciences 41(4):357. https://doi.org/10.1007/s11004-008-9209-x
Pant LM, Mitra SK, Secanell M (2015) Multigrid hierarchical simulated annealing method for reconstructing heterogeneous media. Physical Review E 92(6):063303. https://doi.org/10.1103/PhysRevE.92.063303
Karsanina MV, Gerke KM (2018) Hierarchical Optimization: Fast and Robust Multiscale Stochastic Reconstructions with Rescaled Correlation Functions. Physical Review Letters 121(26):265501. https://doi.org/10.1103/PhysRevLett.121.265501
Chen D, Xu Z, Wang X, He H, Du Z, Nan J (2022) Fast reconstruction of multiphase microstructures based on statistical descriptors. Physical Review E 105(5):055301. https://doi.org/10.1103/PhysRevE.105.055301
Rozman MG, Utz M (2001) Efficient reconstruction of multiphase morphologies from correlation functions. Physical Review E 63(6):1. https://doi.org/10.1103/PhysRevE.63.066701
A. Adam, F. Wang, X. Li, Efficient reconstruction and validation of heterogeneous microstructures for energy applications, International Journal of Energy Research p. er.8578 (2022). https://doi.org/10.1002/er.8578. https://onlinelibrary.wiley.com/doi/10.1002/er.8578
Pant LM, Mitra SK, Secanell M (2014) Stochastic reconstruction using multiple correlation functions with different-phase-neighbor-based pixel selection. Physical Review E 90(2):1. https://doi.org/10.1103/PhysRevE.90.023306
Gerke KM, Karsanina MV, Vasilyev RV, Mallants D (2014) Improving pattern reconstruction using directional correlation functions. EPL (Europhysics Letters) 106(6):66002 https://doi.org/10.1209/0295-5075/106/66002. https://iopscience.iop.org/article/10.1209/0295-5075/106/66002
Shao Q, Makradi A, Fiorelli D, Mikdam A, Huang W, Hu H, Belouettar S (2022) Material Twin for composite material microstructure generation and reconstruction. Composites Part C: Open Access 7:100216 https://doi.org/10.1016/j.jcomc.2021.100216. https://linkinghub.elsevier.com/retrieve/pii/S2666682021001080
Talukdar M, Torsaeter O, Ioannidis M, Howard J (2002) Stochastic reconstruction, 3D characterization and network modeling of chalk. Journal of Petroleum Science and Engineering 35(1–2):1. https://doi.org/10.1016/S0920-4105(02)00160-2
Jiang Z, Chen W, Burkhart C (2013) Efficient 3D porous microstructure reconstruction via Gaussian random field and hybrid optimization. Journal of Microscopy 252(2):135. https://doi.org/10.1111/jmi.12077
Gerke KM, Karsanina MV, Skvortsova EB (2012) Description and reconstruction of the soil pore space using correlation functions. Eurasian Soil Science 45(9):861. https://doi.org/10.1134/S1064229312090049
Zhou XP, Xiao N (2018) 3D Numerical Reconstruction of Porous Sandstone Using Improved Simulated Annealing Algorithms. Rock Mechanics and Rock Engineering 51(7):2135. https://doi.org/10.1007/s00603-018-1451-z
Seibert P, Ambati M, Raßloff A, Kästner M (2021) Reconstructing random heterogeneous media through differentiable optimization. Computational Materials Science 196:110455
Seibert P, Raßloff A, Ambati M, Kästner M (2022) Descriptor-based reconstruction of three-dimensional microstructures through gradient-based optimization. Acta Materialia 227:117667 https://doi.org/10.1016/j.actamat.2022.117667. https://linkinghub.elsevier.com/retrieve/pii/S1359645422000520
Seibert P, Raßloff A, Kalina KA, Gussone J, Bugelnig K, Diehl M, Kästner M (2023) Two-stage 2D-to-3D reconstruction of realistic microstructures: Implementation and numerical validation by effective properties. Computer Methods in Applied Mechanics and Engineering 412:116098 https://doi.org/10.1016/j.cma.2023.116098. https://www.sciencedirect.com/science/article/pii/S0045782523002220
Seibert P, Raßloff A, Kalina K, Ambati M, Kästner M (2022) Microstructure Characterization and Reconstruction in Python: MCRpy. Integrating Materials and Manufacturing Innovation 11(3):450. https://doi.org/10.1007/s40192-022-00273-4
Li X, Zhang Y, Zhao H, Burkhart C, Brinson LC, Chen W (2018) A Transfer Learning Approach for Microstructure Reconstruction and Structure-property Predictions. Scientific Reports 8(1):13461. https://doi.org/10.1038/s41598-018-31571-7
Bhaduri A, Gupta A, Olivier A, Graham-Brady L (2021) An efficient optimization based microstructure reconstruction approach with multiple loss functions. Computational Materials Science 199:110709 https://doi.org/10.1016/j.commatsci.2021.110709. https://www.sciencedirect.com/science/article/pii/S0927025621004365
Bostanabad R (2020) Reconstruction of 3D Microstructures from 2D Images via Transfer Learning. Computer-Aided Design 128:102906. https://doi.org/10.1016/j.cad.2020.102906
Lubbers N, Lookman T, Barros K (2017) Inferring low-dimensional microstructure representations using convolutional neural networks. Physical Review E 96(052111):1
Reck P, Seibert P, Raßloff A, Kästner M, Peterseim D (2023) Scattering transform in microstructure reconstruction. PAMM 23(3):e202300169 https://doi.org/10.1002/pamm.202300169. https://onlinelibrary.wiley.com/doi/10.1002/pamm.202300169
P. Seibert, A. Raßloff, K. Kalina, A. Safi, P. Reck, D. Peterseim, B. Klusemann, M. Kästner, On the relevance of descriptor fidelity in microstructure reconstruction, PAMM p. e202300116 (2023). https://doi.org/10.1002/pamm.202300116. https://onlinelibrary.wiley.com/doi/10.1002/pamm.202300116
Henrich M, Fehlemann N, Bexter F, Neite M, Kong L, Shen F, Könemann M, Dölz M, Münstermann S (2023) DRAGen – A deep learning supported RVE generator framework for complex microstructure models. Heliyon 9(8):e19003 https://doi.org/10.1016/j.heliyon.2023.e19003. https://linkinghub.elsevier.com/retrieve/pii/S2405844023062114
M.A. Groeber, M.A. Jackson, DREAM.3D: A Digital Representation Environment for the Analysis of Microstructure in 3D, Integrating Materials and Manufacturing Innovation 3(1), 56 (2014). https://doi.org/10.1186/2193-9772-3-5
Schneider M (2017) The sequential addition and migration method to generate representative volume elements for the homogenization of short fiber reinforced plastics. Computational Mechanics 59(2):247. https://doi.org/10.1007/s00466-016-1350-7
Mehta A, Schneider M (2022) A sequential addition and migration method for generating microstructures of short fibers with prescribed length distribution. Computational Mechanics. https://doi.org/10.1007/s00466-022-02201-x
C. Lauff, M. Schneider, J. Montesano, T. Böhlke, An orientation corrected shaking method for the microstructure generation of short fiber-reinforced composites with almost planar fiber orientation, Composite Structures p. 117352 (2023). https://doi.org/10.1016/j.compstruct.2023.117352. https://linkinghub.elsevier.com/retrieve/pii/S0263822323006980
P. Seibert, M. Husert, M.P. Wollner, K.A. Kalina, M. Kästner, Fast reconstruction of microstructures with ellipsoidal inclusions using analytical descriptors, ArXiv (2023)
Scheunemann L, Balzani D, Brands D, Schröder J (2015) Design of 3D statistically similar Representative Volume Elements based on Minkowski functionals. Mechanics of Materials 90:185. https://doi.org/10.1016/j.mechmat.2015.03.005
Eshlaghi GT, Egels G, Benito S, Stricker M, Weber S, Hartmaier A (2023) Three-dimensional microstructure reconstruction for two-phase materials from three orthogonal surface maps. Frontiers in Materials 10:1220399 https://doi.org/10.3389/fmats.2023.1220399. https://www.frontiersin.org/articles/10.3389/fmats.2023.1220399/full
L.Y. Wei, S. Lefebvre, V. Kwatra, G. Turk, Eurographics 2009, State of the Art in Example-based Texture Synthesis, State of the Art Report, EG-STAR pp. 93–117 (2009)
L. Gatys, A.S. Ecker, M. Bethge, Texture Synthesis Using Convolutional Neural Networks, arXiv:1505.07376 pp. 1–9 (2015)
P. Seibert, A. Raßloff, Y. Zhang, K. Kalina, P. Reck, D. Peterseim, Reconstructing microstructures from statistical descriptors using neural cellular automata, arXiv:2309.16195 [cond-mat.mtrl-sci] (2023). https://doi.org/10.48550/arXiv.2309.16195
A. Mordvintsev, E. Niklasson, E. Randazzo, Texture Generation with Neural Cellular Automata, arXiv:2105.07299 (2021)
Portilla J, Simoncelli EP (2000) A Parametric Texture Model Based on Joint Statistics of Complex Wavelet Coefficients. International Journal of Computer Vision 40:49
Robertson AE, Kalidindi SR (2021) Efficient Generation of Anisotropic N-Field Microstructures From 2-Point Statistics Using Multi-Output Gaussian Random Fields. SSRN Electronic Journal https://doi.org/10.2139/ssrn.3949516. https://www.ssrn.com/abstract=3949516
Gao Y, Jiao Y, Liu Y (2022) Ultraefficient reconstruction of effectively hyperuniform disordered biphase materials via non-Gaussian random fields. Physical Review E 105(4):045305. https://doi.org/10.1103/PhysRevE.105.045305
D.J. Heeger, J.R. Bergen, Pyramid-Based Texture Analysis/Synthesis, Proceedings of the 22nd annual conference on Computer graphics and interactive techniques (1995)
TetsuyaOdaka/texture-synthesis-portilla-simoncelli. https://github.com/TetsuyaOdaka/texture-synthesis-portilla-simoncelli
LabForComputationalVision/textureSynth (2023). https://github.com/LabForComputationalVision/textureSynth. Original-date: 2016-06-07T18:28:21Z
S. Kench, S.J. Cooper, Generating 3D structures from a 2D slice with GAN-based dimensionality expansion, Nat Mach Intell 3, 299 (2021). https://doi.org/10.1038/s42256-021-00322-1. ArXiv: 2102.07708
Coiffier G, Renard P, Lefebvre S (2020) 3D Geological Image Synthesis From 2D Examples Using Generative Adversarial Networks. Frontiers in Water 2:560598 https://doi.org/10.3389/frwa.2020.560598. https://www.frontiersin.org/articles/10.3389/frwa.2020.560598/full
Phan J, Ruspini L, Kiss G, Lindseth F (2022) Size-invariant 3D generation from a single 2D rock image. Journal of Petroleum Science and Engineering 215:110648
K.H. Lee, G.J. Yun, Microstructure reconstruction using diffusion-based generative models, Mechanics of Advanced Materials and Structures pp. 1–19 (2023). https://doi.org/10.1080/15376494.2023.2198528. https://www.tandfonline.com/doi/full/10.1080/15376494.2023.2198528
C. Düreth, P. Seibert, D. Rücker, S. Handford, M. Kästner, M. Gude, Conditional diffusion-based microstructure reconstruction, Materials Today Communications p. 105608 (2023). https://doi.org/10.1016/j.mtcomm.2023.105608. https://www.sciencedirect.com/science/article/pii/S2352492823002982
J. Song, C. Meng, S. Ermon. Denoising Diffusion Implicit Models (2022). https://doi.org/10.48550/arXiv.2010.02502. arxiv:2010.02502. ArXiv:2010.02502 [cs]
K.H. Lee, G.J. Yun, Multi-plane denoising diffusion-based dimensionality expansion for 2D-to-3D reconstruction of microstructures with harmonized sampling, Preprint (2023). https://doi.org/10.21203/rs.3.rs-3309277/v1
Zheng Q, Zhang D (2022) RockGPT: reconstructing three-dimensional digital rocks from single two-dimensional slice with deep learning. Computational Geosciences 26(3):677. https://doi.org/10.1007/s10596-022-10144-8
Zhang F, He X, Teng Q, Wu X, Cui J, Dong X (2023) PM-ARNN: 2D-TO-3D reconstruction paradigm for microstructure of porous media via adversarial recurrent neural network. Knowledge-Based Systems 264:110333 https://doi.org/10.1016/j.knosys.2023.110333. https://linkinghub.elsevier.com/retrieve/pii/S0950705123000837
Zhang F, Teng Q, He X, Wu X, Dong X (2022) Improved recurrent generative model for reconstructing large-size porous media from two-dimensional images. Physical Review E 106(2):025310. https://doi.org/10.1103/PhysRevE.106.025310
Turner DM, Kalidindi SR (2016) Statistical construction of 3-D microstructures from 2-D exemplars collected on oblique sections. Acta Materialia 102:136 https://doi.org/10.1016/j.actamat.2015.09.011. https://linkinghub.elsevier.com/retrieve/pii/S1359645415006771
Liu L, Yao J, Imani G, Sun H, Zhang L, Yang Y, Zhang K (2023) Reconstruction of 3D multi-mineral shale digital rock from a 2D image based on multi-point statistics. Frontiers in Earth Science https://doi.org/10.3389/feart.2022.1104401. https://www.frontiersin.org/articles/10.3389/feart.2022.1104401/full
Gerke KM, Karsanina MV, Katsman R (2019) Calculation of tensorial flow properties on pore level: Exploring the influence of boundary conditions on the permeability of three-dimensional stochastic reconstructions. Physical Review E 100(5):053312. https://doi.org/10.1103/PhysRevE.100.053312
Briand T, Vacher J, Galerne B, Rabin J (2014) The Heeger & Bergen Pyramid Based Texture Synthesis Algorithm. Image Processing On Line 4:276 https://doi.org/10.5201/ipol.2014.79.https://www.ipol.im/pub/art/2014/79/?utm_source=doi
M.M. McKerns, L. Strand, T. Sullivan, A. Fang, M.A.G. Aivazis, Building a Framework for Predictive Science, arXiv:1202.1056 [cs] (2012). arxiv:1202.1056
M. McKerns, M. Aivazis. pathos: a framework for heterogeneous computing (2023). https://uqfoundation.github.io/project/pathos
C. Commons. Creative Commons licence CC BY 4.0 (2021). https://creativecommons.org/licenses/by/4.0/legalcode
S. Yu, Y. Zhang, C. Wang, W.k. Lee, B. Dong, T.W. Odom, C. Sun, W. Chen, Characterization and Design of Functional Quasi-Random Nanostructured Materials Using Spectral Density Function, Journal of Mechanical Design 139(7) (2017). https://doi.org/10.1115/1.4036582. https://asmedigitalcollection.asme.org/mechanicaldesign/article/139/7/071401/383763/Characterization-and-Design-of-Functional-Quasi
J. Gussone, K. Bugelnig, P. Barriobero-Vila, J.C.d. Silva, P. Cloetens, J. Haubrich, G. Requena, (2023). Ptychotomography datasets of an ultrafine eutectic Ti-Fe-based alloy processed by additive manufacturing, https://doi.org/10.5281/zenodo.7660542. https://zenodo.org/record/7660542
Roters F, Diehl M, Shanthraj P, Eisenlohr P, Reuber C, Wong S, Maiti T, Ebrahimi A, Hochrainer T, Fabritius HO, Nikolov S, Friák M, Fujita N, Grilli N, Janssens K, Jia N, Kok P, Ma D, Meier F, Werner E, Stricker M, Weygand D, Raabe D (2019) DAMASK – The Düsseldorf Advanced Material Simulation Kit for modeling multi-physics crystal plasticity, thermal, and damage phenomena from the single crystal up to the component scale. Computational Materials Science 158:420. https://doi.org/10.1016/j.commatsci.2018.04.030
Böhlke T, Brüggemann C (2001) Graphical Representation of the Generalized Hooke’s Law. Technische Mechanik 21:145
Acknowledgements
The group of M. Kästner thanks the German Research Foundation DFG which supported this work under Grant number KA 3309/18-1. The support of the Institute of Lightweight Engineering and Polymer Technology at the Dresden University of Technology in providing a reference structure for a fiber-reinforced polymer is greatly acknowledged. Some of the presented computations were performed on a PC-Cluster at the Center for Information Services and High Performance Computing (ZIH) at TU Dresden. The authors thus thank the ZIH for generous allocations of computer time.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
P. Seibert: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing - Original draft preparation, Writing - review and editing. A. Raßloff: Software, Validation, Visualization, Writing - review and editing. K. Kalina: Conceptualization, Supervision, Visualization, Writing - review and editing. M. Kästner: Funding acquisition, Resources, Supervision, Writing - review and editing.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Numerical simulation
Numerical simulation
The numerical simulations are performed using the DAMASK [81] simulation kit on a high performance computing cluster. The efficient Fourier-based solver allows to run the simulations directly on the regular grids of the reconstruction results.
In [81], a detailed descriptions of the constitutive modelling is given. Hereafter, the main equations are outlined in brief. The elastic behavior of the individual phases is modeled using a generalized Hooke’s law
It links the second Piola-Kirchhoff stress tensor \(\varvec{S}\) to the elastic Green-Lagrange strain tensor \(\varvec{E}^\text {e}\). \(\varvec{\mathbb {C}}\) denotes the fourth-order stiffness tensor.
The isotropic plastic behavior is modeled by a phenomenological power law
that relates the plastic strain rate \(\dot{\gamma }_\text {p}\) to the initial strain rate \(\dot{\gamma }_0\), the stress exponent n, the Frobenius norm \(\Vert (\bullet )\Vert _\text {F}\) of the deviatoric part \(\varvec{S}^\text {dev} = \varvec{S} - \frac{1}{3} \varvec{I} {{\,\textrm{tr}\,}}(\varvec{S})\) of the second Piola-Kirchhoff stress and the material resistance \(\xi\). The evolution of \(\xi\)
depends on the initial hardening \(h_0\), the initial \(\xi _0\) and final resistance \(\xi _\infty\) and the fitting parameter a.
The chosen values for the conducted simulations of the TiFe and spinodoid structures is summarized in Table 5. The reader is kindly referred to [36] for details on the homogenization.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Seibert, P., Raßloff, A., Kalina, K. et al. Fast descriptor-based 2D and 3D microstructure reconstruction using the Portilla–Simoncelli algorithm. Engineering with Computers (2024). https://doi.org/10.1007/s00366-024-02026-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00366-024-02026-7