Skip to main content
SpringerLink
Log in

Numerical solution of variable-order space-time fractional KdV–Burgers–Kuramoto equation by using discrete Legendre polynomials

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

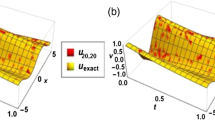
Abstract

In this paper, a new version of the nonlinear space-time fractional KdV–Burgers–Kuramoto equation has been generated via the variable-order (VO) fractional derivatives defined in the Caputo type. A numerical method has been developed based on the discrete Legendre polynomials (LPs) and the collocation scheme for solving this equation. First, the solution of the problem is expanded in terms of the shifted discrete LPs. Then, this expansion and its derivatives, including the classical partial derivatives and the VO fractional partial derivatives are replaced in the equation. Eventually, the operational matrices of the shifted discrete LPs, including the classical derivatives and the VO fractional derivatives (which are derived in this study), and the collocation method are employed to convert the approximated problem into an algebraic system of equations. Some numerical results are given to illustrate the accuracy of the method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Heydari MH, Hooshmandasl MR, Maalek Ghaini FM (2014) An efficient computational method for solving fractional biharmonic equation. Comput Math Appl 68(3):269–287

    Article  MathSciNet  Google Scholar 

  2. Bhrawy AH, Ezz-Eldien SS (2016) A new Legendre operational technique for delay fractional optimal control problems. Calcolo 53(4):521–543

    Article  MathSciNet  Google Scholar 

  3. Sedaghat S, Ordokhani Y, Dehghan M (2012) Numerical solution of the delay differential equations of pantograph type via Chebyshev polynomials. Commun Nonlinear Sci Numer Simul 17:4815–4830

    Article  MathSciNet  Google Scholar 

  4. Salehi F, Saeeidi H, Mohseni Moghadam M (2018) Discrete Hahn polynomials for numerical solution of two-dimensional variable-order fractional Rayleigh-Stokes problem. Comput Appl Math 37:5274–5292

    Article  MathSciNet  Google Scholar 

  5. Canuto C, Hussaini M, Quarteroni A, Zang T (1988) Spectral methods in fluid dynamics. Springer, Berlin

    Book  Google Scholar 

  6. Moradi L, Mohammadi F (2019) A comparative approach for time-delay fractional optimal control problems: discrete versus continuous Chebyshev polynomials. Asian J Control 21(6):1–13

    MathSciNet  Google Scholar 

  7. Moradi L, Mohammadi F (2019) A discrete orthogonal polynomials approach for coupled systems of nonlinear fractional order integro-differential equations. Tbilisi Math J 12(3):21–38

    Article  MathSciNet  Google Scholar 

  8. Heydari MH, Avazzadeh Z (2020) Numerical study of non-singular variable-order time fractional coupled Burgers’ equations by using the Hahn polynomials. Eng Comput. https://doi.org/10.1007/s00366-020-01036-5

    Article  Google Scholar 

  9. Beckman E (1973) Orthogonal polynomials for engineers and physicists. The Golem Press, Boulder

    Google Scholar 

  10. Farrel OJ, Bertram Ross (1963) Solved problem: gamma and beta functions, legendre polynomials, bessel functions. Macmillan, New York

    Google Scholar 

  11. MacRobert RM (1948) Spherical harmonics. Dover, New York

    MATH  Google Scholar 

  12. Horowitz IM (1963) Synthesis of feedback systems. Academic Press, New York

    MATH  Google Scholar 

  13. Morrison N (1969) Introduction to sequential smoothing and prediction. McGraw-Hill, New York

    Google Scholar 

  14. Morrison N (1991) Digital signal processing: theory, applications, and hardware. Computer Science Press, New York

    Google Scholar 

  15. Gong D, Wang X, Wu S, Zhu X (2019) Discrete Legendre polynomials-based inequality for stability of time-varying delayed systems. J Franklin Inst 356:9907–9927

    Article  MathSciNet  Google Scholar 

  16. Samko SG, Ross B (1993) Integration and differentiation to a variable fractional order. Integral Transform Spec Funct 1:277–300

    Article  MathSciNet  Google Scholar 

  17. Hydari MH, Avazzadeh Z, Yang Y, Cattani C (2020) A cardinal method to solve coupled nonlinear variable-order time fractional sine-Gordon equations. Comput Appl Math 39(1):2

    Article  MathSciNet  Google Scholar 

  18. Gómez-Aguilar JF, Atangana A (2019) Time-fractional variable-order telegraph equation involving operators with Mittag-Leffler kernel. J Electromagnet Waves Appl 33(2):165–175

    Article  Google Scholar 

  19. Hosseininia M, Heydari MH, Maalek Ghaini FM, Avazzadeh Z (2018) Two-dimensional Legendre wavelets for solving variable-order fractional nonlinear advection-diffusion equation with variable coefficients. Int J Nonlinear Sci Numeric Simul 19(7–8):793–802

    Article  MathSciNet  Google Scholar 

  20. Roohi R, Heydari MH, Bavi O, Emdad H (2019) Chebyshev polynomials for generalized couette flow of fractional Jeffrey nanofluid subjected to several thermochemical effects. Eng Comput. https://doi.org/10.1007/s00366-019-00843-9

    Article  Google Scholar 

  21. Solís-Pérez JE, Gómez-Aguilar JF, Atangana A (2018) Novel numerical method for solving variable-order fractional differential equations with power, exponential and Mittag-Leffler laws. Chaos Soliton Fract 114:175–185

    Article  MathSciNet  Google Scholar 

  22. Heydari MH (2020) Chebyshev cardinal functions for a new class of nonlinear optimal control problems generated by Atangana-Baleanu-Caputo variable-order fractional derivative. Chaos Soliton Fract 130:109401

    Article  MathSciNet  Google Scholar 

  23. Heydari MH, Atangana A (2019) A cardinal approach for nonlinear variable-order time fractional Schrödinger equation defined by Atangana-Baleanu-Caputo derivative. Chaos Soliton Fract 128:339–348

    Article  Google Scholar 

  24. Heydari MH, Hosseininia M (2020) A new variable-order fractional derivative with non-singular Mittag-Leffler kernel: application to variable-order fractional version of the 2D Richard equation. Eng Comput. https://doi.org/10.1007/s00366-020-01121-9

    Article  Google Scholar 

  25. Heydari MH, Avazzadeh Z (2020) Chebyshev-Gauss-Lobatto collocation method for variable-order time fractional generalized Hirota-Satsuma coupled KdV system. Eng Comput. https://doi.org/10.1007/s00366-020-01125-5

    Article  Google Scholar 

  26. Alimirzaluo E, Nadjafikhah M (2019) Some exact solutions of KdV–Burgers–Kuramoto equation. J Phys Commun 3:035025

    Article  Google Scholar 

  27. Kawahara T (1983) Formation of saturated solitons in a nonlinear dispersive system with instability and dissipation. Phys Rev Lett 51:381–383

    Article  Google Scholar 

  28. Huang F, Liu S (2004) Physical mechanism and model of turbulent cascades in a barotropic atmosphere. Adv Atmos Sci 21:34–40

    Article  Google Scholar 

  29. Cohen B, Krommes J, Tang W, Rosenbluth M (1976) Non-linear saturation of the dissipative trapped-ion mode by mode coupling. Nucl Fusion 16:971–992

    Article  Google Scholar 

  30. Topper J, Kawahara T (1978) Approximate equations for long nonlinear waves on a viscous fluid. J Phys Soc Jpn 44:663–666

    Article  MathSciNet  Google Scholar 

  31. Secer A, Ozdemir N (2019) An effective computational approach based on Gegenbauer wavelets for solving the time-fractional KdV–Burgers–Kuramoto equation. Secer Ozdemir Adv Differ Equ. https://doi.org/10.1186/s13662-019-2297-8

    Article  MATH  Google Scholar 

  32. Gupta AK, Saha Ray S (2014) Traveling wave solution of fractional KdV–Burger–Kuramoto equation describing nonlinear physical phenomena. AIP Adv 4:097120

    Article  Google Scholar 

  33. Safari M, Ganji DD, Moslemi M (2009) Application of He’s variational iteration method and Adomian’s decomposition method to the fractional KdV–Burger–Kuramoto equation. Comput Math Appl 58:2091–2097

    Article  MathSciNet  Google Scholar 

  34. Song L, Zhang H (2007) Application of homotopy analysis method to fractional KDV-burgers-kuramoto equation. Phys Lett A 367:88–94

    Article  MathSciNet  Google Scholar 

  35. Shen S, Liu F, Chen J, Turner I, Anh V (2012) Numerical techniques for the variable order time fractional diffusion equation. Appl Math Comput 218:10861–10870

    MathSciNet  MATH  Google Scholar 

  36. Chen Y, Liu L, Li B, Sun Y (2014) Numerical solution for the variable order linear cable equation with Bernstein polynomials. Appl Math Comput 238:329–341

    MathSciNet  MATH  Google Scholar 

  37. Podlubny I (1999) Fractional differential equations. Academic Press, San Diego

    MATH  Google Scholar 

  38. Abramowitz M, Stegun I (1972) Handbook of mathematical functions. Dover Publications, New York

    MATH  Google Scholar 

  39. Atkinson K (1989) An introduction to numerical analysis, 2nd edn. Wiley, New York

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Shiraz University of Technology, Shiraz, Iran

    M. H. Heydari

  2. Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam

    Z. Avazzadeh

  3. Engineering School (DEIM), University of Tuscia, Viterbo, Italy

    C. Cattani

Authors
  1. M. H. Heydari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Z. Avazzadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. C. Cattani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Z. Avazzadeh.

Ethics declarations

Funding

The financial assistance is not applicable.

Data availability

Data sharing is not applicable to this study.

Conflict of interest

The authors declare that they have no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Heydari, M.H., Avazzadeh, Z. & Cattani, C. Numerical solution of variable-order space-time fractional KdV–Burgers–Kuramoto equation by using discrete Legendre polynomials. Engineering with Computers 38 (Suppl 1), 859–869 (2022). https://doi.org/10.1007/s00366-020-01181-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01181-x

Keywords

Search

Navigation