Elastic Splines II: Unicity of Optimal s-Curves and Curvature Continuity

Abstract

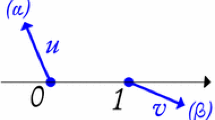
Given points $P_1,P_2,\ldots ,P_m$ in the complex plane, we are concerned with the problem of finding an interpolating curve with minimal bending energy (i.e., an optimal interpolating curve). It was shown previously that existence is assured if one requires that the pieces of the interpolating curve be s-curves. In the present article, we also impose the restriction that these s-curves have chord angles not exceeding $\pi /2$ in magnitude. With this setup, we have identified a sufficient condition for the curvature continuity of optimal interpolating curves. This sufficient condition relates to the stencil angles $\{\psi _j\}$, where $\psi _j$ is defined as the angular change in direction from segment $[P_{j-1},P_j]$ to segment $[P_j,P_{j+1}]$. An angle $\Psi$ ($\approx 37^\circ$) is identified, and we show that if the stencil angles satisfy $\vert {\psi _j} \vert <\Psi$, then optimal interpolating curves are curvature continuous. We also prove that the angle $\Psi$ is sharp. As with the previous article (Borbély and Johnson in Constr Approx 40:189–218, 2014), much of our effort is concerned with the geometric Hermite interpolation problem of finding an optimal s-curve $c_1(\alpha ,\beta )$ that connects $0+i0$ to $1+i0$ with prescribed chord angles $(\alpha ,\beta )$. Whereas existence was previously shown, and sometimes uniqueness, the present article begins by establishing uniqueness when $\vert {\alpha } \vert ,\vert {\beta } \vert \le \pi /2$ and $\vert {\alpha -\beta } \vert <\pi$. We also prove two fundamental identities involving the initial and terminal signed curvatures of $c_1(\alpha ,\beta )$ and partial derivatives, with respect to $\alpha$ or $\beta$, of the bending energy of $c_1(\alpha ,\beta )$.