Robust change-point detection for functional time series based on U-statistics and dependent wild bootstrap

Abstract

The aim of this paper is to develop a change-point test for functional time series that uses the full functional information and is less sensitive to outliers compared to the classical CUSUM test. For this aim, the Wilcoxon two-sample test is generalized to functional data. To obtain the asymptotic distribution of the test statistic, we prove a limit theorem for a process of U-statistics with values in a Hilbert space under weak dependence. Critical values can be obtained by a newly developed version of the dependent wild bootstrap for non-degenerate 2-sample U-statistics.

1 Introduction

Statistical methods for observations consisting of functions are widely discussed since at least the work by Ramsay (1982), and there is a growing interest in recent years because more and more data is available in high resolution that can not be treated as multivariate data. Functional data analysis might even be helpful for one-dimensional time series (see e.g. Hörmann and Kokoszka 2010). Functional observations are often modelled as random variables taking values in a Hilbert space, we recommend the book by Hörmann and Kokoszka (2012) for an introduction.

In this paper, we will propose new methods for the detection of change-points: Suppose that we observe $X_1,\ldots ,X_n$ being a part of a time series $(X_n)_{n\in \mathbb {Z}}$ with values in a separable Hilbert space H (equipped with inner product $\langle \cdot ,\cdot , \rangle$ and norm $\Vert \cdot \Vert =\sqrt{\langle \cdot ,\cdot \rangle }$). The at most one change-point problem is to test the null hypothesis of stationarity against the alternative of an abrupt change of the distribution at an unknown time point $k^\star$: $X_1{\mathop {=}\limits ^{{\mathcal {D}}}}\cdots {\mathop {=}\limits ^{{\mathcal {D}}}}X_{k^\star }$ and $X_{k^\star +1}{\mathop {=}\limits ^{{\mathcal {D}}}}\cdots {\mathop {=}\limits ^{{\mathcal {D}}}}X_{n}$, but $X_1{\mathop {\ne }\limits ^{{\mathcal {D}}}}X_n$ (where $X_i{\mathop {=}\limits ^{{\mathcal {D}}}}X_j$ means that $X_i$ and $X_j$ have the same distribution).

Functional data is often projected on lower dimensional spaces with functional principal components, see (Berkes et al. 2009) for a change in mean of independent data and Aston and Kirch (2012) for a change in mean of time series. Fremdt et al. (2014) proposed to let the dimension on the subspace on which the data is projected grow with the sample size. But is is also possible to use change-point tests without dimension reduction as done by Horváth et al. (2014) under independence, by Sharipov et al. (2016) and Aue et al. (2018) under dependence. Since using the asymptotic distribution would require knowledge of the infinite-dimensional covariance operator, it is convenient to use bootstrap methods. In the context of change-point detection for functional time series, the non-overlapping block bootstrap was studied by Sharipov et al. (2016), the dependent wild bootstrap by Bucchia and Wendler (2017) and the block multiplier bootstrap (for Banach-space-valued times series) by Dette et al. (2020).

Typically, these tests are based on variants of the CUSUM-test, where CUSUM stands for cumulated sums. Such tests make use of sample means and thus, they are sensitive to outliers. For real-valued time series, several authors have constructed more robust tests based on the Mann–Whitney-Wilcoxon-U-test. For the two-sample problem (do the two real-valued samples $X_1,\ldots ,X_{n_1}$ and $Y_1,\ldots ,Y_{n_2}$ have the same location?), the Mann–Whitney-Wilcoxon-U-statistic can be written as

$$\begin{aligned} U(X_1,\ldots ,X_{n_1},Y_1,\ldots ,Y_{n_2}){} & {} =\frac{1}{n_1n_2}\sum _{i=1}^{n_1} \sum _{j=1}^{n_2}{\text {sgn}}(X_i-Y_j)\\{} & {} =\frac{1}{n_1n_2} \sum _{i=1}^{n_1}\sum _{j=1}^{n_2}\frac{X_i-Y_j}{|X_i-Y_j|} \end{aligned}$$

(where 0/0 is set to 0). Chakraborty and Chaudhuri (2017) have generalized this test statistic to Hilbert spaces by replacing the sign by the so called spatial sign:

$$\begin{aligned} U(X_1,\ldots ,X_{n_1},Y_1,\ldots ,Y_{n_2})=\frac{1}{n_1n_2}\sum _{i=1}^{n_1} \sum _{j=1}^{n_2}\frac{X_i-Y_j}{\Vert X_i-Y_j\Vert } \end{aligned}$$

They have shown the weak convergence to a Gaussian distribution for independent random variables. For change-point detection, one encounters several problems: In practice, the change-point is typically unknown, so it is not known where to split the sequence of the observations into two samples. In many applications, the assumption of independence is not realistic, one rather has to deal with time series. Furthermore, the covariance operator is not known.

To deal with these problems, we will study limit theorems for two-sample U-processes with values in Hilbert spaces and deduce the asymptotic distribution of the Wilcoxon-type change-point-statistic

$$\begin{aligned} \max _{k=1,\ldots ,n-1}\Big \Vert \frac{1}{n^{3/2}}\sum _{i=1}^k \sum _{j=k+1}^n\frac{X_i-X_j}{\Vert X_i-X_j\Vert }\Big \Vert \end{aligned}$$

for a short-range dependent, Hilbert-space-valued time series $(X_n)_{n\in \mathbb {Z}}$. Change-point tests based on Wilcoxon have been studied before, but mainly for real-valued observations, starting with Darkhovsky (1976) and Pettitt (1979). Yu and Chen (2022) used the maximum of componentwise Wilcoxon-type statistics. Very recently and independently of our work, Jiang et al. (2022) introduced a test statistic based on spatial signs for independent, high-dimensional observations, which is very similar to the square of our test statistic. However, Jiang et al. (2022) obtained the limit for a growing dimension of the observations and assuming that the entries of each vector form a stationary, weakly dependent time series, while we consider observations in a fixed Hilbert space H and take the limit for a growing number of observations. Furthermore, they use self-normalization instead of bootstrap to obtain critical values.

Let us note that spatial signs have been used for change-point detection before by other authors: Vogel and Fried (2015) have studied a robust test for changes in the dependence structure of a finite-dimensional time series based on the spatial sign covariance matrix.

As the Mann–Whitney-Wilcoxon-U-statistic is a special case of a two-sample U-statistic, authors like (Csörgő and Horváth 1989; Gombay and Horváth 2002) studied more general U-statistics for change point detection under independence and Dehling et al. (2015) under dependence. We will provide our theory not only for the special case of the test statistic based on spatial signs, but for general test statistics based on two-sample H-valued U-statistics under dependence.

As the limit depends on the unknown, infinite-dimensional long-run covariance operator, one would either need to estimate this operator, or one could use resampling techniques. Leucht and Neumann (2013) have developed a variant of the dependent wild bootstrap (introduced by Shao (2010)) for U-statistics. However, their method works only for degenerate U-statistics. As the Wilcoxon-type statistic is non-degenerate, we propose a new version of the dependent wild bootstrap for this type of U-statistic. The bootstrap version of our change-point test statistic is

$$\begin{aligned} \max _{k=1,\ldots ,n-1}\Big \Vert \frac{1}{n^{3/2}}\sum _{i=1}^k\sum _{j=k+1}^n\frac{X_i-X_j}{\Vert X_i-X_j\Vert }(\varepsilon _i+\varepsilon _j)\Big \Vert , \end{aligned}$$

where $\varepsilon _1,\ldots ,\varepsilon _n$ is a stationary sequence of dependent N(0, 1)-distributed multipliers, independent of $X_1,\ldots ,X_n$. We will prove the asymptotic validity of our new bootstrap method. Our variant of the dependent wild bootstrap is similar, but not identical to the variant proposed by Doukhan et al. (2015) for non-degenerate von Mises statistics. Note that this bootstrap differs from the multiplier bootstrap proposed by Bücher and Kojadinovic (2016), as it does not rely on pre-linearization, that means replacing the U-statistic by a partial sum.

2 Main results

We will treat the CUSUM statistic and the Wilcoxon-type statistic as two special cases of a general class based on two-sample U-statistics. Let $h:H^2\rightarrow H$ be a kernel function. We define

$$\begin{aligned} U_{n,k}=\sum _{i=1}^k\sum _{j=k+1}^nh(X_i,X_j). \end{aligned}$$

For $h(x,y)=x-y$, we obtain with a short calculation

$$\begin{aligned} \max _{1\le k< n}\frac{1}{n^{3/2}}\left\| U_{n,k}\right\| =\max _{1\le k < n}\frac{1}{\sqrt{n}}\Big \Vert \sum _{i=1}^k\big (X_i-\frac{1}{n}\sum _{j=1}^n X_j\big )\Big \Vert , \end{aligned}$$

which is the CUSUM-statistic for functional data. On the other hand, with the kernel $h(x,y)=(x-y)/\Vert x-y\Vert$, we get the Wilcoxon-type statistic. Other kernels would be possible, e.g. $h(x,y)=(x-y)/(c+\Vert x-y\Vert )$ for some $c>0$ as a compromise between the CUSUM and the Wilcoxon approach. Before stating our limit theorem for this class based on two-sample U-statistics, we have to define some concepts and our assumptions.

We will start with our concept of short range dependence, which is based on a combination of absolute regularity (introduced by Volkonskii and Rozanov (1959)) and P-near-epoch dependence (introduced by Dehling et al. (2017)). In the following, let H be a separable Hilbert space with inner product $\langle \cdot ,\cdot \rangle$ and norm $\Vert x\Vert =\sqrt{\langle x,x\rangle }$.

Definition 1

(Absolute Regularity) Let $(\zeta _n)_{n\in {\mathbb {Z}}}$ be a stationary sequence of random variables. We define the mixing coefficients $(\beta _m)_{m\in \mathbb {Z}}$ by

$$\begin{aligned} \beta _m=E\Big [\sup _{A\in {\mathcal {F}}_{m}^\infty } \left( P(A|{\mathcal {F}}_{-\infty }^{0})-P(A)\right) \Big ], \end{aligned}$$

where ${\mathcal {F}}_{a}^b$ is the $\sigma$-field generated by $\zeta _{a},\ldots ,\zeta _b$, and call the sequence $(\zeta _n)_{n\in \mathbb {Z}}$ absolutely regular if $\beta _m\rightarrow 0$ as $m\rightarrow \infty$.

Definition 2

(P-NED) Let $(\zeta _n)_{n\in {\mathbb {Z}}}$ be a stationary sequence of random variables. $(X_n)_{n\in {\mathbb {Z}}}$ is called near-epoch-dependent in probability (P-NED) on $(\zeta _n)_{n\in {\mathbb {Z}}}$ if there exist sequences $(a_k)_{k\in {\mathbb {N}}}$ with $a_k \xrightarrow {k \rightarrow \infty } 0$ and $(f_k)_{k\in {\mathbb {Z}}}$ and a non-increasing function $\Phi :(0,\infty ) \rightarrow (0,\infty )$ such that

$$\begin{aligned} {\mathbb {P}}(\Vert X_0-f_k(\zeta _{-k},\ldots ,\zeta _k)\Vert> \epsilon ) \le a_k\Phi (\epsilon ) \,\,\, \forall k\in {\mathbb {N}},\, \epsilon >0. \end{aligned}$$

Definition 3

($L_p$-NED) Let $(\zeta _n)_{n\in {\mathbb {Z}}}$ be a stationary sequence of random variables. $(X_n)_{n\in {\mathbb {Z}}}$ is called $L_p$-NED on $(\zeta _n)_{n\in {\mathbb {Z}}}$ if there exists a sequence of approximation constants $(a_k)_{k\in {\mathbb {N}}}$ with $a_k \xrightarrow {k\rightarrow \infty } 0$ and

$$\begin{aligned} {\mathbb {E}}[\Vert X_0-{\mathbb {E}}[X_0| \mathfrak {F}_{-k}^k] \Vert ^p ]^{\frac{1}{p}} \le a_{k,p}. \end{aligned}$$

P-NED has the advantage of not implying finite moments (unlike $L_p$-NED), which is useful to allow for heavy tailed distributions.

Additionally, we will need assumptions on the kernel:

Definition 4

(Antisymmetry) A kernel $h:H^2\rightarrow H$ is called antisymmetric, if for all $x,y\in H$

$$\begin{aligned} h(x,y)=-h(y,x). \end{aligned}$$

Antisymmetric kernels are natural candidates for comparing two distributions, because if X and $\tilde{X}$ are independent, H-valued random variables with the same distribution and h is antisymmetric, we have $E[h(X,\tilde{X})]=0$, so our test statistic should have values close to 0, see also Račkauskas and Wendler (2020).

Definition 5

(Uniform Moments) If there is a $M>0$ such that for all $k,n \in {\mathbb {N}}$

$$\begin{aligned}{} & {} {\mathbb {E}}[\Vert h\big (f_k(\zeta _{-k},\ldots ,\zeta _k),f_k(\zeta _{n-k},\ldots ,\zeta _{n+k})\big )\Vert _{{H}}^{m}] \le M,\\{} & {} {\mathbb {E}}[\Vert h\big (X_0,f_k(\zeta _{n-k},\ldots ,\zeta _{n+k})\big )\Vert _{{H}}^{m}] \le M,\\{} & {} {\mathbb {E}}[\Vert h\big (X_0,X_n\big )\Vert _{{H}}^{m}] \le M, \end{aligned}$$

we say that the kernel has uniform m-th moments under approximation.

Furthermore, we need the following mild continuity condition on the kernel, which is called variation condition and was introduced by Denker and Keller (1986). The kernel $h(x,y)=(x-y)/\Vert x-y\Vert$ will fulfill the condition, as long as there exists a constant C such that $P(\Vert X_1-x\Vert \le \epsilon )\le C\epsilon$ for all $x\in H$ and $\epsilon >0$. This can be proved along the lines of Remark 2 in Dehling et al. (2022). $P(\Vert X_1-x\Vert \le \epsilon )\le C\epsilon$ for all $x\in H$, $\epsilon >0$ does not hold if the distribution of $X_1$ has points with positive mass, but it still can hold if the distribution is concentrated on finite-dimensional sub-spaces.

Definition 6

(Variation condition) The kernel h fulfills the variation condition if there exist L, $\epsilon _0 > 0$ such that for every $\epsilon \in (0, \epsilon _0)$:

$$\begin{aligned} {\mathbb {E}}\bigg [\Big ( \sup _{\begin{array}{c} \Vert x-X\Vert \le \epsilon \\ \Vert y-\tilde{X}\Vert \le \epsilon \end{array}} \Vert h(x,y)-h(X,\tilde{X})\Vert _{{H}} \Big )^2 \bigg ] \le L\epsilon \end{aligned}$$

Finally, we will need Hoeffding’s decomposition of the kernel to be able to define the limit distribution:

Definition 7

(Hoeffding’s decomposition) Let $h:H\times H \rightarrow {H}$ be an antisymmetric kernel. Let $X,\tilde{X}$ be two i.i.d. random variables with the same distribution as $X_1$. Hoeffding’s decomposition of h is defined as

$$\begin{aligned} h(x,y)= h_1(x)-h_1(y)+h_2(x,y) \, \forall x,y \in H \end{aligned}$$

where

$$\begin{aligned} h_1(x)= & {} \mathbb {E}[h(x,\tilde{X})]\\ h_2(x,y)= & {} h(x,y) - \mathbb {E}[h(x,\tilde{X})] - \mathbb {E}[h(X,y)] = h(x,y) -h_1(x)+h_1(y) \end{aligned}$$

Now we can state our first theorem on the asymptotic distribution of our test statistic under the null hypothesis (stationarity of the time series):

Theorem 1

Let $(X_n)_{n\in {\mathbb {Z}}}$ be stationary and P-NED on an absolutely regular sequence $(\zeta _n)_{n\in {\mathbb {Z}}}$ such that $a_k \Phi (k^{-8\frac{\delta +3}{\delta }})= {\mathcal {O}}(k^{-8\frac{(\delta +3)(\delta +2)}{\delta ^2}})$ and $\sum _{k=1}^\infty k^2 \beta _k^{\frac{\delta }{4+\delta }} < \infty$ for some $\delta >0$. Assume that $h:H^2\rightarrow H$ is an antisymmetric kernel that fulfills the variation condition and is either bounded or has uniform $(4+\delta )$-moments under approximation. Then it holds that

$$\begin{aligned} \max _{1\le k<n} \frac{1}{n^{3/2}} \Big \Vert \sum _{i=1}^k\sum _{j=k+1}^n h(X_i,X_j) \Big \Vert \xrightarrow {{\mathcal {D}}} \sup _{\lambda \in [0,1]} \Vert W(\lambda )-\lambda W(1) \Vert \end{aligned}$$

where W is an H-valued Brownian motion and the covariance operator S of W(1) is given by

$$\begin{aligned} \langle S(x),y\rangle =\sum _{i=-\infty }^\infty {\text {Cov}}\left( \langle h_1(X_0),x\rangle ,\langle h_1(X_i),y\rangle \right) . \end{aligned}$$

For the kernel $h(x,y)=x-y$, we obtain as a special case a limit theorem for the functional CUSUM-statistic similar to Corollary 1 of Sharipov et al. (2016) (although our assumptions on near epoch dependence are stronger). In the next section, we will compare the Wilcoxon-type statistic and the CUSUM-statistic with a simulation study. The proofs of the results can be found in Sect. 5. The next theorem will show that the test statistic converges to infinity in probability under some alternatives, so a test based on this statistic consistently detects these type of changes.

For this, we consider the following model: We have a stationary, $H\otimes H$-valued sequence $(X_n, Z_n)_{n\in \mathbb {Z}}$ and we observe $Y_1,\ldots ,Y_n$ with

$$\begin{aligned} Y_i={\left\{ \begin{array}{ll}X_i \ \ {} &{}\text {for}\ i\le \lfloor n\lambda ^\star \rfloor = k^\star \\ Z_i \ \ {} &{}\text {for}\ i> \lfloor n\lambda ^\star \rfloor = k^\star \end{array}\right. }, \end{aligned}$$

so $\lambda ^\star \in (0,1)$ is the proportion of observations after which the change happens. If the distribution of $X_i$ and $Z_i$ is not the same, then the alternative hypothesis holds: $X_1{\mathop {=}\limits ^{{\mathcal {D}}}}\cdots {\mathop {=}\limits ^{{\mathcal {D}}}}X_{k^\star }$ and $X_{k^\star +1}{\mathop {=}\limits ^{{\mathcal {D}}}}\cdots {\mathop {=}\limits ^{{\mathcal {D}}}}X_{n}$, but $X_1{\mathop {\ne }\limits ^{{\mathcal {D}}}}X_n$. A simple example might be $Z_i=X_i+\mu$, where $\mu \in H$ and $\mu \ne 0$. However, let us point out that not all changes in distribution can be consistently detected. The change is detectable, if $E[h(X_1,\tilde{Z}_1)]\ne 0$ for an independent copy $\tilde{Z}_1$ of ${Z}_1$. For example, with the kernel $h(x,y)=x-y$ and $Z_i=X_i+\mu$ with $\mu \ne 0$, the change is always detectable.

Theorem 2

Let $(X_n, Z_n)_{n\in \mathbb {Z}}$ be P-NED on an absolutely regular sequence $(\zeta _n)_{n\in {\mathbb {Z}}}$ such that $a_k \Phi (k^{-8\frac{\delta +3}{\delta }})= {\mathcal {O}}(k^{-8\frac{(\delta +3)(\delta +2)}{\delta ^2}})$ and $\sum _{k=1}^\infty k^2 \beta _k^{\frac{\delta }{4+\delta }} < \infty$ for some $\delta >0$. Assume that $h:H^2\rightarrow H$ is an antisymmetric kernel that fulfills the variation condition and is either bounded or has uniform $(4+\delta )$-moments under approximation for both processes $(X_n)_{n\in \mathbb {Z}}$ and $(Z_n)_{n\in \mathbb {Z}}$, that $E[\Vert h(X_1,\tilde{Z}_1)\Vert ^{4+\delta }]<\infty$, and that $E[h(X_1,\tilde{Z}_1)]\ne 0$, were $\tilde{Z}_1$ is an independent copy of ${Z}_1$. Then

$$\begin{aligned} \max _{1\le k<n} \frac{1}{n^{3/2}} \Big \Vert \sum _{i=1}^k\sum _{j=k+1}^n h(Y_i,Y_j) \Big \Vert \xrightarrow {{\mathcal {P}}} \infty . \end{aligned}$$

These results on the asymptotic distribution can not be applied directly in many practical applications, because the covariance operator is unknown. For this reason, we introduce the dependent wild bootstrap for non-degenerate U-statistics: Let $(\varepsilon _{i,n})_{i\le n, n\in \mathbb {N}}$ be a rowwise stationary triangular scheme of N(0, 1)-distributed variables (we often drop the second index for notational convenience: $\varepsilon _{i}=\varepsilon _{i,n}$). The bootstrap version of our U-statistic is then

$$\begin{aligned} U_{n,k}^\star =\sum _{i=1}^k\sum _{j=k+1}^nh(X_i,X_j)(\varepsilon _i+\varepsilon _j). \end{aligned}$$

Theorem 3

Let the assumptions of Theorem 1 hold for $(X_n)_{n\in \mathbb {Z}}$ and $h:H^2\rightarrow H$. Assume that $(\varepsilon _{i,n})_{i\le n, n\in \mathbb {N}}$ is independent of $(X_n)_{n\in \mathbb {Z}}$, has standard normal marginal distribution and ${\text {Cov}}(\varepsilon _i,\varepsilon _j)=w(|i-j|/q_n)$, where w is symmetric and continuous with $w(0)=1$ and $\int _{-\infty }^\infty |w(t)|dt<\infty$. Assume that $q_n\rightarrow \infty$ and $q_n/n\rightarrow 0$. Then it holds that

$$\begin{aligned}{} & {} \left( \max _{1\le k<n} \frac{1}{n^{3/2}}\Big \Vert U_{n,k}\Big \Vert , \max _{1\le k<n} \frac{1}{n^{3/2}}\Big \Vert U_{n,k}^\star \Big \Vert \right) \\{} & {} \quad \xrightarrow {{\mathcal {D}}} \bigg (\sup _{\lambda \in [0,1]} \Vert W(\lambda )-\lambda W(1) \Vert ,\sup _{\lambda \in [0,1]} \Vert W^\star (\lambda )-\lambda W^\star (1) \Vert \bigg ) \end{aligned}$$

where W and $W^\star$ are two independent, H-valued Brownian motions with covariance operator as in Theorem 1.

From this statement, it follows that the bootstrap is consistent and it can be evaluated using the Monte Carlo method. If you generate several copies of the bootstrapped test statistic independent conditional on $X_1,\ldots ,X_n$, the empirical quantiles of the bootstrapped test statistics can be used as critical values for the test. For a deeper discussion on bootstrap validity, see Bücher and Kojadinovic (2019). Of course, in practical applications, the function w and the bandwidth $q_n$ have to be chosen. We will apply a method by Rice and Shang (2017) for the bandwidth selection.

Instead of using multipliers with a standard normal distribution, one might also choose other distributions for $(\varepsilon _{i,n})_{i\le n, n\in \mathbb {N}}$. This is done for the traditional wild bootstrap to capture skewness. Under the hypothesis, the distribution of $h(X_i,X_j)$ is close to symmetric for i and j far apart, so we do not expect a large improvement by non-Gaussian multipliers and limit our analysis in this paper to the case of Gaussian multipliers.

3 Data example and simulation results

3.1 Bootstrap procedure

Since no theoretical values of the limit distribution of our test-statistic exist, we perform a bootstrap to find critical values for a test-decision. The procedure to find the critical value for significance level $\alpha \in (0,1)$ is the following:

• Calculate $h(X_i,X_j)$ for all $i<j$

• For each of the bootstrap iterations $t=1,\ldots ,m$:

  • Calculate $h(X_i,X_j)(\varepsilon _i^{(t)}+\varepsilon ^{(t)}_j)$, where $(\varepsilon ^{(t)}_i)_{i<n}$ are random multiplier

  • Calculate $U_{n,k}^{(t)}=\sum _{i=1}^k\sum _{j=k+1}^n h(X_i,X_j)(\varepsilon ^{(t)}_i+\varepsilon ^{(t)}_j)$ for all $k < n$

  • Find $\max \limits _{1 \le k<n} \Vert U_{n,k}^{(t)}\Vert$

• Identify the empirical $\alpha$-quantile $U_\alpha$ of all $\max \limits _{1 \le k<n} \Vert U_{n,k}^{(1)} \Vert ,\ldots ,\max \limits _{1 \le k<n} \Vert U_{n,k}^{(m)} \Vert$

• Calculate $U_{n,k}=\sum _{i=1}^k\sum _{j=k+1}^n h(X_i,X_j)$ for all $1\le k<n$

• Test decision: If $\max \limits _{1\le k<n} \Vert U_{n,k} \Vert > U_{\alpha }$, reject the null hypothesis

To ensure a certain covariance structure within the multiplier (that fulfills the assumptions of the multiplier theorem), we calculate them as

$$\begin{aligned} (\varepsilon ^{(t)}_i)_{i\le n}= A (\eta _i)_{i\le n} \end{aligned}$$

where $\eta _1,\ldots ,\eta _i$ are i.i.d. N(0, 1)-distributed and A is the square root of the quadratic spectral covariance matrix constructed with bandwidth-parameter q (chosen with the method by Rice and Shang (2017) described below). That means $AA^t=B$, where B has the entries

$$\begin{aligned} B_{i,j} = v_{\vert i-j \vert } \;\;\;\;\;\; \forall \, 1 \le i,j \le n \end{aligned}$$

with

$$\begin{aligned}&v_0 = 1 \\&v_i = \frac{25}{12 \pi ^2 (i-1)^2/q^2} \left( \frac{\sin (\frac{6\pi (i-1)/q}{5})}{\frac{6\pi (i-1)/q}{5}} -\cos (\frac{6\pi (i-1)/q}{5})\right) \;\;\;\;\;\; \forall \, 1 \le i \le n-1. \end{aligned}$$

3.2 Bandwidth

We use a data adapted bandwidth parameter $q_{adpt}$ in the bootstrap which is evaluated for each simulated data sample $X_1,\ldots ,X_n$ by the following procedure:

• Calculate $\tilde{X}_1,\ldots ,\tilde{X}_n$ where $\tilde{X}_i=\frac{1}{n-1}\sum _{j=1, j\ne i}^n h(X_i,X_j)$

• Determine a starting value $q_0=n^{1/5}$

• Calculate matrices $V_k = \frac{1}{n}\sum _{i=1}^{n-(k-1)} \tilde{X_i} \otimes \tilde{X_k}$ for $k=1,\ldots , q_0$, where $\otimes$ is the outer product

• Compute $CP_0=V_1+2\sum _{k=1}^{q_0-1}w(k, q_0)V_{k+1}$

        and $CP_1= 2\sum _{k=1}^{q_0-1}k \,w(k, q_0)V_{k+1}$

  w is a kernel function, we use the quadratic spectral kernel

  $w(k,q)= \frac{25}{12 \pi ^2 k^2/q^2} \left( \frac{\sin (\frac{6\pi k/q}{5})}{\frac{6\pi k/q}{5}} -\cos (\frac{6\pi k/q}{5})\right)$

• Receive the data adapted bandwidth

  $$\begin{aligned} q_{adpt} = \Bigg \lceil \left( \frac{3n\sum _{i=1}^d \sum _{j=1}^d {CP_1}_{i,j}}{\sum _{i=1}^d\sum _{j=1}^d{CP_0}_{i,j}+ \sum _{j=1}^d {CP_0}_{j,j}^2 } \right) ^{1/5} \Bigg \rceil \end{aligned}$$

For theoretical details about the data adapted bandwidth we refer to Rice and Shang (2017).

3.3 Data example

We look at data of 344 monitoring stations of the ’Umweltbundesamt’ for air pollutants located all over Germany (Source: Umweltbundesamt, https://www.umweltbundesamt.de/daten/luft/luftdaten/stationen Accessed on 06.08.2020). The particular data is the daily average of particulate matter with particles smaller than $10 \mu m$ ($PM_{10}$) measured in $\mu g / m^3$ from January 1, 2020 to May 31, 2020. This means we have $n=152$ observations and treat the measurements of all stations on one day as a data from ${\mathbb {R}}^{344}$.

Since the official restrictions of the German Government in course of the COVID-19 pandemic came into force on March 22, 2020, an often asked question was whether these restrictions (social distancing, closed gastronomy, closed/reduced work or work from home) had an effect on the air quality in Germany. This question comes from the assumption that the restrictions lead to reduced traffic, resulting in reduced amount of particulate matter.

There are several publications from various countries studying the effects of lockdown measures on air pollution parameters like nitrogen oxides (NO, $NO_2$), ozone ($O_3$) and particulate matter ($PM_{10}$, $PM_{2.5}$). For example, Lian et al. (2020) investigated data from the city of Wuhan, or Zangari et al. (2020) for New York City. Data for Berlin, as for 19 other Cities around the world, are investigated by Fu et al. (2020). They observed a decline in particular matter ($PM_{10}$ and $PM_{2.5}$, only significant for $PM_{2.5}$) in the period of lockdown. But the observed time period is rather short (one month - Mar. 17 to Apr. 19, 2020) and the findings for a densely populated city may not simply be transferred to the whole of Germany. In contrast to that, we use data from measuring stations located across the whole country and over a period of five months.

Looking at the empirical p-values of the CUSUM test and the Wilcoxon-type test (based on spatial signs) resulting from $m=3000$ Bootstrap iterations in Table 1, we see that with CUSUM, the null hypothesis $H_0$ is never rejected for any significance level $\alpha < 0.2$. But the Wilcoxon-type test rejects $H_0$ for significance level $\alpha$ larger than 0.03.

Table 1 Empirical p-values for CUSUM and spatial sign test with data adapted bandwidth. $m=3000$ Bootstrap iterations were used

Since the data exhibits a massive outlier located at January 1 (likely due to New Year’s firework), we repeated the test procedure without the data of this day. We observed that the resulting p-value for the Wilcoxon-type test changed just slightly (Table 2). Whereas the p-value for CUSUM decreased notably - it is now around 0.08. In this example we see that CUSUM is clearly more influenced by the outlier in the data than the spatial signs based test. Evaluation showed that the data adapted bandwidth was set to $q_{adpt}=3$ for both the CUSUM test and the Wilcoxon-type test for both scenarios.

Table 2 Empirical p-values for CUSUM and spatial sign test with data adapted bandwidth for data excluding January 1, 2020. $m=3000$ Bootstrap iterations were used

Fig. 1

Daily average of $PM_{10}$ in $\mu g / m^3$ for 344 monitoring stations from January 1, 2020 to May 31, 2020. Each line corresponds to one station. The blue vertical line is the estimated change-point location. The massive outlier at January 1 could result from New Year’s fireworks

A natural approach to estimate the location $\hat{k}$ of the change-point, is to determine the smallest $1 \le k<n$ for which the test statistic attains its maximum:

$$\begin{aligned} \hat{k} = \min \{k: \Vert \frac{1}{n^{3/2}} U_{n,k} \Vert = \max _{1\le j< n} \Vert \frac{1}{n^{3/2}} U_{n,j} \Vert \} \end{aligned}$$

The maximum of the spatial sign test statistic, which marks our estimated change point, is received at March 15, 2020. (The maximum of the CUSUM statistic is indeed located at the same point.) The estimated change-point in our example lies a week before the official restrictions regarding COVID-19 were imposed. One could argue that the citizen, being aware of the situation, changed their behaviour beforehand, without strict official restrictions. Data projects using mobile phone data (e.g Covid-19 Mobility Project and Destatis) indeed show a decline in mobility preceding the official restrictions on March 22 by around a week. (see https://www.covid-19-mobility.org/de/data-info/, https://www.destatis.de/DE/Service/EXDAT/Datensaetze/mobilitaetsindikatoren-mobilfunkdaten.html)

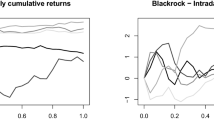
But if we look at our data (Fig. 1), one gets the impression that a change in mean would rather be upwards than downwards, meaning that the daily average pollution increased after March 15, 2020 compared to the beginning of the year. Indeed, after averaging over the 344 monitoring stations and applying the two-sample Hodges-Lehmann estimator to the resulting one-dimensional time series, we estimate the average increase to be 3.8 $\mu g/m^3$. However, our test does not reject the null hypothesis when applied to this one-dimensional time series.

Similar findings about in increase in $PM_{10}$ were made by Ropkins and Tate (2021). They studied the impact of the COVID-19 lockdown on air quality across the UK. While using long-term data (Jan. 2015 to Jun. 2020) from Rural Background, Urban Background and Urban Traffic stations, they observed an increase for $PM_{10}$ and $PM_{2.5}$ while locking down. Noting that this trend is "highly inconsistent with an air quality response to the lockdown", they discussed the possibility that the lockdown did not greatly limit the largest impacts on particulate matter. We assume that the findings are to some extend comparable to Germany due to the similar geographic and demographic characteristics of the countries.

Furthermore, the German ’Umweltbundesamt’ states that traffic is not the main contributor to $PM_{10}$ in Germany (anymore) and other sources of particulate matter (e.g. fertilization, Saharan dust, soil erosion, fires) can overlay effects of reduced traffic (source: https://www.umweltbundesamt.de/faq-auswirkungen-der-corona-krise-auf-die#welche-auswirkungen-hat-die-corona-krise-auf-die-feinstaub-pm10-belastung). It is known that one mayor meteorological effect on particulate matter is precipitation, since it washes the dust out of the air (scavenging). Comparing the data with the meteorological recordings (Fig. 2) another explanation for the change-point gets visible: While January was relatively warm with few precipitation, February and first half of March had much of it. Beginning in the middle of March, a relatively drought period started and lasted through April and May. (Data extracted from DWD Climate Data Center (CDC): Daily station observations precipitation height in mm, v19.3, 02.09.2020. https://cdc.dwd.de/portal/202107291811/mapview)

Fig. 2

Daily rainfall (precipitation) in mm in Germany averaged over 1637 weather stations

Comparing this findings with Fig. 1, we can see that it fits the data quite well. Especially in February and the first half of March, with higher quantity of precipitation, we have relatively low quantity of $PM_{10}$. Beginning with the drought weather, the concentration of $PM_{10}$ goes up and especially the bottom-peaks are now higher than before, meaning that days with a concentration of $PM_{10}$ as low as in the beginning of the year are clearly more rare.

We like to note that this findings do not contradict the satellite data published by ESA (e.g. https://www.esa.int/Applications/Observing_the_Earth/Copernicus/Sentinel-5P/Air_pollution_remains_low_as_Europeans_stay_at_home) which shows a reduced air pollution over Europe in 2020 compared to 2019. While the satellites measure atmospheric pollution, the data of the ’Umweltbundesamt’ is collected at stations at ground level. It is known that there is a difference between these two sorts of pollution.

3.4 Simulation study

In this section we report the results of our simulation study. We compare size and power performance of our test statistic with the well established CUSUM. To do so, we construct different data examples which are described below. Note that we can easily adapt the bootstrap and the adapted bandwidth procedure described above to CUSUM by using $h(x,y)=x-y$ instead of the spatial sign kernel function $h(x,y)=(x-y)/\Vert x-y\Vert$.

3.5 Generating sample

We use a functional AR(1)-process on [0, 1], where the innovations are standard Brownian motions. We use an approximation on a finite grid with d grid points, if not indicated otherwise. To be more precise, we simulate data as follows:

$$\begin{aligned}&X_{-BI}=(\xi _1,\xi _1+\xi _2,\ldots ,\sum _{i=1}^d \xi _i)/\sqrt{d}, \;\;\;\xi _i \text { i.i.d. }{\mathcal {N}}(0,1)\text {-distributed}\\&X_t = a\, \Phi X_{t-1}^{\text {T}} + W_t \;\;\; \forall \; {-BI} <t \le n \\&\text {where } \Phi \in {\mathbb {R}}^{d\times d} \text { with entries } \Phi _{i,j}={\left\{ \begin{array}{ll} i/d^2 &{} i\le j \\ j/d^2 &{} i>j \end{array}\right. } = \min (i,j)/d^2 \\&\text {and } W_t = (\xi ^{(t)}_1,\xi ^{(t)}_1+\xi ^{(t)}_2,\ldots ,\sum _{i=1}^d \xi ^{(t)}_i)/\sqrt{d}, \;\;\; \xi ^{(t)}_i \text { i.i.d. }{\mathcal {N}}(0,1)\text {-distributed} \end{aligned}$$

The scalar $a \in {\mathbb {R}}$ is an AR-parameter, we use $a=1$. The first $(BI+1)$ observations are not used (burn-in period). Through this simulation structure we achieve temproal dependence and spatial dependence. We consider sample sizes $n=100, 200, 250$ for the size and $n=200$ with observations on a grid of size d with $d=100$ if not stated otherwise.

3.6 Size

To calculate the empirical size, data simulation and test procedure via bootstrap is repeated $S=3000$ times with $m=1000$ bootstrap repetitions. We count the number of times the null hypothesis was rejected both for the CUSUM-type and the Wilcoxon-type statistic (based on spatial signs). By using $S=3000$ simulation runs, the standard deviation of the rejection frequencies is always below 1% and is below 0.4% if the true rejection probability is at 5%.

To analyse how good the test statistics performs if outliers are present or if Gaussianity is not given, we study two additional simulations:

• Data simulated as above, but with presence of outliers:

  $$\begin{aligned} Y_i={\left\{ \begin{array}{ll} X_i \;\;\; &{} i \notin \{ 0.2n,0.4n, 0.6n,0.8n\} \\ 10X_i &{} i \in \{ 0.2n,0.4n,0.6n,0.8n\} \end{array}\right. } \end{aligned}$$

• Data simulated similar to the above, but with $\xi _i^{(t)} \sim t_1 \, \forall i\le d,$ $-BI<t\le n$, i.e. heavy tailed data.

As we can see in Table 3, the Wilcoxon-type test and the CUSUM test perform almost similarly under Gaussianity, both are somewhat undersized, especially for a smaller size of $n=100$, but also for $n=200$ or $n=250$. In the presence of outliers or for heavy-tailed data, the rejection frequency of the Wilcoxon-type test does not change much, see Table 4. In contrast, the CUSUM test is very conservative in these situations.

Table 3 Empirical size of CUSUM and spatial sign test with Gaussian data, significance level $\alpha$ and different sample sizes n

Table 4 Empirical size of CUSUM and spatial sign test with significance level $\alpha$, sample size $n=200$ and different distributions

3.7 Power

To evaluate the performance of the test statistics in presence of a change in mean, we construct four scenarios. The sample size is $n=200$ with a change after $k^\star =50$ or $k^\star =100$ observations:

• Scenario 1: Gaussian observations with uniform jump of $+0.3$ after $k^\star$ observations:

  $$\begin{aligned} Y_i={\left\{ \begin{array}{ll} X_i \;\;\; &{} i\le k^\star \\ X_i +0.3u &{} i> k^\star \end{array}\right. } \end{aligned}$$

  where $u=(1,\ldots ,1)^t$.

• Scenario 2: Gaussian observations with sinus-jump after $k^\star$ of observations:

  $$\begin{aligned} Y_i={\left\{ \begin{array}{ll} X_i \;\;\; &{} i\le k^\star \\ X_i + \frac{1}{2\sqrt{2}} (\sin (\pi D/d))_{D\le d} &{} i>k^\star \end{array}\right. } \end{aligned}$$

• Scenario 3: Uniform jump of $+0.3$ after $k^\star$ observations in presence of outlier at 0.2n, 0.4n, 0.6n, 0.8n:

  $$\begin{aligned} Y_i={\left\{ \begin{array}{ll} X_i \;\;\; &{} i<n/2, i \notin \{ 0.2n,0.4n\} \\ 10X_i &{} i \in \{ 0.2n,0.4n\} \\ X_i +0.3u &{} i\ge n/2, i \notin \{ 0.6n,0.8n\} \\ 10X_i +0.3u &{} i \in \{ 0.6n,0.8n\} \end{array}\right. } \end{aligned}$$

• Scenario 4: Heavy tails - In the simulation of $(X_i)_{i \le n}$ we use $\xi _i^{(t)} \sim t_1$ (Cauchy distributed) $\forall i\le d,-BI<t\le n$ and a uniform jump of $+5$ after $k^\star$ observations

As in the analysis under null hypothesis $H_0$, we chose $m=1000$ bootstrap repetitions. The data simulation and test procedure via bootstrap is repeated $S=3000$ times for each scenario and the number of times $H_0$ was rejected is counted to calculate the empirical power. To compare our test-statistic with CUSUM, we calculate the Wilcoxon-type test (spatial sign) and the CUSUM test simultaneously in each simulation run.

Fig. 3

Size-Power-Plot for CUSUM and Spatial Sign Test, Scenario 1–4, sample size $n=200$

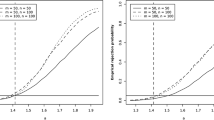
Comparing the size-power plots for both test statistics (Fig. 3), we see that the Wilcoxon-type test (based on spatial signs) outperforms the CUSUM test in all scenarios. As expected, a change in the middle of the data ($k^\star =100$) is detected with higher probability than an earlier change ($k^\star =50$). The difference in the power between the Wilcoxon-type test and the CUSUM test is less pronounced in the Scenarios 1 and 2 with Gaussian data. While the Wilcoxon-type test is not much affected by the outliers in Scenario 3, size and power of the CUSUM-test are reduced, so that the spatial sign based test shows clearly more empirical power. In Scenario 4 with heavy tails, we see that the CUSUM test barely provides any empirical power at all. Even for $\alpha =0.1$ CUSUM shows an empirical power $<0.04$. In heavy contrast, the Wilcoxon-type test shows relatively large empirical power (note that the jump is larger compared to the other scenarios).

For exact values of the empirical power in each scenario, see Table 6 in the appendix. In the appendix can also be found a short examination of the behaviour of the test statistics if the change-point lies even more closely to the beginning of the observations ($k^\star =30$). Here shall just be noted that the Wilcoxon-type test loses power if the change point lies closer to the edge, but still has similar power compared to the CUSUM-test. In the case of one-dimensional observations, Dehling et al. (2020) have also observed that changes not in the middle of the data can not be detected as good with the Wilcoxon-type change-point test. Finally, we consider the case that d is larger than n. The size of both tests is not affected stronlgy by this, see Table 5. The Wilcoxon-type test suffers less loss in power than the CUSUM test if $d=350$.

Table 5 Empirical size of CUSUM and spatial sign based test for different significance level $\alpha$, Scenario 5 with $d=350$, $n=150$

4 Auxilary results

4.1 Hoeffding decomposition and linear part

The proofs will make use of Hoeffding’s decomposition of the kernel h, so recall that Hoeffding’s decomposition of h is defined as

$$\begin{aligned} h(x,y)= h_1(x)-h_1(y)+h_2(x,y) \, \forall x,y \in H, \end{aligned}$$

where

$$\begin{aligned} h_1(x)= & {} \mathbb {E}[h(x,\tilde{X})]\\ h_2(x,y)= & {} h(x,y) - \mathbb {E}[h(x,\tilde{X})] - \mathbb {E}[h(X,y)] = h(x,y) -h_1(x)+h_1(y) \end{aligned}$$

where $X,\tilde{X}$ are independent copies of $X_0$. It is well known that $h_2$ is degenerate, that means $\mathbb {E}[h_2(x,\tilde{X})]=\mathbb {E}[h_2(X,y)]=0$, see e.g. Section 1.6 in the book of Lee (2019).

Lemma 1

(Hoeffding’s decomposition of $U_{n,k}$) Let $h:H\times H \rightarrow {H}$ be an antisymmetric kernel. Under Hoeffding’s decomposition it holds for the test statistic that

$$\begin{aligned} U_{n,k}= \sum _{i=1}^k \sum _{j=k+1}^n h(X_i,X_j) = \underbrace{n \sum _{i=1}^k(h_1(X_i)-\overline{h_1(X)})}_{\text {linear part}} + \underbrace{\sum _{i=1}^k\sum _{j=k+1}^n h_2(X_i,X_j)}_{\text {degenerate part} } \end{aligned}$$

where $\overline{h_1(X)} = \frac{1}{n}\sum _{j=1}^n h_1(X_j).$

Proof

To prove the formula for $U_{n,k}$, we use Hoeffding’s decomposition for h:

$$\begin{aligned} U_{n,k}&=\sum _{i=1}^k \sum _{j=k+1}^n h(X_i,X_j) = \sum _{i=1}^k\sum _{j=k+1}^n [h_1(X_i)-h_1(X_j)+h_2(X_i,X_j) ] \\&= \sum _{i=1}^k \sum _{j=k+1}^n [h_1(X_i)-h_1(X_j)] + \sum _{i=1}^k \sum _{j=k+1}^n h_2(X_i,X_j) \\&= (n-k)h_1(X_1)-\sum _{j=k+1}^n h_1(X_j)+\cdots +(n-k)h_1(X_k)-\sum _{j=k+1}^n h_1(X_j) \\&\quad + \sum _{i=1}^k \sum _{j=k+1}^n h_2(X_i,X_j) \\&= n h_1(X_1)-\sum _{j=1}^n h_1(X_j)+\cdots +n h_1(X_k)-\sum _{j=1}^n h_1(X_j) \\&\quad + \sum _{i=1}^k \sum _{j=k+1}^n h_2(X_i,X_j) \\&= n\Big (\sum _{i=1}^k[h_1(X_i)-\frac{1}{n}\sum _{j=1}^n h_1(X_j)]\Big )+\sum _{i=1}^k \sum _{j=k+1}^n h_2(X_i,X_j) \\&= n \sum _{i=1}^k \Big (h_1(X_i)-\overline{h_1(X)}\Big ) + \sum _{i=1}^k \sum _{j=k+1}^n h_2(X_i,X_j). \end{aligned}$$

$\square$

To use existing results about partial sums, we need to investigate the properties of the sequence $(h_1(X_n))_{n\in \mathbb {Z}}$.

Lemma 2

Under the assumptions of Theorem 1, $(h_1(X_n))_{n\in {\mathbb {Z}}}$ is $L_2$-NED with approximation constants $a_{k,2}={\mathcal {O}}(k^{-4\frac{\delta +3}{\delta }})$.

Proof

By Hoeffding’s decomposition for h it holds that $\forall x,x' \in H$

$$\begin{aligned} \Vert h_1(x)-h_1(x')\Vert =\Vert {\mathbb {E}}[h(x,\tilde{X})]-\mathbb {E}[h(x',\tilde{X})]\Vert \end{aligned}$$

Let $X,\tilde{X}$ be independent copies of $X_0$. Then by Jensen’s inequality for conditional expectations and the variation condition

$$\begin{aligned}&\mathbb {E}\bigg [\Big ( \sup _{\Vert x-X\Vert \le \epsilon } \Vert h_1(x)-h_1(X)\Vert _{{H}}\Big )^2\bigg ] \nonumber \\&\quad = \mathbb {E}\bigg [\Big (\sup _{\Vert x-X\Vert \le \epsilon } E\big [\Vert h(x,\tilde{X})-h(X,\tilde{X})\Vert \big | X\big ]\Big )^2\bigg ] \nonumber \\&\quad \le \mathbb {E}\bigg [\Big (\sup _{\Vert x-X\Vert \le \epsilon } \Vert h(x,\tilde{X})-h(X,\tilde{X})\Vert \Big )^2\bigg ] \nonumber \\&\quad \le \mathbb {E}\bigg [\Big (\sup _{\begin{array}{c} \Vert x-X\Vert \le \epsilon \\ \Vert y-\tilde{X}\Vert \le \epsilon \end{array}} \Vert h(x,y)-h(X,\tilde{X})\Vert \Big )^2 \bigg ] \le L\epsilon . \end{aligned}$$

(1)

We introduce the following notation: Let $X_{n,k}=f_k(\zeta _{n-k},\ldots ,\zeta _{n+k})$ and $\tilde{X}_{n,k}$ and independent copy of this random variable. Now, we can find the approximation constants of $(h_1(X_n))_n$ by using (1) and some further inequalities:

$$\begin{aligned}&\mathbb {E}[\Vert h_1(X_0)-\mathbb {E}[h_1(X_0)|\mathfrak {F}_{-k}^k]\Vert ^2] \le \mathbb {E}[\Vert h_1(X_0)-h_1(X_{0,k})\Vert ^2] \\&\quad = \mathbb {E}[ \Vert h_1(X_0)-h_1(X_{0,k})\Vert ^2 {\textbf {1}}_{\{\Vert X_0-X_{0,k}\Vert>s_k \}} ]\\&\qquad +\mathbb {E}[ \Vert h_1(X_0)-h_1(X_{0,k})\Vert ^2 {\textbf {1}}_{\{\Vert X_0-X_{0,k}\Vert \le s_k \}}] \\&\quad \le \mathbb {E}[ \Vert h_1(X_0)-h_1(X_{0,k})\Vert ^2 {\textbf {1}}_{\{\Vert X_0-X_{0,k}\Vert>s_k \}} ] \\&\qquad + \underbrace{\mathbb {E}\bigg [\Big (\sup _{\Vert X_0-X_{0,k}\Vert \le s_k} \Vert h_1(X_0)-h_1(X_{0,k})\Vert \Big )^2\bigg ]}_{\overset{(1)}{\le } Ls_k} \\&\quad \le \left\| \Vert h_1(X_0)-h_1(X_0,k) \Vert ^2 \right\| _{\frac{2+\delta }{2}}+\left\| {\textbf {1}}_{\{\Vert X_0-X_{0,k}\Vert>s_k \}} \right\| _{\frac{2+\delta }{\delta }} + L s_k \\&\hspace{50pt}\text {by H}\ddot{\textrm{o}}\text {lder's inequality} \\&\quad = \left\| \Vert h_1(X_0)-h_1(X_0,k) \Vert ^2 \right\| _{\frac{2+\delta }{2}}+ {\mathbb {P}}(\Vert X_0-X_{0,k} \Vert > s_k)^{\frac{\delta }{2+\delta }} + Ls_k \\&\quad \le \mathbb {E}[ \Vert h_1(X_0)-h_1(X_{0,k})\Vert ^{2+\delta } ]^{\frac{2}{2+\delta }} + (a_k\Phi (s_k))^{\frac{\delta }{2+\delta }} + L s_k \;\;\; \text {since}\, (X_n)_n\, \text {is P-NED} \\&\quad =\mathbb {E}\left[ \left\| \mathbb {E}[h(X_0,\tilde{X}_0) | X_0,X_{0,k}] - \mathbb {E}[h(X_{0,k},\tilde{X}_{0,k})|X_0,X_{0,k}] \right\| ^{2+\delta } \right] ^\frac{2}{2+\delta } (a_k\Phi (s_k))^{\frac{\delta }{2+\delta }} \\&\qquad + L s_k \\&\quad \le \mathbb {E}\left[ \mathbb {E}[ \Vert h(X_0,\tilde{X}_0)-h(X_{0,k},\tilde{X}_{0,k}) \Vert ^{2+\delta } | X_0,X_{0,k}] \right] ^{\frac{2}{2+\delta }} (a_k\Phi (s_k))^{\frac{\delta }{2+\delta }} + Ls_k \\&\hspace{50pt}\text {by Jensen's inequality} \\&\quad = \left( \mathbb {E}[\Vert h(X_0,\tilde{X}_0)-h(X_{0,k},\tilde{X}_{0,k}) \Vert ^{2+\delta } ]^{\frac{1}{2+\delta }} \right) ^2 (a_k\Phi (s_k))^{\frac{\delta }{2+\delta }} +Ls_k \\&\quad \le \left( \mathbb {E}[\Vert h(X_0,\tilde{X}_0)\Vert ^{2+\delta }]^{\frac{1}{2+\delta }} + \mathbb {E}[\Vert h(X_{0,k},\tilde{X}_{0,k})\Vert ^{2+\delta }]^{\frac{1}{2+\delta }} \right) ^2 (a_k\Phi (s_k))^{\frac{\delta }{2+\delta }} +Ls_k \\&\hspace{50pt} \text {by Minkowski's inequality} \\&\quad \le (M^{\frac{1}{2+\delta }}+M^{\frac{1}{2+\delta }} )^2 (a_k\Phi (s_k))^{\frac{\delta }{2+\delta }} +Ls_k \\&\hspace{50pt} \text {by the uniform moment condition, choose}\, s_k=k^{-8\frac{3+\delta }{\delta }} \\&\quad \le C (k^{-8 \frac{(3+\delta )(2+\delta )}{\delta ^2}})^{\frac{\delta }{2+\delta }} +L k^{-8\frac{3+\delta }{\delta }} \;\;\; \text {by the assumption on the P-NED coefficients} \\&\quad = C k^{-8 \frac{3+\delta }{\delta }}. \end{aligned}$$

By taking the square root, we get the result:

$$\begin{aligned} \left( \mathbb {E}[\Vert h_1(X_0)-\mathbb {E}[h_1(X_0)| \mathfrak {F}_{-k}^k]\Vert ^2] \right) ^{\frac{1}{2}} \le C k^{-4 \frac{3+\delta }{\delta }} =: a_{k,2}. \end{aligned}$$

Since it holds that $a_{k,2} \xrightarrow {k\rightarrow \infty } 0$, $(X_n)_{n\in {\mathbb {Z}}}$ is $L_2$-NED. $\square$

Proposition 1

Under Assumptions of Theorem 1 it holds:

$$\begin{aligned} \Big ( \frac{1}{\sqrt{n}} \sum _{i=1}^{\left\lfloor {n\lambda }\right\rfloor } h_1(X_i) \Big )_{\lambda \in [0,1]} \Rightarrow (W(\lambda ))_{\lambda \in [0,1]} \end{aligned}$$

where $(W(\lambda ))_{\lambda \in [0,1]}$ is a Brownian motion with covariance operator as defined in Theorem 1.

Proof

We want to use Theorem 1 (Sharipov et al. 2016) for $(h_1(X_n))_{n\in \mathbb {Z}}$, so we have to check the assumptions:

Assumption 1: $(h_1(X_n))_{n\in \mathbb {Z}}$ is $L_1$-NED.

We know by Lemma 2 that $(h_1(X_n))_{n\in \mathbb {Z}}$ is $L_2$-NED. Thus, $L_1$-NED follows by Jensen’s inequality:

$$\begin{aligned} \mathbb {E}[\Vert h_1(X_0)-\mathbb {E}[h_1(X_0)|\mathfrak {F}_{-k}^k]\Vert ]&\le \mathbb {E}[\Vert h_1(X_0)-\mathbb {E}[h_1(X_0)| \mathfrak {F}_{-k}^k] \Vert ^2]^{\frac{1}{2}} \le a_{k,2} \end{aligned}$$

So, $(h_1(X_n))_{n\in \mathbb {Z}}$ is $L_1$-NED with constants $a_{k,1}=a_{k,2}=Ck^{-4\frac{3+\delta }{\delta }}$.

Assumption 2: Existing $(4+\delta )$-moments.

This follows from the assumption of uniform moments under approximation:

$$\begin{aligned} \mathbb {E}[\Vert h_1(X_0) \Vert ^{4+\delta }]&= \mathbb {E}[\Vert \mathbb {E}[h(X_0,\tilde{X}_0)| X_0] \Vert ^{4+\delta } ] \\&\le \mathbb {E}[ \mathbb {E}[\Vert h(X_0,\tilde{X}_0) \Vert ^{4+\delta } | X_0 ]] \;\;\; \text {by Jensen's inequality} \\&= \mathbb {E}[\Vert h(X_0,\tilde{X}_0) \Vert ^{4+\delta }] \le M < \infty \end{aligned}$$

In the case that h is bounded, the same holds for $h_1$.

Assumption 3: $\sum _{m=1}^{\infty } m^2 a_{m,1}^{\frac{\delta }{3+\delta }} < \infty$

$$\begin{aligned} \sum _{m=1}^{\infty } m^2 a_{m,1}^{\frac{\delta }{3+\delta }} = C \sum _{m=1}^{\infty }m^2(m^{-4\frac{3+\delta }{\delta }})^{\frac{\delta }{3+\delta }} = C \sum _{m=1}^{\infty } m^2 m^{-4} = C \sum _{m=1}^{\infty } m^{-2} < \infty \end{aligned}$$

Assumption 4: $\sum _{m=1}^{\infty } m^2 \beta _m^{\frac{\delta }{4+\delta }} < \infty$.

This holds directly by the assumed rate on the coefficients $\beta _m$.

We have checked that all assumptions for Theorem 1 (Sharipov et al. 2016) are fulfilled and since $\mathbb {E}[h_1(X_0)]=0$ because h is antisymmetric, the statement of the theorem follows. $\square$

4.2 Degenerate part

Lemma 3

Under the assumptions of Theorem 1, there exists a universal constant $C>0$ such that for every $i,k,l\in {\mathbb {N}}$, $\epsilon >0$ it holds that

$$\begin{aligned} \mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X_{i,l},X_{i+k+2l,l})\Vert ^2]^{\frac{1}{2}} \le C(\sqrt{\epsilon }+\beta _k^{\frac{\delta }{2(2+\delta )}}+(a_l\Phi (\epsilon ))^{\frac{\delta }{2(2+\delta )}} ), \end{aligned}$$

where $X_{i,l} = f_l(\zeta _{i-l},\ldots ,\zeta _{i+l})$.

Proof

By Lemma D1 (Dehling et al. 2017) there exist copies $(\zeta '_n)_{n\in {\mathbb {Z}}}$, $(\zeta ''_n)_{n\in {\mathbb {Z}}}$ of $(\zeta _n)_{n\in {\mathbb {Z}}}$ which are independent of each other and satisfy

$$\begin{aligned} \mathbb {P}((\zeta '_n)_{n\ge i+k+l}=(\zeta _n)_{n\ge i+k+l})=1-\beta _k \;\;\; \text {and} \;\;\; \mathbb {P}((\zeta ''_n)_{n\le i+l}=(\zeta _n)_{n\le i+l})=1-\beta _k \end{aligned}$$

(2)

Define

$$\begin{aligned}&X'_i= f( (\zeta '_{i+n})_{n\in {\mathbb {Z}}}) \; , \;\; \; X''_i= f( (\zeta ''_{i+n})_{n\in {\mathbb {Z}}}) \\&X'_{i,l}=f_l(\zeta '_{i-l},\ldots ,\zeta '_{i+l}) \; , \;\;\; X''_{i,l}=f_l(\zeta ''_{i-l},\ldots ,\zeta ''_{i+l}) . \end{aligned}$$

With the help of these, we can write

$$\begin{aligned}&\mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X_{i,l},X_{i+k+2l,l}) \Vert ^2]^{\frac{1}{2}} \nonumber \\&\quad \le \mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X''_i, X'_{i+k+2l}) \Vert ^2]^{\frac{1}{2}} \end{aligned}$$

(3)

$$\begin{aligned}&\quad + \mathbb {E}[\Vert h_2(X''_i, X'_{i+k+2l})-h_2(X''_{i,l}, X'_{i+k+2l,l}) \Vert ^2]^{\frac{1}{2}} \end{aligned}$$

(4)

$$\begin{aligned}&\quad + \mathbb {E}[\Vert h_2(X''_{i,l}, X'_{i+k+2l,l})-h_2(X_{i,l},X_{i+k+2l,l})\Vert ^2]^{\frac{1}{2}} \end{aligned}$$

(5)

by using the triangle inequality. We will look at the three summands separately. For abbreviation, we define

$$\begin{aligned} B= & {} \{ (\zeta '_n)_{n\ge i+k+l} = (\zeta _n)_{n\ge i+k+l}, \,(\zeta ''_n)_{n\le i+l} = (\zeta _n)_{n\le i+l} \}\\ B^c= & {} \{ (\zeta '_n)_{n\ge i+k+l} \ne (\zeta _n)_{n\ge i+k+l} \text { or } (\zeta ''_n)_{n\le i+l} \ne (\zeta _n)_{n\le i+l} \} \end{aligned}$$

$$\begin{aligned} (3)&= \mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X''_i, X'_{i+k+2l}) \Vert ^2]^{\frac{1}{2}} \end{aligned}$$

$$\begin{aligned}&\le \;\; \mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X''_i, X'_{i+k+2l}) \Vert ^2 {\textbf {1}}_{B^c}]^{\frac{1}{2}} \end{aligned}$$

(3.A)

$$\begin{aligned}&\;\;\; + \mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X''_i, X'_{i+k+2l}) \Vert ^2 {\textbf {1}}_{B}]^{\frac{1}{2}}. \end{aligned}$$

(3.B)

For (3.A), we use Hölder’s inequality together with our assumptions on uniform moments under approximation and get

$$\begin{aligned} (3.A)&\le \mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X''_i,X'_{i+k+2l})\Vert ^{\frac{2(2+\delta )}{2}}]^{\frac{2}{2(2+\delta )}}\mathbb {P}(B^c )^{\frac{\delta }{2(2+\delta )}} \\&\le \left( \mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})\Vert ^{2+\delta }]^{\frac{1}{2+\delta }} + \mathbb {E}[\Vert h_2(X''_i, X'_{i+k+2l})\Vert ^{2+\delta }]^{\frac{1}{2+\delta }}\right) \\&\hspace{20pt} \cdot \big ( \mathbb {P}( \{ \zeta '_n)_{n\ge i+k+l} \ne (\zeta _n)_{n\ge i+k+l} \}) + \mathbb {P}( \{ (\zeta ''_n)_{n\le i+l} \ne (\zeta _n)_{n\le i+l} \}) \big ) ^{\frac{\delta }{2(2+\delta )}} \\&\le 2 M^\frac{1}{2+\delta }(2\beta _k^{\frac{\delta }{2(2+\delta )}}) \\&\le C \beta _k^{\frac{\delta }{2(2+\delta )}}, \end{aligned}$$

where we used property (2) of the copied series $(\zeta '_n)_{n\in {\mathbb {Z}}}$, $(\zeta ''_n)_{n\in {\mathbb {Z}}}$ for the second to last inequality. For (3.B), we split up again:

$$\begin{aligned} (3.B)&\le \; \mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X''_i,X'_{i+k+2l})\Vert ^2 {\textbf {1}}_B \\&\hspace{100pt} {\textbf {1}}_{\{ \Vert X_i-X''_i\Vert \le 2\epsilon , \, \Vert X_{i+k+2l}-X'_{i+k+2l} \Vert \le 2\epsilon \}} ]^{\frac{1}{2}} \\&\;\; +\mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X''_i,X'_{i+k+2l})\Vert ^2 {\textbf {1}}_B \\&\hspace{100pt} {\textbf {1}}_{\{ \Vert X_i-X''_i\Vert> 2\epsilon \, \text {or} \, \Vert X_{i+k+2l}-X'_{i+k+2l} \Vert > 2\epsilon \}} ]^{\frac{1}{2}}. \end{aligned}$$

For the first summand, we use variation condition. For the second, notice that on B:

$$\begin{aligned} \Vert X_i-X''_i \Vert \le \Vert X_i- X_{i,l}\Vert + \Vert X_{i,l}-X''_i \Vert =\Vert X_i -X_{i,l} \Vert +\Vert X''_{i,l}-X''_i \Vert \end{aligned}$$

and

$$\begin{aligned} \Vert X_{i+k+2l}-X'_{i+k+2l} \Vert&\le \Vert X_{i+k+2l}- X_{i+k+2l,l}\Vert + \Vert X_{i+k+2l,l}-X'_{i+k+2l} \Vert \\&=\Vert X_{i+k+2l} -X_{i+k+2l,l} \Vert +\Vert X'_{i+k+2l,l}-X'_{i+k+2l} \Vert . \end{aligned}$$

So,

$$\begin{aligned} (3.B)&\le \sqrt{L2\epsilon } \\&\hspace{10pt} + \mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X''_i,X'_{i+k+2l})\Vert ^2 {\textbf {1}}_{\{\Vert X_i-X_{i,l} \Vert> \epsilon \}}]^{\frac{1}{2}} \\&\hspace{10pt} + \mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X''_i,X'_{i+k+2l})\Vert ^2 {\textbf {1}}_{\{\Vert X''_i-X''_{i,l} \Vert> \epsilon \}}]^{\frac{1}{2}} \\&\hspace{10pt} + \mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X''_i,X'_{i+k+2l})\Vert ^2 {\textbf {1}}_{\{\Vert X_{i+k+2l}-X_{i+k+2l,l} \Vert> \epsilon \}}]^{\frac{1}{2}} \\&\hspace{10pt} + \mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X''_i,X'_{i+k+2l})\Vert ^2 {\textbf {1}}_{\{\Vert X'_{i+k+2l}-X'_{i+k+2l,l} \Vert> \epsilon \}}]^{\frac{1}{2}} \\&\le \sqrt{L2\epsilon }+ 4 \cdot 2M^{\frac{1}{2+\delta }}(\mathbb {P}(\Vert X_i-X_{i,l}\Vert > \epsilon ))^{\frac{\delta }{2(2+\delta )}} \\&\hspace{50pt}\text {by our moment assumptions and H}\ddot{\textrm{o}}\text {lder's inequality} \\&\le \sqrt{L2\epsilon } +4 \cdot 2M^{\frac{1}{2+\delta }} (a_l\Phi (\epsilon ))^{\frac{\delta }{2(2+\delta )}} \;\;\; \text {since}\, (X_n)_{n\in \mathbb {Z}}\, \text {is P-NED} \\&\le C\left( \sqrt{\epsilon }+(a_l\Phi (\epsilon ))^{\frac{\delta }{2(2+\delta )}} \right) \end{aligned}$$

Combining the results for (3.A) and (3.B) we get

$$\begin{aligned} (3) \le (3.A)+(3.B) \le C \left( \beta _k^{\frac{\delta }{2(2+\delta )}} +\sqrt{\epsilon }+(a_l\Phi (\epsilon ))^{\frac{\delta }{2(2+\delta )}} \right) . \end{aligned}$$

We can now look at (4). Again, we split the term into two summands, (similar as for (3)) we use the variation condition for the first and Hölder’s inequality for the second summand:

$$\begin{aligned} (4)&= \mathbb {E}[\Vert h_2(X''_i, X'_{i+k+2l})-h_2(X''_{i,l}, X'_{i+k+2l,l}) \Vert ^2 ]^{\frac{1}{2}} \\&\le \;\;\;\; \mathbb {E}[\Vert h_2(X''_i, X'_{i+k+2l})-h_2(X''_{i,l}, X'_{i+k+2l,l}) \Vert ^2 \\&\hspace{100pt}{} {\textbf {1}}_{\{ \Vert X''_i-X''_{i,l}\Vert \le \epsilon ,\, \Vert X'_{i+k+2l}-X'_{i+k+2l,l} \Vert \le \epsilon \}} ]^{\frac{1}{2}} \\&\hspace{11pt} + \mathbb {E}[\Vert h_2(X''_i, X'_{i+k+2l})-h_2(X''_{i,l}, X'_{i+k+2l,l}) \Vert ^2 \\&\hspace{100pt} {\textbf {1}}_{\{ \Vert X''_i-X''_{i,l}\Vert> \epsilon \, \text {or} \, \Vert X'_{i+k+2l}-X'_{i+k+2l,l} \Vert> \epsilon \}} ]^{\frac{1}{2}} \\&\le \sqrt{L\epsilon } + \left( \mathbb {E}[\Vert h_2(X''_i,X'_{i+k+2l}) \Vert ^{2+\delta }]^{\frac{1}{2+\delta }} +\mathbb {E}[\Vert h_2(X''_{i,l},X'_{i+k+2l,l})\Vert ^{2+\delta }]^{\frac{1}{2+\delta }}\right) \\&\hspace{50pt} \cdot \left( \mathbb {P}(\Vert X''_i-X''_{i,l}\Vert> \epsilon ) + \mathbb {P}(\Vert X'_{i+k+2l}-X'_{i+k+2l,l} \Vert > \epsilon ) \right) ^{\frac{\delta }{2(2+\delta )}} \\&\le \sqrt{L\epsilon } + 2M^{\frac{1}{2+\delta }}(2a_l\Phi (\epsilon ))^{\frac{\delta }{2(2+\delta )}} \;\; \text {since}\, (X_n)_{n \in {\mathbb {Z}}}\, \text {is P-NED} \\&\le C\left( \sqrt{\epsilon } + (a_l\Phi (\epsilon ))^{\frac{\delta }{2(2+\delta )}}\right) \end{aligned}$$

Lastly, we split up (5) as well:

$$\begin{aligned} (5)&= \mathbb {E}[ \Vert h_2(X''_{i,l},X'_{i+k+2l,l})-h_2(X_{i,l},X_{i+k+2l,l})\Vert ^2]^{\frac{1}{2}}\\&\le \;\;\; \mathbb {E}[ \Vert h_2(X''_{i,l},X'_{i+k+2l,l})-h_2(X_{i,l},X_{i+k+2l,l})\Vert ^2 {\textbf {1}}_{B^c}]^{\frac{1}{2}} \\&\hspace{11pt} + \mathbb {E}[ \Vert h_2(X''_{i,l},X'_{i+k+2l,l})-h_2(X_{i,l},X_{i+k+2l,l})\Vert ^2 {\textbf {1}}_{B}]^{\frac{1}{2}}. \end{aligned}$$

Since on B it is $X_{i+k+2l,l}=X'_{i+k+2l,l}$ and $X_{i,l}=X''_{i,l}$, the second summand equals zero. For the first summand, we use Hölder’s inequality again and the properties of $(\zeta '_n)_{n\le i+l}$, $(\zeta ''_n)_{n\le i+l}$, see (2):

$$\begin{aligned} (5)&\le 2M^{\frac{1}{2+\delta }} \big (\mathbb {P}(\{(\zeta '_n)_{n \ge i+k+l} \ne (\zeta _n)_{n \ge i+k+l} \}) \!+\! \mathbb {P}( \{(\zeta ''_n)_{n\le i+l} \ne (\zeta _n)_{n\le i+l} \}) \big )^{\frac{\delta }{2(2+\delta )}} \\&\le 2M^{\frac{1}{2+\delta }}(2\beta _k)^{\frac{\delta }{2(2+\delta )}} \le C \beta _k^{\frac{\delta }{2(2+\delta )}} \end{aligned}$$

We can finally put everything together:

$$\begin{aligned}&\mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X_{i,l}, X_{i+k+2l,l})\Vert ^2]^{\frac{1}{2}} \le (3)+(4)+(5) \\&\quad \le C \left( \beta _k^{\frac{\delta }{2(2+\delta )}}+\sqrt{\epsilon } +(a_l\Phi (\epsilon ))^{\frac{\delta }{2(2+\delta )}}\right) + C\left( \sqrt{\epsilon }+ (a_l\Phi (\epsilon ))^{\frac{\delta }{2(2+\delta )}} \right) + C \beta _k^{\frac{\delta }{2(2+\delta )}} \\&\quad \le C \left( \sqrt{\epsilon } + \beta _k^{\frac{\delta }{2(2+\delta )}} + (a_l\Phi (\epsilon ))^{\frac{\delta }{2(2+\delta )}}\right) \end{aligned}$$

$\square$

Lemma 4

Under the assumptions of Theorem 1 it holds for any $n_1< n_2< n_3 < n_4$ and $l= \left\lfloor {n_4^{\frac{3}{16}}}\right\rfloor$:

$$\begin{aligned} \mathbb {E}\bigg [\Big (\sum _{n_1 \le i \le n_2}\sum _{n_3 \le j \le n_4} \Vert h_2(X_i,X_j)-h_2(X_{i,l},X_{j,l})\Vert \Big )^2 \bigg ]{}^{\frac{1}{2}}\le C(n_4-n_3)n_4^{\frac{1}{4}} \end{aligned}$$

Proof

The important step of the proof is to bound the left hand side expectation from above by a sum of $\mathbb {E}[\Vert h_2(X_i,X_j) - h_2(X_{i,l},Y_{j,l} )\Vert ^2]^{1/2}$ terms. We can then use Lemma 3 to achieve the stated approximation. First note that

$$\begin{aligned}&E\bigg [\Big (\sum _{n_1 \le i \le n_2}\sum _{n_3 \le j \le n_4} \Vert h_2(X_i,X_j)-h_2(X_{i,l},X_{j,l})\Vert \Big )^2 \bigg ]{}^{\frac{1}{2}}\\&\le E\bigg [\Big (\sum _{1 \le i \le j-1}\sum _{n_3 \le j \le n_4} \Vert h_2(X_i,X_j)-h_2(X_{i,l},X_{j,l})\Vert \Big )^2 \bigg ]{}^{\frac{1}{2}}. \end{aligned}$$

For any fixed j it is

$$\begin{aligned} \mathbb {E}\bigg [ \sum _{1\le i < j} \Vert h_2(X_i,X_j) \Vert \bigg ] = \mathbb {E}\bigg [ \sum _{k=1}^{j-1} \Vert h_2(X_{j-k},X_j) \Vert \bigg ] \le \mathbb {E}\bigg [ \sum _{k=1}^{n_4} \Vert h_2(X_{j-k},X_j) \Vert \bigg ]. \end{aligned}$$

And for j there are at most $(n_4-n_3)$ possibilities. So

$$\begin{aligned} \mathbb {E}\bigg [ \sum _{n_3 \le j \le n_4} \sum _{1 \le i < j} \Vert h_2(X_i,X_j) \Vert \bigg ] \le (n_4-n_3) \mathbb {E}\bigg [ \sum _{k=1}^{n_4} \Vert h_2(X_{j-k},X_j) \Vert \bigg ]. \end{aligned}$$

The analog holds for $h_2(X_{i,l},X_{j,l})$. Thus,

$$\begin{aligned}&\mathbb {E}\bigg [\Big (\sum _{1 \le i< j, n_3\le j \le n_4} \Vert h_2(X_i,X_j)-h_2(X_{i,l},X_{j,l})\Vert \Big )^2 \bigg ]{}^{\frac{1}{2}}\nonumber \\&\quad \le \sum _{n_3\le j\le n_4} \sum _{1\le i<j} \mathbb {E}[ \Vert h_2(X_i,X_j)-h_2(X_{i,l},X_{j,l})\Vert ^2]{}^{\frac{1}{2}}\nonumber \\&\quad \le (n_4-n_3) \sum _{k=1}^{n_4} \mathbb {E}[\Vert h_2(X_{j-k},X_j)-h_2(X_{j-k,l},X_{j,l}) \Vert ^2 ]{}^{\frac{1}{2}}\nonumber \\&\quad \le (n_4-n_3) \sum _{k=1}^{n_4} C \left( \sqrt{\epsilon } +\beta _{k-2l}^{\frac{\delta }{2(2+\delta )}} + (a_l\Phi (\epsilon )){}^{\frac{\delta }{2(2+\delta )}}\right) \;\; \text {by Lemma}\,3. \end{aligned}$$

(6)

Now set $\epsilon =l^{-8\frac{3+\delta }{\delta }}$ and define $\beta _k=1$ if $k<0$. Then by our assumptions on the approximation constants and the mixing coefficients

$$\begin{aligned} (6)&= C(n_4-n_3)\sum _{k=1}^{n_4} \left( l^{-8\frac{3+\delta }{\delta }\frac{1}{2}}+\beta _{k-2l}{}^{\frac{\delta }{2(2+\delta )}}+(a_l\Phi (l^{-8\frac{3+\delta }{\delta }})){}^{\frac{\delta }{2(2+\delta )}}\right) \\&\le C(n_4-n_3) \sum _{k=1}^{n_4} \left( l^{-4\frac{3+\delta }{\delta }}+\beta _{k-2l}{}^{\frac{\delta }{2(2+\delta )}}+l^{-4\frac{3+\delta }{\delta }} \right) \\&\le C (n_4-n_3) \Big ( \sum _{k=1}^{n_4} l^{-4} + \sum _{k=1}^{2l-1} \underbrace{\beta _{k-2l}^{\frac{\delta }{4+\delta }}}_{=1} +\sum _{k=2l}^{n_4} \beta _{k-2l}^{\frac{\delta }{4+\delta }} \Big ) \\&\le C (n_4-n_3) \Big (n_4 l^{-4}+2l + \underbrace{\sum _{k=2l}^{n_4} (k-2l)^2 \beta _{k-2l}^{\frac{\delta }{4+\delta }}}_{< \infty } \Big )\\&\le C (n_4-n_3) n_4^{\frac{1}{4}}. \end{aligned}$$

So the statement of the lemma is proven. $\square$

Lemma 5

Under the assumptions of Theorem 1, it holds for any $n_1<n_2<n_3<n_4$ and $l= \left\lfloor {n_4^{\frac{3}{16}}}\right\rfloor$:

$$\begin{aligned} \mathbb {E}\bigg [\Big ( \sum _{n_1\le i \le n_2,\, n_3\le j\le n_4} \Vert h_{2,l}(X_{i,l},X_{j,l})-h_2(X_{i,l},X_{j,l}) \Vert \Big )^2\bigg ]{}^{\frac{1}{2}}\le C (n_4-n_3) n_4^{\frac{1}{4}} \end{aligned}$$

where $h_{2,l}(x,y)= h(x,y)-\mathbb {E}[h(x,\tilde{X}_{j,l})]-\mathbb {E}[h(\tilde{X}_{i,l},y)]\;\;\; \forall i,j,\in {\mathbb {N}}$ and $\tilde{X}_{i,l}=f_l(\tilde{\zeta }_{i-l},\ldots ,\tilde{\zeta }_{i+l})$, where $(\tilde{\zeta }_n)_{n\in \mathbb {\zeta }}$ is an independent copy of $(\zeta _n)_{n\in \mathbb {\zeta }}$.

Proof

For $(\tilde{\zeta }_n)_{n\in {\mathbb {Z}}}$ an independent copy of $(\zeta _n)_{n\in \mathbb {\zeta }}$, write $\tilde{X}_i=f((\tilde{\zeta }_{i+n})_{n\in {\mathbb {Z}}})$. So $(\tilde{X}_i)_{i\in {\mathbb {Z}}}$ is an independent copy of $(X_n)_{n\in \mathbb {Z}}$. We will use Hoeffding’s decomposition and rewrite $h_2$ as $h_2(x,y)=h(x,y)-\mathbb {E}[h(x,\tilde{X}_j)]-\mathbb {E}[h(\tilde{X}_i,y)]$ and similarly for $h_{2,l}$. By doing so, we obtain

$$\begin{aligned}&\mathbb {E}[\Vert h_{2,l}(X_{i,l},X_{j,l})-h_2(X_{i,l},X_{j,l}) \Vert ^2]{}^{\frac{1}{2}}\nonumber \\&\quad = \mathbb {E}[\Vert \;\; h(X_{i,l},X_{j,l})- \mathbb {E}_{\tilde{X}}[h(X_{i,l},\tilde{X}_{j,l})]- \mathbb {E}_{\tilde{X}}[h(\tilde{X}_{i,l},X_{j,l})] \nonumber \\&\qquad - h(X_{i,l},X_{j,l})+ \mathbb {E}_{\tilde{X}}[h(X_{i,l},\tilde{X}_j)]+\mathbb {E}_{\tilde{X}}[h(\tilde{X}_i,X_{j,l})] \Vert ^2 ]{}^{\frac{1}{2}}\nonumber \\&\quad \le \;\; \mathbb {E}[\Vert h(X_{i,l},\tilde{X}_{j,l})-h(X_{i,l},\tilde{X}_j) \Vert ^2 ]{}^{\frac{1}{2}} \end{aligned}$$

(7)

$$\begin{aligned}&\qquad +\mathbb {E}[\Vert h(\tilde{X}_{i,l},X_{j,l})-h(\tilde{X}_i,X_{j,l}) \Vert ^2]{}^{\frac{1}{2}}. \end{aligned}$$

(8)

Here $\mathbb {E}_{\tilde{X}}$ denotes the expectation with respect to $\tilde{X}$, $\mathbb {E}=\mathbb {E}_{X,\tilde{X}}$ is the expectation with respect to X and $\tilde{X}$. We bound the two terms separately, starting with (8):

$$\begin{aligned}&\mathbb {E}[\Vert h(\tilde{X}_{i,l},X_{j,l})-h(\tilde{X}_i,X_{j,l}) \Vert ^2]{}^{\frac{1}{2}}\\&\quad \le \mathbb {E}[\Vert h(\tilde{X}_{i,l},X_{j,l})-h(\tilde{X}_i,X_j) \Vert ^2 ]{}^{\frac{1}{2}}\end{aligned}$$

(8.A)

$$\begin{aligned}&+ \mathbb {E}[\Vert h(\tilde{X}_i,X_{j,l})-h(\tilde{X}_i,X_j)\Vert ^2]{}^{\frac{1}{2}}\end{aligned}$$

(8.B)

Now, for the first summand, we obtain

$$\begin{aligned} (8.A)&= \mathbb {E}[\Vert h(\tilde{X}_{i,l},X_{j,l})-h(\tilde{X}_i,X_j) \Vert ^2 {\textbf {1}}_{\{\Vert \tilde{X}_i-\tilde{X}_{i,l}\Vert \le \epsilon ,\; \Vert X_j-X_{j,l}\Vert \le \epsilon \}}]{}^{\frac{1}{2}}\\&+ \mathbb {E}[\Vert h(\tilde{X}_{i,l},X_{j,l})-h(\tilde{X}_i,X_j) \Vert ^2 {\textbf {1}}_{\{\Vert \tilde{X}_i-\tilde{X}_{i,l}\Vert> \epsilon \, \text {or} \, \Vert X_j-X_{j,l}\Vert> \epsilon \}}]{}^{\frac{1}{2}}\\&\le \sqrt{L\epsilon }+\mathbb {E}[\Vert h(\tilde{X}_{i,l},X_{j,l})-h(\tilde{X}_i,X_j)\Vert ^{2+\delta } ]^{\frac{1}{2+\delta }} \\&\hspace{70pt}\cdot \left( \mathbb {P}(\Vert \tilde{X}_i-\tilde{X}_{i,l} \Vert> \epsilon )+\mathbb {P}(\Vert X_j-X_{j,l} \Vert > \epsilon )\right) \end{aligned}$$

by using the variation condition for the first summand and Hölder’s inequality for the second. By our moment and P-NED assumptions

$$\begin{aligned} (8.A) \le \sqrt{L\epsilon } + 2M^{\frac{1}{2+\delta }}(2a_l\Phi (\epsilon ))\le C\left( \sqrt{\epsilon }+ (2a_l\Phi (\epsilon )){}^{\frac{\delta }{2(2+\delta )}}\right) . \end{aligned}$$

For (8.B) we use similar arguments:

$$\begin{aligned} (8.B)&\le \mathbb {E}[\Vert h(\tilde{X}_i,X_{j,l})-h(\tilde{X}_i,X_j)\Vert ^2 {\textbf {1}}_{\{ \Vert X_j-X_{j,l}\Vert> \epsilon \}}]{}^{\frac{1}{2}}\\&+ \mathbb {E}[\Vert h(\tilde{X}_i,X_{j,l})-h(\tilde{X}_i,X_j)\Vert ^2 {\textbf {1}}_{\{ \Vert X_j-X_{j,l}\Vert \le \epsilon \}}]{}^{\frac{1}{2}}\\&\le \mathbb {E}[\Vert h(\tilde{X}_i,X_{j,l})-h(\tilde{X}_i,X_j)\Vert ^{2+\delta }]^{\frac{1}{2+\delta }} \cdot \mathbb {P}(\Vert X_j-X_{j,l}\Vert > \epsilon ){}^{\frac{\delta }{2(2+\delta )}}+ \sqrt{L\epsilon } \\&\le 2M^{\frac{1}{2+\delta }}(a_l\Phi (\epsilon )){}^{\frac{\delta }{2(2+\delta )}}+\sqrt{L\epsilon } \le C\left( \sqrt{\epsilon } + (a_l\Phi (\epsilon )){}^{\frac{\delta }{2(2+\delta )}}\right) \end{aligned}$$

Putting these two terms together, we get

$$\begin{aligned} (8) \le C\left( \sqrt{\epsilon } + (a_l\Phi (\epsilon )){}^{\frac{\delta }{2(2+\delta )}}\right) . \end{aligned}$$

Bounding (7) works completely analogous, just with i and j interchanged, so

$$\begin{aligned} (7) \le \left( \sqrt{\epsilon } + (a_l\Phi (\epsilon )){}^{\frac{\delta }{2(2+\delta )}}\right) . \end{aligned}$$

All together this yields

$$\begin{aligned} \mathbb {E}[\Vert h_{2,l}(X_{i,l},X_{j,l})-h_2(X_{i,l},X_{j,l}) \Vert ^2]{}^{\frac{1}{2}}\le (7)+(8) \le C\left( \sqrt{\epsilon } + (a_l\Phi (\epsilon )){}^{\frac{\delta }{2(2+\delta )}}\right) .\\ \end{aligned}$$

So we finally get that

$$\begin{aligned}&\mathbb {E}[( \sum _{n_1\le i\le n_2,\; n_3\le j\le n_4} \Vert h_{2,l}(X_{i,l},X_{j,l})-h_2(X_{i,l},X_{j,l}) \Vert )^2]{}^{\frac{1}{2}}\\&\quad \le \mathbb {E}[ ( \sum _{1\le i<j,\; n_3\le j\le n_4} \Vert h_{2,l}(X_{i,l},X_{j,l})-h_2(X_{i,l},X_{j,l}) \Vert )^2 ]{}^{\frac{1}{2}}\\&\quad \le \sum _{1\le i<j,\; n_3\le j\le n_4} \mathbb {E}[\Vert h_{2,l}(X_{i,l},X_{j,l})-h_2(X_{i,l},X_{j,l}) \Vert ^2]{}^{\frac{1}{2}}\\&\quad \le \sum _{1\le i<j,\; n_3\le j\le n_4} C\left( \sqrt{\epsilon } + (a_l\Phi (\epsilon )){}^{\frac{\delta }{2(2+\delta )}}\right) \\&\quad \le C (n_4-n_3)\sum _{k=1}^{n_4}\left( \sqrt{\epsilon }+(a_l\Phi (\epsilon )){}^{\frac{\delta }{2(2+\delta )}}\right) \le C (n_4-n_3)n_4^{\frac{1}{4}} \end{aligned}$$

where the last line is achieved by setting $\epsilon =l^{-8\frac{3+\delta }{\delta }}$ and similar calculations as in Lemma 4. $\square$

Lemma 6

Under the assumptions of Theorem 1, it holds for any $n_1<n_2<n_3 < n_4$ and $l= \left\lfloor {n_4^{\frac{3}{16}}}\right\rfloor$:

$$\begin{aligned} \mathbb {E}\bigg [\Big ( \big \Vert \sum _{n_1\le i \le n_2,\, n_3\le j\le n_4} h_{2,l}(X_{i,l},X_{j,l})\big \Vert \Big )^2 \bigg ] \le C (n_4-n_3)n_4^{\frac{3}{2}}. \end{aligned}$$

For the definition of $h_{2,l}$, see Lemma 5.

Proof

In this proof, we want to use Lemma 1 (Yoshihara 1976), which is the following: Let $g(x_1,\ldots ,x_k)$ be a Borel function. For any $0 \le j \le k-1$ with

for some $\tilde{\delta } > 0$, where $I = \{i_1,\ldots ,i_j\}$, $I^C = \{i_{j+1},\ldots ,i_k\}$ and $X'$ an independent copy of X, it holds that

$$\begin{aligned} \left| \mathbb {E}[g(X_{i_1,l},\ldots ,X_{i_k,l})]- \mathbb {E}[g(X_{I,l}, X'_{I^C,l})] \right| \le 4 M^{1/(1+\tilde{\delta })} \beta _{(i_{j+1}-i_j)-2l}^{\tilde{\delta }/(1+\tilde{\delta })}. \end{aligned}$$

(Y)

Now, for the proof of the lemma, first observe that we can rewrite the squared norm as the scalar product and thus:

$$\begin{aligned}&\mathbb {E}[\Vert \sum _{n_1\le i\le n_2,\, n_3\le j\le n_4} h_{2,l}(X_{i,l},X_{j,l})\Vert ^2] \nonumber \\&\quad = \mathbb {E}[\langle \sum _{n_1\le i\le n_2,\, n_3\le j\le n_4} h_{2,l}(X_{i,l},X_{j,l}), \sum _{n_1\le i\le n_2,\, n_3 \le j\le n_4} h_{2,l}(X_{i,l},X_{j,l})\rangle ] \nonumber \\&\quad = \underset{(i_1 \ne i_2) \,\text {or}\, (j_1 \ne j_2) \,\text {or both} }{\sum _{n_1\le i_1 \le n_2,\, n_3 \le j_1\le n_4} \sum _{n_1\le i_2 \le n_2,\, n_3 \le j_2\le n_4}} \mathbb {E}[\langle h_{2,l}(X_{i_1,l},X_{j_1,l}), h_{2,l}(X_{i_2,l},X_{j_2,l}) \rangle ] \end{aligned}$$

(9)

$$\begin{aligned}&\qquad + \sum _{n_1\le i \le n_2,\, n_3 \le j\le n_4} \mathbb {E}[\langle h_{2,l}(X_{i,l},X_{j,l}), h_{2,l}(X_{i,l},X_{j,l}) \rangle ] \end{aligned}$$

(10)

We know by the uniform moments under approximation that (10) is bounded by the following:

$$\begin{aligned} (10)&= \sum _{n_1\le i \le n_2,\, n_3 \le j\le n_4} \mathbb {E}[\Vert h_{2,l}(X_{i,l},X_{j,l}) \Vert ^2 ] \le (n_2-n_1)(n_4-n_3) M \\&< n_4 (n_4-n_3) M \end{aligned}$$

For (9) we use the above mentioned lemma of Yoshihara (1976). Note that by the double summation, we have three different cases to analyse: $(i_1\ne i_2)$ or $(j_1 \ne j_2)$ or both. Universal, let $m=\max (j_1-i_1, j_2-i_2)$, first assume that $m=j_1-i_1$ and let $\tilde{\delta }=\delta /2 > 0$.

First case: $i_1 \ne i_2$ and $j_1 \ne j_2$

Define the function $g(x_1,x_2,x_3,x_4):=\langle h_{2,l}(x_1,x_2),h_{2,l}(x_3,x_4) \rangle$ and check that ($\Diamond$) holds true for $I=\{i_1\}$ and $I^C = \{j_1, i_2, j_2 \}$:

$$\begin{aligned}&\mathbb {E}[\vert g(X_{i_1,l}, X'_{j_1,l}, X'_{i_2,l}, X'_{j_2,l}) \vert ^{1+\tilde{\delta }}] \le \mathbb {E}[\Vert h_{2,l}(X_{i_1,l}, X'_{j_1,l}) \Vert ^{1+\tilde{\delta }} \Vert h_{2,l}(X'_{i_2,l}, X'_{j_2,l}) \Vert ^{1+\tilde{\delta }}] \\&\quad \le \mathbb {E}[\Vert h_{2,l}(X_{i_1,l}, X'_{j_1,l}) \Vert ^{2(1+\tilde{\delta })}]^{1/2} \mathbb {E}[\Vert h_{2,l}(X'_{i_2,l}, X'_{j_2,l}) \Vert ^{2(1+\tilde{\delta })}]^{1/2} \le M \end{aligned}$$

by our moment assumptions and $\delta = \tilde{\delta }/2$. Here, we first use the Cauchy-Schwarz inequality and then Hölder’s inequality. Now (Y) states that

$$\begin{aligned} \left| \mathbb {E}[ g(X_{i_1,l}, X_{j_1,l}, X_{i_2,l}, X_{j_2,l}) ] - \mathbb {E}[g(X_{i_1,l}, X'_{j_1,l}, X'_{i_2,l}, X'_{j_2,l})] \right| \le C \beta _{m-2l}^{\tilde{\delta }/(1+\tilde{\delta })} \end{aligned}$$

(11)

The second expectation equals 0, which can be seen by using the law of the iterated expectation:

$$\begin{aligned}&\mathbb {E}[g(X_{i_1,l}, X'_{j_1,l}, X'_{i_2,l}, X'_{j_2,l})] = \mathbb {E}[\mathbb {E}[g(X_{i_1,l}, X'_{j_1,l}, X'_{i_2,l}, X'_{j_2,l})| X'_{j_1,l}, X'_{i_2,l}, X'_{j_2,l} ]] \nonumber \\&\quad = \mathbb {E}[\mathbb {E}[\langle h_{2,l}(X_{i_1,l}, X'_{j_1,l}), h_{2,l}(X'_{i_2,l}, X'_{j_2,l}) \rangle | X'_{j_1,l}, X'_{i_2,l}, X'_{j_2,l} ] ] \nonumber \\&\quad = \mathbb {E}[ \langle \mathbb {E}[ h_{2,l}(X_{i_1,l}, X'_{j_1,l}) | X'_{j_1,l}, X'_{i_2,l}, X'_{j_2,l} ], h_{2,l}(X'_{i_2,l}, X'_{j_2,l}) \rangle ] \end{aligned}$$

(12)

since $h_{2,l}(X'_{i_2,l}, X'_{j_2,l})$ is measurable with respect to the inner (conditional) expectation. In general it holds for random variables X, Y that $\mathbb {E}[ \langle Y,X \rangle | \mathfrak {B}]=\langle Y, \mathbb {E}[X|\mathfrak {B}] \rangle$ if Y is measurable with respect to $\mathfrak {B}$. So,

$$\begin{aligned} (12) = \mathbb {E}[ \langle \underbrace{\mathbb {E}[ h_{2,l}(X_{i_1,l}, X'_{j_1,l}) | X'_{j_1,l}, X'_{i_2,l}, X'_{j_2,l} ]}_{=\; 0 \text { because}\, h_{2,l}\, \text {is degenerated}}, h_{2,l}(X'_{i_2,l}, X'_{j_2,l}) \rangle ] = 0. \end{aligned}$$

Plugging this into (11), we get that

$$\begin{aligned} \mathbb {E}[\langle h_{2,l}(X_{i_1,l}, X_{j_1,l}), h_{2,l}(X_{i_2,l}, X_{j_2,l})\rangle ] \le \left| \mathbb {E}[ g(X_{i_1,l}, X_{j_1,l}, X_{i_2,l}, X_{j_2,l})] \right| \le C \beta _{m-2l}^{\tilde{\delta }/(1+\tilde{\delta })} . \end{aligned}$$

We repeat the above argumentation for the other two cases:

Second case: $i_1 \ne i_2$ but $j_1=j_2$

Define the function $g(x_1,x_2,x_3):= \langle h_{2,l}(x_1,x_2), h_{2,l}(x_3,x_2) \rangle$ and check that ($\Diamond$) holds true for $I=\{i_1\}$ and $I^C=\{j_1,i_2\}$:

$$\begin{aligned}&\mathbb {E}[\vert g(X_{i_1,l},X'_{j_1,l}, X'_{j_2,l}) \vert ^{1+\tilde{\delta }}] \\&\quad \le \mathbb {E}[\Vert h_{2,l}(X_{i_1,l}, X'_{j_1,l}) \Vert ^{2(1+\tilde{\delta })}]^{1/2} \mathbb {E}[\Vert h_{2,l}(X'_{i_2,l}, X'_{j_1,l}) \Vert ^{2(1+\tilde{\delta })}]^{1/2} \le M \end{aligned}$$

Here, (Y) states that

$$\begin{aligned} \left| \mathbb {E}[g(X_{i_1,l}, X_{j_1,l}, X_{i_2,l})] -\mathbb {E}[g(X_{i_1,l}, X'_{j_1,l}, X'_{i_2,l})] \right| \le C \beta _{m-2l}^{\tilde{\delta }/(1+\tilde{\delta })} \end{aligned}$$

(13)

Again, the second expectation equals zero:

$$\begin{aligned} \mathbb {E}[g(X_{i_1,l}, X'_{j_1,l}, X'_{i_2,l})]&= \mathbb {E}[\mathbb {E}[\langle h_{2,l}(X_{i_1,l},X'_{j_1,l}), h_{2,l}(X'_{i_2,l},X'_{j_1,l}) \rangle \vert X'_{i_2,l}, X'_{j_1,l} ] ] \\&= \mathbb {E}[ \langle \underbrace{\mathbb {E}[h_{2,l}(X_{i_1,l},X'_{j_1,l}) \vert X'_{i_2,l}, X'_{j_1,l}]}_{=0}, h_{2,l}(X'_{i_2,l},X'_{j_1,l}) \rangle ] \\&= 0 \end{aligned}$$

Plugging this into (13), we get that

$$\begin{aligned} \mathbb {E}[\langle h_{2,l}(X_{i_1,l},X_{j_1,l}), h_{2,l}(X_{i_2,l},X_{j_1,l}) \rangle ] \le \left| \mathbb {E}[g(X_{i_1,l}, X_{j_1,l}, X_{i_2,l})] \right| \le C \beta _{m-2l}^{\tilde{\delta }/(1+\tilde{\delta })}. \end{aligned}$$

Third case: $j_1\ne j_2$ but $i_1=i_2$

Define the function $g(x_1,x_2,x_3):= \langle h_{2,l}(x_1,x_2), h_{2,l}(x_1,x_3) \rangle$. Checking that ($\Diamond$) holds true for $I=\{i_1\}$ and $I^C=\{j_1,j_2\}$ works completely similar to the second case. And noting that we have to condition on $X_{i_1,l}, X'_{j_2,l}$ in this case, yields:

$$\begin{aligned} \mathbb {E}[\langle h_{2,l}(X_{i_1,l},X_{j_1,l}), h_{2,l}(X_{i_1,l},X_{j_2,l}) \rangle ] \le \left| \mathbb {E}[g(X_{i_1,l}, X_{j_1,l}, X_{j_2,l})] \right| \le C \beta _{m-2l}^{\tilde{\delta }/(1+\tilde{\delta })} \end{aligned}$$

We can conclude for the quadratic term:

$$\begin{aligned}&\mathbb {E}[\Vert \sum _{n_1\le i \le n_2,\, n_3 \le j\le n_4} h_{2,l}(X_{i,l},X_{j,l})\Vert ^2 ] \nonumber \\&\quad =\underset{(i_1 \ne i_2) \,\text {or}\, (j_1 \ne j_2) \,\text {or both} }{\sum _{n_1\le i_1 \le n_2,\, n_3 \le j_1\le n_4} \sum _{n_1\le i_2\le n_2,\, n_3\le j_2\le n_4}} C \beta _{m-2l}^{\tilde{\delta }/(1+\tilde{\delta })} + n_4(n_4-n_3)M \end{aligned}$$

(14)

For a fixed m we have the following possibilities to choose:

Since we assumed $m=j_1-i_1$, there are

• at most $n_2-n_1 < n_4$ possibilities for $i_1$, so only 1 possibility for $j_1$

• at most $(n_4-n_3)$ possibilities for $j_2$, so at most m possibilities for $i_2$, since by the definition of m the value $j_2-i_2$ is smaller (or equal) than m.

So, recalling that $\delta = \tilde{\delta }/2$, we have

$$\begin{aligned}&\underset{(i_1 \ne i_2) \,\text {or}\, (j_1 \ne j_2) \,\text {or both} }{\sum _{n_1\le i_1\le n_2,\, n_3\le j_1\le n_4} \sum _{n_1\le i_2\le n_2,\, n_3\le j_2\le n_4}} C \beta _{m-2l}^{\tilde{\delta }/(1+\tilde{\delta })}\\&\quad \le C (n_4-n_3)n_4 \sum _{m=1}^{n_4} m \beta _{m-2l}^{\frac{\delta }{2+\delta }} = C (n_4-n_3) \left( \sum _{m=1}^{2l-1}m \underbrace{\beta _{m-2l}^{\frac{\delta }{2+\delta }}}_{=1} + \sum _{m=2l}^{n_4} \beta _{m-2l}^{\frac{\delta }{2+\delta }} \right) \\&\quad \le C (n_4-n_3)n_4 \left( \sum _{m=1}^{2l-1} m + \sum _{m=2l}^{n_4} (m-2l)\beta _{m-2l}^{\frac{\delta }{2+\delta }}+ \sum _{m=2l}^{n_4} 2l\beta _{m-2l}^{\frac{\delta }{2+\delta }}\right) \\&\quad \le C (n_4-n_3)n_4 \left( (2l)^2 + \sum _{m=2l}^{n_4} (m-2l)\beta _{m-2l}^{\frac{\delta }{2+\delta }}+2l \sum _{m=2l}^{n_4}(m-2l)\beta _{m-2l}^{\frac{\delta }{2+\delta }}\right) \\&\quad = C (n_4-n_3)n_4 \left( l^2 + (1+2l)\sum _{m=2l}^{n_4}(m-2l)\beta _{m-2l}^{\frac{\delta }{2+\delta }}\right) \\&\quad \le C (n_4-n_3)n_4 \left( l^2 + (2l)^2\sum _{m=2l}^{n_4} (m-2l) \beta _{m-2l}^{\frac{\delta }{2+\delta }}\right) \;\;\; \text {for}\, l>\frac{1}{2}\\&\quad \le C (n_4-n_3)n_4 \Big ( l^2 + l^2 \underbrace{\sum _{m=2l}^{n_4}(m-2l)^2 \beta _{m-2l}^{\frac{\delta }{2+\delta }}}_{<\infty } \Big ) \\&\quad \le C (n_4-n_3) n_4 l^2 \le C (n_4-n_3) n_4^{\frac{3}{2}} . \end{aligned}$$

So $(14) \le C (n_4-n_3) n_4^{\frac{3}{2}}$. If $m=j_2 -i_2$, it works very similar. Just a few comments on what changes: We get in the first case $I=\{i_1,j_1,j_2\},\; I^C = \{j_2\}$, which leads to defining the function $g(X_{i_1,l},X_{j_1,l}, X_{i_2,l}, X'_{j_2,l} ):= \langle h_{2,l}(X_{i_1,l},X_{j_1,l}), h_{2,l}(X_{i_2,l}, X'_{j_2,l} )\rangle$ and conditioning on $X_{i_1,l},X_{j_1,l}, X_{i_2,l}$. For the second case it is $I = \{i_1,i_2\},\; I^C =\{j_2\}$. We define $g(X_{i_1,l}, X'_{j_2,l}, X_{i_2,l}):= \langle h_{2,l}(X_{i_1,l}, X'_{j_2,l}), h_{2,l}(X_{i_2,l}, X'_{j_2,l}) \rangle$ and condition on $X_{i_2,l}, X'_{j_2,l}$. In the third case it is $I=\{i_1,j_1\},\; I^C=\{j_2\}$, function $g(X_{i_1,l}, X_{j_1,l}, X'_{j_2,l}):= \langle h_{2,l}(X_{i_1,l}, X_{j_1,l}), h_{2,l}(X_{i_1,l}, X'_{j_2,l}) \rangle$ and we condition on $X_{i_1,l},X_{j_1,l}$.

This proves the lemma. $\square$

Proposition 2

Under the assumptions of Theorem 1, it holds that

• (a)
  $$\begin{aligned}&E\bigg [\Big ( \max _{1 \le n_1 < n} \big \Vert \sum _{i=1}^{n_1}\sum _{j=n_1+1}^n h_2(X_i,X_j) \big \Vert \Big )^2 \bigg ]{}^{\frac{1}{2}}\le C s^2 2^{\frac{5s}{4}}\\&\quad \text {for}\, s\, \text {large enough that}\, n\le 2^s. \end{aligned}$$
• (b)
  $$\begin{aligned} \max _{1\le n_1 < n} \frac{1}{n^{3/2}} \Big \Vert \sum _{i=1}^{n_1}\sum _{j=n_1+1}^n h_2(X_i,X_j) \Big \Vert \xrightarrow {\text {a.s.}} 0 \;\;\; \text {for } n\rightarrow \infty . \end{aligned}$$

Proof

Part a) We split the expectation with the help of the triangle inequality into three parts:

$$\begin{aligned}&\mathbb {E}\bigg [\Big ( \max _{1 \le n_1< n} \Vert \sum _{i=1}^{n_1}\sum _{j=n_1+1}^n h_2(X_i,X_j) \Vert \Big )^2 \bigg ]{}^{\frac{1}{2}}\nonumber \\&\quad \le \mathbb {E}\bigg [ \Big ( \max _{1 \le n_1 < n} \sum _{i=1}^{n_1} \sum _{j=n_1+1}^n \Vert h_2(X_i,X_j)-h_2(X_{i,l},X_{j,l}) \Vert \Big )^2 \bigg ]{}^{\frac{1}{2}} \end{aligned}$$

(15)

$$\begin{aligned}&\quad + \mathbb {E}\bigg [\Big ( \max _{1 \le n_1 < n} \sum _{i=1}^{n_1} \sum _{j=n_1+1}^n \Vert h_{2,l}(X_{i,l},X_{j,l})-h_2(X_{i,l},X_{j,l}) \Vert \Big )^2 \bigg ]{}^{\frac{1}{2}} \end{aligned}$$

(16)

$$\begin{aligned}&\quad + \mathbb {E}\bigg [\Big ( \max _{1 \le n_1 < n} \Vert \sum _{i=1}^{n_1} \sum _{j=n_1+1}^n h_{2,l}(X_{i,l},X_{j,l}) \Vert \Big )^2 \bigg ]{}^{\frac{1}{2}} \end{aligned}$$

(17)

We want to use Lemmas 4–6 to bound the three terms. Because the summands of (15) are all positive, we have by Lemma 4

$$\begin{aligned} (15) \le \mathbb {E}\bigg [ \Big (\sum _{j=1}^{n} \sum _{i=1}^{j-1} \Vert h_2(X_i,X_j)-h_2(X_{i,l},X_{j,l}) \Vert \Big )^2 \bigg ]\le Cn^{5/4}. \end{aligned}$$

(16) can be bounded in the same way, using Lemma 5. For (17), the idea is to rewrite the double sum. First note that for $n_1<n_2$

$$\begin{aligned}&\sum _{i=1}^{n_2} \sum _{j=n_2+1}^n h_{2,l}(X_{i,l},X_{j,l})-\sum _{i=1}^{n_1} \sum _{j=n_1+1}^n h_{2,l}(X_{i,l},X_{j,l})\\&\quad =\sum _{i=n_1+1}^{n_2} \sum _{j=n_2+1}^n h_{2,l}(X_{i,l},X_{j,l})-\sum _{i=1}^{n_1} \sum _{j=n_1+1}^{n_2} h_{2,l}(X_{i,l},X_{j,l}). \end{aligned}$$

So we can conclude by Lemma 6 that

$$\begin{aligned}&\mathbb {E}\bigg [\Big ( \Vert \sum _{i=1}^{n_2} \sum _{j=n_2+1}^n h_{2,l}(X_{i,l},X_{j,l})-\sum _{i=1}^{n_1} \sum _{j=n_1+1}^n h_{2,l}(X_{i,l},X_{j,l}) \Vert \Big )^2\bigg ]\\&\quad \le (n_2-n_1)n^{3/2}\le (n_2-n_1)2^{3s/2} \end{aligned}$$

as $n\le 2^s$. By Theorem 1 (Móricz 1976) (which also holds in Hilbert spaces) it follows that

$$\begin{aligned} \mathbb {E}\bigg [\Big ( \max _{1 \le n_1 < n} \Vert \sum _{i=1}^{n_1} \sum _{j=n_1+1}^n h_{2,l}(X_{i,l},X_{j,l}) \Vert \Big )^2 \bigg ] \le Cs^2 2^{5s/2} \end{aligned}$$

and by taking the square root

$$\begin{aligned} (17) = \mathbb {E}\bigg [\Big ( \max _{1 \le n_1 < n} \Vert \sum _{i=1}^{n_1} \sum _{j=n_1+1}^n h_{2,l}(X_{i,l},X_{j,l}) \Vert \Big )^2 \bigg ]{}^{\frac{1}{2}}\le C s^{\frac{3}{2}}2^{\frac{5s}{4}} \le Cs^2 2^{\frac{5s}{4}}. \end{aligned}$$

This yields all together

$$\begin{aligned} \mathbb {E}\bigg [\Big ( \max _{1 \le n_1 < n} \Vert \sum _{i=1}^{n_1}\sum _{j=n_1+1}^n h_2(X_i,X_j) \Vert \Big )^2 \bigg ]{}^{\frac{1}{2}}\le Cs^2 2^{\frac{5s}{4}} \end{aligned}$$

Part b) Recall that s is chosen such that $n\le 2^s$ and thus $n^{\frac{3}{2}} \le 2^{\frac{3s}{2}}$. To prove almost sure convergence, it is enough to prove that for any $\epsilon >0$

$$\begin{aligned} \sum _{s=1}^{\infty }\mathbb {P}\Big ( 2^{-\frac{3s}{2}} \max _{1\le n_1<n} \big \Vert \sum _{s=1}^{n_1}\sum _{j=n_1+1}^n h_2(X_i,X_j) \big \Vert > \epsilon \Big ) < \infty \end{aligned}$$

We do this by using Markov’s inequality and our result from a):

$$\begin{aligned}&\sum _{s=1}^{\infty }\mathbb {P}\Big ( 2^{-\frac{3s}{2}} \max _{1\le n_1<n} \Vert \sum _{s=1}^{n_1}\sum _{j=n_1+1}^n h_2(X_i,X_j) \Vert > \epsilon \Big ) \\&\quad \le \frac{1}{\epsilon ^2}\sum _{s=1}^{\infty } \mathbb {E}\bigg [\Big (2^{-\frac{3s}{2}}\max _{1\le n_1<n} \Vert \sum _{s=1}^{n_1}\sum _{j=n_1+1}^n h_2(X_i,X_j) \Vert \Big )^2 \bigg ]\\&\quad = \frac{1}{\epsilon ^2}\sum _{s=1}^{\infty } 2^{-3s} \mathbb {E}\bigg [\Big (\max _{1\le n_1<n} \Vert \sum _{s=1}^{n_1}\sum _{j=n_1+1}^n h_2(X_i,X_j) \Vert \Big )^2 \bigg ]\\&\quad \le \frac{1}{\epsilon ^2} \sum _{s=1}^{\infty } 2^{-3s}(Cs^2 2^{\frac{5s}{4}})^2 \;\;\; \text {by part a)} \\&\quad = \frac{C}{\epsilon ^2} \sum _{s=1}^{\infty } s^4 2^{-\frac{s}{2}} < \infty \end{aligned}$$

By the Borel–Cantelli lemma follows the almost sure convergence

$$\begin{aligned} \max _{1\le n_1 < n} \frac{1}{n^{3/2}} \Vert \sum _{i=1}^{n_1}\sum _{j=n_1+1}^n h_2(X_i,X_j) \Vert \xrightarrow {\text {a.s.}} 0 \;\;\; \text {for } n\rightarrow \infty . \end{aligned}$$

$\square$

4.3 Results under alternative

Recall our model under the alternative:

$(X_n, Z_n)_{n\in \mathbb {Z}}$ is a stationary, $H\otimes H$-valued sequence and we observe $Y_1,\ldots ,Y_n$ with

$$\begin{aligned} Y_i={\left\{ \begin{array}{ll}X_i \ \ {} &{}\text {for}\ i\le \lfloor n\lambda ^\star \rfloor = k^\star \\ Z_i \ \ {} &{}\text {for}\ i> \lfloor n\lambda ^\star \rfloor = k^\star \end{array}\right. }, \end{aligned}$$

so $\lambda ^\star \in (0,1)$ is the proportion of observations after which the change happens. We assume that the process $(X_i,Z_i)_{i\in {\mathbb {Z}}}$ is stationary and P-NED on an absolutely regular sequences $(\zeta _n)_{n\in {\mathbb {Z}}}$.

Let $h: H \times H \rightarrow H$ be an antisymmetric kernel and assume that $\mathbb {E}[h(X_0,\tilde{Z}_0)] \ne 0$, where $\tilde{Z}_0$ is an independent copy of $Z_0$ and independent of $X_0$. Since $X_0$ and $\tilde{Z}_0$ are not identically distributed, Hoeffding’s decomposition of h equals

$$\begin{aligned} h(x,y) = h_1^\star (x)-h_1(y)+h_2^\star (x,y) \end{aligned}$$

where

$$\begin{aligned} h_1(x)&=\mathbb {E}[h(x,X_0)]\; , \;\;\;\;\; h_1^\star (x)=\mathbb {E}[h(x,Z_0)] \end{aligned}$$

(18)

$$\begin{aligned} h_2^\star (x,y)&= h(x,y)-h_1^\star (x)+h_1(y) \end{aligned}$$

(19)

So it holds for the test statistic $U_{n,k^\star }(Y):= \sum _{i=1}^{k^\star }\sum _{j=k^\star +1}^n h(Y_i,Y_j)$ that

$$\begin{aligned} U_{n,k^\star }(Y)&= \sum _{i=1}^{k^\star }\sum _{j=k^\star +1}^n h(X_i,Z_j) \\&= \sum _{i=1}^{k^\star }\sum _{j=k^\star +1}^n\big ( h_1^\star (X_i)-h_1(Z_j) +h_2^\star (X_i,Z_j)\big ) \\&= (n-k^\star ) \sum _{i=1}^{k^\star } h_1^\star (X_i) - k^\star \sum _{j=k^\star +1}^n h_1(Z_j) + \sum _{i=1}^{k^\star }\sum _{j=k^\star +1}^n h_2^\star (X_i,Z_j). \end{aligned}$$

Lemma 7

Let the Assumption of Theorem 2 hold for $(X_i,Z_i)_{i\in {\mathbb {Z}}}$ and let $h_2^\star$ as defined in (19). Then it holds that

$$\begin{aligned} \frac{1}{n^{3/2}}\Vert \sum _{i=1}^{k^\star } \sum _{j=k^\star +1}^n h_2^\star (X_i,Z_j)+\mathbb {E}[h(X_0,\tilde{Z}_0) \Vert \xrightarrow {\text {a.s.}} 0 \;\;\; \text {for } n\rightarrow \infty , \end{aligned}$$

where $\tilde{Z}_0$ is an independent copy of $Z_0$ and independent of $X_0$.

Proof

Notice that $h_2^\star (x,z)+ \mathbb {E}[h(X_0,\tilde{Z}_0)$ is degenerated since $\mathbb {E}[h_1^\star (X_0)]= \mathbb {E}[h(X_0,\tilde{Z}_0)]$ and

$$\begin{aligned}{} & {} E\big [ h_2^\star (X_0,z)+ \mathbb {E}[h(X_0,\tilde{Z}_0)] \big ]\\{} & {} \quad =E\big [ h(X_0,y)-h_1^\star (X_0)-h_1(y)+\mathbb {E}[h(X_0,\tilde{Z}_0)] \big ]\\{} & {} \quad =h_1(y)-\mathbb {E}[h(X_0,\tilde{Z}_0)]-h_1(y)+\mathbb {E}[h(X_0,\tilde{Z}_0)]=0 \end{aligned}$$

and similarly $\mathbb {E}[h_2^\star (x,\tilde{Z}_0)+ \mathbb {E}[h(X_0,\tilde{Z}_0)] = 0$. So we can prove the lemma along the same arguments as under the null hypothesis. $\square$

Lemma 8

Under the assumption of Theorem 2 it holds that

$$\begin{aligned} \Big ( \frac{1}{\sqrt{n}} \sum _{i=1}^{\left\lfloor {n\lambda }\right\rfloor }\big ( h_1^\star (X_i)-\mathbb {E}[h(X_0,\tilde{Z}_0)]\big ) \Big )_{\lambda \in [0,1]} \Rightarrow (W_1(\lambda ))_{\lambda \in [0,1]} \end{aligned}$$

and

$$\begin{aligned} \Big ( \frac{1}{\sqrt{n}} \sum _{i=1}^{\left\lfloor {n\lambda }\right\rfloor }\big ( h_1(Z_i)+\mathbb {E}[h(X_0,\tilde{Z}_0)]\big )\Big )_{\lambda \in [0,1]} \Rightarrow (W_2(\lambda ))_{\lambda \in [0,1]} \end{aligned}$$

where $(W_1(\lambda ))_{\lambda \in [0,1]}$, $(W_2(\lambda ))_{\lambda \in [0,1]}$ are Brownian motions with covariance operator as defined in Theorem 1.

Proof

The proof follows the steps of Theorem 1. So, we have to check the assumptions of Theorem 1 (Sharipov et al. 2016). We will do this for $h^\star _1(X_i)$, for $h_1(Z_i)$ everything holds similarly. First note that $\mathbb {E}[h_1^\star (X_0)]=\mathbb {E}[h(X_0,\tilde{Z}_0)]$.

Assumption 1: $(h_1^\star (X_n))_{n \in {\mathbb {Z}}}$ is $L_1$-NED.

Along the lines of the proof of Lemma 2 we can show that $(h_1^\star (X_n))_{n\in {\mathbb {Z}}}$ is $L_2$-NED with approximating constants $a_{k,2}= {\mathcal {O}}( k^{-4\frac{3+\delta }{\delta }})$. By Jensen’s inequality it follows that $(h_1^\star (X_n))_{n\in {\mathbb {Z}}}$ is $L_1$-NED with approximating constants $a_{k,1}=a_{k,2}$.

Assumption 2: Existing $(4+\delta )$-moments.

Recall that $h_1^\star (x)=\mathbb {E}[h(x,\tilde{Z}_0)]$, so by Jensen inequality

$$\begin{aligned} E\left[ |h_1^\star (X_i)|^{4+\delta }\right] \le E[|h(X_1,\tilde{Z}_1)|^{4+\delta }]<\infty \end{aligned}$$

Assumption 3: $\sum _{m=1}^{\infty } m^2 a_{m,1}^{\frac{\delta }{3+\delta }} \le \infty$ follows similar as in Theorem 1.

Assumption 4: $\sum _{m=1}^{\infty } m^2 \beta _m^{\frac{\delta }{4+\delta }} < \infty$ is assumed in Theorem 2.

$\square$

Corollary 1

Under assumptions of Theorem 1, it holds that

$$\begin{aligned} \frac{1}{n^{3/2}} \sum _{i=1}^{k^\star }\sum _{j=k^\star +1}^n \big (h_1^\star (X_i)-h_1(Z_j)-2\mathbb {E}[h(X_0,\tilde{Z}_0)]\big ) \end{aligned}$$

is stochastically bounded.

Proof

This follows from Lemma 8 above:

$$\begin{aligned}&\bigg |\frac{1}{n^{3/2}} \sum _{i=1}^{k^\star }\sum _{j=k^\star +1}^n\big ( h_1^\star (X_i)-h_1(Z_j)-2\mathbb {E}[h(X_0,\tilde{Z}_0)]\big )\bigg | \\&\quad \le \bigg |\frac{1}{n^{1/2}} \sum _{i=1}^{k^\star } h_1^\star (X_i)-\mathbb {E}[h(X_0,\tilde{Z}_0)]\bigg | +\bigg | \frac{1}{n^{1/2}} \sum _{j=k^\star +1}^n h_1(Z_j)+\mathbb {E}[h(X_0,\tilde{Z}_0)] \bigg | \end{aligned}$$

Both summands converge weakly to a Gaussian limit and are stochastically bounded. $\square$

4.4 Dependent wild bootstrap

Proposition 3

Let $(\varepsilon _i)_{i\le n, n \in {\mathbb {N}}}$ be a triangular scheme of random multiplier independent from $(X_i)_{i \in {\mathbb {Z}}}$, such that the moment condition $\mathbb {E}[| \varepsilon _i | ^2] < \infty$ holds.

Then under the Assumptions of Theorem 1, it holds that

$$\begin{aligned} \max _{1\le k < n} \frac{1}{n^{3/2}} \big \Vert \sum _{i=1}^{k}\sum _{j=k+1}^n h_2(X_i,X_j)(\varepsilon _i+\varepsilon _j) \big \Vert \xrightarrow {\text {a.s.}} 0 \;\;\; \text {for } n\rightarrow \infty \end{aligned}$$

Proof

The statement follows along the line of the proofs of the Lemmas 5 to  6 and Proposition 2. For this, note that by the independence of $(\varepsilon _i)_{i\le n, n \in {\mathbb {N}}}$ and $(X_i)_{i \in {\mathbb {Z}}}$ and by Lemma 3

$$\begin{aligned}&\mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})(\varepsilon _{i}+\varepsilon _{i+k+2l})-h_2(X_{i,l}, X_{i+k+2l,l}(\varepsilon _{i}+\varepsilon _{i+k+2l}))\Vert ^2]^{\frac{1}{2}}\\&\quad = \mathbb {E}[\Vert h_2(X_i,X_{i+k+2l})-h_2(X_{i,l},X_{i+k+2l,l}\Vert ^2]^{\frac{1}{2}} \cdot \mathbb {E}[(\varepsilon _{i}+\varepsilon _{i+k+2l})^2]^{\frac{1}{2}} \\&\quad \le C(\sqrt{\epsilon }+\beta _k^{\frac{\delta }{2(2+\delta )}} +(a_l\Phi (\epsilon ))^{\frac{\delta }{2(2+\delta )}} ) \end{aligned}$$

From this, we can conclude that for any $n_1< n_2< n_3 < n_4$ and $l= \left\lfloor {n_4^{\frac{3}{16}}}\right\rfloor$:

$$\begin{aligned} \mathbb {E}\bigg [\Big (\sum _{n_1 \le i \le n_2}\sum _{n_3 \le j \le n_4} \Vert h_2(X_i,X_j)-h_2(X_{i,l},X_{j,l})(\varepsilon _{i} +\varepsilon _{j})\Vert \Big )^2 \bigg ]{}^{\frac{1}{2}}\le C(n_4-n_3)n_4^{\frac{1}{4}} \end{aligned}$$

as in Lemma 4. Similary, we obtain (making use of the independence of $(\varepsilon _i)_{i\le n}$ and $(X_i)_{i \in {\mathbb {Z}}}$ again)

$$\begin{aligned}&\mathbb {E}[\Vert h_{2,l}(X_{i,l},X_{j,l})-h_2(X_{i,l},X_{j,l})(\varepsilon _i+\varepsilon _j)\Vert ^2]\\&\quad =\mathbb {E}[\Vert h_{2,l}(X_{i,l},X_{j,l})-h_2(X_{i,l},X_{j,l}) \Vert ^2] \mathbb {E}[(\varepsilon _i+\varepsilon _j) ^2] \le C\left( \sqrt{\epsilon } + (a_l\Phi (\epsilon )){}^{\frac{\delta }{2(2+\delta )}}\right) \end{aligned}$$

and along the lines of the proof of Lemma 5 for any $n_1<n_2<n_3<n_4$ and $l= \left\lfloor {n_4^{\frac{3}{16}}}\right\rfloor$:

$$\begin{aligned} \mathbb {E}\bigg [\Big ( \sum _{n_1\le i \le n_2,\, n_3\le j\le n_4} \Vert h_{2,l}(X_{i,l},X_{j,l})-h_2(X_{i,l},X_{j,l}) (\varepsilon _i+\varepsilon _j)\Vert \Big )^2 \bigg ] {}^{\frac{1}{2}}\!\! \le \! C (n_4-n_3) n_4^{\frac{1}{4}}. \end{aligned}$$

With the same type of argument, we also obtain the analogous result to Lemma 6:

$$\begin{aligned} \mathbb {E}\bigg [\Big ( \Vert \sum _{n_1\le i \le n_2,\, n_3\le j\le n_4} h_{2,l}(X_{i,l},X_{j,l})(\varepsilon _i+\varepsilon _j)\Vert \Big )^2 \bigg ] \le C (n_4-n_3)n_4^{\frac{3}{2}} \end{aligned}$$

and then we can proceed as in the proof of Proposition 2. $\square$

Lemma 9

Under the assumptions of Theorem 3, for any $t_0=0<t_1<t_2,\ldots ,t_k=1$ and any $a_1,\ldots ,a_k\in H$

$$\begin{aligned}{} & {} {\text {Var}}\bigg [\frac{1}{\sqrt{n}}\sum _{j=1}^k\sum _{i=\lfloor nt_{j-1}\rfloor +1}^{\lfloor nt_j\rfloor }\langle a_j,h_1(X_i)\varepsilon _i\rangle \Big | X_1,\ldots ,X_n\bigg ]\xrightarrow {{\mathcal {P}}}\\{} & {} {\text {Var}}\bigg [\sum _{j=1}^k\langle a_j,W(t_j)-W(t_{j-1})\rangle \bigg ] \end{aligned}$$

Proof

To simplify the notation, we introduce a triangular scheme $V_{i,n} =\langle a_j,h_1(X_i)\rangle$ for $i=\lfloor nt_{j-1}\rfloor +1,\ldots ,i=\lfloor nt_{j}\rfloor$. By our assumptions, ${\text {Cov}}(\varepsilon _i,\varepsilon _j)=w(|i-j|/q_n)$, so we obtain for the variance condition on $X_1,\ldots ,X_n$:

$$\begin{aligned}&{\text {Var}}\bigg [\frac{1}{\sqrt{n}}\sum _{j=1}^k\sum _{i=\lfloor nt_{j-1}\rfloor +1}^{\lfloor nt_j\rfloor }\langle a_j,h_1(X_i)\varepsilon _i\rangle \Big | X_1,\ldots ,X_n\bigg ]\\&\quad =\sum _{i=1}^n\sum _{l=1}^nV_{i,n}V_{l,n}{\text {Cov}}(\varepsilon _i,\varepsilon _l) =\sum _{i=1}^n\sum _{l=1}^nV_{i,n}V_{l,n}w(|i-l|/q_n). \end{aligned}$$

This is the kernel estimator for the variance, which is consistent even for heteroscedastic time series under the assumptions of Jong and Davidson (2000). The $L_2$-NED follows by Lemma 2. Note that the mixing coefficients for absolute regularity are larger than the strong mixing coefficients used by Jong and Davidson (2000), so their mixing assumption follows directly from ours. $\square$

Proposition 4

Under the assumptions of Theorem 3, we have the weak convergence (in the space $D_{H^2}[0,1]$)

$$\begin{aligned} \bigg (\frac{1}{\sqrt{n}}\sum _{i=1}^{[nt]}(h_1(X_i),h_1(X_i)\varepsilon _i)\bigg )_{t\in [0,1]}\Rightarrow (W(t), W^\star (t))_{t\in [0,1]} \end{aligned}$$

where W and $W^\star$ are independent Brownian motions with covariance operator as in Theorem 1.

Proof

We have to prove finite-dimensional convergence and tightness. As the tightness for the first component was already established in the proof of Theorem 1 of Sharipov et al. (2016), we only have to deal with the second component. The tightness of the partial sum process of $h_1(X_i)\varepsilon _i$, $i\in \mathbb {N}$, can be shown along the lines of the proof of the same theorem: For this note that by the independence of $(\varepsilon _i)_{i\le n}$ and $X_1,\ldots ,X_n$

$$\begin{aligned}{} & {} \left| E\left[ \langle h_1(X_i)\varepsilon _i,h_1(X_j)\varepsilon _j\rangle \langle h_1(X_k)\varepsilon _k,h_1(X_l)\varepsilon _l\rangle \right] \right| \\{} & {} \quad =\left| E\left[ \langle h_1(X_i),h_1(X_j)\rangle \langle h_1(X_k),h_1(X_l)\rangle \right] E[\varepsilon _i\varepsilon _j\varepsilon _k\varepsilon _l]\right| \\{} & {} \quad \le 3\left| E\left[ \langle h_1(X_i),h_1(X_j)\rangle \langle h_1(X_k),h_1(X_l)\rangle \right] \right| , \end{aligned}$$

the rest follows as in Lemma 2.24 of Borovkova et al. (2001) and in the proof of Theorem 1 of Sharipov et al. (2016).

For the finite dimensional convergence, we will show the weak convergence of the second component conditional on $h_1(X_i)\varepsilon _i$, $i\in \mathbb {N}$, because the weak convergence of the first component is already established in Proposition 1. By the continuity of the limit process, it is sufficient to study the distribution for $t_1,\ldots ,t_k\in {\mathbb {Q}}\cap [0,1]$ and by the Cramér-Wold-device and the separability of H, it is enough to show the convergence of the condition distribution of $\frac{1}{\sqrt{n}}\sum _{j=1}^k\sum _{i=[nt_{j-1}]+1}^{[nt_j]}\langle a_j,h_1(X_i)\varepsilon _i\rangle$ for $a_1,\ldots ,a_k$ from a countable subset of H. Conditional on $X_1,\ldots ,X_n$, the distribution of $\frac{1}{\sqrt{n}}\sum _{j=1}^k\sum _{i=[nt_{j-1}]+1}^{[nt_j]}\langle a_j,h_1(X_i)\varepsilon _i\rangle$ is Gaussian with expectation 0 and variance converging to the right limit in probability by Lemma 9.

Using a well-known characterization of convergence in probability, for every subseries there is another subseries such that this convergence holds almost surely. So we can construct a subseries that the almost sure convergence holds for all k, $t_1,\ldots ,t_k\in {\mathbb {Q}}\cap [0,1]$ and all $a_1,\ldots ,a_k$ from the countable subset of H, so we can find a subseries such that the convergence of the finite-dimensional distributions holds almost surely. Thus, the finite-dimensional convergence of the conditional distribution holds in probability and the statement of the proposition is proved. $\square$

5 Proof of main results

Proof of Theorem 1

We will bound the maximum from above by the sum of the degenerate and the linear part, using Hoeffding’s decomposition, as shown in Lemma 1:

$$\begin{aligned}&\max _{1\le k<n} \frac{1}{n^{3/2}} \Vert U_{n,k} \Vert = \max _{1\le k<n} \frac{1}{n^{3/2}} \Vert n \sum _{i=1}^k(h_1(X_i)-\overline{h_1(X)})+\sum _{i=1}^k\sum _{j=k+1}^n h_2(X_i,X_j) \Vert \\&\le \max _{1\le k<n} \frac{1}{n^{3/2}} \Vert n \sum _{i=1}^k(h_1(X_i)-\overline{h_1(X)})\Vert + \max _{1\le k<n} \frac{1}{n^{3/2}} \Vert \sum _{i=1}^k\sum _{j=k+1}^n h_2(X_i,X_j) \Vert \end{aligned}$$

by triangle inequality. For the degenerate part, we can use the convergence to 0 from Proposition 2:

$$\begin{aligned} \max _{1\le k<n} \frac{1}{n^{3/2}} \Vert \sum _{i=1}^k\sum _{j=k+1}^n h_2(X_i,X_j) \Vert \xrightarrow {P} 0 \end{aligned}$$

since convergence in probability follows from almost sure convergence.

Now observe that we can write the linear part as

$$\begin{aligned}&\max _{1\le k<n} \frac{1}{n^{3/2}} \Vert n \sum _{i=1}^k(h_1(X_i)-\overline{h_1(X)})\Vert = \max _{\lambda \in [0,1]} \frac{1}{n^{3/2}} \Vert n \sum _{i=1}^{\left\lfloor {n\lambda }\right\rfloor }(h_1(X_i)-\overline{h_1(X)})\Vert \\&\quad = \max _{\lambda \in [0,1]} \frac{1}{n^{3/2}} \Vert n \sum _{i=1}^{\left\lfloor {n\lambda }\right\rfloor }h_1(X_i) -n \left\lfloor {n\lambda }\right\rfloor \frac{1}{n}\sum _{j=1}^n h_1(X_j) \Vert \\&\quad = \max _{\lambda \in [0,1]} \Vert \frac{1}{\sqrt{n}} \sum _{i=1}^{\left\lfloor {n\lambda }\right\rfloor } h_1(X_i) - \frac{\left\lfloor {n\lambda }\right\rfloor }{n^{3/2}} \sum _{j=1}^n h_1(X_j) \Vert \\&\quad \approx \sup _{\lambda \in [0,1]} \Vert \underbrace{\frac{1}{\sqrt{n}} \sum _{i=1}^{\left\lfloor {n\lambda }\right\rfloor } h_1(X_i)}_{=: x(\lambda )} -\frac{\lambda }{\sqrt{n}} \sum _{j=1}^n h_1(X_i) \Vert \;\;\; \text {for}\, n\, \text {large enough}\\&\quad = \sup _{\lambda \in [0,1]} \Vert x(\lambda )- \lambda x(1) \Vert \end{aligned}$$

We know by Proposition 1 that

$$\begin{aligned} (x(\lambda ))_{\lambda \in [0,1]} \xrightarrow {{\mathcal {D}}} (W(\lambda ))_{\lambda \in [0,1]} \end{aligned}$$

By the continuous mapping theorem it follows that $(x(\lambda )-\lambda x(1))_{\lambda \in [0,1]} \xrightarrow {{\mathcal {D}}} (W(\lambda )-\lambda W(1))_{\lambda \in [0,1]}$. And thus we can finally conclude that

$$\begin{aligned} \max _{1\le k<n} \frac{1}{n^{3/2}} \Vert U_{n,k} \Vert \xrightarrow {{\mathcal {D}}} \sup _{\lambda \in [0,1]} \Vert W(\lambda )-\lambda W(1) \Vert . \end{aligned}$$

$\square$

Proof of Theorem 2

We can bound the maximum from below using the reverse triangle inequality and then make use of previous results:

$$\begin{aligned}&\max _{1\le k\le n} \Vert \frac{1}{n^{3/2}} U_{n,k}(Y) \Vert \ge \Vert \frac{1}{n^{3/2}} U_{n,k^\star }(Y) \Vert \;\;\;\;\;\;\text {where}\, k^\star =\left\lfloor {n\lambda ^\star }\right\rfloor \\&\quad = \Vert \frac{1}{n^{3/2}} \big ( U_{n,k^\star }(Y) -k^\star (n-k^\star ) \mathbb {E}[h(X_0,\tilde{Z}_0)] \big ) + \frac{k^\star (n-k^\star )}{n^{3/2}} \mathbb {E}[h(X_0,\tilde{Z}_0)]\Vert \\&\quad \ge \Big \vert \Vert \frac{1}{n^{3/2}} ( U_{n,k^\star }(Y) -k^\star (n-k^\star ) \mathbb {E}[h(X_0,\tilde{Z}_0)] )\Vert - \Vert \frac{k^\star (n-k^\star )}{n^{3/2}} \mathbb {E}[h(X_0,\tilde{Z}_0)]\Vert \Big \vert \\&\quad \text {by using the reverse triangle inequality} \\&\quad = \Big \vert \Vert \frac{1}{n^{3/2}} \sum _{i=1}^{k^\star } \sum _{j=k^\star +1}^n \big (h_1^\star (X_i)-h_1(Z_j) + h _2(X_i,Z_j) - \mathbb {E}[h_2(X_i,Z_j)]\big ) \Vert \\&\quad - \Vert \frac{k^\star (n-k^\star )}{n^{3/2}} \mathbb {E}[h(X_0,\tilde{Z}_0)]\Vert \Big \vert \\&\quad \ge \Vert \frac{k^\star (n-k^\star )}{n^{3/2}} \mathbb {E}[h(X_0,\tilde{Z}_0)]\Vert \\&\quad - \Vert \frac{1}{n^{3/2}} \sum _{i=1}^{k^\star } \sum _{j=k^\star +1}^n\big ( h_1^\star (X_i)-h_1(Z_j) -2 \mathbb {E}[h(X_0,\tilde{Z}_0)]\big ) \Vert \\&\quad - \Vert \frac{1}{n^{3/2}} \sum _{i=1}^{k^\star } \sum _{j=k^\star +1}^n h _2(X_i,Z_j) +\mathbb {E}[h(X_0,\tilde{Z}_0)] \Vert \end{aligned}$$

by using the reverse triangle inequality again. By Corollary 1 we know that

$$\begin{aligned} \Vert \frac{1}{n^{3/2}} \sum _{i=1}^{k^\star } \sum _{j=k^\star +1}^n h_1^\star (X_i)-h_1(Z_j) - 2\mathbb {E}[h_1^\star (X_i)-h_1(Z_j)] \Vert \end{aligned}$$

is stochastically bounded. And by Lemma 7 it holds that

$$\begin{aligned} \Vert \frac{1}{n^{3/2}} \sum _{i=1}^{k^\star } \sum _{j=k^\star +1}^n h _2(X_i,Z_j) + \mathbb {E}[h_2(X_i,Z_j)] \Vert \xrightarrow {n \rightarrow \infty } 0 \end{aligned}$$

But since $\mathbb {E}[h(X_0,\tilde{Z}_0)] \ne 0$ the last part diverges to infinity:

$$\begin{aligned} \Vert \frac{1}{n^{3/2}} k^\star (n-k^\star ) \mathbb {E}[h(X_0,\tilde{Z}_0)] \Vert \approx \Vert \sqrt{n} \lambda ^\star (1-\lambda ^\star ) \mathbb {E}[h(X_0,\tilde{Z}_0)] \Vert \xrightarrow {n \rightarrow \infty } \infty , \end{aligned}$$

and thus $\max \limits _{1\le k\le n} \Vert \frac{1}{n^{3/2}} U_{n,k}(Y) \Vert \xrightarrow {n \rightarrow \infty } \infty$. $\square$

Proof of Theorem 3

Because the convergence in distribution of $\max \limits _{1\le k<n} \frac{1}{n^{3/2}}|| U_{n,k}||$ has already been established in Theorem 1, it is enough to prove the convergence in distribution of $\max \limits _{1\le k<n} \frac{1}{n^{3/2}}|| U_{n,k}^\star ||$ conditional on $X_1,\ldots ,X_n$. For this, we apply the Hoeffding decomposition:

$$\begin{aligned}{} & {} \frac{1}{n^{3/2}}U_{n,k}^\star =\frac{1}{n^{3/2}}\sum _{i=1}^k\sum _{j=k+1}^n h(X_i,X_j)(\varepsilon _i+\varepsilon _j)\\{} & {} \quad =\frac{1}{n^{3/2}}\sum _{i=1}^k\sum _{j=k+1}^n (h_1(X_i)-h_1(X_j)(\varepsilon _i+\varepsilon _j)+\frac{1}{n^{3/2}}\sum _{i=1}^k\sum _{j=k+1}^n h_2(X_i,X_j)(\varepsilon _i+\varepsilon _j) \end{aligned}$$

The second sum converges to 0 by Proposition 3. The first summand can be split into three parts with a short calculation:

$$\begin{aligned}{} & {} \frac{1}{n^{3/2}}\sum _{i=1}^k\sum _{j=k+1}^n (h_1(X_i)-h_1(X_j))(\varepsilon _i+\varepsilon _j)=\frac{1}{\sqrt{n}} \left( \sum _{i=1}^kh_1(X_i)\varepsilon _i+\frac{k}{n}\sum _{i=1}^nh_1(X_i)\varepsilon _i\right) \\{} & {} \quad +\frac{1}{n^{3/2}}\sum _{i=1}^kh_1(X_i)\sum _{j=1}^n\varepsilon _j +\frac{1}{n^{3/2}}\sum _{i=1}^nh_1(X_i)\sum _{j=1}^k\varepsilon _j \end{aligned}$$

By Proposition 4 and the continuous mapping theorem, we have the weak convergence

$$\begin{aligned} \max _{1\le k<n} \left\| \frac{1}{\sqrt{n}}\left( \sum _{i=1}^kh_1(X_i)\varepsilon _i +\frac{k}{n}\sum _{i=1}^nh_1(X_i)\varepsilon _i\right) \right\| \Rightarrow \sup _{\lambda \in [0,1]}\left\| W^\star (\lambda )-\lambda W^\star (1)\right\| \end{aligned}$$

conditional on $X_1,\ldots ,X_n$. For the second part, note that

$$\begin{aligned} {\text {Var}}\left( \frac{1}{n}\sum _{i=1}^n \varepsilon _i\right)= & {} \frac{1}{n^2}\sum _{i,j=1}^nw(|i-j|/q_n)\\\le & {} \frac{1}{n}\sum _{i=-n}^n |w(i/q_n)| \approx \frac{q_n}{n}\int _{-\infty }^\infty |w(x)|dx\rightarrow 0 \end{aligned}$$

for $n\rightarrow \infty$ by our assumptions on $q_n$. So $\frac{1}{n}\sum _{i=1}^n \varepsilon _i\rightarrow 0$ in probability and

$$\begin{aligned} \max _{k=1,\ldots ,n}\Big |\frac{1}{n^{3/2}}\sum _{i=1}^kh_1(X_i)\sum _{j=1}^n\varepsilon _j \Big |=\max _{k=1,\ldots ,n}\Big |\frac{1}{n^{1/2}}\sum _{i=1}^kh_1(X_i)\Big | \Big |\frac{1}{n}\sum _{j=1}^n\varepsilon _j\Big |\rightarrow 0 \end{aligned}$$

for $n\rightarrow \infty$ in probability using the fact that $\frac{1}{n^{1/2}}\sum _{i=1}^kh_1(X_i)$ is stochastically bounded, see Proposition 1. For the third part, we consider increments of the partial sum and bound the variance of increments similar as above by

$$\begin{aligned} {\text {Var}}\left( \sum _{i=l+1}^k \varepsilon _i\right) \le Ckq_n. \end{aligned}$$

Because the $\varepsilon _i$ are Gaussian, it follows that

$$\begin{aligned} \mathbb {E}\left[ \Big (\sum _{i=l+1}^k\varepsilon _i\Big )^4\right] \le C(kq_n)^2. \end{aligned}$$

By Theorem 1 of Móricz (1976), we have

$$\begin{aligned} \mathbb {E}\left[ \max _{k=1,\ldots ,n}\Big (\sum _{i=1}^k\varepsilon _i\Big )^4\right] \le C(nq_n)^2. \end{aligned}$$

and $\frac{1}{n}\max _{k=1,\ldots ,n}|\sum _{i=1}^k\varepsilon _i|\rightarrow 0$ in probability because $q_n/n\rightarrow 0$. So

$$\begin{aligned} \max _{k=1,\ldots ,n}\Big |\frac{1}{n^{3/2}}\sum _{i=1}^nh_1(X_i)\sum _{j=1}^k\varepsilon _j\Big | =\Big |\frac{1}{n^{1/2}}\sum _{i=1}^nh_1(X_i)\Big |\max _{k=1,\ldots ,n}\Big |\frac{1}{n} \sum _{j=1}^k\varepsilon _j\Big |\xrightarrow {n\rightarrow \infty }0 \end{aligned}$$

which completes the proof. $\square$

Appendix

In the following, we give some more information on the simulation results. To demonstrate that our test can also be applied when the dimension of the observations is larger than the sample size, we have simulated the Gaussian autoregressive process as before, but with sample size $n=150$ on a grid of $d=350$. The size of the CUSUM test and the Wilcoxon-type test (based on spatial signs) is given in Table 5. As before, we used $S=3000$ simulation runs with $m=1000$ bootstrap repetitions.

In Table 6, we give the numerical values used for Fig. 3 as well as some additional results on the power of the tests. For Scenario 1 (Gaussian observations with uniform jump), we study a jump in the beginning of our time series after $k^\star =30$ observations (total sample size $n=200$). For such an early change, we see a drastic decline in power for both statistics. Spatial sign nevertheless keeps a small advantage over CUSUM in this scenario.

Scenario 5 is the same as Scenario 1, but with sample size $n=150$, $k^\star =75$ and grid size $d=350$. We see a reduction of power for both statistics compared to Scenario 1. Nevertheless, we can still observe that the Wilcoxon-type test provides a greater empirical power than CUSUM.

Table 6 Empirical power of CUSUM test (CUS.) and spatial sign based test (Sp.S.) for different significance level $\alpha$ and different time of change $k^\star$, Scenario 1 to 4 (Sc1–Sc4 ) with sample size $n=200$, Scenario 5 (Sc5) with $n=150$