1 Introduction

When we wish to reliably evaluate the causal effects of a treatment variable on an outcome variable, one of the fundamental principles in observational and experimental studies is that

“if one is interested in the total (direct and indirect) effect of the exposure on the outcome, then intermediate variables should not be adjusted for as they are part of the effect of interest and adjusting for them would bias this effect.” (Zeegers et al. 2016)

“In short, conditioning on post-treatment variables can ruin experiments; we should not do it. ” (Montgomery et al. 2018)

These statements provide clear instructions, but some researchers and practitioners have provided an alternative view that intermediate variables (post-treatment variables) can reveal several causal quantities (Pearl 2001, 2009) and elucidate the data-generating process in mediation analysis (Cox 1960; Imai et al. 2011; MacKinnon 2008). In the context of nonparametric identification problems of causal effects, the front-door criterion (Pearl 2009) and its extensions (Kuroki and Miyakawa 1999a; Tian and Pearl 2002) are powerful tools for resolving this contradiction from the viewpoint of the multiple stage evaluation method. Remarkably, the front-door criterion, which focuses on intermediate variables, enables us to identify causal effects even when a set of covariates is insufficient to derive reliable estimates of causal effects.

When cause–effect relationships between random variables can be represented by a linear structural equation model (a linear SEM), the total effect is one of the important measures for evaluating causal effects. Intuitively, the total effect can be interpreted as the change in the expected value of the outcome variable when the treatment variable is changed by one unit via external intervention. To evaluate the total effect, statistical researchers in the field of linear SEMs have provided various identification conditions and estimation methods (e.g., Brito 2004; Chan and Kuroki 2010; Chen 2017; Henckel et al. 2019; Kuroki and Pearl 2014; Maathuis and Colombo 2015; Nandy et al. 2017; Pearl 2009; Perković 2018; Tian 2004).

In the framework of Gaussian linear SEMs, when the ordinary least squares (OLS) method is utilized to estimate total effects in the situation where a set of random variables that satisfies the front-door criterion is observed, Kuroki (2000) formulated the exact variance of the estimated total effect. Kuroki and Cai (2004) compared the asymptotic variance of the estimated total effect under several graphical identification conditions. In addition, Cox (1960) and Kuroki and Hayashi (2014, 2016) showed that if a treatment variable is linearly associated with an outcome variable through an intermediate variable then the regression coefficient of the treatment variable on the outcome variable in a single linear regression model can be estimated more accurately by a joint linear regression model based on the intermediate variable. Assuming that a univariate intermediate variable satisfies the front-door criterion, Hui and Zhongguo (2008) and Ramsahai (2012) compared the front-door, back-door (Pearl 2009), and extended back-door (Lauritzen 2001) criteria based on asymptotic variances of the estimated total effects. Nanmo and Kuroki (2021) provided a formula to predict future values of the outcome variable when conducting external intervention.

Here, as Hernán and Robins (2020, p. 7) stated

“the average causal effect, defined by a contrast of means of counterfactual outcomes, is the most commonly used population causal effect. However, a population causal effect may also be defined as a contrast of functionals, including medians, variances, hazards, or CDFs of counterfactual outcomes. In general, a population causal effect can be defined as a contrast of any function of the marginal distributions of counterfactual outcomes under different actions or treatment values. For example, the population causal effect on the variance is defined as \(var(Y^{a=1})-var(Y^{a=0})\),”

when we wish to characterize the distributional change introduced by external intervention, there is no reason to limit our causal understanding to the change in the expected value of the outcome variable. In practice, it is important to estimate the expected value of the outcome variable due to external intervention (the causal effect on the mean), and it is often necessary to evaluate the variation (variance) of the outcome variable due to external intervention (the causal effect on the variance) as well. For example, in the field of quality control, to suppress the defective rate of products effectively, it is necessary to bring the outcome variable closer to the target value by external intervention, thereby reducing the variation (or minimizing the variance) of the outcome variable as much as possible. In this situation, Kuroki (2008, 2012) and Kuroki and Miyakawa (1999b, 1999c, 2003) discussed what happens to the variance of the outcome variable when applying external intervention.

Regarding the estimation accuracy of the causal effect on the variance, when the OLS method is utilized to estimate the total effect, Kuroki and Miyakawa (2003) formulated the asymptotic variance of the consistent estimator of the causal effect on the variance and discussed how the asymptotic variance differs with different sets of random variables that satisfy the back-door criterion (Pearl 2009). In addition, Shan and Guo (2010, 2012) studied the results of Kuroki and Miyakawa (2003) from the perspective of different types of external intervention. Kuroki and Nanmo (2020) applied the results of Kuroki and Miyakawa (2003) to predict future value of the outcome variable when conducting external intervention. Here, it is noted that the existing estimators of the causal effect on the variance are consistent but not unbiased. Estimation accuracy problems are essential issues related to statistical causal inference, and thus, it is important to formulate the unbiased estimator of the causal effect on the variance, together with the exact variance. This is because the reliable evaluation of estimation accuracy of the causal effect on the variance is essential for the success of statistical data analysis, which aims to evaluate the casual effects of external intervention on the outcome variable.

In this paper, we assume that cause–effect relationships between random variables can be represented by a Gaussian linear SEM and the corresponding directed acyclic graph (DAG). In the situation where we observe a set of random variables that satisfies the front-door criterion, when the OLS method is utilized to estimate the total effect, we formulate the unbiased estimator of the causal effect on the variance, i.e., the unbiased estimator of the variance of the outcome variable with external intervention in which a treatment variable is set to a specified constant value. In addition, we provide the variance formula of the unbiased estimator of the causal effect on the variance. The variance formula proposed in this paper is exact, in contrast to those in most previous studies on estimating causal effects.

2 Preliminaries

2.1 Graph terminology

A directed graph is a pair \(G=(V,E)\), where V is a finite set of vertices and E, which is a subset of \({V}\times {V}\) of pairs of distinct vertices, is a set of directed edges (\(\rightarrow \)). If \((a,b)\in E\) for \(a, b\in {V}\), then G contains the directed edge from vertex a to vertex b (denoted by \(a\rightarrow b\)). If there is a directed edge from a to b \((a \rightarrow b)\), then a is said to be the parent of b and b the child of a. Two vertices are adjacent if there exists a directed edge between them. A path between a and b is a sequence \(a=a_{0}, a_{1}, \ldots , b=a_{m}\) of distinct vertices such that \(a_{i-1}\) and \(a_{i}\) are adjacent for \(i=1, 2, \ldots , m\). A directed path from a to b is a sequence \(a=a_{0}, a_{1}, \ldots , b=a_{m}\) of distinct vertices such that \(a_{i-1}\rightarrow a_{i}\) for \(i=1, 2, \ldots , m\). If there exists a directed path from a to b, then a is said to be an ancestor of b and b a descendant of a. When the set of descendants of a is denoted as de(a), the vertices in \(V{\backslash }{(de(a){\cup }\{a\})}\) are said to be the nondescendants of a. If two edges on a path point to a, then a is said to be a collider on the path; otherwise, it is said to be a noncollider on the path. A directed path from a to b, together with the directed edge from b to a, forms a directed cycle. If a directed graph contains no directed cycles, then the graph is said to be a DAG. Let \(G_{\underline{a}}\) be the DAG obtained by deleting all the directed edges emerging from a in DAG G, and let \(G_{\overline{a}}\) be the DAG obtained by deleting all the directed edges pointing to a in DAG G.

Let A, B and S be three disjoint subsets of vertices in a DAG G, and let p be any path between a vertex in A and a vertex in B. Here, path p is said to be blocked by (a possibly empty) set S if either of the following conditions is satisfied:

  1. (1)

    p contains at least one noncollider that is in S;

  2. (2)

    p contains at least one collider that is not in S and has no descendant in S.

S is said to d-separate A from B in G if and only if S blocks every path between a vertex in A and a vertex in B.

2.2 Gaussian linear structural equation model

In this paper, we assume that cause–effect relationships (data generating process) between random variables can be represented by a Gaussian linear SEM and the corresponding DAG . Such a DAG is called a causal path diagram, which is defined as Definition 1. Here, we refer to vertices in the DAG and random variables of the Gaussian linear SEM interchangeably.

Definition 1

(Causal path diagram) Consider a DAG \(G=({V}, {E})\), for which a set \({ V}=\{V_{1},V_{2},\ldots ,V_{m}\}\) of random variables and a set E of directed edges are given. Then, DAG G is referred to as the causal path diagram if the random variables are generated by a Gaussian linear SEM

$$\begin{aligned} V_{i}=\alpha _{v_i}+\sum _{V_{j}{\in }{\textrm{pa}}(V_{i})}\alpha _{v_{i}v_{j}}V_{j}+\epsilon _{v_{i}},\quad i=1, 2,\ldots , m, \end{aligned}$$
(1)

satisfying the constraints entailed by DAG G. Here, \(\textrm{pa}(V_{i})\) is a set of parents of \(V_{i}\in {V}\) in DAG G. In addition, when “(\('\))” stands for a transposed vector/matrix, letting \({0}_{m}=(0,0,\ldots ,0)'\) be an m-dimensional zero vector whose ith element is zero for \(i=1,2,\ldots ,m\), \({ \epsilon }_{v}=(\epsilon _{v_{1}}, \epsilon _{v_{2}},\ldots , \epsilon _{v_{m}})'\) denotes a set of random variables, which is assumed to follow the m dimensional Gaussian distribution with the mean vector \({0}_{m}\) and the positive diagonal variance-covariance matrix \(\Sigma _{\epsilon _v \epsilon _v}\). In addition, the constant parameters \(\alpha _{v_i}\) and \(\alpha _{v_{i} v_{j}}\) for \(i,j=1,2,\ldots ,m\) \((i\ne j)\) are referred to as the intercept of \(V_{i}\) and the causal path coefficient of \(V_j\) on \(V_i\), respectively. \(\square \)

Here, note that V of Definition 1 represents the set of both observed and unobserved variables.

It is known that if Z d-separates X from Y in the causal path diagram G, then X is conditionally independent of Y given Z in the corresponding Gaussian linear SEM (e.g., Pearl 2009).

For \(X,Y\in {V}\) \((X\ne Y)\), consider external intervention in which X is set to be the constant value \(X=x\) in Gaussian linear SEM (1), denoted by \(\text{ do }(X=x)\). According to the framework of the structural causal models (Pearl 2009), \(\text{ do }(X=x)\) mathematically indicates that the structural equation for X is replaced by \(X=x\) in Gaussian linear SEM (1). Then, let \({V}=\{X, Y\}\cup {Z}\) be the set of random variables in the causal path diagram G, where \(\{X, Y\}\) and Z are disjoint. When f(x, y, z) and \(f(x|\text{ pa }(x))\) denote the joint probability distribution of \((X,Y,{ Z})=(x,y,{z})\) and the conditional probability distribution of \(X=x\) given \(\text{ pa }(X)=\text{ pa }(x)\), respectively, the interventional distribution of \(Y=y\) under \(\text{ do }(X = x)\), which is denoted by \(f(y|\text{ do }(X=x))\), is defined as

$$\begin{aligned} f(y|\hbox {do}(X=x)) =\int _{z}\frac{f(x,y,\hbox { z })}{f(x|\text{ pa }(x))}d \hbox {z} \end{aligned}$$
(2)

(Pearl 2009). When Eq. (2) can be uniquely determined from the probability distribution of observed variables, it is said to be identifiable. Based on Eq. (2), Kuroki (2008, 2012) and Kuroki and Miyakawa (1999b, 1999c) defined the causal effect of X on the mean of Y and the causal effect of X on the variance of Y as

$$\begin{aligned} \left. \begin{array}{c} {\displaystyle E(Y|\text{ do }(X=x))=\mu _{y|x}=\int _y yf(y|\text{ do }(X=x))\,dy,}\\ {\displaystyle \text{ var }(Y|\text{ do }(X=x))=\sigma _{yy|x}=\int _y (y-\mu _{y|x})^2f(y|\text{ do }(X=x))\,dy,} \end{array}\right\} \end{aligned}$$
(3)

respectively. Then, in the Gaussian linear SEM (1), the first derivative of \(E(Y|\text{ do }(X=x))\) regarding x, namely,

$$\begin{aligned} \frac{\displaystyle d E(Y|\text{ do }(X=x))}{\displaystyle dx}= \tau _{yx} \end{aligned}$$
(4)

is called the total effect of X on Y. Graphically, the total effect \(\tau _{yx}\) is interpreted as the total sum of the products of the causal path coefficients on the sequence of directed edges along all directed paths from X to Y. If the total effect \(\tau _{yx}\) can be uniquely determined from variances and covariances of observed variables, then it is said to be identifiable.

Then, the front-door criterion is a well-known graphical identification condition of the total effect (Pearl 2009).

Definition 2

(Front-door criterion) Let \(\{X,Y\}\) and S be the disjoint subsets of V in DAG G. If S satisfies the following conditions relative to an ordered pair (X, Y) in DAG G, then S satisfies the front-door criterion relative to (X, Y):

  1. (a)

    S d-separates X from Y in DAG \(G_{\overline{X}}\);

  2. (b)

    an empty set d-separates X from S in DAG \(G_{\underline{X}}\);

  3. (c)

    X d-separates S from Y in DAG \(G_{\underline{S}}\).

\(\square \)

In this paper, random variables on the directed path from X to Y are referred to as intermediate variables, whereas nondescendants of X are often referred to as covariates. In particular, when a subset of covariates satisfies d-separates X from Y in DAG \(G_{\underline{X}}\), such a subset is said to be sufficient or satisfies the back-door criterion relative to (X.Y); otherwise, it is said to be insufficient.

When S satisfies the front-door criterion relative to (X, Y), the interventional distribution of \(Y = y\) under \(\text{ do }(X = x)\), is identifiable and is given by

$$\begin{aligned} f(y|\text{ do }(X=x)) =\int _{s}\left( \int _{x^*}f(y|x^*,\hbox { s })f(x^*)dx^*\right) f(\hbox { s }|x)d\hbox {s} \end{aligned}$$
(5)

(Pearl 2009). Here, \(f(y|x^*,{s})\), \(f(x^*)\) and f(s|x) are the conditional probability distribution of \(Y=y\) given \(X=x^*\) and \({S}={s}\), the marginal probability distribution of \(X=x^*\), and the conditional probability distribution of \({S}={s}\) given \(X=x\), respectively.

3 Formulation

3.1 Joint linear regression model

To proceed with our discussion, we define some notation. We denote n as the sample size. For univariates X and Y and a set of random variables S, let \({\mu }_{x}\) and \({\mu }_{y}\) be the means of X and Y, respectively. In addition, \(\sigma _{xy}\) (\(\sigma _{yx}=\sigma _{xy}\)), \(\sigma _{xx}\) and \(\sigma _{yy} \) represent the covariance between X and Y, the variance of X and the variance of Y, respectively. Furthermore, let \(\Sigma _{xs}\) (\(\Sigma _{sx}=\Sigma '_{xs}\)), \(\Sigma _{ys}\) (\(\Sigma _{sy}=\Sigma '_{ys}\)), and \(\Sigma _{ss}\) be the cross-covariance vector between X and S, the cross-covariance vector between Y and S and the variance-covariance matrix of S, respectively. Then, in Gaussian linear SEM (1), when \(\Sigma _{ss}\) is invertible and \(\sigma _{xx}\) is not zero, the conditional covariance \(\sigma _{xy{\cdot }s}\) (\(\sigma _{yx.s}=\sigma _{xy.s}\)) between X and Y given S, the conditional variance \(\sigma _{xx{\cdot }s}\) of X given S, the conditional variance \(\sigma _{yy{\cdot }s}\) of Y given S, the conditional variance \(\sigma _{yy{\cdot }x}\) of Y given X, the conditional cross-covariance vector \(\Sigma _{ys.x}\) (\(\Sigma _{sy.x}=\Sigma '_{ys.x}\)) between Y and S given X, and the conditional variance–covariance matrix \(\Sigma _{ss.x}\) of S given X are formulated as

$$\begin{aligned} \left. \begin{array}{ccc} \sigma _{xy.s}{=}\sigma _{xy}-\Sigma _{xs}\Sigma ^{-1}_{ss}\Sigma _{sy},&{} \sigma _{xx.s}{=}\sigma _{xx}-\Sigma _{xs}\Sigma ^{-1}_{ss}\Sigma _{sx},&{} \sigma _{yy.s}{=}\sigma _{yy}-\Sigma _{ys}\Sigma ^{-1}_{ss}\Sigma _{sy},\\ \sigma _{yy.x}{=}\sigma _{yy}-\frac{\displaystyle \sigma ^2_{xy}}{\displaystyle \sigma _{xx}},&{}\Sigma _{ys.x}=\Sigma _{ys}-\frac{\displaystyle \sigma _{yx}}{\displaystyle \sigma _{xx}}\Sigma _{xs},&{} \Sigma _{ss.x}=\Sigma _{ss}-\frac{\displaystyle \Sigma _{sx}\Sigma _{xs}}{\displaystyle \sigma _{xx}}, \end{array} \right\} \end{aligned}$$
(6)

respectively. In addition, when \(\Sigma _{ss.x}\) is invertible and \(\sigma _{xx.s}\) is not zero, the conditional variance \(\sigma _{yy.xs}\) of Y given \(\{X\}\cup {S}\) is represented by

$$\begin{aligned} \sigma _{yy.xs}=\sigma _{yy.s}-\frac{\sigma ^2_{xy.s}}{\sigma _{xx.s}}=\sigma _{yy.x}-\Sigma _{ys.x}\Sigma ^{-1}_{ss.x}\Sigma _{sy.x}. \end{aligned}$$
(7)

When S satisfies the front-door criterion relative to (X, Y), to estimate the total effect, according to Eq. (5), consider the joint linear regression model, namely,

$$\begin{aligned} Y= & {} \beta _{y.sx}+\beta _{yx.xs}X^*+B_{ys.xs}{S}+\epsilon _{y.xs}, \end{aligned}$$
(8)
$$\begin{aligned} {S}= & {} B_{s.x}+B_{sx.x}X+ \epsilon _{s.x}, \end{aligned}$$
(9)

where \(\epsilon _{y.xs}\) is the random error of regression model (8) that follows a Gaussian distribution with mean zero and variance \(\sigma _{yy.xs}\), while \(\beta _{y.xs}\), \(\beta _{yx.xs}\), and \(B_{ys.xs}\) are the regression intercept, the regression coefficient of \(X^*\), and the regression coefficient vector of S in regression model (8), respectively. In addition, letting q be the number of random variables in S, \(\epsilon _{s.x}\) is a random error vector of regression model (9) that follows the q dimensional Gaussian distribution with the mean vector \(0_{q}\) and the positive definite variance-covariance matrix \(\Sigma _{ss.x}\), while \(B_{s.x}\) and \(B_{sx.x}\) are the regression intercept vector and regression coefficient vector of X in regression model (9), respectively. Here, regression model (8) is obtained by referring to \({\displaystyle \left( \int _{x^*}f(y|x^*,s)f(x^*)dx^*\right) }\) of Eq. (5), and regression model (9) is obtained by referring to \({\displaystyle f(s|x)}\) of Eq. (5). Furthermore, according to the standard assumptions of regression analysis, in regression model (8), \(\epsilon _{y.xs}\) is assumed to be independent of both \(X^*\) and S. Similarly, in regression model (9), \(\epsilon _{s.x}\) is assumed to be independent of X. Here, \(\epsilon _{y.xs}\) is also assumed to be independent of \(\epsilon _{s.x}\). Then, \(\beta _{yx.xs}\), \(B_{ys.xs}\), \(B_{sx.x}\) and \(B_{xs.s}\) are represented as \(\beta _{yx.xs}=\sigma _{xy.s}/\sigma _{xx.s}\), \(B_{ys.xs}=\Sigma _{ys.x}\Sigma ^{-1}_{ss.x}\), \(B_{sx.x}=\Sigma _{sx}/\sigma _{xx}\) and \(B_{xs.s}=\Sigma _{xs}\Sigma ^{-1}_{ss}\), respectively. Note that X and \(X^*\) represent the same treatment variable but play different roles: \(X^*\) is used as a covariate to estimate the causal effect of S on Y in regression model (8), whereas X is designed to conduct external intervention \(\text{ do }(X=x)\) in regression model (9). From Eqs. (8) and (9), the total effect \(\tau _{yx}\) is identifiable and is given by

$$\begin{aligned} \tau _{yx}=B_{ys.xs}B_{sx.x} \end{aligned}$$
(10)

(Pearl 2009) and

$$\begin{aligned} \mu _{y|x}=\mu _y+B_{ys.xs}B_{sx.x}(x-\mu _x),\quad \sigma _{yy|x}=\sigma _{yy.x}+\beta ^{2}_{yx.xs}\sigma _{xx} \end{aligned}$$
(11)

from Kuroki (2008, 2012).

3.2 Results

For univariates X and Y and a set of random variables S, let \(\hat{\mu }_{x}\) and \(\hat{\mu }_{y}\) be the sample means of X and Y, respectively. In addition, \(s_{xy}\) \((s_{yx}=s_{xy})\), \(s_{xx}\), \(s_{yy}\), \(S_{ss}\), \(S_{xs}\) \((S_{sx}=S'_{xs})\) and \(S_{ys}\) \((S_{sy}=S'_{ys})\) represent the sum-of-cross products between X and Y, the sum-of-squares of X, the sum-of-squares of Y, the sum-of-squares matrix of S, the sum-of-cross products vector between X and S, and the sum-of-cross products vector between Y and S, respectively. Furthermore, when \(S_{ss}\) is invertible and \(s_{xx}\) is not zero, we denote

$$\begin{aligned} \left. \begin{array}{ccc} s_{xy.s}=s_{xy}-S_{xs}S^{-1}_{ss}S_{sy},&{} s_{xx.s}=s_{xx}-S_{xs}S^{-1}_{ss}S_{sx},&{} s_{yy.s}=s_{yy}-S_{ys}S^{-1}_{ss}S_{sy},\\ s_{yy.x}=s_{yy}-\frac{\displaystyle s^2_{xy}}{\displaystyle s_{xx}},&{}S_{ys.x}=S_{ys}-\frac{\displaystyle s_{yx}}{\displaystyle s_{xx}}S_{xs},&{} S_{ss.x}=S_{ss}-\frac{\displaystyle S_{sx}S_{xs}}{\displaystyle s_{xx}}, \end{array} \right\} \qquad \qquad \end{aligned}$$
(12)

respectively \((S_{sy.x}=S'_{ys.x})\). In addition, when \(S_{ss.x}\) is invertible and \(s_{xx.s}\) is not zero, we let

$$\begin{aligned} s_{yy.xs}=s_{yy.s}-\frac{s^2_{xy.s}}{s_{xx.s}}=s_{yy.x}-S_{ys.x}S^{-1}_{ss.x}S_{sy.x}. \end{aligned}$$
(13)

Then, based on the OLSs method, the unbiased estimators of \(\beta _{yx.xs}\), \({B}_{ys.xs}\) and \(B_{sx.x}\) of Eqs. (8) and (9) are given by \(\hat{\beta }_{yx.xs}=s_{xy.s}/s_{xx.s}\), \(\hat{B}_{ys.xs}=S_{ys.x}S^{-1}_{ss.x}\) and \(\hat{B}_{sx.x}=S_{sx}/s_{xx}\), respectively. Here, letting n and q be the sample size and the number of random variables in S, respectively, for \(q<n-2\),

$$\begin{aligned} \left. \begin{array}{c} {\displaystyle \hat{\sigma }_{yy.xs}=\frac{s_{yy.xs}}{n-q-2},\quad \hat{\Sigma }_{ss.x}=\frac{1}{n-2}S_{ss.x},\quad \hat{\Sigma }_{ss}=\frac{1}{n-1}S_{ss},}\\ {\displaystyle \hat{\sigma }_{yy.x}=\frac{s_{yy.x}}{n-2},\quad \hat{\sigma }_{xx.s}=\frac{s_{xx.s}}{n-q-1},\quad \hat{\sigma }_{xx}=\frac{1}{n-1}s_{xx},} \end{array}\right\} \end{aligned}$$
(14)

are unbiased estimators of \({\sigma }_{yy.xz}\), \(\Sigma _{ss.x}\), \(\Sigma _{ss}\), \(\sigma _{yy.x}\), \(\sigma _{xx.s}\), and \(\sigma _{xx}\), respectively.

Under random sampling, when S satisfies the front-door criterion relative to (X, Y), consider a situation where \(\tau _{yx}={B}_{ys{\cdot }xs}{B}_{sx.x}\) is estimated using the unbiased estimators \(\hat{B}_{ys{\cdot }xs}\) of \({B}_{ys{\cdot }xs}\) and \(\hat{B}_{sx.x}\) of \({B}_{sx{\cdot }x}\) in Eqs. (8) and (9), i.e., \(\hat{\tau }_{yx}=\hat{B}_{ys{\cdot }xs}\hat{B}_{sx.x}\). Then, the exact variance of the estimated total effect \(\hat{\tau }_{yx}=\hat{B}_{ys{\cdot }xs}\hat{B}_{sx.x}\) is given by

$$\begin{aligned} \text{ var }(\hat{\tau }_{yx})= & {} \text{ var }(\hat{B}_{ys{\cdot }xs}\hat{B}_{sx.x})\nonumber \\= & {} \frac{1}{(n-3)\sigma _{xx}}B_{ys{\cdot }xs}\Sigma _{ss{\cdot }x}B^{\prime }_{ys{\cdot }xs}+\frac{\sigma _{yy{\cdot }xs}}{(n-q-3)\sigma _{xx{\cdot }s}}-\frac{\sigma _{yy{\cdot }xs}}{(n-3)\sigma _{xx}},\qquad \end{aligned}$$
(15)

where n is the sample size and q \((<n-3)\) is the number of random variables in S (Kuroki 2000). In addition, regarding the mean \(E\left( \hat{\mu }_{y|x}\right) \) and variance \(\text{ var }\left( \hat{\mu }_{y|x}\right) \) of the estimated causal effect \(\hat{\mu }_{y|x}\) of X on the mean of Y, i.e.,

$$\begin{aligned} \hat{\mu }_{y|x}=\hat{\mu }_{y}+\hat{B}_{ys.xs}\hat{B}_{sx.x}(x-\hat{\mu }_x). \end{aligned}$$
(16)

The following theorem was derived by Nanmo and Kuroki (2021):

Theorem 1

Suppose that S satisfies the front-door criterion relative to (X, Y) in the Gaussian linear SEM (1) with corresponding DAG G. When the regression parameters in Eqs. (8) and (9) are estimated via the OLS method, for

$$\begin{aligned} \hat{\mu }_{y|x}=\hat{\mu }_{y}+\hat{B}_{ys.xs}\hat{B}_{sx.x}(x-\hat{\mu }_x), \end{aligned}$$
(17)

we obtain

$$\begin{aligned} E\left( \hat{\mu }_{y|x}\right) =\mu _{y}+{B}_{ys.xs}B_{sx.x}(x-\mu _x)={\mu }_{y|x} \end{aligned}$$
(18)

and

$$\begin{aligned}{} & {} \text{ var }(\hat{\mu }_{y|x})=\frac{1}{n}\left( \sigma _{yy.x}+\beta ^2_{yx.xs}\sigma _{xx}\right) \nonumber \\{} & {} \quad +\left( \frac{\sigma _{yy.xs}}{(n-q-3)\sigma _{xx.s}}{-}\frac{\sigma _{yy.xs}}{{(n-3)\sigma _{xx}}}{+}\frac{B_{ys.xs}\Sigma _{ss.x}B_{ys.xs}^{\prime }}{(n-3)\sigma _{xx}}\right) \left( (x-\mu _{x})^2{+}\frac{\sigma _{xx}}{n}\right) ,\nonumber \\ \end{aligned}$$
(19)

where n is the sample size and q \((<n-3)\) is the number of random variables in S. \(\square \)

In contrast, some practitioners may use

$$\begin{aligned} \tilde{\sigma }_{yy|x}=\hat{\sigma }_{yy.x}+\hat{\beta }^2_{yx.xs}\hat{\sigma }_{xx} \end{aligned}$$
(20)

to evaluate the causal effect \(\sigma _{yy|x}\) of X on the variance of Y. However, Eq. (20) is the consistent but not unbiased estimator of \(\sigma _{yy|x}\). Regarding the unbiased estimator \(\hat{\sigma }_{yy|x}\) of \(\sigma _{yy|x}\), the following theorem is derived:

Theorem 2

Suppose that S satisfies the front-door criterion relative to (X, Y) in Gaussian linear SEM (1) with corresponding DAG G. When the regression parameters in Eqs. (8) and (9) are estimated via the OLS method, for

$$\begin{aligned} \hat{{\sigma }}_{yy|x}=\hat{\sigma }_{yy.x}+\hat{\beta }^2_{yx.xs}\hat{\sigma }_{xx}- \frac{\hat{\sigma }_{yy.xs}\hat{\sigma }_{xx}}{s_{xx.s}}, \end{aligned}$$
(21)

we obtain

$$\begin{aligned} E\left( \hat{{\sigma }}_{yy|x}\right) =\sigma _{yy.x}+\beta ^2_{yx.xs}\sigma _{xx}={{\sigma }}_{yy|x} \end{aligned}$$
(22)

and

$$\begin{aligned}{} & {} \text{ var }(\hat{{\sigma }}_{yy|x})= \frac{2(B_{ys.xs}\Sigma _{ss.x}B'_{ys.xs})^2}{n-2}+\frac{2(\beta ^2_{yx.xs}\sigma _{xx})^2}{n-1}+\frac{2\sigma ^2_{yy.xs}}{n-q-2} \nonumber \\{} & {} \quad \times \left( \left( \frac{n-q-2}{n-2}\right) ^2-2\frac{n-q-2}{(n-1)(n-2)}E\left( \frac{s_{xx}}{s_{xx.s}}\right) +\left( \frac{1}{n-1}\right) ^2E\left( \left( \frac{s_{xx}}{s_{xx.s}}\right) ^2\right) \right) \nonumber \\{} & {} \quad +\frac{2\sigma ^2_{yy.xs}}{(n-1)^2} E\left( \left( \frac{s_{xx}}{s_{xx.s}}\right) ^2\right) +\frac{4\sigma ^2_{yy.xs}}{(n-1)(n-2)}\left( E\left( \frac{s_{xx}}{s_{xx.s}}\right) -1\right) +\frac{2q\sigma ^2_{yy.xs}}{(n-2)^2} \nonumber \\{} & {} \quad + 4\sigma _{yy.xs} (\beta _{yx.xs},B_{ys.xs}) \left( \begin{array}{cc} \left( \frac{\displaystyle 1}{\displaystyle n-1}\right) ^2E\left( \frac{\displaystyle s^2_{xx}}{\displaystyle s_{xx.s}}\right) &{} -\frac{\displaystyle \Sigma _{xs}}{\displaystyle n-2}\\ -\frac{\displaystyle \Sigma _{sx}}{\displaystyle n-2} &{} \frac{\displaystyle \Sigma _{ss.x}}{\displaystyle n-2} \end{array} \right) \left( \begin{array}{c} \beta _{yx.xs}\\ B'_{ys.xs} \end{array} \right) , \end{aligned}$$
(23)

where n is the sample size and q \((<n-5)\) is the number of random variables in S,  and

$$\begin{aligned} E\left( \frac{\displaystyle s_{xx}}{s_{xx.s}}\right)= & {} \frac{(n-3)\sigma _{xx.s}+(n-1)B_{xs.s}\Sigma _{ss}B'_{xs.s}}{(n-q-3)\sigma _{xx.s}}, \end{aligned}$$
(24)
$$\begin{aligned}{} & {} E\left( \left( \frac{\displaystyle s_{xx}}{s_{xx.s}}\right) ^2\right) = 1+2\frac{q\sigma _{xx.s}+(n-1)B_{xs.s}\Sigma _{ss}B'_{xs.s}}{(n-q-3)\sigma _{xx.s}}+\frac{4(n-1)\sigma _{xx.s}B_{xs.s}\Sigma _{ss}B'_{xs.s}}{(n-q-3)(n-q-5)\sigma ^2_{xx.s}}\nonumber \\{} & {} \qquad +\frac{2q\sigma ^2_{xx.s}+2(n-1)(B_{xs.s}\Sigma _{ss}B'_{xs.s})^2 +(q\sigma _{xx.s}+(n-1)B_{xs.s}\Sigma _{ss}B'_{xs.s})^2}{(n-q-3)(n-q-5)\sigma ^2_{xx.s}}, \end{aligned}$$
(25)
$$\begin{aligned}{} & {} E\left( \frac{\displaystyle s^2_{xx}}{\displaystyle s_{xx.s}}\right) =(n-q-1)\sigma _{xx.s}{ +2q\sigma _{xx.s}}+{2(n-1)}B_{xs.s}\Sigma _{ss}B'_{xs.s}+\frac{4(n-1)\sigma _{xx.s}B_{xs.s}\Sigma _{ss}B'_{xs.s}}{(n-q-3)\sigma _{xx.s}}\nonumber \\{} & {} \qquad +\frac{2q\sigma ^2_{xx.s}+2(n-1)(B_{xs.s}\Sigma _{ss}B'_{xs.s})^2 +(q\sigma _{xx.s}+(n-1)B_{xs.s}\Sigma _{ss}B'_{xs.s})^2}{(n-q-3)\sigma _{xx.s}}. \end{aligned}$$
(26)

\(\square \)

Here, from “Appendix”, note that the assumption of Gaussian random variables in Eq. (1) is not necessary to derive Eq. (21), but necessary to derive Eq. (23).

For a large sample size n such as \(n^{-2}\simeq 0\), the consistent estimator \(\tilde{\sigma }_{yy|x}\) of \({\sigma }_{yy|x}\) can be given by

$$\begin{aligned} \tilde{\sigma }_{yy|x}=\hat{\sigma }_{yy.x}+\hat{\beta }^2_{yx.xs}\hat{\sigma }_{xx} \end{aligned}$$
(27)

and the asymptotic variance is given by

$$\begin{aligned}{} & {} \text{ a.var }(\hat{{\sigma }}_{yy|x})= \frac{2(B_{ys.xs}\Sigma _{ss.x}B'_{ys.xs})^2}{n}+\frac{2(\beta ^2_{yx.xs}\sigma _{xx})^2}{n} +\frac{2\sigma ^2_{yy.xs}}{n}\nonumber \\{} & {} \qquad + \frac{4\sigma _{yy.xs}}{n} (\beta _{yx.xs},B_{ys.xs}) \left( \begin{array}{cc} \frac{\displaystyle \sigma ^2_{xx}}{\displaystyle \sigma _{xx.s}}&{} -\displaystyle \Sigma _{xs}\\ -\Sigma _{sx} &{}\Sigma _{ss.x} \end{array} \right) \left( \begin{array}{c} \beta _{yx.xs}\\ B'_{ys.xs} \end{array} \right) \end{aligned}$$
(28)

from \(\sigma _{xx}=\sigma _{xx.s}+B_{xs.s}\Sigma _{ss}B'_{xs.s}\).

4 Numerical experiments

Fig. 1
figure 1

Causal path diagram

Full size image

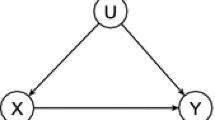
Numerical experiments were conducted to examine the statistical properties of the estimated causal effect on the variance for sample sizes \(n=10, 25, 50\) and 100. For simplicity, let X, Y, S and U be the treatment variable, the outcome variable, the intermediate variable that satisfies the front-door criterion relative to (X, Y) and the covariate that satisfies the back-door criterion relative to (X, Y) (Pearl 2009), respectively, based on Fig. 1, and consider the Gaussian linear SEM of the form

$$\begin{aligned} \left. \begin{array}{lll} Y=\alpha _{ys}S+\alpha _{yu}U+\epsilon _{y.su},&{} &{}S=\alpha _{sx}X+\epsilon _{s.x}\\ X=\alpha _{xu}U+\epsilon _{x.u},&{}&{}U=\epsilon _{u} \end{array}\right\} , \end{aligned}$$
(29)

where \(\epsilon _{x.u}\), \(\epsilon _{y.su}\), \(\epsilon _{s.x}\), and \(\epsilon _{u}\) independently follow Gaussian distributions with mean zero and variance \((1-\alpha ^2_{xu})\), \((1-\alpha ^2_{ys}-\alpha ^2_{yu}-2\alpha _{ys}\alpha _{yu}\alpha _{sx}\alpha _{xu})\), \((1-\alpha ^2_{sx})\), and 1, respectively. In addition, letting \(\alpha _{yu}=\alpha _{ys}=0.5\), \(\alpha _{xu}\) and \(\alpha _{sx}\) are given as:

Case 1: \(\alpha _{xu}=-0.9\), \(\alpha _{sx}=0.1\); Case 2: \(\alpha _{xu}=-0.1\), \(\alpha _{sx}=0.1\)

Case 3: \(\alpha _{xu}=0.1\), \(\alpha _{sx}=0.1\);    Case 4: \(\alpha _{xu}=0.9\), \(\alpha _{sx}=0.1\)

Case 5: \(\alpha _{xu}=-0.9\), \(\alpha _{sx}=0.9\); Case 6: \(\alpha _{xu}=-0.1\), \(\alpha _{sx}=0.9\)

Case 7: \(\alpha _{xu}=0.1\), \(\alpha _{sx}=0.9\);    Case 8: \(\alpha _{xu}=0.9\), \(\alpha _{sx}=0.9\)

Here, it is known that the total effect can be estimated as \(\hat{\beta }_{yx.xu}\) when U is observed and U satisfies the back-door criterion relative to (X, Y) (Pearl 2009). When the back-door criterion is applied to estimate the total effect, \(\alpha _{xu}=\pm 0.9\) implies a situation where multicollinearity occurs, but \(\alpha _{xu}=\pm 0.1\) does not. However, note that U is not observed in our situation. In this situation, when the front-door criterion is applied to estimate the total effect, \(\alpha _{sx}=\pm 0.9\) implies a situation where multicollinearity occurs, but \(\alpha _{sx}=\pm 0.1\) does not. When \(\alpha _{sx}\) and \(\alpha _{xu}\) have the same size but different signs, parametric cancellation occurs (Cox and Wermuth 2014), where \(\beta _{yx.x}=0\) and \(\tau _{yx}\ne 0\) hold. When parametric cancellation occurs, the variance \(\text{ var }(Y|\text{ do }(X=x))\) of Y with external intervention takes a larger value than the variance \(\text{ var }(Y|X=x)\) of Y without external intervention (Kuroki 2012). In contrast, when \(\alpha _{sx}\) and \(\alpha _{xu}\) have the same sign, the total effect is overestimated by the simple regression model. When \(\alpha _{xu}\) has a larger size than \(\alpha _{sx}\) and a different sign, the sign of the estimated simple regression coefficient is different from that of the total effects.

We simulated n random samples from the four-dimensional Gaussian distribution with a zero mean vector and the correlation matrices generated from each case. Then, regarding the causal effects on the variance, we evaluated both the unbiased estimator (21) and the consistent estimator (27) 50,000 times based on \(n=10, 25, 50\), and 100. Table 1 reports the basic statistics of Eqs. (21) and (27) for each case.

Table 1 Numerical experiments
Full size table

First, in the “Estimates” rows of Table 1, for each case, the consistent estimators were highly biased in the smaller sample sizes but became less biased in the larger sample sizes. In particular, the bias reduction speed based on the sample size largely depended on the correlation between X and S: it seems that it was slower when X is highly correlated with S. In contrast, the unbiased estimators were close to the true values even for small sample sizes. However, as seen from the “Minimum” rows of Table 1, except for the sample size \(n=10\) of Case 1, the minimum values of the unbiased estimators were negative for \(n=10\) but not for the larger sample size; the consistent estimators did not take negative values. In addition, both the “Minimum” and “Maximum” rows of Table 1 show that when X was highly correlated with S, the sample ranges of the unbiased estimators were wider than those of the consistent estimators in the smaller sample sizes. However, the sample ranges became close to those of the consistent estimators in the larger sample sizes.

Second, the “Variance” and “Equation (23)/(28)” rows of Table 1 show that the exact variance was relatively close to the empirical variances of the unbiased estimator for any sample size. In contrast, the asymptotic variances were not close to the empirical variances of the unbiased or consistent estimators in the smaller sample sizes but became closer to them as the sample size increased. However, compared to Cases 1–4, in Cases 5–8, the differences between the asymptotic variances and the empirical variances were significant even for \(n=100\). In addition, the exact and asymptotic variances in Cases 3, 4, 7, and 8 were smaller than those in Cases 2, 1, 6, and 5, respectively. The distributional characteristics of the estimated causal effect on the variance depended on the difference between the signs of the total effect \(\tau _{yx}\) and the spurious correlation \(\beta _{yx. x}-\tau _{yx}\). Notably, it seems that if the sign of the total effect was different from that of the spurious correlation, then the estimation accuracy of the causal effect on the variance may have been worse.

Third, it seems that both unbiased and consistent estimators were highly skewed and heavy-tailed in the small sample size, but converged to the Gaussian distributions slowly when the sample sizes were larger for Cases 5–8. In contrast, it seems that both unbiased and consistent estimators in Cases 1–4 converged to the Gaussian distributions faster than Cases 5–8. This implies that the convergence of these estimators to the Gaussian distribution depended on the multicollinearity between X and S with a small sample size.

5 Conclusion

In this paper, when causal knowledge is available in the form of a Gaussian linear SEM with the corresponding DAG, we considered a situation where the total effect can be estimated based on the front-door criterion. In this situation, when the OLS method is utilized to estimate the total effect, we formulated the unbiased estimator of the causal effect on the variance, together with the exact variance. The estimated causal effect on the variance used in Nanmo and Kuroki (2021) is consistent but not unbiased. With small sample sizes, using the consistent estimator may lead to misleading findings in statistical causal inference. The proposed estimator would help avoid this problem, and the results of our method would help statistical practitioners appropriately predict what would happen to the outcome variable when conducting external intervention.

Future work should involve extending our results to a joint intervention that combines several single external interventions. In addition, the numerical experiments showed that one drawback of the proposed unbiased estimator is that it can have a negative value in a small sample size. One suggestion for overcoming this problem is to use \(\max \{0,\hat{\sigma }_{yy|x}\}\) instead of \(\hat{\sigma }_{yy|x}\) to evaluate the causal effect on the variance. However, noting that \(\max \{0,\hat{\sigma }_{yy|x}\}\) is not an unbiased estimator, developing a more efficient unbiased estimator of the causal effect on the variance is another potential topic for future research.