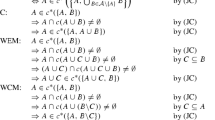Skip to main content
SpringerLink
Log in

Essentiality and convexity in the ranking of opportunity sets

  • Original Paper
  • Published:
Social Choice and Welfare Aims and scope Submit manuscript

Abstract

This paper studies a class of binary relations on opportunity sets which we call opportunity relations (ORs). These are reflexive and transitive (pre-orders) and further satisfy a monotonicity and desirability condition. Associated with each OR is an essential element operator (Puppe, J Econ Theory 68:174–199, 1996). Our main results axiomatically characterise three important classes of ORs: those for which any opportunity set lies in the same indifference class as its set of essential elements—the essential ORs; those whose essential element operator is the extreme point operator for some closure space (Ando, Discrete Math 306:3181–3188, 2006)—the closed ORs; and those whose essential element operator is the extreme point operator for some abstract convex geometry (Edelman and Jamison, Geometriae Dedicata 19:247–270, 1985)—the convex ORs. Our characterisation of convex ORs generalises the analysis of Klemisch-Ahlert (Soc Choice Welf 10:189–207, 1993). Our results also provide complementary perspectives on the well-known characterisation of closure operators by Kreps (Econometrica 47:565–577, 1979), as well as the recent work of Danilov and Koshevoy (Order 26:69–94, 2009; Soc Choice Welf 45:51–69, 2015).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. For example, by Barberà et al. (2004) and Dowding and Hees (2009).

  2. See Kashiwabara et al. (2005).

  3. We use the term “operator” in the sense of Danilov and Koshevoy (2009, Definition 1). That is, an operator is a mapping from \(2^{X\phantom {^T}}\) into itself.

  4. Koshevoy (1999) proved that the class of path independent choice functions on X (Plott 1973) coincides with the class of extreme point operators for ACGs on X.

  5. We thank an anonymous referee for emphasising the value of this aspect of the paper, and for encouraging us to further clarify these links.

  6. Klemisch-Ahlert (1993, p.196) provides three justifications for assuming that the value of a set is the same as that of its convex hull.

  7. In particular, \(\succsim \) need not reflect actual or hypothetical choice behaviour. The individual need not anticipate facing a choice of opportunity sets (as opposed to a choice from an opportunity set). The binary relation \(\succsim \) may instead reflect her preferences over the opportunities with which the world chooses to present her—preferences over what she might be offered, rather than inclinations to choose. This distinction is potentially important for analysing conceptions of freedom.

  8. Since M implies reflexivity we could replace “pre-order” in Definition 1 with “transitive binary relation”.

  9. See, for example, Puppe (1996, p. 178) and Puppe and Xu (2010, p. 671). A notable exception is van Hees (2010).

  10. None of the following reasons is original to the present author, of course.

  11. In other words, nothing would be lost by replacing D with the No Dummy condition of Danilov et al. (2015): \(\left\{ x\right\} \succ \emptyset \) for every \(x\in X\).

  12. Nehring and Puppe (1999) say that x is “essential at \(A\diagdown x\)” if \(x\in e_{\succsim }\left( A\right) \). We follow Puppe’s (1996) terminology in the present paper. The related notion of an eligible element was introduced by van Hees (2010). However, his eligible element mapping \(e:2^{X}\rightarrow 2^{X}\) is treated as exogenous data, logically separate from the pre-order \(\succsim \), though the axioms in van Hees (2010) restrict the relationship between the two objects.

  13. The INE acronym comes from Puppe and Xu (2010). Puppe (1996) calls this property Axiom I, which has less mnemonic value.

  14. Property (iii) is a strengthening of the well-known Aizerman (or Outcast) condition on choice functions. In our context, this latter condition would require \(e_{\succsim }\left( B\right) \subseteq e_{\succsim }\left( A\right) \) whenever \(e_{\succsim }\left( A\right) \subseteq B\subseteq A\) (Moulin 1985).

  15. Property (ii) sharpens the “main content” of Puppe (1996, Proposition 1), and also Fact 7.1 in Nehring and Puppe (1999).

  16. The same property also appears, in a slightly weaker version, in Nehring and Puppe (1999), and in heavily disguised form in Nehring and Puppe (1998). Nehring and Puppe’s (1999) weaker version of CCN is called the Irrelevance of Inessential Elements (IIE) property. It allows CCN to be violated if \(x\sim y\sim \left\{ x,y\right\} \) or if \(A\diagdown \left\{ x,y\right\} =\emptyset \). Our Example 1 satisfies IIE. Note also that if \(\succsim \) is an OR satisfying CCN then \(x\sim y\sim \left\{ x,y\right\} \) implies \(x=y\) (otherwise CCN and D are in contradiction). Nehring and Puppe’s (1998) Strict Properness is essentially equivalent to CCN, though applied to so-called weak extended partial orders (WEPOs). Nehring and Puppe (1998) work with extended binary relations on X, which are subsets of \(2^{X}\times X\), rather than \(2^{X}\times 2^{X}\). The WEPOs are a particular class of extended binary relations. We may transform a binary relation \(\succsim \subseteq 2^{X}\times 2^{X}\) into an extended binary relation \(Q\subseteq 2^{X}\times X\) (and vice versa) by specifying that \(\left( A,x\right) \in Q\) iff \(A\succsim A\cup x\). Under this transformation, \(\succsim \) satisfies CCN iff Q satisfies Strict Properness.

  17. Example 2 shows that EM is not necessary for (i). A necessary and sufficient condition is the following: for all \(A\subseteq X\) and all \(x,y\in X\),

    $$\begin{aligned} A\sim A\cup x\sim A\cup y \Rightarrow A\sim A\cup \left\{ x,y\right\} \end{aligned}$$
    (5)

    To see the sufficiency of (5), note that the proof of Lemma 6(i) does not use the full strength of EM—only (5) is required. To see the necessity, suppose there exist \(A\subseteq X\) and \(x,y\in X\) such that \(A\sim A\cup x\sim A\cup y\) but \(A\cup \left\{ x,y\right\} \succ A\). Then \(A\cup \left\{ x,y\right\} \subseteq \sigma _{\succsim }\left( A\right) \), so M and transitivity give \(\sigma _{\succsim }\left( A\right) \succ A\).

  18. However, Nehring and Puppe (1999) apply CC to binary relations contained within a restricted subset of \(2^{X}\times 2^{X}\). The Monotonicity condition on WEPOs (Nehring and Puppe 1998) can also be translated (via the rule of translation noted previously) into the following version of CC: \(A\subseteq B\) and \(A\succsim A\cup x\) imply \(B\succsim B\cup x\).

  19. Suppose \(B\succ B\diagdown C\) and let \(C=\left\{ c_{1},\ldots ,c_{n}\right\} \). By M and transitivity there exists some \(k^{*}\in \left\{ 1,\ldots ,n-1\right\} \) such that

    $$\begin{aligned} B\diagdown \left\{ c_{1},\ldots ,c_{k^{*}}\right\} \succ B\diagdown \left\{ c_{1},\ldots ,c_{k^{*}+1}\right\} \text {.} \end{aligned}$$

    Then, using M, transitivity and (6) we have:

    $$\begin{aligned} A\succsim A\diagdown \left\{ c_{1},\ldots ,c_{k^{*}}\right\} \succ A\diagdown \left\{ c_{1},\ldots ,c_{k^{*}+1}\right\} \succsim A\diagdown C \end{aligned}$$

    and hence \(A\succ A\diagdown C\).

  20. See also Nehring and Puppe (1999, footnote 3).

  21. See also Danilov and Koshevoy (2009, Proposition 5).

  22. It can be shown that the extreme point operator for any closure space on X is the essential element operator for some OR.

  23. It also satisfies conditions (Cont) and (Ext) of DKS.

  24. More precisely, Kreps studies weak orders on \(2^{X}\diagdown \left\{ \emptyset \right\} \) that satisfy M and (8). The latter, as we have observed, is equivalent to EM (given M and transitivity). If we use D to extend such a weak order to \(2^{X}\), we obtain a complete ClOR.

  25. Lemma 1 in Puppe (1996) assumes that \(\succsim \) satisfies his Axiom F, but the proof that \(\succsim ^{*}\) is transitive (ibid., p.195) does not make use of Axiom F.

  26. In a similar vein, Nehring and Puppe (1998, Theorem 4.1) apply Kreps (1979) to characterise the weak extended partial orders (WEPO’s) associated with ClOR’s. Given an OR, \(\succsim \), its associated WEPO consists of the pairs \(\left( A,x\right) \) such that \(A\succsim ^{*}x\), where \(\succsim ^{*}\) is the dominance relation for \(\succsim \). A yet-more-distant relative of the same basic result, but expressed in the idiom of modal logic, is presented in Gekker and Hees (2006).

  27. Only Player 2’s payoffs are shown as Player 1’s payoffs are redundant to the analysis.

  28. In fact, consider any finite, two-player game. Let n be the number of pure strategies available to Player 1 and let \(X\subseteq \mathbb {R}^{n}\) be the set of (Player 2) payoff vectors corresponding to each of Player 2’s pure strategies. It is not hard to show that the following defines an anti-exchange closure operator:

    $$\begin{aligned} \kappa ^{*}\left( A\right) \ =\ \mathrm {co}( A+\mathbb {R}_{-}^{n}) \cap X\ =\ (\mathrm {co}( A) +\mathbb {R}_{-}^{n}) \cap X\text {.} \end{aligned}$$

  29. The fact that this decision-maker ranks sets by the cardinality of their closure may strike the reader as odd. Why should adding a strictly dominated strategy, for example, increase the value of the strategic opportunity set? While this may seem odd, it is nevertheless consistent with the well-known decoy (or attraction) effect (Clippel and Eliaz 2012). That said, any monotone pre-order satisfying \(A\sim \kappa ^{*}\left( A\right) \) for all \(A\subseteq X\) and \(A\succ B\) for all \(A,B\in 2^{X}\) with \(\kappa ^{*}\left( B\right) \subset \kappa ^{*}\left( A\right) \) will suit our purpose just as well.

  30. In particular, property (CC2) of a closure operator ensures that M is satisfied.

  31. To ensure a payoff greater than 3 when Player 1 chooses \(\beta \), Player 2 must place probability greater than \(\frac{1}{2}\) on a when mixing over a and d. But then the payoff to this mixture will be less than \(\frac{5}{2}\) when Player 1 chooses \(\alpha \).

  32. Properties M and \(\alpha \) already imply both F and INE (cf, Puppe 1996, Lemma 2). Our Theorem 2 shows that F is redundant to Puppe’s Lemma 1.

  33. With some effort, one can also perceive Nehring and Puppe’s (1998) Theorem 5.2 as an essentially equivalent result for WEPO’s.

  34. Condition (17) is equivalent to the Lattice Equivalence (LE) condition in DKS, given the Union property and the finiteness of X.

  35. To verify (C1), suppose \(\sigma \left( A\right) =A\) and \(\sigma \left( B\right) =B\). Two applications of (CC2) gives

    $$\begin{aligned} \sigma \left( A\cap B\right) \subseteq \sigma \left( A\right) \cap \sigma \left( B\right) =A\cap B\text {.} \end{aligned}$$

    Since \(A\cap B\subseteq \sigma \left( A\cap B\right) \) by (CC1), we are done.

  36. The second equality may be justified as follows. If \(x\in \sigma _{\mathcal {K}}\left( A\diagdown x\right) \) then (CC1) implies \(A\subseteq \sigma _{\mathcal {K}}\left( A\diagdown x\right) \) so (CC2) and (CC3) give

    $$\begin{aligned} \sigma _{\mathcal {K}}\left( A\right) \subseteq \sigma _{\mathcal {K}}\left( \sigma _{\mathcal {K}}\left( A\diagdown x\right) \right) =\sigma _{\mathcal {K}}\left( A\diagdown x\right) \text {.} \end{aligned}$$

    Hence \(\sigma _{\mathcal {K}}\left( A\right) =\sigma _{\mathcal {K}}\left( A\diagdown x\right) \) by (CC2). Conversely, if \(\sigma _{\mathcal {K}}\left( A\right) =\sigma _{\mathcal {K}}\left( A\diagdown x\right) \) then \(A\subseteq \sigma _{\mathcal {K}}\left( A\diagdown x\right) \) by (CC2) and hence \(x\in \sigma _{\mathcal {K}}\left( A\diagdown x\right) \).

  37. If \(x\in X\diagdown A\), then \(x\notin e_{\mathcal {K}}\left( A\cup x\right) \) clearly implies \(x\in \sigma _{\mathcal {K}}\left( A\right) \). Conversely, suppose \(x\in \sigma _{\mathcal {K}}\left( A\right) \). Then \(A\cup x\subseteq \sigma _{\mathcal {K}}\left( A\right) \) by (CC1), and hence, using (CC2) and (CC3):

    $$\begin{aligned} \sigma _{\mathcal {K}}\left( A\cup x\right) \subseteq \sigma _{\mathcal {K}}(\sigma _{\mathcal {K}}\left( A\right) ) =\sigma _{\mathcal {K}}\left( A\right) \text {.} \end{aligned}$$

References

  • Ando K (2006) Extreme point axioms for closure spaces. Discrete Math 306:3181–3188

    Article  Google Scholar 

  • Barberà S, Bossert W, Pattanaik PK (2004) Ranking sets of objects. In: Barberà P Hammond, Seidl C (eds) Handbook of utility theory, vol 2. Kluwer Academic, Dordrecht

    Chapter  Google Scholar 

  • Bossert W, Ryan MJ, Slinko A (2009) Orders on subsets rationalised by abstract convex geometries. Order 26(3):237–244

    Article  Google Scholar 

  • Danilov V, Koshevoy G (2009) Choice functions and extensive operators. Order 26:69–94

    Article  Google Scholar 

  • Danilov V, Koshevoy G, Savaglio E (2015) Hyper-relations, choice functions, and orderings of opportunity sets. Soc Choice Welf 45:51–69

    Article  Google Scholar 

  • De Clippel G, Eliaz K (2012) Reason-based choice: a bargaining rationale for the attraction and compromise effects. Theor Econ 7(1):125–162

    Article  Google Scholar 

  • Dowding K, van Hees M (2009) Freedom of choice. In: Anand P, Pattanaik PK, Puppe C (eds) Handbook of rational and social choice. Oxford University Press, Oxford

    Google Scholar 

  • Edelman PH, Jamison RE (1985) The theory of convex geometries. Geometriae Dedicata 19:247–270

    Article  Google Scholar 

  • Gekker R, van Hees M (2006) Freedom, opportunity and uncertainty: a logical approach. J Econ Theory 130:246–263

    Article  Google Scholar 

  • Kashiwabara K, Nakamura M, Okamoto Y (2005) The affine representation theorem for abstract convex geometries. Comput Geom 30(2):129–144

    Article  Google Scholar 

  • Klemisch-Ahlert M (1993) Freedom of choice: a comparison of different rankings of opportunity sets. Soc Choice Welf 10:189–207

    Article  Google Scholar 

  • Koshevoy G (1999) Choice functions and abstract convex geometries. Math Soc Sci 38:35–44

    Article  Google Scholar 

  • Kreps DM (1979) A representation theorem for ‘preference for flexibility’. Econometrica 47:565–577

    Article  Google Scholar 

  • Kukushkin N (2004) Path independence and Pareto dominance. Econ Bull 4(3):1–3

    Google Scholar 

  • Moulin H (1985) Choice functions over a finite set: a summary. Soc Choice Welf 2:147–160

    Article  Google Scholar 

  • Nehring K, Puppe C (1998) Extended partial orders: a unifying structure for abstract choice theory. Ann Oper Res 80:27–48

    Article  Google Scholar 

  • Nehring K, Puppe C (1999) On the multi-preference approach to evaluating opportunities. Soc Choice Welf 16:41–63

    Article  Google Scholar 

  • Plott CR (1973) Path independence, rationality and social choice. Econometrica 41:1075–1091

    Article  Google Scholar 

  • Puppe C (1996) An axiomatic approach to ‘preference for freedom of choice’. J Econ Theory 68:174–199

    Article  Google Scholar 

  • Puppe C, Xu Y (2010) Essential alternatives and freedom rankings. Soc Choice Welf 35:669–685

    Article  Google Scholar 

  • Ryan MJ (2014) Path independent choice and the ranking of opportunity sets. Soc Choice Welf 42:193–213

    Article  Google Scholar 

  • Sen AK (1971) Choice functions and revealed preference. Rev Econ Stud 38:307–317

    Article  Google Scholar 

  • van Hees M (2010) The specific value of freedom. Soc Choice Welf 35:687–703

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Economics, Auckland University of Technology, Auckland, New Zealand

    Matthew Ryan

Authors
  1. Matthew Ryan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Matthew Ryan.

Additional information

My thanks to the Editor and two anonymous referees for thoughtful comments on an earlier draft. All remaining shortcomings are entirely the author’s responsibility.

Appendices

Appendices

The following Appendices review some basic facts about closure spaces and abstract convex geometries. Further details, including omitted proofs, can be found in Edelman and Jamison (1985).

A Closure spaces

Given a finite set X, a closure space on X is a collection \(\mathcal {K}\) of subsets of X satisfying, for all \(A,B\subseteq X\):

  1. (C0)

    \(\emptyset ,X\in \mathcal {K}\),

  2. (C1)

    If \(\left\{ A,B\right\} \subseteq \mathcal {K}\), then \(A\cap B\in \mathcal {K}\).

We take X as given from now on and omit the qualifier “on X” when discussing closure spaces.

A closure space is an abstract generalisation of the notion of closing a set with respect to some underlying operation, such as forming linear combinations. The elements of \(\mathcal {K}\) are interpreted as the subsets of X which are closed with respect to the underlying operation. They are therefore called the closed subsets of X.

Given a closure space \(\mathcal {K}\) and a set \(A\subseteq X\), we define \(\sigma _{\mathcal {K}}\left( A\right) \) to be the smallest element of \(\mathcal {K}\) containing A. This is well-defined by (C1):

$$\begin{aligned} \sigma _{\mathcal {K}}\left( A\right) \ =\ \bigcap \left\{ B\in \mathcal {K}\ \left| \ A\subseteq B\right. \right\} \text {.} \end{aligned}$$

We say that \(\sigma _{\mathcal {K}}\left( A\right) \) is the closure of A. It is easy to see that \(\mathcal {K}\) and \(\sigma _{\mathcal {K}}\) contain the same information: given \(\sigma _{\mathcal {K}}\) we may recover \(\mathcal {K}\) by the rule: \(A\in \mathcal {K}\) iff \(\sigma _{\mathcal {K}}\left( A\right) =A\).

More generally, we call \(\sigma :2^{X}\rightarrow 2^{X}\) a closure operator if it satisfies, for all \(A,B\subseteq X\):

  1. (CC0)

    \(\sigma \left( \emptyset \right) =\emptyset \),

  2. (CC1)

    \(A\subseteq \sigma (A)\),

  3. (CC2)

    \(A\subseteq B\) implies \(\sigma (A)\subseteq \sigma (B)\),

  4. (CC3)

    \(\sigma (\sigma (A))=\sigma (A)\).

If \(\sigma \) is a closure operator, then it is easily shown that the collection

$$\begin{aligned} \mathcal {K}_{\sigma }\ =\ \{ A\in 2^{X}\ \left| \ \sigma \left( A\right) =A\right. \} \end{aligned}$$

is a closure space;Footnote 35 and given any closure space \(\mathcal {K}\), it is clear that \(\sigma _{\mathcal {K}}\) satisfies (CC0)–(CC3). Indeed:

Theorem A.1

Given a closure space \(\mathcal {K}\), the operator \(\sigma _{\mathcal {K}}\) is a closure operator and \(\mathcal {K}=\mathcal {K}_{\sigma _{\mathcal {K}}}\).

Proof

We already observed that \(\sigma _{\mathcal {K}}\) is a closure operator. If \(A\in \mathcal {K}\), then \(\sigma _{\mathcal {K}}\left( A\right) =A\). Conversely, if \(\sigma _{\mathcal {K}}\left( A\right) =A \) then A is the intersection of sets in \(\mathcal {K}\) and hence \(A\in \mathcal {K}\). \(\square \)

Given a closure space \(\mathcal {K}\), we may also define an operator \(e_{\mathcal {K}}:2^{X}\rightarrow 2^{X}\) as follows:Footnote 36

$$\begin{aligned} e_{\mathcal {K}}\left( A\right)= & {} \{ x\in A\ \vert \ \sigma _{\mathcal {K}}\left( A\right) \ne \sigma _{\mathcal {K}}( A\diagdown x) \} \nonumber \\= & {} \{ x\in A\ \vert \ x\notin \sigma _{\mathcal {K}}( A\diagdown x) \} \end{aligned}$$
(18)

The elements of \(e_{\mathcal {K}}\left( A\right) \) are called the extreme points of A.

The closure operator \(\sigma _{\mathcal {K}}\) can be recovered from \(e_{\mathcal {K}}\) as follows:Footnote 37

$$\begin{aligned} \sigma _{\mathcal {K}}\left( A\right) \ =\ A\cup \{ x\in X\diagdown A\ |\ x\notin e_{\mathcal {K}}\left( A\cup x\right) \} \end{aligned}$$
(19)

Thus, \(\mathcal {K}\), \(\sigma _{\mathcal {K}}\) and \(e_{\mathcal {K}}\) all encode the same information.

We should also mention the recent work of Danilov and Koshevoy (2009), who study pairs of operators \(\left( \sigma ,e\right) \) satisfying \(e\left( A\right) \subseteq A\subseteq \sigma \left( A\right) \) for any \(A\in 2^{X}\) and related by the analogue of condition (18):

$$\begin{aligned} x\in e\left( A\right) \ \ \ \Leftrightarrow \ \ \ x\notin \sigma ( A\diagdown x) \end{aligned}$$
(20)

Danilov and Koshevoy do not assume that these operators are derived from an underlying closure space. By directly investigating the duality (20), they are able to map properties of \(\sigma \) into the corresponding properties of e and vice versa, obtaining a novel characterisation of closure operators (Danilov and Koshevoy 2009, Lemma 2) and a new derivation of Ando’s (2006) axiomatisation of the extreme point operators associated with closure spaces (Danilov and Koshevoy 2009, Proposition 5). We comment on a connection between their Lemma 2 and our characterisation of closed opportunity relations in Sect. 4.1.

B Abstract convex geometries

An abstract convex geometry (ACG) is a closure space for which the closure operation has the (algebraic) flavour of forming a convex hull. If \(\mathcal {K}\) is an ACG, then the elements of \(\mathcal {K}\) are usually referred to as the convex subsets of X, rather than the closed sets.

Formally, an ACG is a closure space \(\mathcal {K}\) that satisfies:

  1. (C2)

    If \(A\in \mathcal {K}\diagdown \left\{ X\right\} \), then \(A\cup x\in \mathcal {K}\) for some \(x\in X\diagdown A\).

The sense in which (C2) captures the idea of convexity is clarified by the following important result:

Theorem B.1

If \(\mathcal {K}\) is an ACG, then the associated closure operator \(\sigma =\sigma _{\mathcal {K}}\) satisfies:

  1. (CC4)

    For any \(A\subseteq X\) with \(\sigma \left( A\right) =A\) and any \(x,y\in X\diagdown A\) with \(x\ne y\), if \(y\in \sigma (A\cup x)\), then \(x\notin \sigma (A\cup y)\).

    Conversely, if \(\sigma \) is a closure operator satisfying (CC4), then \(\mathcal {K}_{\sigma }\) satisfies (C2).

Condition (CC4) is called the anti-exchange property.

Edelman and Jamison (1985) provide a range of other conditions on a closure space that are equivalent to the anti-exchange property of its associated closure operator. For our purposes, the most important of these is the following generalisation of the Minkowski–Krein–Milman property:

Theorem B.2

(Edelman and Jamison, Theorem 2.1) A closure space \(\mathcal {K}\) is an ACG iff \(\sigma _{\mathcal {K}}\left( A\right) =\sigma _{\mathcal {K}}\left( e_{\mathcal {K}}\left( A\right) \right) \) for any \(A\subseteq X\).

Thus, the extreme points of A “carry” the convex hull (closure) of A.

Recall that Ando (2006) and Danilov and Koshevoy (2009) give an axiomatic characterisation of the class of extreme point operators associated with closure spaces. Given an operator within this class, Danilov and Koshevoy (2009, Proposition 5, Corollary 3) provide necessary and sufficient conditions for it to be the extreme point operator for some ACG. We discuss a connection between their result and our characterisation of convex opportunity relations in Sect. 5.1.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ryan, M. Essentiality and convexity in the ranking of opportunity sets. Soc Choice Welf 47, 853–877 (2016). https://doi.org/10.1007/s00355-016-0994-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00355-016-0994-8

Keywords

Search

Navigation