Single-dipped preferences with satiation: strong group strategy-proofness and unanimity

Abstract

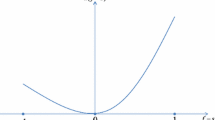
We study the problem of the location of a public facility that generates negative externalities. We consider that agents have single-dipped preferences with satiation: each agent considers a location as the worst, the “dip”, and the farther the location is from the dip, the better for the agent. In addition, an agent might be indifferent between all the locations sufficiently far from his dip, reaching his highest level of satisfaction. We characterize the family of strongly group strategy-proof and unanimous rules. Opposite to previous results without satiation, the locations selected are not necessarily at the extremes of the alternatives’ space.

Appendix

Lemma 1

Let $b\in \{0,T\}$ and $R\in {\mathcal {R}}_{D}^{n}$ be such that $U(R)=\emptyset$. If $E(b;R)\not =\emptyset$, then $\#E(b;R)=1$.

Proof

Let $b=0$ and $R\in {\mathcal {R}}_{D}^{n}$ be such that $U(R)=\emptyset$ and $E(0;R)\not =\emptyset$. Then, there exists at least one alternative $a\in P(R)$, such that $aR_{i}0$ for all $i\in N$ and $aP_{j}0$ for some $j\in N$. Since $U(R)=\emptyset$, then $N_{0}(R)\not =\emptyset$ and $N_{T}(R)\not =\emptyset$. By definition $0\not \in E(0;R)$.

First, take any $i\in N_{0}(R)$. By definition, $0P_{i}T$ and any $x\in [0,l(R_{i})]$ is such that $xI_{i}0$, and any $k\in (l(R_{i}),T]$ is such that $0P_{i}k$. Hence, no alternative $k^{\prime }\in (l_{min}(R_{N_{0}(R)}),T]$ belongs to E(0; R). As $E(0;R)\not =\emptyset$ and $0\not \in E(0;R)$, $E(0;R)\subseteq (0,l_{min}(R_{N_{0}(R)})]$. Hence, any alternative $a\in E(0;R)$ is such that $aI_{i}0$ for each $i\in N_{0}(R).$

Second, take any $i\in N_{T}(R)$. Then, $TP_{i}0$ and any alternative $y\in [h(R_{i}),T]$ is such that $yP_{i}0$. Notice that for each $i\in N_{T}(R)$, $\max W(0;R_{i})=cI_{i}0$ and any $w\in$ $W(0;R_{i})\diagdown \{c\}$ is such that $0P_{i}w$. Hence, for every agent $i\in N_{T}(R)$ it should be that if $a\in E(0;R)$, then $a\in [c,T]$. Therefore, $E(0;R)\subseteq [\overline{c}(R),T]$.

If $N_{0T}(R)=\emptyset$ and as $U(R)=\emptyset$, then $l_{min}(R_{N_{0}(R)})<h_{max}(R_{N_{T}(R)})$. Furthermore, $E(0;R)\subseteq (0,l_{min}(R_{N_{0}(R)})]\cap [\overline{c}(R),T]$. As it should be that for all $i\in N_{0}(R),a\in E(0;R)$ is such that $aI_{i}0$, then it can not be that an alternative $z\in (h_{max}(R_{N_{T}(R)}),T]$ belongs to E(0; R), because $0P_{i}z$ for any $i\in N_{0}(R)$. Therefore, $\overline{c} (R)\le l_{min}(R_{N_{0}(R)})\$and $E(0;R)\subseteq (0,l_{min}(R_{N_{0}(R)})]$.

We can distinguish between two cases:

Case (i) $\overline{c}(R)<$ $l_{min}(R_{N_{0}(R)})$. By definition, $a>b>d(R_{i})$ implies that $aP_{i}bP_{i}d(R_{i})$. Hence, for any alternative $x>\overline{c}(R)$ it is that $xR_{i}\overline{c}(R)$ for each $i\in N_{T}(R)$ and $xP_{j}\overline{c}(R)$ for some $j\in N_{T}(R)$. Then, $l_{min}(R_{N_{0}(R)})R_{i}\overline{c}(R)P_{i}0$ for all $i\in N_{T}(R)$ and $l_{min}(R_{N_{0}(R)})P_{j}\overline{c}(R)P_{i}0$ for some $j\in N_{T}(R)$. Furthermore, $l_{min}(R_{N_{0}(R)})I_{i}0$ for all $i\in N_{0}(R)$. Any other alternative $y\in (0,l_{min}(R_{N_{0}(R)}))$ is such that $l_{min}(R_{N_{0}(R)})P_{i}y$ for some $i\in N_{T}(R)$; hence $y\not \in P(R)$. We conclude that $l_{min}(R_{N_{0}(R)})=E(0;R)$ (Fig. 9).

Fig. 9

$E(0;R)\not =\emptyset$, $N_{0T}(R)=\emptyset$, and $\overline{c} (R)< l_{min}(R_{N_{0}(R)})$

Case (ii) $\overline{c}(R)=l_{min}(R_{N_{0}(R)})$. Then $(0,l_{min}(R_{N_{0}(R)})]\cap [\overline{c}(R),T]=$ $E(0;R)=\overline{ c}(R)=l_{min}(R_{N_{0}(R)})$ (Fig. 10).

Fig. 10

$E(0;R)\not =\emptyset$, $N_{0T}(R)=\emptyset$, and $\overline{c} (R)=$ $l_{min}(R_{N_{0}(R)})$

Suppose that $N_{0T}(R)\not =\emptyset$. Then, $i\in N_{0T}(R)$ it should be that $0I_{i}T$ and any $x\in [0,l(R_{i})]\cup [h(R_{i}),T]$ is such that $xI_{i}0$, and any $y\in (l(R_{i}),h(R_{i}))$ is such that $0P_{i}y$. Hence, no alternative $y\in (l(R_{i}),h(R_{i}))$ belongs to E(0; R). Then, for any $a\in E(0;R)$ and any $i\in N_{0T}(R)$ it should be that $aI_{i}0$. Hence, $E(0;R)\subseteq U(R_{N_{0T}(R)})\diagdown \{0\}$ and $[0,l_{min}(R_{N_{0T}(R)})]\cup [h_{max}(R_{N_{0T}(R)}),T]\subseteq U(R_{N_{0T}(R)})$.

Adding up, when $N_{0T}(R)\not =\emptyset$, $N_{0}(R)\not =\emptyset$ and $N_{T}(R)\not =\emptyset$, then $E(0;R)\subseteq (0,l_{min}(R_{N_{0}(R)})]\cap [\overline{c}(R),T]\cap U(R_{N_{0T}(R)})$. In such case, we distinguish between two cases:

Case (iii) $l_{min}(R_{N_{0}(R)})\le l_{min}(R_{N_{0T}(R)})$. For any $a\in E(0;R)$ it should be that $aI_{i}0$ for all $i\in N_{0}(R)\cup N_{0T}(R)$. Any alternative $x\in (0,l_{min}(R_{N_{0}(R)})]$ accomplishes this latter condition. Furthermore, any $y\in U(R_{N_{0T}(R)})\diagdown [0,l_{min}(R_{N_{0}(R)})]$ is such that $0P_{i}y$ for all $i\in N_{0}(R)$ although $0I_{i}y$ for all $i\in N_{0T}(R)$. As $E(0;R)\not =\emptyset$, $N_{0}(R)\not =\emptyset$, and $N_{T}(R)\not =\emptyset$, $\overline{c} (R)\le l_{min}(R_{N_{0}(R)})<T$. Hence $E(0;R)\subseteq (0,l_{min}(R_{N_{0}(R)})]$. By definition, $a>b>d(R_{i})$ implies $aP_{i}bP_{i}d(R_{i})$. Since $d(R_{i})\le \overline{c}(R)\le$ $l_{min}(R_{N_{0}(R)})$, for any $i\in N_{T}(R)$ and any alternative $e> \overline{c}(R)$, $eP_{i}\overline{c}(R)$. Furthermore $\overline{c} (R)R_{i}0$ for all $i\in N_{T}(R)$ and $\overline{c}(R)P_{j}0$ for some $j\in N_{T}(R)$. Then, $l_{min}(R_{N_{0}(R)})P_{i}\overline{c}(R)P_{i}0$ for some $i\in N_{T}(R)$ and $l_{min}(R_{N_{0}(R)})R_{i}0$ for all $i\in N$. We conclude that $l_{min}(R_{N_{0}(R)})=E(0;R)$ (Fig. 11).

Fig. 11

$E(0;R)\not =\emptyset$, $N_{0T}(R)\not =\emptyset$, and $l_{min}(R_{N_{0}(R)})\le l_{min}(R_{N_{0T}(R)})$

Fig. 12

$E(0;R)\not =\emptyset$, $N_{0T}(R)\not =\emptyset$, and $l_{min}(R_{N_{0}(R)})>l_{min}(R_{N_{0T}(R)})$. There is no alternative $x\in U(R_{N_{0T}(R)})$ such that $x\in (l_{min}(R_{N_{0T}(R)}),l_{min}(R_{N_{0}(R)})]$

Case (iv) $l_{min}(R_{N_{0}(R)})>l_{min}(R_{N_{0T}(R)})$. For any $a\in E(0;R)$ it should be that $aI_{i}0$ for all $i\in N_{0}(R)\cup N_{0T}(R)$. Any alternative $x\in (0,l_{min}(R_{N_{0T}(R)})]$ accomplishes this latter condition, however, it is not the unique interval with this property. There might exist a preference profile $R\in {\mathcal {R}}_{D}^{n}$ where there exist an interval $[h(R_{j}),l(R_{j^{\prime }})]$ for $j,j^{\prime }\in N_{0T}(R)$, $j\not =j^{\prime }$ such that any alternative $y\in [h(R_{j}),l(R_{j^{\prime }})]$ is such that $y\not \in (0,l_{min}(R_{N_{0T}(R)}))$ and $yI_{i}0$ for all $i\in N_{0}(R)\cup N_{0T}(R)$. This opens the possibility of three subcases:

(iv.a) There is no alternative $x\in U(R_{N_{0T}(R)})$ such that $x\in (l_{min}(R_{N_{0T}(R)}),l_{min}(R_{N_{0}(R)})]$. Hence, for any $y\in (l_{min}(R_{N_{0T}(R)}),l_{min}(R_{N_{0}(R)})]$ it is that $0R_{i}y$ for all $i\in N_{0T}(R)$ and $0P_{j}y$ for some $j\in N_{0T}(R)$. Hence, $y\not \in E(0;R)$. Furthermore, any alternative $z\in (l_{min}(R_{N_{0}(R)}),T]$ is such that $0R_{i}z$ for all $i\in N_{T}(R)$ and $0P_{j}z$ for some $j\in N_{T}(R)$. Hence, $z\not \in E(0;R)$. Therefore, any $a\in E(0;R)$ should be such that $a\in [\overline{c} (R),l_{min}(R_{N_{0T}(R)})]$. Since $d(R_{i})\le \overline{c}(R)\le$ $l_{min}(R_{N_{0T}(R)})$, for any $i\in N_{T}(R)$ and any alternative $e\ge \overline{c}(R)$, $eR_{i}\overline{c}(R)$ and $eP_{j}\overline{c}(R)$ for some $j\in N_{T}(R)$. Then, $l_{min}(R_{N_{0T}(R)})P_{i}\overline{c} (R)P_{i}0$ for some $i\in N_{T}(R)$ and $l_{min}(R_{N_{0T}(R)})R_{i}0$ for all $i\in N$. We conclude that $l_{min}(R_{N_{0T}(R)})=E(0;R)$ (Fig. 12).

Fig. 13

$E(0;R)\not =\emptyset$, $N_{0T}(R)\not =\emptyset$, and $l_{min}(R_{N_{0}(R)})>l_{min}(R_{N_{0T}(R)})$. There is no $l(R_{j^{\prime }})\in U(R_{N_{0T}(R)})$ for $j^{\prime }\in N_{0T}(R)$ such that $l(R_{j^{\prime }})>l_{min}(R_{N_{0}(R)})$

Fig. 14

$E(0;R)\not =\emptyset$, $N_{0T}(R)\not =\emptyset$, and $l_{min}(R_{N_{0}(R)})>l_{min}(R_{N_{0T}(R)})$. There exist $l(R_{j^{\prime }})\in U(R_{N_{0T}(R)})$ for $j^{\prime }\in N_{0T}(R)$ such that $l(R_{j^{\prime }})\ge l_{min}(R_{N_{0}(R)})$

(iv.b) There exists an alternative $x\in U(R_{N_{0T}(R)})$ such that $x\in (l_{min}(R_{N_{0T}(R)}),l_{min}(R_{N_{0}(R)})]$ and there is no interval $[h(R_{j}),l(R_{j^{\prime }})]\subset U(R_{N_{0T}(R)})$ for $j,j^{\prime }\in N_{0T}(R)$ such that $l(R_{j^{\prime }})>l_{min}(R_{N_{0}(R)})>h(R_{j})>l_{min}(R_{N_{0T}(R)})$. First, notice that $x\not =l_{min}(R_{N_{0}(R)})$ as there is no a unanimous interval for $N_{0T}(R)$ that includes that alternative. Furthermore, as any $a\in E(0;R)$ should accomplish that $aI_{i}0$ for all $i\in N_{0}(R)\cup N_{0T}(R)$, then $a\in (0,l_{min}(R_{N_{0}(R)}))$. As $N_{T}(R)\not =\emptyset$, then $a\in [\overline{c}(R),l_{min}(R_{N_{0}(R)}))$. Let $\overline{l} (R_{N_{0T}(R)})=\underset{i\in N_{0T}(R)}{\max }\{\max l(R_{i}):l(R_{i})\in U(R_{N_{0T}(R)})$ and $l(R_{i})<l_{min}(R_{N_{0}(R)})\}$. As $E(0;R)\not =\emptyset$ it should be that $\overline{l}(R_{N_{0T}(R)})\ge \overline{c}(R)$, otherwise there is no alternative $y\in [\overline{c}(R),l_{min}(R_{N_{0}(R)}))$ such that $yI_{i}0$ for any $i\in N_{0T}(R)$. Adding up, $l_{min}(R_{N_{0}(R)})>\overline{l}(R_{N_{0T}(R)})\ge \overline{c }(R)\le l_{min}(R_{N_{0T}(R)})$ and any $a\in E(0;R)$ is such that $a\in [\overline{l}(R_{N_{0T}(R)}),l_{min}(R_{N_{0}(R)}))$. However, no alternative $z\in (\overline{l}(R_{N_{0T}(R)}),l_{min}(R_{N_{0}(R)}))$ belongs to $U(R_{N_{0T}(R)})$. Hence, we conclude that $\overline{l} (R_{N_{0T}(R)})=E(0;R)$ (Fig. 13).

(iv.c) There exists an alternative $x\in U(R_{N_{0T}(R)})$ such that $x\in (l_{min}(R_{N_{0T}(R)}),l_{min}(R_{N_{0}(R)})]$ and there is an interval $[h(R_{j}),l(R_{j^{\prime }})]\subset U(R_{N_{0T}(R)})$ for $j,j^{\prime }\in N_{0T}(R)$ such that $l(R_{j^{\prime }})\ge l_{min}(R_{N_{0}(R)})>l_{min}(R_{N_{0T}(R)})>h(R_{j})$. First, notice that $h(R_{j})\not =l_{min}(R_{N_{0T}(R)})$ and that $l_{min}(R_{N_{0}(R)})I_{i}0$ for all $i\in N_{0T}(R)\cup N_{0}(R)$. For any $a\in E(0;R)$ it should be that $aI_{i}0$ for all $i\in N_{0T}(R)\cup N_{0}(R)$, hence, $a\in U(R_{N_{0T}(R)})$ and $a\le l_{min}(R_{N_{0}(R)})$. As $N_{T}(R)\not = \emptyset$, $a\ge \overline{c}(R);$ therefore $\overline{c}(R)\le l_{min}(R_{N_{0}(R)})$. In particular, $l_{min}(R_{N_{0}(R)})R_{i}0$ for all $i\in N_{T}(R)$ and $l_{min}(R_{N_{0}(R)})P_{j}0$ for some $j\in N_{T}(R)$. By definition, for any other alternative y such that $d(R_{i})<y<l_{min}(R_{N_{0}(R)})$, there exists an agent $i^{\prime }\in N_{T}(R)$ such that $l_{min}(R_{N_{0}(R)})P_{i^{\prime }}y$. Hence, we conclude that $E(0;R)=l_{min}(R_{N_{0}(R)})$ (Fig. 14).

A symmetric argument can be used for the case where $U(R)=\emptyset$ and $E(T;R)\not =\emptyset$. $\square$