Matching structure and bargaining outcomes in buyer–seller networks

Abstract

We examine the relationship between the matching structure of a bipartite (buyer–seller) network and the (expected) shares of the unit surplus that each connected pair in this network can create. We show that in different bargaining environments, these shares are closely related to the Gallai–Edmonds Structure Theorem. This theorem characterizes the structure of maximum matchings in an undirected graph. We show that the relationship between the (expected) shares and the Structure Theorem is not an artefact of a particular bargaining mechanism or trade centralization. However, this relationship does not necessarily generalize to non-bipartite networks or to networks with heterogeneous link values.

1 Introduction

In this note, we examine the relationship between the matching structure of a bipartite (buyer–seller) network and the expected shares of the unit surplus that each connected pair in this network can create. As we discuss below, these shares are closely related to a celebrated result in graph theory, the Gallai–Edmonds (GE hereafter) Structure Theorem. Although the recurrent appearance of this theorem in different bargaining contexts is intriguing and hints at a deeper connection between the economic power of player-nodes and their classification in the GE partition, a specific bargaining framework may lie behind this connection. Particularly, the examination of some proposed non-cooperative mechanisms reveals that they are (implicitly) centralized and, hence, conducive to outcomes that maximize the number of trades. As the GE theorem characterizes the structure of maximum matchings in a graph, its connection to the outcome of a centralized bargaining game may appear unsurprising. However, we show that some recently proposed and completely decentralized protocols lead also to equilibrium payoffs that reflect the GE partition. Furthermore, we show that several cooperative solution concepts, which are driven by the competition among players and coalitions, lead to results that confirm the essential importance of the Structure Theorem. Given its pervasiveness in a rich variety of bargaining environments, we believe that the Structure Theorem should take its rightful place as a fundamental result at the intersection of graph and game theory.

2 Gallai–Edmonds Structure Theorem

The theorem characterizes the structure of maximum matchings in a graph (network) G = {N,L} that consists of the set N of nodes (vertices) and the set L of links (edges). G is connected when there is a path between every pair of nodes in N and it is disconnected otherwise. A disconnected graph consists of connected subgraphs (components) and, possibly, singleton nodes. An induced subgraph G(T) consists of all edges with both ends in the set $\hbox {T}\subseteq \hbox {N}$. A matching m(G) in G is a set of links from L such that no two links in m(G) cover the same node (i.e., the links in m(G) are pairwise disjoint). A perfect matching covers all vertices in N. A maximum matching is a matching with maximal cardinality. Most importantly for our purposes, the Structure Theorem uniquely partitions the set of nodes N into three subsets, $N = \hbox {D}\cup \hbox {A}\cup \hbox {C}$. The set D contains vertices that are not covered by at least one maximum matching. All vertices in $\hbox {N}\backslash \hbox {D}$ that are linked to at least one node in D are collected in the set A, while the set $\hbox {C} = \hbox {N}\backslash (\hbox {D}\cup \hbox {A})$ contains all remaining nodes. In the analysed trading environments, nodes in the set D (A) have a relatively weak (strong) bargaining position, while the nodes in C have an intermediate bargaining strength. We will refer to the nodes in the set D (A) as under-demanded (over-demanded) and to the nodes in the set C as perfectly matched.

Buyer–seller networks belong to the important class of bipartite networks. In such networks, vertices can be divided into two subsets (say, buyers and sellers) with no connections between nodes in the same subset. In this special case, the GE Structure Theorem allows for sharper conclusions than the general version of this result. For a connected bipartite network G = {N,L}, the GE partition of the set of nodes $\hbox {N}= \hbox {D}\cup \hbox {A}\cup \hbox {C}$ has the following important properties,¹

• 1. $\hbox {N}^{\mathrm{G}}(\hbox {D}$’) $\subseteq \hbox {A}$ for all D’$\subseteq$D, i.e., all nodes in D are linked to the nodes in A only.

• 2. $|\hbox {N}^{\mathrm{G}}(\hbox {A}$’$)| > |\hbox {A}$’| for all A’$\subseteq$A and $|\hbox {N}^{\mathrm{G}}(\hbox {C}')| \ge |\hbox {C}'|$ for all $\hbox {C}'\subseteq \hbox {C}$

• 3. Every maximum matching m(G) consists of a perfect matching in C and a matching of A into D, i.e., all vertices in A are covered, at least one vertex in D is not. Therefore, |m(G)| = |C|/2 + |A|.

• 4. Edges between C and A never belong to a maximum matching,

where |T| denotes the cardinality of the set T and $\hbox {N}^{\mathrm{G}}(\hbox {T})$ is the set of nodes that are connected in G to at least one node in the set T.

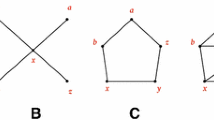
As noted by Corominas-Bosch (2004), the GE partition gives rise to a unique decomposition of a bipartite graph into three disjoint components that can be described as excess demand, excess supply and balanced components. For example, under-demanded buyer (seller) nodes belong to the set D in an excess demand (supply) component. Figure 1 illustrates the GE partition/decomposition.

Fig. 1

GE partition/decomposition. The bipartite network that connects sellers {1,2,3,4,5} with buyers {6,7,8,9,10} is GE decomposed into a balanced (G1), an excess supply (G2) and an excess demand (G3) component. The GE partition is A $=$ {5,8}, D $=$ {3,4,9,10}, C $=$ {1,2,6,7}

3 Non-cooperative mechanisms

In what follows, we consider a generic non-cooperative bargaining game BG(G) on a bipartite graph G= {N, L} with the bipartition N= $\hbox {B}\cup \hbox {S}$. For simplicity, we will often refer to G as a buyer-seller network and to the nodes in the set B (S) as buyers (sellers). Each link (b,s)$\in \hbox {L}$ represents a unit (trade) surplus for the buyer $\hbox {b}\in \hbox {B}$ and the seller $\hbox {s} \in \hbox {S}$.

Several papers consider different bargaining formats in the BG(G). In Corominas-Bosch (2004), players bargain over the unit surplus following a multilateral protocol, in which at any date all players from one side of the market (sellers or buyers) call out prices and the connected agents on the other side of the market simultaneously respond to the offers. When the discount factor approaches one, there is a subgame perfect equilibrium (SPE hereafter) in this game, in which the payoffs to the players in the sets A, D and C of the GE partition converge to 1, 0 and 1/2, respectively. Corominas-Bosch (2004) shows that this SPE corresponds to a selection of the Walrasian outcome and refers to it as the reference solution.

Building on the results in Demange et al. (1986), Kranton and Minehart (2001) propose an ascending-bid simultaneous auction game on a buyer-seller network, where each seller owns one unit of a homogenous good (of no value to her) and buyers have heterogeneous valuations². In the special case of identical valuations for all buyers, this auction induces the GE decomposition (partition) of the bipartite network (of the set of nodes in this network). The goods are sold at the clearing price of zero in all excess supply and balanced sub-networks. In the excess demand subnetworks the clearing price is one. These prices imply the same payoffs as the reference solution in Corominas-Bosch (2004) except for the nodes in the balanced subnetworks.

Finally, Polanski (2007) describes a bilateral bargaining game, in which a maximum number of linked buyer–seller pairs is matched randomly and each matched pair bargains according to the protocol proposed by Rubinstein and Wolinsky (1985). This bargaining game has a unique SPE, in which players’ payoffs are determined by the GE partition: The expected SPE payoffs for players in the set A (D) are above (below) 1/2, while players in the set C expect 1/2. In an example, he shows also that this result does not generalize to non-bipartite graphs.

In all these mechanisms, the GE partition (decomposition) plays a crucial role. However, all of them are (implicitly) centralized as they all force outcomes that maximize the number of trades. This centralization may be the driving force behind the close relationship between the bargaining outcomes and the structure theorem.

Recently, fully decentralized bargaining games on networks have been proposed. As we show below, the equilibrium outcomes in these games also lend support to the GE partition as the key determinant of the expected shares.

Abreu and Manea (2012a, b) study an infinite horizon game, in which pairs of players connected by a (not necessarily bipartite) network are randomly matched to bargain over a unit surplus. One of the players (the proposer) in the matched link is chosen randomly (with equal probability) to make an offer to the other player (the responder) specifying a division of the unit surplus. If the responder accepts the offer, the two players exit the game with the (discounted) shares agreed on. All links that cover at least one of the agreeing nodes are then removed from the network. The matched players (and their links) remain in the game in case of disagreement. Independently of whether agreement is reached or not, the game proceeds to the next date. Abreu and Manea (2012a) extend this game to an alternative model, in which individual players are selected according to some probability distribution, and a chosen player can select a neighbour with whom to bargain. The authors show that a Markov perfect equilibrium (MPE hereafter) always exists in their game but MPEs are not necessarily efficient. Efficiency can be achieved by using non-Markovian strategies. In the Appendix, we prove the following proposition that specifies the payoff ranges in the efficient (non-Markovian) SPE constructed by Abreu and Manea (2012a).³

Proposition 1

For a bipartite network G = {N,L}, there is a SPE in the Abreu and Manea (2012a, b) game such that the expected limit SPE payoffs $\mathbf{x} \in \mathrm{R}^{|\mathrm{N}|}$, when the discount factor approaches one, verify,

$$\begin{aligned} x_k \le 1/2\; if \; k\in D, x_k \ge 1/2\; if\; k\in A, x_k =1/2 \; if \; k\in C, \end{aligned}$$

(1)

where the sets A, D and C result from the GE partition of the set of nodes N.

Manea (2011) considers a different decentralized bargaining game on the network G: In each period t, a link in G is selected randomly (with a positive probability) and one of the players (the proposer) in this link is chosen randomly (with equal probability) to make an offer to the other player (the responder) specifying a division of the unit surplus. If the responder accepts the offer, the two players exit the game with the (discounted) shares agreed on. Next period two new players assume the same positions in the network. If the responder rejects the offer, the two players remain in the game for the next period. In period t+1, the game is repeated with the set of players consisting of the ones from period t, with the departing players being replaced by their replicas if an agreement obtains in period t. Note that, unlike games discussed previously, links are not successively removed from G as the game progresses but remain in place for the entire (infinite) history of the game.

Manea (2011) shows that this game has a unique SPE outcome, which is stationary. In the Appendix, we prove that the unique limit SPE payoffs in this game depend in a clear-cut manner on the GE partition.

Proposition 2

For a bipartite network G = {N,L}, the expected limit payoffs $\mathbf{x} \in {\mathrm{R}}^{|\mathrm{N}|}$ in a SPE of the Manea (2011) game verify,

$$\begin{aligned} x_k < 1/2\; if\; k\in D, x_k > 1/2 \; if \; k\in A, x_k =1/2 \; if \; k\in C, \end{aligned}$$

(2)

where the sets A, D and C result from the GE partition of the set of nodes N.

4 Cooperative environments

The Structure Theorem reappears naturally in cooperative environments, i.e., when no particular bargaining protocol is prescribed. Recall that in the bargaining game BG(G) on the graph G, the players in the set $\hbox {N}= \hbox {S}\cup \hbox {B}$ are embedded in a bipartite network G= {N, L} and each link $(\hbox {b,s})\in \hbox {L}$ represents one unit of surplus. We can interpret this situation as a transferable utility (TU) game with the characteristic function v that assigns to each coalition $\hbox {T}\subseteq \hbox {N}$ the cardinality of a maximum matching m(G(T)) in the induced subgraph G(T),

$$\begin{aligned} v\left( T \right) =\left| {m\left( {G\left( T \right) } \right) } \right| \qquad for\; all\;T \subseteq N. \end{aligned}$$

We will refer to this TU game as TU-BG(G). We note that this game is zero-normalized, $v\left( {\left\{ i \right\} } \right) =0$, and that it is an instance of assignment games (Shapley and Shubik 1971), in which each pair of nodes can create a unit surplus if it is connected and zero otherwise.

The best-known set-valued solution for TU games is the core, which assigns to every TU game $\left( {N,v} \right)$ the set of undominated payoff vectors $\{ x\in R^{\left| N \right| }:\sum _{i\in N} x_i =v\left( N \right) \; and\; \sum _{i\in T} x_i \ge v( T$) $\; for\; all\; \hbox {T} \subseteq \hbox {N} \}$. As the TU-BG(G) is an instance of assignment games, its core is nonempty (Shapley and Shubik 1971). In their Proposition 3.2, Kleinberg and Tardos (2008) show that a core outcome (which they call a stable outcome) of TU-BG(G) satisfies,

Result 1

If $\mathbf{x} \in \mathrm{R}^{|\mathrm{N}|}$ is in the core of TU-BG(G) for a bipartite G= {N, L} then,

$$\begin{aligned} x_k =0 \; if \; k\in D\; and \;x_k =1\; if \; k\in A, \end{aligned}$$

(3)

where the sets A and D result from the GE partition of the set of nodes N in G.

While core allocations deliver clear-cut results for all nodes in the sets A and D, they are compatible with a continuum of values allocated to nodes in the set C. In particular, the worst core allocation for sellers (buyers) in this subset is zero.

Incidentally, the last result also applies to the nucleolus (Schmeidler 1969) of the TU-BG(G) as the latter lies in the nonempty core. Moreover, the fact that this game is an assignment game allows for a generalization of Result 1 to the kernel (Davis and Maschler (1965)) and to the bargaining set (Aumann and Maschler 1964). For assignment games, Driessen (1998) showed that the kernel lies in the core, while Solymosi (1999); Solymosi and Raghavan 2001) proved for these games that the core coincides with the bargaining set. Therefore, we have the following result.

Result 2

If $\mathrm{x} \in \mathrm{R}^{|\mathrm{N}|}$ belongs to the bargaining set/kernel or is equal to the nucleolus of TU-BG(G) for a bipartite graph G= {N, L} then,

$$\begin{aligned} x_k =0 \; if\; k\in D \; and\; x_k =1\; if \; k\in A, \end{aligned}$$

where the sets A and D result from the GE partition of the set of nodes N in G.

Kleinberg and Tardos (2008) refine the set of stable (core) outcomes by demanding that they are computed by the Nash bargaining solution. They show that the resulting balanced outcomes always exist in bipartite graphs. As a subset of the set of stable outcomes, balanced outcomes satisfy also our condition (3). Bayati et al. (2014) devise a dynamic mechanism that converges rapidly to a balanced outcome. Their results provide a dynamic justification for balanced outcomes and hence for the payoffs (3), showing that agents bargaining with each other in a realistic local manner can find such outcomes quickly. The extension of the Nash bargaining solution in Kleinberg and Tardos (2008) is identical to the symmetrically pairwise bargained outcomes, first proposed by Rochford (1984). She shows that these outcomes are equal to the intersection of the core and the kernel. In case of assignment games, this intersection reduces to the kernel (Driessen 1998). Furthermore, the competitive price vector and allocation in Kranton and Minehart (2000), i.e., a price vector and allocation that satisfy “supply equals demand” conditions in a buyer-seller network, boil down to the core outcome and the corresponding payoffs (3), when all links have unit values.

The above results demonstrate a clear and compelling relationship between the Structure Theorem and “competitive” solutions. However, other standard cooperative solutions for TU-BG(G), namely the Shapley value (Shapley 1953) and the position value⁴ (Borm et al. 1992), are not driven by competitive forces. Can they be similarly related to the Structure Theorem nevertheless? As the following example shows this is, generally, not the case. Consider the bipartite graph G= {N, L} in Fig. 2 with the set of vertices N= {1,...,13} and the set of links,

$$\begin{aligned} \hbox {L}=\left\{ {\left( {\hbox {i},\hbox {i}+1} \right) :\hbox {i}=1,\ldots ,12} \right\} \cup \left\{ {\left( {7,\hbox {i}} \right) :\hbox { i}=2,4,10,12} \right\} , \end{aligned}$$

where all odd (even) nodes belong to the set D (A) of the GE partition. In particular, the node 7 has the largest degree (i.e., it is covered by the largest number of links) and belongs to the set D, while all its neighbours are in the set A.

Fig. 2

A bipartite graph with all odd (even) nodes belonging to the set D (A) of the GE partition

The Shapley and the position value for the node 7 are (approximately) 0.55 and 0.70, respectively, while these values for its neighbour node 6 are 0.49 and 0.42. Therefore, these solutions are at odds with the Structure Theorem as they assign a lower value to a node in the set A as compared to the node in the set D. The reason seems to be that the Shapley and the position value capture the individual connectivity of players (node 7 is covered by six and node 6 by two links) rather than the more subtle competitive tension that is determined by the entire connection structure.

5 Conclusions

In this note, we argue that the GE Structure Theorem is an essential graph-theoretical tool in the analysis of network-restricted bargaining games, where each connected pair can create a unit surplus. We have shown that a rich variety of cooperative and non-cooperative solutions lead to qualitatively similar results for excess demand and excess supply (sub)networks. It seems, therefore, that we can use the GE partition independently of the bargaining mechanism or solution concept to classify nodes in a bipartite network as relatively weak (under-demanded), strong (over-demanded) or balanced (perfectly matched) with respect to their (expected) shares of the surplus. While this classification is fairly clear-cut for nodes in the first two classes (shares below or above 1/2, respectively), the situation of the nodes in the last class is somehow ambiguous and will, generally, depend on the particular bargaining mechanism.

The restriction to bipartite networks, where all matches generate the same surplus, allow us to focus on topological properties of such networks that are important in two-sided, network-restricted bargaining situations. The role of the Structure Theorem does not necessarily generalize to non-bipartite networks or to networks with heterogeneous link values [see, e.g., Polanski and Vega Redondo (2013) for a generalization of the Manea (2011) model in this direction].

As the Structure Theorem characterizes maximum matchings in a graph, it seems natural to relate it to efficient bargaining outcomes. However, this relationship can be elusive. Firstly, efficiency is sometimes difficult to define. This is, for example, the case in the dynamic game in Manea (2011), where an infinite number of players enter and leave the game. Furthermore, efficiency itself does not automatically align with the Structure Theorem as illustrated in our example of the (efficient) Shapley values. It seems that for the GE to matter, we need an outcome that is both, “efficient” and “competitive”.

Appendix

Proof of Proposition 1

We use in this proof the results in Theorem 1 and Proposition 2 in Abreu and Manea (2012a)—AM afterwards. Theorem 1 shows that their bargaining game on the graph G admits a limit SPE with efficient agreements along any equilibrium path and expected limit payoffs $\upsilon ^{*}(G)$. Proposition 2 states that $\upsilon _i^*(G)\ge 1/2\hbox { if }i$ is always efficiently matched in G.

Since all agreements in the AM construction are efficient, players who are always efficiently matched, stay efficiently matched after any such agreement. Hence, all players in the set $\hbox {A}\cup \hbox {C}$ in the original network G remain in $\hbox {A}\cup \hbox {C}$ for any network that arises in subgames on the equilibrium path (see step 1 in the proof of AM’s Proposition 2).

The following argument applies when G is bipartite. Take a player $i\in D$. Eventually, this player will either be isolated or reach an agreement with some player j. Since G is bipartite, i has only links to players in the original $\hbox {A}\cup \hbox {C}$ so j belongs to the original $\hbox {A}\cup \hbox {C}$. Thus, j is also in $\hbox {A}\cup \hbox {C}$ for the network in which i and j reach the agreement. By Proposition 2 in AM, j’s limit payoff in this network must be at least 1/2, which means that i’s maximum limit payoff from the agreement cannot exceed 1/2. Since i can only become isolated or reach an agreement that leaves him at most 1/2 in the course of the game, i’s limit expected payoff cannot exceed 1/2.

Similarly, the nodes in the set C are always efficiently matched and bargain over the unit surplus with the nodes in the set $\hbox {A}\cup \hbox {C}$ only and, hence, their expected limit payoffs cannot exceed 1/2. Therefore, the only possible payoff for the nodes in C is 1/2. $\square$

Proof of Proposition 2

First, we delete in a bipartite network G all links that connect two nodes in the set A or a node in the set A to another node in the set C of the GE partition. This decomposes G into three types of components: Balanced components, where all nodes belong to C, excess supply components with all sellers in D and all buyers in A and excess demand components with all sellers in A and all buyers in D (see, e.g., Fig. 1). In this GE decomposition of the graph G, we consider the limit equilibrium payoffs of the bargaining game played on each component separately.

By Theorem 5 in Manea (2011), all nodes in a balanced component (i.e., nodes in the set C) get the equilibrium limit payoffs of 1/2. This is because such a component has a perfect matching (property 3. of the GE partition) and, hence, is quasi-regularizable (Berge 1981).

In order to show that the equilibrium payoffs to the over-demanded buyers in an excess supply component (i.e., to the nodes in the set A in this component) are greater than 1/2, we apply the Algorithm $\hbox {A}^{\mathrm{BS}}(\hbox {G})$ in Manea (2011). This algorithm constructs a partition $\{B_1 ,\ldots ,B_{\bar{\mathrm{s}}}\}$ of buyers in this component such that (see his Proposition $3^{\mathrm{BS}})$,

$$\begin{aligned} \hbox {r}_{s+1} =\frac{|N^{G_{s+1} }\left( {B_{s+1} } \right) |}{\left| {B_{s+1} } \right| }>\frac{|N^{G_s }\left( {B_s } \right) |}{\left| {B_s } \right| }=\hbox {r}_s ,\hbox {s}=1,\ldots ,\text{ s }-1, \end{aligned}$$

where $G_{s+1}\; (G_1 =G)$ is obtained by removing from $G_s$ the set $B_s$ of buyers, the set $N^{G_s }\left( {B_s } \right)$ of adjacent sellers and all links covering at least one of the removed nodes.

As for any subset B’ of buyers in an excess supply component $|\hbox {N}^{\mathrm{G}}(\hbox {B}')| > |\hbox {B}'|$ by the property 2. of the GE partition, we have that,

$$\begin{aligned} \hbox {r}_{\bar{\mathrm{s}}} >\cdots >\hbox {r}_1 > 1. \end{aligned}$$

It follows, then, by the Theorem $4^{\mathrm{BS}}$, that each buyer in the subset $B_s$ will get a limit equilibrium payoff,

$$\begin{aligned} \hbox {x}_s =\frac{\hbox {r}_s}{1+\hbox {r}_s}>\frac{1}{2}. \end{aligned}$$

As by our construction under-demanded sellers in an excess supply component trade only with over-demanded buyers in the same component, the latter players (who all belong to the set D) obtain payoffs strictly below 1/2. By a symmetric argument, the payoff intervals for the nodes in the set A and D can be shown in each excess demand component.

We showed, therefore, that if the bargaining game is played separately on each of the components that result from the GE decomposition of G, then the limit equilibrium payoffs satisfy (2).

For sufficiently high discount factors, we can construct equilibria in the bargaining game on G, which generate the desired limit outcomes, as follows: Within each component of the GE decomposition players behave as if the game was played on this component only and there is a perpetual disagreement in all cross-component (i.e., A-A and A-C) links. The disagreement is rational as the sum of the limit payoffs (2) for each pair of nodes covered by a cross-component link exceeds 1 (note that the matching probabilities are irrelevant for the computation of the limit SPE payoffs as long as they are positive for each link, see Manea (2011)).

As the bargaining game on G has unique limit SPE payoffs (Lemma 6, Manea 2011), they must coincide with the payoffs in the constructed limit SPE. $\square$