Abstract
In card-based cryptography, designing AND protocols in committed format is a major research topic. The state-of-the-art AND protocol proposed by Koch, Walzer, and Härtel in ASIACRYPT 2015 uses only four cards, which is the minimum permissible number. The minimality of their protocol relies on somewhat complicated shuffles having non-uniform probabilities of possible outcomes. Restricting the allowed shuffles to uniform closed ones entails that, to the best of our knowledge, six cards are sufficient: the six-card AND protocol proposed by Mizuki and Sone in 2009 utilizes the random bisection cut, which is a uniform and cyclic (and hence, closed) shuffle. Thus, a question has arisen: “Can we improve upon this six-card protocol using only uniform closed shuffles?” In other words, the existence or otherwise of a five-card AND protocol in committed format using only uniform closed shuffles has been one of the most important open questions in this field. In this paper, we answer the question affirmatively by designing five-card committed-format AND protocols using only uniform cyclic shuffles. The shuffles that our protocols use are the random cut and random bisection cut, both of which are uniform cyclic shuffles and can be easily implemented by humans.
Similar content being viewed by others
Introduction
Card-based cryptography started from the “five-card trick” presented by den Boer in 1989 [2]. This card-based protocol performs a secure AND computation using two black cards  and three red cards
and three red cards  , where their backs
, where their backs  are all identical. This paper begins by introducing the five-card trick.
are all identical. This paper begins by introducing the five-card trick.
The Five-Card Trick
In card-based cryptography, manipulating Boolean values entails the use of the following encoding:

That is, the left card being black represents 0, and the left card being red represents 1. According to this encoding rule (1), Alice can put her private input bit \(a\in \{0,1\}\) on a table using two cards  , keeping its value hidden:
, keeping its value hidden:

Such a pair of face-down cards is called a commitment to a bit \(a\in \{0,1\}\). Similarly, Bob can put a commitment to his private input bit \(b\in \{0,1\}\) on the table, keeping its value secret from Alice (and others). Given the commitments to \(a\in \{0,1\}\) and \(b\in \{0,1\}\), along with a helping card  , the five-card trick [2] proceeds as follows.
, the five-card trick [2] proceeds as follows.
-
1.
Put the helping red card between the two input commitments, apply a NOT computation to the left commitment (to a) by swapping the positions of its two cards, so that we have a commitment to the negation \(\bar{a}\), and turn over the middle red card:

Note that the three cards in the middle will be
 , i.e., three red cards will be consecutive only when \(a = b = 1\), namely, \(a\wedge b=1\).
, i.e., three red cards will be consecutive only when \(a = b = 1\), namely, \(a\wedge b=1\). -
2.
Apply a random cut (denoted by \(\langle \cdot \rangle \)) to the sequence of the five cards:

A random cut, meaning a cyclic shuffling operation, uniformly randomly shifts the positions of the sequence without changing the orderFootnote 1. Mathematically, one permutation is uniformly randomly selected from
$$\begin{aligned} \{\mathsf {id},\,(1\,2\,3\,4\,5),\,(1\,2\,3\,4\,5)^2,\,(1\,2\,3\,4\,5)^3,\,(1\,2\,3\,4\,5)^4\}, \end{aligned}$$and the selected permutation is applied to the sequence of the five cards, where \(\mathsf {id}\) is the identity permutation and \((i_1\,i_2\,\dots \,i_\ell )\) represents a cyclic permutation. (Nobody knows the selected permutation.)
-
3.
Reveal the five cards. If the three red cards
 are consecutive (apart from cyclic rotation), then \(a \wedge b = 1\). Otherwise, \(a \wedge b = 0\).
are consecutive (apart from cyclic rotation), then \(a \wedge b = 1\). Otherwise, \(a \wedge b = 0\).
This is the five-card trick, which is simple and elegant. Although the five-card trick is extremely useful as mentioned, it has one drawback: it cannot deal with a logical conjunction of three or more variables, where players \(P_1,P_2,\dots ,P_n\) with \(n\ge 3\) want to conduct a secure multiparty AND computation. To overcome such a limitation, researchers have designed “committed-format AND protocols,” which are able to perform secure AND computation of three or more inputs.
The Six-Card AND Protocol in Committed Format
A committed-format AND protocol should produce a commitment to \(a \wedge b\):

from the input commitments to a and b. In contrast to the five-card trick, the output is obtained as a commitment to \(a \wedge b\), keeping its value secret; hence, the output commitment can be used as the input for another computation. There are many existing committed-format AND protocols in the literature (as shown in Table 1). Among these, we herein introduce the Mizuki–Sone protocol [10], which is considered to be the simplest for humans to execute. This protocol uses two helping cards  and proceeds as follows.
and proceeds as follows.
-
1.
Put the two helping cards between two input commitments, and turn them over:

-
2.
Rearrange the order of the sequence as:

-
3.
Apply a random bisection cut denoted by \(\left[ \, \cdot \, | \, \cdot \, \right] \), i.e., bisect the sequence of the six cards and shuffle the two halves:

Mathematically, the permutation \(\mathsf {id}\) or \((1\,4)(2\,5)(3\,6)\) is selected with a probability of 1/2, and the selected permutation is applied to the sequence of the six cards.Footnote 2
-
4.
Rearrange the order of the sequence as:

-
5.
Reveal the two left-most cards; then, a commitment to \(a \wedge b\) is obtained, depending on the order of the two face-up cards
 and
and  :
: 
This is the six-card AND protocol in committed format [10]. Given n input commitments to \(x_1,x_2,\dots ,x_n\), and executing such a committed-format AND protocol \(n-1\) times, a secure AND computation of n variables can be conducted, i.e., we can obtain a commitment to \(x_1\wedge x_2\wedge \cdots \wedge x_n\).
Known Results and Our Contribution
As discussed previously, committed-format AND protocols are a useful and indispensable primitive, and designing such AND protocols is a major research topic in the field of card-based cryptography. As enumerated chronologically in Table 1, there are many committed-format AND protocols. The Mizuki–Sone protocol proposed in 2009 [10] (and described in Section 1.2) is the fourth committed-format AND protocol in literature; it uses six cards, which are fewer than the previous three protocols [3, 13, 17] require; furthermore, as shown in the fourth column of Table 1, the Mizuki–Sone protocol is the first committed-format AND protocol that terminates in a finite number of shuffles (actually, it terminates after a single shuffle, namely, a random bisection cut, as indicated in Sect. 1.2).
After the invention of the Mizuki–Sone six-card AND protocol in 2009, it had been a challenging open question to determine whether one could construct an AND protocol (in committed format) with five cards or less. In 2015, Koch, Walzer, and Härtel [7] succeeded in answering the question appropriately; i.e., they presented a four-card AND protocol in committed format, which is the fifth protocol, as shown in Table 1. Their four-card protocol is optimal in terms of the number of required cards, because we need four cards for arranging two input commitments, as long as we follow the encoding (1). As shown in the fourth column of Table 1, their four-card AND protocol does not terminate with a fixed number of shuffles, indicating that it is a Las Vegas algorithm. In addition, they constructed a five-card AND protocol that terminates with a finite number of shuffles; see the sixth protocol shown in Table 1. Furthermore, they proved that there is no four-card committed-format AND protocol with a finite number of shuffles. Therefore, when we focus our attention on finite-runtime protocols, the five-card AND protocol in committed format is optimal in terms of the number of cards.
Now, let us revisit Table 1, which contains columns regarding shuffles being uniform, cyclic, and/or closed. Note that the first four protocols (from 1993 to 2009) all have the answer “yes.” We formally define the uniformity, cyclicity, and closedness of shuffles. Following the formal computation model of card-based protocols [8], a shuffle action is specified by a set \(\varPi \) of permutations and a probability distribution \({\mathcal {F}}\) on \(\varPi \):
if \({\mathcal {F}}\) is uniform, we say that the shuffle is uniform; if \(\varPi \) is a cyclic subgroup (of the symmetric group), we say that it is cyclic; if \(\varPi \) is a subgroup, we say that it is closed. For example, the random bisection cut that the Mizuki–Sone protocol uses can be formally written as:
Thus, a random bisection cut is surely a uniform and cyclic (and hence, closed) shuffle. The first three protocols [3, 13, 17] in Table 1 utilize only random cuts, which are also uniform and cyclic.
On the other hand, the two Koch–Walzer–Härtel protocols [7] use non-uniform and/or non-closed shuffles, such as:
and
Recently, Koch [5], as well as Ruangwises and Itoh [16], independently modified the Koch–Walzer–Härtel protocols to obtain protocols using only uniform shuffles, although those shuffles are non-closed; see the seventh and eighth protocols, as shown in Table 1. Thus, it is relatively difficult for humans to practically implement the existing four-card and five-card protocols. Note that Koch and Walzer [6] showed that any uniform closed shuffles can be implemented by human hands with the help of a secure implementation of the random cut (such as the Hindu cut [18, 19]).
Therefore, a natural question has arisen:
Can we construct a committed-format AND protocol with five cards or less using only uniform closed shuffles?
This is one of the most important open problems in card-based cryptography.
In this paper, we will answer this question affirmatively, i.e., we will design five-card AND protocols in committed format using only uniform closed shuffles (see the last two rows in Table 1). The shuffles that our protocols use are random cuts and random bisection cuts, both of which can be easily implemented by humans, as mentioned above. Hence, we believe that humans can effortlessly execute our protocols. Specifically, we propose two protocols: in Sect. 2, we present a five-card AND protocol whose expected number of shuffles is seven, while in Sect. 3, we improve upon the protocol, such that the expected number of shuffles can be reduced to 4.5 (although the construction is somewhat complicated).
An earlier version of this study was presented and appeared as a conference paper [1]. This present paper is extended compared to the conference paper: This paper provides another novel five-card AND protocol using a less number of shuffles and verify the correctness and security of the protocol. Section 3 is devoted to these new findings.
First Five-Card AND Protocol Using Only Uniform Cyclic Shuffles
In this section, we construct a five-card committed-format AND protocol using only uniform cyclic shuffles.
Idea
Here, we explain the idea behind our protocol.
Recall Steps 1 and 2 of the five-card trick:

Let the middle card be revealed, and assume that it happens to be  :
:

Then, there are four possibilities:

After turning the middle card face down, denote the sequence of cards by

for the sake of convenience [for example, the two left-most cards are not a commitment to a bit for the cases of (i) and (iii)]. Note that in cases (ii) and (iv), the first pair of cards can be regarded as a commitment to x, the second pair can be regarded as a commitment to y, and it holds that \(x \oplus y = a \wedge b\). Therefore, by applying the four-card XOR protocol [10] to the first four cards, one can obtain a commitment to \(x \oplus y = a \wedge b\) in these two cases. Even in cases (i) and (iii), we can continue the computation without leaking any information. The details will be revealed in the next subsection.
Description
Here, we provide the complete description of our protocol.
-
1.
Execute Step 1 of the five-card trick:

-
2.
Execute Step 2 of the five-card trick:

-
3.
Reveal the middle card, i.e., the third card. If the face-up card is
 , turn it over and return to Step 2. If it is
, turn it over and return to Step 2. If it is  , go to the next step. (The probability that
, go to the next step. (The probability that  appears is 2/5.)
appears is 2/5.) -
4.
Turn over the card
 :
: 
-
5.
Apply the procedure of the four-card XOR protocol [10] to the four left-most cards, as follows.
-
(a)
Rearrange the order as:

-
(b)
Apply a random bisection cut to the four left-most cards:

-
(c)
Rearrange the order again as:

-
(a)
-
6.
Reveal the two left-most cards.
-
(a)
If \( \ \mathrm{or}\ \) appears, then we have a commitment to \(a \wedge b\):
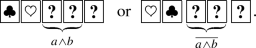
In the latter case, a NOT computation (which involves swapping the positions of two cards) brings a commitment to \(a \wedge b\).
-
(b)
If
 appears, then turn them over:
appears, then turn them over: 
rearrange the order as:

and return to Step 2. (The probability that
 appears is 1/2.)
appears is 1/2.)
-
(a)
This is our committed-format AND protocol. Since this protocol has loops, it does not terminate within a fixed number of shuffles; that is, it is a Las Vegas algorithm. The expected number of shuffles is seven, as follows. Let \({N_\mathrm {RC}}\) and \({N_\mathrm {RBC}}\) be the expected numbers of random cuts and random bisection cuts, respectively; then,
and
hence, we have \({N_\mathrm {RC}} = 5\) and \({N_\mathrm {RBC}} = 2\).
Pseudocode
The following is a pseudocodeFootnote 3 for our protocol, where we define:
and we simply write \((\mathsf {shuf}, \varPi )\) rather than \((\mathsf {shuf}, \varPi , {\mathcal {F}})\) if \({\mathcal {F}}\) is uniform; \((\mathsf {perm},{\pi })\) means to permute the sequence of cards according to \(\pi \), \((\mathsf {turn},{T})\) means to turn over all the cards in T, \((\mathsf {result},{i,j})\) means to terminate the protocol with an output commitment consisting of the ith and jth cards, and “visible seq.” means what are seen when looking at the sequence of cards on the table.

In the next subsection, we confirm that our protocol definitively produces a commitment to \(a \wedge b\) without leaking any information about a and b.
Correctness and Security
In this subsection, we verify the correctness and security of the protocol proposed in the previous subsections.
To this end, we make use of the KWH-tree, which is an excellent tool developed by Koch, Walzer, and Härtel [7]. That is, if one can write the KWH-tree satisfying some properties for a protocol, then it automatically implies that the protocol is correct and secure; see [7, 9] for the details.
We describe the KWH-tree for our five-card AND protocol in Fig. 1. The first box in Fig. 1 corresponds to an initial sequence, consisting of two input commitments and a helping red card; \(X_{00},\,X_{01},\,X_{10}\), and \(X_{11}\) represent the probabilities of \((a,b)=(0,0)\), \((a,b)=(0,1)\), \((a,b)=(1,0)\), and \((a,b)=(1,1)\), respectively. In the second box (and below), we write \(X_{0}\) rather than \(X_{00}+X_{01}+X_{10}\) and write \(X_{1}\) instead of \(X_{11}\). A polynomial, such as \(\frac{1}{5}X_{0}\) and \(\frac{1}{3}X_{1}\), represents the conditional probability that the current sequence is the one next to the polynomial, given the view seen on the table. Looking at the two boxes at the bottom, one can see that a commitment to \(a \wedge b\) is definitively obtained. Furthermore, in each box, the sum of all polynomials is equal to \(X_{0}+X_{1}\), implying that no information about a and b leaks.
Thus, the KWH-tree in Fig. 1 guarantees that our protocol is correct and secure.
Optimality of Our Protocol
As presented above, we constructed a five-card AND protocol in committed format using random cuts and random bisection cuts that are sufficiently practical for humans to implement, solving an important open problem [6, 7]. Therefore, we have the following theorem.
Theorem 1
There exists a 5-card expected-finite-runtime AND protocol in committed format with only uniform cyclic shuffles.
Given that the previous “practical” AND protocol [10] uses six cards, as mentioned in Section 1.2, our protocol reduced the number of required cards from six to five, and one might presume that the contribution of this protocol is only incremental. However, we believe that this is not the case. One reason for this is that a “practical” committed-format AND protocol with five cards or less has been solicited for many years since the six-card AND protocol [10] appeared in 2009. Another reason is that our five-card AND protocol using only uniform cyclic shuffles is the best possible, because the following lower bounds have been found.
Theorem 2
[4] There is no five-card finite-runtime AND protocol in committed format with only closed shuffles.
Theorem 3
[4] There is no four-card expected-finite-runtime AND protocol in committed format with only uniform closed shuffles.
Theorem 3 implies that we need at least five cards to have a protocol using only uniform closed shuffles; moreover, even though we have five cards, Theorem 2 dictates that we cannot have a finite-runtime protocol. Thus, considering five-card expected-finite-runtime protocols is the only possible option. Consequently, Theorems 1, 2, and 3 together imply that, in this context, our proposed protocol is optimal.
Another Five-Card Protocol Using a Less Number of Shuffles
Recall that our five-card AND protocol presented in Sect. 2 uses seven shuffles on average. In this section, we show that one can decrease the number of required shuffles to 4.5 by designing a somewhat complicated protocol.
Idea and Description
Remember Step 3 of our first protocol presented in Section 2.2: If the face-up card is  , go back to the previous step to apply a random cut again; only when the face-up card is
, go back to the previous step to apply a random cut again; only when the face-up card is  , move forward. Therefore, if we can move forward even if the face-up card is
, move forward. Therefore, if we can move forward even if the face-up card is  , we have a chance to reduce the number of required shuffles. This is the main idea behind our second protocol.
, we have a chance to reduce the number of required shuffles. This is the main idea behind our second protocol.
Figure 2 is the (partial) KWH-tree of our second five-card AND protocol, which uses a less number of shuffles compared to the first protocol (presented in Sect. 2), as follows.
Comparing Fig. 2 with Fig. 1 (that is, contrasting the KWH-tree of the second protocol with that of the first protocol) reveals that they are similar: The first box and the second box named (A) in Fig. 2 are the same as the ones in Fig. 1, and box (B) and all the boxes following box (C) (including (C) itself) are also the same as the ones in Fig. 1. The only difference appears after box (B): while it always goes back to (A) after (B) in the first protocol (namely, Fig. 1), there are three possibilities in the second protocol (namely, Fig. 2) via the “See Fig. 3 box” part. That is, it goes back to (A) with a probability of 1/6, it terminates with a probability of \(1/3 + 1/6\), and it goes to (C) with a probability of 1/3. This contributes to reducing the expected number of trials, as imagined.
Specifically, to count the expected number of shuffles, let \(N_A\) be the expected number of shuffles from box (A) to the end of the protocol, and let \(N_C\) be the expected number of shuffles from box (C) to the end. Then,
and
and hence, we have \(N_A = 3.5\). Therefore, the total number of shuffles is \(1 + N_A = 4.5\) on average.
The details of the “See Fig. 3 box” part are shown in Fig. 3. Thus, Figs. 2 and 3 complete the description of our second five-card AND protocol (whose pseudocode will be presented in the next subsection). Because we can easily confirm that the KWH-tree for our second protocol also satisfies the required properties, it is correct and secure.
Pseudocode
The following is a pseudocode for the second protocol.

Conclusion
In this paper, we first constructed a five-card AND protocol in committed format using only random cuts and random bisection cuts. This nicely has closed the open problem, and our protocol is optimal, as shown in Theorems 1, 2, and 3.
In addition, whereas our five-card AND protocol in Sect. 2 uses seven shuffles on average, we were successful in reducing the expected number of shuffles from 7 to 4.5 with the same number of cards (five) and the same allowed shuffles (uniform cyclic shuffles) by changing part of the protocol.
It is an intriguing open problem to determine whether we can reduce the expected number of shuffles to less than 4.5 with the same conditions.
All the protocols mentioned thus far in this paper can be executed publicly: every operation by players is supposed to be conducted with all eyes fixed on how the cards are manipulated. In contrast, there is another model wherein players are allowed to use “private” operations: it is known that such a somewhat strong assumption results in protocols with fewer cards, e.g., [11, 12, 14, 15, 20].
Notes
Technically, describing this pseudocode is redundant, but it will allow easy reference.
References
Abe, Y., Hayashi, Y., Mizuki, T., Sone, H.: Five-card AND protocol in committed format using only practical shuffles. In: Proceedings of the 5th ACM ASIA Public-Key Cryptography Workshop, APKC ’18, pp. 3–8. ACM, New York, NY, USA (2018). https://doi.org/10.1145/3197507.3197510
den Boer, B.: More efficient match-making and satisfiability: the five card trick. In: Quisquater, J.J., Vandewalle, J. (eds.) Advances in Cryptology–EUROCRYPT ’89, Lecture Notes in Computer Science, vol. 434, pp. 208–217. Springer, Berlin (1990). https://doi.org/10.1007/3-540-46885-4_23
Crépeau, C., Kilian, J.: Discreet solitary games. In: Stinson, D.R. (ed.) Advances in Cryptology–CRYPTO ’93, Lecture Notes in Computer Science, vol. 773, pp. 319–330. Springer, Berlin (1994). https://doi.org/10.1007/3-540-48329-2_27
Kastner, J., Koch, A., Walzer, S., Miyahara, D., Hayashi, Y., Mizuki, T., Sone, H.: The minimum number of cards in practical card-based protocols. In: Takagi, T., Peyrin, T. (eds.) Advances in Cryptology–ASIACRYPT 2017, Lecture Notes in Computer Science, vol. 10626, pp. 126–155. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_5
Koch, A.: The landscape of optimal card-based protocols. Cryptology ePrint Archive, Report 2018/951 (2018). https://eprint.iacr.org/2018/951
Koch, A., Walzer, S.: Foundations for actively secure card-based cryptography. In: Farach-Colton, M., Prencipe, G., Uehara R (eds.) 10th International Conference on Fun with Algorithms (FUN 2021), vol. 157, pp. 17:1, 17:23, Schloss Dagstuhl–Leibniz-Zentrum für Informatik, Germany (2020). https://doi.org/10.4230/LIPIcs.FUN.2021.17
Koch, A., Walzer, S., Härtel, K.: Card-based cryptographic protocols using a minimal number of cards. In: Iwata, T., Cheon, J.H. (eds.) Advances in Cryptology–ASIACRYPT 2015, Lecture Notes in Computer Science, vol. 9452, pp. 783–807. Springer, Berlin (2015). https://doi.org/10.1007/978-3-662-48797-6_32
Mizuki, T., Shizuya, H.: A formalization of card-based cryptographic protocols via abstract machine. Int. J. Inf. Secur. 13, 15–23 (2014). https://doi.org/10.1007/s10207-013-0219-4
Mizuki, T., Shizuya, H.: Computational model of card-based cryptographic protocols and its applications. In: IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, vol. E100-A, pp. 3–11. The Institute of Electronics, Information and Communication Engineers (2017)
Mizuki, T., Sone, H.: Six-card secure AND and four-card secure XOR. In: Deng, X., Hopcroft, J.E., Xue, J. (eds.) Frontiers in Algorithmics, Lecture Notes in Computer Science, vol. 5598, pp. 358–369. Springer, Berlin (2009). https://doi.org/10.1007/978-3-642-02270-8_36
Nakai, T., Shirouchi, S., Iwamoto, M., Ohta, K.: Four cards are sufficient for a card-based three-input voting protocol utilizing private permutations. In: Shikata, J. (ed.) International Conference on Information Theoretic Security, ICITS 2017, Lecture Notes in Computer Science, vol. 10681, pp. 153–165. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-72089-0_9
Nakai, T., Tokushige, Y., Misawa, Y., Iwamoto, M., Ohta, K.: Efficient card-based cryptographic protocols for millionaires’ problem utilizing private permutations. In: Foresti, S., Persiano, G. (eds.) Cryptology and Network Security, CANS 2016, Lecture Notes in Computer Science, vol. 10052, pp. 500–517. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-48965-0_30
Niemi, V., Renvall, A.: Secure multiparty computations without computers. Theor. Comput. Sci. 191, 173–183 (1998). https://doi.org/10.1016/S0304-3975(97)00107-2
Ono, H., Manabe, Y.: Card-based cryptographic protocols with the minimum number of cards using private operations. In: Zincir-Heywood, N., Bonfante, G., Debbabi, M., Garcia-Alfaro, J. (eds.) Foundations and Practice of Security, Lecture Notes in Computer Science, vol. 11358, pp. 193–207. Springer, Cham (2019)
Ono, H., Manabe, Y.: Card-based cryptographic protocols with the minimum number of rounds using private operations. In: Pérez-Solà, C., Navarro-Arribas, G., Biryukov, A., Garcia-Alfaro, J. (eds.) Data Privacy Management, Cryptocurrencies and Blockchain Technology. Lecture Notes in Computer Science, vol. 11737, pp. 156–173. Springer, Cham (2019)
Ruangwises, S., Itoh, T.: AND Protocols Using only Uniform Shuffles. Computer Science—Theory and Applications. Lecture Notes in Computer Science, vol. 11532, pp. 349–358. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-19955-5_30
Stiglic, A.: Computations with a deck of cards. Theor. Comput. Sci. 259, 671–678 (2001). https://doi.org/10.1016/S0304-3975(00)00409-6
Ueda, I., Miyahara, D., Nishimura, A., Hayashi, Y., Mizuki, T., Sone, H.: Secure implementations of a random bisection cut. Int. J. Inf. Sec. 19(4), 445–452 (2020). https://doi.org/10.1007/s10207-019-00463-w
Ueda, I., Nishimura, A., Hayashi, Y., Mizuki, T., Sone, H.: How to implement a random bisection cut. In: Martín-Vide, C., Mizuki, T., Vega-Rodríguez, M.A. (eds.) Theory and Practice of Natural Computing, Lecture Notes in Computer Science, vol. 10071, pp. 58–69. Springer International Publishing, Cham (2016). https://doi.org/10.1007/978-3-319-49001-4_5
Watanabe, Y., Kuroki, Y., Suzuki, S., Koga, Y., Iwamoto, M., Ohta, K.: Card-based majority voting protocols with three inputs using three cards. In: 2018 International Symposium on Information Theory and Its Applications (ISITA), pp. 218–222 (2018). https://doi.org/10.23919/ISITA.2018.8664324
Acknowledgements
We thank the anonymous referees, whose comments have helped us to improve the presentation of the paper. This work was supported by JSPS KAKENHI Grant number JP17K00001.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
An earlier version of this study was presented at the 5th ACM ASIA Public-Key Cryptography Workshop, APKC 2018, Korea, June 4, 2018, and appeared in the Proceedings of the 5th ACM ASIA Public-Key Cryptography Workshop, pp. 3–8, 2018 [1].
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Abe, Y., Hayashi, Yi., Mizuki, T. et al. Five-Card AND Computations in Committed Format Using Only Uniform Cyclic Shuffles. New Gener. Comput. 39, 97–114 (2021). https://doi.org/10.1007/s00354-020-00110-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00354-020-00110-2






 , i.e., three red cards will be consecutive only when
, i.e., three red cards will be consecutive only when 
 are consecutive (apart from cyclic rotation), then
are consecutive (apart from cyclic rotation), then 



 and
and  :
: 


 , turn it over and return to Step 2. If it is
, turn it over and return to Step 2. If it is  , go to the next step. (The probability that
, go to the next step. (The probability that  appears is 2/5.)
appears is 2/5.) :
: 



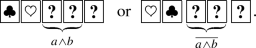
 appears, then turn them over:
appears, then turn them over: 

 appears is 1/2.)
appears is 1/2.)

