The combined influence of spin and roughness frequency on sphere aerodynamics

Abstract

The lift and drag of spinning spheres roughened with macro-roughness elements are examined. The velocity field of these same spheres in flight is measured with particle image velocimetry (PIV). Several spheres with varying roughness are examined at various spin rates and fixed Reynolds number. Unlike previous studies, where the roughness height is varied, in the present work, the number of roughness elements is varied. The PIV datasets are used to determine the boundary layer separation points for each case. Comparing the lift and drag to the separation points reveals that (1) the separation points become more asymmetric with spin (the Magnus effect), (2) The drag increases with the size of the wake, and (3) the drag increases with the asymmetry of the separation points, meaning that lift on spheres is accompanied by increased drag. Scant evidence of this third effect has been reported previously. Additionally, it is shown that, counter to smooth spheres, the force transmitted to the surface through the roughness elements leads to significant drag. The drag is shown to increase with the number of roughness elements while the lift decreases. Results have implications for understanding aerodynamic forces on bluff bodies with roughness and passive control of aerodynamic forces through roughness element frequency rather than the traditional roughness height.

1 Introduction

Understanding the behavior of spheres travelling through a fluid is vital to many applications, including the trajectory of sports balls (Mehta 1985; Pallis and Mehta 2003; Clanet 2015), ocean engineering (Jetly et al. 2018), and other engineering problems. While the influence of dimpled surfaces (e.g., golf balls), and smooth spheres are well researched (Crabill et al. 2019; Aoki et al. 2010; Achenbach 1972; Sakib and Smith 2020), the current understanding of roughened spheres is less developed. Specifically, little is known regarding how a varying roughness spacing changes the effective roughness of a surface, and how the interaction(s) of roughness and spin affect lift and drag.

Considering the aerodynamic forces on a sphere from a control volume perspective, the lift and drag are a result of the pressure and shear distributions over the sphere surface. For non-creeping flow, the boundary layer separates from the sphere surface (Fage and Committee 1936), and the force of the fluid on the sphere is dominated by the forces due to the fluid pressure, which are influenced by the boundary layer separation locations.

To facilitate the discussion of locations on a sphere surface, Fig. 1 defines the Cartesian and spherical coordinates used in this study where $z$ is aligned with $\overrightarrow {{\mathbf{V}}} _{\infty }$ (the velocity vector of the sphere,) and $y$ is along $\overrightarrow {\mathbf {\omega }}$ (the spin vector). For this experiment, we identified the separation locations on the sphere in three dimensions by illuminating a cross-section of the flow at a given plane which passes through the sphere center and lies along z. To match experimental parameters, we define the observation angle $\theta$ as the cross-section of the flow along one hemisphere. Subsequently, the polar angle $\phi$ describes the rotation from the sphere translation velocity vector along a given $\theta$. To reduce redundancy, the limits of these coordinates are: $0^{\circ }\le \theta <360^{\circ }$ and $0\le \phi \le 180^{\circ }$.

Fig. 1

Coordinate system for defining points (red dot) on the surface of a sphere travelling in the $z$ direction rotating about $y$. The observation angle $\theta$ describes the rotation from the x axis about the z axis to a point projection on the x-y plane and the polar angle $\phi$ describes the rotation to a point from the z axis

A non-dimensional spin rate, S, is used in this study based on the ratio of the largest tangential velocity of the sphere surface ($|\overrightarrow {{\mathbf{V}}} _{T} | = |\overrightarrow {{\mathbf{\omega }}} |D/2$, D is the sphere diameter), relative to the sphere translational velocity magnitude,

$$S = \frac{{|\overrightarrow {{\mathbf{\omega }}} |D}}{{2|\overrightarrow {{\mathbf{V}}} _{\infty } |}}.{\text{ }}$$

(1)

Because the flow around a smooth sphere has little dissipation prior to separation, the relationship between pressure and velocity is well described by Bernoulli’s equation. Specifically, the fluid pressure is greatest at the forward stagnation point near $\phi =0^{\circ }$ and decreases with increasing $\phi$ until a point near the maximum cross-sectional area where the relative fluid velocity is greatest. After this point where the relative fluid velocity is greatest, the pressure increases with increasing $\phi$ until separation. The base pressure after the separation point and up to $\phi =180^{\circ }$ is near the pressure directly prior to separation (Heisler 2002). Therefore, for a given $\overrightarrow {{\mathbf{V}}} _{\infty }$, delaying separation increases the base pressure, decreasing the pressure difference between the front and back of the sphere, therefore decreasing drag.

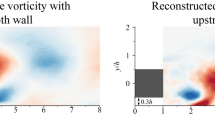
For spheres with asymmetric behavior (e.g., spheres with spatially varying surface features or relative velocity due to spin), separation asymmetry about the y axis leads to an asymmetric pressure distribution and a resulting lift force. Figure 2 shows the asymmetric separation of the boundary layer in the spin plane (the plane normal to the spin vector which passes through the middle of the sphere), where separation occurs earlier on the lower surface than the upper surface. As the low pressure region along the upper surface is longer than for the lower surface, the pressure difference causes an upward lift force.

Fig. 2

Experimental measurement of the spin plane velocity field (black vectors) over a smooth rotating sphere at Re$=1.67 \times 10^5$. The separation point asymmetry leads to the low pressure region over the upper surface extending further than on the lower surface. This asymmetry causes lift in the upward direction $x$, indicated by the white arrow

The location of separation is dependent on the mixing of free stream and boundary layer momentum (Kays and Crawford 1993). Because of this, separation from spheres near transition (Re $=10^5$) occurs at significantly larger $\phi$ for a turbulent boundary layer than for a laminar boundary layer. This phenomenon, combined with the influence of separation on the lift and drag, leads to a range of Reynolds numbers where the drag and lift are highly sensitive to small changes in Reynolds number and asymmetry (respectively referred to as the “drag crisis" and “spin crisis" (Lyu et al. 2022)).

The stability of the boundary layer can be degraded through surface roughness, dimples, and trip wires leading to a delay in separation and a reduction in drag near the critical Reynolds number. Among these methods, surface roughness and dimples are the only passive controls that have been studied for a rotating sphere. While dimpled surfaces reduce the stability of the viscous sub-layer, roughness elements can eliminate the viscous sub-layer (Choi et al. 2008; Kays and Crawford 1993; Choi 2015; Beratlis et al. 2018; Son et al. 2011). Because of this distinction, roughness elements are a unique problem from the better-understood dimpled surface.

This also suggests that the earlier spatial development of the turbulent boundary layer leads to an earlier separation (in $\phi$) for super-critical Reynolds numbers. Several studies have shown that this effect leads to increased drag for supercritical roughened spheres compared to smooth or dimpled spheres (Achenbach 1974; Norman and McKeon 2011; Kensrud and Smith 2010).

Kensrud and Smith (2018) investigated uniformly roughened, rotating spheres where roughness $\kappa$ is defined as the ratio of roughness element height to sphere diameter. They found that the lift increased with an increase in spin rate and roughness at the Reynolds of $1.9\times {10}^{5}$. At the same Reynolds number, the drag on the spheres with higher roughness increased with increasing spin, with the line of best fit following a slope of $0.44*S$ for $\kappa =1.65\times {10}^{-4}$. The drag on smooth and lightly roughened ($\kappa =6.39\times {10}^{-5}$) spheres decreased with increasing spin.

In an effort to better understand non-uniform textures, Norman and McKeon (2011) considered the influence of a single cylindrical stud protruding from the surface of a smooth sphere (traditional $\kappa$ from 0.01 to 0.04). Their key result was to show that in the sub-critical regime, the single stud has a significant influence on lift and a minimal impact on drag. Specifically, the results showed that in the supercritical regime, the boundary layer downstream of the stud separated earlier than along the smooth edge of the sphere, indicating that the instability caused by the stud enhances the boundary layer instability. This finding confirms earlier observations that added turbulence in the supercritical regime can lead to earlier separation than a smooth sphere.

Considering previous work, several research gaps exist. While prior work has shown that increasing roughness element size decreases the critical Reynolds number, less focus has been given to the influence of varied roughness outside the strips considered by Barlow (2008), the single roughness element considered by Norman and McKeon (2011), and the skewness measure of sports ball roughness from Haake et al. (2007). As research on flat plates identified the influence of roughness spacing on boundary layer development (Jia et al. 1998), potential exists for varied spacing of constant size roughness elements to achieve results similar to Achenbach (1974) without a maximally dense roughness spacing. Further, we are not aware of any studies that have considered the pressure drag on rough surfaces where force is transmitted to the surface through pressure drag on individual roughness elements (Kays and Crawford 1993). Finally, prior research has only considered separation points in the spin plane. This limitation has prevented researchers from analyzing the correlation of wake area to drag (Sakib and Smith 2020). Considering separation outside the spin plane concurrent with lift and drag measurements could confirm or challenge the current expected relationship between wake shape and aerodynamics.

To fill these research gaps, this study further develops the understanding of roughened sphere aerodynamics by (1) deploying experimental methods that do not interfere with the pressure gradient (i.e., launched spheres rather than wind-tunnel studies), (2) examining the difference between varied roughness element spacing and established, fully rough results, (3) making the effects of roughness more easily observable by using roughness elements which are larger than traditional sand-grain roughness, (4) including observations of the less understood rotating sphere (and thereby the asymmetric wake) in three dimensions, and 5) comparing three-dimensional wake shape to lift and drag.

2 Methods

To accomplish the objectives of this study, we require in situ measurements of the lift, drag, and velocity field, for a prescribed Reynolds number and spin rate of roughened spheres. Test spheres were of diameter 71.9 mm to match the available launching hardware (made for baseballs) and were 3D printed plastic with a five-minute acetone vapor bath to reduce the printed surface roughness. The final microscopic roughness of the chemically treated sphere surfaces were $R_{a} \le 10\;\mu {\text{m}}$, which provides fully “smooth" sphere behavior at the Reynolds numbers used in this study ($\kappa \le 1.4 \times 10^{{ - 4}}$) (Achenbach 1974). Macroscopic roughness elements were similar to those in prior work (Norman and McKeon 2011): cylinders of height 1.27 mm and radius 2.54 mm resulting in a traditional roughness of $\kappa =1.8\times {10}^{-2}$. This roughness is near the largest sand-grain roughness examined by Achenbach (1974) and also coincides with the roughness size of some sports balls (e.g. baseballs).

We define the roughness element frequency as the number of roughness elements ($N$) along the spin plane. Prior studies (Norman and McKeon 2011; Jackson et al. 2020) solely considered the separation points in the spin plane and found these points to correlate well with lift. For the sphere surface outside the spin plane, the roughness element spacing was approximately uniform. Figure 3 shows a drawing of each test sphere.

Fig. 3

Drawings for each test sphere from the spin plane projection, from $N=12$ on the far left to $N=24$ on the far right. Roughness frequency is denoted N according to the number of roughness elements along the spin plane. Roughness element height and radius were constant across roughness frequencies

Measuring the flow fields and forces in situ eliminated the effects of mounting devices on the flow (i.e., a wind-tunnel mounting sting) and the influence of blockage ratio (Achenbach 1974). A pneumatic air cannon similar to that used in the study of Kensrud and Smith (2018) was employed to repeatably launch spheres through still air at a prescribed velocity and spin rate. Referring to Fig. 4, spin was imparted on the sphere leaving the cannon tip through the difference in friction along the “smooth” and “sticky” sides of the flexible tip. The velocity and spin rate of a sphere were dependent on the cannon pressure and depth of the sphere in the launcher tip.

Fig. 4

A drawing of the cannon for launching spheres at a prescribed velocity and spin rate

Fixing the Reynolds number to near-critical at the nominal value of $1.65\times {10}^{5}$ isolated the two variables of primary interest: roughness spacing (varied by $N$) and $S$ (varied by cannon pressure and tip depth). To identify the influence of these parameters on the lift, drag, and boundary layer separation points, a force measurement and a PIV system (each described below) gathered multiple observations for each combination of the parameters described by Table 1.

Table 1 Experiment parameters

The surface fractions of roughness element projection area to total area ($f_{A,N}$) for each roughness frequency are: $f_{A,N=12}=6.2\%$, $f_{A,N=16}=12.2\%$, $f_{A,N=20}=16.5\%$, and $f_{A,N=24}=22.7\%$. Due to the symmetry of the sphere geometries and relative surface velocities about the spin plane, we assumed the separation points were symmetric about the spin plane, allowing us to approximate the full three-dimensional separation point curves ($0^{\circ }\le \theta <360^{\circ }$) by only measuring the flow field on $0^{\circ }\le \theta \le 180^{\circ }$.

2.1 Aerodynamic force measurements

Lift and drag forces were found by measuring the trajectory of each sphere at discrete locations using infrared sensors comprising three speed gates. Each speed gate consisted of two vertical sensors (to measure speed) and one angled sensor (to measure the ball’s vertical location). The vertical speed sensor pairs in each speed gate were 0.7 m apart, while the distance between the first and third speed gate was 12.1 m. The speed sensor locations were accurate to within $7.9\times 10^{-4}$ m, while time was measured to within $1.25\times 10^8$ s, resulting in the systematic uncertainty of the mean drag and lift coefficients at 0.002 and 0.001, respectively (95%). Each ball was projected four times, where the 95% confidence interval of the mean of the drag and lift coefficients were 0.006 and 0.016, respectively. A high-speed video camera (Phantom V711) recorded each shot at 2000 fps to verify orientation and spin rate (within ± 15 rpm).

Since the vertical displacement of the trajectory was small (0.05 m), the ball was assumed to be traveling in the horizontal plane, and acceleration due to drag was taken from the horizontal motion of the sphere. The error from this assumption was two orders of magnitude smaller than the random uncertainty of the mean drag coefficient. The change in ball speed over the 12.1 m trajectory was also small (less than 5% of the projected speed) so that its coefficient of drag could be considered constant and its motion was fit to a second-order polynomial as a function of time from the six known horizontal locations. (The change in the sphere drag and lift coefficients over the 12.2 m trajectory were less than 0.008 and 0.003, respectively, and comparable to the random uncertainty of the mean lift coefficient.) The ball’s vertical motion was also fit to a second-order polynomial from its three known vertical locations. The drag and lift force were found from the product of the acceleration and ball mass, where gravity was subtracted from the vertical acceleration.

2.2 Flow field measurements

A LaVision PIV system provided flow field measurements of the launched spheres. Before launching a sphere, the still air in a test section was seeded with submicron-diameter fluid particles generated by a theater fogger. To trigger the PIV system, a pair of LED lasers and phototransistors operated in the path of the launched spheres. When a sphere blocked both of the lasers, a timing unit triggered the PIV image capture. A thin sheet of seed particles was illuminated by two aligned double-pulsed New Wave Solo III Nd:YAG lasers (50 mJ/3–5 ns at 532 nm wavelength), one above and one below the ball, fired simultaneously. Using two laser pairs eliminated the shadow of the sphere. The particle images were acquired with a LaVision sCMOS camera (16 bit, 2560×2160 pixels) and Nikon 105 mm lens, resulting in a scale factor of 19.7 pixels/mm. For each launch, the PIV system captured a single image pair at ${\text{d}}t = 10\mu$s leading to maximum particle displacements near 10 pixels.

Separation points were described by the observation angle ($\theta$), which is the arc along $0^{\circ } \le \phi < 180^{\circ }$ at a fixed $\theta$ according to Fig. 1. Each planar PIV image provided the separation points in the plane which passes through the center of the sphere and is parallel to $\mathbf {\vec{V}_\infty }$ at a given $\theta$ and $\theta +180^{\circ }$. To measure the separation point around the entire sphere, the pneumatic launcher tip was rotated relative to the fixed laser plane as demonstrated by Fig. 5.

Fig. 5

Example of the pneumatic launcher tip orientation providing separation points at different observation angles $\theta$. For this example, looking from the test section toward the pneumatic launcher, orienting the launcher tip at $45^{\circ }$ to the laser plane provided the planar velocity field around the sphere at $\theta =45^{\circ }$ and $\theta =225^{\circ }$

Each PIV image pair was processed through a PIV algorithm to identify the boundary layer separation point location $\phi _{s}$ for a given $\theta$. The FFT-based cross-correlation processing included multiple passes with image deformation. The first two passes were completed with 64 pixel interrogation region pairs and five subsequent 32 pixel interrogation region passes at 87% overlap. Figure 6 shows the PIV velocity field results for an image pair capturing the spin plane flow field around the $N=16$ roughness frequency at $S=0.053$.

Fig. 6

A single PIV observation of the separation points at $\theta =0^{\circ }$ and $\theta =180^{\circ }$ for the $N=16$ roughness frequency

The processed PIV results informed manual inspection of the raw image pairs for the onset of particles in reverse flow along the sphere surface. Using the raw image data allowed us to overcome the resolution limits in PIV processing and noise issues along the roughened sphere boundary.

3 Results and discussion

3.1 Aerodynamic force results

We measured the lift and drag on the spheres at an average Re$= 1.67 \times 10^5$. Shot-to-shot velocity variation led to a Reynolds number standard deviation of 0.02 $\times 10^5$. Lift coefficient as a function of S is shown in Fig 7 for all roughness frequencies. Lift was fit to the model $C_L = aS^{b}$, and these results are shown as curves in the figure. A natural question is how these results compare to those of a baseline such as a smooth sphere or sand-grain roughened sphere. Near the Reynolds number we observed, prior studies show that the retreating surface on a smooth or lightly roughened sphere maintains a laminar boundary layer. As demonstrated in Fig 7, lower roughness values and the early separation of the laminar boundary layer result in a reverse Magnus effect (Barlow 2008).

Fig. 7

Lift Coefficient versus spin rate for each roughness frequency at $\textrm{Re}=1.67\times {10}^{5}$. Fits to $C_L = aS^{b}$ are shown solid curves with the data. Results of Barlow (2008) at Re$=2\times 10^5$ are shown in dotted lines

Lift was found to increase with spin (Barlow 2008; Kensrud and Smith 2018). At a given spin rate, lift was found to decrease with roughness frequency. The dependence of lift on S is not linear, and the contribution of spin to lift for each given roughness frequency is largest at the lowest spin rates (i.e., $0\le S \le 0.10$). The dimensionless spin rate and roughness frequency were combined to a single parameter $S^{C_1}N^{C_2}$, as shown in Fig. 8. The lift increased at all spin rates indicating the separating boundary layer is turbulent on all sides of the sphere, eliminating the potential for the reverse Magnus effect (Barlow 2008). From a nonlinear least squares fit (Virtanen et al. 2020) of the lift data we have $C_1=0.42$ and $C_2=-0.31$. It is important to note that this relationship is limited to roughness frequency values (N) near those observed in this study, and may not hold at the limits of smooth spheres and/or significantly higher roughness frequency.

Fig. 8

Lift coefficient versus ratio of spin rate to roughness frequency at $\textrm{Re}=1.67\times {10}^{5}$

Turning to drag, Fig. 9 demonstrates that the drag coefficient generally increases linearly with increasing spin as previously observed for roughened spheres (Kensrud and Smith 2018). Further, the drag increases with increasing roughness frequency.

Fig. 9

Drag coefficient versus spin rate for each roughness frequency at $\textrm{Re}=1.67\times {10}^{5}$

As shown in Fig. 9, the drag coefficient is lowest for the $N=12$ until $S>0.2$, at which point the drag coefficient for $N=12$, $N=16$, and $N=20$ roughness frequencies are similar. The $N=16$ and $N=20$ cases are similar across the spin rates measured. Finally, the $N=24$ roughness frequency has the greatest drag coefficient at all spin rates observed and remains distinct from the other roughness frequencies until $S\ge 0.25$. Due to the nature of the measurement method, no information regarding the time-dependent lift or drag coefficients is available.

3.2 Separation point results

PIV images and velocity vector fields provided instantaneous measurements of the flow field at each spin rate and laser plane for the average Reynolds number $1.61 \pm 0.01 \times {10}^{5}$. These separation points are used to assess the wake and are now compared to the lift and drag forces. The average separation points for each observation angle $\theta$, spin rate, and roughness frequency are shown in Fig. 10. Note, that an increase in $\phi _s$ indicates delayed separation.

Fig. 10

Spherical coordinate description of average separation points $\phi _s$ versus observation angle $\theta$ and target spin rate $S$ for each roughness frequency at $\textrm{Re}=1.61\times {10}^{5}$. Uncertainty bands indicate the 95% confidence interval of the mean

The uncertainty bands in Fig. 10 indicate the combined uncertainty of mean (i.e., $u_{{{\text{mean}}}} = [u_{{{\text{rand}}}}^{2} + u_{{{\text{sys}}}}^{2} ]^{{1/2}}$) due to the random uncertainty in the measurement ($u_{{{\text{rand}}}}$), and the systematic uncertainty in the method ($u_{{{\text{sys}}}}$). In this experiment, the systematic uncertainty of the separation points is low relative to the random uncertainty. Specifically, the time-dependent nature of the instantaneously measured separation point is the primary contributor to the uncertainty in the separation points and subsequent analysis using the separation points.

Comparing across the plots for different N in Fig. 10, the separation points at all $\theta$ occur earlier (i.e., at lower $\phi$) for the higher roughness frequency spheres. This observation is consistent with the study conducted by Norman and McKeon (2011) which included measurements of the boundary layer separation location after a single cylindrical roughness element. Specifically, the single roughness element placed prior to separation aided the turbulent transition of the boundary layer. For super-critical spheres, the earlier transition to turbulence resulted in earlier spatial development of the boundary layer and induced earlier separation. In the context of this study, increasing roughness frequency may result in earlier spatial development of the boundary layer which would explain why increased roughness frequency leads to earlier boundary layer separation for a fixed spin rate.

Analyzing within each value of N in Fig. 10, the separation points near the spin plane ($\theta =0^{\circ },180^{\circ }$), move with spin in the direction of increasing/decreasing relative velocity. Specifically, the separation points on the advancing side ($\theta =180^{\circ }\pm 45^{\circ }$) move to smaller $\phi$ with increasing spin, and the separation points on the retreating side ($\theta =0^{\circ }\pm 45^{\circ }$) move to larger $\phi$ with increasing spin. Finally, the separation points along the spin axis $\theta =90^{\circ }$ and (assuming symmetry) $\theta =270^{\circ }$, which has no relative surface velocity change due to spin, remained approximately constant across all spin rates.

The separation points moving in the direction of relative surface velocity may also be explained by a mechanism similar to increased roughness frequency causing earlier separation from super-critical spheres. Specifically, the boundary layer development may be increased/decreased by an increase/decrease in the local Reynolds number determined by relative surface velocity. This would explain the movement of separation points in the direction of relative velocity changes for all S and N.

3.3 Summarizing three-dimensional separation points

Boundary layer separation from a spinning sphere is a 3-D phenomenon, even in the mean. To concisely describe the 3-D wake, we identified the separation centroid (mean coordinate vector of the observed separation points around the sphere), at each observed roughness frequency and spin rate. Figure 11 demonstrates the curve of separation points from a sphere (black circle) and the resulting centroid of the separation points (black point) described by the separation centroid location vector (blue).

Fig. 11

The separation centroid (black point) of given separation points (black circle). The blue vector describes the separation centroid position

Applying the coordinates defined in Fig. 1 and reiterated in 11, the x-component of the vector describing the separation centroid measures the asymmetry of the wake and is expected to correlate to lift. Similarly, the area of the wake is described by the area of the spherical cap defined by the x and z components of the separation centroid vector:

$$\begin{aligned} A_w=2\pi (1-\sqrt{{\bar{X}}^2+{\bar{Z}}^2}) \end{aligned}$$

(2)

where the sphere is of unit radius. The wake area $A_w$ measures the size of the separated region of the flow and is expected to correlate to drag.

We determine the Cartesian x-coordinate of the wake averaged for $m$ observations over observation angles $\theta _i$ through:

$$\begin{aligned} {\bar{X}}=\frac{1}{m}\sum \limits _{i=1}^{m}{{\frac{r}{R}\textrm{sin}}(\theta _i){\textrm{cos}}(\phi _{{s},i})}, \end{aligned}$$

(3)

where the radius is of unit length ($\frac{r}{R}=1$).

Figure 12 shows the separation centroid x components, ${\bar{X}}$, across all observation angles for each spin rate and roughness frequency. The separation asymmetry magnitude increases with increasing spin and decreasing roughness frequency. This is expected, where the more downward shifted wake, indicated by separation centroid in an increasingly negative $x$ direction, corresponds to greater lift forces.

Fig. 12

Separation centroid x components versus spin rate across all roughness frequencies at $\textrm{Re}=1.61\times {10}^{5}$. Uncertainty bands indicate the 95% confidence interval of the mean

When relating wake shape to drag, prior studies have noted that the mean wake width correlates to the drag for non-rotating spheres (Achenbach 1974). However, for rotating or otherwise asymmetric spheres, the wake width is not measurable on a single plane. As a result, prior studies have considered the wake width [$360^{\circ }-(\phi _{s,\theta =0^{\circ }}+\phi _{s,\theta =180^{\circ }})$] in the spin plane, and have not found strong relationships between wake width and drag (Sakib and Smith 2020).

In the present study, we attempt to address this issue by describing the three-dimensional wake area which requires the separation centroid z-component (${\bar{Z}}$). Specifically, averaging the separation point z-coordinate at each of the m measured planes around the sphere surface:

$$\begin{aligned} {\bar{Z}}=\frac{1}{m}\sum \limits _{i=1}^{m}{{\frac{r}{R}\textrm{cos}}(\phi _{s,i})}. \end{aligned}$$

(4)

Figure 13 shows the wake area for each roughness frequency and spin rate. Increased roughness frequency results in earlier separation (higher $A_w$) across spin rates and is expected to correlate to increased drag. This finding agrees with prior observations, that an increased roughness leads to earlier separation and higher drag for super-critical spheres.

Fig. 13

Wake area versus spin rate for all roughness frequencies at $\textrm{Re}=1.61\times {10}^{5}$. Uncertainty bands indicate the 95% confidence interval of the mean

3.4 Relating forces and separation points

The lift coefficient is found to have a linear relationship with the x separation centroid ${\bar{X}}$ for all roughness frequencies and spin rates. The spin plane separation asymmetry method used in prior studies (Sakib and Smith 2020; Lyu et al. 2022; Aoki et al. 2010) fitted to the data from this study resulted in a poor fit ($R^2=0.43$, not shown). The separation centroid x component is a significant predictor of lift force across roughness frequencies as shown in Fig. 14.

Fig. 14

Lift coefficient versus separation centroid x component for all roughness frequencies and spin rates. Uncertainty bands indicate the 95% confidence interval of the mean

This is expected, as the surface pressure has a nonlinear dependence on $\phi$ (Cengel and Cimbala 2017). Further, this explains why the larger wakes associated with higher roughness frequency lead to lower lift at the same spin rate and difference in spin plane separation angles. The strong correlation between simple wake asymmetry and lift in prior studies is likely due to the focus on specific spheres (i.e. all measurements in a similar roughness).

Turning to drag, the wake area is expected to correlate to drag. Fitting the wake area component and drag force measurements across all roughness frequencies and observed spin rates gives a weak fit as shown in Fig. 15.

Fig. 15

Drag coefficient versus wake area for all roughness frequencies and spin rates. Uncertainty bands indicate the 95% confidence interval of the mean

Comparing across each roughness frequency in Fig. 15, however, the increased drag does correlate to the wake area. Specifically, the $N=24$ roughness frequency has the greatest drag, and largest wake area, while $N=12$ has the lowest overall drag and smallest wake area. Further, the $N=16$ and $N=20$ roughness frequencies show very similar wake areas and have similar drag values. Overall, these results indicate that the wake area may describe the differences in drag for the different roughness frequencies, but is convolved with other variables relating to spin rate.

Attempting to relate drag to wake area is based on an a priori assumption that skin friction is small, as reported in previous studies on smooth sphere drag (Son et al. 2011). However, the macroscopic roughness elements used in this study may apply significant force to the sphere. Kays and Crawford (1993) note that for a sufficiently high roughness Reynolds number “... the [viscous] sublayer disappears entirely, which accounts for the fact that viscosity is no longer a significant variable. But this also means that the shear stress must be transmitted to the wall by some mechanism other than viscous shear. This different mechanism is quite obviously pressure drag directly on the roughness elements...." While their discussion is focused on microscopic roughness elements, we conjecture that the present macroscopic elements behave the same way.

Prior research also suggests that the spin parameter correlates to a decrease in base pressure, resulting in an increase in drag for rotating spheres (Kray et al. 2012). Further, the surface pressure coefficient before separation is dependent on local velocity and Reynolds number (Briggs 1959; Beratlis et al. 2012). We conjecture that the wake orientation (i.e. the separation centroid x component ${\bar{X}}$) may also correlate with the drag on the roughened spheres as a result.

We assume the drag force of the fluid on these rough spheres has three components:

• 1. Pressure drag on the roughness elements. This will likely be a function of the fluid velocity local to each roughness element in addition to the number of roughness elements exposed to the attached boundary layer.

• 2. Form drag on the sphere due to the difference in attached surface pressures and base pressure that scales on the wake area $A_w$. This is the largest contributor to drag for smooth spheres.

• 3. Pressure drag on the sphere due to the difference in attached surface pressures and base pressure which scales on the separation centroid x component. This is drag associated with lift on spinning spheres.

To explore the relative importance of these components, we propose a semi-empirical model with several unknown parameters which estimates the weighted drag contributions of roughness element drag ($\alpha C_{D{\tau }}$), form drag determined by $A_w$ ($\beta C_{DA_w}$), and drag related to wake orientation as determined by ${\bar{X}}$ ($\zeta C_{D{\bar{X}}}$):

$$C_{D} = \alpha C_{{D\tau }} + \beta C_{{{\text{DA}}_{w} }} + \zeta C_{{D\bar{X}}} .{\text{ }}$$

(5)

Fitting to the drag and separation points at each observed roughness frequency and spin rate provides an estimate of the model parameters.

To model the pressure drag on individual roughness elements, we identified the mean number of roughness elements exposed to the attached boundary layer $n$ based on the separation points for each roughness frequency and spin rate. The region of exposed roughness elements contributing to n for the $N=16$, $S=0.13$ parameter set is shown in Fig. 16.

Fig. 16

Example spin plane PIV result demonstrating the regions of separated flow in the wake (red), and attached flow (green). The number of roughness elements in the attached flow region determines the count of exposed roughness elements n

For each exposed roughness element, we assumed that the drag is a function of the fluid velocity relative to the sphere surface: $V_{{{\text{rel}}}} = (1 - Sx)V_{\infty }$ where x is the Cartesian coordinate of the center of the roughness element on the sphere surface. To estimate the overall drag contribution from the roughness elements, we passed the number of exposed roughness elements through the distribution of relative velocities over the sphere surface identified by Monte Carlo simulation. The total drag of the roughness elements $F_{D{\tau }}$ is the sum of the drag on each roughness element (i),

$$F_{{D\tau }} = \sum\limits_{i}^{n} {\frac{1}{2}} \rho |V_{{{\text{rel}},i}} |^{2} A_{r} C_{{{\text{Dr}}}} ,$$

(6)

where $A_{r} = 6.45 \times 10^{{ - 6}} {\text{m}}^{2}$ and $C_{{{\text{Dr}}}} = 0.5$ indicate the frontal area and drag coefficient of the roughness elements, respectively. Note, that the roughness drag force conversion to a force coefficient for the model fit is consolidated into the weighting factor $\alpha$.

To identify the values of $\alpha$, $\beta$, and $\zeta$, we used the dual annealing global optimization method from the Python-based Scipy optimization module (Virtanen et al. 2020) and minimized the mean-square error of the composite measure and drag across each roughness frequency and spin rate. Figure 17 demonstrates that the result of the optimization identified a strong fit of the composite measure ($R^2=0.90$) to the drag coefficient.

Fig. 17

Drag coefficient versus composite measure across all roughness frequencies and spin rates

Overall, adding the number of roughness elements within the attached boundary layer and the wake orientation to the drag measurement significantly increased the strength of fit between drag and proposed measures of drag. To evaluate the relative contributions of each drag component, Fig. 18 shows the absolute weighted components $C_{{{\text{Di}}}}$ for each observation of total drag.

Fig. 18

Drag component contribution versus total drag across all roughness frequencies ($N=12$, $N=16$, $N=20$, and $N=24$) and spin rates

These results show that while form drag ($\beta C_{DA_w}$) is the most important contributor, the roughness element drag ($\alpha C_{D{\tau }}$) and wake orientation, or lift component ($\zeta C_{D{\bar{X}}}$) are significant components of overall drag for rotating, roughened spheres. For each N, five spin values were tested (with the exception of four spin values for $N=12$ due to hardware limitations). The lift component is most sensitive to spin followed by the form drag component. The drag on the roughness elements is not sensitive to spin.

Considering the contribution of the pressure drag on individual roughness elements to the overall drag, the pressure difference over each roughness element may also explain decreasing lift with increased roughness frequency. Specifically, the “drag" acting on the roughness elements on the advancing side ($\theta =180 \pm 90^{\circ }$) of the sphere may negatively impact the overall lift (since they act in the $-x$ direction), while the drag on the roughness elements on the retreating side ($\theta =0 \pm 90^{\circ }$) may positively impact the overall lift.

However, the roughness elements which would have the greatest contribution to lift (near $\phi =0^{\circ }$) are nearest the stagnation region and likely to experience the least pressure drag. The contribution of the roughness element drag to total lift is also subject to factors such as local boundary layer thickness, interactions between roughness elements, and similar issues which are not measurable through the methods in this study.

As a final consideration, since the pressure distribution around a rotating, smooth sphere can be approximated analytically, a model was developed that integrates the surface pressure over the entire surface by estimating the (1) the surface pressure prior to separation with dissipation fitted to the data by $c_p = {C_1}V_{\phi ,\theta }^{C_2}$, and (2) the base pressure as the average of the pressure directly prior to separation. However, this model, bounded by realistic values of surface pressure, provided a worse fit to the data than the simplified model in Eq. 5. This result suggests a key area for future work; measuring the surface pressure over a roughened, rotating surface.

4 Conclusion

This study examined the influence of roughness element frequency on the boundary layer separation and aerodynamic forces of a spinning sphere at a constant Reynolds number ($1.65\times 10^5$). Flow visualization through PIV on multiple planes through the center of the ball captured the three-dimensional separation points. PIV results demonstrated that the asymmetry of separation points increases with spin, and the area of the wake increases with roughness frequency. Force measurement through trajectory analysis demonstrated that lift increases with spin and decreases with roughness frequency.

The relationship between separation points and lift is well described by the mean location of the separation points in the lift direction. Drag increased with wake area as expected from prior studies. However, our analysis showed wake area does not wholly explain the differences in drag for rotating, roughened spheres. Rather, we identified an increase in drag with an increase in wake asymmetry (meaning the mechanism generating lift also generates drag). We also identified a significant contribution of roughness elements drag to total drag, which is a less-reported phenomenon and may contribute to the uniqueness of super-critical drag on roughened spheres when compared to smooth or dimpled spheres. Results demonstrate that the spacing of constant height roughness elements is an important variable for descriptions of roughness to predict lift and drag, and the drag on rotating spheres is not only dependent on wake area but also on roughness element drag and orientation of the wake.