Wall shear stress measurement using a zero-displacement floating-element balance

Abstract

The floating-element (FE) principle, introduced nearly a century ago, remains one of the most versatile direct wall shear stress measurement methods. Yet, its intrinsic sources of systematic error, associated with the flow-exposed gap, off-axis load sensitivity, and calibration, have thus far limited its widespread application. In combination with the lack of standard designs and testing procedures, measurement reliability still hinges heavily on individual judgement and expertise. This paper presents a framework to curb these limitations, whereby the design and operation of a FE balance are leveraged by an analytical model that attempts to capture the behaviour and predict the relative contribution of the systematic sources of error. The design is based on a parallel-shift linkage and a zero-displacement force-feedback system. The FE has a surface area of $200\times 200\,$ mm, and measurement sensitivity is adjustable depending on the surface condition and the Reynolds number. It is thus suitable for application in a wide range of low-speed, boundary-layer wind tunnels, small or large scale. Measurements of the skin friction coefficient over a smooth wall show a remarkable agreement with oil-film interferometry, especially for ${\rm Re}_{\theta } > 1.3 \times 10^4$. The discrepancy relative to the empirical Coles–Fernholz relation ($\kappa = 0.39$ and $C = 4.352$) is within $0.5\,$%, and the level of uncertainty is below $1\,$% for a confidence interval of $95\,$%.

1 Introduction

The importance of accurate estimates of wall shear stress $\tau _w$ cannot be overstated. Often expressed in terms of the friction velocity $U_{\tau } = (\tau _w/\rho )^{1/2}$, where $\rho$ is the density of the fluid, it is a fundamental scaling parameter, crucial to our understanding and modelling of wall-bounded turbulent flows (Townsend 1976). The wall shear stress can be inferred using indirect methods based on velocity measurements. Yet, their application is limited to canonical flows so long as established hypotheses about the turbulence structure remain valid (Clauser 1956; Perry and Joubert 1963; Walker 2014; Womack et al. 2019). For example, wall similarity and total stress methods should only be applied to high Reynolds number boundary layers, developing over smooth or mildly rough surfaces under neutral equilibrium and zero-pressure-gradient conditions. Many flows of interest, however, do not meet these criteria, in which case the accuracy of the estimates quickly deteriorates, and direct wall shear stress measurement methods become the preferred choice.

Introduced by Kempf (1929) nearly a century ago, the FE principle is arguably the most versatile direct measurement method. Not only is it independent of the flow conditions—as it does not make assumptions about the structure of turbulent boundary layers or requires a flow-based calibration—it is also independent of the test surface. Following the seminal work of Dhawan (1951), several devices have been developed with application to low and high-speed flows under nonzero-pressure-gradient, surface heat, and mass transfer conditions (Winter 1979). While designs can be markedly different because of the unique features of each facility and application, virtually all the basic concepts and solutions today stem from this early stage of development. Modern devices thus share similarities but typically enjoy improved sensitivity, stability, and signal-to-noise ratio (SNR) by using more sophisticated signal-conditioning systems and large-scale facilities. At the same time, technology also allowed for miniaturisation of the FE for local measurement of wall shear stress fluctuations over smooth walls (Sheplak et al. 2004; Ding et al. 2018).

Despite development efforts, the FE balance is still not widespread owing to significant experimental challenges. Measurements are inherently subject to diverse sources of error, predominantly of a systematic nature (Brown and Joubert 1969; Allen 1977, 1980). Design and correct operation thus require a comprehensive understanding of the mechanisms through which they come about to eliminate them or otherwise subtract their contribution from the measurement a posteriori. As FE balances are traditionally tailored to meet specific requirements, and development is subject to time and budget constraints, error sensitivity may vary wildly and is seldom reported or included in uncertainty propagation analyses. Combined with the lack of formal testing procedures or guidelines, measurement quality hinges heavily on individual judgement and expertise. Adopting a standard design could address some of these shortcomings but remains unlikely as there is no market for FE balances, in contrast to other measurement instruments (e.g. hot-wire anemometers and flow imaging systems).

This paper presents a framework for designing and operating FE balances centred around an analytical model which attempts to capture the behaviour and predict the relative contribution of systematic error sources that could be overlooked. The FE balance is designed for application to low-speed, boundary-layer flows and draws inspiration from the Kelvin balance, featuring a zero-displacement force-feedback system (Smith and Walker 1959; Acharya et al. 1985; Kameda et al. 2008). The surface area is $200\times 200\,$ mm, and measurement sensitivity is adjustable, depending on the surface condition and the Reynolds number, for optimal resolution and SNR. Following a thorough discussion of the potential sources of systematic error and their driving mechanisms in Sect. 2, the analytical model of the FE balance is derived in Sect. 3. The experimental methods, including calibration and uncertainty propagation analysis, are detailed in Sect. 4. Finally, Sect. 5 presents measurements of the skin friction coefficient of a smooth-wall boundary layer, obtained using the FE balance and oil-film interferometry (OFI) for validation purposes.

2 Potential error sources

FE balances measure the streamwise force component $F_w$ acting on a finite area of the test surface S that is structurally independent and free to move in the planar directions. The measurements are subject to diverse sources of error, which can be classified into four categories: (i) pressure-driven forces acting on non-parallel surfaces to the flow, (ii) off-axis load sensitivity, (iii) SNR, and (iv) calibration (including offset, sensitivity, hysteresis, and linearity errors). The first two are especially detrimental to conventional devices with $S \gtrsim \mathcal {O}(1)\,$ $\textrm{cm}^{2}$ and become gradually less important with miniaturisation for $S \lesssim \mathcal {O}(1)\,$ mm$^{2}$. The reader may refer to Sheplak et al. (2004) for an in-depth analysis of the effect of scale.

Fig. 1

Schematic illustration of the effect of the streamwise pressure gradient (blue), the pressure difference between the top and the underside of the FE (red), the cavity-induced flow (yellow), and the weight of the FE (green). Free-body diagrams a represent pressure-driven forces acting on a FE that is parallel to the test surface or misaligned by $\alpha$, and b the off-axis load vectors depending on the mechanical arrangement of the balance, single-axis or parallel-shift linkage, and the horizontal inclination of the test surface $\gamma$. A dashed line indicates that the corresponding load vector does not affect the measurement

The first category stems from the flow-exposed gap and the potential misalignment of the FE with the surrounding test surface. Schematically illustrated in Fig. 1, the combined action of the streamwise pressure gradient across the FE (blue force vector) and the cavity-induced flow (yellow force vector) creates a spurious streamwise force component, which depends on the geometry of the cavity and on the boundary-layer flow above (Brown and Joubert 1969). There have been few attempts to fully characterise this error contribution because of the challenge of systematically varying the relevant parameters. The most comprehensive study by Allen (1977) shows how the gap width b and the protrusion of the FE relative to the test surface $\varDelta _y$ affect the accuracy of the measurement. The experiments were performed under zero-pressure-gradient conditions so the effect of the cavity-induced flow could be isolated. He found that while the error becomes increasingly significant with protrusion, error sensitivity is reduced the wider the gap is, providing the flow remains undisturbed. Based on his observations and an investigation by Gaudet and Winter (1973), on the drag produced by spanwise-aligned grooves, Winter (1979) suggested that the viscous-scaled gap width $U_{\tau }b/\nu$ should not exceed 100, at which point the shear stress across the gap is about three times the undisturbed value. Besides the effect of the flow-exposed gap, a parallel misalignment of the FE can be equally detrimental, causing the normal net force arising from the pressure difference between the top and the underside to be no longer vertical and exhibit a streamwise component (red force vector).

Also illustrated in Fig. 1, off-axis load sensitivity depends essentially on the mechanical arrangement of the FE balance. Specifically, on its ability to single out the surface drag from the spurious effect of additional forces acting perpendicularly to the flow direction. A case in point is the negative impact of uneven static-pressure distributions on single-axis FE balances, like those of Fowke (1969), Allen (1977), Krogstad et al. (1992), and Krogstad and Efros (2010), to name a few. Under nonzero-pressure-gradient conditions or in the extreme case of a wall-mounted cube as the roughness pattern unit, the resulting surface pressure distribution creates a pitching moment (blue-coloured moment vector), which single-axis FE balances are unable to decouple from that produced by the streamwise force component. Similarly, a pitching moment is created as the FE is displaced under load, and the centre of gravity becomes offset from the pivot point (green force vector). Designs featuring a parallel-motion linkage (Dhawan 1951; Kameda et al. 2008; Ferreira et al. 2018) are immune to uneven static-pressure distributions but, owing to their kinematics, are equally affected by an offset of the centre of gravity. They are additionally sensitive to the wall-normal component of the pressure difference between the top and the underside of the FE (red force vector) as the FE remains parallel to the flow direction, unlike single-axis configurations. The effect of off-axis loading becomes less pronounced the farther the pivot point is from the wall, but it still stands as a source of systematic error. Only planar-supported FE configurations using air bearings (Ozarapoglu 1973; Baars et al. 2016) or a pool of liquid (Sadr and Klewicki 2000) are intrinsically insensitive. Nevertheless, their design and operation are inevitably more complex.

The SNR is typically limited by the size of the FE that ensures local measurement of wall shear stress, by the turbulent nature of boundary-layer flows, and the mechanical vibrations induced by the flow and the wind tunnel drive unit. It can be improved by scaling up the FE or by using more sophisticated sensors and signal-conditioning systems that are sensitive yet immune to the noise sources mentioned above. The FE balance from Baars et al. (2016) is notable for its large dimensions and consequently better SNR than equivalent, smaller devices. Its surface area is $3\,$m$^2$, and the ratio of the mean of the signal $\mu$ to its standard deviation $\sigma$ ranges between 25 and 40. Comparatively, that from Ferreira et al. (2018) has an area of $0.04\,$m$^2$ and $\mu /\sigma$ ranges between 1–5. While there is undoubtedly an advantage in using large-scale facilities in terms of SNR, they are seldom available and less practical or cost-effective for systematically testing different surface conditions. In this case, improving the performance of the sensor and signal conditioning is preferable, and it appears to be the main driving factor for better SNR and stability of modern devices.

Having considered and designed for mitigating error contributions (i) through (iii), errors associated with calibration, including offset, sensitivity, hysteresis, and linearity errors, may represent the most significant part of the total uncertainty in the measurement (Ferreira et al. 2018). Notably, the conventional calibration procedure using a weight and pulley arrangement is a simple and effective method but not without limitations. Besides the uncertainty in the applied weight, the static friction of the pulley implies that the force experienced by the FE balance is lower than the force of the suspended weight. It is thus essential to know the static-friction coefficient of the pulley as reported by the manufacturer or by taking measurements whenever possible (Baars et al. 2016). Friction may, additionally, introduce a hysteresis effect, causing the FE balance to exhibit seemingly different responses depending on the loading direction.

3 The floating-element balance

3.1 Sensitivity and resolution

Fig. 2

Estimate of the surface drag over the FE (left-vertical axis) and the local streamwise pressure gradient (right-vertical axis), assuming the velocity profile of the smooth-wall, turbulent boundary layer follows the 1/7th power law distribution

The size of the FE greatly influences the utility of the balance. Not only is it a crucial aspect in determining sensitivity and resolution it also dictates what surface conditions could be tested. Designs featuring a small, circular FE are limited to smooth walls or homogeneous roughness, like sandpaper, whose characteristic length scale is significantly smaller than the diameter. They are unsuitable for spatially varying surface roughness at $\delta$-scale, such as spanwise-heterogeneous (Vanderwel and Ganapathisubramani 2015; Wangsawijaya et al. 2020) or regular-distributed, obstacle arrays (Cheng and Castro 2002; Ferreira and Ganapathisubramani 2020). These surfaces are often represented by a repeating square pattern that can be easily reproduced and pieced together on the wind tunnel floor. For unbiased measurements of the wall shear stress, the FE must house an integer number of pattern units—one at the very least—so it is optimal to be square-shaped of side l as large as the dimension of an arbitrary roughness pattern, typically comparable to the boundary-layer thickness. Given the specifications of the wind tunnel at the University of Southampton, $l = \mathcal {O}(\delta ) = 200\,$ mm, ensuring, at the same time, local measurement of wall shear stress.

To estimate the full-scale load and resolution of the FE balance, let us consider a turbulent boundary layer developing over a smooth wall with a vertical distribution of the longitudinal velocity given by the $1/7^{th}$ power law. The evolution of the integral parameters, namely, the displacement thickness $\delta ^*$ and the skin friction coefficient $C_f$, can be written as a function of the local Reynolds number ${\rm Re}_x = U_{\infty }\,x/\nu$, where x is the development length from the tripping point. Accordingly,

$$\begin{aligned} \frac{\delta ^*}{x} \ = \ 0.046\,Re_x^{-1/5} \end{aligned}$$

(1)

and

$$\begin{aligned} C_f \ = \ 0.0576\,Re_x^{-1/5}. \end{aligned}$$

(2)

Given the dimensions of the test section with constant cross-sectional area A and perimeter P, it follows from mass conservation that

$$\begin{aligned} \frac{dU_{\infty }}{dx} \ = \ \frac{P\,U_{\infty }}{A-P\,\delta ^*}\,\frac{d\delta ^*}{dx}, \end{aligned}$$

(3)

and, in the freestream, where the flow is irrotational,

$$\begin{aligned} \frac{dp_{\infty }}{dx} \ = \ -\,\rho U_{\infty }\,\frac{dU_{\infty }}{dx}. \end{aligned}$$

(4)

Equations 1 through 4 are used to estimate the surface drag over the FE and the local streamwise pressure gradient at $x = 9\,$m (refer to Fig. 6) for freestream velocities ranging from 5 to $50\,$m s$^{-1}$. The results are shown in Fig. 2 as a function of the unit Reynolds number. For optimal measurement resolution, the full-scale (FS) load should be comparable to the maximum expected surface drag over the FE. While the latter does not seem to exceed $120\,$mN for a smooth wall, it may be significantly higher for rough walls, up to one order of magnitude (e.g. Ferreira et al. 2018; Esteban et al. 2022). It would thus be advantageous for the system to provide the ability to tune its sensitivity according to the surface condition and Reynolds number. For a smooth wall, taking a conservative estimate of $150\,$mN FS and a target resolution of $5\,\upmu$N, 1/1000th of the minimum expected load, the required noise-free bit resolution is 15.

3.2 Design

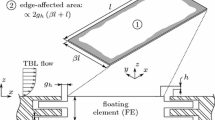
The mechanical arrangement of the FE balance, shown in Fig. 3, is based on a parallel-motion linkage. Two pairs of stainless-steel leaf springs, fixed on the upstream and downstream sides, support the FE such that it only moves freely in the streamwise direction. They are $50\,$ $\upmu$m thick by $1\,$ mm wide, and the free length $a = 20\,$ mm. This mechanism behaves dynamically like a simple pendulum and, as explained in Sect. 2, its kinematics ensures that measurements are insensitive to uneven static-pressure distributions. Alignment of the FE with the test surface is adjusted via three vertical-translation stages with a resolution of $0.5\,\upmu$m. It was positioned slightly recessed by sliding a go/no-go gauge block across the gap such that $-10\,$ $\upmu$m $<\varDelta _y<0$. The width of the gap $b=0.5\,$ mm and the thickness of the FE $t=3\,$ mm. Given these dimensions and the empirical analysis from Allen (1977), the spurious streamwise force component arising from the cavity-induced flow in and out of the test section should remain negligible since $b/l = 2.5\times 10^{-3}$ and $\varDelta _y/\delta = \mathcal {O}(10^{-4})$. At the same time, the gap should not appreciably disturb the flow development as its viscous-scaled width $U_{\tau }b/\nu = \mathcal {O}(10)$. A dashpot filled with mineral oil was added for increased damping. The wetted area of the blade is $7\,$% of the surface area of the FE.

The measurement principle consists of tracking the position of the FE and minimising its deviation from a set point by creating an equal and opposite reaction to the surface drag. The position of the FE is measured using a capacitive displacement sensor with an effective resolution of $20\,$nm, and the reaction force is produced by a neodymium magnet and a custom-made solenoid. A closed-loop, proportional-integral controller¹ regulates the flow of current through the solenoid, which is linearly proportional to the induced electromagnetic force. The controlled current source is bidirectional, allowing the system to push or pull the FE. It interfaces with a microcontroller via a 16-bit digital-to-analog converter (DAC) whose output range is software-selectable. The sensitivity of the FE balance, determined by the output range the DAC, is therefore adjustable for optimal measurement resolution, depending on the test surface and the local Reynolds number. Sensitivity can also be adjusted by varying the spacing between the solenoid and the magnet. It becomes higher the wider the spacing is as the induced electromagnetic force is reduced for the same current level. The maximum rated output of the current source is $\pm 500\,$ mA. Placed $1\,$ mm apart, the corresponding maximum induced force between the magnet and the solenoid is approximately $1\,$ N. The solenoid has a measured DC resistance of $3.2\, \Omega$ and inductance $1150\,\upmu$H. The output range of the DAC was set such that the full-scale load of the FE balance is approximately 300 mN, over twice as high as the maximum expected surface drag, and resolution $5\,\upmu$N.

Fig. 3

Simplified drawing of the FE balance, including the top view (at the bottom) and the section view along A-A (at the top). The FE is supported via two pairs of leaf springs (1) mounted on the upstream and downstream sides, and a set of three translation stages (2) allow adjusting the planar alignment with the test section to within $0.5\,$µm. The FE balance features a dashpot (3) for added damping and improved SNR. The solenoid (5) and proximity sensor (7) are mounted on a linear stage (4) which allows adjusting their position relative to the permanent magnet (6)

3.3 Analytical model

Fig. 4

Schematic representation of the FE balance. $F_e$ is the actuation force produced by the solenoid, $F_w$ is the surface drag, and $F_n$ and $F_t$ are the pressure-based normal and tangential force components, respectively. The movement of the FE, displaced under load, is prescribed by the length of the leaf springs l and the angle $\phi$. The horizontal inclination of the test surface is indicated by the angle $\gamma$

Figure 4 shows a schematic of the FE balance where the parallel-motion linkage is represented as a simple pendulum of mass m and length a at an arbitrary angular displacement $\phi$. The angle $\gamma$ represents the horizontal inclination of the test surface. The parallel misalignment of the FE may be safely neglected as $\varDelta _y/l < 5\times 10^{-5}$, and so is the effect of the leaf springs whose spring constant is an order of magnitude lower than the stiffness of the pendulum linearised around $\phi = 0$. The model attempts to capture the systematic sources of error discussed in Sect. 2, associated with pressure-driven forces acting on non-parallel surfaces to the flow and off-axis load sensitivity. Accordingly, the free-body diagram includes the weight of the FE mg, the surface drag $F_w$, the electromagnetic force $F_e$, the net force due to the streamwise pressure gradient

$$\begin{aligned} F_t \ = \ -\,\frac{dp_{\infty }}{dx}\,t\,l^2, \end{aligned}$$

(5)

and the wall-normal force component arising from the pressure difference between the top and the underside of the FE

$$\begin{aligned} F_n \ = \ \varDelta p_y\,S. \end{aligned}$$

(6)

It then follows, from the moment balance around the pivot point, that the relative systematic error in the measurement of surface drag is expressed as

$$\begin{aligned} \begin{aligned} \epsilon \ = \ \frac{1}{F_w}\bigg [F_t\,+\,F_n\,\tan (\phi -\gamma )\,-\,mg\,\frac{\sin {\phi }}{\cos {(\phi -\gamma )}}\bigg ], \end{aligned} \end{aligned}$$

(7)

which, for small angles, reduces to

$$\begin{aligned} \begin{aligned} \epsilon \ = \ \frac{1}{F_w}\,\bigg [ \underbrace{F_t}_{\begin{array}{c} \\ \epsilon _{i} \end{array}} \,+\, \underbrace{F_n\,\frac{\varDelta _x-a\,\gamma }{a+\varDelta _x\,\gamma }}_{\begin{array}{c} \\ \epsilon _{ii} \end{array}} \,-\, \underbrace{mg\,\frac{\varDelta _x}{a+\varDelta _x\,\gamma }}_{\begin{array}{c} \\ \epsilon _{iii} \end{array}} \bigg ]. \end{aligned} \end{aligned}$$

(8)

Considering the smooth-wall, boundary-layer flow outlined in Sect. 3.1, Eq. 8 may be used to assess the relative importance and behaviour of these sources of error and establish effective mitigation strategies. The first term on the right-hand side (RHS) $\epsilon _i$ models the effect of the streamwise pressure gradient. As shown in Fig. 5 (solid-yellow line), its magnitude is independent of the unit Reynolds number $U_{\infty }/\nu$, contributing to a uniform vertical shift of the skin friction coefficient. Naturally, it becomes negligible under nominally zero-pressure-gradient (ZPG) conditions, for example, by adjusting the dimensions of the test section to conform with the flow development (Baars et al. 2016). However, this requirement severely limits the utility of the FE balance, and few existing facilities offer this capability. An alternative approach proposed by Frei and Thomann (1980) and Hirt et al. (1986) involves sealing the flow-exposed gap with liquid held in place by surface tension. They derived analytical expressions for predicting the net force due to surface tension when the FE is displaced under load, creating asymmetric upstream and downstream menisci. While this arrangement may be especially suitable for a zero-displacement FE balance, as the menisci would remain unchanged regardless of the surface drag, the comparably larger dimensions of the present device make it challenging to maintain the machining tolerances and surface finish necessary for a well-designed liquid seal. Since neither above is a viable option, the effect of the pressure gradient on the measurement of surface drag is estimated and subtracted a posteriori using Eq. 5.

The second term on the RHS of Eq. 7$\epsilon _{ii}$ models the combined effect of the wall-normal force component $F_n$, the inclination of the test surface $\gamma$, and the steady-state error of the control system $\varDelta _x$ (i.e. the average deviation of the FE from the set point). For illustration purposes, let us assume the wind tunnel runs at a slight overpressure, such that the local static-pressure coefficient in the test section $\varDelta p_y/ q$, where q is the freestream dynamic pressure, is approximately 0.06.² Fig. 5 shows that a horizontal inclination of $0.05^{\circ }$, corresponding to the measurement uncertainty indicated in Table 2, would induce a significant error in the measurement of the surface drag (solid-red line), comparable in absolute terms to the effect of the streamwise pressure gradient (solid-yellow line). In contrast, the effect of the steady-state error, taking a conservative estimate of $1\,$ $\upmu$m, given the resolution of the system, is much less significant (dashed-red line). For accurate measurements, it is thus crucial to equalise the static pressure between the test section and the FE balance and to ensure its horizontal alignment. In the experimental setup described in Sect. 4.1, the static pressure is passively equalised using silicon tubing connecting the FE balance to the test section, which decreased $\varDelta p_y/ q$ by approximately $85\,$% to $8\times 10^{-3}$. Other studies have used blowers for active pressure equalisation (Baars et al. 2016; Ferreira et al. 2018), but this was deemed unnecessary.

The third source of systematic error $\epsilon _{iii}$ is associated with the weight of the FE, which acts as a restoring force. Similarly to $\epsilon _{ii}$, this term is a function of the horizontal inclination of the test surface $\gamma$ and the steady-state error of the control system $\varDelta _x$. Yet, the former has a minimal effect because it only appears in the denominator and is considerably smaller than $a\varDelta _x$. Taking the mass of the FE $m = 0.612\,$kg and $\varDelta _x = 1\,$ $\upmu$m, Fig. 5 shows that $\epsilon _{iii}$ is most significant in the lower range of Reynolds numbers and gradually decreases for larger values (solid-blue line). Its contribution can be kept within acceptable levels by carefully tuning the control system such that $\varDelta _x \ll 1\,$ $\upmu$m. Otherwise, like $e_i$, it can be quantified and subtracted from the measurement as the control variable $\varDelta x$ is readily available.

Fig. 5

The relative systematic error as a function of the unit Reynolds number (black), modelled given the smooth-wall boundary layer flow outlined in Sect. 3.1. Coloured lines represent each term on the RHS of Eq. 8

3.4 Stability and frequency response

Measurement stability is affected by drift and creep, causing the readout of the FE balance to change over time. The first is driven by environmental factors, like temperature and vibration, which affect the flow conditions and the response of the measurement instrument. It can be minimised in a well-controlled environment by continuously monitoring key parameters throughout the experiment. In contrast, creep is an intrinsic property of the measurement instrument, describing the change in output from its gradual deformation under load over an extended period. To assess the creep behaviour of the FE balance, four loading conditions were applied over a period of one hour, sampling at a frequency of $16\,$Hz. The test was performed in a temperature-controlled room, and the FE balance was mounted on an anti-vibration table. The results, summarised in Table 1, reveal a marginal creep behaviour up to $50\,\%$ of the full-scale load, which exceeds the maximum expected smooth-wall drag. A temperature-controlled fan ensured the current source operated at a set temperature, regardless of the loading condition.

Table 1 Output change for a period of $1\,$h for selected loading conditions, normalised by the mean output value $\xi$ and by the rated output value $\xi _{\rm FS}$. $\varDelta T$ indicates the temperature difference between the controlled current source and the room

The resonance frequency $f_n$ and damping coefficient c of the FE balance were estimated by performing a set of motion-decay tests. They involve measuring the decaying signal over time following a controlled disturbance and, assuming the system behaves like a simple pendulum, fitting a simple harmonic motion equation through a least-squares regression. Tests were performed first without the dashpot and later with it in place: The resonance frequency $f_n$ remained approximately constant at $3.7\,$Hz, whereas the damping coefficient increased from 10.6 to $13.2\,$% of the critical damping, contributing to attenuate the peak amplitude response (at resonance frequency) approximately $20\,$%.

4 Experimental methods

To assess the accuracy of the FE balance, the wall shear stress measurements are compared against those obtained from OFI and indirect estimates from hot-wire measurements of the streamwise velocity profile, taken at the same downstream location. This section describes the setup and calibration of the FE balance but only briefly addresses the experimental aspects of OFI and hot-wire anemometry. This work follows the convention that x, y, and z are the streamwise, wall-normal, and spanwise directions, respectively.

4.1 Wind-tunnel setup

Fig. 6

Schematic representation of the working section comprising five interchangeable modules. A square section of the floor was removed at the measurement location to accommodate the FE balance and a clear acrylic window for OFI (not represented). Pressure taps were drilled around the cutout to measure the local streamwise pressure gradient $dp/dx = 2(p_2 - p_1)$ and the static-pressure difference between the top and the underside of the FE $\varDelta p_y = p_4 - p_3$. On the bottom-right corner is a side view of the setup for OFI, illustrating the relative position of the camera and the sodium lamp

Experiments were conducted in the newly commissioned, closed-return wind tunnel at the University of Southampton. This facility features a flow-conditioning section with an area-contraction ratio of 7:1 followed by a 12-m-long working section, $1.2\,$m wide by $1\,$m high. Immediately following the contraction, hot-wire velocity measurements in the freestream show that the turbulence intensity remains consistently lower than $0.1\,$% up to $45\,$m s$^{-1}$. Boundary layers are established directly on the wind tunnel floor and develop under a slightly favourable pressure gradient, owing to the fixed cross-sectional area. A zigzag strip is used to trigger the laminar-to-turbulent transition.

The measurements were taken $9\,$m downstream of the contraction, as indicated in Fig. 6. The floor was cut out along the centreline to accommodate the FE balance and a clear acrylic window for OFI. They are flush mounted with the test surface and securely fastened using through-hole countersunk bolts. The FE balance is additionally supported by a heavy-duty pedestal, which contributes to mitigating the adverse effects of vibration and improving SNR. As the cutout is marginally wider than the housing of the FE or the acrylic window, the clearance was sealed off to prevent flow disturbances using a light-duty sellotape, whose thickness is estimated to be less than 5 wall units. Static-pressure taps were drilled around the cutout, $250\,$ mm from the centre, to measure the local streamwise pressure gradient ${\rm d}p/{\rm d}x = 2(p_2 - p_1)$ and the static-pressure difference between the top and the underside of the FE $\varDelta p_y = p_4 - p_3$. To minimise $\varDelta p_y$, the FE was connected to the test section at a location transversely aligned with $p_3$ via 10-mm-diameter silicon tubing.

4.2 Static calibration

The FE balance was calibrated using a set of weights and the string-pulley arrangement illustrated in Fig. 3. The weights were measured using an analytical balance (Fisherbrand™ PAS214C), calibrated in situ with M1-class weights. It has a resolution of $0.1\,$mg and the linearity and repeatability errors are 0.2 and $0.1\,$mg, respectively. The pulley (ME-9450 PASCO Scientific) has a groove diameter of $50\,$ mm and is mounted beneath the working section, aligned with the centreline. Removing the lid provides access to the interior of the balance, exposing a fitting mounted to the FE. The fitting receives a 40-mm-long stud bolt, which sticks out from underneath, and a 0.19-mm-diameter nylon string is looped around it and strung over the pulley. A notch prevents the string from sliding off.

Since the strength of the magnetic field inside the air core solenoid is linearly proportional to the applied current, and the spacing between the solenoid and the permanent magnet remains unchanged, the response of the FE balance is essentially linear. The electromagnetic force may, therefore, be expressed as $F_e = kV$, where k is the linear sensitivity coefficient, and V is the DAC output voltage that regulates the controlled current source. Two crucial aspects were taken into account in the calibration: The first is the friction in the string-pulley arrangement, which causes the force experienced by the FE balance $F_2$ to be marginally lower than the gravitational force acting on the suspended weight $F_1$. The ratio of magnitude between these forces is described by the modified Capstan equation (Stuart 1961)

$$\begin{aligned} \frac{F_2}{F_1} \ = \ \exp {\left[ \theta \,(\mu _0 + \mu _1\,F_1^{-1})\right] }, \end{aligned}$$

(9)

where $\theta = \pi /2$ is the wrap angle of the string around the pulley and $\mu _0$ and $\mu _1$ are, respectively, the zeroth-order and linear-inverse friction coefficients measured following the procedure detailed in appendix A. The second detrimental factor is the steady-state error of the control system, whose effect is captured by the analytical model outlined in Sect. 3.3. Eliminating the pressure terms in Eq. 8 and assuming the FE balance is horizontally aligned, such that $\gamma = 0$, it follows that

$$\begin{aligned} F_2 \ = \ k\,V\,+\,mg\,\frac{\varDelta _x}{a}. \end{aligned}$$

(10)

The second term on the RHS of Eq. 10 is a source of systematic error that should remain negligible with adequate control of the actuation system. Nevertheless, as $\varDelta _x$ is continuously monitored for control purposes and is readily available, its contribution was quantified and subtracted before fitting the data.

Pre and post-calibrations were performed, sampling each data point at $128\,$HZ over $2\,$min to average out noise. The results are shown in Fig. 7. Seven loading combinations were applied with nominal values 5, 10, 20, 40, 60, 110, and $160\,$mN, taking the local gravity acceleration $g = 9.81084\,$m s$^{-2}$ from the land gravity survey data by the British Geological Survey. Given the uncertainty associated with the weights and the friction in the string-pulley arrangement, the weighted least-squares regression yielded a linear sensitivity coefficient $k = 0.1063\,\textrm{N} \textrm{V}^{-1} \pm 0.02\text {\%}$. The maximum absolute and relative deviations are $37.9 \upmu$N and $0.36\,$%, respectively. The average value of $\varDelta _x$ across all data points is on the order of $1\,$nm, representing a maximum relative error of $0.01\,$%.

Fig. 7

a Pre and post-calibration data as a function of the readout of the FE balance. The black-solid line is expressed by Eq. 10 where $k = 0.1047\,\textrm{N} \textrm{V}^{-1}\pm 0.02\text {\%}$. b The relative residual error of the fit as a function of the electromagnetic force kV

4.3 Data acquisition

Measurements of the surface drag over the FE were carried out for freestream velocities ranging from 10 to $45\,$m s$^{-1}$, in increments of $5\,$m s$^{-1}$. They were repeated seven times under identical test conditions to achieve statistical significance. Once switched on, the FE balance was given time to reach a set equilibrium temperature, maintained throughout the measurements within $\pm 0.5$ $^\circ$ C. A shakedown period of 3 min followed, ramping up the freestream velocity to 45 m s$^{-1}$ and back down again to ensure the first data point was taken under the same conditions as that of every subsequent repetition. The settling time following the shakedown and between repetitions is 30 min. Each data point was sampled at 128 Hz over 1 min, corresponding to a minimum of $T \delta / U_{\infty } = 4\times 10^3$ boundary-layer turnover times. The freestream was gradually increased every 5 min, allowing the system to adjust to the new loading condition.

4.4 Uncertainty propagation

Table 2 Resolution and uncertainty associated with the input quantities used to infer wall shear stress. Values specified by the sensor manufacturer or estimated to a confidence interval of 95 %

The present uncertainty analysis follows the guide to the expression of uncertainty in measurement from the International Bureau of Weights and Measures (BIPM et al. 2008). Uncertainty estimates of relevant quantities were obtained depending on the experimental method, yet only those pertaining to the FE balance are detailed here.

To quantify the uncertainty in the measurement of the surface drag experienced by the FE, Eq. 8 is recast such that the contribution of the systematic error sources identified in Sect. 3.3 is subtracted from the output of the balance. Thus,

$$\begin{aligned} \begin{aligned} F_w \ = \ F_e\,+\, \underbrace{2\,\varDelta p_x\,t\,l^2}_{\begin{array}{c} \\ F_{i} \end{array}}\,-\, \underbrace{\varDelta p_y\,S\,\frac{\varDelta _x\,-\,a\,\gamma }{a\,+\,\varDelta _x\,\gamma }}_{\begin{array}{c} \\ F_{ii} \end{array}}\,+\,\\ \,+\,\underbrace{mg\,\frac{\varDelta _x}{a\,+\,\varDelta _x\,\gamma }}_{\begin{array}{c} \\ F_{iii} \end{array}}, \end{aligned} \end{aligned}$$

(11)

where $F_t$ and $F_n$ were replaced by Eqs. 5 and 6, respectively, $\phi \simeq \varDelta _x/a$, and $p_{\infty }/dx \simeq 2\varDelta p_x$, given the streamwise distance between pressure taps 1 and 2, indicated in Fig. 6. In Eq. 11, $F_w$ is written as a function of $N = 11$ uncorrelated quantities $x_i$, which are either constant or were directly measured throughout the experiment. The associated uncertainty is estimated as the positive square root of the combined variance, expressed as

$$\begin{aligned} u_c^2(F_w) \ = \ \sum _{i=1}^N\,u_{x_i}^2(F_w), \end{aligned}$$

(12)

where

$$\begin{aligned} u_{x_i}^2(F_w) \ = \ \left( {\frac{\partial F_w(x_i)}{\partial x_i}}\right) ^2\,u^2(x_i), \end{aligned}$$

(13)

and $u(x_i)$ is the uncertainty associated with each independent quantity, listed in Table 2. Once $u_c^2(F_w)$ is computed, the uncertainty associated with the friction velocity $U_{\tau } = (F_w/S/\rho _{\infty }) ^ {1/2}$ can be estimated. It is assumed that air approximates ideal gas behaviour, so its density $\rho _{\infty } = p_{\infty }/R/T_{\infty }$, where $p_{\infty }$ is the atmospheric pressure, $T_{\infty }$ is the room temperature, and $R = 287.05$J kg$^{-1}$ K$^{-1}$ is the specific gas constant. The combined variance of the friction velocity becomes

$$\begin{aligned} \begin{aligned} u_c^2(U_{\tau }) \ = \ u_{F_w}^2\,(U_{\tau })\,+\, u_{p_{\infty }}^2(U_{\tau })\,+\, u_{T_{\infty }}^2(U_{\tau })\,+\,\\ \,+\,u_{S}^2(U_{\tau }). \end{aligned} \end{aligned}$$

(14)

In a similar manner, the combined variance of the skin friction coefficient $C_f = F_w / S / q_{\infty }$ is given by

$$\begin{aligned} u_c^2(C_f) \ = \ u_{F_w}^2(C_f)\,+\,u_{q_{\infty }}^2(C_f)\,+\,u_{S}^2(C_f). \end{aligned}$$

(15)

Fig. 8

Uncertainty budget for the measurement of surface drag over the FE as a function of the unit Reynolds number, comparing the relative contribution of the individual terms on the RHS of Eq. 11

Fig. 9

Uncertainty budget for the measurement of skin friction coefficient as a function of the unit Reynolds number

Figure 8 shows the uncertainty budget for the measurement of $F_w$, comparing the relative contribution of the individual terms on the RHS of Eq. 11. The leading factors $u^2_{F_i}(F_w)$ and $u^2_{F_{ii}}(F_w)$ represent approximately $75\,$% of the combined variance at low Reynolds numbers and over $99\,$% in the upper range. $u^2_{F_i}(F_w)$ is primarily driven by the error in the measurement of the streamwise static-pressure difference across the FE $u^2_{\varDelta p_x}(F_i)$, and $u^2_{F_{ii}}(F_w)$ by the measurement error in the horizontal alignment of the FE balance $u^2_{\gamma }(F_{ii})$, as $u^2_{\varDelta p_y}(F_{ii})$ and $u^2_{\varDelta _x}(F_{ii})$ are relatively small. These factors exhibit similar behaviour because of their pressure-based nature, scaling quadratically with the freestream velocity. In contrast, the uncertainty factor associated with the electromagnetic force $u^2_{F_e}(F_w)$ is dominated by calibration errors independent of the flow conditions. Its relative magnitude peaks at $23\,$% and gradually decreases with the Reynolds number to negligible values in the upper range.

The uncertainty budget for the measurement of $C_f$ is given in Fig. 9. $u^2_{F_w}(C_f)$ is consistently the most significant factor, except for low Reynolds numbers where measurement repeatability is poorer, representing up to $40\,$% of the combined variance. Notably, $u^2_S(C_f)$ lies between 10 and $20\,$%, indicating there is an appreciable contribution from the dimensional tolerance of the FE. The uncertainty factor associated with the measurement of the freestream dynamic pressure $u^2_{q_{\infty }}(C_f)$ remains negligible across the entire range of Reynolds numbers.

4.5 Oil-film interferometry

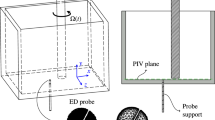
Introduced by Squire (1961), OFI was popularised as a direct wall shear stress measurement method by Tanner and Blows (1976). They showed that the thinning rate of a flow-exposed oil film is linearly proportional to the wall shear stress, providing the film is sufficiently thin for pressure drag to have a negligible contribution. The thinning rate is measured by interferometry, whereby the light waves reflected by the upper and lower boundaries of the film interfere with one another, creating a fringe pattern of light and dark bands with wavelength proportional to the thickness of the film. This measurement method is independent of the flow conditions and was shown to provide accurate estimates of the skin friction coefficient—typical uncertainty is $\pm 2\,$% (Tanner and Blows 1976; Naughton and Sheplak 2002; Segalini et al. 2015)—making it ideal as a benchmark against which to compare the present FE balance.

The experimental setup is depicted in Fig. 6. The measurements were taken at the same downstream location as the FE balance, replaced by a 20-mm-thick clear acrylic window for optical access. The light source was a monochromatic sodium lamp with a wavelength of $589\,$nm, mounted underneath the working section at a $41\,^\circ$ angle with the vertical direction. The dynamic viscosity of the oil was calibrated for a wide temperature range using a TA Instruments DHR3 Rheometer. Snapshots of the oil film were taken using a 16-MP LaVision Imager LX camera, mounted opposite the light source and fitted with a $200\,$ mm Nikon lens. The sampling rate is $1\,$Hz and the spatial resolution approximately $24\,$ $\upmu$m. The fast Fourier transform (FFT) was applied to the oil-film interferograms to determine the fringe spacing corresponding to the dominant peak of the power spectrum (Ng et al. 2007). OFI measurements were repeated three times under similar test conditions.

4.6 Hot-wire anemometry

The streamwise velocity profile was measured over the FE using an Auspex A55P05 hot-wire (HW) probe, featuring a 5- $\upmu$m-diameter Tungsten wire, shouldered on either side by copper-plated sections such that its active length is 1 mm and the effective length-to-diameter ratio 200. The probe was driven by a Dantec StreamLine Pro CTA (constant temperature anemometry) system, set to an overheat ratio of 1.8, and its output signal was sampled at $30\,$ kHz using an NI USB-6212 data-acquisition system. Pre- and post-calibrations were performed in situ, taking reference velocity measurements in the freestream using a Pitot-static tube, mounted alongside the HW and connected to an FCO 560 micromanometer. The velocity profiles consist of 35 data points, distributed logarithmically near the wall and linearly in the wake region. Each data point was sampled for at least $10^4$ boundary-layer turnover times to converge the energy contained in the large scales.

5 Results

5.1 Skin friction coefficient

Fig. 10

a The smooth-wall skin friction coefficient as a function of the momentum-based Reynolds number ${\rm Re}_{\theta }$ (lower x-axis) and the linear Reynolds number Re (upper x-axis). The black-dashed line represents the Coles–Fernholz skin friction relation with $\kappa = 0.39$ and $C = 4.352$, and the shaded regions the 95 % uncertainty bounds. b The relative difference between the measurements and the skin friction relation. The grey-shaded region indicates a $\pm 1$ % deviation

Direct measurements of the skin friction coefficient and the associated uncertainty estimates are shown in Fig. 10 as a function of the unit Reynolds number and the momentum-based Reynolds number ${\rm Re}_{\theta }$. A baseline is established by fitting the Coles–Fernholz relation (Fernholz 1971) to the OFI measurements, expressed as

$$\begin{aligned} C_f \ = \ 2\,\left[ \frac{1}{\kappa }\,\log (Re_{\theta })\,+\,C\right] ^{-2}, \end{aligned}$$

(16)

where the von Kármán constant $\kappa = 0.39$ (Marusic et al. 2013) and the fitting parameter $C = 4.352$. Alternatively, setting $\kappa = 0.38$ yields $C = 3.682$. Given the mean square error of approximately 0.5 %, the general trend appears to be accurately captured despite the comparably larger measurement uncertainty — 2.5 % for a confidence interval of $95\,$%, assuming a normal error distribution.³ Measurements from the FE balance show a remarkable agreement with OFI and closely follow the empirical relation to within 0.5 % for ${\rm Re}_{\theta } > 1.3\times 10^4$. The estimated uncertainty is typically lower than 1 %, notably better than that associated with OFI. The values diverge from the expected trend at low Reynolds numbers, exceeding the uncertainty band of $1.4\,$% for ${\rm Re}_{\theta } = 8.9 \times 10^3$, where the relative deviation is about 6.1 % or 0.38 mN in absolute terms.

A similar behaviour is visible in the measurements of Ferreira et al. (2018) and Baars et al. (2016), included in “Appendix B”. It is presumably the symptom of a systematic error that was underestimated or overlooked. Although it might be impossible to identify its source, a few assumptions can be made about its nature, considering the analysis presented in Sect. 3.3. The mechanism is likely not pressure-driven. Otherwise, its magnitude would scale quadratically with the unit Reynolds number, evenly affecting the values of the skin friction coefficient. Quantification of the systematic error terms in Eq. 8, discussed in the following Sect. 5.2, convincingly rules out any effect of the streamwise pressure gradient or the pressure difference between the top and the underside of the FE, which might not have been entirely eliminated. It also indicates a minimal effect of the steady-state error $\varDelta _x$, which was not only subtracted from the measurements but would have instead manifested as a repeatability error. A calibration error is equally unlikely because the magnitude of the residuals shown in Fig. 7 does not explain such a large deviation.

It would be reasonable to assume that the effect of the cavity-induced flow, not included in the model outlined in Sect. 3.3, might be important. However, the data is inconsistent with findings from Gaudet and Winter (1973), who show that the ratio of the drag coefficient across the gap, defined based on the surface area $b\,l$, to the undisturbed skin friction coefficient increases logarithmically with the Reynolds number $b^+$. They provide an empirical expression which can be modified to quantify the relative error contribution due to the cavity-induced flow $\epsilon _{iv}$ given the dimensions of the FE. Accordingly,

$$\begin{aligned} \epsilon _{iv} \ = \ \frac{2\,b}{l} \, [\log (b^+) - 1], \end{aligned}$$

(17)

for $b^+ > 10$. Equation 17 exhibits the opposite trend to the discrepancy between the measurements of the FE balance and the Coles-Fernholz relation, which is most significant for ${\rm Re}_\theta = 8.9 \times 10^3$ and drops off to negligible values (below $0.5\,$%) for ${\rm Re}_{\theta } > 1.3 \times 10^4$.

The preceding argument based on observations by Gaudet and Winter (1973) alone is insufficient to conclusively rule out an effect of the cavity-induced flow, which remains a plausible yet unlikely candidate. Additional literature is scarce. Spazzini et al. (1999) and more recently Perez et al. (2022) are two examples where the cavity dimensions are shown to strongly influence the local flow behaviour. They attempt to quantify the systematic error in measuring the skin friction coefficient using cavity hot-wire probes. The analyses are thus centred around point-wise velocity measurements rather than the global drag coefficient of the cavity, making it challenging to translate their results in the present context.

Also included in Fig. 10 are the values inferred using the Clauser-chart fitting method (Clauser 1956), which assumes the mean velocity profile in the overlap region follows a universal logarithmic distribution with a von Kármán constant $\kappa = 0.39$ and a wall intercept $A = 4.3$ (Marusic et al. 2013). This method consistently overestimates the skin friction coefficient, showing a relative deviation from the Coles–Fernholz relation of about $5\,$%. Although the associated uncertainty was not estimated, reported values typically fall between 5 to $10\,$% (Schultz and Flack 2005; Klewicki 2007), depending, amongst other factors, on the extent of the logarithmic layer and the error in the parameters $\kappa$ and A.

5.2 Systematic error sources

Fig. 11

Measured relative contribution of the systematic error terms defined in Eq. 8 as a function of the linear Reynolds number. $\epsilon _{ii}$ and $\epsilon _{iii}$ are multiplied by a factor of 100

Figure 11 shows the measured relative contribution of the spurious force components, subtracted from the electromagnetic force. As predicted by the analytical model derived in Sect. 3.3, the systematic error due to the favourable streamwise pressure gradient across the FE $e_i$ leads to the overestimation of the skin friction coefficient by approximately 7 %. Its magnitude is independent of the Reynolds number but is considerably larger than expected. This discrepancy stems from additional sources of pressure loss, such as the effect of the corners of the test section that were not included in the model. The remaining systematic error contributions are insignificant, mainly because the horizontal inclination of the FE balance $\gamma$ is nominally zero and the typical steady-state error $\varDelta _x$ across the measurement range is on the order of 10 nm, instead of 1  $\upmu$m, as conservatively assumed in Fig. 5. While $e_{ii}$ may be small, equalising the static pressure between the top and the underside of the FE proved crucial in mitigating the associated measurement uncertainty.

5.3 Effect of protrusion

Additional measurements were taken to assess the sensitivity of the balance to the protrusion of the FE $\varDelta _y$, adjusted using a set of linear stages to within 0.5  $\upmu$m, as illustrated in Fig. 3. The results are summarised in Table 3. Positive and negative values of $\varDelta _y$ indicate the FE is either standing proud from the test surface or recessed, respectively. The difference in skin friction coefficient relative to the reference measurements, presented in Sect. 5.1, was averaged across the range of Reynolds numbers, as the effect of protrusion is essentially uniform. In agreement with observations by Allen (1977), $\varDelta C_f$ is proportional to $\varDelta _y$. Positive protrusions create a high-pressure region on the leading edge of the FE and a low-pressure region on the trailing edge, yielding a positive net force. Conversely, negative protrusions yield a negative net force. The relative discrepancy is nearly 1 % for a protrusion as small as 20  $\upmu$m, which does not exceed 2 wall units at the highest Reynolds number, highlighting the importance of carefully aligning the FE with the surrounding test surface. Linearising around $\varDelta _y=0$ yields a sensitivity factor $d C_f / d \varDelta _y \approx 0.953$ m$^{-1}$ or $d C_f / d (\varDelta _y/\delta _{99}) \approx 0.124$. For reference, O’Donnel (1964) reported a measurement error of approximately $1\,$% for a protrusion of $12.7\,$ $\upmu$m ($b/l = 5\times 10^{-3}$) and Allen (1977) 2.9 $\upmu$m ($b/l = 2\times 10^{-3}$).

Table 3 Difference in skin friction coefficient $\varDelta C_f$, averaged across the measurement range of Reynolds numbers, as a function of the protrusion of the FE $\varDelta _y$

6 Summary

This work documents the development of a FE balance for application to low-speed boundary-layer flows over smooth or rough walls. An analytical model was derived to assess the relative significance and behaviour of its intrinsic sources of systematic error and establish effective mitigation strategies concerning design and operation. The mechanical arrangement, based on the parallel-motion linkage, in combination with the zero-displacement force-feedback system, makes the FE balance immune to off-axis loading, providing it is horizontally aligned and the steady-state error of the controller is sufficiently small, i.e. $\varDelta _x = \mathcal {O}(10\,\textrm{nm})$. The sensitivity is adjustable depending on the surface condition and the Reynolds number to ensure optimal measurement resolution and improve SNR. Given the flow-exposed gap, the FE balance is subject to the direct action of the pressure gradient and the cavity-induced flow. However, the first was estimated and subtracted from the measurement and the second was minimised by carefully aligning the FE with the surrounding test surface, $\varDelta _y^+ = \mathcal {O}(1)$, and by making the gap as wide as possible without disturbing the flow development, $b^+ = \mathcal {O}(10)$.

Measurements of the skin friction coefficient of a smooth-wall boundary layer obtained using the FE balance agree within uncertainty with OFI, and the relative discrepancy from the Coles–Fernholz relation ($\kappa = 0.39$ and $C = 4.352$) is consistently lower than $0.5\,$%, for ${\rm Re}_{\theta } > 1.3 \times 10^4$. The combined uncertainty for a confidence interval of $95\,$% typically does not exceed $1\,$%. The leading factors across the entire measurement range are associated with errors in estimating the effect of the streamwise pressure gradient and the horizontal inclination of the FE balance. Calibration and repeatability errors are only significant at low Reynolds numbers. Despite the comprehensive analysis of the systematic sources of error, the measurements appear to diverge from the expected trend for ${\rm Re}_{\theta } < 1.3 \times 10^4$, and it is unclear what could be the cause. An effect of the flow-exposed gap seems unlikely, yet, as discussed in Sect. 5.1, it cannot be confidently ruled out for the lack of definite evidence.

The expected performance of the FE balance should be better for rough-wall boundary layers. Not only is the SNR likely to improve, but the relative magnitude of the systematic sources of error should decrease with the added resistance (i.e. $\varDelta U^+$), given they are independent of the surface condition. Measurement repeatability should become the most important source of uncertainty, as demonstrated by Ferreira et al. (2018). Crucially, pressure measurements $p_1$ through to $p_3$, used to estimate the local pressure gradient and the pressure difference between the top and the underside of the FE, may no longer be taken on the surface. They should instead be taken using Pitot-static probes mounted in the freestream.

Appendices

Appendix A: Friction in the string-pulley arrangement

Fig. 12

Ratio of magnitude between the gravitational force acting on the suspended weight $F_1$ and the force experienced by the FE balance $F_2$. Solid line is the weighted squares regression of Eq. 18, and the dashed lines indicate the $95\,$% uncertainty bounds

The ratio of magnitude between the gravitational force acting on the suspended weight $F_1$ and the force experienced by the FE balance $F_2$ (refer to Fig. 6) is described by the modified Capstan equation (Stuart 1961)

$$\begin{aligned} \frac{F_2}{F_1} \ = \exp {\left[ \theta \,(\mu _0 + \mu _1\,F_1^{-1})\right] }, \end{aligned}$$

(18)

where $\theta = \pi /2$ is the wrap angle of the string around the pulley and $\mu _0$ and $\mu _1$ are, respectively, the zeroth-order and linear-inverse friction coefficients. The latter were estimated by measuring the change in the output of a load cell mounted in two different configurations: horizontally and vertically aligned. In the first configuration, calibrated weights were hung directly from the load cell using a 0.19-mm-diameter nylon string, whereas, in the second, the string was strung over the pulley as it would for in situ calibration of the FE balance. Six loading combinations ranging from 5 to 200 mN were applied, and the measurements were repeated nine times for both configurations to achieve statistical significance. Equation 18 was fit through the data by minimising the weighted sum of squared residuals, yielding $\mu _0 = 5.1\times 10^{-4} \pm 4.2\times 10^{-4}$ and $\mu _1 = -8.2\times 10^{-2} \pm 2.4\times 10^{-2}$ mN. The uncertainty level in the coefficients was estimated to a confidence interval of $95\,$%, assuming normal distribution. As shown in Fig. 12, the friction in the string-pulley arrangement can have an appreciable effect, especially for $F_1 < 10$ mN. The values of surface drag presented in Sect. 5 fall within the range of $F_1$.

Appendix B: Published measurements of skin friction coefficient

Figure 13 shows how the smooth-wall skin friction coefficients from Baars et al. (2016) and Ferreira et al. (2018) compare against the present measurements.

Fig. 13

The smooth-wall skin friction coefficient as a function of the momentum-based Reynolds number ${\rm Re}_{\theta }$. The black-dashed line represents the Coles–Fernholz skin friction relation with $\kappa = 0.39$ and $C = 4.352$, and the shaded region the 95 % uncertainty bounds