1 Introduction

Yacht sails are thin, flexible wings with three free sharp edges. Their design and the aerodynamics of sails have been described within the reviews of Milgram (1998), Larsson (1990) and Viola (2013). Modern sloops, i.e. yachts with one mast, sail with one mainsail attached to the mast and one headsail in front of it. The mainsail is attached to a mast by the leading edge, while headsails, such as jibs, genoas and spinnakers, are fixed only by the three corners and have a sharp leading edge. Headsails are trimmed near the ideal angle of attack, preventing leading-edge separation or enabling flow reattachment shortly downstream.

We define the true wind and apparent wind angle (\(\beta _t\) and \(\beta _a\), respectively) as the angles between boat heading and the wind velocity at 10-m height, as observed from an earth-fixed and a boat-fixed frame, respectively (Fig. 1). A boat is traditionally said to sail upwind or downwind when \(\beta _t\) is lower or greater than \(90^{\circ }\), respectively. Sails used in upwind conditions such as jibs, where the drag has a negative component along the sailed course, have relatively low camber to prevent trailing edge-separation (Viola 2013; Biancolini et al. 2014), and the aerodynamic forces can be accurately computed with panel methods (Milgram 1968; Gentry 1971). In contrast, when sailing downwind, and the drag has a positive component along the sailed course, highly cambered sails such as spinnakers are used to increase the total lift, as the increased drag results in none or in a marginal speed penalty associated with the boat heeling. This work focuses on the aerodynamics of spinnakers used in downwind conditions.

Fig. 1
figure 1

Schematic drawing of the relative sail position, the velocity triangle defining the apparent wind velocity, and the boat-fixed coordinate system

Full size image

Significant advances in spinnaker design were made in the 1990 s when asymmetric spinnakers were first developed for racing purposes (Fallow 1996; Milgram 1998). This period coincides with developments in both the first twisted-flow wind tunnels (Flay and Vuletich 1995) and the application of Computational Fluid Dynamics (CFD) to downwind sails design (Hedges et al. 1996). Since then, spinnakers have been the subject of substantial research with both CFD (Viola 2009; Viola et al. 2014; Lasher and Sonnenmeier 2008; Richards 1997; Nava et al. 2018), wind tunnel testing (Bot et al. 2014; Viola 2009; Richards et al. 2001; Lasher et al. 2005; Augier et al. 2021; Aubin et al. 2018; Richards and Lasher 2008; Schutt 2017; Hawkins 1998; Campbell 2014), and full-scale, on-water measurements (Viola and Flay 2012; Deparday et al. 2014; Viola and Flay 2010; Motta 2015; Masuyama and Fukasawa 1997; Deparday et al. 2018). Two findings are particularly relevant to the present work.

First, modelling the flexibility of the sail is not essential at low \(\beta _a\). All of the above-cited CFD studies consider a rigid spinnaker, which is also the case for several wind tunnel tests such as those of Hawkins (1998), Lasher et al. (2005), Richards and Lasher (2008), Bot et al. (2014) and Schutt (2017). The study of Viola and Flay (2009) was the first to show that the extra drive force achieved, allowing the leading edge to curl, vanishes as \(\beta _a\) decreases. This was further confirmed by Aubin et al. (2018) and Augier et al. (2021). In mild sea conditions and for a steady course where \(\beta _a<{90}^{\circ }\), spinnakers’ flexibility is negligible (Viola and Flay 2009; Gerhardt et al. 2011).

The second relevant finding is that the sail twist can be adjusted to model the effect of the apparent wind twist (Arredondo-Galeana et al. 2023). Boats sail in the atmospheric boundary layer (ABL) such that the wind speed increases with height. Therefore, the flow velocity experienced by the boat as it moves through the ABL varies both in magnitude and direction (Viola 2013). In some specialised wind tunnels, twisting vanes are used to twist the flow upstream of a static model (Flay and Vuletich 1995; Fossati et al. 2006; Graf and Müller 2009). This is possible when small models are used compared to the test section size. In other facilities, it is common practice to entirely neglect the apparent wind twist in wind (Lasher et al. 2005; Campbell 2014; Schutt 2017; Bot et al. 2014; Aubin et al. 2018) and water (Arredondo-Galeana and Viola 2018) tunnels. Alternatively, in lieu of twisting the onset flow, the sail geometry itself can be twisted in order to achieve the expected incidence at any spanwise section. The validity of this approach was demonstrated by Arredondo-Galeana et al. (2023), who tested a set of sails generated by twisting a reference sail shape by different extents. They found that, despite the massive flow separation, the slope of the lift with the angle of attack is independent of the twist, in agreement with strip theory. While more research is needed to explore the limitations of this approach, this assumption is adopted in this work (further detailed in Sec. 2.1), and its further analysis is left to future studies.

The comparison between the surface pressure distributions computed with CFD and measured in a wind tunnel and at full scale has been reported by Viola and Flay (2011), while Viola et al. (2014) compared the forces and surface pressure distributions computed with CFD and measured on a flexible and a rigid spinnaker with a nominally identical shape. Both studies show large discrepancies, revealing the inherent challenges in testing highly separated flow on such complex three-dimensional curved wings and highlighting the need for high-quality experimental data to validate numerical simulations. The flow field around spinnakers has never been measured on full-scale spinnakers, where only force (Masuyama et al. 2009; Deparday et al. 2014; Motta 2015) and pressure measurements (Viola and Flay 2012; Motta et al. 2014; Deparday et al. 2016) have been undertaken. To gain further insights into the flow field around spinnakers and enable quantitative validation of CFD simulations, Particle Image Velocimetry (PIV) has recently been undertaken in water tunnels. Water tunnel experiments have been performed both on two-dimensional spanwise sections of spinnakers (Bot et al. 2016; Bot 2020; Souppez et al. 2022, 2019; Souppez and Viola 2022; Souppez et al. 2021), and on three-dimensional downwind sails (Arredondo-Galeana and Viola 2018; Arredondo-Galeana et al. 2023).

Thanks to the increasing availability of facilities equipped with fast prototyping capabilities, water tunnels and PIV instrumentation, these tests have the potential to become a common design tool for validating CFD simulations of high-performance spinnakers. However, all previous PIV studies have been characterised by a lower Reynolds number than full-scale, larger models with respect to the test section than typically recommended by wind and water tunnel guidelines, and the absence of the mainsail, which is typically sailed together with the spinnaker. In this study, we aim to provide some guidance on these aspects, as well as to gain new insights into the flow around spinnakers. Specifically, this paper aims to address the following research questions.

  1. (1)

    Due to the limitations of the facility or of the load balance, and to limit the stress on the model, the average-chord-based Reynolds number Re that has been tested in water tunnels is of the order of \(10^4\), \(O(10^4)\) (Arredondo-Galeana and Viola 2018; Arredondo-Galeana et al. 2023). Conversely, for similar considerations, \(Re=O(10^5)\) in wind tunnel tests (Gerhardt et al. 2011; Viola and Flay 2011; Bot et al. 2014; Viola and Flay 2010; Viola et al. 2014), while \(Re=O(10^6)\) for full-scale spinnakers (Collie 2006; Braun et al. 2016; Deparday et al. 2018; Viola and Flay 2012). Whether testing at such low Reynolds numbers allows Reynolds-independent force prediction and effective design methodologies is yet to be determined.

  2. (2)

    On circular cylinders, the drag curve versus Re shows a sharp drop, known as the drag crisis, for a critical Reynolds number. This is associated with the occurrence of laminar-to-turbulent transition in the boundary layer. Specifically, the flow is subcritical when the laminar boundary layer separates, and the separated shear layer turns to turbulent in the wake, while the flow is transcritical when the laminar-to-turbulent transition occurs in the boundary layer, resulting in turbulent separation (Schewe 1983). In contrast, for highly cambered two-dimensional circular arcs, the force crisis (lift and drag) with increasing Reynolds number is due to suppressed relaminarisation. In fact, the pressure distribution on the suction side of the arc features two characteristic suction peaks: a first one due to the sharp leading edge and a second one further downstream due to the arc curvature. The flow separates at the sharp leading edge, and reattachment occurs shortly downstream, forming a leading-edge separation bubble (LESB). The reattached boundary layer eventually separates before the trailing edge, a feature here referred to as trailing-edge separation. In subcritical conditions, the favourable pressure gradient associated with the second suction peak and the inherent flow acceleration result in relaminarisation of the boundary layer (Souppez et al. 2022). CFD simulations (Collie 2006; Nava et al. 2017) and pressure measurements (Viola and Flay 2011, 2012; Bot et al. 2014) have shown that the characteristic double suction peak also occurs on three-dimensional spinnakers, and CFD simulations (Viola et al. 2014; Nava et al. 2018) and PIV measurements (Arredondo-Galeana and Viola 2018; Arredondo-Galeana et al. 2023) have shown that the LESB is formed. However, whether the force crisis and the associated relaminarisation occurs on three-dimensional spinnakers have never been shown.

  3. (3)

    The blockage ratio is the ratio of the frontal area of the geometry \(A_F\) to the cross-section area of the test section \(A_S\). Barlow et al. (1999) suggests a maximum blockage ratio of 0.075 for wind tunnel tests, while Lasher et al. (2005) recommended 0.050 or lower for spinnakers. However, to increase the Reynolds number, the signal-to-noise ratio of load measurements, and the spatial resolution of PIV measurements, higher blockage ratios than the previously cited guidelines have been employed (Bot et al. 2016; Marchand et al. 2017; Bot 2020; Arredondo-Galeana and Viola 2018; Arredondo-Galeana et al. 2023). While established blockage corrections are unable to correctly predict the unconstrained forces for lift-generating bodies experiencing significant trailing-edge separation, Souppez et al. (2022) successfully established empirical linear extrapolations for \(A_F/A_S\) as high as 0.25 for nominally two-dimensional, transitional flow conditions. Whether a similar approach can be successful for spinnaker sails is yet to be established.

  4. (4)

    Water tunnel tests have been undertaken without the mainsail (Arredondo-Galeana and Viola 2018; Arredondo-Galeana et al. 2023), thereby neglecting the upwash it generates. Spinnakers alone have also been tested in wind tunnels (Aubin et al. 2018; Augier et al. 2021; Gauvin and Banks 2020; Lasher et al. 2005). However, whether it is possible to account for the absence of the mainsail by correcting the angle of attack of the spinnaker in isolation remains to be ascertained.

The purpose of this study is to address the aforementioned open questions (1–4) and provide guidelines for future water tunnel tests of model-scale spinnakers. To this end, six models of a spinnaker are tested in a water tunnel. Experiments are undertaken at three blockage ratios up to 0.094, at average-chord-based Reynolds numbers between 5 870 and 61 870, and both with and without the presence of the mainsail.

The remainder of this paper is structured as follows. Sec. 2 presents the research methodology, including the sails employed, water tunnel facility, and experimental setups. Results are presented in Sec. 3, first considering the effect of the blockage, then the Re dependency, and finally, the presence or absence of the mainsail. Finally, the main findings are summarised in Sec. 4.

2 Methodology

In this section, we describe the spinnaker geometry and associated sailing conditions (Sec. 2.1), the water tunnel (Sec. 2.2), and the methodology to measure forces and the flow velocity fields (Sec. 2.3 and 2.4, respectively).

2.1 Sail models

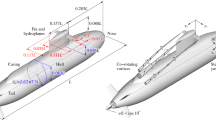
The tested geometries are based on the design of Braun et al. (2016) for the McCurdy & Rhodes 48’ sloop Carina, having an overall length of 14.70 m. At the design conditions considered here, the boat sails at \(\beta _a={85}^{\circ }\) at a boat speed \(V_b={4.06}\text {m}\,\text {s}^{-1}\) in a wind speed \(V_t={6.17}\text {m}\,\text {s}^{-1}\) at \(Z_\text {ref}={10}\,\text {m}\) from sea level. The full-scale surface area of the spinnaker is \(A={175}\,\text {m}^{2}\), the vertical span is \(s={16.27}\,\text {m}\), and the Reynolds number based on the average chord (\({{\bar{c}}}\equiv A/s\)) is \(Re={4326\,069}\). In Sect. 3.3, we will investigate the effect of the mainsail on the aerodynamics of the spinnaker. The full-scale surface of the mainsail is \(A_\textrm{main}={58.04}\,{\text {m}^2}\), and the span is \(s_\textrm{main}={17.84}\,{\text {m}}\).

While sailing, a spinnaker can be trimmed in different ways by adjusting the relative position of the three corners at which the sail is fixed to the boat. Here, we consider two different trims of the same sail, \({\text{T}}_{1}\) and \({\text{T}}_{2}\) (Fig. 2). The sail designers (Braun et al. 2016) identified \({\text{T}}_{1}\) as the optimum sail trim providing the design boat speed, while \({\text{T}}_{2}\) is the sail shape achieved by moving the aft corner of the sail 0.50 m towards the stern (on board, this would be practically executed by shortening the spinnaker sheet).

Fig. 2
figure 2

The two tested sail geometries: a trim \({\text{T}}_{1}\), and b trim \({\text{T}}_{2}\) of the tested spinnaker with adjusted twist. Both the boat-fixed O’(X, Y, Z) and the sail-fixed O(x, y, z) frames of reference are shown

Full size image

Three model sizes of \({\text{T}}_{1}\) are made at a scale \(\lambda =\)83.44:1, 100.13:1 and 125.16:1. A fourth model is made by mirroring the largest model about the XY-plane to undertaken flow measurements throughout the whole span of the sail despite the large spanwise curvature leading to shadow areas (further detailed in Sec. 2.2). Two mirrored large models are also made of \({\text{T}}_{2}\).

Both trims are low aspect ratio (\(A_R\equiv s^2/A\)), highly cambered wings. Specifically, on a horizontal section at midspan, the maximum camber-to-chord ratio is \(y_c/c=0.31\) and 0.28 for \({\text{T}}_{1}\) and \({\text{T}}_{2}\), respectively, and the chordwise position of the maximum camber (i.e. the draft) is at 0.509 of the local chord c for both (Fig. 3; Table 1 and 2). At the design condition, the angle of attack \(\alpha\) of the horizontal section at midspan is \(33.62^{\circ }\) for \({\text{T}}_{1}\) and \(38.10^{\circ }\) for \({\text{T}}_{2}\).

Fig. 3
figure 3

Mid-span cross section of the \({\text{T}}_{1}\) model and O(x, y, z) frame of reference

Full size image
Table 1 Geometric definition of the four models
Full size table
Table 2 Geometric definition of the mid-span section of the four models
Full size table

In the ABL, the true wind velocity \(\varvec{V_t}\) increases with height (Z). As the boat sails with velocity \(\varvec{V_b}\), it experiences an apparent wind speed \(\varvec{V_a}(Z)=\varvec{V_t}(Z)-\varvec{V_b}\). For the present boat at full scale conditions, \(\varvec{V_a}\) increases by \({0.87}\,\text {m}\,\text {s}^{-1}\) in magnitude and rotates anticlockwise by \(7.81^{\circ }\) (with reference to Fig. 1) from the bottom to the top section of the spinnaker.

Instead, in the water tunnel, the onset flow velocity is uniform and the model is fixed. Hence, as mentioned in the Introduction (Sec. 1), we follow the approach of Arredondo-Galeana et al. (2023), where the original sail design is modified to ensure that, for every horizontal section at coordinate Z, the angle of attack \(\alpha (Z)\) between the chord and \(\varvec{V_a}(Z)\) is the same in the water tunnel and at full-scale conditions. This is achieved by rotating each horizontal sail section around the leading edge. The relative velocity \(\varvec{V_a}(Z)\) is computed assuming the velocity profile of the ABL is (Cook 1986)

$$\begin{aligned} \varvec{V_t}(Z)=\varvec{V_t}\left( Z_{\textrm{ref}}\right) \frac{\ln \left( Z / Z_{0}\right) }{\ln \left( Z_{\textrm{ref}} / Z_0\right) }, \end{aligned}$$
(1)

where the reference height \(Z_{\textrm{ref}}\) is 10 m and the roughness length \(Z_{0}\) is \(5.097\times 10^{-5}\) m.

Furthermore, to investigate the effect of the angle of incidence, the model is rigidly rotated around Z by an angle \(\eta\), and experiments are undertaken for a range of \(\eta\) values. Hence, \(\eta\) is the angle between the chord of the rotated sails and the chord of the sail at the design position of the sail.

All spinnakers and mainsail models were 3D printed using fused filament fabrication, i.e. layer plastic deposition, on a Zortrax M200 (small and medium \({\text{T}}_{1}\) models) and a Zortrax M300 (large \({\text{T}}_{1}\) and \({\text{T}}_{2}\) and mainsail models) 3D printer. For the largest spinnakers, two mirrored models were manufactured for each trim. This is to enable PIV measurement over a full range of spanwise sections, as further discussed in Sec. 2.2. The spinnaker model thickness (t) was 3.00 mm for the largest models, 2.50 mm for the medium-size model, and 2.00 mm for the small model. This yields a thickness-to-average-chord ratio \(t/{{\bar{c}}}=0.0233\), and a local thickness-to-chord ratio \(t/c\le 0.04\), but for the top 12% of the sail because the chord decreases up to vanishing at the top head of the sail. The mainsail model thickness was 2 mm. All models were sanded with 2500 grit wet and dry sandpaper, as adopted in previous work Souppez et al. (2022). The large \({\text{T}}_{1}\) and \({\text{T}}_{2}\) spinnakers, which were used for PIV measurements, were then coated with Rhodamine B (to minimise laser light reflection) and clear acrylic, before being sanded with 2500 grit wet and dry sandpaper.

2.2 Water tunnel

The water tunnel is 8 m long, 0.4 m wide, and 0.9 m deep with a flat horizontal bed. The static water level was 0.34 m. Tests were undertaken at \({5870}\le Re_{{{\bar{c}}}} \le {61\,870}\) (Sec. 3.2), with all other experiments conducted at \(Re={32\,210}\). In this latter condition, the free-stream velocity for the small, medium, and large spinnakers, denoted with the subscript S, M, and L, respectively, was \(U_{\infty , S}={0.361}{\,\text {m}\,\text {s}^{-1}}\), \(U_{\infty , M}={0.289}{\,\text {m}\,\text {s}^{-1}}\) and \(U_{\infty , L}={0.241}{\,\text {m}\,\text {s}^{-1}}\). The streamwise turbulence intensity (\(T_u\)), measured with laser Doppler velocimetry, was \(T_{u,S}=0.0281\), \(T_{u,M}=0.0369\), and \(T_{u,L}=~0.0459\).

Each spinnaker model was tested with a horizontal spanwise axis, vertically centred on the water column and spanned horizontally and centrally across the width of the water tunnel. For the large \({\text{T}}_{1}\) model, both the tip and the foot of the sail were at 102 mm from the walls of the tunnel. The forces were only marginally sensitive to the model position in the water tunnel. In fact, by placing the foot of the large \({\text{T}}_{1}\) model at \(\eta ={0}^{\circ }\) and \(Re_{{\overline{c}}}={32\,210}\), from 2.5 mm to 152.5 mm from the water tunnel wall, the lift and the drag varied by less than 1% and 1.5%, respectively. Note that the foot of the full-scale sail is at 3.5 m from the water plane, that is 83 mm at the scale of the large \({\text{T}}_{1}\) model. Hence, the ground effect was found to be marginal.

A 395 mm wide by 800 mm long skim plate was employed to avoid free surface deformation. For force measurements, the suction side was oriented downwards (Fig. 4a), while PIV measurements were taken with the suction side upwards to illuminate the suction side with the laser (Fig. 4b). The same orientation was employed for mainsail tests (Fig. 4c).

Fig. 4
figure 4

Schematic of the experimental setup for a force measurements, b PIV measurements, and c mainsail

Full size image

PIV measurements of the large \({\text{T}}_{1}\) and \({\text{T}}_{2}\) models were undertaken at five spanwise sections \(z/s=0.05, 0.37, 0.57, 0.70\) and 0.88, where z is parallel to Z and has the origin at the lowest point of the spinnaker (Fig. 2). The values of \(z/s=0.05, 0.37\) and 0.70 were selected to match the work of (Braun et al. 2016). Intermediate data are provided as close as possible to midspan, namely \(z/s=0.57\), and at 7/8th of the span (\(z/s=0.88\)) as per Arredondo-Galeana and Viola (2018). The flow on the midspan section (\(z/s=0.50\)) could not be measured due to the shadow resulting from the double curvature of the geometry. The focus on the upper half of the span is due to its greater impact on the overall performance of the sail (Arredondo-Galeana and Viola 2018).

Because of the high spanwise curvature of the spinnaker, not all spanwise sections were visible to the PIV camera for a single model. Consequently, two mirrored geometries were employed. The first one was placed with the head of the sail towards the PIV camera to visualise the upper half of the span. The second one was located with the foot of the sail towards the PIV camera, so that the flow fields on the lower half of the span could be visualised.

2.3 Force measurements

Forces were measured with a six-axis force/torque sensor. For each tested condition, forces were recorded at 1000 Hz for 120 s. Experiments were repeated with and without the support bracket. The lift and drag were taken as the difference between the two time-averaged measurements. The lift and drag coefficients are \(C_L\equiv 2L/\rho AU_{\infty }^2\) and \(C_D\equiv 2D/\rho AU_{\infty }^2\), respectively, where L and D are the time-averaged measured lift and drag forces, respectively; \(\rho\) is the water density at the median temperature recorded during the experiments in accordance with the ITTC (2011) freshwater properties; A is the surface area of the suction side of the sail (see Table 1); and \(U_{\infty }\) is the time-averaged streamwise velocity measured with laser Doppler velocimetry in an empty water tunnel at the same impeller power as the tests undertaken with the model. The uncertainty quantification inherent to the lift and drag coefficients is detailed in supplementary information and will be represented as vertical error bars in this paper. Horizontal error bars for the rotation angle will not be shown for clarity given their negligible magnitude (\(\pm {0.025}^{\circ }\)).

2.4 Particle image velocimetry

PIV measurements were taken parallel to the onset flow and orthogonal to the spinnakers on the suction side of the sail. The PIV experiments were undertaken using a 200 mJ Nd:YAG pulsed laser (Solo 200XT) at a 532 nm wavelength. Silver-coated hollow glass spheres, with a nominal diameter of 14\(\upmu\)m and a specific gravity of 1.7 were illuminated by the 2 mm laser sheet created using a -20 mm sheet optic. No free surface deformation or model vibration was noticed during the experiments.

Two fields of view (FoV) were employed: a wide field of view to capture the wake, and a narrow one focused on the geometry. Their respective sizes were 255.2 mm \(\times\) 215.3 mm, and 163.5 mm \(\times\) 137.8 mm. Images were recorded at 15 Hz using a 5.5 Megapixel sCMOS camera with a resolution of 2560 px \(\times\) 2160 px, and fitted with a 532 nm filter, and a Nikkor f/4, 50 mm lens. The time between frames was 1000\(\upmu\)s. For each tested condition, 500 images were acquired, where an image is defined as two frames. Pre-processing in the form of sliding background subtraction was applied with a 12 px filter length. For post-processing, a multi-pass (decreasing size) cross-correlation was adopted, with one initial pass having a 96 px \(\times\) 96 px interrogation window and 50% overlap, before three 32 px \(\times\) 32 px passes with a 75% overlap. As such, a velocity vector is ascertained for an 8 px \(\times\) 8 px window. This yields velocity fields with a spatial resolution of 0.798 mm, corresponding to 0.0062c for the wide field of view. The spatial resolution of the narrow field of view is 0.511 mm, or 0.0040c. The error in the velocity measurements is considered to be driven by the error in pixel displacement, as quantified in supplementary information. At \(Re={32\,210}\), the flow velocity uncertainty is ± 0.0279\(U_{\infty }\) for the wide field of view and ± 0.0181\(U_{\infty }\) for the narrow field of view.

3 Results

This section is organised as follows. We first discuss the effect of blockage (Sec. 3.1), then the existence of a critical Reynolds number (Sec. 3.2), and the difference between testing with or without the mainsail (Sec. 3.3). Finally, we discuss the differences between the trims \({\text{T}}_{1}\) and \({\text{T}}_{2}\) (Sec. 3.4).

3.1 Blockage

The frontal area, and therefore blockage ratio, varies with the angle of rotation \(\eta\). For the range of incidences considered, namely \({-9}^{\circ }<\eta <{9}^{\circ }\), the blockage ratio is \(0.080<A_F/A_S<0.094\) for the large model, \(0.056<A_F/A_S<0.065\) for the medium model, and \(0.036<A_F/A_S<0.042\) for the small model.

Here an empirical linear blockage correction is sought, including solid blockage, wake blockage, and the effect of blockage streamline curvature. For every geometry, a linear fit of the force coefficient with \(A_F/A_S\) is achieved using the least squares method for each rotation angle, \(\eta =-9^{\circ }, -6^{\circ }, -3^{\circ }, 0^{\circ }, 1^{\circ }, 2^{\circ }, 3^{\circ }, 4^{\circ }, 5^{\circ }, 6^{\circ }, 7^{\circ }, 8^{\circ }\) and \(9^{\circ }\) at \(Re=32~210\). This is presented for the measured lift and drag coefficient in Fig. 5a and b, respectively. For clarity, results are presented in \({3}^{\circ }\) increments for \(\eta\).

Fig. 5
figure 5

Force coefficients versus the blockage ratio a–b; and measured c–d and corrected e–f force coefficients versus the rotation angle \(\eta\) for \(Re={32\,210}\)

Full size image

Both force coefficients are shown to increase with increasing \(A_F/A_S\). This is interpreted as the combined effect of solid and wake blockage (Barlow et al. 1999). First, solid blockage caused by the test section being obstructed by a comparatively large model leads to a higher local flow speed, and thus higher force coefficients. Secondly, wake blockage, whereby further acceleration of the flow results from the obstruction created by the wake downstream of the body.

Extrapolating the linear fits for each \(\eta\) to \(A_F/A_S=0\) yields the corrected lift and drag coefficients, \(C_{L\textrm{cor}}\) and \(C_{D\textrm{cor}}\), respectively, plotted versus \(\eta\) in Fig. 5c and d, respectively, including the extrapolated coefficients. Next, for every \(\eta\), \(C_{L\textrm{cor}}/C_L\) and \(C_{D\textrm{cor}}/C_D\) versus the blockage ratio \(A_F/A_S\) are fitted with a linear regression, yielding to the slopes \(a_L\) and \(a_D\), respectively. The corrected force coefficients are then given by

$$\begin{aligned} C_{L_\textrm{cor}}=\left( a_L\frac{A_F}{A_S}+1\right) C_L, \end{aligned}$$
(2)

and

$$\begin{aligned} C_{D_\textrm{cor}}=\left( a_D\frac{A_F}{A_S}+1\right) C_D. \end{aligned}$$
(3)

The collapse of the corrected lift and drag coefficients for each model and \(\eta\) is shown in Fig. 5e and f, respectively. The corrected lift is, on average, within \(-\)0.20%, 0.55% and \(-\)0.22% of the extrapolated values for the large, medium, and small spinnakers, respectively. The corrected drag is, on average, within \(-\)0.33%, 0.68% and \(-\)0.32% of the extrapolated values for the large, medium, and small spinnakers, respectively. There is a noticeable decline in the extrapolate lift coefficient (Fig. 5e) for \(\eta >{3}^{\circ }\). This is associated with the spinnaker stalling at \(z/s=0.57\) and 0.70 for \(\eta =6^{\circ }\) and \(9^{\circ }\), a behaviour not observed at \(\eta ={3}^{\circ }\), as revealed by the flow fields in Sec. 3.3.

3.2 Critical Reynolds number

In this section, we first present the effect of the Reynolds number on the forces (Sec. 3.2.1), then on the flow velocity field (Sec. 3.2.2) and finally on the turbulent kinetic energy (Sec. 3.2.3).

3.2.1 Force crisis

The lift and drag coefficients for the three models and values extrapolated for \(A_F/A_S=0\) are presented in Fig. 6a and b, respectively, versus Re. It is noted that \(Re={61\,870}\) could only be achieved for the large model, as the higher stream velocities required for the medium and small spinnakers resulted in visible model vibrations.

Fig. 6
figure 6

Lift a and drag b coefficients versus the Reynolds number at \(\eta ={0}^{\circ }\)

Full size image

There is a noticeable step change in the force coefficients for \(Re\ge 22~940\) for all model sizes and, therefore, blockage ratios. The step change in force coefficients corresponds to the critical Reynolds number. These results are consistent with those observed by Souppez et al. (2022) on the circular arc, where the lift coefficient increases by approximately 1.15 to 1.32 times at \({53\,530}\le Re \le {150\,000}\) at angles of attack from \({10}^{\circ }\) to \(25^{\circ }\). However, the drag coefficient decreases with increasing Reynolds number on the circular arc as the trailing edge separation shifts downstream and the wake thickness decreases. Conversely, the drag increases with increasing Reynolds number on the present spinnaker. This is associated with a step increase of circa 170% in the magnitude of the aerodynamic force, as well as a rotation towards the drag direction of circa \(5^{\circ }\). The underlying physics for the step change in the lift and drag with increasing Reynolds number is discussed in Sec. 3.2.3.

The force measurement uncertainty shown in Fig. 6 is higher at both low and high Re because of the increasing bias error with decreasing Re, and the increasing precision error with increasing Re. In fact, model vibration and the amplitude of the force fluctuations increased with increasing Re. Thus, we will focus on \(Re={16\,320}\) and \({32\,210}\), which are markedly lower and higher than the critical Reynolds number, respectively, but have relatively low uncertainty.

3.2.2 Velocity field

Figure 7 shows contours of the magnitude of the planar velocity field \({{\varvec{u}}=(u,v)}\) and streamlines on five sections at the subcritical \(Re={16\,320}\) and at the transcritical \(Re={32\,210}\). On the suction side of the highest sail sections, for both Reynolds number conditions (Fig. 7a and b), an attached boundary layer develops till around the location of the maximum camber. The LESB is not present or sufficiently small to be not visible with the present resolution. The boundary layer on the pressure side (not visible in Fig. 7) separates at the trailing edge.

Fig. 7
figure 7

Time-averaged streamlines and contours of velocity magnitude for the large \({\text{T}}_{1}\) model at \(Re={16\,320}\) (left column) and \({32\,210}\) (right column), at \(z/s=0.88\) a–b, \(z/s=0.70\) c–d, \(z/s=0.57\) e–f, \(z/s=0.37\) g–h and \(z/s=0.05\) (i-j), for \(\eta ={0}^{\circ }\). Laser shadow areas are coloured in grey. The red crosses indicate the location of the fore corner of the sail (tack) at \(z/s=0\). The red diamonds show the trailing-edge separation point

Full size image

At \(z/s=0.70\) and 0.57, and \(Re={16\,320}\) (Fig. 7c and e), the near wake identified by the low-speed region (in blue) expands after the separation point (red diamond) reaching a higher frontal area than \(A_S\), as typical of the subcritical flow regime. Conversely, the near wake is narrower and deflected towards the pressure side (downwards) at the transcritical \(Re={32\,210}\) (Fig. 7d and f). The shift from subcritical to transcritical is associated with a downward shift of the separation point (red diamond) (Tank et al. 2021). The location of the point of trailing-edge separation is taken as the closest point to the surface of the spinnaker where the tangential velocity vanishes, as defined by Fujiwara et al. (2020). At \(z/s=0.37\), where the angle of attack is higher than on the highest sections, the LESB is markedly visible (Fig. 7g and h).

3.2.3 Turbulent kinetic energy

Here, we employ the turbulent kinetic energy \(\kappa =(\overline{u'^2}+\overline{v'^2})/2\) to characterise the laminar or turbulent nature of the flow field, where \(\overline{u'^2}\) and \(\overline{v'^2}\) are the variances of the streamwise and in-plane streamnormal velocity components. Because of the planar PIV instrumentation, and given the marginal loss of out-of-plane particle pairs thanks to the short time interval between PIV frames (Appendix 2), the variance of the out-of-plane velocity (\(\overline{w'^2}\)) is neglected. The threshold identifying turbulent flow is \(\kappa >10^{-2}U_{\infty }^2\). The laminar-to-turbulent transition results in an increase in \(\kappa\) of one or more orders of magnitude. As such, the exact value of the threshold is unimportant. The threshold has proven applicable to flat plates (Crompton and Barrett 2000), foils (Lee et al. 2015), and circular arcs (Souppez et al. 2022), and is resilient to both low and high levels of free-stream turbulent intensity (Langari and Yang 2013). Contours of \(\kappa /U_{\infty }^2\) are presented in Fig. 8 for \(Re={16\,320}\) and \(Re={32\,210}\).

In Fig. 8a, c and e, the red diamond in a white contour region reveals laminar trailing-edge separation on the highest sections of the sail (\(z/s=0.88, 0.70\) and 0.57) at the subcritical \(Re={16\,320}\). Conversely, on the right column of Fig. 8, the red diamond within a blue contour region reveals the turbulent nature of the trailing-edge separation at the transcritical \(Re={16\,320}\).

In Sec. 3.2.2, Fig. 7g and h shows a visible LESB at \(z/s=0.37\). Here, in Fig. 8g and h, turbulent kinetic energy is observed at the leading edge, revealing the turbulent nature of the LESB, akin to two-dimensional circular arcs (Souppez et al. 2022). In subcritical regime (\(Re={16\,320}\), Fig. 8g) relaminarisation due to the accelerated flow resulting from the large camber is visible downstream of the LESB and upstream of the boundary layer transition, ultimately leading to the turbulent separation. This behaviour is not observed in the transcritical regime (\(Re={32\,210}\), Fig. 8h). This is consistent with the relaminarisation downstream of the LESB previously observed on circular arcs (Souppez et al. 2022).

Fig. 8
figure 8

Contours of non-dimensional turbulent kinetic energy of the large \({\text{T}}_{1}\) model at \(Re={16\,320}\) (left column) and \({32\,210}\) (right column), at \(z/s=0.88\) a–b, \(z/s=0.70\) c–d, \(z/s=0.57\) e–f, \(z/s=0.37\) g–h and \(z/s=0.05\) i–j, for \(\eta ={0}^{\circ }\). Flow regions with \(\kappa < 10^{-2}U_{\infty }^2\) are white. Laser shadow areas are coloured in grey. The red crosses indicate the location of the fore corner of the sail (tack) at \(z/s=0\). The red diamonds show the trailing-edge separation point

Full size image

3.3 Mainsail effect

In this section, we explore the difference in the forces experienced by a spinnaker and the flow field around it when tested in isolation or together with the mainsail, as it would be sailed. In Sec. 3.3.1 we discuss the forces, and in Sec. 3.3.2 we discuss the velocity field.

3.3.1 Forces

The presence of the mainsail causes an upwash on the spinnaker. The increase in circulation is expected to yield a higher angle of attack for a spinnaker with the mainsail present compared to a spinnaker in isolation. This was shown by Collie (2006) through three-dimensional CFD simulations of a spinnaker with and without a mainsail at \(\beta _a={90}^{\circ }\) and a full-scale Reynolds number of \(3.31\times 10^{6}\). Collie (2006) found that the maximum lift coefficient \(C_{L_\textrm{max}}\) in the absence of a mainsail is 10.8% lower and occurs at a \(2.6^{\circ }\) greater incidence with the apparent wind than with the mainsail present. Similar results are found in the present study. Once forces are corrected for blockage, the \(C_{L_\textrm{max}}\) of the large \({\text{T}}_{1}\) model at \(Re=32~210\) without the mainsail is 7.8% lower, and it occurs at \(3^{\circ }\) greater incidence than when the model is tested with the mainsail. These results are shown in Fig. 9, where \(C_L\) is normalised with \(C_{L_\textrm{max}}\) and plotted versus \(\eta\) for both the spinnaker with and without the mainsail and for both the present results and those of Collie (2006).

Fig. 9
figure 9

Blockage-corrected lift coefficient normalised by its maximum value versus the rotation angle for the large \({\text{T}}_{1}\) model with and without the mainsail at \(Re=32~210\), and comparison with the three-dimensional CFD simulations of Collie (2006) on a spinnaker with and without mainsail at \(\beta _a={90}^{\circ }\) and \(Re=3.31\times 10^{6}\)

Full size image

The lift and drag coefficients are also shown, non-normalised with their maximum value and versus the rotation angle \(\eta\) in Fig. 10a and b, respectively, and their ratio is shown in Fig. 10c. We also show the drive force coefficient along the sailed course of the boat, \(C_X\) (Fig. 10d), and the side force coefficient orthogonal to the sailed course, \(C_Y\) (Fig. 10e), as well as their ratio (Fig. 10f). The sailed course is parallel to the longitudinal axis of the boat as the leeway angle is zero in the present design conditions (Braun et al. 2016). Therefore, \(C_X=C_L\sin \beta _a-C_D\cos \beta _a\), and \(C_Y=C_L\cos \beta _a+C_D\sin \beta _a\). The results present both the measured coefficients and the extrapolated values for \(A_F/A_S=0\). For extrapolated results with the mainsail, the correction is applied, taking into account the increased \(A_F/A_S\) arising from the presence of the mainsail. However, because of its small frontal area and overlap with the spinnaker, the results are only marginally sensitive to whether the mainsail is considered or not.

Once the measurements have been corrected for the blockage, \(C_L\), \(C_L/C_D\), \(C_X\) and \(C_X/C_Y\) are maximum at \(\eta ={0}^{\circ }\) without the mainsail. It is noted that the maximum value of \(C_L/C_D\) at \(\eta ={0}^{\circ }\) is consistent with the design specifications (Braun et al. 2016). As suggested by the comparison with Collie (2006) (Fig. 9), \(C_L\), \(C_L/C_D\) and \(C_X\) are maximum at \(\eta ={3}^{\circ }\) without the mainsail. The maximum \(C_L\) and \(C_D\) could be estimated by assuming an upwash of \(3^{\circ }\), i.e. increasing \(\eta\) from \({0}^{\circ }\) with the mainsail present to \({3}^{\circ }\) with the spinnaker in isolation, within 1.72% and 1.32%, respectively, which are within the experimental uncertainty. However, while \(C_D\) and \(C_Y\) have minima at \(\eta ={3}^{\circ }\) with the mainsail, they decrease monotonically for increasing \(\eta\) without the mainsail. Hence, the force trends could be substantially mispredicted.

While there is no other experimental data for the sail under consideration, the values presented in Fig. 10 appear consistent with published work on different downwind yacht sail geometries. The highest \(C_L\) have been reported for \({50}^{\circ } \le \beta _a \le {55}^{\circ }\) where \(1.3 \le C_L \le 1.6\) and \(0.4 \le C_D \le 0.6\) (Arredondo-Galeana et al. 2023; Campbell 2014; Viola et al. 2014; Viola and Flay 2009), with lower \(C_L\) values and higher \(C_D\) values achieved for higher \(\beta _a\), including \(0.6 \le C_L \le 1.1\) and \(0.5 \le C_D \le 0.8\) for \({80}^{\circ } \le \beta _a \le {110}^{\circ }\) (Campbell 2014; Claughton et al. 2008; Richards et al. 2001; Hedges et al. 1996; Braun et al. 2016), and \(0.3 \le C_L \le 0.9\) and \(0.6 \le C_D \le 1\) for \({120}^{\circ } \le \beta _a \le {150}^{\circ }\) (Campbell 2014; Hedges et al. 1996; Richards et al. 2001).

Fig. 10
figure 10

Lift a and drag b coefficients and their ratio c, as well as drive d and side e force coefficients and their ratio f versus the rotation angle measured with the large \({\text{T}}_{1}\) model at \(Re={32\,210}\) with and without the mainsail present. Both measured and extrapolated data for \(A_F/A_S=0\) are presented

Full size image

3.3.2 Velocity field

Figure 11 depicts the flow fields at \(z/s=0.88, 0.70, 0.57, 0.37\) and 0.05 for the large \({\text{T}}_{1}\) model at \(Re={32210}\) with mainsail and in isolation at \(\eta =0^{\circ }, 3^{\circ }, 6^{\circ }\) and \(9^{\circ }\). The results confirm the conclusions of the previous section (Sec. 3.3.1) that the effect of the mainsail cannot be accounted for by a constant upwash of, say, \(3^{\circ }\). For example, by increasing the rotation angle such that the isolated spinnaker generates the same lift and drag as the spinnaker with the mainsail, the flow around the sails would still miss the circulation due to the mainsail. This is shown by the visibly higher flow velocity on the suction side of the spinnaker when the mainsail is present compared to the spinnaker in isolation at any of the tested \(\eta\) in Fig. 11.

Fig. 11
figure 11

Time-averaged streamlines and contours of velocity magnitude for the large \({\text{T}}_{1}\) model at \(Re={32\,210}\) with the mainsail in the left column, and without the mainsail in subsequent columns at \(\eta =0^{\circ }, 3^{\circ }, 6^{\circ }\) and \(9^{\circ }\), respectively. Each row corresponds to a different spanwise section: \(z/s=0.88\) a–e, \(z/s=0.60\) f–j, \(z/s=0.57\) k–o, \(z/s=0.37\) p–t and \(z/s=0.05\) u–y. Laser shadow areas are coloured in grey. The red crosses indicate the location of the fore corner of the sail (tack) at \(z/s=0\). The red diamonds show the trailing-edge separation point

Full size image

The channel between the spinnaker and the mainsail sees opposing induced velocities from the circulations of the spinnaker and the mainsail. Hence, the mainsail tends to increase the flow rate through the channel—an effect that cannot be recovered by increasing the rotation angle of the spinnaker in isolation.

On the three highest sections (\(z/s=0.57, 0.70, 0.88\)), the time-averaged wake of the spinnaker is characterised by a single closed recirculation region with streamlines originating from the suction side of the sail (Fig. 11, rows 1-3). Conversely, at the lowest sections (\(z/s=0.05\)), which are at a higher angle of attack, two counter-rotating recirculation regions are formed (Fig. 11, bottom row).

3.4 Trim comparison

From a design perspective, the differences between trim \({\text{T}}_{1}\) and \({\text{T}}_{2}\) are small. At the model-scale, the difference between the two models is a displacement of the aft corner of the sail of less than 6 mm. This results in a slightly flatter sail and higher angles of attack (Tables 1 and 2). At the design condition, trim \({\text{T}}_{\text{1}}\) is expected to result in a higher boat speed than trim \({\text{T}}_{2}\) Braun et al. (2016). However, the flattening of \({\text{T}}_{2}\) means it would be expected to perform better in stronger wind conditions than the design conditions. For this reason, these two trims were considered by Braun et al. (2016) as a benchmark case to assess the precision of different design tools. Here we show that the precision of the present force and PIV measurements are sufficient to clearly identify the differences between the two trims.

Blockage-corrected force measurements of large \({\text{T}}_{1}\) and large \({\text{T}}_{2}\) models at \(Re={32\,210}\) for \({-9}^{\circ }\le \eta \le {9}^{\circ }\) are presented in Fig. 12. Both models are tested in isolation without the mainsail. The differences in \(C_L\) and \(C_D\) are greater than the measurement uncertainty but for \(C_D\) at \(\eta >0\), where the average difference in drag between the two trims are smaller than 4.8% because both are dominated by flow separation. Similar conclusions can be drawn for \(C_X\) and \(C_Y\). Importantly, the trade-off between the two sails versus \(\eta\) is clearly identified both in terms of \(C_L/C_D\) and \(C_X/C_Y\), where \({\text{T}}_{1}\) performs better than \({\text{T}}_{2}\) at low \(\eta\) and vice versa at high \(\eta\). The two sails perform almost identically at \(\eta ={2}^{\circ }\) and \(3^{\circ }\). As both models were tested in isolation, the shift of the crossover at \(\eta\) between \(2^{\circ }\) and \(3^{\circ }\) is consistent with the design expectation that the crossover is at the design condition (\(\eta =0\)) when the mainsail is present.

Figure 13 presents the PIV measurements for both the \({\text{T}}_{1}\) and \({\text{T}}_{2}\) model at each measurement section at \(\eta ={3}^{\circ }\). The flow field around the two models is qualitatively similar, with a larger region of low-speed flow in the wake of \({\text{T}}_{2}\) because of the higher angles of attack. At \(z/s=0.37,\) this also results in a visibly larger LESB.

Despite the higher lift generated by \({\text{T}}_{1}\), the velocity contours reveal higher flow velocity on the suction side of the \({\text{T}}_{2}\) model. This is due to the higher blockage of \({\text{T}}_{2}\), for which the flow field cannot be corrected. This is the main limitation of the current approach. In fact, while we showed that the force measurements can be corrected for the blockage, the PIV measurements cannot be corrected, and the blockage effect is significant.

Fig. 12
figure 12

Lift a and drag b coefficients and their ratio c, as well as drive d and side e force coefficients and their ratio f versus the rotation angle measured with the large \({\text{T}}_{1}\) and \({\text{T}}_{2}\) models at \(Re={32\,210}\) without the mainsail present

Full size image
Fig. 13
figure 13

Time-averaged streamlines and contours of velocity magnitude for the large \({\text{T}}_{1}\) model (left column) and \({\text{T}}_{2}\) models (right column) at \(Re={32\,210}\), each tested in isolation at \(\eta ={3}^{\circ }\). Each row corresponds to a different spanwise section: \(z/s=0.88\) a–b, \(z/s=0.60\) c–d, \(z/s=0.57\) e–f, \(z/s=0.37\) (g-h) and \(z/s=0.05\) i–j. Laser shadow areas are coloured in grey. The red crosses indicate the location of the fore corner of the sail (tack) at \(z/s=0\). The red diamonds show the trailing-edge separation point

Full size image

4 Conclusions

In this paper, we investigated the aerodynamics of downwind yacht sails with water tunnel tests of rigid models, undertaking force and PIV measurements. We tested spinnaker models with and without the mainsails at an average-chord-based Reynolds numbers ranging from 5 870 to 61 870, and blockage ratios ranging from 0.036 to 0.094.

A critical Reynolds number of around 22 940 is identified, below which relaminarisation occurs on the suction side of the spinnaker downstream of the leading-edge separation bubble. The reattached laminar boundary layer separates upstream of the trailing edge, and upstream of where it separates when relaminarisation does not occur. Suppression of the relaminarisation results in a twofold increase in the lift. To the Author’s knowledge, this is the first evidence that the force crisis on spinnakers is due to suppressed relaminarisation with increasing Re (previously observed on circular arcs), as opposed to the laminar-to-turbulent transition of the boundary layer on cylindrical shapes. Relaminarisation is due to the two suction peaks associated with the sharp leading edge and the sail curvature, respectively: the first adverse pressure gradient results in separation and transition, while the subsequent favourable pressure gradient results in relaminarisation of the reattached boundary layer.

The critical Reynolds number decreases with increasing incidence and is insensitive to the blockage ratio. The lift and the drag remain constant within 1.24% and 1.81%, respectively, at any tested Reynolds number value above the critical value. While this suggests that forces might become Reynolds-number independent at Reynolds number as low as 22 940, this should be verified in future works by extending the range of the Reynolds number to higher values.

The presence of the mainsail is found critical to correctly predict the forces and the flow field around the spinnaker. The average upwash of the mainsail on the spinnaker is quantified at about \(3^{\circ }\). A rotation of \(3^{\circ }\) of the spinnaker model tested in isolation results in the same life forces (within 1.72%) as those experienced by the spinnaker model when tested in the presence of the mainsail. However, the trends of the drag and side force with the angle of incidence are different, as are the velocity fields. Specifically, the mainsail circulation results in substantially higher velocity on both sides of the spinnaker.

Finally, we found that the force and PIV measurements are able to correctly detect the differences between two candidate optimal sail trims that provide the same performances at the design wind speed condition, but each is predicted to be optimal at either higher or lower wind speeds.

Overall we concluded that water tunnel tests are a suitable design tool for spinnaker sails that could provide both accurate validation for CFD simulations, as well as insights into the flow field. High blockage is not recommended because of the significant effect on critical performance indices such as the lift. Tests can be undertaken at relatively low Reynolds numbers as long as they are higher than the critical value, which will need to be assessed for each sail and flow condition. Finally, while this study focused specifically on yacht sails, the results are applicable to any three-dimensional highly cambered wing.