1 Background and objectives

A wide range of large scale liquid flow-measurement situations is characterized by extremely challenging environmental conditions, which in turn limits the number of measurable quantities and accordingly diminishes the extractable information content for a given measurement campaign. These conducted experimental efforts mostly have to deal with extremely difficult optical and mechanical access, as well as particularly adverse thermal and chemical conditions, as encountered, e.g., in hydrological field tests, geothermal reservoir exploration and pipeline monitoring (see, e.g., Gillette and Kolpa 2008; Klepikova et al. 2014; Bauer 2014; Helbig and Zarrouk 2012; Renner and Messar 2006). In geothermal plants, for instance, heat reservoirs located in the earth’s crust are used to generate electrical energy and heating energy from the natural heat of the earth. An important method for investigating heat reservoirs is the measurement of volumetric flow in boreholes that penetrate a heat reservoir. Today, the distributed quantification of volume fluxes and corresponding flow velocities appears rather premature as compared to the more elaborated means for a distributed investigation of state variables such as e.g. the temperature. A fiber-optic cable as flow sensor introduces the opportunity to build a several meter long distributed flow sensor for boreholes and other flow-measurement applications. Especially, in boreholes, this would decrease the measurement effort enormously compared to a point sensor which must be moved meter by meter for each single measurement point. Additionally, as the measurement electronics are located on the surface, the probe may be applied in the deepest boreholes with surrounding temperatures in the order of 100 degree Celsius.

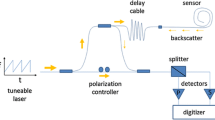
Fiber-optic-based distributed temperature sensing (DTS) has been developed since the 1980 s, initially being used as a downhole tool for oil and gas. DTS has shown to be a precise and robust tool for spatially distributed temperature measurements (Kersey 2000; Li et al. 2004; Ukil et al. 2011). Research over the last two decades has led to great improvements in measurement resolution, applicability and affordability, so that DTS is now more and more frequently used to investigate hydrological systems (see Selker et al. 2006; Hausner et al. 2011; Banks et al. 2014; Bense et al. 2016). Particularly, DTS-evaluation approaches on the grounds of the temperature sensitive Raman anti-Stokes backscatter enjoy increasing attention and gain importance in the community, where the application of heated fiber cables (i.e., so-called hybrid cables comprised of fiber optics and high-resistance conductors) further increases the signal-to-noise-ratio as elaborated by Briggs et al. (2012); Banks et al. (2014); Bense et al. (2016) and Van De Giesen et al. (2012), for instance. Their applications range from the evaluation of groundwater flow into streams to downhole heat-pulse tests, but remain largely limited to temperature-distribution quantification along the cable, thus inside the boreholes.

Note that the general measurement strategy of DTS is comparable to Doppler-Lidar systems (Light detection and ranging), since either approach emits laser bursts and determines the distance to the observed location from the latency between burst emission the arrival of the scattered light (cp. Fernando et al. 2007). In contrast to the Doppler-based velocity determination (for the Lidar approach), the DTS approach evaluates the ratio between anti-Stokes and Stokes scatter intensities to estimate the local temperature for the given scatter location inside the fiber-optic cable. Interestingly, a heated cable in crossflow and the corresponding interrelationships between kinematic and thermodynamic conditions of the surrounding flow are well-known and extensively elaborated in the context of flow measurements via hot-wire anemometry (HWA) (see, e.g., Stainback and Nagabushana 1993; King 1914; Comte-Bellot 1976; Bruun 1995 for more details on HWA).

This conceptual similarity has already been tested for air-velocity estimations by means of different glass fiber temperature-measurement technologies: fiber Bragg grating (FBG) and optical frequency domain reflectory (OFDR) are Rayleigh-based methods, which are—among other influential factors—sensitive to strain and temperature, but provide good spatial and dynamic resolution as shown by Palmieri and Schenato (2013). FBGs are imprinted Bragg reflectors in short segments of the optical fiber, reflecting a narrow wavelength peak of a swept laser, which is shifted, if the grating period is changed due to stress and/or temperatures change. Therefore, FBGs enable point measurements of temperature at each optical grating along the fiber (see, e.g., Selker et al. 2006). OFDR evaluates the characteristic Rayleigh backscatter of a glass fiber, which might be either converted into temperature changes or strain information (given the other influence is eliminated). Jewart et al. (2006); Gao et al. (2011) and Chen et al. (2014), among others, used a light source to heat the fibers and FBGs to measure directly temperature. Liu et al. (2015) followed a similar approach but used a modified Fabry-Pérot interferometer for the temperature measurement. Due to the restricted heating power, the maximum air velocity remained below 20 m/s.

The glass fiber may be inserted in a stainless-steel capillary, which can be connected to an electric circuit and heated by joule heating. Wylie et al. (2012) and Chen et al. (2012) achieved air velocity measurements up to 10 m/s with this setup and glass fiber temperature measurements via Brilluion Scattering and OFDR, respectively. The concept of Chen et al. (2012) was verified and operated successfully up to Mach numbers of \(M=0.5\) in a wind tunnel by Ohanian et al. (2019).

To combine the above achievements of measurements in air with the rough environment of the target application, the objective of the present work revolves around the idea to treat data as received from classical—and robust—fiber-optical thermography (DTS) in a similar way as the well established thermal anemometry (HWA) so as to convert the recorded Raman scatter from the fiber-optic cables into distributed velocity information inside (geothermal) boreholes and aquifers.

It is hypothesized that the sensor cable may be appropriately wound around a borehole-sensor probe and take immediate advantage of the known heat transfer law of cylinders in crossflow. To test this hypothesis, the similarities of either measurement technique (DTS and HWA) and inherently involved limitations of the hot-wire analogy for an advanced DTS post-processing in borehole flows are outlined in a combined analytical/experimental feasibility study. For the sake of limited experimental and fabrication complexity of a borehole-mimicking test rig, the current proof-of-concept experiments exclude transverse aquifer flow across the boreholes and solely concentrate on the axial velocity around sensor probes along boreholes.

2 Experimental procedure

Two experiments were conducted. First, the main experiments focus on the practical application and provide the attempt to validate the measurement concept in a simplified model-borehole test rig with a double-packer probe prototype (see, e.g., Solexperts-AG 2015 for more information on double-packers). An additional second set of experiments particularly addresses the interplay of underlying heat transfer phenomena with a purpose-built horizontal cylinder probe in a water channel.

Fig. 1
figure 1

Sketch and relevant quantities of the considered simplified double-packer probe equipped with a hybrid fiber-optic cable; a cable and involved thermal quantities, b cable orientation around a double-packer probe section

Full size image

A cartoon of the applied hybrid cable and its wound arrangement around a double-packer probe is shown in Fig. 1. As indicated in Fig. 1a, the cable mimics a heated cylinder in crossflow, where the crossflow direction of the velocity u is aligned with the borehole axis \(z_\text {B}\). For orientation purposes, both cylindrical coordinate systems for the cable (\(r-\phi -z\)) and the borehole (\(r_\text {B}-\phi _\text {B}-z_\text {B}\)) are displayed. The cable is supplied with the electric power \(P_\text {el}\), which is converted to heat in the high-resistance conductors of the hybrid cable. Accordingly, it may increase the cable temperature T and is converted into convective and conductive heat fluxes, the latter being mostly significant at regions with large temperature gradients along the cylinder axis, e.g., when the cable enters the water from the air. Radiation phenomena are excluded for brevity.

Fig. 2
figure 2

Sketch of the borehole test rig at ISTM comprised of a big water tank, a borehole section, a simplified double-packer probe as carrier for the hybrid DTS cable and a pump; geometry and operating parameters are added to the sketch for clarity

Full size image

The cable is wound helically with diameter D and pitch angle \(\Theta\) around a simplified double-packer borehole probe (cp. Solexperts-AG 2015) with sufficient spacing \((D-D_\text {P})/2\) to ensure an undisturbed flow around the probe of diameter \(D_\text {P}\), cp. Figure 1b. Obviously, the probe is intrusive as the flow is disturbed by the wound, heated cable. Depending on velocity and heating power, a thermal wake will occur, which is perturbed by unsteady (Re-dependent) vortex structures. Accordingly assuming sufficient mixing and thus quasi constant temperature normal to the flow direction, the increase in temperature of the water along the complete probe length \(L_\text {P}\) was calculated for different heating powers and velocities. Figure 3 shows that the water temperature increases only significantly for the smallest velocity. At higher velocities, the increase is below \(0.1\,\mathrm {^\circ C}\) for all heating powers. Due to this small intensity of the thermal wake and a small helix angle, it is expected that the heat transfer of the helix is comparable to a cylinder in crossflow. Furthermore, the influences on the heat transfer are expected to be the same in the test rig and in the real application; thus, an extensive calibration of the probe will cover these effects without unraveling them.

Fig. 3
figure 3

The temperature difference of the water downstream of the probe to the water upstream of the probe \(\Delta T_\textrm{probe}\) is calculated with the assumption of ideal mixing normal to the flow direction. Except for the smallest velocity, the temperature increase is very small indicating a small influence of the thermal wake

Full size image

The equipped probe is inserted into the borehole-mimicking test rig as displayed in Fig. 2. This test rig consists of a drainpipe with diameter \(D_\textrm{B}\) and Length \(L_\textrm{B}\) as the borehole section, which is vertically mounted in a large water tank. Various circumferentially oriented holes at the bottom of the pipe and the insertion of a Linn MXH pump result in a vertically circulating water flow rate \(\dot{V}\) through the pipe against gravity g. Flow rate \(\dot{V}\) and water temperature \(T_\infty\) are measured with a Kobold Messring MIN1220 flow meter attached to the hose between the pipe and the pump. An AP-sensing N43856B DTS system is used to supply the fiber-optic cable with laser bursts, record the Raman scatter and convert the signals to temperature estimates, which are initially assumed to be constant across the cable cross section.

Fig. 4
figure 4

Sketch of the center plane of the rectangular open water channel (not to scale). PIV measurements are performed in this plane to determine the upstream velocity. A horizontal cylinder is inserted perpendicular to the flow direction for temperature sensing and heating

Full size image

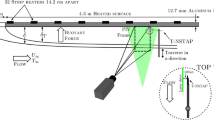
The second experiments are performed in an open water channel as depicted in Fig. 4. It is comprised of perspex walls for optical access and is equipped with a brass tube, which can be operated as heating and sensing probe. The channel has a rectangular cross section with a lateral length of 120 mm and is filled with distilled water. To measure the flow velocity upstream of the cylinder with particle image velocimetry (PIV), the water is seeded with \(57\) μm polyamide particles, which are illuminated and recorded with a Quantel Evergreen Laser and pco.edge 5.5 sCMOS Camera, respectively. The light sheet optics span an \(x-y\) plane in the center of the water channel (Fig. 4). Preceding to the experiments, the flow upstream of the probe has been investigated for all velocities of the measurement series. It was steady, and no turbulences were detected. As the probe should measure, the upstream velocity in its future application the flow around the probe is not of interest and not evaluated. The desired velocity information are estimated from 24 interrogation areas of \(128\times 128\) px (\(11.6\times 11.6\) mm) upstream of the cylinder, which are evaluated with PIVview software and averaged across 10 image pairs per measurement to ensure velocity standard deviations \(\sigma _u<5\%\) of the respective flow speeds u. The interrogation areas overlap by 4% and the time delay between consecutive frames is varied from \(0.02-0.1\) s to ensure a pixel displacement in the range of 8–20 px.

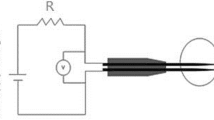
The design of the custom-built heated cylinder is sketched in Fig. 5. It consists of a stainless-steel capillary surrounded by four isolated heating wires, which are fixed by one layer of duct tape. The glass fiber is inserted into the cavity of the capillary. Note that this hand-made probe is inevitably comprised of fabrication imperfections, which lead to varying gaps between the isolated heating-wire packages and an eccentricity of the inner part inside the brass pipe. Three times two type T thermocouples are fixed at the steel capillary, the duct tape and the brass pipe, respectively, using adhesive strips. The temperature of the ambient water is measured downstream of the cylinder using two PT1000 sensors. All temperature sensors are evaluated using a NI cDAQ-9188 with NI 9219 and NI 9213 modules. The manufacturers declare a limiting deviation of 0.035 K for the PT1000 sensors and 0.5 K for the type T thermocouples. With the PT1000 measurements set as ground truth, the thermocouples were offset calibrated at \(20\,^\circ\)C, reducing the limiting deviation to 0.2 K in the relavant measurement range of 20–35 K.

Fig. 5
figure 5

Sketch of the ideal design of the custom-built heating and temperature-sensing cylinder. From inside to outside, the cylinder consists of a steel capillary containing a glass fiber, four isolated sets of heating wires, a layer of duct tape for fixation and a brass pipe. The cavities are filled with distilled water and the temperatures are measured at two locations inside the cylinder, a third at the surface, and a fourth inside the water

Full size image

3 Analytical procedure and results

Firstly, the HWA procedure is recapped and compared to the results of the borehole-mimicking test rig. Subsequently, an extended procedure is proposed and elaborated, which takes radial heat transport phenomena into account and also provides a comparison to the results of the water channel experiments. To benchmark all results in the end, they are compared to the \({Nu}-{Re}\) relations of King and Gnielinski. King provides the first analytical solution based on potential theory, and Gnielinski gives an empirical correlation based on experiments which were conducted in similar scales and the same working fluid for heat exchanger research.

3.1 Common HWA procedure

The combination of energy equation, Fourier’s law of heat transfer and Nusselt correlations leads to a measurement equation according to \(u=u(P_\textrm{el}, \Delta T)\) between the desired velocity information u, the given input power \(P_\textrm{el}\) and the cable-surface temperature T.

If only convective heat transfer \(\dot{Q}_\text {conv}\) from the cable to the fluid is considered, the steady energy equation around the horizontal cylinder yields

$$\begin{aligned} 0 = P_\textrm{el} - \dot{Q}_\textrm{conv}. \end{aligned}$$
(1)

Radiative heat transfer from the cylinder to the fluid is several magnitudes smaller than the convective heat transfer and is therefore neglected. Conductive heat transport along the cylinders axis is neglected, because it is only relevant at regions with temperature gradients along the cylinder axis, i.e., at the water–air boundary of the cable, which in the present setup is sufficiently far away from the investigated cable section (see Örlü and Vinuesa 2017). Fourier’s law of heat transfer relates the transferred heat \(\dot{Q}_\textrm{conv}\) to the temperature difference \(\Delta T=T\,-\,T_\infty\) of the cylinders wall and the fluid, with the lateral surface \(A\,=\,\pi \,d\,l\) of the cable with length l and the heat transfer coefficient \(\alpha\), i.e.,

$$\begin{aligned} \dot{Q}_\textrm{conv} = \alpha A (T - T_\infty )\overset{{{\hbox {Eq}.~(1)}}}{\equiv }P_\text {el}. \end{aligned}$$
(2)

The heat transfer coefficient is velocity dependent, which is usually expressed in a dimensionless form using empirical Nusselt number correlations in the form of \(Nu\,=\,f(Re,\,Gr,\,Pr)\). Grashof and Reynolds numbers are dimensionless products describing the driving forces of the flow. They are used in the present context to distinguish between natural and forced convection. In case of free convection, the flow is dominated by buoyancy forces and described by the Grashof number: \(Nu\,=\,f(Gr,\,Pr)\). In forced-convection dominated cases, the flow is consequently described by the Reynolds number: \(Nu\,=\,f(Re,\,Pr)\). According to Collis and Williams (1959), free convection can be neglected for \({Re}\,>\,{Gr}^{1/3}\) (see also Durst 2008), which holds true for all parameter combinations with operating pump, cp. Figure 6b. Consequently, the remainder of the derivation concentrates on forced convection. The most common correlation used for HWA is the so-called King’s law (cp. King 1914) which is theoretically derived using the potential flow assumption and may be simplified to

$$\begin{aligned} {Nu}= \frac{1}{\pi } + \sqrt{\frac{2}{\pi }} \sqrt{Re Pr}. \end{aligned}$$
(3)

for \(Re\,Pr\,>\,0.08\) (cp. Collis and Williams 1959). In practice the relationship is calibrated as

$$\begin{aligned} {Nu}\,= A + B\, Re^C \end{aligned}$$
(4)

to account for neglected heat flow phenomena and real flow phenomena. A more recent correlation based on experiments with macroscopic tubes as horizontal cylinders is given by Gnielinski (1975) as

$$\begin{aligned} Nu_\text {l}=0.3 + \sqrt{Nu_\text {l\,lam}^2 + Nu_\text {l\,turb}^2} \end{aligned}$$
(5)

with

$$\begin{aligned}&Nu_\text {l\,lam} = 0.664\, Re_\text {l}^{1/2} Pr^{1/3} \end{aligned}$$
(6)
$$\begin{aligned}&{Nu}_\text {l\,turb} = \frac{0.037\, Re_\text {l}^{0.8} Pr}{1+2.443\, Re_\text {l}^{-0.1} (Pr^{2/3}-1)}. \end{aligned}$$
(7)

Note that different characteristic length definitions are given in liteature for this problem. Gnielinsky, used the half of the cylinders perimeter πd/2 as characteristic length to build \({Re}_\text {l}\) and \({Nu}_\text {l}\). In the following Re, Gr, and Nu are calculated with the cables or cylinders diameter d as characteristic length. Note also that Re is calculated with the averaged velocity of the annular channel.

Employing these \({Nu}-{Re}\) relationships the velocity can be expressed as a function of supplied electric power and measured temperature difference \(u(P_\text {el},T-T_\infty )\). The velocity-temperature relation has been tested in the borehole-mimicking test rig for various parameter combinations of input power per cable length and flow rates in the range of \(P_\text {el}/l=3.7\,-\,20.4\) W/m and \(\dot{V}=0\,-\,50\) l/min (\(Re=0\,-\,365\)), as will be discussed below.

The observed interplay between normalized flow rate \(\dot{V}\) through the borehole and the measured temperature difference \(\Delta T=T\,-\,T_\infty\) between cable and flow, thus heat transfer \(\dot{Q}_\text {conv}\), is shown in Fig. 6 with additional parametrization of the supplied electric input power per cable length. The \({Re}-{Nu}\) diagram of Fig. 6a reveals mixed results dependent on the heating powers. For heating powers of \(11.4\,\text {W/m}\) and less, the Nusselt number is not increasing monotonously. It is hypothesized that this trend is caused by temperature-measurement errors which are most influential at low heating powers and higher velocities. The results at higher heating powers exhibit the expected concave, monotonic increase in Nu over Re with only one exception. Especially, the results at higher heating powers indicate the general validity of the above cylinder-in-crossflow assumption for further post-processing of the DTS-data in view of velocity estimates. However, it is important to mention that the determined Nusselt numbers are an order of magnitude below Kings law and Gnielinksky Eq. (3, 5), which implies a significant overestimation of \(\Delta T\). The assumption of a homogeneous temperature distribution across the cable cross section, therefore, has to be retro-actively considered an oversimplification for the given problem and radial heat conduction must accordingly be considered as explained in the following.

Fig. 6
figure 6

Measured temperature differences for the tested combinations of flow rate \(\dot{V}\) and electric input powers \(P_\text {el}/l\) plotted as non-dimensional quantities: a The Nu–Re diagram connects velocity with temperature difference; b the Gr–Re diagram indicates the influence of natural convection on the given problem

Full size image

3.2 Extended procedure by radial heat conduction

In steady heat transfer analysis with heat-conduction inside a wall and heat-convection outside the wall, the Biot number Bi may be considered as an insightful ratio between the resistances of heat-conduction inside the cylinder and heat-convection at the cylinder surface. For HWA applications, the heat-convection resistance is dominant, which is equivalent to \(Bi\ll 1\) and, in turn, confirms the validity of the assumption of a constant temperature across the wire’s cross section. For the considered hybrid cable, in contrast, the Biot number increases by several orders of magnitude as elaborated along the following estimation.

Assuming the similarity of a cylinder in crossflow with identical Nusselt and Reynolds numbers for both applications, the Biot-number change can be estimated for both cases with the values given in Table 1.

Table 1 The values for the Biot number calculation of the hybrid cable and the hot-wire are the characteristic length L, the heat conductivity of the surrounding fluid (water and air) \(\lambda _\textrm{fl}\), the heat conductivity of the wall (cable isolation and, e.g., tungsten) \(\lambda _\textrm{w}\) and wall thickness s
Full size table

The Biot number for a planar surface according to

$$\begin{aligned} Bi = \frac{\alpha ~s}{\lambda _w} = \frac{\text{Nu}~\lambda _{fl}}{L} \, \frac{s}{\lambda _w} \end{aligned}$$
(8)

is considered for the present estimation. Equation (8) states the interplay of heat conductivity of the wall \(\lambda _\textrm{w}\), the wall thickness s and the heat transfer coefficient \(\alpha\), where the latter is additionally replaced the Nusselt number Nu, the heat conductivity of the fluid \(\lambda _\textrm{fl}\) and the characteristic length scale L. For identical Nusselt numbers, the Biot-number ratio \(Bi_\textrm{hc}/Bi_\textrm{hw}\) between the hybrid cable and the hot-wire is given by

$$\begin{aligned} \frac{Bi_\textrm{hc}}{Bi_\textrm{hw}} = \! \underbrace{ \!\frac{\text{Nu}_\textrm{hc}}{\text{Nu}_\textrm{hw}}\!}_{{ 1}} \ \underbrace{ \!\frac{\lambda _\textrm{fl,hc}}{\lambda _\textrm{fl,hw}}\!}_{{3\cdot 10^1}} \ \underbrace{ \!\frac{\lambda _\textrm{w,hw}}{\lambda _\textrm{w,hc}} }_{{3.5\cdot 10^3\!}} \ \underbrace{ \!\frac{L_\textrm{hw}}{L_\textrm{hc}}\!}_{{ 10^{-3}}} \ \underbrace{ \!\frac{s_\textrm{hc}}{s_\textrm{hw}}\!}_{{ 10^3 }} \!\approx 10^5. \end{aligned}$$
(9)

Obviously, the Biot number increases by five orders of magnitude from hot-wire to hybrid cable due to the change of fluid and the change of wall material. The increased thermal conductivity of water compared to air decreases the convective heat transfer resistance and the decreased thermal conductivity of the wall increases the heat conduction resistance. The change of the geometric length scale does not influence the Biot number. Note, however that the response time of the sensor is expected to increase significantly in cases, where unsteady modeling is considered.

This estimation saliently demonstrates \(Bi>1\) for the hybrid cable, which indicates heat-conduction resistance to be dominant. Therefore, most of the measured temperature difference drops within the cables sheath and the relevant temperature difference for the calculation of the Nusselt number is accordingly smaller.

To characterize this intra-cable temperature drop more rigorously, the second set of experiments has been conducted under well-adjustable conditions in a water channel (see Fig. 4). The temperature measurements \(T_1\), \(T_3\), and \(T_\infty\) are used to measure the Biot number. Note, that the self-built probe design, cp. Figure 5, is not rotationally symmetric and the heat source is located between the measurement positions of \(T_1\) and \(T_3\), which adds additional uncertainty to the calculation of the heat-conduction resistance in comparison with smooth and homogeneous planar or annular surfaces. With \(R_\text {cond}\) and \(R_\text {conv}\) as heat conduction and convection resistances, respectively, the heat flux can be expressed as

$$\begin{aligned} \dot{Q} = \frac{1}{R_\text {cond}} (T_1 - T_3) = \frac{1}{R_\text {conv}} (T_3 - T_\infty ). \end{aligned}$$
(10)

This equation can be converted into a Biot-number expression

$$\begin{aligned} Bi = \frac{R_\text {cond}}{R_\text {conv}} = \frac{T_1 - T_3}{T_3 - T_\infty } \end{aligned}$$
(11)
Fig. 7
figure 7

Results of the water channel experiments; a \(Bi-Re\) diagram for varying power per cable length \(P_\textrm{el}/l\), which emphasizes the dominant heat-conduction resistance of the probe (\(Bi>1\)); b \(\Delta T-Re\) plot for the \(P_\textrm{el}/l=22.5\) W/m measurement series reveals that the relevant temperature difference for the velocity measurement is only a small fraction of the total temperature difference

Full size image

based on the measured temperature differences, which is used to calculate Bi for the results of the experiments in the water channel. While the heat-convection resistance decreases with increasing flow velocity, the heat-conduction resistance is independent of flow velocity changes. Thus, a monotonic increase in Bi over Re is expected and revealed by the results (see Fig. 7a). The practical consequences are exemplarily emphasized for the temperature measurements of the \(P_\textrm{el}/l=22.5\) W/m experiments in Fig. 7b. The total measured temperature difference between the glass fiber in the probe center and the environment, \(T_1-T_\infty\), consists of a dominant nearly constant offset of \(T_1-T_3\approx 25\) K inside the probe and an accordingly diminished relevant temperature difference for the velocity measurement in the range of \(0.4<T_3-T_\infty <2.0\) K.

For this experiment Re is computed with the local velocity estimate from above-outlined complementarily-conducted PIV measurements and Nu is calculated with the temperature difference between the cylinders surface and the environment \(T_3-T_\infty\). Figure 8 finally shows the results of the water channel experiment and the 20.4 W/m results of the borehole test rig experiment in a \({Re}-{Nu}\) diagram in comparison with the correlations of King and Gnielinski. The experimental results of the water channel are depicted with circular markers. They range in the same order of magnitude as both correlations and moreover reveal very good agreement with the Gnielinski correlation. The 20.4 W/m curve of the borehole test rig experiment (*) is an order of magnitude below the correlations, as the measured temperature difference is underestimated due to the neglection of heat conduction within the hybrid cables sheath. The temperature drop may be calculated with the known heat flow of the outer isolation layer of the cable using a layer thickness of 1 mm and a heat-conduction coefficient of 0.19 W/(m K) were used. (**) displays the results when this calculated constant temperature offset is subtracted from the measured temperature difference. The results seem to fit nicely to the other measurements and the Gnielinski correlation. However, only a slight variation of the assumed cable isolation layer thickness of 0.1 mm would move the corrected line significantly.

Fig. 8
figure 8

Comparison of the water channel measurements (◦ marker), the borehole test rig experiments (x marker, before (*) and after (**) offset correction), and the correlations of King (1914) and Gnielinski (1975)

Full size image

4 Discussion and conclusions

The results of the first experiments in the borehole-mimicking test rig do already demonstrate the expected concave and monotonously increasing behaviour between the measured Nusselt and Reynolds numbers, cp. Figure 6. This relation proves the validity of the measurement concept for the desired purpose, even though the Nusselt numbers are significantly smaller than expected from HWA-literature perspective. The initially adapted assumption of constant temperature across the cylinder—as fully valid for HWA—has been hypothesized to be a strong oversimplification. To elaborate the influence of temperature gradients within and heat transfer around the considered hybrid cable further, a second experiment has been conducted, which revealed the following two insights. Firstly, the heat conduction inside the cable has been identified to predominate the overall temperature difference of the measurement with accordingly large Biot numbers (\(Bi>1\)), which confirms the above hypothesis. Secondly, the heat transfer of the considered system comprised of measurement equipment and test scenario can be well estimated by means of the Nusselt correlation as proposed by Gnielinski (1975). The first take home, i.e., \(Bi>1\), is a remarkable conclusion, since the measurement principle builds upon heat convection, which has been successfully shown, despite heat conduction predominating the problem. Fortunately, the heat conduction is only a function of the supplied power, constant geometry and material parameters, where any mild influence of the latter has been neglected at the present proof-of-concept level. Thus, the temperature offset inside the cable must only be known for the given system, i.e., cable and heating power, and subtracted from the measured temperature difference between glass fiber and environment.

The second take home, i.e., the validity of Gnielinski’s Nu(Re) correlation for the given problem, allows an analytic-empiric analysis of the dimensional measurement range of velocities

$$\begin{aligned} u=u(\Delta T, \dot{Q}/l, Nu(Re), d, \nu , \lambda _\text {fl}) \end{aligned}$$
(12)

and the derivation of corresponding temperature-measurement uncertainties. With the simplified assumption \(\sqrt{{Re}}\propto {{Nu}}\) and constant material properties of water the relevant influences on the velocity

$$\begin{aligned} u \propto \left( \frac{1}{\Delta T} \frac{\dot{Q}}{l} \right) ^2 \frac{1}{d} \end{aligned}$$
(13)

are revealed. For a given velocity the resulting temperature difference will increase for increasing heat flux \(\dot{Q}/l\) and/or decreasing diameter d. This interplay of phenomena is emphasized for varying heat fluxes per length and diameters in the measurement map as shown in Fig. 9 according to Gnielinski’s Nu(Re) correlation.

The diagram shows that the curves with higher heat flux per length \(\dot{Q}/l\) and smaller diameters d appear to have the best measurement range. It is worth to recap that a diameter reduction is equivalent to an effectively higher heat flux per cylinder surface area \(Q/(\pi d l)\). For the desired borehole application, however, the diameter must be sufficiently large to ensure mechanical robustness of the sensor in the expected harsh conditions. Furthermore, the heat flux should not significantly heat up the fluid within the borehole, which suggests an iterative measurement strategy—starting from small heat fluxes until the actually occurring velocities can be resolved.

Fig. 9
figure 9

Dimensional map of the measurement range for a horizontal cylinder based on Gnielinski’s Nu(Re) correlation for varying heat fluxes per length \(\dot{Q}/l\) and diameters d. The measurement range increases with increasing \(\dot{Q}/l\) and decreasing d, where the latter effectively increases the heat flux per surface area \(\pi d l\)

Full size image

It is important to note that the measurement range of each configuration in Fig. 9 is inherently limited by the measurement precision of the temperature difference between the cylinders surface and the environment. Due to the steep slopes for small temperature differences, small temperature-measurement errors will lead to large velocity measurement errors. Very large temperature differences, in contrast, approach the purposely-neglected effect of natural convection. Recall from Fig. 6b and corresponding discussion that all conducted experiments exceed the \(Re>Gr^{1/3}\) condition (see Collis and Williams 1959), thus rendering natural convection negligible. The only exception, however, is the quiescent-water test run (\(Re=0\)), which is buoyancy dominated as expected. This exception—even though beyond the purpose of the present work—consequently outlines that a possible investigation of very small Reynolds numbers as occur, e.g., for aquifer monitoring implies that a consideration of natural convection will become mandatory in an accordingly adapted processing approach.

As a technical note, typical DTS systems, as the AP-sensing N43856B system used in the present work, have a rather coarse minimum spatial resolution in the range of \(\approx 0.5\,\textrm{m}\), which renders the identification of local temperature phenomena particularly challenging. Even though obviously sufficient for the proof-of-concept setup in the present work and quasi-steady temperatures along the spiral probe in vertical flow, the distinction of different temperatures around the probe perimeter in case of transverse flow across a borehole encountering superimposed aquifer fluxes seems very difficult and expensive with standard DTS as elaborated by, e.g., Thomcraft et al. (1992); Dyer et al. (2012) and Bazzo et al. (2016). The additional application of FBG technology is considered a promising alternative or even extension to the presently operated DTS setup. Future efforts accordingly foresee a combined DTS/FBG application to address both, resolved temperatures—thus spatial velocity resolution for transverse flows—around the perimeter of the double-packer probe and further accuracy improvements for the temperature-measurement procedure itself.