Investigation of turbulent superstructures in Rayleigh–Bénard convection by Lagrangian particle tracking of fluorescent microspheres

Abstract

We present spatially and temporally resolved velocity and acceleration measurements of turbulent Rayleigh–Bénard convection (RBC) in the entire fluid sample of square horizontal cross section with length $L=320$ mm and height $H=20$ mm, resulting in an aspect ratio of $\Gamma =H/L=16$. The working fluid was water with a Prandtl number of Pr=7 and the Rayleigh number was set to ${\text{Ra}}= 1.1\times 10^6$. In order to minimize surface reflections, we used fluorescent polyethylene microspheres as tracer particles that were imaged at a rate of 19 Hz by six cameras. From the images, the particle positions, velocities, and accelerations were determined via the ‘Shake-The-Box’ (STB) Lagrangian particle tracking algorithm. With this approach, we could simultaneously track more than 300,000 particles and hence study the resulting turbulent structures in the Eulerian and Lagrangian frames while resolving the smallest spatial and temporal scales of the flow.

1 Introduction

Thermal convection describes fluid flow that is driven by temperature gradients. It plays a major role as an efficient heat transport mechanism in nature and industry and is the driving force behind large-scale flow systems in many geo- and astrophysical settings. Convection is usually studied numerically and experimentally in an idealized model system, in which a horizontal fluid layer of height H is confined by a warm plate from below and a cold plate from above. This system is known as Rayleigh–Bénard convection (RBC) and has been studied for over a century (see, e.g., Bénard (1900); Rayleigh (1916); Kadanoff (2001); Ahlers et al. (2009)).

When the temperature difference $\Delta =T_b-T_t$ between the bottom ($T_b$) and the top ($T_t$) is sufficiently small, relevant physical properties of the fluid can be assumed to be constant and the system is only governed by two dimensionless control parameters, namely the Rayleigh number Ra and the Prandtl number Pr, defined as

$${\rm Ra} = \frac{{g\alpha \Delta H^{3} }}{{\nu \kappa }}\quad{\text{ and }}\quad {\rm Pr} = \frac{\nu }{\kappa }.$$

(1)

Here, g, $\alpha$, $\nu$ and $\kappa$ denote the gravitational acceleration, the isobaric thermal expansion coefficient, the kinematic viscosity, and the thermal diffusivity, respectively. The Rayleigh number indicates the ratio between the driving buoyancy and the damping mechanisms, i.e., momentum and thermal diffusion, whereas Pr is the ratio of the latter two. Next to Ra and Pr also the geometrical constraints play a role as they control the influence of the lateral boundaries on the system. For a given geometry, this is expressed by the aspect ratio between the lateral dimension L and the height $\Gamma =L/H$.

For small Ra, the flow is laminar and RBC serves as a model system to study pattern formation (see, e.g., Bodenschatz et al. (2000); Weiss et al. (2014)). In fact, for a laterally extended fluid layer ($\Gamma \gg 1$), convection sets in at a critical value ${\text{Ra}}_c=1708$ in the form of stationary periodic rolls with a wave number of $k_c = 3.117/H$ (wavelength of $\lambda _c = 2\pi /k_c\approx 2H$). With increasing thermal driving, the initially steady rolls become dynamic, chaotic and finally, at sufficiently large Ra, the flow turns turbulent. Most investigations that are focusing on this regime aim to understand how and how much heat is transported from the bottom to the top as a function of the applied temperature difference (Kraichnan 1962; Kadanoff 2001; Ahlers et al. 2009).

In order to increase the thermal driving and also for practical reasons, turbulent convection is predominantly studied in boxes or cylinders of a lateral extent similar to their height $\Gamma \approx 1$. In these cases, the flow is dominated by a large-scale convection roll, in which warm fluid rises on one side and cold fluid sinks at the opposite side (Ciliberto et al. 1996; Shang et al. 2003; Bosbach et al. 2021). As typical for turbulent flows, the kinetic energy of the large-scale structure is transferred into smaller eddies and eventually dissipated into heat in the smallest eddies. Warm (cold) fluid volumes, the so-called plumes, rise (sink) from the bottom (top) and carry potential energy, which is converted into kinetic energy of the large roll.

Many different aspects of such laterally confined systems have been investigated in the past (see, e.g., Ahlers et al. (2009); Lohse and Xia (2010); Chillà and Schumacher (2012)). Such aspects of interest include the characterization of the flow close to the boundary, the warm (cold) plumes that rise (fall) due to their buoyancy, or the shape and dynamics of the large-scale convection roll. For this, the velocity was measured using classical techniques such as laser Doppler velocimetry (LDA) for local measurements with high temporal resolution (e.g., du Puits et al. (2007, 2009)), two-dimensional particle image velocimetry (PIV, e.g., Xia et al. (2003); Sun et al. (2005, 2005)) if spatial resolution was required, or shadowgraphy (Funfschilling et al. 2008; Bosbach et al. 2012) for spatially resolved information about the temperature field.

It was only rather recently that researchers have started to focus on the largest scales of the flow structure and investigated how it changes when given more space in lateral direction, i.e., when the influence of the lateral sidewalls becomes smaller (see, e.g., Bailon-Cuba et al. (2010); Pandey et al. (2018); Stevens et al. (2018)). It was observed that in these cases, structures are hidden in the turbulent flow that resemble the convection rolls close to convection onset. These structures become visible in particular in the vertical velocity and the temperature field upon averaging over sufficiently long time scales and they are called turbulent superstructures (TSS). Albeit the turbulent superstructures are less coherent and less ordered than their laminar counterpart at small Ra, they have a well-defined wavelength as well. Simulations by Pandey et al. (2018) suggest that the wavelength increases with Ra from $\lambda \approx 2H$ close to convection onset to $\lambda \approx 6H$ for the fully turbulent regime. However, the exact value depends on the aspect ratio $\Gamma$ as well and can only be reached in sufficiently wide domains, i.e., large $\Gamma$ (Stevens et al. 2018). The dynamics, shape, or even the size of the TSS are so far not understood. Only recently have first attempts been made to model the increase in wavelength by adding a noise term, representing the vigorous turbulent fluctuations, to the Swift–Hohenberg model (Ibbeken et al. 2019).

Investigating such large aspect ratio systems is important to better understand many natural systems such as the Earth’s atmosphere where the height of which is rather small compared to its lateral dimensions. However, they are difficult to address in direct numerical simulations, as the performance of computers is limited and even nowadays still insufficient to resolve both the largest and the smallest relevant length scales simultaneously over a sufficient time span. While in experiments, it is on the one hand possible to make long time measurements, it is, on the other hand, also rather complicated to measure the entire velocity field with sufficiently high spatial resolution. Hence, information about details of the flow has been gained by direct numerical simulation (see, e.g., Kooij et al. (2018)), accepting the limitations discussed above.

However, the development of fast high-resolution cameras, the increasing computational power, high-power pulsed LED, and the development of smart flow measurement techniques have significantly enhanced the spatial resolution available from experiments (see for an overview Raffel et al. (2018); Schröder and Schanz (2023)). First volumetric Lagrangian particle tracking (LPT) measurements in RBC have been conducted by Ni and coworkers about a decade ago in the bulk region (Ni et al. 2011, 2012), which revealed spatially resolved statistical properties of the flow. With the ‘Shake-The-Box’ (STB) algorithms, Schanz et al. (2016) proposed a method, which enables to track hundreds of thousand particles with sub-pixel resolution. With such high seeding density, one could not only measure spatially resolved statistical properties of the flow but one could also probe the flow as function of time. This technique has successfully been used for volumetric measurements of the three-dimensional velocity field in RBC by Bosbach et al. (2021), Godbersen et al. (2021), Bosbach et al. (2022) as well as by Paolillo et al. (2021). The focus of these investigations was to analyze the shape and the dynamics of the large-scale circulation in cylindrical container of small aspect ratios between diameter (D) and height (H) of $\Gamma =1$ and 0.5, respectively.

Also very recently, experimental measurements of turbulent RBC in large aspect ratio cells have been conducted by Moller et al. (2021, 2022) by using thermochromic liquid crystal particles. The particle temperatures were determined from their color, and velocities were measured via stereoscopic particle image velocimetry. While this technique could successfully measure the three velocity components and the temperature simultaneously, hence also calculated the vertical heat flux with rather good spatial resolution, measurements were done only along two horizontal planes of the cell (at mid-height and close to the top plate). In this experiment, the authors could follow the dynamics of the turbulent superstructures over up to $10^4$ free-fall times ($t_{f}=\sqrt{H/g\alpha \Delta }$).

Here, we present an RBC experiment in a large aspect ratio cell of $\Gamma =16$. This aspect ratio is large enough so that the natural wave number of the TSS is expected to be independent of the lateral dimension of the container (Stevens et al. 2018). Via particle tracking in the entire volume, we determine the complete three-dimensional velocity field with a spatial resolution similar to the Kolmogorov length and a temporal resolution 18 times higher than the Kolmogorov time. From these measurements, we decompose the flow field in the slowly moving large-scale turbulent superstructures and the faster small-scale fluctuations.

The paper is organized as follows. In the next section, we describe in detail the experimental setup and the measurement and evaluation techniques. In Sect. 3, we show an analysis of the morphology and the dynamics of the turbulent superstructures. The paper ends with a summary and an outlook.

2 Experimental setup

In order to generate turbulent superstructures in RBC that can be investigated with optical, volumetric measurement methods, such as time-resolved LPT, we designed and built a Rayleigh–Bénard cell with variable sidewalls and a transparent cooling plate. The experimental setup is sketched in Fig. 1(a). The Rayleigh–Bénard cell has a quadratic horizontal cross section of side length $L=320$ mm. The sidewalls of the cell were made out of transparent acrylic which functioned as spacer between the bottom and top plates and hence define the height H of the convection cell. The bottom plate was 30 mm thick and made out of aluminum, which was electrically heated via a carbon fiber fabric glued at its bottom and thermally insulated from below with 15-cm-thick polypropylene foam. Four resistance temperature detectors were embedded inside the bottom, distributed evenly so that each thermistor was placed in the center of a quadrant of 160 mm $\times$ 160 mm. For this, blind holes were drilled from underneath up to 1 mm below the interface with the working fluid and filled with thermal grease, into which the thermistor was pushed. The measured temperatures from these thermometers were fed into a PID feedback loop for regulating the heat input into the bottom plate to keep $T_b$ constant within ±5 mK.

The top plate was a 0.5-mm-thin borosilicate glass for providing optical access. It was cooled by pumping cooling water at a well-defined temperature through a cavity above its top. The temperature of the cooling water was regulated by a chiller and is kept constant to within $\pm 10$ mK. The entire cell was leveled with respect to gravity to within $0.2^o$.

We used distilled water as the working fluid to which sodium chloride was added (0.25 percent in mass) in order to fine adjust its density to that of the seeding particles. The temperature at the top ($T_\textrm{t}$) and bottom ($T_\textrm{b}$) plates were regulated so that their mean $T_\textrm{m}=(T_\textrm{b}+T_\textrm{t})/2$ stayed constant at $T_m=20.0\pm 0.01$ $^o$C, resulting in ${\textit{Pr}}=7.0$. The cell height was given by the sidewall that was used and hence could easily be adapted. Here, we present results from a cell with height of $H=20$ mm corresponding to an aspect ratio of $\Gamma =L/H=16$. The applied temperature difference between the bottom and the top plate was set to $\Delta =10$ K resulting in ${\text{Ra}}=1.1\times 10^6$.

Since the top plate is cooled from above by the cooling liquid and heated from below by the working fluid, a temperature difference occurs across the 0.5 mm thick borosilicate plate (heat conductivity $\lambda _{b}=1.2$ W/m$\cdot$K) which can be estimated for a given heating power of 200 W to be $0.08\Delta$. The cooling flow over the top plate is sufficiently strong, and one can consider the top plates top surface to be nearly isothermal. Then, temperature inhomogeneities at its bottom occur due to the spatially varying heat fluxes. In order to quantify these inhomogeneities, we analyzed the spatial variations of the Nusselt number close to the top and bottom boundary layer, which were found to amount to 35% (Emran and Shishkina 2020, 2023) of the mean Nusselt number. Therefore, we expect that the temperature inhomogeneities at the interface between the top plate and the fluid to amount to $\pm 0.03\,\Delta$ (rms).

The bottom plate is different, as a spatially constant heat flux is provided by the carbon heater at its bottom. Furthermore, the larger heat conductivity of the aluminum also allows heat transport in lateral directions and hence an equilibration of the temperature. Therefore, in order to estimate spatial temperature inhomogeneities we consider the measurements of the four temperature sensors embedded in the bottom plate. They differ from their mean value by $\pm 0.03\,\Delta$ suggesting the bottom plate to be similar homogeneous as the top plate.

Another possible source of large-scale inhomogeneities could be introduced in the cooling bath since the cooling liquid heats up when it flows over the top plate, hence creating a positive temperature gradient along the flow direction. In our experiment, the pumping rate of the cooling water was sufficiently fast to avoid significant lateral temperature gradients of the top plate. We have measured the temperature of the cooling fluid at the inlet $T_\textrm{in}$ and the outlet $T_\textrm{out}$ (green vertical lines in Fig. 1a), and their difference did not exceed 0.1 K. We note, however, that at this point nothing is known about the sensitivity of the large-scale flow pattern with respect to inhomogeneities of the boundary conditions.

Fig. 1

Experimental setup. a: Schematic of the experimental setup. The two green vertical lines represent the location of the thermistor array which measure the temperature of the cooling water when it enters the cooling chamber ($T_\textrm{in}$) and when it leaves the cooling chamber ($T_\textrm{out}$). b: Image of the convection cell upon illumination from the side with UV light. The orange color is emitted light from the fluorescent microspheres shown in (c). c: Image of the $\approx 50\mu$m large fluorescent polyethylene microsphere that were used for seeding the flow (Image copyright by Cospheric LLC). d: Side view of the rectangular convection cell

For time-resolved LPT, we seeded the fluid with fluorescent polyethylene microspheres of diameter $d \approx 45 - 53\,\mu$m as tracer particles (UVPMS-BO-1.00 by Cospheric LLC), which were illuminated by two pulsed UV-LED arrays (by LaVision). The illumination was further enhanced by placing flat mirrors in opposition to the UV-LED (see also Fig. 2). We have illuminated the fluid parallel to the bottom plate and hence absorption can only occur at the particles, because water is transparent in the spectral range of the UV-LED. We have pulsed with 19 Hz and a pulse energy of 97 mJ per LED module. Hence both LED modules together emit a total illumination power of 3.7 W. However, as the area of the LED is much larger than the area of the sidewall of the cell by a factor of about 5, the total amount of energy that enters the cell is less than 0.8 W. This is rather small compared to the 200 W heating power produced by the bottom plate. In addition, we also conducted similar experiments with a smaller framerate but the same pulse energy. There, we did not observe any changes in the flow.

The particles had a density of $\rho =1.00\times 10^3$kg/m$^3$, to which the density of the working fluid was matched and hence the particles can be considered neutrally buoyant. The particles absorb light in the near UV range and emit at wavelengths longer than 580 nm. By placing a long-pass filter (3 mm thick Perspex ‘orange’, 550 nm) on the top of the flow distributor of the cooling liquid, we filtered out light scattered directly by surfaces of the apparatus. This has significantly increased the image quality and altogether enabled LPT measurements in the shallow fluid layer where reflections from the boundaries were unavoidable.

We have used six scientific sCMOS cameras (Imager sCMOS by LaVision, 2560  $\times$  2160 px) to image the particles from different angles between 7$^o$ and 28$^o$ with respect to the vertical axis, hence covering a total aperture of about 55$^o$. The four most outer cameras were equipped with 60 mm lenses (Zeiss Makro-Planar 2.8/60), the two inner cameras were combined with 50 mm lenses (Zeiss Planar T* 1.4/50). These lenses were mounted on the cameras via Scheimpflug adapters to account for the oblique viewing angles and hence to minimize the depth of field required for volumetric imaging of the particles.

For calibration of the camera system, we designed and manufactured a dedicated calibration cell, which allowed us to position a two-layer calibration target at vertical distances $z=0$ and H from the real bottom plate while mimicking the optical path of light in the actual RBC apparatus as closely as possible (Fig. 2). In addition, we also performed a volumetric self-calibration (Wieneke 2008) and a calibration of the particle imaging (optical transfer function (Schanz et al. 2012)) during an actual measurement with low seeding density. In this way, we could map the real-world coordinate system to the camera image with sub-pixel precision ($\sim$ 0.1 px).

Fig. 2

Calibration cell that was put in place of the actual RBC apparatus with calibration target

From the camera snapshots and the previously determined calibration matrix, the position of the microspheres as well as their velocity and acceleration was calculated as a function of time by using the Shake-The-Box algorithm (Schanz et al. 2013, 2016). Specifically, the DLR implementation of the Variable-Timestep-STB processing (Schanz et al. 2021) was applied to the images that showed particle peaks in a density of approx. $N_\textrm{I} = 0.06$ particles-per-pixel (ppp). This allowed tracking of more than 300,000 particles for an extended time span. The gained raw particle positions were filtered using the TrackFit approach (Gesemann et al. 2016), with a crossover frequency calibrated from the position spectrum of the unfiltered tracks. This procedure allows to quantify the average position accuracy, being approx. 7 $\mu$m for the x- and y-coordinates and 20 $\mu$m for the z-coordinate in case of the raw tracks. The filtering process roughly halves the given values.

We used the Lagrangian particle field to further calculate highly resolved Eulerian velocity fields using the data assimilation method FlowFit (Gesemann et al. 2016). FlowFit returns a continuous three-dimensional velocity field by minimizing a cost function comprised of the residual of the particle velocity at a given position and the velocity of the field, which also takes the incompressible continuity and Navier–Stokes equations into consideration. In the case presented here, we calculated the velocity on a grid of overlapping 3rd order B-splines, with spacing between neighboring knots of 1 mm, which amounts roughly to one Kolmogorov length ($\eta \approx 1$ mm). On average, the velocity and acceleration of 0.14 particles were used to calculate the velocity in one unit cell of the grid. The regularization via the governing equations hence increases the reconstructed spatial resolution beyond the sampling by the particles by a factor of about 2.

During an experimental run, the temperature of the cooling bath and the bottom plate was set to their desired temperatures and sufficient time was given until the plates have adjusted to their desired temperature (at least 30 min). After that, the previously injected tracer particles were dispersed by magnetically moving a thin rod close to the bottom plate. The flow was then given sufficient time ($\approx 1800\,t_f$), so that the introduced fluid motion could fully decay and the resulting flow was purely driven by thermal gradients. We took snapshots with a frequency of 19 Hz which are roughly 18 images per Kolmogorov time $t_\eta =\sqrt{\nu /\varepsilon }$, with $\varepsilon$ representing the average energy dissipation rate. For the dataset discussed below, we took 38,000 snapshots with each camera, covering a time span of 2,000 $t_f$.

3 Results

As already stated above, our study focuses on the morphology and the dynamics of the largest structures in the flow with the slowest dynamics, i.e., the turbulent superstructures.

Fig. 3

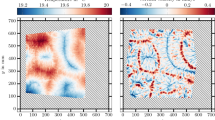
a and b: Horizontal and vertical cross sections of 2 mm and 4 mm thickness of a single snapshot of the tracked particles. The color of each point denotes the vertical velocity in units of $u_f$, i.e., red for the rising particles, and blue for sinking particles (see colorbar). c and d: Horizontal and vertical cross sections of snapshots of the Eulerian velocity field. Colors are vertical velocity in units of $u_f$. a and c Show horizontal cross sections at mid-height ($z=0.5\pm 0.05$ H). (b and d) show vertical cross sections at y=8H, i.e., around the horizontal dashed line in (a). Note that the ratio of the x- and z-axis in (b and d) is not preserved for better visibility. Movies of the particles and the Eulerian velocity field are provided as supplemental material online

Figure 3 shows horizontal (a) and vertical (b) cross sections of snapshots of the tracked particles. In both figures, all particles are shown that were tracked and are located within a thin slice that is 2 mm (a) or 4 mm (b) wide at a given time. The color of the data points corresponds to their vertical velocity in units of the free-fall velocity $u_\textrm{f}=\sqrt{g\alpha \Delta H}$ (i.e., a hypothetical velocity that is reached by a fluid parcel after a distance H under constant acceleration $g\alpha \Delta /2$). In this representation, areas where warm fluid rises (red) and where cold fluid sinks (blue) can be clearly distinguished.

We show in Fig. 3(c and d) the reconstructed Eulerian velocity field that was calculated from the particle field in Fig. 3(a and b) via FlowFit. The vertical velocity along the horizontal cross section appears rather chaotic and spatial coherence is lost over short length scales, due to the turbulent motion of the flow (see also supplementary material).

In the vertical cross section (Fig. 3b and d) on the other hand, we see that warm (red) upflow and cold (blue) downflow occurs in rather narrow regions that are very coherent in the vertical direction. We note that coherent regions of upflow or downflow are not equally spaced, as one would expect from equally spaced convection rolls. This is because of the different orientations of the largest rolls with respect to the plane considered here.

Having the velocity data of the particles we can start to make some more quantitative analysis. First, we look at averaged vertical profiles of the horizontal ($\langle u^2+v^2\rangle$) and vertical ($\langle w^2\rangle$) turbulent kinetic energy (TKE) (Fig. 4a). For this, data were averaged over time and the horizontal coordinate and the result is normalized by $u_\textrm{f}$. The shape of these profiles are typical and as expected for Rayleigh–Bénard convection. The maxima of the horizontal TKE are located rather close to the top and bottom, which is a result of the largest convection pattern that span the entire vertical extent of the cell. Due to these structures, shear boundary layers occur close to the top and bottom plate, which can be considered laminar since the shear stress therein is too small to render them turbulent (Grossmann and Lohse 2000; Ahlers et al. 2009). However, due to hot and cold plumes that detach from the bottom and top plates, the boundary layers are constantly perturbed by these frequent ejections of highly buoyant fluid. The vertical TKE (red) has a maximum at mid-height, which again is in congruence with the observation of the large-scale structures (see also Fig. 6). The largest accelerations occur near the top and bottom plates, where temperature gradients and therefore also buoyancy are largest (see red dashed line in Fig. 4b. Subsequently, the largest vertical velocity has to occur in the vertical center before pressure gradients close to the opposite plate decelerates the fluid.

Fig. 4

Vertical profiles of the spatially and temporally averaged horizontal and vertical turbulent kinetic energy (TKE) as a function of the vertical distance from the bottom plate

The maximal TKE corresponds to velocities of about 0.09 $u_f$ for the horizontal and 0.08 $u_f$ for the vertical component. These values can be used for a rough estimate of an eddy turnover time for eddies of the size similar to the cell height, resulting in $\tau _{to}\approx 50\,t_f$.

Another view to the same physical quantities that we would like to discuss in the following, are the distributions of the velocity and the accelerations, which can be considered as an additional quality check. Hereto, we show the probability density functions (PDF) of the three velocity components $\mathcal {P}(u)$ (blue), $\mathcal {P}(v)$ (red), $\mathcal {P}(w)$ (green) in Fig. 5(a,b,c) as well as the three components of the accelerations $\mathcal {P}(a_x)$ (blue), $\mathcal {P}(a_y)$ (red), $\mathcal {P}(a_z)$ (green) in Fig. 5(d,e,f) close to the bottom plate ($z = 0.1H$—Fig. 5a,d), at mid-height ($z=0.5H$—Fig. 5b,e), and close to the top plate ($z=0.9H$—Fig. 5c,f). The distributions were calculated considering data from the entire horizontal domain and over a duration of ~ 2000 $t_\textrm{f}$.

Let us focus first on the PDFs at mid-height. The statistics of the horizontal velocity components ($\mathcal {P}(u)$ and $\mathcal {P}(v)$) are very similar and follow a near-Gaussian distribution (black line). This is symptomatic for isotropic turbulence (see, e.g., Wilczek et al. (2011)) and caused by the fact that the horizontal velocity components at mid-height are a result of the breakup of larger eddies, and the influence of the top and bottom boundaries on these components is weak. For the vertical component, a qualitatively different distribution $\mathcal {P}(w)$ is found. While small velocity values follow a normal distribution, as well, its tails are much higher as many particles have much larger velocities as what would be expected for isotropic turbulence. This is explained by the existence of up- and down-draft regions where warm (cold) fluid rises (sinks) due to buoyancy. All three acceleration components at mid-height show non-Gaussian distributions with strong tails, which is also typical for isotropic turbulence (see, e.g., Mordant et al. (2004)). The tails for $a_z$ are slightly larger than for the horizontal accelerations, which is expected because of buoyancy that leads to acceleration in vertical direction, whereas no body forces act in horizontal direction. Overall, the PDFs at mid-height are very symmetric with respect to positive and negative values.

The PDFs close to the bottom (Fig. 5a and d) and the top (c and f) are very similar considering the up-down symmetry of the system and hence we only discuss the PDFs at the bottom shown in Fig. 5(a and d). Let us first focus on the PDFs of the horizontal velocities $\mathcal {P}(u)$ (blue) and $\mathcal {P}(v)$ (red). Both are rather similar, symmetric and close to a Gaussian curve, albeit with a slightly broader maximum. The calculation of the PDF was done by using data from almost the entire height of the boundary layer, and we consider here the horizontal components, whose statistics should be governed by shear effects. While this does not explain a Gaussian distribution, we at least note that the horizontal velocities in a turbulent shear layer show positive skewness close to the wall and negative skewness at the top end of the boundary layer (see, e.g., Stevens et al. (2014); Durst et al. (1987)). Both contributions might cancel out, leading to a symmetric distribution when averaged over the entire boundary layer height.

However, we also note that there are small systematic differences between the PDFs of both components. In particular $\mathcal {P}(u)$ (blue) appears slightly asymmetric and is a bit higher for small positive values and a bit lower at small negative values close to the bottom plate (Fig. 5b). Interestingly, this situation is reversed close to the top plate (Fig. 5c), and hence suggests a weak large-scale flow that moves fluid along the bottom plate in positive x-direction and at the top plate in negative x-direction.

The PDF of the vertical component $\mathcal {P}(w)$ (red) is non-symmetric in a very characteristic way reflecting the asymmetry between warm line-shaped rising plumes that are ejected from the bottom plate and colder plumes that are impacting into the bottom boundary layer from above (see also Fig. 6a). The stretched line plumes have velocities in the range of 0.05...0.1 $u_f$, hence causing a bulge in the PDF at these values (Fig. 5a). For larger velocities $\mathcal {P}(w)$ decays quickly, whereas the left tail for negative velocities decays much slower, caused by the large velocities of impacting plumes.

The PDFs of the three components of the accelerations close to the bottom are shown in Fig. 5(d). The PDFs of the two horizontal components (blue and red) are almost equal as it is also true for the left tail of the vertical component. While negative vertical accelerations are caused by pressure gradients and shear forces, positive accelerations are caused in addition by the buoyancy of the warm plumes, which leads to an abundance of positive acceleration.

Fig. 5

Probability density functions of the different velocity components (a,b, and c) as well as of the acceleration (d, e, and f), close to the bottom plate (a and d), at mid-height of the cell (b and e) and close to the top plate (c and f). Different colors mark the components of the velocity and acceleration in x- (blue), y- (red) and z-direction (green). The black solid lines in (a,b, and c) are Gaussian distribution plotted as a guide to the eye. Accelerations in (d, e, and f) were normalized by the buoyancy $\alpha g \Delta$, which for the presented experiments here had a value of $\alpha g \Delta = 0.0203$. See also the supplemental material for vertically resolved probability density functions

Large-scale structures in turbulent systems are usually affiliated with longer time scales, whereas small-scale fluctuations occur on short time scales. As we are mainly interested in characterizing the largest flow structures, i.e., the TSS, we average the instantaneous velocity fields over various time intervals in the following. For best observing the turbulent superstructures this time interval should be long enough, so that small-scale fluctuations are averaged out, but not so long that the intensity of the interesting pattern is reduced. This is crucial, since also the largest structures are dynamic and both move and deform rather randomly in time. Therefore, in an ideal and perfectly symmetric system, no mean flow is expected to occur after averaging over sufficiently long time intervals.

We show in Fig. 6 horizontal slices of the vertical velocity field at mid-height (left column) and close to the bottom plate (right column, z=0.1 H). The velocity close to the top plate is not shown here, but it looks very similar to the velocity at the bottom, just color-inverted due to the up-down symmetry of the system. Figure 6(a) displays snapshots, whereas Fig. 6(b and c) presents velocity fields that were averaged over $\approx 26$ (b) and $\approx 53$ (c) free-fall times.

Fig. 6

Eulerian field of the vertical velocity component (in units of $u_f$) at mid-height (left column) and right above the bottom plate at z=0.1H (right column). Row a shows snapshots, b An average over 26 free-fall times and c An average over 53 free-fall times

Let us first focus on the snapshots shown in Fig. 6(a), where we see clear qualitative differences between the velocity fields at mid-height and close to the bottom. One sees that at mid-height (left), the blue (sinking) and red (rising) structures are rather symmetric in shape and distribution, whereas at the bottom (right), a network of red thin line-like structures exists with patches of blue areas enclosed by them. These line structures are formed by rising warm plumes and the interaction between them. The dominant length scale at the bottom is determined by the spacing of these line plumes. Larger patterns are not easily visible in the snapshots.

Upon averaging over 26 or even 53 free-fall times (Fig. 6b and c) the long-living large-scale structures become more pronounced and appear as a complex network of cellular and roll-like structures, which we refer to as TSS. The flow field at the bottom and the mid-height looks now more similar in the averaged flow fields. Since the TSS themselves move and change in time, the structures become more fuzzy when averaging over even longer time spans.

For a better understanding on how temporal averaging affects the large and small length scales, we show in Fig. 7 the azimuthal average of the two-dimensional Fourier transform of the vertical velocity at mid-height (dashes lines) as well as close to the bottom plate (solid lines). The different colors are results from different averaging time spans (see legends). In general, one sees that the Fourier transform at mid-height shows distinct maxima. Even though the maxima are clearly visible, its wave number k is not very well resolved, due to the finite aspect ratio of our cell ($\Gamma =16$), which results in a resolution of $\Delta k=2\pi /\Gamma =0.393$. The wave number at which the maximum occurs for small averaging times ($\tau < 53t_f$) is $k=2.4$, which is within the range of length scales where the superstructures are expected to occur. The critical wave number at the onset of convection for a laterally infinite extended fluid layer is $k_c=3.117$ (right dashed vertical line in Fig. 7) at a critical Rayleigh number ${\text{Ra}}_c=1708$ (see e.g., Bodenschatz et al. (2000)). With increasing Ra, the flow becomes unsteady, chaotic and turbulent and the pattern increase in size, corresponding to the reduction in the wave number k. So far it has not been thoroughly investigated how the wave number of these superstructures depend on Ra, Pr, and $\Gamma$. However, recent numerical investigations (Pandey et al. 2018; Stevens et al. 2018) suggest that with increasing $\Gamma$ and Ra, the wave number of the turbulent superstructures asymptotically approaches $k_{turb}=1$ (left dashed vertical line in Fig. 7). Any large-scale convection pattern that occurs in a sufficiently large cell is expected to have a typical wave number somewhere in between these two limits, i.e., $k_\textrm{turb}< k < k_\textrm{c}$.

Fig. 7

Azimuthally averaged Fourier spectrum of time-averaged vertical velocity field. The dashed lines are calculations for a horizontal plane at z=H/2. The solid lines are calculations for a horizontal cross section near the bottom plate. Different colors mark different duration over which the velocity was average (see legends). The solid colored points mark the maxima of the Fourier transform at mid-height. The inset shows the wave number with the maximal Fourier signal at mid-height as a function of the averaging time

The Fourier spectra of the vertical velocity field close to the bottom plate exhibit much broader peaks, but the location of them is similar and as well close to $k_{max}\approx 2.4$. Both, the mid-height Fourier spectra and that taken close to the bottom change upon time-averaging such that the intensity at larger k (small-scale structure) is suppressed. The suppression is stronger the longer the time interval over which was averaged. We show in Fig. 7 Fourier spectra of various averages over time intervals up to $\tau _\textrm{op}=194\,t_\textrm{f}$. One can consider a good time interval for averaging as the one that sufficiently suppresses wave numbers larger than $k_\textrm{max}$, without reducing the peak at $k_\textrm{max}$. This is given for averaging times of $\tau _\textrm{op} =53\,t_\textrm{f}$ (greenish curves). Averaging over longer times leads to a reduction in the intensity at wave number $k_\textrm{max}$ and subsequently to a change of the location of the maxima toward smaller wave numbers. The location of the wave number with the largest intensity is shown in the inset of Fig. 7 as a function of the averaging time. Such an optimal timescale for averaging reflects the maximal time scales on which the superstructures can be considered to be steady, whereas they are dynamic on longer time scales.

We note that the interval of $\tau _\textrm{op}=53\,t_f$ corresponds to 1000 time steps in our experiment, and is not a very precise measure but rather a convenient value to separate the turbulent superstructures from the smaller fast fluctuations. Interestingly, this time also corresponds to the eddy turnover time of the largest eddies. At this point we do not yet have an explanation for this relation between both time scales, or at least we do not see an obvious reason why the large-scale structures should not be stable on longer time scales. On the other hand, however, one would not expect the superstructures to change on smaller time scales than the eddy turnover time, because in thermal convection, the large-scale structure is determined by the location of warm and cold plumes. Since temperature is advected by the flow itself, a rearrangement of the large structure cannot be faster than the travel time of the fluid parcel over the corresponding length scales, i.e., the eddy turnover time.

We now want to deduce the relationship between typical time scales of the bespoken structure and their size. For this, we decompose the spatiotemporal dataset of the vertical velocity in its most important contributions via proper orthogonal decomposition (POD) (see, e.g., Lumley (1967); Berkooz et al. (1993)). This method represents the temporal evolution of an m-dimensional signal $\textbf{u}(t) = [u_1(t),u_2(t),\dots , u_m(t)]$ as a linear combination of the most important fundamental modes ($[{\varvec{\phi }_1},{\varvec{\phi }_2},\dots ,{\varvec{\phi }_n}]$):

$$\begin{aligned} \left[ \begin{array}{c} \textbf{u}(t_1)\\ \textbf{u}(t_2)\\ : \\ \textbf{u}(t_n) \end{array} \right] = \left[ \begin{array}{cccc} A_{11} &{} A_{12} &{} \dots &{}A_{1m} \\ A_{21} &{} A_{22} &{} \dots &{}A_{2m} \\ : &{} : &{} : &{} : \\ A_{n1} &{} A_{n2} &{} \dots &{}A_{nm} \\ \end{array} \right] [{\varvec{\phi }_1},{\varvec{\phi }_2},\dots ,{\varvec{\phi }_n}] \text{. } \end{aligned}$$

(2)

Here, the $A_{ik}$ are the kth time coefficients for the ith mode. The modes are ordered according to their contribution to the total turbulent kinetic energy (the eigenvalues of the covariance matrix) in decreasing relevance. Note that the individual POD modes ($\phi _i$) strongly depend on the time interval considered.

This is neatly demonstrated in Fig. 8, where isosurfaces are shown of the first POD mode calculated from the three-dimensional vertical velocity over a time period of $\approx 5t_f$ (Fig. 8a and c) and over $\approx 50 t_f$ (Fig. 8b and d). Shown are isosurfaces surrounding volumes with a vertical velocity larger than 0.025 $u_f$ (red) and smaller than -0.025 $u_f$ (blue).

Fig. 8

Isosurfaces of the 1st POD mode at $-0.025$ $u_f$ (blue) and 0.025 $u_f$ (red) that was calculated from the evolution of the vertical velocity field over a time interval of $\approx 5 t_f$ (a and c) and $\approx 50 t_f$ (b and d). a and b: View from the top. c and d: View from the bottom, with an inverted x-direction to better compare with the top view

The blue volumes are rather thin at the top (Fig. 8a and b) and widen toward the bottom (Fig. 8c and d), while the red updraft areas are wide at the top and narrow at the bottom. This up-down symmetry is due to the qualitative difference between regions where plumes form and detach from the boundary layer (plume ejection regions) and regions where they reach the opposite plate (plume impacting regions).

Similar to Fig. 6, we clearly see in Fig. 8 that the dominant structures become larger and more pronounced, while small-scale pattern disappears when longer time scales are considered (comparing Fig. 8 a and b). In fact, the 1st POD mode is the time-averaged vertical velocity field. In contrast to a simple average, by performing a POD the small-scale structures are not lost, but are instead available in the higher-order modes. Therefore, we want to look now at these higher-order modes, and see over which time scales they exist.

Since the flow structure is rather coherent in vertical direction and since we are mostly interested in the horizontal flow structure, from now on we apply the POD only on the vertical velocity component along a horizontal plane at mid-height, calculated over $\approx 50 t_f$. The first mode, again, is the same as the averaged velocity field shown in Fig. 6(c). The small-scale fluctuations that occur on short time scales, which were averaged out in Fig. 6(c) are visible in Fig. 9(b-f). There, one can clearly see how the structures become smaller with increasing mode number.

We further observe that the structures become more isotropic with increasing mode number. The dominant patterns in Fig. 9(a) consist of rather long extended ridges, denoting the large-scale convection rolls. Also, the structures visible in the 2nd (b) and 3rd mode (c), albeit smaller, show elongated red and blue patches, which are still somehow aligned over short distances. However, the alignment gets more and more lost for higher modes and also the structures themselves become more and more round. This is because in turbulence the directional bias of the largest scales are lost when energy is transferred to smaller scales, at which the flow becomes isotropic.

Fig. 9

a–f: First 6 POD modes of the 2d-vertical velocity field at mid-height, calculated over $\approx 50 t_{f}$. The color code mark POD value in units of $u_{f}$

Of course, just calculating the individual POD modes is only helpful if we also consider their relative contribution to the flow, i.e., their eigenvalues. The eigenvalue spectrum of all modes is shown in Fig. 10(a), plotted on a semi-log plot. The first eigenvalue is significantly larger than the second eigenvalue by a factor of 1.5, indicating the strong contribution of the TSS to the total kinetic energy. The higher modes decay, initially exponentially with their mode number, but the decay slows down at around the 45th eigenvalue (black vertical line in Fig. 10a).

We have seen already in Fig. 9 that the visible structure in each mode becomes smaller with increasing mode number. In order to quantify the size of the pattern in each mode, we calculated the two-dimensional spatial Fourier transform which we then average over all possible orientations, in order to get a wave number spectrum for each mode. The result is shown in Fig. 10(b). The two down-pointing red arrows mark wave numbers $k_c=3.117$, i.e., the critical wave number for the convection rolls at their onset for an infinite system (Bodenschatz et al. 2000), and $k_{turb}=1$, which is the wave number that is expected for the larges structures at large Ra in spatially extended systems (Stevens et al. 2018).

In this figure, the maximum of the power spectra for mode 1 is rather close to $k\approx 2$ and hence somewhere in between these two values and similar to what was reported already above. The maximum for higher modes moves toward larger wave numbers, i.e., small structures, as was shown already in Fig. 9. The width of the peaks also broadens significantly in the same way.

Fig. 10

Properties of the POD modes shown in Fig. 9. a: Eigenvalue spectrum. The red dashed line marks an exponential decay. The black vertical line at 45 marks the mode at which the eigenvalues decay slower. Both lines are meant as guides to the eyes. b: Spatial Fourier spectra of the first ten POD modes (color coded, see legend). The two red down-pointing arrows mark critical wave numbers for the onset of convection ($k_c=3.117$) and $k_{turb}=1$ c: Temporal evolution of the time coefficient of the first 10 POD modes. Colors as in (b). d: Fourier transform of the time coefficients shown in (c). Line colors are as in (b and c). Colored bullets mark the calculated maxima

The higher modes are not only characterized by smaller structures, but also by faster dynamics as is shown by evolution of their corresponding coefficients in time in Fig. 10(b). The time coefficients of the most dominant mode (dark blue) are always positive as the largest structure does not change sign over the time interval of the analysis, which is expected since it is the most dominant and most stable mode. The time coefficients of higher modes, however, oscillate with increasing frequencies. The exact frequencies are shown in the temporal Fourier spectrum in Fig. 10(d). There, the maxima are marked with colored bullets and a monotonic shift of the maxima to the right with increasing mode number, as well as a decrease in spectral power is clearly visible.

The POD here was performed over a time $\approx 50\,t_f$ which corresponds to the eddy turnover time for eddies of size H. We also have calculated the POD for much longer times ($\approx 500\,t_f$ ), when the time coefficients are no longer oscillating but more chaotic, which suggests that they are not related to any eddy turnover time anymore.

Since we now have calculated the temporal and spatial spectra for each POD mode we can consider the relation between time and length scales by directly comparing frequencies and wave numbers with the largest spectral energy. This is shown in Fig. 11, where we plot the frequency with the largest Fourier power $\omega _\textrm{max}$ of a given mode against the wave number with the largest power $k_\textrm{max}$. In fact, for lower modes, where $\omega _\textrm{max}$ was small, we determined the exact frequency by fitting a cosine function to the time coefficients directly, in order to avoid spectral leakage. For larger $\omega _\textrm{max}$, we fitted a parabolic function to the power spectra close to their maxima in order to increase the spectral resolution. The maxima in the spatial spectra (Fig. 10b), however, are broad, and we therefore have identified the maximum $k_\textrm{max}$ by fitting a convenient function of the form $a(x-x_0)^b\exp (-cx)$ to the data close to the maximum, from which we could analytically determine its maximum (red point in inset Fig. 11).

Fig. 11

Dispersion relation between the dominant frequency $\omega _\textrm{max}$ and the dominant wave number $k_\textrm{max}$ for the different POD modes. The solid line represents a parabolic fit to the data of the form $0.01x^2$. $k_\textrm{max}$ was estimated from the maximum of a smooth function that was fit to the data in Fig. 10(b). The green dot marks the wavelength of the turbulent superstructures. Since its characteristic frequency is longer than half the duration over which the POD was conducted, this value is rather meaningless here and was not used for the parabolic fit. Inset: Spatial Fourier spectrum of the 3rd mode (blue bullets) to which a function of the form $a(x-x_0)^b\exp (-cx)$ was fitted (black solid line) in order to estimate the dominant wave number $k_{max}$ (red bullet)

We see that the increase in $\omega _\textrm{max}$ is not linear but rather follows a power law with larger exponents. We have fitted a parabolic function to the data resulting in a coefficient of 0.01.

Overall, we see that the TSS can be well separated from the turbulent background by proper orthogonal decomposition and occur as the first eigenmode with a wave number $k \approx 1$ as previously reported by others for such large-scale structures. The turbulent background is represented by higher-order modes which also show a significant faster dynamic.

4 Conclusion and outlook

We have presented spatially and temporally resolved velocity measurements of all three components of the entire flow field in Rayleigh–Bénard convection. By studying the flow in a rectangular cell with an aspect ratio between its lateral dimension and height of $\Gamma =L/H=16$, we have investigated the shape and dynamics of the large-scale turbulent superstructures. The working fluid was water at $T_m=20.0^o$C, which was seeded with 50 $\mu$m large fluorescent polyethylene microspheres. We used pulsed UV-LED for illumination of the particles and observed their motion from different angles with 6 sCMOS cameras. The position, the velocity and the acceleration of the observed particles was calculated using the Shake-The-Box algorithm and the complete three-dimensional Eulerian velocity and acceleration fields were calculated via FlowFit.

Using these techniques, we could clearly see the line pattern formed by rising plumes close to the bottom plate. Upon temporal averaging, the large-scale turbulent superstructures (TSS) were revealed and found to have a typical wave number of $k\approx 2$, which is in accordance to what has been as previously observed in numerical simulations (Pandey et al. 2018; Stevens et al. 2018). We have further separated the slowly varying large-scale pattern from the faster small-scale pattern by using proper orthogonal decomposition of the vertical velocity field. There, the mode corresponding to the largest eigenvalue contains the turbulent superstructure. The first eigenvalue is about 1.5 times larger than the second eigenvalue and consecutive eigenvalues quickly decrease nearly exponentially for the first 40 eigenvalues.

With the setup presented here, it is possible to generate TSS and observe their evolution with ‘Shake-The-Box’ particle tracking in Rayleigh–Bénard cells of large aspect ratios $\Gamma$. Hence in the future, we plan to acquire and analyze more data in order to answer questions such as, whether the TSS can also be detected in Lagrangian properties, and how efficient particles located in one TSS are transported to neighboring rolls. We also want to investigate how their morphology and dynamics change with the control parameters, most importantly Ra and $\Gamma$. In fact, we have already successfully conducted measurements with the same setup in a $\Gamma =8$ cell as well as for Rayleigh numbers in the range $1\times 10^5\lesssim {\text{Ra}}\lesssim 13\times 10^6$. We will present according results in future publications.