Design and performance of an ultra-compact, low-speed, low turbulence level, wind tunnel for aerodynamic and animal flight experiments

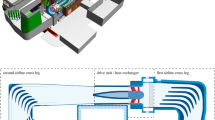
Abstract

We present a novel closed-circuit ultra-compact wind tunnel with an 8:1 contraction ratio and high flow quality. Its overall footprint area is less than half that of a conventional tunnel with the same test section size and same contraction ratio, enabling significantly smaller material and construction costs. The tunnel’s key features which enable the small footprint include a two-dimensional main diffuser, a minimum-length contraction, and expanding turning vanes with a 1.167:1 ratio in corner two and an aggressive 1.875:1 ratio in corner four. Separation in the latter is prevented using a screen and honeycomb integrated into each vane passage—the first time this has been used in a wind tunnel. The tunnel exhibits excellent flow quality with less than $\pm 1$% mean flow variation in the test section core and a freestream turbulence level of 0.03% at 12 m/s over a 4 Hz–20kHz bandwidth.

Graphical abstract

1 Introduction

Low-speed wind tunnels with low levels of freestream turbulence are desirable testing facilities in both academic and industrial laboratories for pursuing a wide variety of experimental goals. The majority of tests in such facilities are for engineering and physical science applications including testing of vehicle and wing configurations as well as fundamental fluid mechanics. For these applications, models are tested over extended periods of time and used for detailed experiments that might include measurements of surface pressure and/or flow field measurements using Pitot, hot-wire, or Particle Image Velocimetry (PIV). In a “low-speed” facility, defined (somewhat arbitrarily) as one where the Mach number is less than $\sim \!0.2$ so that the flow can be considered incompressible, testing velocities span the range of $\sim \!5$–$50\,\mathrm{m/s}$.

A more unusual application that has seen increased interest in the past few years is that of animal flight testing; for such biological flight experiments, birds or bats are trained to fly in the tunnel, while a variety of tests including, for example, kinematic (e.g., wing motion) and velocity field (e.g., wake measurements), are conducted. For such applications, testing velocities tend to be lower than in aerodynamic testing (most animals fly at velocities below 15–$20\,\mathrm{m/s}$), but apart from this constraint, the facility requirements for animal flight share many of the same goals as for engineering testing, including good flow uniformity, low turbulence levels, optical access to the test section and good control of temperature over a wide range of flow speeds and over a long testing duration.

The design of low-speed, low-turbulence wind tunnels has evolved over the past century, but has always involved tradeoffs between flow quality (uniformity and turbulence levels) against power consumption, construction costs, and size. Extensive reviews are given by Bradshaw and Pankhurst (1964); Cattafesta et al. (2010). Larger contraction ratios are desirable to achieve low turbulence levels, but a large contraction ratio requires extensive expansion of the flow from the test section, through the fan and back to the settling chamber, screens and contraction. Achieving such expansion without boundary layer separation in the diffusers usually requires shallow expansion angles, and this leads to long flow paths and consequently a large facility footprint. A common approach to reduce the facility size has been the use of a wide-angle final diffuser, in which separation is prevented by the use of some number of screens or perforated plates, at the cost of somewhat greater power consumption and possibly a greater turbulence level compared to a conventional diffuser. More recently, innovations by Lindgren et al. which allow reduction of the overall tunnel size are vertically expanding 2D diffusers (Lindgren et al. 1998), and expanding (diffusing) corner vanes (Lindgren and Johannson 2004). This approach also reduces design complexity and construction costs due to the increased use of rectangular flow elements.

Expanding the flow in the turning vanes at each corner comes with the risk of flow separation due to the strong adverse pressure gradient. This risk can be eliminated using the screened expanding vane concept of Drela et al. (2020) in which separation in a cascade with the very large expansion ratio of 2:1 is suppressed by means of a screen placed perpendicular to the flow at the exit of each vane passage. This concept was successfully demonstrated in both scale experiments and numerical simulations (Drela et al. 2020) as well as in an apparatus to inject a gust into a low-speed water flume (Corkery et al. 2018). The concept has not yet been used in the primary flow loop of a large test facility.

In this manuscript we describe a new wind tunnel facility at Brown University that is designed for both animal flight and engineering aeromechanics applications. As such it needs to exhibit good flow quality over a wide speed range and have a testing section that is suitable for a diverse series of experiments. These include measurements of aerodynamic forces on fixed models, flow field measurements using hot-wire anemometers and laser-based diagnostics such as PIV, and measurements of the kinematics and dynamics of birds and bats in free flight.

The wind tunnel design presented here incorporates, for the first time, all of the following recent design innovations: vertically expanding second and main diffusers, a weakly expanding vane in corner 2 before the fan, and a strongly expanding screened vane in corner 4 before the flow-conditioning screens and contraction. Another innovation is that Corner 4 integrates the honeycomb into its vane assembly, thus eliminating the length a separate honeycomb would add to the screen section. Lastly the design also features a minimum-length contraction leading into the test section. All these features are aimed at giving the smallest possible tunnel footprint for the required test section size and contraction ratio. The paper will give an overview of the design philosophy and design techniques used for the tunnel components and present the measurements of the flow quality in the test section.

2 Design considerations

2.1 Overall layout and design

As is often the case with wind tunnel design, two main factors that drove the present design were the tension between (i) the available space to locate the facility and (ii) the desired contraction ratio and test section dimensions. The current tunnel is housed entirely in an existing building, which limited the overall tunnel length to 15.8 meters. The maximum test section size is then constrained by the desired contraction ratio and also by the length required by the diffusers to expand to the necessary settling chamber dimensions without risk of flow separation.

For the present tunnel, flowpath design iterations traded between the flow quality requirements and the space constraints, guided by quasi-1D integral boundary layer calculations to gauge the flow separation margins (see discussion below). 3D RANS calculations of the entire final flowpath were performed as a design verification.

The final tunnel layout is shown in Fig. 1. Corners 1 and 3 are conventional (non-expanding), Corner 2 expands slightly, and Corner 4 expands very aggressively which is enabled by the screened vanes. The main diffuser is two-dimensional and expands only vertically. A minimum-length contraction is also used. These design features give an ultra-compact tunnel which has only about 40% of the footprint area, and hence also lower construction costs, than an equivalent conventional-design tunnel with the same test section size. The specific design considerations for each component of the tunnel are discussed next.

Fig. 1

Wind tunnel layout, viewed from above. The flow direction is clockwise. The overall tunnel footprint is 15.8 by 6.3 m. The main diffuser at top expands only vertically, which is not visible in this view. The strongly expanding Corner 4 is in the lower right

2.2 Fan section

A fiberglass/epoxy transition section is used to change from a square to round cross section for the axial fan. The same section shape, in reverse, is used to convert back to a square section downstream of the fan. The annular flow area between the fan case and the motor nacelle is nearly the same as the square area immediately upstream and downstream of the fan.

The airflow is driven using a commercially available nine-bladed axial fan (Twin City) powered by a 125 HP AC motor (TECO) and a variable frequency drive (ABB ACH550). The fan blade angles can be manually adjusted to suit the desired operating characteristics. Since this facility is intended to operate extensively at low speeds, the blade angles were set at an intermediate angle which reduces the maximum achievable speed in the tunnel and decreases the mechanical efficiency of the fan. However, by increasing the fan RPM at a given freestream velocity, it provides a more stable flow at low speeds, suitable for animal flight experiments.

2.3 Diffusers

For the flowpath portion immediately after the test section, a length reduction shrinks the tunnel footprint, while width reduction does not. Therefore, a conventional three-dimensional design was used here for this first diffuser, with an area ratio of 1.67:1 and a wall half-angle of $3^\circ$. This relatively “safe” combination compensates for the thicker than usual boundary layers created by the relatively long test section.

In contrast to the first diffuser, both a small length and a small width are at a premium in the return leg of the tunnel. Hence, for the main diffuser after the fan a two-dimensional design was chosen, with a constant width and a vertical expansion. The area ratio is 1.875:1 and the wall expansion half-angle is $7.7^\circ$, which is a very aggressive combination. Hence, a wire-mesh screen is added about one-third down the expansion to suppress flow separation (Mehta 1979; Farell and Xia 1990). The heat exchanger located at the diffuser end also acts as a second diffuser screen to suppress flow separation there.

2.4 Corner vanes

The 0.322m chord turning vanes in Corner 1 have a pitch/chord ratio of 0.55, and are designed using the viscous/inviscid MISES cascade code (Giles and Drela 1987) to operate without significant separation over the entire tunnel operating speed range, as shown in Fig. 2. The lowest tunnel speed causes the most difficulty with laminar separation, so to address this the vane is shaped to have a weak adverse pressure gradient over most of the suction surface. This intentionally destabilizes the boundary layer and thus encourages it to undergo transition at chord Reynolds numbers down to 38 000 (3000/inch) without laminar separation bubble bursting. The unavoidable penalty is some loss of laminar flow at the highest speeds. The pressure surface is designed for mostly laminar flow, and to meet manufacturing constraints. The vanes are extruded aluminum, which requires a minimum thickness of roughly 0.15in at the trailing edge. At maximum tunnel speed the predicted loss coefficient is 0.025, which is 20% more than what’s possible (0.021) for an aerodynamically ideal vane with a sharp trailing edge. This extra loss is, however, small in real terms, consuming only 0.07% of the tunnel drive power.

Fig. 2

Optimized Corner 1 vane with computed displacement surfaces and $C_p$ distributions from MISES, for minimum (top) and maximum (bottom) tunnel speeds. The flow parameters, including the loss coefficient, ($\omega$) computed by MISES are shown in the legend

The Corner 2 vanes are physically the same as in Corner 1, but are staggered and angled differently to expand the flow area by the ratio 1.17:1 while giving the necessary $90^\circ$ turning. The pitch/chord ratio is also reduced to 0.50, which compensates for the area expansion and prevents flow separation, at least according to the 2D MISES simulations. A debris screen positioned at the exit of Corner 2, immediately upstream of the fan section, helpfully acts to suppress any possible 3D separation from the Corner 2 vane/wall intersections from going into the fan.

Corner 3 vanes are a conventional non-expanding type, with a constant thickness. Based on MISES simulations, their designed shape is a simple $94^\circ$ circular arc with a straight trailing edge extension, and a pitch/chord of 0.40. The constant thickness and simple shape were chosen to be compatible with inexpensive rolled sheet steel construction. Their additional loss compared to the alternative fully optimized shape vanes is less than 0.005% of total drive power, which is an acceptably small penalty given their considerable construction cost savings.

Corner 4 features the screened expanding turning vane (Drela et al. 2020), which is the most innovative aspect of the tunnel design, and is the one which enables most of the tunnel footprint reduction. The specific vane design used here has a very aggressive expansion ratio of 1.875:1, and a pitch/chord ratio of 0.33. A constant thickness and a simple arc plus trailing edge extension shape are also used here for low cost. This vane concept has wire screening installed over each vane-passage exit to suppress flow separation which would otherwise occur inside each passage, as diagrammed in Fig. 3. Honeycomb is also installed in the vane passage immediately upstream of the screen, and suppresses any streamwise vorticity which might be produced in the vane passages. There is one honeycomb piece in each vane passage, and this has the screen attached to it prior to installation (Fig. 4). The combined honeycomb+screen sections are installed in the vanes much like filter elements, and if necessary they can be replaced just as easily. This modular system avoids the high cost and structural-support difficulties of the typical large single-piece honeycomb used in conventional tunnels. In effect, Corner 4 combines the functions of a turning vane, a wide-angle diffuser, and a honeycomb, all with a near-zero added streamwise flow length.

Fig. 3

Screened expanding turning vane cascade of corner 4, with flow area ratio of 1.875:1. MISES $C_p$ distributions show screen pressure drop. The displacement-body surfaces along the vane show the boundary layer thinning effect of the screen within the flow passage

Fig. 4

Section of screened vane, viewed from downstream. The screen covers the honeycomb section and is positioned in between two turning vanes (painted blue)

2.5 Contraction

The design goal for the 8:1 contraction is to obtain the shortest possible distance between the last screen and the start of the test section without any laminar flow separation. A traditional high-order polynomial definition was found to have inadequate design freedom for this task, so roughly 50 x, r (streamwise-radial) coordinate pairs, interpolated by a cubic spline, define the wall shape. Initial axisymmetric design was performed by iterating geometric construction and inverse calculations with specified wall $C_p(s)$, using the viscous/inviscid MTFLOW code which is an axisymmetric version of MISES.

The contraction starts at the last screen but very slowly at first, so that the initial wall curvatures are small and the resulting adverse pressure gradients are kept below the laminar separation threshold. The slow initial contraction then makes the large end of the contraction function as a settling chamber, and it also minimizes the potential-flow distortion over the screen face, which in turn minimizes the total-pressure distortions leaving the screen. As the centerline favorable gradient gradually overcomes the wall adverse gradient, the contraction rate is progressively increased up to the maximum contraction rate of $\mathrm{d}r/\mathrm{d}x = -1.25$ at the inflection point. This is limited mainly by the suction peak and resulting adverse pressure gradient which appears on the convex wall just ahead of the test section entry. The final contraction length/width ratio is only 0.67:1, significantly shorter than the 1:1 ratio of conventional tunnels.

The initial axisymmetric channel design was converted to the necessary square cross-section channel, and fillets were also added, such that the flow area distribution was preserved. The resulting 3D wall shapes and the fillet widths were then fine-tuned using the QUAPDAN panel code (Youngren et al. 1983), together with quasi-1D integral boundary layer calculations to check for separation. Figure 5 shows the surface speed contours from QUADPAN on one quadrant of the final contraction design.

The fillets serve to weaken the superposition of the 2D wall pressure gradients at the corners, which avoids laminar separation and secondary flow development which would otherwise occur there. To maximize their benefit the fillets are “flared” such that they are widest near the contraction inflection, and taper upstream to a point at the last screen and also taper partially downstream into the test section. The flaring reduces the maximum surface speed on each fillet to only 1.09 times the test-section velocity, compared to 1.14 which would occur on a constant-width, or straight, fillet. The maximum surface speed ratio on the midlines is 1.05, shown in Fig. 6. The adverse pressure gradients past these modest overspeeds are very easily handled by the very thin turbulent boundary layers at those locations.

Fig. 5

Surface speed contours, $Q = V/V_{screen}$, where $V_{screen}$ is the velocity leaving the last screen, shown on the lower quadrant of the contraction, computed with QUADPAN. The section from x = $-$3.0 to +0.61 (m) is shown, where $x = 0$ represents the start of the test section. The two magenta lines are slices for line plots in Fig. 6

Fig. 6

Surface speed versus x along slice lines shown in Fig. 5. Test section begins at $x=0$

2.6 Turbulence screens

Five stainless steel, seamless turbulence-reducing screens are installed just upstream of the contraction. Following the recommendations of Groth and Johansson (1988), the screens have varying mesh size, as indicated in Table 1. The resistance factor, K, of each screen is based on Groth and Johansson (1988)’s correlation data and was used as the first guess for the pressure drop associated with the screens (see Sect. 2.10).

Table 1 Turbulence-reducing screens specifications

2.7 Test section

The test section (Fig. 7) is designed to be reconfigurable to handle many different types of tests and instrumentation. It is comprised of three interchangeable modules, each measuring 1.2 x 1.2 ms in cross section and 1.4 ms in length. All four sides have removable panels so that a variety of wall, floor and ceiling systems can be easily installed, including clear panels for optical access or structural panels, from which to mount models from the side, top or bottom of the working section. Mounting rails for cameras, lasers, etc., run along the top of each module. Gull-wing doors on the two side walls facilitate easy access to the test section for model installation and adjustment. A removable frame in between each of the test section modules can be used to mount additional screens, or instrumentation. The test section has corner fillets that are matched with those of the contraction and decrease in size as one moves downstream to account for boundary layer growth in the working section.

Fig. 7

Photograph of test section, looking from the downstream end. The entire test section is enclosed in “the White House” which can be used as a Biosafety-II room during animal flight testing. One of the adjustable pressure-equalization slots is visible at the far left side of the photo

One of the test section modules is fitted with an Aerolab Model Positioning System (MPS) and sting assembly which provides a computer-controlled Pitch & Yaw system for aerodynamic model testing.

2.8 Heat exchanger and instrumentation

The heat exchanger, located upstream of Corner 3, serves to control the air temperature in the test section. The cooling liquid is a water–glycol mixture connected to a dedicated chiller located outside the laboratory building.

Several sensors are used to monitor and control the tunnel operation. Temperature thermistors are located in the test section, the “settling chamber” at the end of the contraction, and immediately upstream and downstream of the heat exchanger. The temperature of the coolant is also monitored at the entrance and the exit of the heat exchanger. A high-accuracy pressure transducer (Mensor CPT6100) measures the differential pressure between static rings located at the entrance and exit of the contraction and is used to measure the test section speed at speeds greater than 10 m/s. A Pitot tube, mounted in the test section and monitored by a 1-Torr Baratron 170 is used to measure velocities below 10 m/s. Sensors for ambient humidity and absolute pressure are located in the large portion of the contraction. All aspects of the wind tunnel operation—speed, temperature, etc., are controlled using a custom-written MATLAB App, which has a graphical user interface, logs the tunnel conditions, and can also be called by custom MATLAB scripts.

2.9 Considerations for engineering and animal flight experiments

As mentioned in the introduction, the wind tunnel will be used for two key research objectives—(i) animal flight research and (ii) engineering research and model testing. The desired qualities for animal flight experiments are similar to those for engineering and physics experiments—low turbulence levels and good freestream uniformity. Good performances (velocity stability, uniformity and turbulence levels) are desirable at low speeds, relevant to animal flight (2–15 m/s) as well as at higher speeds (10–50 m/s) typical for engineering experiments. Several features of the facility design make these two distinct applications feasible and convenient:

• The test section modules are separated by removable frames, allowing wire-mesh screens to be placed immediately upstream of module 2 and downstream of module 3 for animal flight testing. Although this raises the turbulence level in the test section by a moderate amount, it creates a flight area approximately 2.5 ms long in which birds or bats can fly, but from which they cannot “escape” into the rest of the wind tunnel volume (i.e., into the turning vanes and the fan). The screens are easily removed after animal testing so that the turbulence level is again at its minimal level.

• The test section is enclosed in “the White House”—a biosafety level II enclosure that is held at negative pressure, drawing air in through an air filter in the ceiling and exhausting the air through two HEPA-filters at the ground level. This configuration ensures that the testing space is isolated from the rest of the laboratory space so that (i) any animal that accidentally escapes the test section will not be lost to the rest of the lab, and (ii) that any infectious agent that might be introduced by the animals during testing is contained within the testing volume and is filtered from the air before it can pose a risk to un-vaccinated personnel in the larger laboratory space outside. The White House also provides optical isolation for laser light being used in the test section for PIV.

• The cooling system is sized to maintain approximately ambient temperature conditions, even at high test section speeds. This control is critical for engineering testing at high speeds. However, the cooling system can also be used to achieve a range of temperatures at low speeds which are more appropriate for animal flight experiments. By running the cooling system at its highest capacity while still operating the tunnel at low speeds, the ambient temperature of the test section can be lowered to as low as 10$^\circ$C. Conversely, if one runs the tunnel empty for a few minutes at the highest speed without any cooling, the air temperature in the test section rises (quickly), after which low-speed animal flight experiments can be performed at the elevated temperatures before the tunnel cools down.

2.10 Performance predictions and measurements

Initial tunnel flowpath design was performed by a interacting boundary layer theory (IBLT) analysis, with the tunnel idealized as a variable-area axisymmetric channel with an inviscid core flow and an axisymmetric boundary layer (BL) developing on the inside wall. With tunnel mass flow fixed, the local core velocity depends only on the local total temperature and pressure, and on the local geometric channel flow area minus the viscous displacement area. The latter is in turn governed by integral BL equations Drela and Giles (1987) which depend on the core flow velocity, and include BL thinning terms due to screens and the fan as described in (Drela 1996). The inviscid and BL equations are thus strongly coupled, and can be integrated into separated regions, if any.

In addition to predicting energy losses in the wall BLs, the model allows for three types of tunnel design features associated with the screen terms: Type-i features are turning vanes, which impose a core total pressure loss but do not affect the tunnel wall BL. Type-ii features are screens, heat exchangers and honeycombs, which impose a core total pressure loss and also thin the incoming BL. The only type-iii feature is the fan which increases the total pressure and also thins the incoming BL. Each element is parameterized by a loss/BL thinning parameter, K (see Drela (1996) for more details). The strongly coupled core-flow and BL equations are integrated simultaneously, with an overall flowpath solution being obtained in less than one second on a laptop computer. The outputs are the core flow velocity and BL development along the entire channel, and also the additional losses of the screens and turning vanes.

Figure 8 shows the predicted distribution of total pressure and BL parameters around the tunnel circuit, for a test section velocity of 30 m/s. Despite its relatively simple physics modeling, the method gives quite reasonable and useful results with great economy. This makes it a very fast design tool for evaluating the approximate performance of the wind tunnel, its energy efficiency, and in particular for providing an estimate of the health of the BLs on the tunnel walls.

The top panel of Fig. 8 summarizes (schematically) the wind tunnel geometry in both the horizontal and vertical dimensions; $x = 0$ represents the start of the test section. The vertical lines indicate the approximate positions of key features of the tunnel: blue lines represent turning vanes (type-i features); red lines represent screens/honeycomb/heat exchangers (type-ii features); the fan is represented by a green line (type-iii feature). Initial values of the loss factor, K, for each feature were obtained from a variety of sources. Numerical simulations using MISES Giles and Drela (1987) were used to predict the two-dimensional losses in the turning vanes. Screen losses were estimated, as described earlier, using correlations by Groth and Johansson (1988). Other features (honeycomb, heat exchanger, etc.) were estimated based on simple laminar flow analysis, and prior experience. The loss factors are, in general, Reynolds number dependent, and so the loss coefficients were tweaked to match the experimentally measured total pressure distribution (Fig. 8b, green symbols). These measurements will be discussed in more detail in the following section.

Figure 8c shows the predicted core velocity (pink line), and the kinematic shape parameter, $H_k$ (Drela and Giles 1987). In aerodynamic design, $H_k$ is a critical parameter, indicating how close the BL is to separation, which in a wind tunnel can be disastrous for flow stability, noise and turbulence levels. For the current design, we see that the predicted shape factor rises during each of the geometric expansions, but consistently stays below a value of 2.0 which is a typical threshold value for turbulent BL separation. (Drela 2014). The presence of the heat exchanger at the end of the primary diffuser ($x = 25$m) provides a downstream resistance which helps to suppress separation in the aggressive 2D vertical diffuser. The screen positioned halfway down the main diffuser ($x = 20$m) provides additional guarantees with this regard, but incurs minimal pressure loss.

Fig. 8

Overall performance of the wind tunnel at a representative speed of 30 m/s. The top panel shows the tunnel geometry in the horizontal and vertical directions. Panel 2 shows the total pressure distribution around the tunnel circuit. The solid lines represent the IBLT predictions while the symbols are the measured values. The total pressure coefficient, $C_{Pt}$, is normalized by the dynamic pressure in the test section with a reference pressure such that $C_{Pt} = 1$ exiting the fan. Panel 3 shows the flow characteristics—core velocity and boundary layer shape factor, H, predicted by the IBLT computation

3 Measured performance

3.1 Total pressure distribution

Static pressure measurements were made at 14 positions around the tunnel circuit. This was combined with the local dynamic pressure—calculated by estimating the core velocity in that section based on the test section velocity and the tunnel geometry (Fig. 8a)—to give the total pressure around the loop. These are shown in Fig. 8b and compared with the computed values using the IBLT code. Recall that the loss coefficients for the IBLT code were tweaked to optimize agreement and so good agreement is to be expected. The values for the loss coefficients for the $U = 30$m/s case are shown in Table 2.

Table 2 Lumped parameter loss factor, K, for each flow element used in the IBLT model. The values were initially based on published correlations, MISES simulations and simple flow analysis, but were adjusted to match static pressure measurements made at 30 m/s (Fig. 8b). The agreement with measurement was robust to modest changes in K, and relatively insensitive to test section velocity

The purpose of this exercise is to assess the relative losses associated with different component of the tunnel design, and for this goal the calculation and measurement is extremely informative. As one would expect the high speed sections of the tunnel, the test section, and the first two turning corners account for most of the losses, although the fourth corner (with the integrated screen and honeycomb) and the five turbulence screens are also responsible for a large pressure loss. The impact of the debris screen and the diffuser screen have minimal effect on the energy losses. We also note optimal values of K did not change significantly over a wide range of test section velocities, and the agreement with experimental measurements of $C_p$ was generally very good.

3.2 Power factor

The measured aerodynamic power factor of the wind tunnel, shown in Fig. 9, is the power injected by the fan, compared with the total kinetic energy flux through the test section. We calculate this as the fan total pressure rise (Fig. 8b) normalized by the dynamic pressure in the test section. The actual electrical power required will be somewhat higher, due to both the non-ideal electrical efficiency of the fan motor (which is close to unity) and, more significantly, the non-ideal mechanical efficiency of the axial fan (which, for fixed a fan blade angle, is strongly dependent on the fan RPM). However, the electrical power was not easily available and so here we report only on the aerodynamic power factor of the tunnel. We find that the aerodynamic power factor improves to about 39% at 50 m/s. If we assume that a typical axial fan efficiency is 85% when the fan blade angles are appropriately tuned, this will yield a total power factor of 45%—comparable to that reported by the KTH-BTL tunnel (Lindgren and Johansson 2002).

Fig. 9

Measured aerodynamic power factor for the wind tunnel as a function of test section velocity. The power factor is defined as the pressure rise across the fan, normalized by the dynamic pressure in the test section. Since we do not measure the electrical power, this does not include losses due to the fan, electric motor and Variable Frequency Drive (VFD)

3.3 Flow uniformity

The flow uniformity was assessed by measuring the velocity variation using a Pitot tube which was traversed over the central core of the test section (i.e., away from the wall boundary layers, and in the regions where “production measurements” would be conducted). The results are shown for a freestream velocity of 12 m/s in Fig. 10, and were very similar both quantitatively and qualitatively at other speeds. The uniformity of the flow is generally good. There is a general trend of higher measured speeds toward the top-inside corner, but this might be due to a slow and steady rise in the tunnel temperature ($0.2^\circ$ C) over the long duration of the uniformity experiment (6 h) which lowers the density slightly and for a fixed fan rotation speed, would be consistent with the observed rise in speeds. Despite this, the standard deviation of the mean flow is approximately 0.5%, and the maximum variation in mean flow less than $\pm 1\%$. Even with this variation, the values, are not as low as those reported by Lindgren and Johannson (2004), and the source of this variation needs to be further explored.

Fig. 10

Mean flow variation, in percent, measured using a pitot tube over the central portion of the test section at $U=12$m/s

3.4 Turbulence levels

Turbulence levels in the test section were measured using a hot wire probe, sensitive to streamwise velocity fluctuation, positioned at the center line of the tunnel, at free stream velocities ranging from 2 to 24 m/s. For the turbulence level vs speed, 180 s of data were recorded at 40 kHz. A different data acquisition configuration was used for spatial scans of the turbulence level, which were recorded for 60 s at 17.5 kHz. There were no discernible differences between the results obtained using these different sittings. The anemometer voltages were converted to velocities using a fifth-order polynomial calibration. Velocity fluctuation spectra and turbulence levels were computed using a Welch estimate (50% overlap, Hanning window) for two different low-pass cutoff frequencies: 4 Hz and 0.1 Hz.

A representative power spectrum recorded at the center line of the test section at a freestream velocity of 12 m/s is shown in Fig. 11. As expected the dominant contribution to the turbulence comes at low frequencies, but there is a slight “bulge” in the 100–200 Hz range, and a few discrete spikes which can be related to the fan rotation frequency, the blade passage frequencies associated with this speed and electrical interference. We did not filter these spikes out. There is no contribution to the overall turbulence level from frequencies above 4 kHz. Integrating over all frequencies gives a turbulence level of Tu = 0.024% for a 4Hz cutoff, and 0.047% over the wider bandwidth to 0.1 Hz. A sample spatial distribution of velocity fluctuations, measured at 10 m/s using a two-axis traverse, is shown in Fig. 12. There is no indication of any coherent spatial pattern to the freestream turbulence within the test section.

Fig. 11

Sample turbulence spectrum in the center of the test section, $(y,z) = (0,0)$. Freestream velocity, $U = 12 \,\mathrm{m/s}$, Red: 0.03 Hz– 8.5 kHz bandwidth, Blue: 4.0 Hz-$-$8.5 kHz bandwidth

Fig. 12

Spatial distribution of turbulence, $u'/U$ (in percent), measured using a hot wire anemometer over the central portion of the test section at $U = 10$m/s. (4Hz - 8.5 kHz bandwidth). Note that the “hot spot” on the right side of the plot is due to the wake shed from pitot tube that protrudes from the side wall of the test section and measures the freestream velocity

The variation of the overall turbulence level (4–20,000 Hz bandwidth) was measured at the centerline of the test section over a range of freestream velocities and is shown in Fig. 13. The turbulence levels are very low, rising from 0.022% at 4 m/s to 0.045% at 25 m/s. When the lower frequencies are included (0.1 − 20,000 Hz bandwidth), the overall turbulence level was slightly higher, and fluctuated between 0.040 and 0.045%, but was independent of the freestream velocity, suggesting that these low frequency “breathing” modes are not speed-related. One might expect the risk of separation somewhere in the tunnel to diminish with increasing speed, and so the increase in turbulence level with free stream velocity is somewhat surprising. However, similar trends have been observed in other facilities (Hunt et al. 2010; Quinn et al. 2017), and the low levels of turbulence are extremely encouraging. At comparable speeds, the (streamwise) turbulence levels in the current facility are lower than those reported in the ASU Klebanoff-Saric tunnel (Hunt et al. 2010), the UIUC Low-turbulence tunnel (Selig et al. 2011), the Stanford animal flight tunnel (Quinn et al. 2017) and the KTH-BLT tunnel (Lindgren and Johannson 2004) (which also has expanding corners). They are comparable to values reported in the KTH-MTL tunnel (Lindgren and Johansson 2002).

Fig. 13

Streamwise velocity turbulence levels, $u'/U$ (4 Hz - 20 kHz bandwidth), measured at the tunnel centerline, as a function of the free stream velocity, U

4 Conclusions and outlook

Although the design and construction of a new low-turbulence low-speed wind tunnel is not generally a publication-worthy event, several very novel features of this tunnel make it of substantial interest to the experimental fluid mechanics, aerodynamics and animal flight research communities. Some of the design features—the modestly expanding corner two, for example—are not new, but still relatively uncommon. Similarly, the short contraction is not completely new, but its present computational design (as opposed to traditional empirical polynomial design) pushes its length down to the physically feasible limit while maintaining demonstrably low losses. In contrast, the corner four screened vanes with integrated honeycomb demonstrated here are completely novel, and this is the first test facility to incorporate and exploit this innovative design feature.

All of these features result in a remarkably compact design which enables a large test section for a given tunnel footprint, which is especially attractive when valuable lab space is at a premium. Furthermore, mostly rectangular flow segments, rolled steel sheet vane profiles in corners three and four, and the elimination of a large monolithic honeycomb all contribute to material and construction cost reductions. All these features make an appreciable difference to facility and institutional budget planning.

The flow results are, in general, very promising. Although the flow uniformity is not as low as some other test facilities, the variations might be alleviated by some adjustments to the honeycomb thickness in the fourth corner which can even out flow variations. Offsetting these concerns, however are the turbulence levels, which are spectacular, with streamwise velocity fluctuations as low as any reported in the recent literature. In addition, although key performance metrics are provided, further details are still needed to complete the facility description. These include measurements of temperature uniformity, flow angularity, and cross-stream turbulence components. These will be reported on in future publications.

In summary, although the facility is still new and we are still learning about its performance over the full range of operating speeds, all indications are that the innovative aspects of the design have performed as expected, without significant surprises, and that the flow quality is excellent. A new wind tunnel, with the same design features but over twice the size has already been constructed at MIT, and we anticipate that these will be the first of many such designs to enter service in the years to come.