Interpreting single-point and two-point focused laser differential interferometry in a turbulent jet

Abstract

Focused laser differential interferometry (FLDI) and its relative two-point FLDI (2pFLDI) are used to make density fluctuation and velocity measurements, respectively, in a canonical, round turbulent air jet ($U_\mathrm{jet}=300$ m/s, $d=3.2$ mm, $Re_\mathrm{d}=8.6\times 10^4$). Both techniques are seedless, non-intrusive, inexpensive (< $5k), and insensitive to vibrations. The FLDI signal is proportional to the phase difference between two closely spaced laser beams passing through the flow. The phase difference is created by index of refraction gradients in the flow, integrated along the beam paths. Transfer functions for interpreting the FLDI signal are proposed as an accurate method for predicting the response in an arbitrary flow. A procedure for applying these transfer functions to a turbulent jet is developed. The procedure is able to model FLDI’s response to fluctuations in the jet with error on the order of 10–50% across a $\sim \, 100$ kHz band. The transfer functions provide a simple method for estimating the FLDI & 2pFLDI spatial resolution along the optical axis, which is a strong function of disturbance scale, based on three instrument parameters: (1) the laser wavelength, $\lambda _0$, (2) the beam separation, $\Delta x_1$, and (3) the beam radius at the focus, $w_0$. For the 2pFLDI employed in this work ($\lambda _0=633$ nm, $\Delta x_1=145\,\mu$m, $w_0=3\,\mu$m), the resolution ranges from 1cm for a 0.9mm disturbance wavelength to 5cm for a 5.5mm disturbance wavelength. The spatiotemporal resolution depends on the convection velocity of the disturbances, as well as the spatiotemporal amplitude variation in the disturbances themselves. We model the velocity and spatial amplitude distribution with Gaussian functions based on historical jet studies and we measure the amplitude variation with frequency directly via FLDI. This leads to 1cm resolution for the smallest timescales measured (100 kHz) up to 5cm resolution for the largest time scales measured (1kHz). 2pFLDI’s relatively large spatial resolution complicates comparisons of velocity measurements to those made using hot-wires. The methods, modeling, and procedures outlined in this work provide a framework for interpreting future FLDI and multi-point FLDI measurements.

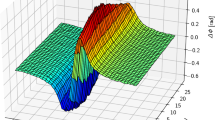
Graphical abstract

A derivation of FLDI transfer functions, Eq. 18

Beginning with the argument of the z-axis integral in Eq. 17, which we will call Z, we have:

$$\begin{aligned}&Z=\int _0^{2\pi }\int _0^\infty I_0(r,\theta )\rho (\mathbf{x} _1,t)rdrd\theta - \nonumber \\&\quad \int _0^{2\pi }\int _0^\infty I_0(r,\theta )\rho (\mathbf{x} _2,t)rdrd\theta \end{aligned}$$

(42)

Plug in the definition of beam intensity profile $I_0$ (Eq. 12), the density field model $\rho (x,y,z,t)$ (Eq. 10) and the definitions of the beam paths $\mathbf{x} _1$ and $\mathbf{x} _2$ (Eq. 15 and Eq. 16):

$$\begin{aligned}&Z=\int _0^{2\pi }\int _0^\infty \frac{2}{\pi w^2 }\exp \left( -\frac{2r^2}{w^2}\right) g(z)\times \nonumber \\&\quad \int _{-\infty }^\infty A(f)\exp \left[ i\left( k_x\left( x+\frac{\Delta x_1}{2}\right) -2\pi ft+\psi \right) \right] dfrdrd\theta -\nonumber \\&\quad \int _0^{2\pi }\int _0^\infty \frac{2}{\pi w^2 }\exp \left( -\frac{2r^2}{w^2}\right) g(z)\times \nonumber \\&\quad \int _{-\infty }^\infty A(f)\exp \left[ i\left( k_x\left( x-\frac{\Delta x_1}{2}\right) -2\pi ft+\psi \right) \right] dfrdrd\theta \end{aligned}$$

(43)

Next, exchange the order of integration and re-arrange some terms:

$$\begin{aligned}&Z=g\int _{-\infty }^\infty A\int _0^\infty \frac{2r}{\pi w^2 }\exp \left( -\frac{2r^2}{w^2}\right) \times \nonumber \\&\quad \int _0^{2\pi }\exp \left[ i\left( k_x\left( x+\frac{\Delta x_1}{2}\right) -2\pi ft+\psi \right) \right] d\theta drdf- \nonumber \\&\quad g\int _{-\infty }^\infty A\int _0^\infty \frac{2r}{\pi w^2 }\exp \left( -\frac{2r^2}{w^2}\right) \times \nonumber \\&\quad \int _0^{2\pi }\exp \left[ i\left( k_x\left( x-\frac{\Delta x_1}{2}\right) -2\pi ft+\psi \right) \right] d\theta drdf \end{aligned}$$

(44)

Re-arrange more terms and convert from Cartesian to polar coordinates using $x=rcos(\theta )$:

$$\begin{aligned}&Z=g\int _{-\infty }^\infty A \left( \exp \left[ i\left( k_x\left( +\frac{\Delta x_1}{2}\right) -2\pi ft+\psi \right) \right] \times \right. \nonumber \\&\quad \int _0^\infty \frac{2r}{\pi w^2}\exp \left( -\frac{2r^2}{w^2}\right) \int _0^{2\pi }\exp (ik_xr\cos \theta )d\theta dr- \nonumber \\&\quad \exp \left[ i\left( k_x\left( -\frac{\Delta x_1}{2}\right) -2\pi ft+\psi \right) \right] \times \nonumber \\&\quad \left. \int _0^\infty \frac{2r}{\pi w^2}\exp \left( -\frac{2r^2}{w^2}\right) \int _0^{2\pi }\exp (ik_xr\cos \theta )d\theta dr \right) df \end{aligned}$$

(45)

Re-arrange terms and evaluate the integral over $\theta$:

$$\begin{aligned}&Z=g\int _{-\infty }^\infty A \exp \left[ i(-2\pi ft+\psi )\right] \times \nonumber \\&\quad \left( \exp \left[ \frac{ik_x\Delta x_1}{2}\right] -\exp \left[ \frac{-ik_x\Delta x_1}{2}\right] \right) \times \nonumber \\&\quad \int _0^\infty \frac{2r}{\pi w^2}\exp \left( -\frac{2r^2}{w^2}\right) 2\pi J_0(k_xr)drdf \end{aligned}$$

(46)

where $J_0$ is the Bessel function of the first kind. Next, we evalute the subtraction of the two exponential terms and evaluated the integral over beam radius, r. For more detail on this integral evaluation, see the next subsection, appendix 1.

$$\begin{aligned}&Z=g\int _{-\infty }^\infty A \exp \left[ i(-2\pi ft+\psi )\right] \times \nonumber \\&\quad 2i\sin \left( \frac{k_x\Delta x_1}{2}\right) \exp \left( -\frac{k_x^2w^2}{8}\right) df. \end{aligned}$$

(47)

Finally, re-arrange to get the argument of the z-axis integral in Eq. 18.

1.1 A.1 Evaluation of integral over beam radius, r

Start with the integral over r in Eq. 46, which we will call $\mathcal {R}$:

$$\begin{aligned} \mathcal {R}=\int _0^\infty \frac{4r}{w^2}\exp \left( -\frac{2r^2}{w^2}\right) J_0(k_xr)dr \end{aligned}$$

(48)

Using the definition of the Bessel function of the first kind, $J_0$:

$$\begin{aligned} \mathcal {R}=\frac{4}{w^2}\int _0^\infty r\exp \left( -\frac{2r^2}{w^2}\right) \left[ \sum _{n=0}^{\infty }\frac{\left( -k_x^2r^2/4\right) ^n}{(n!)^2}\right] dr \end{aligned}$$

(49)

Expand out the sum:

$$\begin{aligned} \mathcal {R}=\frac{4}{w^2}\int _0^\infty r\exp \left( -\frac{2r^2}{w^2}\right) \left[ 1-\frac{k_x^2r^2}{4}+\frac{k_x^4r^4}{64}-...\right] dr \end{aligned}$$

(50)

Re-arrange:

$$\begin{aligned}&\mathcal {R}=\frac{4}{w^2}\left[ \int _0^\infty r\exp \left( -\frac{2r^2}{w^2}\right) dr- \right. \nonumber \\&\quad \frac{k_x^2}{4}\int _0^\infty r^3\exp \left( -\frac{2r^2}{w^2}\right) dr+ \nonumber \\&\quad \left. \frac{k_x^4}{64}\int _0^\infty r^5\exp \left( -\frac{2r^2}{w^2}\right) dr-...\right] \end{aligned}$$

(51)

Evaluate the integrals over r:

$$\begin{aligned} \mathcal {R}=\frac{4}{w^2}\left[ \frac{w^2}{4}-\frac{k_x^2}{4}\left( \frac{w^4}{8}\right) +\frac{k_x^4}{64}\left( \frac{w^6}{8}\right) -...\right] \end{aligned}$$

(52)

Finally, we have:

$$\begin{aligned} \mathcal {R}=1-\frac{k_x^2w^2}{8}+\frac{k_x^4w^4}{128}-... \end{aligned}$$

(53)

Recognizing the Taylor’s series expansion, we have

$$\begin{aligned} \mathcal {R}=\exp \left( -\frac{k_x^2w^2}{8}\right) . \end{aligned}$$

(54)