Simultaneous determination of particle size, velocity, and mass flow in dust-laden supersonic flows

Abstract

The particle mass concentration and -mass flow rate are fundamental parameters for describing two-phase flows and are products of particle number, -size, -velocity, and -density. When investigating particle-induced heating augmentation, a detailed knowledge of these parameters is essential. In most of previous experimental studies considering particle-induced heating augmentation, only average particle mass flow rates are given, without any relation to measured particle sizes and -velocities within the flow or any indication of measurement uncertainty. In this work, particle number, individual particle sizes, and velocities were measured in a supersonic flow by means of shadowgraphy and particle tracking velocimetry (PTV). The goals are to determine measurement uncertainties, a particle velocity-size relation, and the spatial distribution of number, size, velocity, and mass flow rate across the nozzle exit. Experiments were conducted in a facility with a nozzle exit diameter of 30 mm, at Ma_∞ = 2.1 and Re_∞ = 8.2e7 1/m. Particles made of Al₂O₃ and up to 60 µm in size were used for seeding. Particle mass flow rates up to 50 kg/m² s were achieved. It is shown that an additional correction procedure reduced common software uncertainties regarding shadowgraphy particle size determination from 14% to less than 6%. Discrepancies between calculated particle velocities and experimental data were found. In terms of spatial distribution, larger particles and a higher mass flow rate concentrate in the flow center. The determined particle mass flow rate uncertainty was up to 50% for PTV; for shadowgraphy, it was less than 17%.

Graphical abstract

1 Introduction

The particle mass concentration (c_m), or the particle mass flow rate (G_p), as well as the particle volume concentration c_v, are fundamental parameters for describing two-phase flows. These parameters have, e.g., significant impact on the choice of particle-flow coupling in terms of particle motion simulation (Crowe 2006; Ling et al. 2013), but also on experimental heat flux measurements. Previous studies showed that in supersonic and hypersonic flows, the presence of particles can cause significantly higher heat transfer rates compared to particle-free flows (Bakum and Komarova 1971; Fleener and Watson 1973; Kudin et al. 2013; Osipov et al. 2001; Polezhaev et al. 1992; Vasilevskii and Osiptsov 1999). This phenomena is called “particle-induced heating augmentation” or “heating augmentation.”

A linear dependence between c_m and the heating augmentation was demonstrated by (Bakum and Komarova 1971; Osipov et al. 2001; Polezhaev et al. 1992; Vasilevskii and Osiptsov 1999). Additionally, the authors of (Kudin et al. 2013) found an asymptotic behavior of heating augmentation for large c_m. Particle shielding effects in front of the probe are given as reasons for it. As it is concluded in (Bakum and Komarova 1971) and measured in (Kudin et al. 2013; Vasilevskii and Osiptsov 1999), small particles (< 0.23 µm and < 0.15 µm, respectively) do not contribute to particle-induced heating augmentation. It was stated that due to the negligible velocity lag between particle and flow velocity, these particles do not impact on probe surfaces. The authors of (Alkhimov et al. 1982) found that heating augmentation effects with particles < 25 µm are negligible as long as c_m < 0.5–1%.

The Supersonic and Hypersonic Technologies Department of DLR, Cologne, intends to investigate particle-induced heating augmentation effects in more detail. As it can be seen from the literature, an accurate knowledge of the parameters c_m or G_p, as well as individual particle characteristics, are essential for these investigations (Bakum and Komarova 1971; Fleener and Watson 1973; Kudin et al. 2013; Osipov et al. 2001; Polezhaev et al. 1992; Vasilevskii and Osiptsov 1999).

How have the parameters c_m / G_p been determined in the past? As it turns out, most of the experimental campaigns determined an average mass flow concentration for each run by dividing the particle discharge of the facility seeding system by the test time and the flow cross-sectional area (Fleener and Watson 1973; Kudin et al. 2013; Polezhaev et al. 1992; Vasilevskii and Osiptsov 1999). This procedure assumes that no particles remain in the facility, and that G_p is constant over time and over the flow cross section. Nonetheless, the authors of (Fleener and Watson 1973) reported significant variations in G_p occurred during some runs. In (Vasilevskii and Osiptsov 1999), time and spatial resolved particle mass flow rates were determined by measuring a particle scattering signal in front of the probe. In that study, it was concluded that the particle mass flow rate is constant across the flow section. However, for smaller facilities, as it was shown in (Kudin et al. 2013), G_p is higher close to the symmetry axis. A kind of a particle catcher probe was often used during pretests as an additional calibration measurement method for leveling the average c_m for each run, but no indication of the capturing efficiency was given in any study.

As it is shown in Eq. (3–1), G_p correlates strongly with particle size. However, all of the studies provide only the nominal mean particle sizes, which were measured before insertion into the wind tunnel facilities. The study described in (Kudin et al. 2013) is the only one which additionally analyzed captured particle sizes. The study measured a particle size decrease, which is stated to be a consequence of particle break-up.

Particle velocity was determined experimentally only in some of the studies (Dunbar et al. 1975; Kudin et al. 2013); most of the studies defined it with analytical formulations. The question arises of how accurate these analytics are, since comparisons made in (Dunbar et al. 1975; Molleson and Stasenko 2017) have indicated discrepancies.

In summary, there is no data set related to heating augmentation, where all particle characteristics, namely number, size, and velocity, were measured simultaneously, although all of them affects G_p.

The first overall purpose of this work is to infer G_p from all the above-mentioned particle characteristics for a specific test condition by means of shadowgraphy. The determination of the radial G_p distribution at the nozzle exit, named “distribution profile” or “profile” in the following, is the second overall purpose of this work. Therefore, a combination of shadowgraphy and PTV were used: accurate particle characteristics, measured with shadowgraphy, were taken to convert PTV velocity data across the entire nozzle exit flow into size and G_p profiles.

Measurement uncertainties for the respective particle characteristics were derived, the discrepancy in experimentally and numerically determined particle velocity at the nozzle exit was identified, and a spatial resolved G_p profile across the flow cross area was reconstructed. The latter one was compared to a scattering signal as it was done by (Vasilevskii and Osiptsov 1999).

The detailed determination of G_p, presented here, is essential for future particle-induced heating augmentation effect analysis, which will not be content of this work.

In the following, first the experimental tools are described in detail. After the mathematical definition of G_p, measurement uncertainties for particle velocity, size, and number as well as the size of the measurement volume are evaluated. Then, a relation between particle size and particle velocity at the nozzle exit, named “velocity-size relation” in the following, is analyzed, which is used to convert velocity data from PTV into size data. In the end, the reconstructed G_p profiles are discussed.

2 Experimental tools

2.1 Test facility GBK

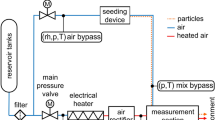
The multiple phase flow facility (GBK) is a small test facility integrated into DLR’s supersonic wind tunnel infrastructure in Cologne, Germany (Gawehn et al. 2010). It is a fully automated blow down facility, using dried high-pressurized air from reservoir tanks. A sketch of the principal GBK facility is illustrated in Fig. 1. Variable measurement sections can be feeded with two air flows: a heatable pure air flow, named “main” flow, and an unheated flow, named “bypass” flow in the following. An electrical heater with a maximum electrical power of 191 kW can heat the main air flow up to 800 K. Afterward, an air rectifier reduces the main flow turbulence. The bypass flow is equipped with an in-house developed seeding device for particle dispersion.

Fig. 1

Sketch of the GBK facility

GBK’s maximum design air pressure is 5.4 MPa, and the maximum total air flow rate (main + bypass) is approximately 1.5 kg/s. Several measuring points exist to fully determine the GBK flow. Total pressure (p₀) and total temperature (T₀) were determined in the measurement section, which is described in Sect. 2.1.1.

2.1.1 GBK measurement section

The GBK measurement section is part of the GBK facility and can be designed and set up variably. In this work, it contained a cross-sectional adapter, a mixing chamber, an ideal-contoured nozzle, a test chamber, and a diffusor pipe. A sketch of the implemented measurement section is given in Fig. 2.

Fig. 2

Sectional side view of the GBK measurement section

The stagnation chamber had a diameter of 70.3 mm. The measurement section maximum temperature was 573 K, limited by its sealings. Just before the stagnation chamber, the heatable main flow was mixed with the cold two-phase bypass flow. For additional particle mass flow calibration purposes, a circular conical particle injection collection probe was located at the position where the cold particle bypass flow was injected into the heated pure air flow. Geometric details of the particle injection and the particle injection collection probe tip can be found in Fig. 3. Its position was optimized in terms of minimizing gravity-based particle losses in pipes or pipe bending losses (Baron and Willeke 2001). A closed container was mounted at the outlet of the injection collection probe. Here, it was assumed that due to the particle inertia, particles were caught with it. After the measurements were finished, it was noticed that particle seeding also occurred in the shut down phase, which was not recorded and differed from run to run. This again had influence on the collected particle mass in the injection collection probe and the particle discharge within the seeding device. So, unfortunately, these data were excluded from further processing.

Fig. 3

Geometric details of the particle injection

A 1.1 mm diameter type K thermocouple close to the nozzle was used for T₀ measurements. To avoid particle deposit in a Pitot tube, p₀ was reconstructed by means of the wall pressure close to the T₀ sensor, total air mass flow, and T₀ measurements. The reconstructed p₀ value agreed well to the total pressure measurements upstream of the cross-sectional adapter.

The 111.9-mm-long, ideal-contoured Ma = 2.1 nozzle with 30 mm nozzle exit diameter ended in a sealed test chamber, with dimensions of 388 × 390 × 744 mm. The nozzle contour can be found in Fig. 18 of Sect. 3.5. The test chamber pressure (p_a) was measured with multiple pressure sensors in the test chamber. This chamber had a convex shape in the y–z-plane, allowing optical access in 10° inclination steps to ensure window related reduced aberration (see Fig. 5). Additional windows provided optical access from all sides.

This facility was designed to investigate particle–probe interactions and heating augmentation effects in the future. So, also a fast flow probe insertion system was implemented. The probe mount was attached to two vertical rail carriages, allowing a high freedom degree of illumination. The full insertion of the probe into the flow took around 75 ms. The probe position was determined with a Laser-based distance sensor. The probe itself was axisymmetric (cylindrical) and had a hemispherical-shaped tip with 12 mm in diameter. The tip was made of stainless steel, namely 1.4539. The probe length, from tip to its mount, was 60 mm. It was located approximately 5 mm downstream of the nozzle exit.

The distance between diffusor pipe and nozzle exit plane was 147 mm. All relevant test parameters can also be found in the tables of Sect. 2.4.

2.1.2 Operation range

Considering the GBK and the presented measurement section setup in Sect. 2.1.1, the operation range of GBK was defined, see Fig. 4. The nozzle flow remained fully established down to p_a ~ 0.05 MPa.

Fig. 4

Operation range of GBK facility

2.2 Non-intrusive measurement techniques

The overall purpose of this work is to infer G_p from relevant particle characteristics, namely number, size, and velocity. For simultaneous particle size and velocity measurements, a shadowgraphy system was used. Since it is capable of both, particle characterization and shock visualization, it is an appropriate technique also for future heating augmentation tests. Particle size determination in the micron size range requires large optical magnifications for shadowgraphy. This typically constraints the measurement to a small field-of-view (FOV). Since another purpose of this work is to determine the radial G_p distribution in the complete nozzle exit flow, an additional particle image velocimetry (PIV) setup was used.

2.2.1 Shadowgraphy

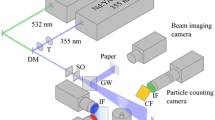
The high magnification shadowgraphy system consisted of two Lavision Imager sCMOS cameras (named C1 and C2, respectively), mounted on a long distance microscope K2 Distamax of Infinity Photo-Optical Company. The sCMOS cameras had a pixel size of 6.5 µm and a maximum number of pixels of 2560 × 2160 px². To avoid double exposure by the 100 Hz laser system, only a centered sensor area of 2560 × 1060 px² for C1 and C2 was used, leading to an image rate of 50 Hz for each camera. The cameras were recording one after the other, resulting in a shadowgraphy recording rate of 100 Hz. The long distance microscope was further equipped with a ‘Zoom Module’, an optical beam splitter and a CF-1b lens, leading to a magnification of 211.2 px/mm for C1 and C2. In this setup, the implemented CF-1b lens offered the highest available resolution in the image centers, but the coma effect in the image edges reduced the evaluable image size.

The aperture of the long distance microscope was set to be half open. C1 and C2 were equipped with an 564 nm long pass filter. For velocity uncertainty determination of the shadowgraph system, also PIV recordings were acquired with C1 and C2, for which the long pass filters were replaced with 532 nm band pass filters.

For shadowgraphy background illumination, a shadow diffusor of Dantec Dynamics GmbH was implemented, providing short pulse background illuminations with a maximum illumination area of 112 mm in diameter. The diffusor was fed with light from the PIV laser (see Sect. 2.2.2), so, both non-intrusive measurement techniques recorded simultaneously (C1 and C3) with the same double-image time separation of 400 ns. The shadow diffusor was placed 695 mm away from the nozzle axis. The detected particle shadow displacement was between 25 and 40 px.

2.2.2 PIV / PTV

The PIV camera (named C3 in the following) was a PCO 1600 with a Nikkon Nikkor tele lens, providing a magnification of 40.6 px/mm. The camera pixel size was 7.4 µm, and the lens aperture was set to f/11. A Scheimpflug adapter was used to correct the focus plane angle. Distancing rings provided the required short focal length. The active sensor pixel area was reduced to 168 × 1600 px² to avoid double exposures by the 100 Hz laser system. The resulting image rate of C3 was 50 Hz. The detected PIV particle displacement was between 5 and 10 px.

The PIV and shadowgraph illumination source was a SpitLight DPSS 250 PIV Laser system of InnoLas Laser GmbH, with a pulse rate of 100 Hz and a maximum pulse of energy of 120 mJ. With a set of half-wave plates and beam splitters, the energy for shadow and PIV illumination was controlled.

The PIV light beam was redirected by several mirrors and was generated by one cylindrical lens with focal length of 500 mm. This lens was placed ahead of the particle section so that the PIV illumination came vertically from top to bottom (see Fig. 5). The PIV light sheet was around 5 mm wide and parallel to achieve homogenous illumination intensity across the nozzle. The laser sheet thickness was determined by aid of a scale to be approx. 1 mm.

Fig. 5

Front view on PIV and shadowgraphy measurement system in the GBK facility

The time separation between the PIV double images was set to 400 ns. It was controlled by an additional photodiode. The timing of laser and cameras as well as the camera data acquisition was controlled by a PTU-X timing unit of Lavision GmbH and the software DaVis 10.1.

In Fig. 6, the resulting FOVs are sketched: C3 was used for PIV covering the entire nozzle exit flow, C1 and C2 were used for high-resolution image acquisition on the symmetry axis. In the ongoing analysis, only data in front of the probe bow shock were evaluated. So, the applied shadowgraphy FOV in front of the shock wave on the symmetry axis was 1 × 3 mm². The respective PTV FOV was 1 × 27.5 mm². The FOV was smaller than the nozzle exit diameter, because an essential thermocouple blocked C3’s view on the nozzle exit. The origin of the coordinate center was put on the probe tip.

Fig. 6

FOV of the cameras (left), raw shadowgraphy image and data field (right)

In (Vasilevskii and Osiptsov 1999), the G_p profile in the nozzle exit flow was determined by aid of a scattered light profile. For comparison, this profile was calculated in this study by summing intensities of all C3 images.

2.3 Particles

Two different kinds of particle materials were used for seeding. For velocity uncertainty estimation purposes, the finest available material was chosen which was made of MgO. For G_p determination, particles made of Al₂O₃ were chosen because the available material contained mostly particles > 15 µm, so that most of the particles could be detected by shadowgraphy.

Prior to the tests, these materials were analyzed externally by Microtrac GmbH with a ‘PartAn SI’ and a ‘S3500’, applying dynamic image analysis and laser diffraction, respectively. For Al₂O₃, the results of the dynamic image analysis are referenced in this work; laser diffraction results are used describing MgO, since the dynamic image analysis quantitatively detects only particles > 2 µm which will unconsider most of the MgO particles. For both analyses, both materials were diluted into water. The wet dilution possibly dispers particles < 0.5 µm while the dry dilution does not. So, only minor differences in particle size distribution between dry and wet dilution for larger particles like the Al₂O₃ material were assumed. Nonetheless, MgO particles may tend to smaller sizes in the wet diluted analysis. For the ongoing work, that size shift is of minor importance since the MgO particles were not used for particle mass flow rate determination.

Number and volume distributions of both particle materials can be found in Figs. 7, 8, 9 and 10. Specific diameters describing particle size distributions are listed in Table 1

Fig. 7

Cumulative and differential particle number distribution of Al₂O₃ particles, measured with a ‘PartAn SI’ by Microtrac Gmbh

Fig. 8

Cumulative and differential particle volume distribution of Al₂O₃ particles measured with a ‘PartAn SI’ by Microtrac Gmbh

Fig. 9

Cumulative and differential particle number distribution of MgO particles, measured with a ‘S3500’ by Microtrac Gmbh

Fig. 10

Cumulative and differential particle volume distribution of MgO particles, measured with a ‘S3500’ by Microtrac Gmbh

Table 1 Specific diameters of particle materials

In Figs. 7, 8, 9 and 10, the green lines represent the cumulative particle distributions up to a specific particle size, which is given on the x-axis. As an example, approx. 60% of the entire Al₂O₃ particle volume is spread on particles < 30 µm (see Fig. 8). The red bins are the particle distribution histogram and represent the gradient of the green line. To get a probability density function, the particle number distribution histogram of Figs. 7 and 9 can be used.

For Al₂O₃ particle density ρ_p, a value of 3950 kg/m³ was chosen (Molleson and Stasenko 2017; Vasilevskii et al. 2002). Since they were not used for particle mass flow rate calculations, no particle density was required for MgO particles.

Before filling them into the seeding device, both particle materials were stored in airtight containers at room temperature. To avoid any change in particle size distributions due to preparation, they were filled into the seeding device directly, meaning that there was no additional treatment like heating or sieving.

2.4 Test conditions

The GBK allows running tests continuously, so that steady state flow conditions were established. The facility was heated up until desired T₀ and p₀ values were achieved. Then, the seeding device was activated for 3 s. Just 0.5 s after seeding started, the probe was injected into the flow for 2 s. The measurement time started when the probe reached its measurement position on the symmetry axis. It was observed that the test chamber pressure p_a increased when the probe was located within the flow. Because of reference purposes of, e.g., future particle–probe experiments, where all boundary conditions should kept similar, and because the pressure increase may have an impact on the nozzle exit flow conditions, data were evaluated only when the probe was positioned into the flow.

In total, ten runs (named N10–N19) at the given flow conditions with varying G_p were conducted. The nominal flow and test conditions are given in Tables 2 and 3, respectively. In Table 2, the mix bypass temperature is given for non-seeded flow, since the presence of particles in the bypass line affected the temperature signal. Here, it was assumed that the gas temperature did not change. In Table 3, the run to run variation of nominal flow conditions is given in brackets.

Table 2 GBK air flow conditions

Table 3 Nominal test conditions

3 Analysis

3.1 Particle mass flow rate

The particle mass flow rate G_p can be determined with the following formulation, assuming spherical particles and the same particle density for all particles:

$$G_{p } \left( {t,X,Y} \right) = \frac{4}{3}\pi \frac{{\rho_{p} }}{LxLy}\mathop \sum \limits_{i = 1}^{{n_{p} \left( {t,X,Y} \right)}} \frac{{\left( {\frac{{d_{p i} }}{2}} \right)^{3} V_{p i} }}{{z_{i} }}, \left[ {G_{p} } \right] = \frac{kg}{{m^{2} s}}$$

(3-1)

An illustrative explanation of the parameters is given in Fig. 11. The volume-of-interest (VOI) has the dimensions Ly, Lx, and a thickness z. It is located at the position X and Y. All particles which are located in VOI at time t are summarized with n_p (t,X,Y). The parameter ρ_p is the particle density which is assumed to be constant for all particles. The individual particle size and velocity are expressed with d_p and V_p, respectively. For shadowgraphy, the VOI thickness z is the shadowgraph depth-of-focus (DOF) which again is dependent on d_P. For PTV, z is the light sheet thickness, because it is smaller than the DOF of the PTV system.

Fig. 11

Sketch of volume-of-interest (VOI) for G_p determination

Data are shown on the x–y measurement plane, while, e.g., G_p is referenced on the y–z reference plane. It is obvious that the definition of VOI has influence on the measured G_p. Larger VOI result in smooth G_p values, while small VOI sizes compared to particle size lead to mostly zero values with sporadic extrema for G_p, especially in low particle concentration flows.

The particle mass concentration c_m is determined by:

$$c_{m} = \frac{{G_{p} }}{{\rho_{g} V_{g} }}$$

(3-2)

The parameter V_g is the gas velocity and ρ_g is the gas density.

The particle volume concentration c_v is the particle mass concentration multiplied by the flow/particle density ratio:

$$c_{v} = c_{m} \frac{{\rho_{g} }}{{\rho_{p} }} = \frac{{G_{p} }}{{\rho_{p} V_{g} }}$$

(3-3)

So, for uncertainty estimation of G_p all the respective parameters in Eq. (3–1) and their respective uncertainties have to be determined. Therefore, an extensive python program was written. Generally, all the uncertainty calculations were performed following the linear-error-propagation theory, implemented in a python package by (Lebigot 2021).

3.2 Particle velocity

In terms of PTV and shadowgraphy evaluation with DaVis 10.1 by LaVision GmbH, particle velocity is determined with a particle tracking algorithm. While for PIV uncertainty estimation the correlation statistics method (Wieneke 2015) is used in DaVis, there is no uncertainty calculation tool for PTV measurements. So, a work-around was developed for estimating velocity uncertainties for PTV and shadowgraphy measurements.

PIV analyses of C1/2 and C3 with tracer particles made of MgO were performed. For preprocessing, a spatial-time filter was used for background noise reduction. The PIV interrogation window was 8 × 8 px, and the particle image size was around 5 px for C1/C2; for C3, the PIV interrogation window was 3 × 3 px and the particle images 1–2 px. The idea was that each PIV interrogation window should contain only one particle image to infer the velocity uncertainty for each particle. With the help of the correlation statistics method, a PIV uncertainty vector field was generated. The DaVis PTV algorithm was used for particle localization. The PIV uncertainty value at the PTV found particle position was referred to be the PTV uncertainty. This procedure is a very conservative PTV error estimation approach. As a result, the mean C1/C2/shadow velocity uncertainty is 0.2 px (2.4 m/s). The same procedure was repeated for C3 and resulted in a mean velocity uncertainty of 0.1 px (4.9 m/s) for small tracer particle images.

However, the seeding of large particles led to much larger particle images up to 8 px and the scattered intensity was often in the cameras saturating range which caused additional imaging artifacts, especially on the first frame of C3. Again, PTV uncertainty for C3 was interpolated from PIV evaluations with an interrogation window size of 8 × 8 px for larger Al₂O₃ particles. This interrogation window size was a trade-off between the large particle image sizes (large interrogation window size) and the idea that each interrogation window should contain only one particle image (small interrogation window size due to high particle concentrations). The relative PTV velocity uncertainty depending on particle velocity is depicted in Fig. 12. Here, the mean velocity uncertainty over several velocity classes is illustrated. The data were taken across the entire nozzle exit of the reference test. The bars indicate the velocity uncertainty interquartile range (IQR). Figure 12 clearly shows that the lower the particle velocity (= the larger the particles, as shown in Sect. 3.5), the higher the relative velocity uncertainty. The velocity uncertainty for large particles is much larger compared to usual tracer particles.

Fig. 12

Adapted PTV uncertainty for different particle velocities across the entire nozzle exit, C3

3.3 Particle size

For determination of individual particle sizes, the shadowgraphy system was used and its data were evaluated with DaVis ParticleMaster-Shadow v.10.1.0. This software has been widely used for particle and bubble characterization, e.g., in (Berg et al. 2006) and follows the processing steps of image normalization, denoising, binarization, and filtering (Lavision Gmbh 2019).

For measuring small particles down to 10 µm in size, a high optical magnification was required, resulting in limited DOF of the shadowgraphy system. As a consequence, many particle shadows were slightly out-of-focus which again influenced the detected particle size. This behavior is illustrated in Fig. 13. It shows a part of LaVision’s shadow calibration target containing dark dots in the size range of 10–200 µm in diameter. In the top left image, the calibration target was in focus (z = 0 mm), in the top right image (z = −1 mm) and in the bottom right image (z = −2 mm), it was moved out of focus. The blue circles indicate the particle size, detected with the ParticleMaster-Shadow software. Unfocussed particles were sized and shaped incorrectly at high magnifications. Figure 13 also shows that the minimum detectable dot size is between 10 and 20 µm, since the 10 µm dots were not detected (six dots in each image center).

Fig. 13

Calibration dots analyzed with LaVision Particlemaster—Shadowgraphy: a z = 0.0 mm, b z = −1.0 mm, c z = −2.0 mm (Lavision Gmbh 2019)

In the following, the particle/calibration target dot diameter, provided by DaVis ParticleMaster-Shadow without application of an additional size correction, is named d_{p detected} or d_{p uncorrected}. If the size correction is applied, it is named d_{p corrected} or just d_p. Since the calibration target dot diameter is known a priori, this diameter is referenced to be d_{p True}. Because d_{p corrected} depends on the size correction quality, it does not need to be the same as d_{p True}.

The detected and true dot size are quantified in Fig. 10. The parameter “gradient slope” (GS) is defined within the ParticleMaster-Shadow software. It is a measure of particle contour sharpness which again is a measure of particle defocus position. The parameter GS is defined as the normalized intensity decrease per pixel at the detected particle/dot rim (Lavision Gmbh 2019). While 100 and 200 µm unfocussed dots with low GS were detected to be larger, smaller particles were mostly undersized.

The defocus level, expressed by GS, has a strong nonlinear influence on the detected dot size, see Fig. 14. The detected dot size d_{p detected} is a function of the GS and the true dot size d_{p True} itself. Furthermore, if the image quality is not homogeneous, it is also a function of the dot location within the image. Because the FOV of this investigation was small, it was assumed that spatial effects could be neglected. Dots became larger when they were moving out of focus. This effect was detectable for the largest investigated dots with 200 µm diameter. However, for smaller dots, the detected dot size decreased with decreasing GS. Moreover, there was an offset between true dots size and detected dot size. To reduce size determination uncertainty, a correction was applied which also influences the measurement volume (see Sect. 3.4.1).

Fig. 14

Dependence between GS, detected diameter and true diameter of the calibration target dots

For the z-position dependent size correction, the experimental data of dots with size between 20 and 60 µm were considered since the correlation between detected dot size, true dot size, and GS was similar for these size classes. This correlation is described with the following generic exponential term:

$$\frac{{d_{{p\;{\text{detected}}}} }}{{d_{{p\;{\text{True}}}} }} = a + b* e^{{ - c*\frac{{{\text{GS}}}}{{{\text{GS}}_{\max } }}}},\;\; a,b,c = f(d_{{p\; {\text{True}}}} )$$

(3-4)

In Eq. (3–4), d_{p detected}/ d_{p True} is the ratio between detected and true dot/particle size and GS_max is the maximum gradient slope, depending on d_{p True} which is described with the formula:

$$GS_{\max } = f + \frac{g - f}{{1 + \left( {\frac{{d_{{p\;{\text{True}}}} }}{h}} \right)^{i} }}$$

(3-5)

The GS_max value for the investigated dot sizes is shown in Fig. 14 as a red, dotted line. The generic parameters f,g,h, and i in Eq. (3–5) for GS_max determination can be found with a curve fit on the existing data.

Since the generic parameters a, b, and c in Eq. (3–4) depend on d_{p True,} first these parameters were fitted to the 20, 40, and 60 µm data and then, a linear regression was performed for a, b, and c. So, it is assumed that:

$$a = a_{0} + a_{f} * d_{p\;True} ,\;\;b = b_{0} + b_{f} * d_{p\;True} ,\;\;c = c_{0} + c_{f} * d_{p\;True} .$$

(3-6)

The dot size correction is illustrated in Fig. 15. The dots in the plot belong to a true dot size class, depending on their color. In the background, a “rainbow” is plotted, from which each stripe represents a corrected particle size class. Each dot was reordered into these corrected size stripes. Since there was a spread for every true dot size class, the corrected size stripes are 5 µm wide. Unfortunately, the calibration target did not contain dots between 10 and 20 µm in size. So, the size correction was extrapolated to a 15 µm size stripe, because several particles in the flow runs fell in that stripe. For lower GS, the polynomial fit gets inaccurate so that a minimum GS was defined. This limit is indicated with a red, dashed line in Fig. 15. This minimum GS affected the measurement volume, see Sect. 3.4.1.

Fig. 15

“Rainbow” plot for size correction: The dot color indicates its true size of 20, 40, and 60 µm, the y-axis represents the uncorrected detected dot size, and each rainbow stripe represents the corrected dot size

3.3.1 Shadowgraphy uncertainty

The application of the size correction leads to lower size errors. This is quantified by its mean and standard deviation:

$$\overline{\varepsilon }_{{d_{{p\; {\text{corr}}}} }} = \left| {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \frac{{d_{{p\; {\text{corrected}}, i}} - d_{{p\; {\text{True}}}} }}{{d_{{p\; {\text{True}}}} }}}}{n}} \right|$$

(3-7)

$$\sigma_{{d_{{p\; {\text{corr}}}} }} = \left| {\mathop \sum \limits_{i = 1}^{n} \left( {\frac{{d_{{p\; {\text{corrected}}, i}} - d_{{p\; {\text{True}}}} }}{{d_{{p\; {\text{True}}}} }} - \overline{\varepsilon }_{{d_{{p\; {\text{corr}}}} }} } \right)^{2} } \right|$$

(3-8)

The mean and standard deviation size errors for the uncorrected data were calculated in a similar manner. Table 4 lists mean and standard deviation size errors before (uncorrected) and after size correction (corrected), regarding the calibration target dots. The size correction leads to significant lower mean and standard deviation size errors, except for the smallest dots with 20 µm in diameter, where the standard deviation error is slightly increased. This is caused by the correction size stripe width of 5 µm which is 25% of the absolute size of 20 µm.

Table 4 Size uncertainty before and after calibration, C1

As a conclusion, the size errors were significantly minimized in the range of 20–60 µm. Regarding the selected measurement setup and the selected software settings, a standard deviation size error of 2.5 µm, corresponding to the half of the chosen corrected size stripes, was used for the ongoing analysis.

As visualized in Fig. 13, there is a minimum detectable particle size for shadowgraphy, which was between 10 and 20 µm in this study. It was assumed that only particles > 20 µm can all be identified and that most, but not all, of the smaller particles were “invisible” for shadowgraphy. Regarding the cumulative particle volume distribution of the Al₂O₃ particles (see Fig. 8, green line), the “invisible” cumulative volume up to d_p = 10 µm was < 1%; for d_p = 20 µm it was ~ 17%. Multiplying this volume distribution with particle velocity, the cumulative particle mass flow rate contribution up to a specific particle size can be determined (see Eq. (3–1)). Considering the velocity-size relation, introduced in Sect. 3.5, for particle velocity, the invisible G_p of shadowgraphy was up to 18%.

In contrast, it was assumed that PTV detects all particles of every size, since also the MgO tracer particles with a mean particle size of 0.2 µm were registered in the PIV experiments (see Sect. 3.2).

3.4 Volume-of-Interest (VOI)

The VOI (see Fig. 11) depends on the spatial resolution of the measurement plane (hence Lx and Ly) and the measurement depth in z-axis. For the shadowgraphy system, the measurement depth was its DOF. For PTV, the light sheet thickness (z_PTV) limited the measurement volume, because it was smaller than the PTV DOF. The determination of both parameters is described in the following.

3.4.1 Shadowgraphy DOF

The maximum shadowgraphy DOF is the range in z-direction where particles can still be detected and accurately sized. The size correction, described in Sect. 3.3, introduced a minimum GS of dots/particles which limited the DOF. For DOF determination, the LaVision calibration target was shifted on z-axis from -3 to 3 mm. The relation between GS, DOF, and true dot size is illustrated in Fig. 16. The brightened dots fell below the minimum GS, so they could not be accurately sized; all other dots were valid for size correction. The DOF is the range between the valid dots with the lowest and highest z position. The smaller the true dot size, the smaller is the DOF.

Fig. 16

Relation between GS and z position for different calibration dot sizes, C1. Brightened dots fall below the minimum GS limit (see Fig. 15)

The relation between DOF and true dot size is plotted in Fig. 17, showing that a linear dependence between DOF and true dot size is an appropriate approximation, as it was also reported in (Berg, Deppe, Michaelis, Voges and Wissel 2006, Kashdan et al. 2003). Dots > 60 µm provided a larger DOF then the investigated z-range, so they were excluded from the linear fit. The resulting factor between DOF and dot size is:

$$\frac{{{\text{DOF}}}}{{d_{{p\; {\text{True}}}} }} = 65. 36\frac{m}{m}$$

(3-9)

Fig. 17

DOF depending on calibration dot size, C1

It was assumed that its uncertainty is negligible.

3.4.2 PTV light sheet thickness

The PTV light sheet thickness was determined by aid of a scale to be approximately 1 mm. This was controlled by comparing PTV and shadowgraphy data. To do so, the amount of detected particles number concentration per measurement volume (PpV) of PTV and shadowgraphy were set equal, by varying the PTV light sheet thickness. As described in Sect. 3.3.1, shadowgraphy could only detect all particles > 20 µm. To take this lack of particles < 20 µm into account, these particles were also excluded from PTV data by considering only particles with velocities in the range of 350 – 400 m/s (see velocity-size relation, Fig. 19). The mean PTV light sheet thickness of nine runs, excluding N14 because of its outlier character, was determined to be z_PTV = 1.66 mm ± 0.28 mm.

3.5 Particle velocity-size relation

The shadowgraphy system is capable of identifying particle size and velocity in a small FOV. The correlation between particle size and particle velocity is named “velocity-size relation.” Since the PTV system measures only particle velocities, the idea was to apply the velocity-size relation from shadowgraphy to the velocity data from PTV to achieve radial particle size and G_p distributions profiles across the nozzle exit. Therefore, a monotonic function describing the velocity-size relation had to be found. On the one hand, this can be done with a simple curve fit, optimized on the experimental data. On the other hand, particle motion simulations on the symmetry axis through the entire convergent-divergent nozzle possibly allowing additional conclusions about the particle density, so this procedure was selected in the following.

Depending on particle size, density, and drag model, a single particle trajectory was calculated. From this single trajectory, the particle velocity was extracted at the nozzle exit. Multiple extracted velocities, depending on particle size, were merged to a single velocity-size relation curve. This calculated monotonic curve was then used for converting PTV velocity data into particle size and G_p data. It was assumed that the velocity-size relation was independent of radial flow location.

For particle motion computation, the local flow states, e.g., velocity or density, were required. These parameters were calculated with the help of the isentropic gas equations, local Mach numbers, as well as experimental determined p₀ and T₀. For computation, the local Mach number on the symmetry axis of the convergent-divergent nozzle was taken. Three Mach number modeling approaches were compared: isentropic Mach number calculation based on the nozzle expansion ratio (1D), methods of characteristics (MOC), and an axisymmetric flow calculation with the DLR Tau code (Gerhold et al. 1999) without viscous effects. The resulting Mach number profiles, as well as the radius contour of the nozzle, can be found in Fig. 18. The Mach number profile based on TAU shows agreement with the supersonic solution of MOC. Because the TAU simulation is more sophisticated and contained also data in the subsonic regime, its Mach profile was used for particle motion calculation. The simulations started at the beginning of the convergent part of the nozzle. It was assumed that the initial particle velocity was in equilibrium with the surrounding flow for every particle size, so v_p,x0 = 24.39 m/s.

Fig. 18

Nozzle contour and Mach Number contours along the nozzle axis, calculated with different methods

For modeling the particle motion, only the dominating drag forces were considered. This procedure is one-way-coupled: only the surrounding fluid affects the particle motion, but not vice-versa. So, the particle motion can be expressed as follows:

$$m_{p} *\frac{{dV_{p} }}{dt} = \frac{\pi }{8}* d_{p}^{2} * \rho_{g} *C_{D} *\left( {V_{g} - V_{p} } \right)* \left| {V_{g} - V_{p} } \right|$$

(3-10)

Here, m_p is the mass of the particle and C_D is the particle drag coefficient. In Eq. (3–10), particles are assumed to be spherical. For solving this ordinary differential equation, a fourth-order Runge–Kutta scheme was used.

Three drag correlations were taken into account, namely Henderson (Henderson 1976), Parmar (Parmar et al. 2010), and Loth (Loth et al. 2021) drag correlation. Their formulations are given in the Appendix.

In Fig. 19, relations between particle velocity and particle size are illustrated. The orange markers belong to experimental data gained with shadowgraphy. Here, only particles with a detected centricity > 90% were included. Centricity is the ratio between short and long axis of the detected shadow. It was assumed that a high centricity value results in a high sphericity of the particle. With this constraint, particles from all ten runs were summed up to be 2567.

Fig. 19

Particle velocity vs. particle size 2.5 mm downstream of the nozzle exit, assuming different drag models and particle densities

The size error bars correspond to the “rainbow” stripe width of the additional shadowgraphy size correction; the velocity error bars represent the IQR of particle velocity for the respective size classes. The light blue marker indicates PTV velocity measurements with tracer particles made of MgO, whose size is set to be 0.2 µm.

The dotted lines belong to calculations with different drag models and a Al₂O₃ pure substance density of ρ_p = 3950 kg/m³. The “kink” in the Henderson relation is caused by the change of subsonic to transonic formulation for particles > 55 µm at the nozzle exit. As visible in Fig. 19, results from all three drag models did not agree very well with experimental data if the Al₂O₃ pure substance density was used. As a consequence, the calculated relations were fitted to the experimental data by adapting ρ_p, following a procedure similar to the one described in (Williams et al. 2015) for PIV particle characterization. The relations with adapted ρ_p are indicated with the dash-dotted lines; the red, green, and blue lines belong to the Henderson, Parmar, and Loth drag model, respectively.

The optimized particle density was less than a half of 3950 kg/m³ for all three drag correlations (see legend of Fig. 19). The adaption of ρ_p led to good agreement of experiment and theory. It must be noted that the optimized particle density depends on the selected particles and the chosen drag model.

Although a reduction in the particle density is possible due to, e.g., agglomerations, there is not enough evidence for this drastic reduction by half. Further investigations, including the check of the one-way-coupling validity as well as particle density measurements, are necessary.

For the ongoing calculation of G_p, following Eq. (3–1), particle density was assumed to be ρ_p = 3950 kg/m³. Nonetheless, for the conversion of PTV velocity data into size data, the velocity-size relation considering the adapted particle density with the Loth drag model (blue dash-dotted line in Fig. 19) was used for conversion of PTV velocity into size data, since it considers the largest experimental data base and provided the largest Knuden number Kn regime; velocity calculations for particles < 4 µm using the Parmar model suffered, because the maximum defined Kn = 0.01 for this model was exceeded within the nozzle (see Eq. (9–13)).

3.6 Particle distribution profiles at the nozzle exit

For the following analyses, the VOI height Ly was set to 1 mm, its length Lx was 1 mm, corresponding to the selected FOV length. In the following, time-averaged particle distributions are shown for the run named N11 (Figs. 20, 21, 22 and 23). The G_p distributions of the other runs are shown  in Figs. 24, 25, 26, 27, 28, 29, 30, 31 and 32 in the  Appendix.

In Fig. 20, the spatial distribution of particle number across the nozzle exit is plotted. Regarding the PTV data, in the inner jet core between y = −2 to 2 mm, the PpV is slightly lower than in the rest of the jet core between of y = −7 to 7 mm. At y = 12 mm, a PpV maximum is achieved. The shadowgraphy PpV is lower than for PTV. It must be noted that in Fig. 20 all particles with velocities > 310 m/s are considered, while for the determination of the PTV VOI (see Sect. 3.4.2), only particles in a specific velocity range were regarded.

Fig. 20

Spatial distribution of particle number concentration across the nozzle section

In Fig. 21, the solid blue line indicates the mean velocity and the blue filling the standard error of the arithmetic mean, called uncertainty in the following, of the PTV measurement. The respective values of the shadow evaluation are shown in dark blue. The dashed cyan line indicates the theoretical isentropic gas velocity at the nozzle exit. The orange line represents the velocity distribution measured with MgO tracer particles. The red dashed line indicates a sensor, limiting C3’s visibility on the nozzle exit flow.

Fig. 21

Spatial particle velocity distribution across the nozzle exit, run N11

Spatial resolved particle size distributions are plotted in Fig. 22. Applying the velocity-size relation, shown in Fig. 19, on every single particle of the PTV data led to significant particle size uncertainties, compared to shadowgraphy. In the flow center, meaning in the range of y = −7 to 7 mm, the mean PTV detected particle size is around 20 µm, whereas in the outer flow areas it is 2 µm. The time-averaged particle size of PTV in the flow center is lower than those for shadowgraphy, which is 28 µm on the flow symmetry axis.

Fig. 22

Particle size distribution, run N11

The high G_p plateau exists in the range of y = −7 to 7 mm. In the outer regions (|y|> 10 mm), it is very low for all runs, similar to the particle size distributions.

The uncertainties of PTV based G_p estimation are relatively large and up to 50%. The upper bound of shadowgraphy standard deviation of the arithmetic mean was multiplied by 1/(1–0.18) to consider the invisible G_p amount of shadowgraphy (see Sect. 3.3.1). As a result, the maximum shadowgraphy uncertainty is less than 17%. The shadowgraph G_p mean is lower than those of PTV. However, both techniques coincide within their uncertainty range.

For comparison, the G_p profile was also calculated using the velocity-size relation based on the Henderson drag model (see Sect. 3.5; yellow drawings in Fig. 23). It turns out that G_p profile differences are small, compared to the PTV-based G_p profile uncertainties.

Fig. 23

Particle mass flow rate distribution, run N11

A scattered light profile across the nozzle, as it was proposed in (Vasilevskii and Osiptsov 1999), is used for another estimation of G_p distribution. When normalizing this profile on to shadowgraph data, the resulting G_p profile is mostly within the PTV uncertainty range. Regarding the scattered intensity profile at the bottom edge of the nozzle throat (y = −7 mm), G_p is slightly higher than its counterpart at the top edge for this profile. This G_p profile asymmetry tendency can also be seen in the PTV data of run N12 (Fig. 25), N15 (Fig. 28), and N16 (Fig. 29). Generally, the scattered intensity profile underlines the accumulation of G_p in the range of y =−7 to 7 mm. However, PTV data of runs N12 (Fig. 25), N16 (Fig. 29), N17 (Fig. 30), and N18 (Fig. 31) indicate a slight G_p drop in the jet core between y = −2 to 2 mm.

4 Discussion

For particle characterization in a supersonic air flow field, a combination of shadowgraphy and PTV system was used to gain accurate particle data across the nozzle exit flow. High-resolution shadowgraphy is very useful for particle characterization and shock visualization, but its drawback is a minimum detectable particle size and a limited FOV. The amount of the “invisible” particles could only be estimated with a pre-defined particle size distribution. A change of this size distribution within the flow, as reported in (Kudin et al. 2013), was neglected in this work. Assuming that the velocity of the invisible particles can be estimated with adapted numerical formulations, the invisible amount of G_p could be assessed. If particle break-up would occur, the invisible amount of G_p would be higher. Therefore, further particle investigations have to check the particle size distribution within the test facility. However, sufficient particle velocity-size relations could only be achieved if particles were larger than several microns.

In contrast to PTV, one big advantage of shadowgraphy is its clear definition of measurement volume through a DOF analysis.

As shown in this work, size determination of defocused particles led to errors. This problem can be reduced by filtering particles by its gradient slope, a defocus parameter introduced with LaVision’s DaVis ParticleMaster-Shadowgraphy software package, which again comes with a reduction in measurement volume. In this work, an additional shadowgraphy size correction was introduced, which could significantly reduce the size uncertainty from 12% to < 6% for 20 µm particles, and less for larger particles up to 60 µm, coming with only a slight decrease in measurement volume. However, a calibration target containing dots between 10 and 20 µm in size would help to determine additional size correction polynomials also for particles < 20 µm.

Considering only the drag forces described with the Henderson, Parmar, or Loth correlation and assuming particle density to be pure substance density of Al₂O₃, particle motion simulations underestimated particle exit velocities for all investigated particle sizes. This behavior was also reported in (Dunbar et al. 1975), without any comment about the analytical model. In a recent study (Molleson and Stasenko 2017), simulated drag coefficients were lower than its experimentally determined counterparts for particles in two-phase flows. The authors assumed that the differences are likely due to differences in particle surface state and the shape of the particles.

There is a work-around to reduce the differences between experimental and simulated data by reducing the effective particle density as done in (Williams et al. 2015). In that work, nominal particle size and density were fitted to particle response data downstream of an oblique shock. Nonetheless, this procedure opens the question about the “real” density of particles in the flow when analyzing G_p. Referring to Fig. 19, it seems that the detected spherical particles with ~ 60 µm in size tend to lower densities which could be caused by agglomeration.

Further studies have to proof and to adapt the “real” particle density and the corresponding drag model to correctly describe particle motions in the freestream and the shock layer of heat flux probes. The PTV-based data can be helpful to calculate the integral particle mass flow, which again can be compared with particle discharge measurements of the seeding system, as proposed in (Fleener and Watson 1973; Kudin et al. 2013; Polezhaev et al. 1992; Vasilevskii and Osiptsov 1999). The validity of the assumption for one-way-coupled particle motion modeling has to be checked, which can be influenced by high particle number-, and mass concentrations (Ling et al. 2013). Also, the importance of non-steady forces affecting particle motions, as well as the importance of the particle shape have to be discussed.

PTV seems to be a reasonable solution for single particle indication across the entire nozzle flow, but finding an appropriate laser intensity level for its light sheet is challenging: it must be strong enough to illuminate small particles but also weak enough to avoid a camera pixel saturation, when large particles scatter. These overexposure effects have led to high velocity measurement errors, which again are one of the main reasons for large G_p uncertainties. Furthermore, an accurate determination of the PTV light sheet thickness is mandatory, because it has significant impact on the PTV measurement volume. The assumptions of optimum particle counting efficiency and identical PpV for PTV and shadowgraphy, which are required for PTV light sheet thickness determination, have to be discussed. Generally, a thicker light sheet is less sensitive to measurement volume determination, but probably only usable for low particle concentrations. In future studies, an additional procedure has to be set up to proof PTV light sheet thickness.

Regarding the particle distribution profiles in the nozzle, PTV detects more particles than shadowgraphy because of shadowgraphy’s minimum detectable particle size (see Fig. 20). The slight decrease in the PTV PpV between y = −2 to 2 mm might be a consequence of larger particle images which possibly cover smaller particle images on the C3 sensor. The time-averaged velocity profile data indicate that slower particles are concentrated close to the symmetry axis, in the range of y = −7 to 7 mm, while only faster particles close to the gas velocity are located in the outer flow area (see Fig. 21). The larger velocity uncertainty in the center is caused by larger particle images and a larger spread in detected particle velocities.

Applying the adapted velocity-size relation with Loth drag correlation on the PTV velocity profile, particles with high inertia accumulate in the center, while small particles with low inertia are dominating in the outer flow areas (see Fig. 22). The PTV-based size uncertainty is caused by large velocity uncertainties. In the flow center, the time-averaged PTV particle size is lower, but the PTV particle velocity is higher, than their counterpart for shadowgraphy. This again is due to the large amount of “invisible” small and fast particles for shadowgraphy which pushes down the mean PTV particle size and increases the mean PTV particle velocity.

The resulting G_p distribution reaches almost constant levels close to the symmetry axis from y = -−7 to 7 mm (see Fig.  23). Some runs indicate that G_p is slightly lower in the inner jet core, ranging from y = −2 to 2 mm. In the outer areas, it is significantly lower. Assuming that particles are homogeneously distributed within the stagnation chamber, it seems that high inertia particles are accumulating along the convergent nozzle wall until they reach the nozzle throat, which is 22.13 mm in diameter. Up to here, they have been accelerated toward the flow center due to the convergent nozzle profile shape. Behind this point, they are not spread in radial direction again, leading to an accumulation of particles on y-positions slightly closer to the symmetry axis than the nozzle throat radius. This observed phenomenon could be also a consequence of aerodynamic focussing in supersonic nozzles, which was already numerically demonstrated for smaller particle sizes (Shershnev and Kudryavtsev 2019).

The PTV-based G_p distribution uncertainty is up to 50%, and the respective shadowgraphy uncertainty is less than 17%. While the shadowgraphy uncertainty is mainly driven by “invisible” particles, PTV-based G_p uncertainty is mostly caused by the multiplication of uncertain values for the PTV light sheet thickness, particle velocities, and -sizes (see Eq. (3–1)) and the usage of linear error propagation theory. It has to be discussed if this theory is applicable for G_p calculation. A higher amount of detected particles, which can be achieved by, e.g., a higher seeding rate or a longer measurement time, would smooth the time-averaged G_p profile, but it would not reduce the PTV-based G_p uncertainty. This can be seen at the smooth G_p profile of test N17 (see Fig. 30, high G_p and constant measurement time mean high particle number), compared to the G_p profile of run N14 (see Fig. 27, low G_p and constant measurement time mean low particle number). However, a run to run comparison indicates maximum G_p values close to the symmetry axis from y = −7 to 7 mm for almost all runs.

The discrepancy between G_p derived by shadowgraphy and PTV can have several reasons. On the one hand, the application of the velocity-size relation (see Fig. 19) to transform PTV velocities to particle sizes possibly overestimates the size in specific size regimes. From shadowgraphy data, a particle with a velocity of 380 m/s can be down to 25 µm in size, considering the vertical IQR bars of the corresponding data point in Fig. 19. But for the same velocity, the velocity-size relation (and hence, PTV) leads to a particle size of 35 µm (see red dash-dotted line in Fig. 19), which corresponds to a particle with approx. 270% larger volume. To investigate this influence, a comparison of the particle size distribution from shadowgraphy data, from PTV and from external measurements (Fig. 8) may be helpful. Additionally, the velocity-size relation is restricted to spherical particles due to the limitations of the particle motion model, whereas PTV data include also non-spherical particles. On the other hand, the assumed particle counting efficiency of both, shadowgraphy and PTV, can be erroneous. This has an effect on the PTV light sheet thickness determination, which again has a linear influence on the absolute value of G_p from PTV.

The dependence of the radial position on the velocity-size relation is assumed to have minor impacts on G_p, compared to the particle segregation effects: On the one hand, G_p dominating high inertia particles are concentrated in the flow center (y =−7 to 7 mm) where the found velocity-size relation is valid and where radial flow velocity components along their nozzle trajectory are negligible. These particle did not even reach the axial flow component which is considerably larger than the radial flow velocity component. On the other hand, in the outer flow areas, where radial flow velocity components could become more important for the velocity-size relation, mostly low inertia particles were detected which have only minor effects on G_p. Nonetheless, in future studies, velocity-size relations at different radial positions have to be compared.

The particle-scattered-intensity profile, as it was proposed in (Vasilevskii and Osiptsov 1999), seems to be applicable for a quick and fast G_p distribution estimation, although it provides no information about the number concentration, size, and velocity of particles. Possibly due to gravity, at the bottom edge of the nozzle throat (y = −7 mm) the G_p is slightly higher than its counterpart at the top edge for this profile. Although this asymmetry can be also a consequence of non-uniform illumination intensity, or PTV light sheet thickness variation, a tendency to this asymmetry is also detected in three PTV profiles.

Further studies have to check, if the mass flow rate uncertainty can be reduced by several improvements:

• The choice of another flow condition where particle velocities are more dependent on particle size

• An optimization of PTV laser light intensity to avoid large particle saturation effects

• An increase in shadowgraphy resolution to improve velocity-size relation accuracy

However, this work showed that the last two points provide possibly other disadvantages, like a lower signal-to-noise ratio for smaller particles for PTV or a reduction in the shadowgraphy measurement volume.

The gained experiences concerning G_p determination, the quantified uncertainties as well as the distributions of particle velocity, size, and G_p help to improve measurement techniques for individual particle characterization and are a first basis for upcoming heating augmentation analyses.

With the aid of the presented methods, in the short term, future work will focus on several method improvements, suggested in this work, and determination of the “true” particle density for a more accurate G_p determination. Then, attention will be given to shock layers and the resulting probe-impact G_p. The latter parameter will be correlated with experimentally measured stagnation point heat fluxes and compared to existing data considering particle-induced heating augmentation. Finally, it will be checked how the achieved data can be related to impacts of particle laden flows on TPS materials in the Martian atmosphere.

The presented results can also be used as experimental reference of particle composition cold spray simulations, since also here small convergent divergent nozzles are used and a similar investigation focus regarding particle velocity-size relations is addressed (e.g., see (Yin et al. 2016)).

5 Conclusion

Particle mass- and volume concentrations, c_m and c_v, respectively, as well as the particle mass flow rate G_p are of fundamental interest for describing two-phase flows, but also for describing particle-induced heating augmentation effects. For G_p determination, multiple particle characteristics have to be taken into account, namely particle number, size, velocity, and density, as well as measurement volume size. Up to now, no study considering heating augmentation has determined G_p by measuring all of these particle characteristics within the flow, although a detailed knowledge about the particles seem to be essential for describing particle-induced heating augmentation effects.

This work estimated all required measurement uncertainties of particle number, size, velocity, and measurement volume size for a detailed G_p uncertainty analysis, and inferred the G_p distribution profile across the nozzle exit of the small-scaled test facility GBK at the Supersonic and Hypersonic Technologies Department of DLR, Cologne, from single particle characteristics.

A shadowgraphy size correction has been implemented which reduced size measurement uncertainty from 12% to < 6% for particles < 60 µm. Comparing experimental nozzle exit velocities of differently sized spherical particles with one-dimensional one-way-coupled particle motion calculations, a discrepancy has been found which is of fundamental interest for further processing.

Particle size, velocity, and mass flow rate across the nozzle exit of the small-scaled facility have been presented. For particle mass flow rate, PTV-based uncertainties are up to 50%, for shadowgraphy they are less than 17%. Results of both techniques coincide within their uncertainty range. Larger and slower particles are located in the flow center, and only smaller and faster particles are distributed in the outer region of the nozzle exit flow. Experimental results show that the particle mass flow rate is mostly concentrated in an area close to the corresponding nozzle throat diameter. A slight drop of the particle mass flow rate in the inner jet core is measured in four of ten runs.

Appendices

Appendix

1.1 Drag Correlation

1.1.1 General

The relative particle Reynolds number Re_p is:

$${\text{Re}}_{p} = \left( {V_{g} - V_{p} } \right)\frac{{\rho_{g} }}{{\mu_{g} }}d_{p}$$

(9-1)

The relative particle Mach Number Ma_p is defined as:

$$Ma_{p} = \frac{{\left( {V_{g} - V_{p} } \right)}}{{\sqrt {\gamma R T} }}$$

(9-2)

The Knudsen number Kn is:

$$Kn = \sqrt {\frac{\gamma \pi }{2}} Ma_{p}$$

(9-3)

1.1.2 Henderson drag correlation

The drag correlation by Henderson, described in (Henderson 1976), is divided into three expressions, depending on Ma_p.

$$C_{D} (Ma_{p} ,{\text{Re}}_{p} ) = \left\{ {\begin{array}{*{20}l} {C_{{D{\text{sub}}}} \left( {{\text{Re}}_{p} ,Ma_{p} } \right),if\;Ma_{p} \le 1.0} \hfill \\ {C_{{D{\text{trans}}}} \left( {{\text{Re}}_{p} ,Ma_{p} } \right),if\;1.0 < Ma_{p} \le 1.75} \hfill \\ {C_{{D,\sup }} \left( {{\text{Re}}_{p} ,Ma_{p} } \right),if\;Ma_{p} > 1.75} \hfill \\ \end{array} } \right.$$

(9-4)

For Ma_p < 1, the drag coefficient is defined as:

$$\begin{aligned} C_{{D {\text{sub}}}} \left( {Ma_{p} ,{\text{Re}}_{p} } \right) = & 24.0\left\{ {{\text{Re}}_{p} + S\left[ {4.33 + \left( {\frac{{3.65 - 1.53\frac{{T_{p} }}{T}}}{{1.0 + 0.353\frac{{T_{p} }}{T}}}} \right)\exp \left( { - 0.247\frac{{{\text{Re}}_{p} }}{S}} \right)} \right]} \right\}^{ - 1} \\ & \quad + \exp \left( { - \frac{{0.5Ma_{p} }}{{{\text{Re}}_{p}^{0.5} }}} \right)\left[ {\frac{{4.5 + 0.38\left( {0.03{\text{Re}}_{p} + 0.48{\text{Re}}_{p}^{0.5} } \right)}}{{1.0 + 0.03{\text{Re}}_{p} + 0.48{\text{Re}}_{p}^{0.5} }} + 0.1Ma_{p}^{2} + 0.2Ma_{p}^{8} } \right] \\ & \quad + \left[ {(1.0 - \exp \left( { - \frac{{Ma_{p} }}{{{\text{Re}}_{p} }}} \right)} \right]0.6S \\ \end{aligned}$$

(9-5)

With:

$$S = Ma_{p} \sqrt {\frac{\gamma }{2}}$$

(9-6)

For the subsonic regime, the authors of (Henderson 1976) have used experimental data with Re_p up to 1e4. For the regime Ma_p > 1.75, the maximum experimental Rep was 5e3. In this regime, the drag coefficient can be expressed with:

$$C_{D \sup } (Ma_{\infty } ,{\text{Re}}_{\infty dp} ) = \frac{{0.9 + \frac{0.34}{{Ma_{\infty }^{2} }} + 1.86\left( {\frac{{Ma_{\infty } }}{{{\text{Re}}_{\infty dp} }}} \right)^{0.5} \left( {2 + \frac{2}{{S_{\infty }^{2} }} + \frac{1.058}{{S_{\infty } }}\left( {\frac{{T_{p} }}{T}} \right)^{0.5} - \frac{1}{{S_{\infty }^{4} }}} \right)}}{{1 + 1.86\left( {\frac{{Ma_{\infty } }}{{{\text{Re}}_{\infty dp} }}} \right)^{0.5} }}$$

(9-7)

With:

$$S_{\infty } = Ma_{\infty } \sqrt {\frac{\gamma }{2}}$$

(9-8)

The subscript “∞” indicates free stream conditions. So, the free stream Reynolds number Re_∞dp is:

$${\text{Re}}_{\infty dp} = V_{g} \frac{{\rho_{g} }}{{\mu_{g} }}d_{p}$$

(9-9)

The respective free stream Mach Number Ma_∞ is defined as:

$$Ma_{\infty } = \frac{{V_{g} }}{{\sqrt {\gamma R T} }}$$

(9-10)

If 1 < Ma_p < 1.75, the drag coefficient is interpolated linearly:

$$\begin{aligned} C_{{D {\text{trans}}}} = & C_{{D {\text{sub}}}} \left( { Ma_{p} = 1,{\text{Re}}_{p} } \right) \\ & \quad + \frac{4}{3}\left( {Ma_{\infty } - 1} \right)\left( {C_{D \sup } \left( {Ma_{\infty } = 1.75,{\text{Re}}_{\infty dp} } \right) - C_{{D {\text{sub}}}} \left( { Ma_{p} = 1,{\text{Re}}_{p} } \right)} \right) \\ \end{aligned}$$

(9-11)

In this work, it is assumed that the particle temperature T_p is always in equilibrium with the surrounding gas temperature T, so:

$$\frac{{T_{p} }}{T} = 1$$

(9-12)

1.1.3 Parmar drag correlation

The drag correlation by Parmar et al. (Parmar et al. 2010) is based on the following assumptions:

Attention is limited to continuum flows:

$$Kn = \sqrt {\frac{\gamma \pi }{2}} Ma_{p} < 0.01$$

(9-13)

The particle temperature is constant and equal to the surrounding gas temperature:

$$\frac{{T_{p} }}{T} = 1$$

(9-14)

In the limit of zero Mach number, the correlation should approach the following correlation:

$$C_{{D, {\text{std}}}} \left( {{\text{Re}}_{p} } \right) = \frac{24}{{{\text{Re}}_{p} }}\left( {1 + 0.15 {\text{Re}}_{P}^{0.687} } \right) + 0.42 \left( {1 + \frac{42500}{{{\text{Re}}_{p}^{1.16} }}} \right)^{ - 1}$$

(9-15)

Attention is limited to subcritical Reynolds numbers:

$${\text{Re}}_{p} \widetilde{ < }2e5$$

(9-16)

The Mach number is limited to:

$$0 \le Ma_{p} \le 1.75$$

(9-17)

The critical Mach number is defined as:

$$Ma_{p, cr} \approx 0.6$$

(9-18)

The drag correlation consists of three separate correlations:

$$C_{D} (Ma_{p} ,{\text{Re}}_{p} ) = \left\{ {\begin{array}{*{20}c} {C_{{D,std}} \left( {{\text{Re}}_{p} } \right) + \left[ {C_{{D,Ma_{{p,cr}} }} \left( {{\text{Re}}_{p} } \right) - C_{{D,std}} \left( {{\text{Re}}_{p} } \right)} \right]\frac{{Ma_{p} }}{{Ma_{{p,cr}} }},if\;Ma_{p} \le Ma_{{p,cr}} } \\ {C_{{D,sub}} \left( {{\text{Re}}_{p} ,Ma_{p} } \right),if\;Ma_{{p,cr}} < Ma_{p} \le 1.0} \\ {C_{{D,\sup }} \left( {{\text{Re}}_{p} ,Ma_{p} } \right),if\;1.0 < Ma_{p} \le 1.75} \\ \end{array} } \right.$$

(9-19)

Drag coefficients for fixed Mach numbers are:

$$C_{{D, Ma_{p} = 1}} \left( {{\text{Re}}_{p} } \right) = \frac{24}{{{\text{Re}}_{p} }}\left( {1 + 0.118 {\text{Re}}_{P}^{0.813} } \right) + 0.69 \left( {1 + \frac{3550}{{{\text{Re}}_{p}^{0.793} }}} \right)^{ - 1}$$

(9-20)

$$C_{{D, Ma_{p} = 1.75}} \left( {{\text{Re}}_{p} } \right) = \frac{24}{{{\text{Re}}_{p} }}\left( {1 + 0.107 {\text{Re}}_{P}^{0.867} } \right) + 0.646 \left( {1 + \frac{861}{{{\text{Re}}_{p}^{0.634} }}} \right)^{ - 1}$$

(9-21)

$$C_{{D, Ma_{p,cr} }} \left( {{\text{Re}}_{p} } \right) = \frac{24}{{{\text{Re}}_{p} }}\left( {1 + 0.15 {\text{Re}}_{P}^{0.684} } \right) + 0.513\left( {1 + \frac{483}{{{\text{Re}}_{p}^{0.669} }}} \right)^{ - 1}$$

(9-22)

For the supersonic regime, the drag coefficient can be expressed at follows:

$$C_{D, \sup } \left( {{\text{Re}}_{p} , Ma_{p} } \right) = C_{{D, Ma_{p} = 1}} \left( {{\text{Re}}_{p} } \right) + \left[ {C_{{D, Ma_{p} = 1.75}} \left( {{\text{Re}}_{p} } \right) - C_{{D, Ma_{p} = 1}} \left( {{\text{Re}}_{p} } \right)} \right]\xi_{\sup } \left( {{\text{Re}}_{p} ,Ma_{p} } \right)$$

(9-23)

$$\xi_{\sup } \left( {{\text{Re}}_{p} ,Ma_{p} } \right) = \mathop \sum \limits_{i = 1}^{3} f_{i, \sup } \left( {Ma_{p} } \right)\mathop \prod \limits_{{\begin{array}{*{20}c} {j \ne i} \\ {j = 1} \\ \end{array} }}^{3} \frac{{\log {\text{Re}}_{p} - C_{j,\sup } }}{{C_{i,\sup } - C_{j,\sup } }}$$

(9-24)

$$f_{1, \sup } \left( {Ma_{p} } \right) = - 2.963 + 4.392 Ma_{p} - 1.169Ma_{p}^{2} - 0.027Ma_{p}^{3} - 0.233 \exp \left[ {\frac{{1 - Ma_{p} }}{0.011}} \right]$$

(9-25)

$$f_{2, \sup } \left( {Ma_{p} } \right) = - 6.617 + 12.11 Ma_{p} - 6.501Ma_{p}^{2} + 1.182Ma_{p}^{3} - 0.174 \exp \left[ {\frac{{1 - Ma_{p} }}{0.01}} \right]$$

(9-26)

$$f_{3, \sup } \left( {Ma_{p} } \right) = - 5.866 + 11.57 Ma_{p} - 6.665Ma_{p}^{2} + 1.312Ma_{p}^{3} - 0.350 \exp \left[ {\frac{{1 - Ma_{p} }}{0.012}} \right]$$

(9-27)

$$\begin{array}{*{20}c} {C_{1,\sup } = 6.48} \\ {C_{2,\sup } = 8.93} \\ {C_{3,\sup } = 12.21} \\ \end{array}$$

(9-28)

In the intermediate regime, the drag coefficient is defined as:

$$C_{D, sub} \left( {{\text{Re}}_{p} , Ma_{p} } \right) = C_{{D, Ma_{p, cr} }} \left( {{\text{Re}}_{p} } \right) + \left[ {C_{{D, Ma_{p} = 1}} \left( {{\text{Re}}_{p} } \right) - C_{{D, Ma_{p,cr} }} \left( {{\text{Re}}_{p} } \right)} \right]\xi_{sub} \left( {{\text{Re}}_{p} ,Ma_{p} } \right)$$

(9-29)

$$\xi_{\sup } \left( {{\text{Re}}_{p} ,Ma_{p} } \right) = \mathop \sum \limits_{i = 1}^{3} f_{i, sub} \left( {Ma_{p} } \right)\mathop \prod \limits_{{\begin{array}{*{20}c} {j \ne i} \\ {j = 1} \\ \end{array} }}^{3} \frac{{\log {\text{Re}}_{p} - C_{{j,{\text{sub}}}} }}{{C_{{i,{\text{sub}}}} - C_{{j,{\text{sub}}}} }}$$

(9-30)

$$f_{1, sub} \left( {Ma_{p} } \right) = - 1.884 + 8.422 Ma_{p} - 13.70Ma_{p}^{2} + 8.162Ma_{p}^{3}$$

(9-31)

$$f_{2, sub} \left( {Ma_{p} } \right) = - 2.228 + 10.35 Ma_{p} - 16.96Ma_{p}^{2} - 9.840Ma_{p}^{3}$$

(9-32)

$$f_{3, sub} \left( {Ma_{p} } \right) = 4.362 \pm 16.91 Ma_{p} + 19.84Ma_{p}^{2} - 6.296Ma_{p}^{3}$$

(9-33)

$$\begin{array}{*{20}c} {C_{1,sub} = 6.48} \\ {C_{2,sub} = 9.28} \\ {C_{3,sub} = 12.21} \\ \end{array}$$

(9-34)

1.1.4 Loth drag correlation

The drag correlation by Loth (Loth et al. 2021) is divided into two regimes, namely the rarefaction-dominated regime and the compression-dominated regime. In between, the authors of (Loth et al. 2021) indicated a nexus of the drag coefficient at Re_p = 45.

$$C_{D} (Ma_{p} ,\text{Re} _{p} ) = \left\{ {\begin{array}{*{20}c} {\frac{{24}}{{\text{Re} _{p} }}\left( {1 + 0.15\text{Re} _{P}^{{0.687}} } \right)H_{M} + 0.42C_{M} \left( {1 + \frac{{42500}}{{\text{Re} _{p}^{{1.16C_{M} }} }} + \frac{{G_{M} }}{{\text{Re} _{p}^{{0.5}} }}} \right)^{{ - 1}} ,} & {if\;45 < \text{Re} _{p} < \text{Re} _{{p,crit}} } \\ {\frac{{C_{{D,Kn,\text{Re} _{p} }} }}{{1 + Ma_{p}^{4} }} + \frac{{Ma_{p}^{4} C_{{D,fm,\text{Re} _{p} }} }}{{1 + Ma_{p}^{4} }},} & {if\;\text{Re} _{p} \le 45} \\ \end{array} } \right.$$

(9-35)

The parameters for the compression-dominated regime are defined as follows:

$$C_{M} = \left\{ {\begin{array}{*{20}c} {1.65 + 0.65\tanh \left( {4Ma_{p} - 3.4} \right),} & {if\;Ma_{p} < 1.5} \\ {2.18 - 0.13\tanh \left( {0.9Ma_{p} - 2.7} \right),} & {if\;Ma_{p} > 1.5} \\ \end{array} } \right.$$

(9-36)

$$G_{M} = \left\{ {\begin{array}{*{20}l} {20 - 10.9Ma_{p} + 3.29Ma_{p}^{2} + 166Ma_{p}^{3} ,} \hfill & {if\;Ma_{p} < 0.8} \hfill \\ {5 + 40Ma_{p}^{{ - 3}} ,} \hfill & {if\;Ma_{p} > 0.8} \hfill \\ \end{array} } \right.$$

(9-37)

$$H_{M} = \left\{ {\begin{array}{*{20}c} {1 - 0.074Ma_{p} + 0.212Ma_{p}^{2} + 0.0239Ma_{p}^{3} ,} & {if\;Ma_{p} < 1} \\ {0.93 + \frac{1}{{3.5 + Ma_{p}^{5} }},} & {if\;Ma_{p} > 1} \\ \end{array} } \right.$$

(9-38)

The parameters for the rarefaction-dominated regime are defined as follows:

$$C_{{D, Kn,{\text{Re}}_{p} }} = \frac{24}{{{\text{Re}}_{p} }}\left( {1 + 0.115 {\text{Re}}_{P}^{0.687} } \right) f_{Kn}$$

(9-39)

$$f_{ Kn} = \frac{1}{{1 + Kn\left[ {2.514 + 0.8\exp \left( {\frac{ - 0.55}{{Kn}}} \right)} \right]}}$$

(9-40)

$$C_{D, fm} = \frac{{\left( {1 + 2S^{2} } \right) \exp \left( { - S^{2} } \right)}}{{S^{3} \sqrt \pi }} + \frac{{\left( {4S^{4} + 4S^{2} - 1} \right){\text{erf}}\left( S \right)}}{{2S^{4} }} + \frac{2}{3S}\sqrt \pi$$

(9-41)

$$C_{{D, fm, {\text{Re}}_{p} }} = \frac{{C_{D,fm} }}{{1 + \left[ {\frac{{C_{D,fm} }}{{J_{M} }} - 1} \right]\sqrt {\frac{{{\text{Re}}_{p} }}{45}} }}$$

(9-42)

$$J_{M} = \left\{ {\begin{array}{*{20}c} {2.26 - \frac{{0.1}}{{Ma_{p} }} + \frac{{0.14}}{{Ma_{p}^{3} }},} & {if\;Ma_{p} \le 1} \\ {1.6 + \frac{{0.25}}{{Ma_{p} }} + \frac{{0.11}}{{Ma_{p}^{2} }} + \frac{{0.44}}{{Ma_{p}^{3} }},} & {if\;Ma_{p} > 1} \\ \end{array} } \right.$$

(9-43)

The authors of this study assume the following critical Reynolds number for the Loth drag correlation:

$${\text{Re}}_{{p,{\text{crit}}}} \approx 1.5e5$$

(9-44)

Spatial resolved particle mass flow rate distributions

Fig. 24

Particle mass flow rate distribution, run N10

Fig. 25

Particle mass flow rate distribution, run N12

Fig. 26

Particle mass flow rate distribution, run N13

Fig. 27

Particle mass flow rate distribution, run N14

Fig. 28

Particle mass flow rate distribution, run N15

Fig. 29

Particle mass flow rate distribution, run N16

Fig. 30

Particle mass flow rate distribution, run N17

Fig. 31

Particle mass flow rate distribution, run N18

Fig. 32

Particle mass flow rate distribution, run N19