Capsule aerodynamics and shock-wave boundary layer interaction (SBLI) in supersonic and transonic flow

Abstract

Static force and moment measurements are performed on the MarcoPolo-R aero shape in the trisonic wind tunnel TMK. The static stability behaviour of the capsule is characterized in the Mach number range $0.5\le M\le 3.5$ reproducing the Mach and Reynolds conditions of the flight trajectory in the supersonic regime. An aerodynamic database is built based on the experimental results. The flow structure around the capsule is visualised in supersonic tests by means of schlieren imaging. Under certain conditions, development of a complex shock system on the leeward side of the inclined capsule is observed. Oil film technique is used to visualise boundary layer phenomena in connection to this shock system. Numerical simulations with the DLR TAU code are performed to support the interpretation of the flow phenomena under these conditions.

Graphical abstract

Schlieren imaging visualisation of density gradients in supersonic flow. Depending on the test conditions and angle of incidence, a complex shock system is observed on the leeward side of the inclined capsule. Analysis of the shock structure and its impact on aerodynamic coefficients is one subject of the present investigation.

1 Introduction

The most critical part of an Earth return or exploration mission is the entry phase, in which the high kinetic and potential energy of the spacecraft is dissipated. This leads to very high temperatures on the surface of the probe. Commonly, blunt body geometries are chosen for the aerodynamic outer shell, as these generate high drag, quickly decelerate the probe to the terminal velocity, and reduce the magnitude of the occurring heat fluxes.

Capsule-like shapes have proven to be suitable for atmospheric entry on numerous missions. However, the disadvantage of this shape is the low aerodynamic stability, especially in the transonic and subsonic regime. Therefore, a parachute system is usually implemented for the final deceleration phase. Other concepts focus on passive entry systems without a parachute and use crushable material to protect freight from ground impact loads.

The MarcoPolo-R project featured such an alternative concept without a parachute. It was planned as a sample return mission to an organic-rich near-earth asteroid and was a candidate mission in ESA’s Cosmic Vision program (Barucci et al. 2012; Michel et al. 2014). Besides the scientific characterization of the asteroid at multiple scales, a bulk sample should be returned to Earth for laboratory analyses. The ultimate goal was to contribute to the in depth understanding of the early solar system.

Since the aero shell was designed for flight without a parachute system, its shape had to be selected carefully to be aerodynamically stable throughout the complete re-entry trajectory down to transonic and subsonic velocities. Therefore, within the frame of ESA’s MarcoPolo-R Earth Re-Entry Capsule Dynamic Stability Characterization TRP, several experimental campaigns and transient computational simulations were performed (Clopeau et al. 2015).

In the initial shape definition phase, different capsule models from a system study preselection were investigated via free-flight tests in the vertical free jet facility VMK of DLR (Preci and Gülhan 2015; Preci et al. 2015, 2016). The dynamic behaviour of the shapes and their dependency on the position of the Centre of Gravity as well as the shoulder radius was investigated in detail at low Mach numbers. Subsequently, the aero shape based on the Hayabusa geometry (Hiraki and Inatani 2003; Ishii et al. 2008), but with a modified aft section (designed by Astrium DS team, which now belongs to ArianeGroup), was chosen as reference for MarcoPolo-R (Clopeau et al. 2015).

After definition of the general shape, the static aerodynamic parameters of the configuration were to be characterized in wind tunnel tests in the Mach number range $0.5\le M\le 3.5$. This testing was performed in the trisonic wind tunnel TMK of DLR in Cologne. The results were used to support the creation of an aerodynamic database and are presented in this paper. Subsequent to this project, different test conditions were investigated in more detail and numerical simulations were performed. These investigations support the analysis of the observed interaction of the near-normal shock wave within the boundary layer on the convex capsule surface. Houghton et al. (2013) describe this flow phenomenon in detail, identifying three different types of interaction. Shortcomings of numerical simulations in this context have been observed, e.g. by da Mata et al. (2017) in their combined experimental/numerical study on a Microsatellite Launch Vehicle at transonic conditions. They related the interaction types described by Houghton et al. to different flow structures they observed, but were not able to properly rebuild the shock structures numerically.

Similar observations are made by the authors of this study. It proved difficult to set the boundary conditions and simulation parameters in such a way that the structures of the shock boundary layer interaction are sufficiently resolved and experimental and numerical results agree to an acceptable degree. These comparative results show room for improvement in numerical simulations. The results of the additional investigations are also presented and discussed in this study. The findings proved to be less relevant for static capsule aerodynamics, than for investigations on shock boundary layer interaction in supersonic flows near convex surfaces.

ESA’s MarcoPolo-R TRP study was supported by a free-flight test campaign dedicated to determination of the dynamic behaviour of the aero shape at the open range facility of ISL (Dobre and Berner 2015). Furthermore, a transient computational simulation campaign was conducted by CFSE for the evaluation of dynamic derivatives of the aero shape in the subsonic regime (Charbonnier et al. 2015). Although the outcome of the whole study was promising, the MarcoPolo-R mission was not selected as an ESA mission due to financial aspects (Barucci et al. 2012; Michel et al. 2014).

The interest in the aerodynamic behaviour of the Hayabusa-like MarcoPolo-R capsule grew again when the aero shape was selected as baseline configuration for the ESA TRP Modshape (Modelling Capsule Stability accounting for Shape Change) in 2019. The main goal of the Modshape project is to experimentally quantify the impact of the Outer Mold Line changes due to the recession of the Thermal Protection System (TPS) on the flight qualities of the capsule (Neeb et al. 2019). Furthermore, a Hayabusa-like capsule with a passive re-entry system (i.e. without parachute) is chosen as candidate for the Phobos Sample Return mission of ESA’s Mars Robotic Exploration Preparation programme with the launch targeted for $2024/25$ (Centuori et al. 2016; Ferri et al. 2018). The aerodynamic behaviour of the aero shape presented in this paper is relevant in that context. To the knowledge of the authors, no other experimental data exist for the exact geometry investigated in this study.

2 Experimental setup

2.1 Trisonic wind tunnel cologne (TMK)

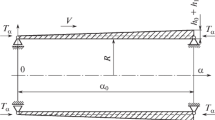
The TMK facility is a trisonic blow down wind tunnel with a rectangular test section of $0.6 \mathrm{m} x 0.6\mathrm{ m}$. It is equipped with large quartz glass windows on opposing sides, providing direct optical access to the test section. As sketched in Fig. 1, air from a pressure reservoir passes a storage heater and a settling chamber and is then accelerated in an adaptable de Laval nozzle. In the test section, the flow conditions are nearly constant. The flow is decelerated downstream in the diffuser system. Depending on Mach and Reynolds conditions, a maximum testing time of up to $60$ seconds is achieved.

Fig. 1

Schematic illustration of the Trisonic Wind Tunnel Cologne (TMK)

The performance map of the facility is given in Fig. 2. The standard Mach number range in the supersonic operation mode is $1.25<M<4.5$. The wind tunnel is operated at a dynamic pressure of ${q}_{\infty }\approx 1 \mathrm{bar}$ in this range. The Mach number is controlled via the adaptable de Laval nozzle. The diffuser is usually fully open. Tests with reduced dynamic pressure or Mach numbers up to $M=5.7$ can be realized by ejecting additional air mass flow downstream the subsonic diffuser and, if necessary, by additionally heating the flow in the storage heater.

Fig. 2

Performance map of the Trisonic Wind Tunnel

For Mach numbers of $0.5<M<1.2,$ an additional transonic test section with perforated walls of variable aperture is installed downstream the supersonic test section. In this case, the wind tunnel is operated at a static pressure of ${p}_{\infty }\approx 1 \mathrm{bar}$ and the Mach number is controlled via the adaptable diffuser downstream the test section. In transonic tests, the perforated walls inhibit the application of optical flow visualisation techniques (e.g. schlieren).

2.2 Facility instrumentation and calibration

The stagnation conditions ${T}_{0}$ and ${p}_{0}$ are measured in the settling chamber of TMK with a type K thermocouple of tolerance class $1$ and a $PMP 4015$ pressure sensor of GE Sensing with a $\pm 0.04 \%$ full scale accuracy. Depending on the test conditions, a sensor with a $3, 10$ or $30$ bar range is used.

The supersonic calibration of the adaptable de Laval nozzle shows that the Mach number in the centreline region of the wind tunnel deviates less than $\pm 0.5 \%$ of the nominal value for $M\ge 2.0$. With decreasing Mach number, the relative error increases to $\pm 0.75 \%$ at $M=1.5$ (Esch 1986).

For transonic tests the Mach number and its uncertainty are calculated from the pressure ratio ${p}_{0}/{p}_{\infty }$ using gas dynamic equations and applying correction factors derived from calibration tests. Thereby, the static pressure ${p}_{\infty }$ in the test section is measured relative to ambient pressure with a $Pm131TC$ differential sensor with a $0.7 \mathrm{bar}$ range with $\pm 0.0012 \mathrm{bar}$ uncertainty.

During a test, the angle of incidence $\alpha$ is continuously varied and measured via an angle transmitter with an accuracy better than $\pm 0.05^\circ$. Additionally, from calibration data, the flow angularity in vertical and horizontal planes $\Delta {\alpha }_{\infty }$ and $\Delta {\beta }_{\infty }$ are known to be less than $\pm 0.25^\circ$. This value might increase near the operating limits of the wind tunnel (Esch 1986).

2.3 Wind tunnel models

The reference aero shape with a diameter of $880\mathrm{ mm}$ is shown in Fig. 3 together with the CAD-design of the wind tunnel model of scale $1:11$. This baseline model has a diameter of ${D}_{\mathrm{\rm Ref}\_1}=80\mathrm{ mm}$. To account for the limited mechanical strength of the wind tunnel balance, a second wind tunnel model with a reduced diameter of ${D}_{\mathrm{\rm Ref}\_2}=70 \mathrm{mm}$ (scale $1:12.57$) is designed. The uncertainty in diameter due to manufacturing is $\Delta {D}_{\rm Ref}=\pm 0.1 \mathrm{mm}$. The reference surfaces are calculated as ${S}_{\mathrm{Ref}}=\pi /4\cdot {D}_{\mathrm{Ref}}^{2}$.

Fig. 3

Reference aero shape (left) and wind tunnel baseline model ϕ80 mm (right)

The Moment Reference Centre ($MRC$) is defined on the centreline of the capsule, $0.25\cdot {D}_{\mathrm{Ref}}$ downstream the stagnation point at a zero degree angle of incidence. The uncertainty of the $MRC$ position in moment estimation is $\pm 0.1 \mathrm{mm}$. If the centre of gravity ($CoG$) coincides with the $MRC$, the pitching moment curves provide a direct reference to the static aerodynamic stability of the capsule.

The wind tunnel models are made from a high strength Aluminium alloy ($3.4345$) and coated with a $30\pm 3 \mathrm{\mu m}$ nickel layer. They have a smooth front surface and are fixed to the balance via adapter and screws on the rearward side. The balance is connected to a $\diameter 18 \mathrm{mm}$ sting and covered by a shell with $\diameter 22 \mathrm{mm}$ (length: $365.6 \mathrm{mm}$). For baseline configuration, the sting to capsule diameter ratio is ${D}_{S}/{D}_{80}=0.275$ and the sting length to capsule diameter ratio is ${L}_{S}/{D}_{80}=4.57$.

From previous capsule tests, a combination of ${D}_{S}/D\le 0.18$ and ${L}_{S}/D>3.55$ has proven to be an ideal compromise to minimize the sting influence on the aerodynamic results. In the current case, the capsule diameter could not be increased further due to mechanical constraints of the balance. Therefore, the sting length was increased to achieve a better ${L}_{S}/D$-ratio. As the diameter ratio further increases for the $70 \mathrm{mm}$ capsule, it is used only for selected tests, mainly with high axial loads.

An inner and outer clearance of $1 \mathrm{mm}$ between shell and model allows for contact-free measurements at all incidence angles, even when aerodynamic loads lead to a slight bending of the sting-balance-system. Nevertheless, a potential contact is surveyed electrically during the wind tunnel tests.

The photographs in Fig. 4 show the baseline model’s front and rear side.

Fig. 4

Photographs of baseline model

2.4 Static aerodynamic measurements

Aerodynamic coefficients are determined with the six-component strain gauge balance $DLR - 0007$ as shown in Fig. 5. A balance of $\diameter 18 \mathrm{mm}$ is chosen as a compromise between high acceptable axial loads and a low model to shell diameter ratio. The distance between the two instrumented sections of the balance for longitudinal and lateral measurements is $100 \mathrm{mm}$.

Fig. 5

Six component balance $\mathbf{D}\mathbf{L}\mathbf{R} - 0007$

Table 1 provides the test range and the maximum error for each component (derived from calibration data) of balance $DLR - 0007$. Different values are given for transonic and supersonic tests (with ejector). This considers the level of the aerodynamic loads in each test series.

Table 1 Technical data of balance $DLR - 0007$

The calibration is performed with the balance-sting constellation. This enables correction of the sting bending with respect to the model’s angle of incidence with an uncertainty better than $\pm 0.1^\circ$.

The base pressure downstream the model is measured relative to ambient pressure with a $PDCR 22$ sensor positioned outside the test section. The sensor is connected via a long, thin tube ($\diameter 1.6 x L 2500\mathrm{ mm}$) guided along the model support system and sting to a pressure port inside the shell (see Fig. 3). The pressure level is assumed to be representative for an average pressure distribution on the model’s base. The sensor’s range is $15 \mathrm{PSID}$ $(\sim 1 \mathrm{bar}$) and its total uncertainty from calibration is $\pm 0.001 \mathrm{bar}$. The sensor was chosen to cover the whole range of test conditions accepting a loss in resolution at low pressure levels.

All pressure, temperature, angle of incidence and balance data are recorded simultaneously with an acquisition rate of $100\, \mathrm{Hz}$. If static aerodynamic measurements are performed, a filter of $10 \, \mathrm{Hz}$ is applied. Raw data are stored during the test together with calibration information. Post-processing is performed after the test with an in-house developed tool.

2.5 Flow visualisation

The schlieren visualisation for supersonic tests in TMK uses a Z-arrangement with a vertical knife edge and a simultaneous recording on two camera systems:

• 1. A monochromatic Photron Fastcam ultima APX-RS (Frame rate: up to $150 \, \mathrm{kHz}$, minimum exposure time: $1 \,\mathrm{\mu s}$, sensor: CMOS, resolution: $1024x1024 \mathrm{px}$, bit depth: $10 \mathrm{bit}$) as well as.

• 2. A monochromatic Prosilica $GE4000$ (Frame rate: up to $5 \, \mathrm{Hz}$ at full resolution, minimum exposure time: $140\mathrm{ \mu s}$, sensor: CCD, res.: $4008x2672 \mathrm{px}$, bit depth: $16 \mathrm{bit}$).

With this line-of-sight method, the three-dimensional flow structures are visualised in two dimensions. Density gradients are integrated along the line of sight (perpendicular to the graph). The schlieren technique differs from the shadowgraph technique by the usage of a knife edge. This results in the density gradient being emphasized orthogonal to that edge.

Additionally, the oil film technique is used for visualisation of surface streamlines in some dedicated tests. In these tests, the model surface is prepared with a thin layer of a special mixture (oil, petroleum, fluorescent pigments) that dries during the test while the flow conditions are kept constant. The pattern created on the model surface is photographed after the test.

3 Experimental test campaign

3.1 Test procedure

For minimizing the loads on the balance in aerodynamic tests, the model is aligned at $\alpha =0^\circ$ for wind tunnel start-up and shut-down. After a short transitional phase of the tunnel, data are recorded at constant flow conditions with the incidence angle altered continuously in the range of $-2.5^\circ \le \alpha \le +25^\circ$ at $2^\circ /s$ up and $3^\circ /s$ down. No dependency of the aerodynamic data on sweep direction or sweep velocity is observed. But, at the low-pressure level in supersonic tests, the base pressure measurement reacts with short delay to sudden pressure changes in the flow field, e.g. at wind tunnel start-up. This is caused by the technically unavoidable long tube length. To account for this, supersonic data are presented for the sweep-down phase, whereby transonic data are presented for the sweep-up phase.

Within supersonic tests, high quality schlieren images are recorded in full resolution at $3 \, \mathrm{Hz}$ and $1 \,\mathrm{ms}$ exp. time (Prosilica) simultaneously with a schlieren video in full resolution at $60 \, \mathrm{Hz}$ and $1 \,\mathrm{\mu s}$ exp. time (Photron). The cameras do not provide a precise time stamp for each frame. Thus, the images cannot be correlated to the measurements directly. Therefore, the corresponding model’s angle of incidence is determined for each individual image during post processing. This is done relative to a horizontal reference using an edge detection algorithm with an uncertainty of approx. $\pm 0.1^\circ$. Analysis of the schlieren recordings proved that oscillations of the shock structures can be neglected in both cases, the short $1\mathrm{ \mu s}$ and the longer $1 \,\mathrm{ms}$ exposure. Both exposure times yield the same result except for a difference in optical resolution. Therefore, only images recorded with the high-resolution Prosilica camera are shown here, with the intensity of images at different Reynolds numbers normalized in post-processing.

Oil film visualisation is performed for certain test conditions. In this case, the model is prepared with the oil layer and set to a specific angle of incidence. This angle is calculated considering the sting bending during the test due to the aerodynamic loads. After wind tunnel start-up, conditions are kept constant until the oil layer has completely dried and cannot be distorted any more during wind tunnel shut-down. For this type of test, the balance in the model is replaced by a rigid adapter. After the test, the oil film pattern is documented via photography.

3.2 Test conditions

Table 2 provides the Mach-Reynolds-conditions of the experiments performed with both capsule sizes in TMK. The given values are averaged across the entire test duration. In Fig. 6, the test conditions are plotted together with the predicted flight trajectory of the sample return capsule.

Table 2 Mach-Reynolds-conditions of wind tunnel tests (Re in millions)

Fig. 6

Test conditions and flight trajectory

The transonic tests in the Mach number range $0.5\le M\le 1.05$ can only be performed at a static pressure of ${p}_{\infty }\approx 1 \mathrm{bar}$ (see section “Trisonic Wind Tunnel Cologne “). Thus, the model Reynolds number differs from the predicted flight trajectory. Most of the supersonic tests are conducted at reduced stagnation pressures using the ejector system of the TMK wind tunnel. This allows exact rebuilding of the nominal re-entry flight trajectory of the capsule in the range $1.3\le M\le 3.5$. To assess a potential Reynolds number influence, an additional aerodynamic test with a higher Reynolds number is performed at $M=1.8$.

Due to the axial load constriction of the balance, the transonic test at $M=1.05$ cannot be performed with the baseline capsule (${D}_{\rm Ref}=0.08 \mathrm{m}$) so that the smaller capsule (${D}_{\rm Ref}=0.07\mathrm{ m}$) is used instead. For analysis of a potential influence of the reduced capsule diameter on the derived coefficients, both capsules are tested at $M=0.95$ and the results are compared. In the supersonic regime, the tests are performed with the smaller capsule up to a Mach number of $M=1.5$. The baseline model is used again for tests at higher Mach numbers up to $M=3.5$ with a common condition at $M=1.5$ for comparison.

The oil film visualisation tests are conducted at selected angles of incidence with the baseline model (${D}_{\rm Ref}=0.08 \mathrm{m}$) at two Mach numbers ($M=0.5$ and $1.5$). The test conditions are comparable to those of the corresponding aerodynamic tests. At $M=1.5$, additional visualisations are performed at a higher Reynolds number condition (i.e. at increased stagnation pressure but unchanged Mach number) to address a potential impact of the boundary layer status on the flow structure. As forces exceed the balance range at this condition, aerodynamic data are not obtained from these tests.

3.3 Coordinate system

The coordinate system given in Fig. 7 is used for definition of the aerodynamic coefficients. Its origin lies in the capsule’s $MRC$ and shows the positive direction of axes, coefficients and angles. At zero-degree incidence and yaw angle, the x-axis is positive against flow direction and the z-axis positive downwards, in direction of the gravitational force. Thus, the y-axis points positive to the right.

Fig. 7

Aerodynamic coordinate system

3.4 Uncertainty analysis

The analysis presented hereafter follows the “Guide to the expression of uncertainty in measurement” proposed by the International Organisation for Standardization (ISO 1995). The focus of this analysis is on the estimation of the measurement chain uncertainties and their impact on the determination of the aerodynamic coefficients. Other sources of uncertainty like the wind tunnel flow quality or the model support interference are not addressed in this section. A similar analysis of the uncertainty of pressure measurements in the TMK wind tunnel has already been presented by Willems (2017).

For the uncertainty analysis, the specific uncertainties related to all relevant parameters are determined first. All pressure measurements are referenced to ambient pressure. The error of the barometric scanner and additional uncertainties from the data acquisition system are expressed in a total uncertainty value for the ambient pressure ${p}_{\mathrm{amb}}$. This error is propagated and increases the uncertainties of the stagnation pressure ${p}_{0}$ as well as the static pressure ${p}_{\infty }$ to the values given in Table 3. The total uncertainty of the base pressure ${p}_{B}$ considers an additional response time uncertainty at low pressure levels. The uncertainties of the stagnation temperature ${T}_{0}$, the supersonic Mach number $M$, the reference diameter ${D}_{\mathrm{ref}}$ and the isentropic coefficient $\kappa$ (Willems 2017) are also listed in the table.

Table 3 Uncertainties of parameters, partially from (Esch 1986; Willems 2017)

The aerodynamic coefficients are calculated from the measured data for a given reference point $\mathrm{MRC}$ and an incidence angle $\alpha$. The uncertainty analysis is performed for both operation modes (supersonic and transonic) of the TMK wind tunnel. In supersonic tests, the flow Mach number is determined by the contour of the adaptable de Laval nozzle. Therefore, it is an input parameter with a known uncertainty. In transonic tests, the Mach number is calculated from a corrected pressure ratio ${p}_{0}/{p}_{\infty }$ using gas dynamic equations. The static pressure ${p}_{\infty }$ is a relevant input parameter in this case.

It is assumed that all parameters are measured with independent and random uncertainties so that the overall error can be calculated from the partial derivatives applying the Gaussian error propagation rule. The calculation is presented in the Annex. As all test parameters are recorded synchronously during one test, the uncertainties are calculated for each data set, i.e. for every time step of the test, separately. In the charts, they are given as vertical error bars.

Two examples of the uncertainty estimation are given in the following:

For a data set in a supersonic test ($M=2.0$, $Re=0.39\cdot {10}^{6}$, $\alpha =25.0^\circ )$, Table 4, a) shows the outcome of the uncertainty analysis. The first block lists the model and wind tunnel parameters ${D}_{\mathrm{ref}}$, $\kappa$, $M$ and ${p}_{0}$ together with the estimated absolute ($\Delta i$) and relative ($\Delta i/i$) uncertainties. In the second block, the measured values and uncertainties of axial ${X}_{f}$ and normal force ${Z}_{f}$, pitching moment ${M}_{f}$ and base pressure ${p}_{B}$ are given. The third block lists the aerodynamic coefficients ${C}_{A}$, ${C}_{N}$, ${C}_{m}$ and ${C}_{{p}_{B}}$ together with the calculated overall uncertainties.

Table 4 Calculated uncertainty values

The pressure level as well as the resulting forces and moments are relatively low with respect to the balance range due to the usage of the wind tunnel’s ejector system within supersonic tests. This leads to relative uncertainty values for the force coefficients ${C}_{A}$ and ${C}_{N}$ of $\pm 1.4\%$, for the pitching moment ${C}_{m}$ of $\pm 2.2\%$ and for the base pressure coefficient ${C}_{{p}_{B}}$ of $\pm 7.8\%$.

Table 4, b) shows the uncertainty calculated for a transonic data set ($M=1.05$, $Re=2.5\cdot {10}^{6}$, $\alpha =25.0^\circ$), where the calculated Mach number uncertainty is below $\pm 0.2\%$. Due to the higher pressure level as well as the related higher forces and moments, the overall uncertainties of the coefficients are smaller than in the supersonic test. They are approximately $\pm 0.4\%$ for ${C}_{A}$ and ${C}_{N}$, $\pm 0.6\%$ for ${C}_{{p}_{B}}$ and $\pm 1.5\%$ for ${C}_{m}$.

Experience shows that the flow quality in the TMK wind tunnel is higher at supersonic conditions than in the transonic test section with its perforated side walls. In the presented uncertainty analysis, such systematic errors are not being accounted for. Therefore, the provided values give only an estimate of the uncertainties of the performed aerodynamic measurements and yield seemingly lower uncertainty values for the transonic testing.

4 Experimental results

The MarcoPolo-R shape is investigated in a wide Mach number range within numerous wind tunnel tests. Aerodynamic data are obtained from static force and moment measurements, and an aerodynamic database is built for the given capsule configuration. The flow structure around the wind tunnel model is investigated applying schlieren and oil film visualisation techniques.

Within this study a huge amount of experimental and numerical data have been generated, which cannot be described in a single publication. Therefore, only a selection of results is presented. In this section, an overview of the general aerodynamic behaviour of the capsule is given by presenting the determined coefficients. The observed tendencies are described. Furthermore, the flow topology is discussed briefly at the example of supersonic schlieren images at $M=1.8$ and $3.0$ as well as a subsonic test case at $M=0.5$ where oil film visualisation is performed.

This section concentrates on experimental results only. A more detailed analysis for $M=1.5$ is given in the following chapter.

4.1 Aerodynamic coefficients

The charts in Fig. 8 show data of tests with the baseline capsule model (${D}_{\rm Ref}=80 \mathrm{mm}$) plotted against the incidence angle $\alpha$. For the axial fore body force coefficient ${C}_{{A}_{FB}}$, results of the smaller capsule model are also shown and indicated accordingly.

Fig. 8

Aerodynamic coefficients: Axial force ${C}_{A}$, base pressure ${C}_{{p}_{B}}$, axial fore body force ${C}_{{A}_{FB}}$, normal force ${C}_{N}$ and pitching moment ${C}_{m}$

First, the axial force coefficient ${C}_{A}$ is shown (a). The coefficient is highest at $\alpha =0^\circ$ and decreases slightly with an increasing angle of incidence. In the subsonic range, the level of ${C}_{A}$ increases with Mach number. In supersonic this trend is reversed. The calculated uncertainties are small and show in supersonic cases only, in which the pressure level is reduced via the ejector system. In transonic regime, the higher-pressure level leads to a better load factor for the balance, thereby yielding smaller uncertainty values (see section “Uncertainty Analysis”).

The axial force coefficient can be divided into a fore body part and a base part:

$${C}_{A}={C}_{{A}_{FB}}+{C}_{{A}_{B}},$$

whereby the base part is calculated from the measured base pressure coefficient as

$${C}_{{A}_{B}}=-{C}_{{p}_{B}}\cdot \frac{{S}_{B}}{{S}_{\rm Ref}}$$

considering the ratio of the base area ${S}_{B}$ to the reference area ${S}_{\rm Ref}$.

The corresponding coefficient ${C}_{{p}_{B}}$ is shown with reversed ordinate axis direction (b). The base pressure is measured inside the shell (Fig. 3) and assumed to be representative for an average pressure distribution on the capsule’s rear side. In this study, the base pressure coefficient is negative by definition and increases with the Mach number. All curves show a slight decrease when the angle of incidence is increased. The uncertainties shown in the graphs amount to several percent, especially at supersonic conditions where the pressure level is low.

The axial fore body force coefficient ${C}_{{A}_{FB}}$ is calculated according to the above equations for an area ratio of ${S}_{B}/{S}_{\rm Ref}=1$ and plotted next (c). Similar to ${C}_{A}$, the fore body part ${C}_{{A}_{FB}}$ is highest around $\alpha =0^\circ$ and decreases with an increasing angle of incidence. Apart from small deviations, the shape of the curves is comparable across all plotted Mach numbers. It just shifts to a higher level when Mach number is increased.

The change in the base pressure with the Mach number leads to the reversed trend in ${C}_{A}$ in the supersonic range. By reducing ${C}_{A}$ to ${C}_{{A}_{FB}}$, thus removing the base pressure’s influence, this trend is eliminated. Additional measurements plotted in the chart show comparable curve characteristics, also for the smaller capsule (suffix “70” in the graph) that has been used for Mach numbers close to unity.

The normal force coefficient ${C}_{N}$ is plotted in a skew Cartesian coordinate system with an inclined ordinate axis (d). At all conditions, the coefficient is zero at $\alpha =0^\circ$ (due to capsule symmetry) and increases with incidence angle and test Mach number. Different curve characteristics are observed depending on the test Mach number.

In the subsonic regime, ${C}_{N}$ shows a rather small positive gradient $d{C}_{N}/d\alpha$ at zero degrees angle of incidence. This gradient increases with the angle up to $\alpha \approx 15^\circ$ and stays nearly constant for higher angles. In contrast, for $M\ge 2.5$, the initial gradient is higher, but continuously decreases with increasing $\alpha$. In the range of $1.5\le M\le 2.0$ all curves start at the origin with a positive gradient, then pass a turning point ($\alpha \approx 20^\circ , 15^\circ , 11^\circ$, respectively) before the gradient turns negative.

This Mach number dependent curve characteristics are also observed for the pitching moment coefficient ${C}_{m}$ that is also plotted in a skew coordinate system (e). For the symmetrical capsule all curves show a pitching moment that is zero at $\alpha =0^\circ$ and then decreases with increasing incidence angle. This gives the capsule a statically stable aerodynamic behaviour in the investigated Mach number range (supposed: $MRC = CoG$). In the subsonic regime ($M\le 0.8$), the Mach number dependency of ${C}_{m}$ is small. This leads to comparable values at different Mach numbers up to an incidence angle of $\alpha \approx 18^\circ$. Above that angle, the capsule’s stability increases with the Mach number. In higher supersonic ($M\ge 2.5$) the absolute value of the gradient $\left|d{C}_{m}/d\alpha \right|$ is initially higher than in subsonic, but constantly decreases with increasing angle. In the range of $1.5\le M\le 2.0$ the gradient’s amount is initially smaller or comparable to the subsonic cases, but changes tendency twice giving two turning points on each curve ($\alpha =8.0^\circ /21.4^\circ$, $6.6^\circ /17.6^\circ$, and $6.7^\circ /{14.6}^\circ$ , respectively).

The above analysis reveals the change in the capsule’s aerodynamic behaviour when decelerating from supersonic to subsonic conditions and thereby underlines the necessity of performing experiments in the complete Mach number range.

4.2 Schlieren visualisation

The schlieren technique is used to visualise density gradients in the flow field. In the TMK it is applicable for Mach numbers of $M\ge 1.25$ . In the test campaign setup, a vertical knife edge in a spherical holder is used. Thus, the density gradients in direction of the inflow are resolved. The orientation of the knife edge leads to compression regions (positive gradients) being visualised as dark areas and acceleration regions (negative gradients) showing as bright areas. In case of high negative gradients, the holder acts as an additional aperture and the corresponding regions unexpectedly appear dark.

Figure 9 shows schlieren images of the capsule at an incidence angle of $\alpha =20^\circ$ and a free stream Mach number of $M=1.8$ (a) as well as $3.0$ (b), respectively. A thick dark region ahead of the capsule (A) is clearly visible in both images. This is the two-dimensional visualisation of the three-dimensional bow shock. Characteristic parameters of that shock wave are its curvature and the relative stand-off distance $\delta /D$ between shock and capsule’s surface. With increasing Mach number, the curvature of the shock is increased as well. At the same time, the stand-off distance decreases in case of the displayed tests from $\delta /D\approx 0.23$ at $M=1.8$ down to $\delta /D\approx 0.11$ at $M=3.0$. It is observed that during all supersonic tests the shock stand-off distance at the stagnation point is almost independent of the incidence angle (if within the investigated range), thus staying approximately constant when the angle is altered.

Fig. 9

Schlieren images

On the stagnation point streamline (arrow in Fig. 9), the bow shock acts as a normal shock. With increasing radial distance, it turns into a curved shock wave and finally into a strong oblique shock. Passing the bow shock, the air flow is decelerated to subsonic speed. Flow direction ahead of the capsule is turned into radial direction and a re-acceleration along the surface takes place. With a sufficiently inclined capsule, the leeward accelerated flow soon returns to supersonic speed. In both displayed cases for $\alpha =20^\circ$ a re-deceleration takes place in a second three-dimensional shock wave (B). The shock forms near the junction between the spherical nose and the conical part of the capsule.

At the capsule’s shoulder the flow expands and re-accelerates. For both Mach numbers, an expansion fan is visible on the windward side (C). Downstream the capsule, the shear layer emanating from the capsule’s shoulder and confining the wake flow, is visible (D, E). On the leeward side, the straight shear layer’s shape (D) implies that there, in both cases, the flow separates at the capsule’s shoulder. On the windward side, the shear layer tends to follow the capsule’s rear contour and curves towards the sting (E). At $M=1.8$ (a) the shear layer smears with increasing distance from the base, whereas at $M=3.0$ (b) the shear layer merges further downstream the capsule (F).

4.3 Oil film visualisation

Schlieren visualisation is not possible in the transonic test section of the TMK. Therefore, by means of oil film visualisation at selected test conditions, at least the surface streamlines can be visualised. Figure 10 shows the oil film images that were photographed after a test at $M=0.5$ and an angle of incidence $\alpha =15^\circ$.

Fig. 10

Oil film visualisation at $M=0.5, \alpha =15^\circ$

The image of the model’s front surface (a) shows a stagnation region (S) where the flow is turned towards radial direction and re-accelerated along the visible streamlines. These lines are curved (B-D) because of the compressibility effects which are higher on the leeward side. The flow pattern is symmetrical to the vertical plane (A) and a circular structure is visible (R) in the oil film visualisation at the sphere-cone-transition.

The side view (b) confirms that structure in the flow pattern. Additionally, the pattern on the sting shows that the wake flow hits the sting at a certain distance downstream the capsule. In the base region (c), a circumferential structure of the oil film pattern is visible that includes two stagnation regions (S) in the symmetry plane. Although the oil film images show surface streamlines of a subsonic test case, similarities in the structure to the supersonic test cases shown in the above schlieren images can be observed.

5 Numerical rebuilding

In the experimental test campaign, a complex interaction between the leeward shock system and the boundary layer on the capsule’s surface is observed, especially at a test Mach number of $Ma=1.5$. The experiments at this Mach number are rebuilt numerically to assist the analysis and interpretation of the test results. The numerical simulations are not the focus of this study. The 2016 version of the flow solver TAU, developed by DLR (Schwamborn and Gerhold 2006; Langer et al. 2014), is used for the simulation.

The TAU code applies the finite volume method to the Navier–Stokes equations. It uses structured, unstructured and hybrid grids. Several one and two equation turbulence models as well as Reynolds stress and DES models are available in the flow solver for simulation of turbulent flows. Laminar and inviscid simulations can be conducted using TAU, too. Besides the perfect gas, real gases as well as reacting flows in equilibrium and chemical and/or thermal non-equilibrium can be simulated. The TAU code provides different techniques for convergence acceleration, such as local time stepping and multigrid approaches.

5.1 Computational domain

In this work, a hybrid grid with $13$ prism layers is generated via the Centaur grid generation software. The prism layers allow sufficient resolution of the boundary layer while keeping the computational costs in an acceptable range. The thickness of the prism layers does not get adjusted during the calculation but is configured before such that the requirements of the respective turbulence models are met. The adaptation routine implemented in TAU is used for local refinement of the mesh to better resolve the shock structures. The grid is also pre-refined in the regions of interest. The symmetry of the test setup is used to reduce the numerical effort by cutting the flow field in half.

The sting holding the sample in the wind tunnel experiments is included in the numerical grid. The connection between sting and model is simplified as a $1 \mathrm{mm}$ gap. The initial grid has a total of $18.5$ million cells and $3.2$ million vertices. It gets adapted during the simulation to $55 - 65$ million cells and $10 - 12$ million vertices. The exact number varies with the simulations. Figure 11 shows a close-up of the initial (a) and a fully adapted grid (b). The high resolution in the area of the detached bow shock and the shock on the model’s shoulder are obvious.

Fig. 11

Initial grid (a) as generated with Centaur Software and an example of a fully adapted grid (b). Here: $M=1.5, \alpha =19^\circ , Re=0.46\cdot {10}^{6}$, laminar flow

The sensitivity of the solution to the grid resolution is assessed by reducing the grid size. As shown in Table 5, the coarse grid (cell count reduced by a factor of five) yields the same aerodynamic coefficients. The general use of the fine grid as baseline is justified by the interest in the secondary shock system. The impact of these shocks on the coefficients is small and below the overall numerical uncertainty. Nevertheless, the shock system requires a high grid resolution for being resolved.

Table 5 Aerodynamic coefficients for different boundary conditions at $M=1.5$ and $\alpha =19^\circ$

5.2 Visualisation of numerical solutions

The commercial Tecplot software is used to visualise the numerical results. Tecplot allows the investigation of most flow properties and effects, including the visualisation of surface tension lines. This enables a comparison with the oil film photographs. However, the software does not provide the necessary functionality to generate schlieren images (integration of the density gradient over the ray of light path). Thus, an in-house developed tool is used for this purpose: the Nice program (Numerical Images for Comparison with Experiments). Nice is dedicated to the calculation of schlieren images from numerical data. The program considers the experimental boundary conditions, such as the orientation and the type of the knife edge. The major simplification used is that the software assumes that the refraction of the light is negligible. This allows an implementation of a computationally efficient ray-tracing algorithm that does not need to change the orientation of the light rays during their passage through the numerical domain. This simplification is found to be negligible for the conditions achievable in the wind tunnel testing in TMK, but could be relevant in case of high density gradients and/or wide test sections. Apart from this simplification, the approach for generating computed schlieren images rebuilds the physical principle.

5.3 Boundary conditions

The cold flow in combination with the low densities in the test section allows utilizing the perfect gas simplifications in the numerical rebuilding. For the low Reynolds number condition ($Re=0.46\cdot {10}^{6})$, a laminar boundary layer is expected and set as baseline. However, due to the turbulence present in the wind tunnel and the test model’s Reynolds number, a fully turbulent flow is assumed in case of the high Reynolds number condition ($Re=2.7\cdot {10}^{6}$). For both, the high and low Reynolds number, the turbulence model is varied to assess its impact on the simulation results and specifically on the capturing of the shock system structure.

The Shear Stress Transport model (SST) of Menter (1994) is the baseline for turbulent modelling. The one equation Spalart–Allmaras (1994) model (SAO) in a TAU specific formulation and the Wilcox (1988) k Ω two equation model (k Ω) are used for comparison. To assess the potential relevance of the anisotropy of the turbulence, the Reynolds stress equation model (RSM) is used as well. The RSM standard formulation of TAU uses the above-mentioned SST model. See (Langer et al. 2014) for the implementation of the turbulence models in TAU.

The computational resources available to the authors are limited, so a stationary modelling of the flow is necessary. As the numerical investigations are intended to support the interpretation of the experimental results, the main interest is the flow before the shoulder. The aft flow has a negligible influence on the forebody flow due to the supersonic Mach number. The stationary modelling is therefore considered acceptable despite the problems in simulating the aft flow.

The laminar simulations show a non-stationary nature in the wake region. This results in the laminar simulations not converging to a stable solution within a reasonable number of iterations. Instead, the aft flow shows an oscillating behaviour. This is contradictory to the stationary simulation approach. The resulting flow and the aerodynamic coefficients vary accordingly with the number of iterations. This is not observed when a turbulence model is used.

Figure 12a gives an impression of a non-converging aft flow showing the numerical schlieren image for the low Reynolds number condition and laminar simulation at $\alpha =19^\circ$ angle of incidence. When the SST turbulence model is applied (b), the non-stationary nature in the wake region disappears and the obtained structure of the secondary shock system before the capsule’s shoulder changes. Increasing the Reynolds number shows no further visual impact on the simulated flow structure (c).

Fig. 12

Num. schlieren images, $M=1.5, \alpha =19^\circ$

These stability issues lead to a fluctuation of the base pressure for the whole angle of incidence range. The degree depends on the capsule orientation. Aerodynamic coefficients that include the base pressure (${C}_{A}$ and ${C}_{{p}_{B}}$) reflect this.

Table 5 shows the aerodynamic coefficients at $M=1.5$ and $\alpha =19^\circ$ for the various turbulence models and the laminar flow at different Reynolds number conditions. Aerodynamic coefficients are extracted from the final solution after the same number of iterations for all cases, unless otherwise stated.

The stable fore body flow results in a low variation of ${C}_{{A}_{FB}}$ for all cases, including the different turbulence settings and Reynolds numbers. The secondary shock structure has a small influence on the fore body force coefficient due to its limited extension and surface pressure impact. In case of the laminar simulations at low Reynolds numbers, the system of multiple shocks yields slightly lower fore body force coefficients.

The base pressure coefficient ${C}_{{p}_{B}}$ shows a higher variation between the different cases as well as within one case at a varying number of iterations. The simulations with higher iteration count show that the numerical solution is not fully converged in the aft flow region after the baseline iteration number. Unfortunately, it is not possible for the authors to run all calculations with a sufficient number of iterations. The same tendency is observed for the low and high Reynolds number condition: a higher number of iterations leads to smaller base pressures, which is reflected in the results in Table 5. Within one simulation, the base pressure coefficient variation is small for turbulent and high for laminar modelling due to the non-stationary aft-flow nature.

A tendency can be observed for the different turbulence models. At both baseline conditions the RSM and the SST model give similar results, while the k Ω model shows a lower and the SAO model a higher base pressure. As the simulations are not fully converged, it is unclear whether this comes from the turbulence models converging at a different rate or if they yield substantially different end results. The laminar simulations give even higher base pressures than the SAO, unless they are allowed to iterate longer. The base pressure coefficient variations transfer directly to ${C}_{A}$.

The normal force coefficient ${C}_{N}$ shows some scattering, but no systematic differences between the different turbulence models. Simulations with the complex shock system with multiple shocks give slightly higher normal force coefficients. This is explained by the reduction in the surface pressure in the shock system region. However, the impact on the coefficient is small.

The moment coefficient ${C}_{m}$ shows some variation of non-systematic nature, while the influence of the shock system on this parameter seems too low to evaluate.

5.4 Numerical results

The trends of the aerodynamic coefficients at $M=1.5$ derived from the numerical results agree with the measured data (Fig. 13). The numerical data points of the fore body force coefficient ${{C}_{A}}_{FB}$ match the experimental curve. This indicates that the numerical rebuilding of the tests captures the major flow phenomena to a sufficient degree. The differences in the fore body force coefficient curves of the high and low Reynolds number conditions are small, as has been observed for the boundary conditions variation at a constant angle of incidence in the previous section. This proves that the secondary shock system, despite being very dissimilar for the two cases (this will be shown and discussed later), has a smaller impact on the coefficient than could have been expected.

Fig. 13

Aerodynamic coefficients at $M=1.5$ derived from numerical results (squares and triangles) compared to wind tunnel measurements (solid lines)

The experimental ${{C}_{A}}_{FB}$ values are calculated from the measured axial force coefficient ${C}_{A}$ by subtraction of ${C}_{{p}_{B}}$. The latter is derived from the base pressure measurement (approximated by the static pressure inside the shell). Thus, the agreement between numerical and experimental fore body force coefficient proves that the approach to approximate the base pressure is reasonable and the corresponding values are accurate.

The issues with the convergence and stability of the after-body flow in the numerical simulation shows in the fluctuation of the base pressure coefficient ${C}_{{p}_{B}}$ over the angle of incidence. As highlighted in the previous section, this mainly concerns the low Reynolds number with its laminar flow. Accordingly, the variations of the coefficient are more pronounced in this case, where numerical and experimental values fit well for low angles of incidence, but an increasing offset is visible at higher angles. In the turbulent boundary layer case, the base pressure coefficient derived from the numerical results shows smaller variations and a low constant offset to the experimental data.

The axial force coefficient ${C}_{A}$ includes the base pressure coefficient, so that the fluctuations and offset can be observed in this coefficient, too. As known from the boundary condition variation, the simulations are not fully converged after the baseline number of iterations. The base pressure coefficient is reduced when the simulation is iterated further (Table 5). The coefficient derived from the single low Reynolds number simulation with a higher iteration count fits the experimental data at $\alpha =19^\circ$. The authors therefore believe that a good agreement of experimental and numerical base pressure as well as axial force coefficient could be achieved in the full range of the angle of incidence with a sufficiently high number of iterations.

The normal force coefficient ${C}_{N}$ and the pitching moment coefficient ${C}_{m}$ are less sensitive to a correct capturing of the after-body flow. Accordingly, they coincide well with the measured data. This is explained by the fact that the surface pressure is significantly higher on the front of the capsule and the numerical issues only concern the rear. A slight difference in the pitching moment is observed between the two numerical cases. The experimental data are fit by the laminar simulation where the application of the turbulence model leads to slightly higher absolute values up to $\alpha \approx 17^\circ$. Above this angle, the coefficients coincide well for both cases.

6 Shock structure analysis

At certain conditions, the shock wave boundary layer interaction leads to a secondary shock system on the leeward side of the capsule that is worth to be further investigated. The analysis is based on experimental and numerical images at an inflow Mach number of $Ma=1.5$ as well as low and high Reynolds number conditions. In a first step, this analysis is performed in the frame of the inclined capsule system and the observed structures are classified with regard to the literature. Then, in a second step, the shock boundary layer interaction is investigated in detail in a more universal frame. Therefore, close-up views of the marked areas in the schlieren images are used.

The following considerations are used for interpretation of our results.

6.1 Classification of shock boundary layer interaction types

According to Houghton et al. (2013), the interaction of a laminar boundary layer with a near-normal shock wave on a convex surface can be categorized in the interaction types shown in Fig. 14. In case of the “multiple-interaction” type (Fig. 14a), a supersonic Mach number close to unity leads to a weak primary shock wave with gradual thickening of the boundary layer before the shock. Compression waves form upstream and join the main shock wave at some distance from the surface. This smears the shock foot. The weak primary shock decelerates the flow to subsonic speed. Downstream the initial shock the boundary layer thickness decreases. This causes local expansion and re-accelerates the flow back to a low supersonic speed. This leads to another weak near-normal shock that develops in a similar way. Depending on the conditions, a varying number of subsidiary shock waves form until the re-accelerated flow stays subsonic. Local boundary layer separation with reattachment may occur below the initial shock wave, but the laminar boundary layer stays attached in general and transition to turbulence is not observed.

Fig. 14

Near-normal shock interaction with laminar boundary layer, sketches reproduced from (Houghton et al. 2013) with permission of the rights holder Elsevier. Copyright 2013, Elsevier, Ltd. All rights reserved. Nomenclature introduced by the authors

With increased inflow Mach number, the first shock becomes stronger and the interaction type eventually changes to the “doublet-interaction” (Fig. 14b). The stronger first shock leads to an increased thickening of the boundary layer accompanied by a laminar separation bubble. The expansion caused by the following boundary layer thinning re-accelerates the flow back to supersonic speed and a second shock wave decelerates the flow to subsonic condition. Transition to turbulence and reattachment of the boundary layer is likely to occur.

At higher Mach numbers, the interaction type transitions to the “$\lambda$-interaction” (Fig. 14c). The stronger initial shock yields a pressure rise high enough for the laminar boundary layer to separate ahead of the shock. Thus, the direction of the flow outside the boundary layer is caused to change, forming an oblique shock wave that joins the main shock at some distance from the surface. The transitional boundary layer downstream the $\lambda$-shaped shock stays detached. This prevents re-acceleration and subsidiary shock waves.

In case of a near-normal shock interacting with a turbulent boundary layer, separation of the boundary layer is less likely to occur (Houghton et al. 2013). The turbulent boundary layer thickens faster ahead of the shock wave. The compression waves are therefore found closer to the shock. The shock foot appears slightly smeared, but a $\lambda$-formation is not observed. Boundary layer thinning downstream the shock, flow re-acceleration and subsidiary shock waves are not to be expected. If the pressure gradient is high, the turbulent boundary layer separates ahead of the shock wave and a $\lambda$-interaction, as described for the laminar boundary layer case, occurs (see Fig. 14c).

6.2 Low Reynolds number condition

Additional aerodynamic tests are performed at the low Reynolds number condition using the ejector system of the wind tunnel. Figure 15 shows four schlieren images taken from a single test with a slowly varying angle of the model. The angle of incidence in these images ranges from 17.7 to 21.5 degrees (a-d). Justified by the slow angle variation in the polar test, stationary conditions are assumed. In addition to the schlieren pictures, the front surface oil film pattern of two angles of incidence is gathered via dedicated tests (j, l). Schlieren images (e–h) and surface tension lines (m-p) derived from laminar numerical simulation at the same conditions and angles complete the figure.

Fig. 15

Experimental and numerical visualisations for low Reynolds number case, $M=1.5, {R}{e}\approx 0.46\cdot {10}^{6}$

At the incidence angle $\alpha =17.7^\circ$, a dark region around the leeward sphere-cone-transition is visible both in the experimental and the numerical schlieren image (Fig. 15a, e). The shock starts to form, but structures could not yet be resolved. This is explained by the low strength of the shock in combination with its three-dimensional structure. The pattern of the surface tension lines (Fig. 15m) reflects this.

When the incidence angle is increased, a shock system of the multiple-interaction type described above forms for $\alpha =19.0^\circ$ (Fig. 15b). Typical for this type, the shocks appear to be slightly smeared. Compression waves ahead of the shocks contribute to this, but also the three-dimensional flow and the curved shape of the shocks in combination with the line-of-sight nature of the schlieren imaging technique. In the experiment, the initial and at least three successive shocks are visible, while the numerical schlieren image (Fig. 15f) only shows the initial and one successive shock wave.

The formation of the multiple-interaction implies that the boundary layer on the capsule’s surface is laminar at the low Reynolds number condition, see (Houghton et al. 2013). There is no transition to turbulence and a local separation bubble develops below the initial shock wave. This is confirmed by the oil film pattern (Fig. 15j). The pattern indicates an attached boundary layer until the foot of the initial shock. The different appearance of the oil streaks right upstream seems to be caused by the compression waves as well as the according early thickening of the boundary layer. The downstream oil accumulation in the central part represents a local separation region. It extends further downstream until the second shock. This behaviour is probably caused by the volume of oil that is accumulated. The pattern implies that, downstream the shock foot, the boundary layer from both sides is transported into the central region. The numerical surface tension lines confirm the separation bubble and the transversal flow (Fig. 15n). Regard that the theoretical cases in the section above consider a two-dimensional flow field, but the surface of the capsule and the surrounding flow are three-dimensional.

A flow structure with elements of the multiple-interaction is observed at $\alpha =20.3^\circ$ (Fig. 15c). The higher incidence angle leads to a further re-acceleration and an increased pre-shock Mach number. The compression waves ahead of the initial shock merge into an oblique shock with increased strength represented by a higher gradient (darker grey level) in the schlieren image. This weakens the second foot of the $\lambda$-shaped shock. Downstream the initial shock, the flow is re-accelerated and one subsidiary shock wave follows. Compared to the previous case, the deceleration by the initial shock is higher. Accordingly, the re-acceleration takes longer and the distance to the subsidiary shock increases. The shock structure is well reproduced in the numerical simulation (Fig. 15g) with only a slightly different shape of the initial shock. Unfortunately, oil film visualisation was not performed at this angle of incidence, so the above interpretation cannot be further supported and comparison with the surface numerical tension lines (Fig. 15o) is not possible.

The capsule configuration differs from the theoretical cases discussed in the previous section in two essential points: the flow structure is highly three-dimensional and there is a discontinuity in the second derivative of the surface at the sphere-cone-transition. Regard that the shock changes its orientation with increasing angle of incidence, thereby moving downstream. However, the front foot of the shock remains ahead of the surface discontinuity at all angles in the experimental and numerical images. This might force the initial shock to adapt a $\lambda$-shape, while without the discontinuity it would be an oblique shock positioned further downstream.

Figure 15d shows the experimental schlieren image for $\alpha =21.5^\circ$. The photograph seems to show a single oblique shock wave with the origin near the sphere-cone-transition and a slight S-shape. A similar shock wave is visible in the numerical schlieren image (Fig. 15h), but a closer look into simulation details at this condition (not shown) reveals that at least in the central part of the flow the shock is still a $\lambda$-shock about to becoming oblique. The second foot is not resolved in the line-of-sight schlieren visualisation.

The oil film pattern in Fig. 15l confirms the existence of boundary layer separation with a visible backflow and—probably—no reattachment in the central region. On both sides, oil accumulation areas are observed. They are interpreted as local separation bubbles with reattachment downstream. The oil film pattern shows a highly complex flow structure on the capsule’s surface that is nicely rebuilt in the numerical simulation. The surface tension lines (Fig. 15p) explain the oil accumulation and show a detachment in the central area. In comparison to the lower angle of incidence case, a higher circumferential extension of the shock foot is observed in the oil film image.

6.3 High Reynolds number condition

A transition of the laminar boundary layer to turbulence is not observed at the low Reynolds number condition, so this point is addressed separately. For this investigation, the Reynolds number is increased by a factor of about $5.5$ to $Re=2.7\cdot {10}^{6}$. This is obtained via increasing the dynamic pressure ${q}_{\infty }$, which leads to a higher load on the model and the support system. The balance therefore had to be replaced by a rigid adapter. Nonetheless, vibrations are observed during the tests and a further increase of the dynamic pressure is not advisable.

One slow motion $\alpha$-sweep and three oil film tests ($\alpha =17.7^\circ /19.0^\circ /21.5^\circ$) are performed at the higher Reynolds number condition. Four schlieren images, recorded at the same angles as in the low Reynolds number case, are shown in the top row of Fig. 16. The third row of this figure shows the photographed front surface oil film patterns. Here, again, the figure is completed with corresponding numerical simulation results.

Fig. 16

Experimental and numerical visualisations for high Reynolds number case, $M=1.5, {R}{e}\approx 2.7\cdot {10}^{6}$

For an angle of incidence of $\alpha =17.7^\circ$, the density gradients in the schlieren image (Fig. 16a) are interpreted as multiple-interaction shock system (Houghton et al. 2013). This effect indicates a laminar boundary layer. The second shock is followed by another weak compression wave, that can just be resolved by the schlieren setup. The first shock is located ahead of the discontinuity on the capsule’s surface (sphere-cone transition), as observed before. The shock system is not correctly reproduced in the numerical simulation (Fig. 16e) because of the fully turbulent modelling of the flow. This suggests that the flow on the capsule’s front remains laminar under the given conditions in the experiment.

The oil film pattern (Fig. 16i) supports the assumption of laminar flow until the shock system, but without early thickening of the boundary layer as has been observed in the low Reynolds number case (Fig. 15j). A very localized separation bubble below the main shock wave with reattachment is indicated in the central region. Downstream, transition to turbulence seems to occur (strip-like pattern). Despite the turbulent modelling, the image of the numerical surface tension lines (Fig. 16m) agrees well with the pattern of the oil film picture. The laminar-turbulent transition is missing due to obvious reasons, so that the main difference is the circumferential extension of the curved shock. This is probably limited in the numerical rebuilding either because of grid resolution constraints or related to the turbulent modelling.

When increasing the incidence angle to $\alpha =19.0^\circ$, the secondary shock system transitions to a doublet-interaction with compression waves ahead and the main shock followed by a small subsidiary shock wave (Fig. 16b). In the oil film pattern in Fig. 16j, a laminar pre-shock boundary layer is indicated. A local separation bubble, which is more pronounced than at the lower incidence angle forms below the main shock wave. Downstream, the oil-film pattern indicates a transitional, attached boundary layer that is only found in the doublet-interaction (Fig. 14b). This boundary layer transition, which is not rebuilt in the fully turbulent numerical simulation, explains the difference in the shock system between numerical and experimental results. The turbulent numerical rebuilding shows a single normal shock with a small oblique part at the foot (Fig. 16f). The extension of the normal shock is very similar to the experiment, but the oblique part of the shock appears smaller in the simulation. The surface tension lines (Fig. 16n) agree well with the oil film traces, again. But, as discussed before, the circumferential extension of the curved shock is reduced in the numerical solution.

At higher incidence angles a shock structure of a $\lambda$-interaction type is found for both the experimental and numerical investigations. The main part of the shock is normal to the surface first ($\alpha =20.3^\circ$, Fig. 16c), then bends and moves downstream ($\alpha =21.5^\circ$, Fig. 16d). Along with the change of the shock’s orientation and position, the extension of the formed $\lambda$-shock grows. Numerical simulations (Fig. 16g, h) show an excellent agreement with the experiment on position, shape and extension of the shock for both incidence angles. Yet, the numerical tools have problems refining the shock further away from the surface, where it becomes weak and diffused (Fig. 16h).

The increasing distance between main shock and onset of the oblique shock wave leads to a growing separation region, that is also reflected in the oil film pattern for $\alpha =21.5^\circ$ (Fig. 16l) and the surface tension lines for both incidence angles (Fig. 16o, p). In this case, the authors interpret the oil film pattern as showing a transition to turbulence already ahead of the shock system and a boundary layer separation probably without downstream reattachment. This fits to the observed agreement between experiment and turbulent CFD simulation.

6.4 Shock boundary layer interaction analysis

The impact area of the leeward shock system on the capsule’s surface is relatively small. Therefore, as has been shown in a previous section, the change in the shock system does not influence the aerodynamic coefficients of the capsule significantly. With the changing interaction of the shock with the boundary layer, a local separation bubble, a transition to turbulence or a complete detachment of the boundary layer can occur. These flow features and the ability to predict them numerically are of minor relevance for the field of capsule aerodynamics. But they are interesting in other research fields where shock boundary layer interaction is concerned. Increasing the capsule’s angle of incidence has a comparable effect on the flow structures as increasing the inflow Mach number.

For analysis of the observed shock boundary layer interaction in a more general context, close-up views of the marked areas of experimental and numerical schlieren images in Figs. 15 and 16 are extracted and plotted horizontally aligned in Figs. 17 and 18. A thin orange line marking the capsule’s surface and a millimetre-scale with its origin (longest tick) at the surface discontinuity in the mid-plane are added.

Fig. 17

Experimental and numerical shock structure details for low Reynolds number case, $M=1.5, {R}{e}\approx 0.46\cdot {10}^{6}$

Fig. 18

Experimental and numerical shock structure details for high Reynolds number case, $M=1.5, {R}{e}\approx 2.7\cdot {10}^{6}$

In case of the low Reynolds number (Fig. 17), a good agreement is observed between experiment and numerical simulation. This justifies the application of the laminar boundary layer condition. At the lowest pre-shock Mach number (Fig. 17a, e), a weak shock starts to form near the surface $1-2 \mathrm{mm}$ ahead of the discontinuity, but details could not be resolved at that condition. A thickening of the boundary layer follows that is hardly visible in the experiment (bright region next to the surface), but clearly observable as a bright region along the wall in the simulation.

Increasing the pre-shock Mach number (Fig. 17b, f) leads to formation of a multiple-interaction with the main shock wave originating at the surface discontinuity. A discrepancy in shock distance and the number of successive shocks between experiment and simulation is visible. This demonstrates the challenge of correctly rebuilding the complex interaction structure at the given conditions. The line-of-sight nature of the schlieren technique in combination with the three-dimensional flow field around the capsule leads to slightly smeared shock structures. The compression waves ahead of each shock add to this effect. It is visible in experiment and simulation that the boundary layer thickens along the shock system. A downstream detachment is not observed. Unfortunately, further details of the boundary layer development along the shock system, as indicated in the illustration of this case in Fig. 14a, could not be resolved.

A further increase in the pre-shock Mach number turns the compression waves ahead of the initial shock into an oblique shock wave that causes higher deceleration. This weakens the second foot of the $\lambda$-shaped shock as can be concluded from the grey level in the experimental and numerical images (Fig. 17c, g). The schlieren visualisation of the three-dimensional oblique shock implies a shock foot $1-2 \mathrm{mm}$ ahead of the discontinuity while the normal part moves downstream. This indicates an impact of the surface discontinuity on the position and structure of the shock system. The increased deceleration across the $\lambda$-shaped shock leads to a downstream shift of the successive shock as it takes longer to re-accelerate the flow to supersonic speed. Position and shape of the first shock wave up to the junction of the normal and oblique part are predicted correctly by the numerical simulation. Discrepancies are found farther away from the surface. The position of the second shock is predicted further downstream than visible in the experimental image.

If the pre-shock Mach number increases further, the angle of the oblique shock becomes smaller and the junction of the oblique and normal part moves away from the surface. An increase in strength of the oblique shock weakens the second foot until, in case of the highest pre-shock Mach number (Fig. 17d, h), only the oblique shock wave remains visible with its origin still $1-2 \mathrm{mm}$ ahead of the discontinuity. The $\lambda$-shape of the shock around the mid-plane (see previous section), is not resolved in the schlieren visualisation. Position and shape of the oblique shock wave coincide well between experiment and simulation.

Despite the complex and three-dimensional flow, it was possible to rebuild the shock boundary layer interaction fairly well numerically at the low Reynolds number using a laminar boundary layer condition. The close-up views visualise that the shock boundary layer interaction starts slightly ahead of the surface discontinuity in all cases. Boundary layer development along the capsule surface is influenced by the discontinuity and thereby affects formation of the different shock systems. Unfortunately, in the present study, neither resolution of the schlieren optic nor the resolution of the numerical simulation allow a deeper analysis of the interaction process around the discontinuity.

In the high Reynolds number case, a turbulent boundary layer was assumed for numerical simulation. The experimental results show a transitional character of the flow field, so that differences in the shock boundary layer interaction structures are visible in Fig. 18.

At the lowest pre-shock Mach number, the schlieren image (Fig. 18a) shows a shock system of the multiple-interaction type that extends less into the far field than the shock observed in the low Reynolds number case (Fig. 17b, f). The normal part of the initial shock wave is found about $1 \mathrm{mm}$ ahead of the sphere-cone-transition. The experimental schlieren image is interpreted to show compression waves ahead of each shock, that are slightly smeared by visualisation effects. Boundary layer thickening is limited to the length of the shock system and shows as a dark gradient in the schlieren image. In contrast to this behaviour, the numerical simulation (Fig. 18e) predicts a single shock wave with an oblique foot. The shock position is approximately at the discontinuity and causes a slight thickening of the boundary layer.

Increasing the pre-shock Mach number leads to a completely different shock system in the schlieren image. The transitional boundary layer downstream in mind (see oil-flow image in Fig. 16j) the system is interpreted as a doublet-interaction (Fig. 18b). The normal part of the main shock wave is found about $2 \mathrm{mm}$ downstream the discontinuity, but the compression waves ahead reach about $4 \mathrm{mm}$ upstream. A small subsidiary shock wave follows. The visible boundary layer thickening is limited to the shock system region, again. In the numerical simulation (Fig. 18f) the increase of the pre-shock Mach number changes the shock structure only slightly: The oblique part and the extension of the shock into the far field grow and the angle of the shock changes to being nearly perpendicular to the surface. Again, boundary layer thickening is very localised.

The fully turbulent assumption does not allow a correct numerical rebuilding of the experimental shock structure at the lower pre-shock Mach numbers described so far. This changes in Fig. 18c, g: A strong shock wave originating at the surface $3-4 \mathrm{mm}$ downstream the discontinuity, normal near the surface and moderately inclined above is found in experiment and simulation at this condition. An oblique shock originates ahead of the discontinuity and joins the main shock to form a $\lambda$-shape. If the pre-shock Mach number is further increased, the main shock moves further downstream and gets inclined, while the oblique shock foot stays attached to the discontinuity (Fig. 18d, h). Thereby, the formed $\lambda$-shape grows. Experiment and simulation show an excellent agreement in position, shape and structure of the shock boundary layer interaction at this condition.

In case of the high Reynolds number and the assumption of a turbulent boundary layer, discrepancies between simulation and experiment occur in the first two cases at a lower pre-shock Mach number, but diminish when the Mach number increases. This is explained by the turbulent boundary layer assumption used for the simulation that does not match reality in the first two cases. The multiple interaction (Fig. 18a) is typical for laminar boundary layers, and the doublet-interaction (Fig. 18b) requires consideration of a laminar-turbulent transition. In the numerical simulation, $\lambda$-formation is not observed in these cases (Fig. 18e, f), but – according to Houghton et al. (2013) – with the pressure gradient high enough, the turbulent boundary layer separates ahead of the shock wave and a $\lambda$-interaction occurs (Fig. 18g, h). Therefore, supported by the transitional structures observed in the oil-film visualisation at $\alpha =21.5^\circ$ (Fig. 16l), the authors assume that laminar-turbulent transition also occurred in the experiment in the two dedicated cases (Fig. 18c, d). This would explain the excellent accordance of the shock-boundary layer interaction between experiment and simulation at these conditions.

7 Conclusion

A combined experimental and numerical study concerning aerodynamic stability behaviour of the MarcoPolo-R aero shell was conducted. By means of numerous wind tunnel tests, static aerodynamic coefficients were determined and implemented in a database. Static stability of the capsule was proven for the complete investigated range. This feature qualified the aero shape as baseline configuration for the ESA TRP Modshape (Neeb et al. 2019), in which changes in the aerodynamics of the capsule due to shape changes caused by TPS recession are investigated. Furthermore, due to the similar front shield geometry, the aerodynamic coefficients determined in the present study could be helpful for the Phobos Sample Return mission design (Centuori et al. 2016; Ferri et al. 2018).

At an inflow Mach number of $M=1.5$, a system of shock waves forms on the leeward side of the inclined capsule, while the structure changes with the incidence angle. The shock system was visualised using schlieren imaging and its footprint on the capsule’s surface was revealed by means of the oil film visualisation technique. Within a numerical simulation the flow structure and the aerodynamic coefficients could be well reproduced at this test condition.

In aerodynamic tests, the Reynolds number was limited to a certain range by the stiffness of the wind tunnel balance. The possible variation was too small to reveal any impact of the Reynolds number on the aerodynamic coefficients. Therefore, additional tests without a balance were performed at an increased Reynolds number and the change in shock structure and surface footprint were visualised. Numerical simulations were performed at the higher Reynolds number, too, and validated against the experimental results in terms of flow structure and surface tension lines. Afterwards, the simulation was used to predict the aerodynamic coefficients for this case. As the shock system is limited in its physical extension, the impact of the phenomenon on the static aerodynamic coefficients of the capsule was found to be negligible. A potential influence on the dynamic stability behaviour of the capsule was not investigated.

Nonetheless, as shock boundary layer interaction is of interest in many fields of aerodynamic research, the authors analysed the interaction structures at low and at high Reynolds number conditions. They were compared to theoretical models of Houghton et al. (2013) and reproduced numerically. The finite computational resources available limited the numerical investigations to stationary simulations.

In the low Reynolds number case, laminar boundary conditions proved to be suitable for a fairly good reproduction of the secondary shock system on the capsule, as no transition to turbulence was observed. In the high Reynolds number case, the experiments revealed an initially laminar boundary layer with a transition to turbulence at the secondary shock system at lower angles of incidence. At higher angles, a transition of the boundary layer was observed already ahead of the shock system thereby causing formation of a $\lambda$-interaction. Yet, aiming the determination of aerodynamic coefficients, fully turbulent boundary conditions for the simulation turned out to reproduce the shock boundary layer interaction sufficiently. Therefore, the authors did not perform a boundary layer transition analysis for the present study. For future research, investigation of the dynamic aspects of the observed shock-boundary layer interaction is recommended.

Appendix

The uncertainty analysis differs with the operational mode of TMK wind tunnel. The used approach is presented exemplarily for the pitch coefficient ${C}_{m}$ in supersonic tests and the base pressure coefficient ${C}_{pB}$ in transonic tests. The same approach can be applied to other aerodynamic coefficients.

1.1 Error estimation for supersonic tests

The supersonic Mach number and its uncertainty are known from calibration tests. Therefore, the pitch coefficient ${C}_{m}=\frac{{M}_{f}}{{q}_{\infty }\cdot {D}_{\rm Ref}\cdot {S}_{\rm Ref}}$ is expressed as a function of the known input parameters $\kappa , M, {p}_{0}, {D}_{\rm Ref}$ and ${M}_{f}$ using gas dynamic equations:

$${C}_{m}=\frac{8}{\pi }\cdot \frac{{M}_{f}}{\kappa \cdot M^{2}\cdot {p}_{0}\cdot {D}_{\rm Ref}^{3}}\cdot {\left(1+\frac{\kappa -1}{2}\cdot {M}^{2}\right)}^{\frac{\kappa }{\kappa -1}}.$$

The sensitivity of the coefficient to errors of the input parameters is given by the partial derivatives:

$${\left[{C}_{m}\right]}_{{M}_{f}}=\frac{\partial {C}_{m}}{\partial {M}_{f}}=\frac{1}{{M}_{f}}\cdot {C}_{m}$$

$${\left[{C}_{m}\right]}_{{D}_{\rm Ref}}=\frac{\partial {C}_{m}}{\partial {D}_{\rm Ref}}=\frac{-3}{{D}_{\rm Ref}}\cdot {C}_{m}$$

$${\left[{C}_{m}\right]}_{{p}_{0}}=\frac{\partial {C}_{m}}{\partial {p}_{0}}=\frac{-1}{{p}_{0}}\cdot {C}_{m}$$

$${\left[{C}_{m}\right]}_{M}=\frac{\partial {C}_{m}}{\partial M}=\frac{2\cdot \left(-2+{M}^{2}\right)}{M\cdot \left(2+{M}^{2}\cdot \kappa -{M}^{2}\right)}\cdot {C}_{m}$$

$${\left[{C}_{m}\right]}_{\kappa }=\frac{\partial {C}_{m}}{\partial \kappa }=\left(\frac{-1}{\kappa }+\frac{\kappa }{2\cdot \left(\kappa -1\right)}\cdot \frac{{M}^{2}}{1+\frac{\kappa -1}{2}\cdot {M}^{2}}+\left(\frac{-1}{{\left(\kappa -1\right)}^{2}}\right)\cdot \mathrm{ln}\left(1+\frac{\kappa -1}{2}\cdot {M}^{2}\right)\right)\cdot {C}_{m}.$$

The uncertainty of ${C}_{m}$ is calculated applying the error propagation rule of Gauss:

$$\Delta {C}_{m}=\sqrt{{{\left(\frac{\partial {C}_{m}}{\partial {M}_{f}}\cdot \Delta {M}_{f}\right)}^{2}+\left(\frac{\partial {C}_{m}}{\partial {D}_{\rm Ref}}\cdot \Delta {D}_{ref }\right)}^{2}+{\left(\frac{\partial {C}_{m}}{\partial {p}_{0}}\cdot \Delta {p}_{0}\right)}^{2}+{\left(\frac{\partial {C}_{m}}{\partial M}\cdot \Delta M\right)}^{2}+{\left(\frac{\partial {C}_{m}}{\partial \kappa }\cdot \mathrm{\Delta \kappa }\right)}^{2}}.$$

1.2 Error estimation for transonic tests

The pressure ratio ${p}_{0}/{p}_{\infty }$ is corrected applying correction factors from calibration tests. Neglecting the influence of this minor correction, the base pressure coefficient ${C}_{pB}=\frac{{p}_{B}-{p}_{\infty }}{{q}_{\infty }}$ can be expressed as a function of the input parameters $\kappa , {p}_{0}, {p}_{\infty }$ and ${p}_{B}$ using gas dynamic equations:

$${C}_{{p}_{B}}=\frac{\kappa -1}{\kappa \cdot {p}_{\infty }}\cdot \frac{{p}_{B}-{p}_{\infty }}{\left[{\left({p}_{0}/{p}_{\infty }\right)}^{\frac{\kappa -1}{\kappa }}-1\right]}$$

The sensitivity to errors of the input parameters is given by the partial derivatives:

$${\left[{C}_{{p}_{B}}\right]}_{{p}_{B}}=\frac{\partial {C}_{{p}_{B}}}{\partial {p}_{B}}=\frac{1}{{p}_{B}-{p}_{\infty }}\cdot {C}_{{p}_{B}},$$

$${\left[{C}_{{p}_{B}}\right]}_{{p}_{0}}=\frac{\partial {C}_{{p}_{B}}}{{\partial p}_{0}}=-\frac{\kappa -1}{\kappa \cdot {p}_{0}}\cdot \frac{{\left({p}_{0}/{p}_{\infty }\right)}^{\frac{\kappa -1}{\kappa }}}{\left[{\left({p}_{0}/{p}_{\infty }\right)}^{\frac{\kappa -1}{\kappa }}-1\right]}\cdot {C}_{{p}_{B}},$$

$${\left[{C}_{{p}_{B}}\right]}_{{p}_{\infty }}=\frac{\partial {C}_{{p}_{B}}}{{\partial p}_{\infty }}=\left[\frac{-1}{{p}_{B}-{p}_{\infty }}+\frac{\kappa -1}{\kappa \cdot {p}_{\infty }}\cdot \frac{{\left({p}_{0}/{p}_{\infty }\right)}^{\frac{\kappa -1}{\kappa }}}{\left[{\left({p}_{0}/{p}_{\infty }\right)}^{\frac{\kappa -1}{\kappa }}-1\right]}-\frac{1}{{p}_{\infty }}\right]\cdot {C}_{{p}_{B}},$$

$${\left[{C}_{{p}_{B}}\right]}_{\kappa }=\frac{\partial {C}_{{p}_{B}}}{\partial \kappa }=\left[\frac{1}{\kappa \cdot \left(\kappa -1\right)}-\frac{{\left({p}_{0}/{p}_{\infty }\right)}^{\frac{\kappa -1}{\kappa }}\cdot \mathrm{ln}\left({p}_{0}/{p}_{\infty }\right)}{{\kappa }^{2}\cdot \left[{\left({p}_{0}/{p}_{\infty }\right)}^{\frac{\kappa -1}{\kappa }}-1\right]}\right]\cdot {C}_{{p}_{B}}$$

The uncertainty of ${C}_{pB}$ is calculated applying the error propagation rule of Gauss:

$$\Delta {C}_{{p}_{B}}=\sqrt{{\left(\frac{\partial {C}_{{p}_{B}}}{\partial {p}_{B}}\cdot \Delta {p}_{B}\right)}^{2}+{\left(\frac{\partial {C}_{{p}_{B}}}{\partial {p}_{0}}\cdot \Delta {p}_{0}\right)}^{2}+{\left(\frac{\partial {C}_{{p}_{B}}}{\partial {p}_{\infty }}\cdot \Delta {p}_{\infty }\right)}^{2}+{\left(\frac{\partial {C}_{{p}_{B}}}{\partial \kappa }\cdot \Delta \kappa \right)}^{2}}$$

Then, the test Mach number is calculated as:

$$M=\sqrt{\frac{2}{\kappa -1}\cdot \left[{\left({p}_{0}/{p}_{\infty }\right)}^{\frac{\kappa -1}{\kappa }}-1\right]}$$

The sensitivity to errors of the input parameters is given by the partial derivatives:

$${\left[M\right]}_{{p}_{0}}=\frac{\partial M}{\partial {p}_{0}}=\left[\frac{\left(\kappa -1\right)}{2\cdot \kappa \cdot {p}_{0}}\cdot \frac{{\left({p}_{0}/{p}_{\infty }\right)}^{\frac{\kappa -1}{\kappa }}}{\left[{\left({p}_{0}/{p}_{\infty }\right)}^{\frac{\kappa -1}{\kappa }}-1\right]}\right]\cdot M.$$

$${\left[M\right]}_{{p}_{\infty }}=\frac{\partial M}{\partial {p}_{\infty }}=\left[\frac{-\left(\kappa -1\right)}{2\cdot \kappa \cdot {p}_{\infty }}\cdot \frac{{\left({p}_{0}/{p}_{\infty }\right)}^{\frac{\kappa -1}{\kappa }}}{\left[{\left({p}_{0}/{p}_{\infty }\right)}^{\frac{\kappa -1}{\kappa }}-1\right]}\right]\cdot M$$

$${\left[M\right]}_{\kappa }=\frac{\partial M}{\partial \kappa }=\frac{1}{2}\left[\frac{-1}{\kappa -1}+\frac{{\left({p}_{0}/{p}_{\infty }\right)}^{\frac{\kappa -1}{\kappa }}}{\left[{\left({p}_{0}/{p}_{\infty }\right)}^{\frac{\kappa -1}{\kappa }}-1\right]}\cdot \frac{1}{{\kappa }^{2}}\cdot \mathrm{ln}\left({p}_{0}/{p}_{\infty }\right)\right]\cdot M$$

The uncertainty of $M$ is calculated applying the error propagation rule of Gauss:

$$\Delta M=\sqrt{{\left(\frac{\partial M}{\partial {p}_{0}}\cdot \Delta {p}_{0}\right)}^{2}+{\left(\frac{\partial M}{\partial {p}_{\infty }}\cdot \Delta {p}_{\infty }\right)}^{2}+{\left(\frac{\partial M}{\partial \kappa }\cdot \Delta \kappa \right)}^{2}}.$$