Shock interaction induced heat flux augmentation in hypersonic flows

Abstract

This paper gives a summary of dedicated experiments on the shock interaction induced heat flux augmentation, by means of tests carried out in the hypersonic wind tunnel H2K. The first test case is devoted to the shock boundary layer interaction on a flat plate. The interaction impact has been varied by changing the free stream parameters and the position of the shock generator, i.e. shock impingement point on the plate. The heat flux distribution has been determined using surface temperature data measured by an infrared camera. The heat flux data combined with free stream flow parameters allow calculation of the Stanton number evolution. The second test case is a double sphere configuration with a variable axial and lateral distance between the spheres. This allowed measurements of the heat flux augmentation induced by a shock-shock interaction along the complete frontal surface of the second sphere, which was hit by the bow shock of the first sphere. Shock-shock and shock-boundary layer interaction effects are studied by means of experiments on the IXV flight configuration with double control flaps. Depending on the test configuration and flow parameters, shock interaction induced heat flux augmentation factors up to seven have been measured.

Graphical abstract

1 Introduction

Hypersonic vehicles are exposed to severe aerothermal loads, which may be the main design driver depending on the trajectory parameters. The high total enthalpy of the decelerated gas in the shock layer, in combination with partially significant velocity gradients at specific vehicle locations, leads to thermal problems. Particularly during hypersonic flights at high altitudes, thermo-chemical non-equilibrium processes within the gas phase may increase the heat flux remarkably, depending on the vehicles surface catalysis. However, there is a lack of reliable data on measured collision rates, and recombination coefficients, i.e. surface catalysis of different materials. These data are essential to validate design tools. Because of uncertainties at this point, most hypersonic vehicle designs use partially very high design margins, which may increase again due to strong heat flux augmentation caused by gas surface interaction effects. One well known effect, linked to an increase in the heat transfer, is the boundary layer transition from laminar to turbulent flow. Roughness induced heat flux augmentation is another design margin driver, since available experimental data are very limited.

In hypersonics, viscous interaction effects play an important role on aerodynamic efficiency and aerothermal heating of the vehicle. Especially the last one is enhanced in case of shock wave induced interactions. Depending on the vehicle configuration shock-shock interaction or shock-boundary layer interaction can cause significant heat flux augmentation. Shock wave–boundary layer interactions (SWBLI) can cause locally increased pressure and thermal loads, causing separations themselves and thus having a great influence onto the aerothermal heating process. Most of the existing publications in this field deal with interactions of shock waves with turbulent boundary layers (Dupont et al. 2006; Schülein 2006; Humble et al. 2009; Helmer 2011; Grilli et al. 2012), some handle the case of interactions of shock waves with laminar boundary layers (Boin et al. 2006; Lüdeke and Sandham 2009; Brown and Boyce 2009) but investigations of the interaction between shock waves and transitional boundary layers are rare (Dolling 2001; Arnal and Delery 2004; Benay et al. 2006; Sandhem et al. 2014; Vanstone et al. 2013).

Jaunet et al. investigated the influence of the wall temperature effects on the shock induced separation behaviour by using particle image velocimetry and hot-wire technique for experiments at Mach 2.3 (Jaunet et al. 2014). Their results indicate the impact of aerothermal heating on the size and low-frequency unsteadiness of shock wave boundary layer interaction (SWBLI). Schülein investigated the shock wave boundary layer interaction by performing heat flux and skin friction measurements on a shock impinged flat plate at Mach 5 (Schülein 2006). His measurements showed a clear difference between the 2D and 3D SWBLI on the heat transfer evolution. Volpaini et al. performed numerical studies to investigate the effect of thermal conditions of the wall on the size of the shock wave boundary layer interaction and frequency of pressure fluctuations (Volpiani et al. 2018). Numerical results indicate, that the thermal behaviour of the incoming boundary layer is the main driver of the interaction length. The same team simulated also the experiments of Schülein by means of high-fidelity numerical computations at different wall temperature to recovery temperature ratios and incidence angles (Volpiani et al. 2020). The three-dimensional effects of the experiments were declared as the source of deviation between numerical simulations and experiments. Another interesting work related to shock induced pressure and heat flux loads has been published by Wang et al. (Wang et al. 2021). This combined experimental and numerical study used a test model consisting of different swept leading edged and ‘V-shaped’ crotches with a nonuniform bluntness. It has been demonstrated that the pressure and heat flux augmentation resulting from shock-shock and shock wave boundary layer interactions can be modulated by means of variations of the ratio of the swept leading-edge radius and stagnation point radius of the crotch.

This paper summarizes results of recent experiments concerning the shock induced heat flux augmentation (SIHFA) in the DLR’s hypersonic wind tunnel H2K. Experiments have been carried out at flow conditions, which have been well characterized using intrusive and non-intrusive measurement techniques. After the description of experimental tools in the first block, the main scientific chapter of the manuscript presents detailed experimental results on different test configurations. Shock wave boundary layer interaction effects on a flat plate configuration in laminar and turbulent hypersonic flow are discussed first. Edney type interactions on the stagnation point of a double sphere configuration and the flaps of a hypersonic vehicle and follow this part. Finally, the preparatory activities for the in-flight measurement of the shock induced heat flux augmentation at a canard in the frame of the hypersonic flight experiment STORT, which will be carried out by the end of 2021 (Gülhan et al. 2021) will be described. The paper is finished with some concluding remarks.

2 Experimental tools

2.1 Hypersonic wind tunnel cologne (H2K)

The hypersonic wind tunnel H2K at the DLR in Cologne is a blow down wind tunnel with test durations of up to 30 s, depending on the flow conditions. The facility is equipped with five contoured nozzles with an exit diameter of 600 mm, i.e. Ma = 5.3, 6, 7, 8.7, 11.2. Dried air passes from a pressure reservoir with a maximum pressure of 45 bars through electrical heaters. To avoid condensation and perform tests at higher enthalpies, the air is heated up by the electrical heaters with a heating capacity of up to 5 MW. It allows running the facility at a maximum total temperature of 1100 K. A scheme of the wind tunnel is shown in Fig. 1.

Fig. 1

Schematic of Hypersonic Wind Tunnel Köln (H2K)

The operational range of the H2K wind tunnel is shown in Fig. 2. Here the performance map with respect to the Mach number and unit Reynolds number Re_U is depicted depending on the total pressure p₀ and the mass flow rate. The thick black bars indicate the available wind tunnel nozzles. The unit Reynolds number is given by the proper choice of the total pressure p₀ and temperature T₀ of the flow.

Fig. 2

Performance map of H2K

2.2 Measurement techniques

The flow field of the hypersonic wind tunnel H2K is well characterized and allows reliable aerodynamic and aerothermal tests at Mach numbers between 5.3 and 11.2. Figure 3 shows the measured Mach number distribution at the exit of contoured nozzles for Mach 6 and 8.7. The data show a homogenous flow core of about 400 mm for both nozzles, which is in the same order for all nozzles with an exit diameter of 600 mm (Mach numbers of 5.3, 6.0, 7.0, 8.7 and 11.2). The Mach number deviations in the core flow are typically below 0.05 (1%) and 0.18 (2%) for Ma = 6 and Ma = 8.7, respectively.

Fig. 3

Mach number profiles at the exit of Mach 6 (left) and Mach 8.7 nozzle (right)

The turbulent intensity and velocity of the inflow were measured with a Laser-2-Focus-Velocimeter (L2F). This method measures at a single point the directional velocity distribution of particles in the flow. As shown in Fig. 4 a laser beam is split into two beams and those are focused on two points with a small offset Δs in flow direction. In case a single particle passes both focus points, the time difference Δt of the reflected light on both detectors allows the determination of the particle velocity. A statistical evaluation allows the elimination of signals from two different particles and the computation of the turbulent intensity (Boutier et al. 1978; Schodl 1979). The measured turbulent intensity is about 0.9% for Mach 5.3, 6.0 and 7.0 and about 1.3% for Mach 8.7.

Fig. 4

Sketch of a Laser-2-Focus-Velocimeter (L2F)

This paper focusses on heat flux measurements based on infrared images. For this purpose, the models are made of Polyether Ether Ketone (PEEK), which is a low conductive high temperature plastic and is a suitable model material for tests in which surface temperatures do not exceed 500 K. This allows distributed measurements on the model surface with less limitations with respect to model manufacturing and handling compared to temperature sensitive paint.

The surface temperature information of the infrared camera needs to be transformed into heat fluxes or Stanton numbers. This is performed by the in-house tool VisualHeatFlow, which is based on a thermal energy balance. The data reduction methodology is outlined in the following.

In the literature, several algorithms can be found to derive heat flux data from surface temperature measurements. Unfortunately, most of these techniques are not perfectly adapted to the application in blow down facilities, which show radiation effects and significantly rising wall temperatures. Furthermore, in order to reduce lateral heat transfer, thick wall models are generally built of artificial resin with low thermal conductivity and temperature dependent material properties.

The heat flux evaluation presented here requires a more advanced approach, starting from the thermal energy balance on a solid volume element and which can be transformed to result in the one-dimensional nonlinear heat equation (Henckels and Gruhn 2004)

$$\frac{\partial T}{{\partial t}} \,= a_{\left( T \right)} \cdot \frac{{\partial^{2} T}}{{\partial y^{2} }} + b_{\left( T \right)} \cdot \left( {\frac{\partial T}{{\partial y}}} \right)^{2}$$

(1)

with the thermal diffusivity

$$a_{\left( T \right)} \,= \frac{{\lambda_{\left( T \right)} }}{{\rho_{\left( T \right)} \cdot c_{\left( T \right)} }}$$

(2)

and

$$b_{\left( T \right)} = \frac{{\frac{{d\lambda_{\left( T \right)} }}{dT}}}{{\rho_{\left( T \right)} \cdot c_{\left( T \right)} }}$$

(3)

with the material density $\rho_{\left( T \right)}$, the specific heat capacity $c_{\left( T \right)}$ and the heat conductivity $\lambda_{\left( T \right)}$. The suffix (T) indicates the temperature dependent properties of the material. To calculate the temperature profile inside the model wall, Eq. (1) can be solved by an explicit finite-difference procedure by marching stepwise through time t = k⋅Δt. The unknown temperature T_i,k+1 (the index i describes equally spaced points in y-direction normal to the surface) at the next time step can be calculated by

$$T_{i,k + 1} = T_{i,k} + \frac{\Delta t}{{\Delta y^{2} }}a_{{\left( {T_{i,k} } \right)}} \left( {T_{i - 1,k} - 2T_{i,k} + T_{i + 1,k} } \right)+ \frac{\Delta t}{{\Delta y^{2} }}\frac{{b_{{\left( {T_{i,k} } \right)}} }}{4}\left( {T_{i - 1,k} - T_{i + 1,k} } \right)^{2}$$

(4)

As initial condition at t = 0 s, a homogeneous temperature distribution inside the model is assumed, i.e. for all points the temperature T_i,0 is set equal to the initial surface temperature T_0,0. The surface temperatures T_0,k measured by the infrared system are applied as boundary condition at the surface for all time points. A second boundary condition at the backside of the computational domain is based on an adiabatic assumption. This numerical procedure provides temperature profiles T_i inside the model wall at each time step k (see also Fig. 5). Based on these profiles, the conductive heat flux $\dot{q}_{w}$ absorbed by the wall can be calculated by Fourier’s law

$$\dot{q}_{w} = \lambda_{{\left( {T_{0,k} } \right)}} \cdot \left. {\frac{dT}{{dy}}} \right|_{y = 0}$$

(5)

Fig. 5

Scheme of heat flux determination from surface temperature evolution

which is solved by a high-order interpolation scheme based on the points in the vicinity of the surface. The convective heat flux $\dot{q}_{c}$ between the flow and the wall can be derived via the heat flux balance at the surface via

$$\dot{q}_{c} = \dot{q}_{r} + \dot{q}_{w} .$$

(6)

The radiative heat flux $\dot{q}_{r}$ between the large surface of the test section, which is assumed at a constant ambient temperature T_U, and the model surface is given by the Stefan-Boltzmann law

$$\dot{q}_{r} = \varepsilon \cdot \sigma \cdot \left( {T_{{\left( {0,k} \right)}}^{4} - T_{U}^{4} } \right).$$

(7)

with the surface emissivity $\varepsilon$ and the Stefan-Boltzmann constant $\sigma$. This thermal data evaluation technique has been proven as an efficient tool to resolve unsteady heat flux loads with an error of typically less than 10% on models in blow down facilities and it showed good agreement to analytical predictions in canonical flow Willems et al. (2015), Willems (2013), Neeb et al. (2015). Further information can be found in Henckels and Gruhn 2004. The image distortion correction is performed using the algorithm of Tsai (1987).

3 Shock interaction induced heat flux augmentation.

3.1 Flat plate in laminar and turbulent hypersonic flow.

This study was performed in the framework of the ESA technology research project “laminar to turbulent transition in hypersonic flows” (Willems et al. 2015). For the experiments, a Mach 6 contoured nozzle with an exit diameter of 600 mm was used. The test gas air is heated with resistance heaters. As shown in Fig. 6, the model consists of the following main parts:

• A flat base plate 600 mm in length and 340 mm in width, with an exchangeable nose with a ramp of 25° towards the underside and different nose radii. All experiments presented here used a sharp leading edge. The leading edge of the base plate is razor-sharp and for sure less than 0.1 mm. The leading edge is grinded regularly during the test campaign.

• Different measuring inserts embedded into the base plate, 400 mm in length and 150 mm in width. One insert made of PEEK was used for the infrared thermography. Two inserts made of steel are equipped with different sensors and described by Willems, 2015.

• A wedge as a shock generator, 190 mm in length and 340 mm in width. It has a leading edge with a radius of 0.1 mm and a ramp to the upside of 25°. The shock generator is movable in flow direction and can be installed at different angles of attack. All H2K experiments with the shock generator were performed with an angle of attack of the shock generator of α = 4^◦.

• The mounting system.

Fig. 6

CAD model with definition of the coordinate system

The mid-point of the leading edge of the base plate’s nose is the origin of the coordinate system used in this paper. The x-axis points in the flow direction, the y-axis is parallel to the leading edge, and the z-axis is the normal vector of the base plate pointing towards the shock generator. The defined coordinate system is also shown in Fig. 6. With respect to the standard H2K support arm, the model was mounted upside down in the test section.

Both positions of the shock generator used for the experiments in H2K are shown in Fig. 7. Due to viscous effects on the shock generator, the generated shock is upstream the estimated position based on the inviscid equations provided by NACA (1953) as shown in Fig. 8.

Fig. 7

Shock generator positions and estimated shock positions

Fig. 8

Comparison of theoretical and real shock position in a Schlieren picture (Re_u = 6·10⁶ and x_shock = 239 mm)

The theoretical Stanton number is based on the free stream conditions computed from measured values of the reservoir conditions and measured wall temperatures. In Fig. 9, the Stanton number distribution for Re_u = 6·10⁶ and x_shock = 239 mm on the PEEK insert is plotted. It shows, that there are differences in the y-direction, which are probably caused by small differences in the inflow as shown in Fig. 3, as they lead to different transition onset positions. Figure 9 also shows some streaks in x-direction which are a hint to longitudinal vortices. A more detailed discussion of the 2D-distributions can be found in Willems, 2015. The analysis here concentrates on the amplification rates along the symmetry plane.

Fig. 9

Example of the Stanton number distribution on the PEEK insert (Re_u = 6·10⁶ and x_shock = 239 mm)

The lower part of Fig. 10 shows the Stanton number distribution of the natural transition for the three flow conditions versus the Reynolds number based on the path length. In addition, the theoretical curves for laminar and turbulent boundary layers are plotted based on the equations of Korkegi (1962) and White (2006) using the Sutherland law, as discussed in Willems and Gülhan 2013. The different inflow conditions lead to different Reynolds numbers for transition onset, as the nose radius is not scaled. Hence the leading edge is relative sharper for smaller unit Reynolds numbers. The upper part of Fig. 10 shows the Stanton number ratio between cases with and without shock impingement. The abscissa is the same as in the lower part. The vertical lines in both parts mark the (theoretic) shock impingement position for the curve of the same colour. While the Stanton number amplification is just slightly above two for an impingement in a turbulent boundary layer (Re_u = 12·10⁶, x_shock = 331 mm), it becomes much larger for an impingement into a transitional boundary layer. For Re_u = 3·10⁶ and x_shock = 239 mm the highest ratio of more than seven is detected. In that case the shock impinges right at the transition onset location. For earlier and later shock positions the amplification is lower. For a shock wave turbulent boundary layer interaction (SWTBLI), there is no prominent peak in the amplification curve, but a plateau. For the transitional cases there is a clear peak after the theoretic shock impingement.

Fig. 10

Stanton number distribution for natural transition and amplification rates of the shockwave boundary layer interaction vs. Re_x

Figure 11 contains the same curves, but they are plotted against Re_u·(x—x_shock) and hence the shapes of the amplifications curves can be compared. It illustrates that the maximum amplification is reached earlier for more turbulent boundary layers. If the shock hits a laminar boundary layer or shortly after transition onset, there is a region with an amplification factors below one, before the theoretic impingement point, that is caused by the separation zone. The downstream parts of the curves are difficult to compare, as they depend on the length of the shock generator and do not scale with the inflow condition. The curves for Re_u = 6·10⁶, x_shock = 331 mm and Re_u = 12·10⁶, x_shock = 239 mm have a similar progression (until 5·10⁵) and reach a similar maximum value. The lower part of the diagram shows, that the shock impingement is at a similar position with respect to the natural transition process for both cases. In contrast to that the increase for Re_u = 3·10⁶ and Re_u = 6·10⁶ with x_shock = 239 mm is quite different, although the highest amplification is similar, but in the first case, the shock impinges before and in the latter case after transition onset.

Fig. 11

Stanton number distribution for natural transition and amplification rates of the shockwave boundary layer interaction vs. Re_u·(x—x_shock)

3.2 Edney type interaction in stagnation point configuration.

It is well known that Edney type shock-shock interaction can lead to significant change in the bow shock characteristics, which may lead to significant heat flux augmentation (Edney, 1968). In order to investigate shock interaction induced heat flux augmentation, at a two-sphere test configuration the heat flux was measured in the hypersonic wind tunnel H2K. The bottom sphere acts as shock generator and can be moved in axial and vertical direction with respect to the top sphere (Fig. 12). The top sphere is made of PEEK to deduce heat flux rate from measured surface temperature distribution using semi-infinite wall assumption as describe in the previous chapter. For the computation of the Stanton number the reservoir temperature T₀ is used, as this definition gives the most stable results over time. As the wall temperatures are high and close to the recovery temperature, a Stanton number based on the latter is very sensitive to the used recovery factor.

Fig. 12

Two sphere test configuration for shock induced heat flux augmentation tests

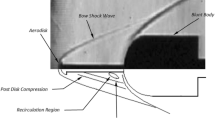
Measured and computed flow parameters of tests are listed in Table 1. The unit Reynolds number of the Mach 7 flow is 2.2 10⁶/m. The facility is started for the configuration of spheres with big distance from each other, which means no shock-shock interaction ahead of the second sphere. After the achievement of the steady state flow condition the first sphere’s vertical motion is started by activation the stepping motor and move the front sphere in the nominal position. Figure 13 shows Schlieren pictures of the test at two different test time points to illustrate the impact of the shock-shock interaction on the shock stand-off distance and strong change of the flow in case of Edney IV interaction in the stagnation point region of the rear sphere. The relative sphere positions and flow parameters of the test with Schlieren picture were slightly different than the pressure value in Table 1, which contains major flow parameters of heat flux measurements.

Table 1 Flow parameters of tests

Fig. 13

Schlieren pictures of the test for two different relative position of spheres to each other

The flow interaction of two spheres in a hypersonic flow field also results in a dramatic change in the heat loads. For different relative positions of both spheres significantly different shock-shock interactions occur. The (logarithmic scaled) Stanton number distribution in Fig. 14 on the rear sphere is computed from temperature data measured with an infrared camera. The shock of the front sphere hits the rear sphere right in the middle, i.e. at the stagnation point. There is a strong interaction zone in front of the rear sphere and a significant increase in the Stanton number on its surface, which is quite sharp.

Fig. 14

Heat flux distribution on the rear sphere without (left) and with shock-shock interaction (right)

As shown in Fig. 15 the heat flux, i.e. Stanton number distribution over the sphere surface at test time point of 7.5 s without shock-shock interaction shows a symmetrical profile with respect to the stagnation point (green line). At time point 19.5 s in in the stagnation point region an Edney IV type shock interaction occurs. It leads to a significant heat flux jump (red line). The blue line represents the normalized heat flux profile of the Edney IV type interaction using the profile with interaction as reference. Again, the shock interaction induced heat flux augmentation at the stagnation point of the rear sphere is more than factor 3.

Fig. 15

Heat flux and heat flux augmentation in the symmetry plane of the rear sphere

3.3 Edney type interaction on control surfaces

In cooperation with industrial partners, ESA performed an experimental atmospheric re-entry technology activity including the in-flight demonstrator called IXV (Intermediate eXperimental Vehicle) (Tumino et al., 2016). Its key mission and system objectives were the design, development, manufacturing, assembling and on-ground to in-flight verification of an autonomous European lifting and aerodynamically controlled re-entry vehicle. Besides guidance, navigation, flight control and aerodynamics, the aerothermodynamic properties of the vehicle played a major role in the design. Big attention was paid to the design of various thermal protection components like control surfaces made of CMC material.

For a better quantification of aerothermal loads on the control surface an experimental study of the IXV configuration has been conducted in the hypersonic wind tunnel H2K Cologne (Neeb et al. 2008). Tests have been carried out at Mach 8.7, three different Reynolds numbers, different flap deflection and angles of attack. The model with a length of 250 mm (without flaps) was made of the thermally low conductive material PEEK. It was placed inside the test chamber with its windward side faced upwards (Fig. 16) and attached to a sting on the lee side which was mounted to the H2K model support arm. As mentioned before, the low thermal conductivity of PEEK allows avoiding any lateral heat dissipation inside the structure and deducing the heat flux rate from the measured surface temperature using the semi-infinite wall assumption. Depending on the flow and model parameters the testing time varied between 8 and 15 s.

Fig. 16

IXV model made of PEEK in the hypersonic wind tunnel H2K

Different sets of flaps for deflection angles of 5°, 10°, 15° and 20° were used. In order to determine the heat flux rate for the complete windward side of the model surface, an infrared (IR) camera ThermaCAM SC3000 with an image rate of 60 frames per second, sensitive to the long-wave infrared range (8–9 µm), has been used. Determination of the heat flux rate and Stanton number from measured surface temperature distributions is described by Neeb et al. 2008. In addition to the infrared measurements the model temperature was monitored with 12 thermocouples, which were flush mounted at distinct model positions.

Test parameters of the runs and the corresponding wind tunnel flow conditions are given in Table 2. The values have been averaged over the useful testing time. All presented runs have been performed at 0° sideslip angle. The given Reynolds number is defined using the model length of 0.25 m as characteristic length L.

Table 2 Averaged wind tunnel flow conditions

3.3.1 Typical distributions along the model

To allow accurate scaling of the infrared mappings, the complete Stanton number distribution on the model surface has been projected onto a 3D mesh. Only data with an IR camera viewing angle smaller than 57° were used for post-processing, to keep the change in temperature due to a change in emissivity below 1.5%. For direct comparisons between different runs, Stanton number distributions along defined slices of constant x- or y- coordinates have been extracted according to Fig. 17.

Fig. 17

Temperature-, convective heat flux- and Stanton number-mappings of run No. 32

Figure 17 contains a view of the model windward side with distributions of the surface temperature, convective heat flux and Stanton number for the medium Reynolds number run No.32 with 15° flap deflection angle and 45° angle of attack. As can be seen the general distribution is comparable for all three quantities. The stagnation region on the windward side near the nose is clearly visible due to increased values (Fig. 17, I). Just in front of the flaps a 3D shaped region with low values can be observed in all three distribution maps (IV). This corresponds to the separated flow region induced by the adverse pressure gradient on the flaps. Near the hinge line of the flaps a sharp increase in all values is visible (V). This is caused by the reattachment shock, which causes high local pressure and heat fluxes. On the deflected flap surfaces in general higher values can be observed due to the higher surface pressure and flow drag. Due to the tilt angle of the flaps a nonuniform flow field can be seen here. The flow is oriented towards the inner edges of the flaps, which causes higher values here due to an acceleration of the flow.

3.3.2 Reynolds number effects

3.3.2.1 15° flaps – Run09, Run32, Run34

To highlight the impact of heat flux augmentation, in the following a Stanton number increase St/St_SP is shown based on the visible stagnation point Stanton number St_SP as reference. Especially for the low angles of attack, it is possible that the complete stagnation region was not visible with the IR set-up. For absolute Stanton number distributions, the reader is referred to Neeb et al. 2008. The highest heat load is located on the flaps for all three Reynolds number cases (Fig. 18, top), with up to approx. 50% larger values compared to the stagnation point values. For the medium and high Reynolds number case this maximum is at the hinge line, whereas for the low Reynolds number case a second peak value is reached at the trailing edge of the flaps. This second peak can be connected to a SWSWI near the flaps, which causes higher pressure and heat loads. This will be described later in more detail. The separation region with the lowest heat flux rate is located immediately in front of the flaps for all three cases. Its beginning can be determined in the Stanton number distribution at the point of increasing negative heat flux gradient and its ending at the point of increasing positive gradient. A decrease in the separation region extension with increasing Reynolds number is visible. This could be confirmed by the corresponding Schlieren images. Numerical studies on a Mach 8 (Wright et al. 2000) flow around a double-cone configuration supports this separation behaviour for transitional interactions, whereas laminar and fully turbulent interactions show an opposite trend. Further downstream, a sharp increase in the heat flux is visible in Fig. 18, top. In the vicinity of the hinge line of the flaps the heat loads increase to a distinctive peak value which is followed by a decreasing curve towards the trailing edge for all three configurations. This is typical for a transitional boundary layer heating and has also been determined in an experimental and numerical study of the Pre-X configuration with a comparable Mach number of 8.9, 45°angle of attack but 20° flap deflection angle and a small Reynolds number of 0.06·10⁶ (Schramm and Reimann 2007). This result supports the transitional flow characterization due to the separation region development.

Fig. 18

Stanton number augmentation distribution for Reynolds number effects and 15° flaps at α = 45°

In the lateral slices along the y-axis (Fig. 18, bottom) the heat flux peak at the flap’s trailing edge is also clearly visible for the case of the low Reynolds number. Here, again up to approx. 50% augmentation compared to the stagnation point values were determined. This is also the case near the inner edges of the flap for the low Reynolds number case, not visible in the longitudinal slices.

3.3.3 Flap deflection effects

The influence of the flap deflection angle on the Stanton number distribution is presented for two different Reynolds number conditions.

3.3.3.1 Medium Reynolds number condition – Run25, Run32, Run30

As visible in Fig. 19, the location of highest heat load changes from the nose region for the 10° flaps to the flap region for the 15° and 20° flap configuration. At maximum, for the 20° flap angles an augmentation of up to 100% compared to the stagnation point level is visible.

Fig. 19

Stanton number augmentation distribution for Flap deflection effects and medium Reynolds number condition α = 45°

The minimum of the Stanton number according to the separation region just in front of the flaps is moving upstream for increasing flap deflection, but stays nearly on a constant level. A distinct “jump” of the minimum is visible for the 20° flap configuration. This is linked to a detachment of the shock in front of the flaps which causes an increase in heat flux already upstream of the hinge line. The level of the heat load is drastically changing when comparing the different flap angle configurations so that the heat flux peak at the hinge line changes from moderate for the 10° flap to a distinct overshoot for the other configurations. The heat flux distribution along the flaps shows the characteristic of a transitional flow for all three configurations, with increasing augmentation impact with increasing flap angle. On the 20° flaps a second peak on a similar maximum is visible directly upstream of the trailing edge which is again correlated to the SWSWI near the flaps. The increase in the overall heat flux level with flap angle is also clearly visible in the lateral slices (Fig. 19, bottom). At the inner edges of the flaps heat flux peaks are visible for all three configurations increasing with increasing flap angle.

3.3.3.2 High Reynolds number condition – Run15, Run27, Run34

Also, for the high Reynolds number condition a similar general heating augmentation tendency with flap angles is visible in Fig. 20. Just ahead of the flaps the heat flux minimum, linked to the separation region, moves upstream for increasing flap deflection due to an increase in adverse pressure gradient. On the flap itself a huge difference of the heat flux level and the characteristics is visible. It changes from the laminar plateau-like characteristic for the 5° flaps to a transitional one with an overshoot at the hinge line and a following decrease towards the trailing edge for the 10° and 15° flaps. At the trailing edge a moderate heat flux peak can be seen for the 10° and 15° flaps (Fig. 20, top). Along the y-axis a heat flux peak is visible at the inner trailing edges for all three flap configurations (Fig. 20, bottom). The level of the heat flux increases again with increasing flap angle. The second heat flux peak at the trailing edge of the 15° flap configuration is again correlated to an impingement resulting from SWSWI on the flap, although with a lower augmentation compared to its equivalent at the medium Reynolds number (Fig. 19).

Fig. 20

Flap deflection effects and high Reynolds number condition, α = 45°

3.3.4 Angle of attack effects

3.3.4.1 15° flaps – Run24, Run09, Run22

To evaluate the influence of the angle of attack on the heat flux distribution of the IXV configuration three different configurations, namely α = 35°, α = 45° and α = 55°, with the 15° flap angle and low Reynolds number condition have been investigated. Figure 21 shows the upper part the results for the longitudinal slices.

Fig. 21

Stanton number augmentation distribution for angle of attack effects, flap angle 15°

With increasing the angle of attack, the downstream movement of the stagnation region peak is clearly visible. The movement from the 35° to 45° case is relatively small due to the high curvature in the nose region, whereas the shift to the 55° case becomes greater. The heat load minimum in the separation region in front of the flaps moves clearly upstream for increasing angle of attack with a distinct “jump” between the 45° and 55° case. This is due to a complete change in the shock system around the flaps, visible in the corresponding Schlieren image, shown in Fig. 22, c.

Fig. 22

Combined Stanton number augmentation mappings and Schlieren images for a the 35°,b the 45° and c the 55° angle of attack case

Just downstream of the heat flux minimum the longitudinal distribution (Fig. 21, top) shows an increase in heat flux values for all three configurations. The 55° case shows an increased heat load upstream the hinge line, comparable to the case of the detached shock in front of the 20° flaps in Fig. 19, top. Again, a second enhanced increase at the hinge line at about 0.245m is visible. Along the flaps themselves the heat flux profile changes from a flat laminar heating for 35° to a transitional characteristic with the distinct increase in heat flux at the hinge line for the 45° and 55° case. For the 45° case the second peak value connected to a SWSWI near the trailing edge is visible as already observed in Fig. 18.

The combined Stanton number and Schlieren images in Fig. 22 show a clear change of shock structure between the three angle of attack cases. Furthermore, it shows clearly the change in SWSWI influence on the heat loads. Figure 22a shows no sign of interference of the SWSWI in the Stanton number distribution on the flaps and Schlieren image for the 35° case. For the α = 45° case the heat load peak, which could already be observed in the longitudinal and lateral slices (Fig. 21), is clearly visible near the flaps’ trailing edges in Fig. 22b. This huge shock induced heat flux augmentation was connected to an Edney V type interaction on the flap (Edney 1968; Olejniczak at al. 1996; Wright et al. 2000; Neeb et al. 2008). Here, locally factor 2 higher heat loads compared to the stagnation point heating can occur. The corresponding Schlieren image shows a disturbance generated by the SWSWI, which impinges the surface in this area. This phenomenon has already been observed in former experimental and numerical studies (Schramm and Reimann 2007).

In Fig. 22 c an interesting multiple shock structure is visible for the α = 55° just ahead of the flaps. Due to the high angle of attack and flap deflection angle several disturbances induced by the SWSWI impinge on the model surface, which cause increased local heat loads. The region with extremely high Stanton numbers expands in the lateral direction along the hinge line of both flaps and reaches even the main model outer part around the flaps. In this region the highest heat loads with values nearly 2.1 times of the stagnation region can be reached.

4 Concluding remarks

This experimental study discussed the role of the Shock Wave—Shock Wave—Interaction (SWSWI) and Shock Wave Boundary Layer Interaction (SWBLI) on the heat flux augmentation in hypersonic flow. The first test case concerning the shock boundary layer interaction on a flat plate shows, that the convective heating can be augmented by factors up to 7 depending on the shock and boundary layer properties. Shock Wave—Shock Wave—Interaction (SWSWI) at the stagnation point of a double sphere configuration allowed measurement of the heat flux augmentation greater than factor 3. The a bit more complex IXV flight configuration allowed measuring both SWSWI and SWBLI simultaneously. In particular a high angle of attack with a large flap angle combination in laminar flow leads to heat flux augmentation by more than factor two. The interaction is weaker in the turbulent hypersonic flow field.

In-flight measurement of the shock wave boundary layer interaction is also part of the coming DLR’s flight experiment called STORT (Key Technologies for High-Speed Return Flights of Launcher Stages), which will fly at hot hypersonic flight conditions using a three-stage sounding rocket configuration (Gülhan et al. 2021). The third stage will fly a suppressed trajectory at Mach numbers above 8 in an altitude range of 45 km to 55 km with a duration of approx. 120 s to generate high integral heat loads on the structure. The forebody of the vehicle consists of high temperature CMC panels which are extensively instrumented with heat flux sensors, thermocouples and pressure sensors along four longitudinal lines every 90° in circumferential direction.

Three fixed canards with a CMC outer shell are used to qualify thermal management concepts (Fig. 23). While an impingement cooling will be integrated in the first canard, the second canard is passively cooled. The third (reference) canard without any cooling will serve to perform a Shock Wave Boundary Layer Interaction (SWBLI) experiment, which requires dedicated instrumentation with fast response time to measure the foot print of the SWBLI around the canard. For the first time a miniaturized IR-camera will measure the canard outer surface temperature in hypersonic flight. Two additional video cameras will monitor the fins of the third stage.

Fig. 23

Third stage of the STORT flight configuration with scientific payloads

As a pre-flight activity, two test models of the reference canard mounted on a flat plate have been manufactured and will be tested in the hypersonic wind tunnel H2K and high enthalpy shock tunnel HEG in the coming weeks. The impact of the canard´s angle of attack, Mach number, Reynolds number and flow are the main parameters on the aerothermal heat flux augmentation that will be measured. Preparatory tests in H2K to specify the measurement set-up clearly showed the footprint of the heat flux augmentation induced by shock boundary layer interaction (SWBLI) on the plate (Fig. 24). As a second step a scaled model of the forebody and canards of the flight configuration will be tested in H2K.

Fig. 24

IR images of the canard, side view (left) and top view (right)