Analysis of the filtering effect of the stochastic estimation and accuracy improvement by sensor location optimization

Abstract

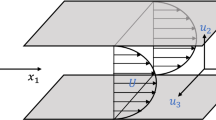
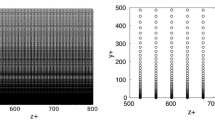
The reconstruction of the flow behind a backward-facing step at a Reynolds number of 60,000 using linear stochastic estimation (LSE) and modified LSE (with or without multi-time-delay) is investigated. In particular, the turbulent spatial integral length scales estimated for several sensor configurations are studied. The estimation of the proper orthogonal decomposition (POD) modes is also performed in order to show the limitations of the SE for complex flows, for which taking into account only a few POD modes may not be enough to represent the flow dynamics. The importance of the sensor locations on the estimation is also emphasized, and the opportunity to use a sensor location optimization algorithm is investigated.

Appendix: Tikhonov regularization

Let us denote N _s the number of time samples used to train the MTD-LSE. The problem of finding the MTD-LSE coefficients A _x coefficients can therefore be arranged in the following matrix system:

$${\text{MA}}\left( \varvec{x} \right) = {\text{U}}\left( \varvec{x} \right)$$

(19)

with:

$${\text{M}} = \left( {\begin{array}{*{20}c} {{\mathbf{E}}\left( {y_{1} ,t_{1} - \tau_{1} } \right)} & \ldots & {\begin{array}{*{20}c} {{\mathbf{E}}\left( {y_{N} ,t_{1} - \tau_{1} } \right)} & \ldots & {{\mathbf{E}}\left( {y_{N} ,t_{1} - \tau_{{N_{d} }} } \right)} \\ \end{array} } \\ \vdots & \ddots & {\begin{array}{*{20}c} \vdots & \ddots & \vdots \\ \end{array} } \\ {{\mathbf{E}}\left( {y_{1} ,t_{{N_{s} }} - \tau_{1} } \right)} & \ldots & {\begin{array}{*{20}c} {{\mathbf{E}}\left( {y_{N} ,t_{{N_{s} }} - \tau_{1} } \right)} & \ldots & {{\mathbf{E}}\left( {y_{N} ,t_{{N_{s} }} - \tau_{{N_{d} }} } \right)} \\ \end{array} } \\ \end{array} } \right)$$

$${\text{A}}\left( \varvec{x} \right) = \left( {\begin{array}{*{20}c} {A_{\varvec{x}} \left( {y_{1} ,\tau_{1} } \right)} \\ \vdots \\ {\begin{array}{*{20}c} {A_{\varvec{x}} \left( {y_{N} ,\tau_{1} } \right)} \\ \vdots \\ {A_{\varvec{x}} \left( {y_{N} ,\tau_{{N_{d} }} } \right)} \\ \end{array} } \\ \end{array} } \right)$$

$${\text{U}}\left( \varvec{x} \right) = \left( {\begin{array}{*{20}c} {u\left( {\varvec{x},t_{1} } \right)} \\ \vdots \\ {u\left( {\varvec{x},t_{{N_{s} }} } \right)} \\ \end{array} } \right)$$

In classical LSE, the system (19) is solved using the ordinary least square (OLS) method. In the OLS, one looks to minimize the loss function defined by the L ₂-norm of the residual ${\text{MA}}\left( \varvec{x} \right) - {\text{U}}\left( \varvec{x} \right)$:

$$f\left( {A,U} \right) = ||{\text{MA}}\left( \varvec{x} \right) - {\text{U}}\left( \varvec{x} \right)||^{2}$$

(20)

However, this system is ill-posed and the matrix M can be very ill-conditioned. In such conditions, the resulting model can be overfitted. The error obtained on the training data set is much lower than the error obtained on data outside the training data set. Thus, it may become better to compute an approximate solution using a nearby system that is less sensitive to perturbations that the initial one. To do so, the loss function is penalized. Using the Tikhonov regularization, the loss function is penalized using the L ₂-norm and becomes:

$$f\left( {A,U} \right) = ||MA\left( \varvec{x} \right) - U\left( \varvec{x} \right)||^{2} + ||LA\left( \varvec{x} \right)||^{2}$$

(21)

Then, the coefficients A(x) are solution of the following regularized system:

$$\left( {M^{T} M + L^{T} L} \right)A\left( x \right) = M^{T} U\left( x \right)$$

(22)

where L is called the Tikhonov matrix. Most often, L is taken such as being proportional to the identity matrix: L = αI. Such matrix is used in this work. And the regularization parameter α is determined by cross-validation (more details can be found in Abu-Mostafa et al. 2012).

In comparison with the OLS where A(x) satisfies the minimization problem $\min_{{A\left( \varvec{x} \right) \in R^{{N.N_{d} }} }} \left( ||{MA\left( \varvec{x} \right) - U\left( \varvec{x} \right)^{2} } \right)$, using the Tikhonov regularization A(x) satisfies the minimization problem:

$$\min_{{A\left( \varvec{x} \right) \in R^{{N.N_{d} }} }} \left(||{MA\left( \varvec{x} \right) - U\left( \varvec{x} \right||)^{2} + \propto^{2} ||U\left( \varvec{x} \right)||^{2} } \right).$$

In our case, only one regularization parameter is used for the complete system formed with A the matrix containing all the columns A(x) for all x of the field to estimate and U all the columns U(x).