Skip to main content
SpringerLink
Log in

Time-resolved stereo PIV measurements of the horseshoe vortex system at multiple locations in a low-aspect-ratio pin–fin array

  • Research Article
  • Published:
Experiments in Fluids Aims and scope Submit manuscript

Abstract

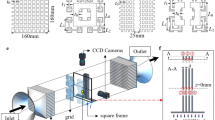
Pin–fin arrays are a type of cooling feature found in heat exchangers, with elements (generally cylindrical or square) that span between two endwalls. Flow around the pin–fins generates highly turbulent mixing that increases convective heat transfer from the pins to the cooling flow. At the junction of a pin–fin and the endwall, a complex flow known as the horseshoe vortex (HSV) system is present. Although the HSV is a well-studied phenomenon, its behavior is not understood in the highly turbulent flow of a pin–fin array. Furthermore, the presence of close confining endwalls for low-aspect-ratio (short) pin–fins may have an impact on HSV dynamics. The present study utilized time-resolved stereo particle image velocimetry to examine the fluid dynamics of the HSV system in rows 1, 3, and 5 of a low-aspect-ratio pin–fin array, for a range of Reynolds numbers. In the first row, instantaneous flowfields indicated a clearly defined HSV at the leading edge, with dynamics similar to previous studies of bluff-body junction flows. The time-averaged HSV system moved closer to the pin with increasing Reynolds number, with more concentrated vorticity and turbulent kinetic energy (TKE). For downstream rows, there was a significant increase in the amount of mid-channel vorticity, with levels on the same order as the value in the core of the HSV. The time-averaged HSV system in downstream rows showed minimal variation with respect to either Reynolds number or row location. Regions of maximum streamwise and wall-normal turbulent fluctuations around the HSV were a result of its quasiperiodic oscillation between so-called backflow and zero-flow modes, which were present even in downstream rows despite the extremely high mid-channel turbulence. In the downstream rows, normalized TKE across the entire field of view decreased with increased Reynolds number, likely due to dissipation rates proportionally outpacing increases in mean channel velocity and Reynolds number. The flowfield results from this study corroborate prior findings from heat transfer measurements that indicate a fully developed condition is established at around the fifth row in an array.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Abbreviations

D :

Pin–fin diameter

dt :

Time between S-PIV image-pair exposures

f :

S-PIV sampling frequency

H :

Pin–fin height, H = D

HSV:

Horseshoe vortex

\(\overline{{n^{{\prime }} n^{{\prime }} }}\) :

Variance of component of velocity, n (where n is u, v, or w)

S-PIV:

Stereo particle image velocimetry

Re D :

Reynolds number based on D and U m , \(Re_{D} = \frac{{D*U_{m} }}{\nu}\)

S L :

Streamwise array spacing, S L = 3.46 * D

S w :

Spanwise array spacing, S w = 2 * D

Δt + :

Sampling timestep in inner coordinates, \(\varDelta t^{ + } = \frac{{{\raise0.7ex\hbox{$u_{\tau }^{2}$} \!\mathord{\left/ {\vphantom {1 f}}\right.\kern-0pt} \!\lower0.7ex\hbox{$f$}} }}{\nu}\)

Tu:

Turbulence level, \({\text{Tu}} = \left.\left( {\sqrt {\frac{2}{3}{\text{TKE}} } } \right)\right/U_{m}\)

TKE:

Turbulent kinetic energy, \({\text{TKE}} = \frac{1}{2}\sqrt {\overline{{u^{\prime } u^{\prime } }} + \overline{{v^{\prime } v^{\prime } }} + \overline{{w^{\prime } w^{\prime } }} }\)

u :

Streamwise component of velocity

u τ :

Friction velocity

u + :

Streamwise component of velocity in inner coordinates, \(u^{ + } = \frac{u}{{u_{\tau } }}\)

U m :

Channel mean velocity upstream of array

U max :

Maximum average velocity in the channel, U max = 2 * U m

v :

Endwall normal component of velocity

|V| :

Velocity magnitude

w :

Spanwise component of velocity

X :

Streamwise direction

y + :

Wall-normal direction in inner coordinates, \(y^{ + } = \frac{{yu_{\tau } }}{\nu}\)

Y :

Endwall normal direction

Z :

Spanwise direction

ν :

Kinematic viscosity

References

  • Agui JH, Andreopoulos J (1992) Experimental investigation of a three-dimensional boundary layer flow in the vicinity of an upright wall mounted cylinder (data bank contribution). J Fluids Eng 114:566–576

    Article  Google Scholar 

  • Ames F, Dvorak L (2006) The influence of Reynolds number and row position on surface pressure distributions in staggered pin fin arrays. Paper published in ASME Turbo Expo 2006: Power for Land, Sea, and Air, pp 149–159

  • Ames FE, Dvorak LA, Morrow MJ (2005) Turbulent augmentation of internal convection over pins in staggered-pin fin arrays. J Turbomach 127:183–190

    Article  Google Scholar 

  • Ames FE, Nordquist CA, Klennert LA (2007) Endwall heat transfer measurements in a staggered pin fin array with an adiabatic pin. Paper published in ASME Turbo Expo 2007: Power for Land, Sea, and Air, pp 423–432

  • Ballio F, Bettoni C, Franzetti S (1998) A survey of time-averaged characteristics of laminar and turbulent horseshoe vortices. J Fluids Eng 120:233–242

    Article  Google Scholar 

  • Blair MF (1974) An experimental study of heat transfer and film cooling on large-scale turbine endwalls. J Heat Transf 96(4):524–529. doi:10.1115/1.3450239

    Article  Google Scholar 

  • Borello D, Hanjali K (2011) LES of fluid and heat flow over a wall-bounded short cylinder at different inflow conditions. J Phys: Conf Ser 318:042046

    Google Scholar 

  • Delibra G, Hanjalić K, Borello D, Rispoli F (2010) Vortex structures and heat transfer in a wall-bounded pin matrix: LES with a RANS wall-treatment. Int J Heat Fluid Flow 31:740–753

    Article  Google Scholar 

  • Devenport WJ, Simpson RL (1990) Time-dependent and time-averaged turbulence structure near the nose of a wing-body junction. J Fluid Mech 210:23–55

    Article  Google Scholar 

  • Escauriaza C, Sotiropoulos F (2011) Reynolds number effects on the coherent dynamics of the turbulent horseshoe vortex system. Flow Turbul Combust 86:231–262

    Article  MATH  Google Scholar 

  • Fleming JL, Simpson RL, Cowling JE, Devenport WJ (1993) An experimental study of a turbulent wing-body junction and wake flow. Exp Fluids 14:366–378

    Article  Google Scholar 

  • Giel PW, Thurman DR, Fossen GJV, Hippensteele SA, Boyle RJ (1998) Endwall heat transfer measurements in a transonic turbine cascade. J Turbomach 120:305–313

    Article  Google Scholar 

  • Graziani RA, Blair MF, Taylor JR, Mayle RE (1980) An experimental study of endwall and airfoil surface heat transfer in a large scale turbine blade cascade. J Eng Power 102:257–267

    Article  Google Scholar 

  • Hunt J, Abell C, Peterka J, Woo H (1978) Kinematical studies of the flows around free or surface-mounted obstacles; applying topology to flow visualization. J Fluid Mech 86:179–200

    Article  Google Scholar 

  • Kähler CJ, Scharnowski S, Cierpka C (2012) On the uncertainty of digital PIV and PTV near walls. Exp Fluids 52:1641–1656

    Article  Google Scholar 

  • Kang MB, Kohli A, Thole KA (1999) Heat transfer and flowfield measurements in the leading edge region of a stator vane endwall. J Turbomach 121:558–568

    Article  Google Scholar 

  • Kirkil G, Constantinescu G (2015) Effects of cylinder reynolds number on the turbulent horseshoe vortex system and near wake of a surface-mounted circular cylinder. Phys Fluids 27:075102

    Article  Google Scholar 

  • Lawson SA, Thrift AA, Thole KA, Kohli A (2011) Heat transfer from multiple row arrays of low aspect ratio pin fins. Int J Heat Mass Transf 54:4099–4109

    Article  Google Scholar 

  • Levchenya AM, Smirnov EM, Goryachev VD (2010) RANS-based numerical simulation and visualization of the horseshoe vortex system in the leading edge endwall region of a symmetric body. Int J Heat Fluid Flow 31:1107–1112

    Article  Google Scholar 

  • Metzger D, Haley S (1982) Heat transfer experiments and flow visualization for arrays of short pin fins. Paper published in ASME 1982 International Gas Turbine Conference and Exhibit: V004T009A007-V004T009A007

  • Olcmen SM, Simpson RL (1994) Influence of wing shapes on surface pressure fluctuations at wing-body junctions. AIAA J 32:6–15

    Article  Google Scholar 

  • Ölçmen SM, Simpson RL (2006) Some features of a turbulent wing-body junction vortical flow. Int J Heat Fluid Flow 27:980–993

    Article  Google Scholar 

  • Ostanek J, Thole K (2012a) Effect of streamwise spacing on periodic and random unsteadiness in a bundle of short cylinders confined in a channel. Exp Fluids 53:1779–1796

    Article  Google Scholar 

  • Ostanek J, Thole K (2012b) Wake development in staggered short cylinder arrays within a channel. Exp Fluids 53:673–697

    Article  Google Scholar 

  • Ostanek JK, Thole KA (2012c) Flowfield measurements in a single row of low aspect ratio pin fins. J Turbomach 134:051034

    Article  Google Scholar 

  • Paik J, Escauriaza C, Sotiropoulos F (2007) On the bimodal dynamics of the turbulent horseshoe vortex system in a wing-body junction. Phys Fluids (1994-present) 19

  • Praisner TJ, Smith CR (2006a) The dynamics of the horseshoe vortex and associated endwall heat transfer—part I: temporal behavior. J Turbomach 128:747–754

    Article  Google Scholar 

  • Praisner TJ, Smith CR (2006b) The dynamics of the horseshoe vortex and associated endwall heat transfer—part II: time-mean results. J Turbomach 128:755–762

    Article  Google Scholar 

  • Radomsky RW, Thole KA (2000) High free-steam turbulence effects on endwall heat transfer for a gas turbine stator vane. J Turbomach 122:699–708

    Article  Google Scholar 

  • Sabatino DR, Smith CR (2009) Boundary layer influence on the unsteady horseshoe vortex flow and surface heat transfer. J Turbomach 131:011015–011018

    Article  Google Scholar 

  • Sahin B, Ozturk NA, Gurlek C (2008) Horseshoe vortex studies in the passage of a model plate-fin-and-tube heat exchanger. Int J Heat Fluid Flow 29:340–351

    Article  Google Scholar 

  • Scholten JW, Murray DB (1998) Heat transfer and velocity fluctuations in a staggered tube array. Int J Heat Fluid Flow 19:233–244

    Article  Google Scholar 

  • Simoneau R, Van Fossen G (1984) Effect of location in an array on heat transfer to a short cylinder in crossflow. J Heat Transf 106:42–48

    Article  Google Scholar 

  • Simpson RL (2001) Junction flows. Ann Rev Fluid Mech 33:415–443

    Article  Google Scholar 

  • Wieneke B (2014) Generic a posteriori uncertainty quantification for PIV vector fields by correlation statistics. Paper published in 17th international symposium on applications of laser techniques to fluid mechanics (Lisbon, Portugal)

  • Yates LA, Chapman GT (1992) Streamlines, vorticity lines, and vortices around three-dimensional bodies. AIAA J 30:1819–1826

    Article  MATH  Google Scholar 

Download references

Author information

Author notes

  1. Corey D. Anderson

    Present address: United Technologies–Pratt & Whitney, East Hartford, CT, USA

Authors and Affiliations

  1. Department of Mechanical and Nuclear Engineering, Pennsylvania State University, University Park, PA, 16802, USA

    Corey D. Anderson & Stephen P. Lynch

Authors
  1. Corey D. Anderson
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Stephen P. Lynch
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Stephen P. Lynch.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Anderson, C.D., Lynch, S.P. Time-resolved stereo PIV measurements of the horseshoe vortex system at multiple locations in a low-aspect-ratio pin–fin array. Exp Fluids 57, 5 (2016). https://doi.org/10.1007/s00348-015-2091-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00348-015-2091-7

Keywords

Search

Navigation