1 Introduction

Nowadays, the progress in engineering quantum matter in the laboratory has allowed to gain deeper insights into the dynamic properties of the quantum many-body systems [1,2,3]. These systems with the nearest-adjacent interactions in the lattice sites, like the Ising, Heisenberg and Hubbard models, have fundamental significance in comprehending the strongly correlated systems [4]. Beside the adjacent interactions, there are other types of interactions known as long-range interactions that have a significant effect on the correlated system dynamics. The frustrations and newly discovered essential behaviors which result in unexpected phenomena have led to some studies being focused on systems with long-range interaction [5,6,7]. Additionally, the trapped ion system [8,9,10] has recently been tuned and used to achieve novel models of many-body systems with long-range interaction. Moreover, it is thought that the entanglement of trapped-ion atoms is one of the most efficient and reliable techniques [11].

Some preceding studies have shown many protocols and procedures to achieve correlated and entangled states [12,13,14,15,16]. The engineering procedures to obtain multi-qubit entangled and correlated states have become important in quantum metrology [17], quantum information [18] and computation [19]. Besides, the nonlocality, uncertainty principle and entanglement criteria are the most notable illustrations to distinguish between classical and quantum, and they are also the most interesting aspects of information resources [20, 21]. These criteria are here employed as the primary aim for exploring quantum correlations. Such correlations are studied in this context in particular within natural systems, such as trapped ions with long-range interaction. The tunable ion trap systems are important tools for efficient quantum information techniques [22]. As a result, certain qubit models using the trap-ion lattice have been developed to address significant computing difficulties [23].

However, as far as we know, studying the decoherence effect on interacting many-body systems is critical to both quantum information and metrology [17, 24, 25]. So, a closed or open trap-ion chain will be susceptible to decoherence effects, so the chain cannot be completely shielded from decoherence. Such a decoherence occurs when the closed ions system evolves in a stochastic sequence of identical unitary transformations due to the ions’ intrinsic vibration at small time scales. For this purpose, the present research aims to investigate the formation and robustness of correlations and entanglements among sites occupied by ions under the intrinsic decoherence impact by employing the uncertainty-induced nonlocality, concurrence and Bell function criteria. Such criteria are extremely useful for tracking the arising information in trapped ions with long-range interaction.

The present research is structured as follows: Sect. 2 describes the model of the long-range Paul trap chain and the decoherence trap equation with its solution. Section 3 introduces several criteria for detecting arising information across ion correlations, as well as an examination of their temporal evolution behavior. Section 4 provides our results and draws a few conclusions.

2 Model and ionic vibration equation

2.1 Paul trap chain

A model of linear trap lattice like this can be experimentally achieved with a collection of N ions trapped by magnetic and electric forces in a one-dimensional chain [26,27,28]. The axial direction of the chain is assigned to z-axis, while the x, y-axes are assigned to its radial direction, see Fig. 1a. Each site is here occupied by one ion and has two internal ground hyperfine states (\(|\uparrow \rangle , |\downarrow \rangle\)), and each site is separated from the others by a various distance. The configuration of the interaction of ions between the chain sites is controlled by the laser field’s intensity and polarization, and it transmits via the collective vibration modes, or phonons. Besides, the chain is sensitive to a global magnetic field, \(\vec {M}_{0}\), which can act in any direction. The strength of the magnetic field is simulated via lasers acting on the internal transition of the ions. According to [26, 28], the corresponding Hamiltonian of chain sites is as follows:

$$\begin{aligned} {\hat{H}}_{sk}= & {} \sum _{s,k,\zeta }\wp ^{\zeta }_{s,k}\left[ \frac{m}{2} {\hat{Q}}^{\zeta }_{s}{\hat{Q}}^{\zeta }_{k}+\frac{1}{2m}{\hat{P}}^{\zeta }_{s} {\hat{P}}^{\zeta }_{k}\right] \nonumber \\{} & {} -2\sum _{s,\zeta }\eta _{\zeta }{\hat{Q}}^{\zeta }_{s}| \uparrow \rangle \langle \uparrow |_{s,\zeta }+\sum _{k}\vec {M}_{0}\cdot \vec {\sigma }_{k}, \end{aligned}$$
(1)

where \(\wp ^{\zeta }_{s,k}\) denotes a specific elasticity matrix, \({\hat{Q}}^{\zeta }_{k}\) represents the spatial position operator of each ion at k site in each \(\zeta\) direction, \({\hat{P}}^{\zeta }_{k}\) is the momentum operator corresponding to \({\hat{Q}}^{\zeta }_{k}\), m is the mass of ion, \(\zeta =(x,y,z)\), \(\vec {\sigma }_{k}=({\hat{\sigma }}^{x}_{k},{\hat{\sigma }}^{y}_{k},{\hat{\sigma }}^{z}_{k})\) is the vector of Pauli operators, \(\eta _{\zeta }\) is the coupling of internal states with the motion caused by placing the ions in an off-resonant standing wave, and \(\vec {M}_{0}=(M^{x},M^{y},M^{z})\) with \(M^{x}\) is the energy of the internal state and others can be specified via the action of lasers with the internal transition. In another aspect, we represent \({\hat{Q}}^{\zeta }_{k}\) and \({\hat{P}}^{\zeta }_{k}\) in terms of the rising and lowering of phonons, \({\hat{\Re }}^{\dagger }_{\jmath ,\zeta }\) and \({\hat{\Re }}_{\jmath ,\zeta }\), by means of a specific unitary matrix \(\complement ^{\zeta }\) as: \({\hat{Q}}^{\zeta }_{s}=\sum _{\jmath }\complement ^{\zeta }_{\jmath ,s}\sqrt{\frac{\hbar }{2\,m(N-1)\omega ^{\zeta }_{\jmath }}}({\hat{\Re }}_{\jmath ,\zeta } +{\hat{\Re }}^{\dagger }_{\jmath ,\zeta })\) and \({\hat{P}}^{\zeta }_{s}=-i\sum _{\jmath }\complement ^{\zeta }_{\jmath ,s}\sqrt{\frac{\hbar m}{2(N-1)\omega ^{\zeta }_{\jmath }}}({\hat{\Re }}_{\jmath ,\zeta }-{\hat{\Re }}^{\dagger }_{\jmath ,\zeta })\), with \(\omega ^{\zeta }_{\jmath }\) indicates the energy of \(\jmath\) mode in the \(\zeta\)-direction. Therefore, the chain Hamiltonian (1) with ignoring the constant terms reads:

$$\begin{aligned} {\hat{H}}_{ch}= & {} \sum _{\zeta ,\jmath }\hbar \omega ^{\zeta }_{\jmath } {\hat{\Re }}^{\dagger }_{\jmath ,\zeta }{\hat{\Re }}_{\jmath ,\zeta } -\sum _{\zeta ,\jmath ,s}\chi ^{\zeta }_{\jmath ,s}({\hat{\Re }}_{\jmath ,\zeta } +{\hat{\Re }}^{\dagger }_{\jmath ,\zeta })({\hat{I}} +{\hat{\sigma }}^{\zeta }_{s})\nonumber \\{} & {} +\sum _{k}\vec {M}_{0}\cdot \vec {\sigma }_{k}, \end{aligned}$$
(2)

where \(\chi ^{\zeta }_{\jmath ,s}=\eta _{\zeta }\complement ^{\zeta }_{\jmath ,s}\sqrt{\frac{\hbar }{2m(N-1)\omega ^{\zeta }_{\jmath }}}\) and \(\sum _{s,k}\complement ^{\zeta }_{\jmath ,s}\wp ^{\zeta }_{s,k}\complement ^{\zeta }_{\jmath _{1},k}=(N-1)(\omega ^{\zeta }_{\jmath })^{2}\delta _{\jmath ,\jmath _{1}}\).

Such a above physical realization of the confined ions in this scenario corresponds to the Coulomb chain in Paul traps, which can result in long-range antiferromagnetic interaction in the axial direction. To get this, we perform a unitary transformation \(e^{\digamma }\) with a generator \(\digamma =\sum _{\zeta ,\jmath ,s}\frac{\chi ^{\zeta }_{\jmath ,s}}{\hbar \omega ^{\zeta }_{\jmath }}({\hat{\Re }}_{\jmath ,\zeta }-{\hat{\Re }}^{\dagger }_{\jmath ,\zeta })({\hat{I}} +{\hat{\sigma }}^{\zeta }_{s})\) to system (2). In light of this, the generating Hamiltonian of the linear Paul trap for \(\chi ^{\zeta }_{\jmath ,s}\ll \hbar \omega ^{\zeta }_{\jmath }\), with disregard for the constant terms, can be written as follows:

$$\begin{aligned} {\hat{H}}^{'}_{ch}= & {} e^{\digamma }{\hat{H}}_{ch}e^{-\digamma }\nonumber \\\approx & {} -\sum _{\zeta ,s,k}J^{\zeta }_{s,k}{\hat{\sigma }}^{\zeta }_{s}{\hat{\sigma }}^{\zeta }_{k} +\sum _{k}\vec {M}\cdot \vec {\sigma }_{k}\nonumber \\{} & {} +\sum _{\zeta ,\jmath }\hbar \omega ^{\zeta }_{\jmath }{\hat{\Re }}^{\dagger }_{\jmath ,\zeta }{\hat{\Re }}_{\jmath ,\zeta } \nonumber \\{} & {} +\sum _{\zeta ,\jmath ,s}\sum _{\zeta _{1},\jmath _{1}} \frac{\chi ^{\zeta }_{\jmath ,s}\chi ^{\zeta _{1}}_{\jmath _{1},s}}{2\hbar \omega ^{\zeta _{1}}_{\jmath _{1}}} ({\hat{\Re }}_{\jmath ,\zeta }+{\hat{\Re }}^{\dagger }_{\jmath ,\zeta }) ({\hat{\Re }}_{\jmath _{1},\zeta _{1}}-{\hat{\Re }}^{\dagger }_{\jmath _{1},\zeta _{1}})\nonumber \\{} & {} ({\hat{\sigma }}^{\zeta }_{s}{\hat{\sigma }}^{\zeta _{1}}_{s} -{\hat{\sigma }}^{\zeta _{1}}_{s}{\hat{\sigma }}^{\zeta }_{s}), \end{aligned}$$
(3)

where \(J^{\zeta }_{s,k}=\sum _{\jmath }\frac{\chi ^{\zeta }_{\jmath ,s}\chi ^{\zeta }_{\jmath ,k}}{\hbar \omega ^{\zeta }_{\jmath }}\), \(\zeta =\zeta _{1}\), \(\vec {M}=M_{\zeta }{\hat{e}}_{\zeta }\), \(M_{\zeta }=M^{\zeta }-\frac{\eta ^{2}_{\zeta }}{m\omega ^{2}_{\zeta }}\) represents an overall correction to the amount of global magnetic field, and \(\sum _{\jmath }\frac{\complement ^{\zeta }_{\jmath ,s}\complement ^{\zeta }_{\jmath ,k}}{(N-1)(\omega ^{\zeta }_{\jmath })^{2}}=\frac{1}{\omega ^{2}_{\zeta }}\) with \(\omega _{\zeta }\) is the trapping frequency in \(\zeta\)-direction.

In the harmonic approximation, the displacements around the equilibrium locations can be used to represent the Coulomb repulsion so that the ions occupy the equilibrium positions along the \(\zeta\)-axis. Thus, the coupling strength among ions is specified by the characteristics of the vibrational modes via the second derivatives of the Coulomb interaction with respect to the positions [26, 29]. This means that \(J^{\zeta }_{s,k}=\sum _{\jmath } \frac{\eta ^{2}_{\zeta }\complement ^{\zeta }_{\jmath ,s}\complement ^{\zeta }_{\jmath ,k}}{2\,m(N-1)(\omega ^{\zeta }_{\jmath })^{2}}= -\frac{\eta ^{2}_{\zeta }|\vec {r}^{\zeta }_{s}-\vec {r}^{\zeta }_{k}|^{-p}\top _{\zeta }}{2\,m(N-1)(\omega ^{\zeta }_{\jmath })^{2}}\), where \(|\vec {r}^{\zeta }_{s}-\vec {r}^{\zeta }_{k}|\) is the distance between any two-ion position, \(0<p\le 3\) is a parameter to tune the range of the power-law interactions, \(\vec {r}^{\zeta }_{s}\) is the vector of ions’ equilibrium position, and \(\top _{\zeta }\) is a parameter that quantifies the relative value of Coulomb interaction and trapping potentials for \(s\ne k\) and \(\top _{\zeta }\ll 1\) [26, 28]. In addition, the terms describing the spin-phonon couplings can be neglected in the case of low phonon temperatures [26], so the last two terms of Eq. (3) are not taken into account. As a result, the model governing the spin-spin antiferromagnetic interaction along the z-direction of the confined ions at nearest-neighboring sites or next-to-nearest neighboring sites (i.e., between 1–2, 2–5, 1–3, and so on) is as follows:

$$\begin{aligned} {\hat{H}}= & {} \frac{J}{(N-1)}\sum _{s\ne k}\frac{{\hat{\sigma }}^{z}_{s} {\hat{\sigma }}^{z}_{k}}{|\vec {r}^{z}_{s}-\vec {r}^{z}_{k}|^{p}}\nonumber \\{} & {} +\sqrt{M^{2}_{x}+M^{2}_{z}}\sum _{k}({\hat{\sigma }}^{x}_{k}\sin \theta +{\hat{\sigma }}^{z}_{k}\cos \theta ), \end{aligned}$$
(4)

where \(J=\frac{\eta ^{2}_{z}\top _{z}}{2m(\omega ^{z}_{\jmath })^{2}}\), N is the number of ions, \(M_{x}=M^{x}-\frac{\eta ^{2}_{x}}{m\omega ^{2}_{x}}\), \(M_{z}=M^{z}-\frac{\eta ^{2}_{z}}{m\omega ^{2}_{z}}\), and \(\theta =\arctan (\frac{M_{x}}{M_{z}})\) indicates the angle between the direction of global magnetic field and axial axis. For the Eq. (4), we assumed that the chain is susceptible to magnetic field in any direction across the zx-plane.

In this work, we consider the case of (\(p=2\)) to estimate the long-range antiferromagnetic interaction across two sites that have four possible internal states as: \(\{|\uparrow _{s}\uparrow _{k}\rangle , |\uparrow _{s}\downarrow _{k}\rangle , |\downarrow _{s}\uparrow _{k}\rangle , |\downarrow _{s}\downarrow _{k}\rangle \}\).

Fig. 1
figure 1

Simulation of quantum information with trapped ions. a A schematic setup of the long-range Paul trap, which contains a linear chain of trapped ions restricted by external laser beams and a harmonic potential along the z-direction (axial trapping). b A scheme for describing the intrinsic decoherence in a non-idealistic Paul trap

Full size image

2.2 Decoherence of Paul trap

We here address the non-ideal effects that would arise during the configuration of the Paul trap chain. These effects may arise due to the vibration of ions between sites or be caused by stochastic fluctuations in the laser intensity applied to the ion system, see Fig. 1b. Usually, these effects create an excess electric field on adjacent ions and result in spontaneous decay of the internal spin states, causing intrinsic decoherence inside the Paul lattice. Such a decoherence has the potential to destroy the information that arises between the interacting ions. Thus, the equation describing the dynamics of an ionic vibrational trap can be expressed in a similar form to that considered in Ref. [30] as follows:

$$\begin{aligned} \hat{{\dot{\varrho }}}(t)= & {} \Gamma \biggl [e^{\frac{-i{\hat{H}}}{\hbar \Gamma }} {\hat{\varrho }}(t)e^{\frac{i{\hat{H}}}{\hbar \Gamma }}-{\hat{\varrho }}(t)\biggl ], \end{aligned}$$
(5)

where \({\hat{\varrho }}\) is the density operator of ionic vibration, and \(\Gamma\) denotes the decay rate in dynamics caused by ionic vibration, which is known as an intrinsic decoherence parameter as estimated by Milburn [30]. It should be noted that expanding the preceding series to higher terms than \(\Gamma ^{-2}\) leads to a higher order of decoherence. So, the series of the exponential functions of Eq. (5) expands up to terms in \(\Gamma ^{-2}\) as follows:

$$\begin{aligned} \hbar \hat{{\dot{\varrho }}}(t)\approx & {} i\Big ({\hat{\varrho }}(t){\hat{H}} -{\hat{H}}{\hat{\varrho }}(t)\Big )\nonumber \\{} & {} +\frac{\gamma }{2}\Big (2{\hat{H}}{\hat{\varrho }}(t){\hat{H}} -{\hat{\varrho }}(t){\hat{H}}^{2}-{\hat{H}}^{2}{\hat{\varrho }}(t)\Big ), \end{aligned}$$
(6)

where \(\gamma =\frac{1}{\hbar \Gamma }\) is the decoherence or vibration rate.

2.3 Solving decoherence equation

First, the general solution of Eq. (6) can be expressed in terms of the superoperators, , and , as follows:

(7)

where , , , and \({\hat{\varrho }}(0)\) is the density operator of initial ion-trap system. Second, we assume that the two interacting ions across the chain start with two separate initial states, as follows: (i) In an uncorrelated state \({\hat{\varrho }}(0)=\alpha ^{*}\delta |\uparrow _{s}\uparrow _{k}\rangle \langle \downarrow _{s}\downarrow _{k}|\); (ii) maximally correlated state \(\frac{\{\alpha |\downarrow _{s}\downarrow _{k}\rangle +\delta |\uparrow _{s}\uparrow _{k}\rangle \}\otimes \{\alpha ^{*}\langle \downarrow _{s}\downarrow _{k}| +\delta ^{*}\langle \uparrow _{s}\uparrow _{k}|\}}{\sqrt{(|\alpha |^{2}+|\delta |^{2})(|\alpha ^{*}|^{2}+|\delta ^{*}|^{2})}}\), where \(\alpha\) and \(\delta\) are the particular complex numbers. Thus, we can rewrite the above solution (7) in the following way:

$$\begin{aligned} {\hat{\varrho }}(t)= & {} \sum _{m=0}^{\infty }\biggl (\frac{\gamma t}{\hbar } \biggl )^{m}\bigg [\frac{{\hat{H}}^{m}}{\sqrt{ m!}}\,e^{-i\frac{{\hat{H}}t}{\hbar }}e^{-\frac{\gamma {\hat{H}}^{2}t}{2\hbar }}{\hat{\varrho }}(0) e^{-\frac{\gamma {\hat{H}}^{2}t}{2\hbar }}e^{i\frac{{\hat{H}}t}{\hbar }} \,\frac{{\hat{H}}^{m}}{\sqrt{m!}}\bigg ]. \end{aligned}$$
(8)

Following the action of straightforward calculations with the suggested model, the precise analytical solution of the ionic decoherence equation is given by:

$$\begin{aligned} {\hat{\varrho }}(t)= & {} \sum ^{4}_{m,n=1}\exp \left[ -\left( i\lambda _{mn} +\frac{\gamma \lambda ^{2}_{mn}}{2}\right) t\right] \langle \Theta _{m}|{\hat{\varrho }}(0)|\Theta _{n}\rangle \, |\Theta _{m}\rangle \langle \Theta _{n}|, \end{aligned}$$
(9)

where \(\hbar =1\), \(D=|\vec {r}^{z}_{s}-\vec {r}^{z}_{k}|\), \(M=\sqrt{M^{2}_{x}+M^{2}_{z}}\), and \(\lambda _{mn}=(\lambda _{m}-\lambda _{n})\), with \(\lambda _{1}=-\frac{2J}{D^{2}}, \quad \lambda _{2}=\frac{1}{3D^{2}}\bigl [2J -2(\frac{\varpi _{1}}{\varpi _{2}}-\varpi _{2})\bigl ]\), \(\lambda _{3}=\frac{1}{3D^{2}}\bigl [2J +(\frac{\varpi _{1}}{\varpi _{2}}-\varpi _{2})+i\sqrt{3}(\frac{\varpi _{1}}{\varpi _{2}}+\varpi _{2})\bigl ]\), \(\lambda _{4}=\lambda ^{*}_{3}\), \(\varpi _{1}=-(4J^{2}+3M^{2} D^{4})\), \(\varpi _{2}=(\varpi _{3}+ \sqrt{\varpi ^{3}_{1}+\varpi ^{2}_{3}})^{\frac{1}{3}}\) and \(\varpi _{3}=-J[8J^{2}+9M^{2}D^{4}(1-3\cos ^{2}\theta )]\). In the preceding solution, the states of \(|\Theta \rangle\) represent the eigenstates of Hamiltonian (4) that are given by:

$$\begin{aligned} |\Theta {_1}\rangle= & {} -\frac{1}{\sqrt{2}}\bigl \{|\downarrow _{s}\uparrow _{k} \rangle -|\uparrow _{s}\downarrow _{k}\rangle \bigl \}. \nonumber \\ |\Theta _{j}\rangle= & {} \frac{1}{\eta _{j}}\bigl \{ A_{j}|\downarrow _{s} \downarrow _{k}\rangle + B_{j}|\downarrow _{s}\uparrow _{k}\rangle + B_{j}|\uparrow _{s}\downarrow _{k}\rangle +|\uparrow _{s}\uparrow _{k}\rangle \bigl \}, \end{aligned}$$
(10)

where \(A_{j}=\bigl [D^{4}(\lambda _{j}+M\cos \theta )^{2}-M^{2}D^{4}(1+\sin ^{2}\theta )+4JMD^{2}\cos \theta -4J^{2}\bigl ]/\bigl [2D^{4}M^{2}\sin ^{2}\theta \bigl ]\), \(B_{j}=\bigl [\lambda _{j}D^{4}+2D^{2}M\cos \theta -2J\bigl ]/\bigl [2D^{2}M\sin \theta \bigl ]\) and \(\eta _{j}\) denotes the normalization constants for \(j= 2,3,4\) and \(s\ne k\). In the following context, we use the density operator solution to identify the information that arises across the generated correlation and entanglement in the Paul chain. To do this, various measures’ numerical results are used.

3 Generating information among interacting ions

Here, the generation and detection of information between lattice sites are investigated via the correlation and entanglement of the interacting ions. Some of criteria, like Bell inequality, uncertainty-induced nonlocality (UIN) and concurrence entanglement, are employed to measure the robustness of arisen information at any time. Besides, we discuss the impact of physical quantities of D, J, \(\gamma\) and \(\theta\) on the derived information.

3.1 Information resource criteria

  • Uncertainty-induced nonlocality: Starting, the quantity of skew information for a two-ion state, \({\hat{\varrho }}(t)\), and a local observable, \({\hat{\ell }}\), of ions subsystem is given by [31]:

    $$\begin{aligned} {\hat{S}}_{f}(t)= & {} -\frac{1}{2}\text {Tr}\Bigl (\sqrt{{\hat{\varrho }} (t)}{\hat{\ell }}-{\hat{\ell }}\sqrt{{\hat{\varrho }}(t)}\Bigr )^{2}. \end{aligned}$$
    (11)

    According to [32, 33], this quantity is employed to define the UIN measure to discover the information encoded among any correlated two-ions in the lattice as follows: \({\hat{U}}(t)=\displaystyle \max _{{\hat{\ell }}}{\hat{S}}_{f}(t)\). This implies that the UIN can represent maximal skew information between the local observable and the interacting state of two ions. Thus, the correlation matrix, \({\hat{\Xi }}\), of the ions’ chain state, \({\hat{\varrho }}\), can be used to establish the explicit form of UIN as follows:

    $$\begin{aligned} U(t)= & {} \left\{ \begin{array}{ll} 1-\wedge _{\min }({\hat{\Xi }}), &{}\vec {v}=0; \\ \\ 1-\frac{1}{|\vec {v}|^{2}} \vec {v}\,\,{\hat{\Xi }}\,\,\vec {v}^{\tau }, &{}\vec {v}\ne 0, \end{array} \right. \end{aligned}$$
    (12)

    where \({\hat{\Xi }}=\text {Tr}\{\sqrt{{\hat{\varrho }}(t)}({\hat{\sigma }}^{i}\otimes {\hat{I}})\sqrt{{\hat{\varrho }}(t)}({\hat{\sigma }}^{j}\otimes {\hat{I}})\}\), \(\wedge _{\min }\) indicates the minimal eigenvalue of this matrix, \(\vec {v}=[{\hat{v}}_{i}]\) is the Bloch vector of the ions density operator with \({\hat{v}}_{i}=\text {Tr}\{{\hat{\varrho }}(t)({\hat{\sigma }}^{i}\otimes {\hat{I}})\}\), \({\hat{I}}\) is the identity operator, and \({\hat{\sigma }}_{i}\) are the Pauli matrices for \(i,j= x,y,z\).

  • Bell inequality: To discover the nonlocality of the interaction for any two ions across the lattice, we use the maximal amounts of the Bell inequality measure [34, 35]. Such a maximal function is violated if it is greater than two. As a result, the following inequality can be used to determine the information among the interacted ions across the lattice sites:

    $$\begin{aligned} B(t)= & {} 2\sqrt{\wedge _{1}+\wedge _{2}}-1, \end{aligned}$$
    (13)

    where \(B(t)>1\), \(\wedge _{j}\,(j=1,2)\) refers to the two greatest eigenvalues of the matrix, \({\hat{\emptyset }}^{\dagger }{\hat{\emptyset }}\), which are dependent on the correlation matrix \({\hat{\emptyset }}=\text {Tr}\{{\hat{\varrho }}(t)({\hat{\sigma }}^{i}_{1}\otimes {\hat{\sigma }}^{j}_{2})\}\) for \(i,j=x,y,z\).

  • Concurrence entanglement: Here, to detect the entanglement between ions to give information about protecting data received or sent across sites in linear Paul trap, we employ the concurrence measure, defined as follows [36]:

    $$\begin{aligned} C(t)= & {} \max \{0,\sqrt{\beta_{1}}-\sqrt{\beta_{2}}-\sqrt{\beta_{3}}-\sqrt{\beta_{4}}\,\}, \end{aligned}$$
    (14)

    where \(C\in [0,1]\), \(\beta_{k}\,(k=1,2,3,4)\) denotes the positive eigenvalues of the matrix, \({\hat{\varrho }}(t)({\hat{\sigma }}^{y}_{1}\otimes {\hat{\sigma }}^{y}_{2}){\hat{\varrho }}^{*}(t) ({\hat{\sigma }}^{y}_{1}\otimes {\hat{\sigma }}^{y}_{2})\), and \(\beta_{1}>\beta_{2}>\beta_{3}>\beta_{4}\).

3.2 Temporal evolution of arising information

Figures 2, 3 show the dynamics of U, B and C correlation criteria for the two interacting ions that began in an uncorrelated state under the effect of applied \(\vec {M}\) along x-axis (i.e., \(\theta =\frac{\pi }{2}\)) across the sites. In the absence of decoherence, we find that the system has a high ability to generate information (nonlocalities) in the case of weak interaction coupling and short distances between sites, as shown in Fig. 2a. The correlations of two-site using B, U and C, arise and oscillate irregularly as the time evolves, indicating that different two-trap chain-site correlations can be generated by the proposed system. Such B, U and concurrence measures fluctuate, and their frequencies increase with the increasing of two-ion interaction strength, see Fig. 2c. By increasing the distance between the sites, the fluctuations of C and B-nonlocality of the two sites quickly reduce and become more stable, whereas the oscillations of U correlation persist and become quasi-regular, as shown in Fig. 2b. Moreover, one can observe from Fig. 2d that the two-trap-chain-site correlations improve and become more uniform after increasing J and growing D among sites. The B-nonlocality and concurrence reach their maximal values through long time periods compared to the U reaching its maximal value at short time periods. Because of this, it’s noteworthy to note that the U, B, and concurrence have a strong ability to maintain their maximal values at any value of the impacted parameters, which is in specific periods.

Fig. 2
figure 2

Temporal evolution of the arising information among the ions correlation using B, U and concurrence criteria in the case of \(\gamma =0\) (\(\Gamma \rightarrow \infty\)), \(M=1\), and the two trapped-ion interaction starts initially with the separable state: \({\hat{\varrho }}(0)= |\uparrow _{s}\uparrow _{k}\rangle \langle \downarrow _{s}\downarrow _{k}|\)

Full size image
Fig. 3
figure 3

Temporal evolution of the same criteria as in Fig. 2 but with the vibrational effect, \(\gamma =0.03\)

Full size image

Figure 3 illustrates the impact of the intrinsic vibrational-trapped-ion decoherence (\(\Gamma \rightarrow 33\)) on the two-trap sites correlation dynamics. We observe that the values determining the maximum entanglement between the two sites decrease rapidly for short distances between sites and weak damping compared to the U and B until they reach their stable correlations after a certain time. For large distances among the lattice sites as shown Fig. 3b, we find that the intrinsic decoherence causes a faster decrease in the generated two ions correlations than for small distances. In light of this, it may be said that the decoherence and long two-sites distances have a concurrently destructive impact on the generated two-traps-chain-sites correlations.

Fig. 4
figure 4

Idealistic dynamics of the correlation criteria for any two interacting ions in the zx-plane under a performed magnetic field in an arbitrary direction, starting with the state \({\hat{\varrho }}(0)= |\uparrow _{s}\uparrow _{k}\rangle \langle \downarrow _{s}\downarrow _{k}|\) and \(M=1\)

Full size image

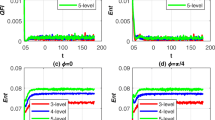
Figure 4 demonstrates the evolution of the two trap sites correlation criteria when the global magnetic field acts in any arbitrary direction inside the zx-plane, and the strength of two ions interaction when they started in an uncorrelated state is fixed. We observe that the applied magnetic field along the zx-plane has a significant effect on the generated correlation and entanglement among any two-ion, resulting in lower maximum values of C, U, and B-nonlocality compared to the values shown in Fig. 2c. Furthermore, as illustrated in Fig. 4c, the entanglement and correlations across the short distance between the sites of ions are extremely fragile due to the magnetic field’s direction approaching from the z-direction (\(\theta \le \frac{\pi }{4}\)). This implies that the magnetic field action along the z-axis or near it may have a negative impact on the two trapped ions correlations. In addition, the U correlation improves significantly with an increase in distances between ions, but the entanglement and B correlation improve frequently and irregularly for any direction of magnetic field, as shown in Fig. 4b, d. This demonstrates emphatically that the magnetic field’s direction has a significant role in controlling the generated quantum two-trap-chain-site correlation dynamics.

Furthermore, we show in Fig. 5 how strong information develops between any two interacting idealistic ions that are maximally entangled at the start time. We note that the criteria begin at their maximal values, as expected from the supposed start state, where \(B(0)=2\sqrt{2}-1\approx 1.8284\) and \(C(0)=U(0)=1\). One can observe that the two sites correlation criteria continue to exhibit irregular oscillatory behavior due to the fact that the strength of the interaction is dependent on the position and direction of the acting global field with the ion axis is: \(\theta =\frac{\pi }{3}\). As shown in Fig. 5a, we discover that, in contrast to the U, the C and B-nonlocality criteria behave similarly to maintain their maximum values over time throughout lattice sites that are close to one another.

Fig. 5
figure 5

Evolution of information produced by the robust correlation for any two-site occupied ions for the cases of \(\Gamma \rightarrow \infty\), \(M=1\), and the two interacting ions are initially in a maximally antisymmetric Bell state: \({\hat{\varrho }}(0)= \frac{1}{2}(|\downarrow _{s}\downarrow _{k}\rangle +|\uparrow _{s}\uparrow _{k}\rangle )\otimes (\langle \downarrow _{s}\downarrow _{k}|+\langle \uparrow _{s}\uparrow _{k}|)\)

Full size image
Fig. 6
figure 6

Dynamics of lossy information arising among the correlation of interacting ions across far or close sites for the cases as Fig. 5 and \(\gamma =0.03\)

Full size image

By increasing the interaction strength among ions across the sites that are close to one another, the loss of the initial maximal two-trap-chain-site entanglement and correlations is decreased, and these become more robust, as shown in Fig. 5c. One can infer from Fig. 5b that the increasing of distance between ion sites (\(D = 1.2\)) with the two-ion interaction strength (\(J=0.5\)) reduces the maximum values of the B-nonlocality and entanglement, whereas the U correlation keeps volatile and more robust. In addition, the strong interacting strength among the sites that are far from each other (\(D=1.2\)) causes an improvement of the correlations between any two idealistic ions, but their maxima of criteria will decline at certain times until the period’s begins, see (Fig. 5d). As a result of the acting magnetic field inside the plane, it can reliably store and transfer some information across any two ions, whether with a far distance between sites and medium exchange coupling or a close distance between sites and strong exchange coupling.

Finally, Fig. 6 discusses the impact of the vibrational on the robust interacting ions (\(J=1\)) that are far from each other or close to each other. We observe that the correlation criteria’s amplitudes and frequencies deteriorate with damping until they eventually reach steady values. Also, we find that the U correlation is more robust versus the decoherence compared to the B correlation and entanglement. Besides, one can find that the effect of decoherence is enhanced at distant sites of ions, so the correlations and entanglement among ions will reach stable values more quickly in this case, see Fig. 6b. We can conclude that the initial maximal two ions correlations will decrease with an increase in the distance between ion sites.

4 Conclusions

We have proposed and thoroughly discussed a former proposal [26, 28] to simulate the generated information among correlated ions inside the vibrational chain of a long-range Paul trap. An analytical solution for the governing equation of decoherence under the vibrational impact of ions has been presented to investigate the information resources that decide by the correlations and entanglement in the Paul trap. It is found that the B, U and concurrence criteria to explore the correlations in the non-vibrational chain have a strong ability to maintain their maximal values when the global magnetic field is acting perpendicularly on the trap. Also, we discovered that the performance of the magnetic field in the axial trap direction (z-axis) or near it may have a negative impact on the information resources between the interacting ions that begin in an uncorrelated state, but they improve when the distance between ions increases. Furthermore, we found that the information arising from the two sites correlations generated by the away ions’ interaction with medium coupling strength and the close ions’ interaction with strong coupling strength, which began in a maximally correlated state, can reliably be stored and transferred across the sites. Finally, we discovered that the effect of the vibrational is severely enhanced at distant sites of ions, and the correlations and entanglement among ions will quickly deteriorate and reach stable values under this effect. Consequently, the measurements of Alice’s obtained from Bob’s information will decrease with an increase in the distance among vibrational ion sites.