High-power, high-brightness solid-state laser architectures and their characteristics

Abstract

The development of high-power diode lasers enabled new solid-state laser concepts such as thin-disk, fiber, and Innoslab lasers based on trivalent ytterbium as the laser-active ion, which resulted in a tremendous increase in the efficiency and beam quality of cw lasers compared to previously used lamp-pumped rod or slab lasers and the realization of ultrafast lasers with several 100 W or even kilowatts of average power. In addition to their beneficial thermo-optical properties, these architectures offer characteristic benefits making them especially suitable to obtain dedicated laser properties. This review article comprises milestone developments, characteristic challenges, and benefits, and summarizes the state of the art of high-power solid-state lasers with the focus on ultrafast lasers.

1 Historical development, general considerations

1.1 The beginnings

In retrospect, it is quite amazing that most of the important concepts in the fields of lasers and nonlinear optics have been proposed within a couple of years since the realization of the first laser. Often, these initially suffered from severe technical limitations that were only overcome with new approaches in the course of time. High-power lasers for instance used to be neodymium rod lasers that were pumped by discharge lamps, which emitted across an extremely large spectrum from NIR to UV into a solid angle of basically 4π, resulting in typical electrical-to-optical laser efficiencies of 2%–3% [1]. The advent of high-power diode lasers around the year 1990 with an emission linewidth of only a few nanometers and a much smaller beam parameter product allowed us to rethink the high-power solid-state laser concept, both in terms of the active material [2, 3] and in terms of laser design. However, the most obvious approach was to simply replace the lamps in rod or slab lasers by diode-laser arrays matched to the absorption band of Nd:YAG at a wavelength of 808 nm and to take advantage of the higher absorption efficiency and the somewhat reduced average quantum defect between pump and laser photons.

T.Y. Fan proposed Yb³⁺ as a substitute for Nd³⁺ despite or because of its intrinsic two-level nature [4]. It has only one hole in the 4f shell. The resulting two electronic levels, ²F_7/2 and ²F_5/2 (spin parallel/antiparallel to the orbital momentum), are further split by the crystal field of a host on the order of several hundreds of inverse centimeters or several k_BT at room temperature and broadened by coupling with acoustic and optical phonons. This system has a number of advantages, the only real disadvantage being the thermal population of the lower laser level of 4% at room temperature according to the Boltzmann factor exp(− ΔE/k_BT). This is why Yb³⁺ doped laser materials are usually referred to as 'quasi-three-level' systems. Room-temperature laser operation was reported in [5] with a longitudinal pumping scheme in a fairly small active volume.

In the same paper, the authors proposed a platelet or active-mirror geometry for improved cooling and reduced thermal lensing. Still for Nd³⁺, Ueda and Uehara [6] proposed the active mirror design (see Fig. 1b; later called 'thin-disk laser') for diode-pumped lasers and alternatively the fiber laser as the two extreme cases of a rod design with maximized surface-to-volume ratio and hence optimized heat extraction. A long-time overlooked paper from the early years of the laser by Basov et al. [7] proposed 'radiating mirrors', see Fig. 1a. Here, the active layer was a thin semiconductor layer, deposited on a massive heat sink with a fully reflecting surface. This was combined with an external output-coupling mirror and pumping at an oblique angle. The main advantages of such a design were mentioned to be the 'effective removal of heat' enabling 'large average powers' and 'high spatial and temporal coherence'.

Fig. 1

The threefold invention of the thin-disk laser: (a) Basov et al. (1966) [7], could not be reprinted due to copyright restrictions, (b) Ueda et al. (19933), reprinted with permission from [6], and (c) Giesen et al. (1994), reprinted by permission from [8] © 1994 Springer Nature

The first experimental results with Yb:YAG as the active medium on a water-cooled copper heat sink were published by Giesen et al. [8], see Fig. 1c. One difference to the earlier active-mirror concepts based on Nd³⁺ was the need to reduce the thickness of the disk as much as possible to reduce the transparency threshold density, i. e., the additional contribution to the laser threshold from the quasi-three-level nature of the energy-level scheme of Yb³⁺. This allowed to reduce the density of the pump power needed for efficient laser operation and the resulting temperature increase of the active medium, which again reduced the three-level threshold. Although not implemented in the first experiments, it was mentioned that more pump passes are needed to further reduce the thickness of the disk while maintaining or even increasing the absorption efficiency for the pump radiation.

This leads back to the remark at the beginning on the importance of technical limitations. The reduction of the thickness of the disk was the key to efficiently operate Yb³⁺ at high (average) power levels at or above room temperature. This could be achieved by increasing the number of pump- passes by making use of a multipass pump optics, often based on a parabolic mirror for focusing and collimating combined with additional optics like prisms to laterally move the pump beam. However, for a given diameter of the pump spot and a given beam-parameter product of the pump radiation, the number of passes through the disk is limited by the available (overall) numerical aperture (NA) of the focusing optics [9]. In this way, the progress in the brightness of the pump diodes directly translated into the progress of the thin-disk laser. A similar argument holds for the demonstration of power scaling. It became only possible with the availability of sufficient pump power at an affordable price and with a reasonable lifetime. Both, the availability of high-brightness and high-power pump diodes, was actually an advantage for Yb³⁺ over Nd³⁺, since the 'aluminum-free' InGaAs/GaAs diodes needed for Yb³⁺ were considered to be more powerful and reliable than the AlGaAs/GaAs diodes needed for Nd³⁺.

Another key aspect for a better and more reliable performance—not so much depending on the progress in other technological fields—was an improved mounting of the disk, replacing the cold-pressed indium by hard-soldering onto expansion-matched CuW heatsinks or gluing the disk onto polycrystalline diamond heatsinks [10].

Many more details on the beginnings of the thin-disk laser can be found in [11]

Yb doping was at that time already well established for fiber lasers, both as laser activator (even with lasing on the so-called 'zero-phonon line' [12], where an inversion exceeding 50% is required) and as sensitizer for Er fiber lasers. Laser results with double-clad pumping, invented for efficient pumping of Nd³⁺ with diode lasers [13], was presented for the first time in 1994 [14], the same year when the first Yb thin-disk laser results were published.

1.2 Properties of the laser ion Yb³⁺

1.2.1 Pumping with InGaAs diode lasers

The pump bands of Yb³⁺ fit perfectly to the preferred spectral emission range of InGaAs laser diodes, which used to be and still are the most reliable and powerful laser diodes available. Due to the comparatively strong coupling of the Yb³⁺ ions to the host lattice, the transitions are quite broad compared to other rare-earth ions, especially at the standard pump transition with wavelengths around 940 nm. This relaxes the requirements in terms of fabrication tolerances and for the temperature stabilization of the pump diodes.

1.2.2 Quantum defect

For high-power lasers, it is essential to keep the temperature of the active medium at a reasonable level by efficiently removing the heat produced by the laser process and by reducing the heat generation in the first place. An unavoidable contribution to the thermal load arises from the quantum defect, i. e., the difference between the energy of the pump and the laser photons. In principle, this can be minimized by reducing the energy difference between the two upper and the two lower levels of the four-level energy scheme, at the extreme ending up at a two-level system. Hence, one has to find a trade-off between the low laser threshold of an 'ideal' four-level-system (the 1.06-µm transition of Nd³⁺) and the reduced quantum defect but increased threshold density of a 'quasi-three-level' system (Yb³⁺). In both cases, one can directly pump the upper laser level (at approx. 870 nm for Nd³⁺ and 970 nm for Yb³⁺), which reduces the quantum defect without increasing the laser threshold. However, pumping is somewhat more difficult in these cases because of the narrower absorption lines. In addition to the reduced heat load, the quasi-three-level operation increases the (differential) laser efficiency so that the overall laser efficiency can be higher despite the elevated laser threshold, provided that the laser concept allows to realize small active volumes and an efficient heat removal.

1.2.3 Further properties

Since there are no further 4f energy levels above the upper laser level ²F_5/2, there is no risk for excited-state absorption (ESA) and perhaps a reduced risk of energy migration, which allows higher doping levels. However, both for higher doping levels and for higher inversion, there seem to be some non-radiative recombination channels, which are not yet fully understood [15,16,17].

Compared to other rare-earth ions, the strong coupling to the lattice of the host material and the resulting comparatively broad absorption and emission lines make pumping with diode-laser arrays easier and allow tuning the laser emission over several tens of nanometers or realizing pulse widths in the range from 100 fs to 1 ps depending on the host crystal and the type of mode locking. The downside are the reduced peak cross sections. Hosts with especially strong electron–phonon coupling usually also exhibit comparatively low thermal conductivities, which makes power scaling of lasers with pulse durations of less than 100 fs even more challenging.

1.3 Geometries for quasi-three-level operation

As outlined by Ueda and Uehara [6], starting from the traditional rod design, there are two options to increase the surface-to-volume ratio and to reduce the volume: reducing the length of the rod, resulting in a disk or reducing the radius of the rod, resulting in a fiber. Another option is to start from a (crystalline) slab and to reduce its thickness, resulting in a so-called Innoslab (for a review see [18]). Pumping is done longitudinally to have the necessary absorption length in a single or double pass.

Another option (not discussed further in this paper) is to run the laser at cryogenic temperatures, e. g., at 80 K by cooling with liquid nitrogen (LN₂) [19]. This makes Yb³⁺ doped materials an almost ideal 4-level system, which removes the need for high pump-power densities and at the same time improves the thermal properties by an order of magnitude enabling the traditional rod geometry. The backside of this approach is the need for a high-vacuum chamber which, on the other hand, is sometimes used for ultra-fast room-temperature laser systems to reduce nonlinear and thermal effects in the cavity.

A special case are semiconductor disk lasers, where the small active volume is realized by quantum wells (QW), which are only a few nanometers thick. The thicker barrier and spacer layers in between the QWs can be used as absorbers. For a good confinement of the electrons and holes in the quantum wells, the energy gap of the barriers has to be larger by typically 20%, which sets the corresponding lower limit for the quantum defect [20].

Coincidentally, a saturable absorber, similar to semiconductor disk lasers (Semiconductor Saturable Absorber Mirror, SESAM) was invented [21, 22], which turned out to be the ideal complement to the disk laser for mode locking.

1.4 Requirements for the pump sources

Before discussing the specific requirements for the pump radiation for disks and fiber lasers, we will summarize briefly the definitions and relationships of parameters, which are equally important for the characterization of the pump beam and the laser beam.

The brightness or radiance is defined as power per area and solid angle ($\frac{P}{A \Omega }$) or intensity per solid angle. It can be shown using the 2nd law of thermodynamics or Liouville's theorem (conservation of the density of particles in phase space) that the brightness of a light source cannot be increased by any passive optical transformation. This applies also to cases where several fiber-coupled sources are coupled using fiber-couplers and/or tapers [23]. Considering the propagation of a light beam of a given power or photon number, this means that the product of beam area $A$ and far-field solid angle $\Omega$ are at best conserved. Likewise, this is true for the beam parameter product ${w}_{0}\Theta$, where ${w}_{0}$ is the near-field beam radius and $\Theta$ is the far-field half angle with (in paraxial approximation, i. e., for small angles, and in air) $A=\pi {w}_{0x}{ w}_{0y}$, $\Omega =\pi {NA}_{x}{ NA}_{y}$, numerical aperture ${{NA}_{x,y}=\Theta }_{x,y}=\frac{{k}_{x,y}}{{k}_{z}}=\frac{{p}_{x,y}}{{p}_{z}}$, ${k}_{x,y}$ being the wave-vector components and ${p}_{x,y}$ the photon momentum components normal to the propagation direction $z$, i. e., the beam radius in the corresponding Fourier or k-space. Both, the Fourier theorem and Heisenberg's uncertainty principle state that there exists a lower boundary for the beam-parameter product: ${w}_{0x,y} {\Theta }_{x,y}={M}_{x,y}^{2}\frac{\lambda }{\pi }$, with ${M}_{x,y}^{2}\ge 1$, if ${w}_{0x,y}$ and ${\Theta }_{x,y}$ are defined as the second-order momentum of their respective intensity distribution. Beams with ${M}^{2}=1$ are termed 'diffraction limited', ${M}^{2}$ is frequently informally called 'beam quality' or 'beam-quality factor' [24]. It is a useful parameter because it is conserved when propagating the beam through 'paraxial' optics. For the correct measurement of the second-order moments and ${M}^{2}$, see ISO 11146 [25].

The challenge posed by the small volume, whether in disk or fiber lasers, is to achieve a high absorption efficiency for the pump radiation with low-brightness pump sources like diode-laser bars or stacks.

Fiber lasers use a double clad-design, where the cladding region of the laser waveguide functions as the core region of the pump waveguide, which is surrounded by a second cladding, which serves as the cladding layer of the pump waveguide (see Fig. 2b). In this way, the waveguides for the pump and for the laser can be separately optimized for the low-brightness pump radiation and the high-brightness laser radiation. A certain asymmetry helps to make sure that most launched pump rays have the chance to cross the doped core of the laser waveguide and to be absorbed—provided the fiber is long enough [13]. An increase of the core diameter further enhances the pump absorption and reduces the necessary fiber length.

Fig. 2

source is given by the cladding area and NA² of the fiber, which cannot be easily increased with pump power: The NA is limited by the available index-of-refraction difference between inner and outer cladding, the fiber diameter is limited by the bending radius the fiber should tolerate

Pumping and cooling geometries of (a) disk and (b) fiber lasers. Shown is a sectional plane through the axis of rotation. In either case, the heat-extraction capability scales linearly with the laser power: In disk lasers the laser-mode area grows proportional to the laser power and likewise does the cooling surface. In fiber lasers, in principle, the fiber length scales with the output power and likewise does the cooling surface. For disk lasers, the pump area grows proportional to the laser-mode area and hence linearly with the output power, which means that the pump power density is independent of the laser power. For fiber lasers, the maximum pump power for a given brightness of the pump

Double-clad fibers typically have a diameter of the (inner) cladding of between 200 and 400 µm and a NA of 0.22, resulting in a beam parameter product of between 0.22 and 0.44 mm·mrad. As outlined above, this sets a maximum beam-parameter product for the pump beam that still allows the pump beam to be efficiently coupled into the fiber, and which is independent of the pump power. Since neither the diameter nor the NA can be increased much further, this means that for higher laser powers and therefore higher pump powers the brightness of the pump source has to grow linearly with respect to laser power.

Double-clad waveguides can also be realize with monocrystalline material, usually with rectangular cross section due to the production process of bonding thin slabs of different doping and/or host crystals, mostly called 'crystalline waveguide lasers'. Similar to silica fibers, they allow double-clad pumping with a small Yb-doped core, an un- or differently doped inner cladding and a low-index outer cladding, e. g. sapphire, for confining the pump radiation. A problem for power scaling could become thermal lensing because of the radial cooling, which affects the modes of the external resonator and may compete with the waveguide for the laser mode. So far, the output power achieved was limited to several 10 W [26, 27].

Another option (not discussed further in this paper) is to stick to the traditional (end-pumped) rod design with the size of the active volume adapted to the quasi-three-level nature of Yb³⁺, usually termed 'single-crystal fiber lasers'. Typical dimensions of the rod are a length of 40 mm, a diameter of 1 mm and 1% doping concentration. They should not be confused with the 'crystalline-waveguide lasers' mentioned above, which have waveguides for both, the laser radiation and the pump radiation. In single-crystal fiber lasers, the laser mode always propagates freely inside the rod without interaction with the rod surface and is defined by the external resonator. For (end-) pumping, there exist principally two modes of operation:

• (1) The rod is used as a waveguide for the pump radiation, justifying somewhat the classification as fiber if 'fiber' stands for 'waveguide'. If the cylindrical surface of the rod is highly reflective, the numerical aperture of the pump radiation can be arbitrarily high and in combination with the relatively large diameter of the rod there are no practical limitations due to the brightness of typical pump lasers. Power scaling is as with 'real' fiber lasers via the rod length keeping the total number of Yb³⁺ and hence the three-level threshold pump power constant. However, there are two features inherited from the traditional transversely pumped rod lasers: The rod is pumped homogeneously across its cross section. This strongly favors multi-mode operation and makes fundamental-mode operation quite ineffective. The highest multi-mode cw output power reported so far was 250 W with a pump power of 570 W and M² = 15 [28]. The resonator was designed to allow transversal modes up to the order of 12, resulting in an M² = 13 if assuming that all modes contribute equally. In the same paper, high extraction efficiency for the amplification of Gaussian beams is reported, but there is no information on the effect of saturation effects on the shape of the beam after amplification. A side note: Using the waveguide effect for pumping was actually the original option considered for pumping thin-disk lasers, in this case in radial direction [29]. There, it was proposed to use a disk, which is only doped in the central region, to avoid the pumping of the outer regions, but it never became really popular. The second feature inherited from the rod laser is the thermal lensing and thermally induced stress birefringence proportional to the pump and laser power because of the radial cooling although—compared to lamp-pumped Nd³⁺ rod lasers—much less pronounced due to the much smaller quantum defect with the combination of Yb³⁺ and diode pumping. In the case of ultrashort pulses, self-focusing may also become an issue with increasing rod length [30].

• (2) Free-space propagation for the pump radiation, at least for the larger and more intense part of the pump beam—as far as the brightness of the pump source allows. This results in a good overlap between the pumped volume and the fundamental laser-mode volume and hence highly efficient for fundamental-mode operation. In addition, the unpumped region serves as a soft aperture. This increases the losses for the higher-order modes in oscillators and reduces the amplification of the wings of Gaussian beams in amplifiers. Since for free-space propagation of the pump radiation inside the rod the beam parameter product has to be reduced inversely proportional to the length of the rod, for power-scaling the brightness of the pump source has to scale with the third power of the extracted laser power. Nevertheless, this design has its strengths for medium-average-power ultrafast amplifiers because of its much larger gain length compared to disk lasers and larger mode-size compared to fiber lasers. Typical extracted average powers are of the order of 100 W with close to diffraction-limited beam quality, pulse energies are of the order of 1 mJ [30,31,32,33,34].

Disk lasers are usually pumped at an angle through the front (see Fig. 2a) using multipass pump optics, which extends the absorption length by the number of passes. Figure 3 shows a schematic drawing and a photo of the second-generation pump optics with four spherical mirrors for four double passes through the disk. The following generations of pump optics are all based on one parabolic mirror, see Fig. 4. N segments on the parabolic mirror are needed for N double passes through the disk if the spots are arranged in one ring or for 2 N double passes if the spots are arranged in two rings. The size of these segments sets a lower limit for the brightness of the pump sources, which is thus determined by the number of double passes N and the area A of the pump spot. For a typical configuration (12 double passes in one ring on the parabolic mirror or 24 double passes on two rings) the maximum usable numerical aperture is roughly NA = 0.08, corresponding to a solid angle of Ω = 0.02 sr.

Fig. 3

Second generation 'eight-pass' thin-disk pump optics using four spherical mirrors for two double-passes in each propagation direction. In a plane opposite the mirrors (near the center of the photo) are the crystalline disk (K) on a TEC-cooled copper heat sink, the pump-fiber end (F; metal jacket), and a mirror (H), which changes the plane of propagation from 1/2 to 3/4. Mirror #4 reverses the propagation direction. The large NA of the mirrors allows to realize a small pump spot with a low-brightness pump source

Fig. 4

source in reversed order, which gives another 12 reflections at the disk. The two green folding prism-pairs shift the collimated beam six times in azimuthal direction, the optional blue folding prism-pair moves the beam in radial direction for another 6 reflections. The number of segments ('cake pieces') on the parabolic mirror (using one ring) corresponds to the number of double passes through the disk, in this case N = 12. The angle φ between the two green prism-pairs determines the number of double passes N according to φ = 2π/N (for one ring). Reprinted with permission from [35] © The Optical Society

Modern '48-pass' thin-disk pump optics using one parabolic mirror (in yellow) for focusing the pump beam onto the disk and recollimating it after being reflected. The red spots mark the positions where the beams hit the parabolic mirror, numbered according to the order of impact. At position #1 the collimated pump beam enters the pump optics, after 12 reflections at the disk, the beam is reversed by an HR mirror at position #24. Not shown is here the path back towards the pump

The main characteristic of the disk laser concept is the laser- and pump-power scaling with constant power density. Assuming a typical pump power density of $\frac{{P}_{\mathrm{pump}}}{A}=10\frac{\mathrm{kW}}{{\mathrm{cm}}^{2}}$ the required brightness (radiance) of the pump radiation is $\frac{{P}_{\mathrm{pump}}}{A \Omega }=500\frac{\mathrm{kW}}{{\mathrm{cm}}^{2} \mathrm{sr}}$ independent of the pump and laser power. The required beam parameter product increases linearly with the radius ${r}_{spot}$ of the pump spot according to ${r}_{\mathrm{spot}}NA$, and amounts to 200 mm·mrad for a pump spot with a diameter of 5 mm. The solid angle roughly scales inversely proportional to the number of pump passes, hence the required brightness of the pump diodes scales linearly with the number of pump passes. Especially for a large number of passes, there are ways to arrange the pump spots somewhat differently on the parabolic mirror, which allows to use the available solid angle more efficiently [9].

1.5 Other gain materials

1.5.1 Materials for disk lasers

With the proposal of Yb as a new laser-active ion, the search for suitable host crystals that lead to the most favorable properties (threshold, gain, etc.) was started. Besides YAG, there are a number of other host crystals, suitable for doping with Yb³⁺. They differ in the resulting crystal field splitting, the coupling to the phonons of the host crystal, and the heat conductivity, to name a few. For high-power operation, the heat conductivity is most important. In this respect, the garnet LuAG and the sesquioxide Lu₂O₃ are promising candidates, because Yb³⁺ and Lu³⁺ are quite similar in size and weight, so that doping only slightly impairs the heat conductivity. Other crystals, with stronger electron-lattice coupling, lead to broader gain spectra of the active ions, useful for tunable lasers and ultrafast lasers, but usually suffer from small gain coefficients and poor thermal properties and are therefore only of limited use for high-power operation. Some of the hosts are also available as ceramics with optical and thermal properties that can compete with their monocrystalline counterpart but can be produced in larger sizes and potentially with higher doping levels.

Since the disk laser turned out to work well with laser materials that have a more or less high transparency threshold, the initial hope was that it would work equally well with other 4-level or quasi-3-level laser materials. Disk lasers with rare-earth ions such as Nd³⁺, Tm³⁺, Ho³⁺, Pr³⁺, and transition-metal ions like Ti³⁺ in Al₂O₃ (sapphire) or Cr²⁺ in ZnSe (for the mid-IR), have been reported, often with output powers and efficiencies well below the standard set by Yb³⁺:YAG [35,36,37,38,39]. The 3d electrons of the transition metal ions strongly couple with the lattice vibrations (phonons) often leading to very wide, but low gain, which makes the operation as disk laser with very short gain and absorption length a challenge. Just from the production process, semiconductors are perfectly suited for the disk laser geometry, both for the gain material (quantum wells or quantum dots) and the highly reflective mirror (Distributed Bragg Reflector, DBR). Usually, the gain has a spectral width of a few tens of nanometers and can easily be shifted by changing the composition of the gain layers, in principle from the near-UV to the mid-IR. Typically, they have to be operated at higher pump power densities than their Yb counterparts, which makes the power scaling by means of larger pump spots more difficult. The power record for one disk is of the order of 100 W at a wavelength near 1 µm and was achieved with InGaAs QWs [40]. The power attained in other spectral regions is much lower. For an overview on semiconductor disk lasers or vertical-external-cavity surface-emitting lasers (VECSEL) see, e. g. [41].

1.5.2 Materials for fiber lasers

The first double-clad fiber lasers were realized with Nd³⁺ doping [13]. With the discovery of Yb³⁺, Nd was quickly replaced, but also other rare-earth dopants like Er³⁺ or Tm³⁺ proved to be quite successful in the near- to mid-IR. Transition-metal ions are not really suitable since their strong coupling to the glass matrix results in mostly non-radiative relaxation. Crystalline semiconductor fibers are challenging to fabricate.

Since we want to focus on power scaling and high-power operation, only Yb lasers are considered in the following.

1.5.3 Mode-locking techniques

Today, mainly passive mode-locking techniques are used as they enable a shorter pulse duration than active mode-locking approaches, which are limited by the bandwidth of the electronics [42]. Laser pulses with a duration well below one picosecond are commonly obtained with Yb:YAG by means of passive mode-locking. While a faster absorber is beneficial to obtain a shorter pulse duration, the lower limit of the pulse duration is determined by the spectral bandwidth of the locked modes and, therefore, closely linked to the gain bandwidth of the laser medium.

Mode-locking can be realized with a variety of different techniques, each exhibiting characteristic properties with respect to (environmental) stability, self-starting, obtainable pulse duration, and technical complexity. The techniques can roughly be grouped into actual saturable absorbers and artificial saturable absorbers.

Saturable absorption occurs in various materials. In the early days laser dyes have been used, later also laser crystals like Cr⁴⁺:YAG for Nd³⁺:YAG lasers ('all-solid-state'). Nowadays, the most common example is the widely used semiconductor saturable absorber mirror (SESAM), sometimes also referred to as a saturable Bragg reflector (SBR) [22]. Less commonly used are saturable absorbers based on carbon nanotubes [43], graphene [44], or quantum dots in glasses [45]. The saturable absorber speed is limited by the material response (intra-band thermalization) being typically on the order of 100 fs [22].

Artificial saturable absorbers are based on nonlinear optical effects that only alter the properties of the laser radiation but do not absorb it. An intensity-dependent transmission is realized by means of another optical element such as an aperture, a polarizer or a dichroic mirror. The most prominent example is Kerr-lens mode-locking (KLM), which uses self-focusing to increase the transmission of an intense pulse through a subsequent aperture [46]. The modulation speed is determined by the nonlinear optical polarization. With a typical response time of the order of 1 fs it can be considered to be instantaneous in most cases [47].

Apart from the type of the modulator, mode-locking can be subdivided into the mechanisms governing the formation of the pulses, which are characterized by the amount of net dispersion being positive (normal) or negative (anomalous) as illustrated by Fig. 5.

Fig. 5

Mode-locking grouped by dispersion regimes with the commonly used nomenclature. Reproduced with permission from [48] © IOP Publishing.  All rights reserved

2 Aspects of power scaling

2.1 General aspects

2.1.1 Disk lasers

The disk laser design, in principle, allows to scale the output power by simply increasing the active area on the disk, keeping the areal densities of pump power, laser power, and heat-flux constant. Early simulations showed that the stress at the interface between the pumped and the unpumped region does not increase in a problematic way [8, 49]. Later on, amplified spontaneous emission was recognized to impose some restrictions on the design of the disk, especially for larger diameters, see discussion below [50]. Power scaling of fundamental-mode lasers is also not as straight-forward, since larger diameters of the mode come along with a reduced power range for stable laser oscillation in the resonator [51]. An additional option for power scaling is to implement several disk modules in one resonator [52]. The power density inside the resonator can be kept unchanged by adapting the output-coupling. Since the gain per pass is low, thin-disk lasers require rather high-intracavity powers (low outcoupling) and low resonator losses for efficient operation. This feature leads to two characteristics. First, thin-disk lasers are highly insensitive to back reflections. Second, in particular cw disk lasers, are ideally suited for intra-cavity frequency doubling (second harmonic generation, SHG). For this, the SHG crystal is placed in or near a waist of the laser beam within the resonator. SHG is used for the output coupling, is self-adjusting, and, therefore, needs to have an SHG efficiency of only a few percent.

2.1.2 Fiber lasers

For fiber lasers, the power by principle scales with the length of the fiber, which determines the amount of heat that can be removed from the fiber and hence the output power that can be generated. The removable heat depends on the temperature increase that can be tolerated inside the fiber and is limited primarily by non-radiative transitions that occur at higher temperatures and ultimately by the melting and rupture of the fiber.

A problem for power scaling of fiber lasers, especially in fundamental-mode operation, arises from the fact that the mode-field area cannot be increased in the same way as the output power. To preserve strict single-mode operation in step-index fibers, the maximum core size is limited to approx. 16 µm (at 1064 nm) due to the minimum NA of about 0.05 that can be produced in practice [53]. Micro-structured (photonic-crystal) fibers allow for very low NAs enabling core sizes exceeding 100 µm [54], but the low NA leads to weak guiding, effectively requiring to keep the fibers straight to avoid bending losses and impeding splicing techniques. Usually, fibers with a very large core are not strictly single-mode but support the propagation of a few-modes. While there are several techniques to suppress the excitation of higher-order modes, high-power operation and the linked thermal effects can lead to transient coupling between these modes, usually referred to as mode instabilities [55,56,57] (see below). The consequence of the limited mode size is that the laser intensity inside the fiber grows with the output power. In combination with the long path length this induces a variety of nonlinear effects at comparatively low power. For a general review on fiber lasers see, e. g. [58,59,60].

The resonator mirrors can be integrated into the active fiber as fiber Bragg gratings (FBG), which makes a very robust design and allows to splice the active fiber directly to a transport fiber. Fiber lasers can be operated as pure oscillators or in various oscillator-amplifier (MOPA) configurations. A similar flexibility exists for the launching of the pump radiation. Because of the finite size of the pump core, the power scaling is, however, somewhat limited and relies on high-brightness pump sources.

For multi-mode operation, the limitation for the mode diameter is strongly relaxed, but the problems with the coupling of the pump radiation still exists. However, this limitation can be easily circumvented by incoherently combining a larger number of single-mode or few-modes fibers into one multi-mode fiber. In this case, all the limits discussed below apply to the single-mode or few-modes fiber lasers only.

2.1.3 Coherent beam combining (CBC)

As already mentioned above in connection with the power scaling of the pump beam, when combining several beams, the brightness of a single beam will be conserved at best and the beam-parameter products, ${w}_{x}{\Theta }_{x}$, ${w}_{y}{\Theta }_{y}$, and correspondingly ${M}_{x}^{2}$, ${M}_{y}^{2}$ of the combined beam at best grows linearly with the number of combined beams, ${N}_{x}$, ${N}_{y}$, in the respective direction, i. e., in two dimensions, ${M}^{2}=\sqrt{{M}_{x}^{2}{M}_{y}^{2}}$ grows proportional to the square root of the total number of combined beams ${N}_{\mathrm{tot}}={N}_{x}{N}_{y}$.

This limit does not exist if the beams have a well-defined phase with respect to each other, in the simplest case identical phases. In this way, the beams can be perfectly superimposed using beam splitters in the reverse direction, the resulting beam parameter product and ${M}^{2}$ are identical to that of a single beam, the total power and hence the brightness grow by a factor of ${N}_{\mathrm{tot}}$. Another option would be to image the nearfield of the array of individually collimated beamlets ('tiled aperture') with a lens into the far-field. Then, depending on the phases, the resulting spot can be moved in the far-field (phased array). Again, the peak brightness in the main spot will be ${N}_{\mathrm{tot}}$ times that of a single beam. However, due to the intensity modulation in the near-field, higher diffraction orders will be generated, resulting in a loss of power in the central peak of the order of 30%–50%. The generation of higher diffractive orders can be reduced by applying diffractive optical elements (DOEs) in the near and or far field.

If, in the case of pulsed lasers, the limitation is only given by the peak power in the amplifier, it is also possible to separate the pulses in time with the help of a delay line and to superimpose the pulses again after amplification with a second delay line (divided pulse amplification, DPA).

In principle, CBC can be used with any type of lasers and any laser architecture, e. g., with diode laser arrays [61, 62]. In practical life, however, because of the limited power of single-frequency diode lasers, solid-state lasers are preferred as coherence or brightness converters, and CBC is used only, where the limits of the solid-state laser concept is reached. This is especially the case in narrow-bandwidth cw fiber lasers, where stimulated Brillouin scattering (SBS) limits the output power (for a review see [60]), and for ultrafast fiber lasers, where the peak power is limited despite strongly stretched pulses (for a review on various CBC schemes see [63]).

For this to work, the phases of the individual beams have to have a well-defined phase with respect to each other and in the end the individual beams have to be combined into one—ideally diffraction-limited—beam.

Phase coupling can be realized by using one common seed laser for the array of power amplifiers, e. g., by splitting the beam with a set of beam splitters [64] or diffractive optical elements (DOEs). In the case of fiber lasers, the array can be made of individual fibers or one multi-core fiber (MCF). If MCFs are designed with core spacings of approximately 50 µm to reduce optical and thermal coupling, they can be used and power-scaled similar to discrete fiber arrays. If the spacing is much smaller, the modes of the individual cores couple and form supermodes with well-defined phases [65]. All these options work with oscillators as well. In addition, a Talbot resonator can be used for self-organized coupling of the individual modes. Relying on supermodes has the advantage that no external phase control is needed to stabilize the (relative) phases.

Beam combining after amplification can be done with the same set of beam splitters as used for splitting the seed beam, just in reversed order. This is called the 'filled aperture' approach because each of the superimposed beams fills the full aperture. The other approach for beam combining is the 'tiled-aperture' or 'phased-array' approach. In this case, the individual beams are separated in the near field, e. g., arranged in a hexagonal array, and superimposed in the far field by focusing with a lens. Due to the intensity modulation in the near field, diffraction occurs that reduces the power in the central peak to come 50–80%. The supermode in multi-core fibers behaves like a 'tiled aperture'. Imaging the supermode into the far field is the simplest method for beam combining, provided the in-phase supermode is dominating.

The most-straight-forward CBC solution in terms of efficiency and scalability is to use individual fibers and beam splitters, both for splitting the seed beam and for combining the amplified beams. This allowed to realize a record of 10 kW average power with femtosecond pulses [66]. The disadvantage is the high complexity of the setup. The overall power is then limited only by the number of individual amplifiers that can be combined and the power-handling capabilities of the beam combiners. With increasing number, the combining efficiency may slowly deteriorate due to position, angle, and phase tolerances. Controlling and optimizing the phases of the individual elements may also become more difficult for N > 100. The power scalability of the monolithic MCF/supermode approach is less obvious. Besides thermal issues, the favorite in-phase supermode seems to be similarly limited by self-focusing as the mode in a single-core fiber. However, this limit should not apply for the anti-phase supermode [67].

2.2 Thermally induced effects and limitations

2.2.1 Disk lasers

Thermal aberrations in disk lasers are minimized by the thin-disk design, which favors a one-dimensional heat flow and a temperature gradient almost collinear with the axis of the laser beam. Nevertheless, there is a temperature step between the pumped volume and the surrounding unpumped area. The resulting wavefront distortions lead to diffraction losses that are noticeable in fundamental-mode operation. Apart from these aspherical aberrations, there are also spherical distortions (similar to a thermal lens) due to the bending of the disk-heatsink assembly (bi-metal effect), which affects the stability range of the resonator. As the stability range is inversely proportional to the diameter of the mode field area [51, 68], this might be a concern especially for single-mode lasers and hence also in the case of power scaling of mode-locked lasers. Another possible aberration is caused by the heating of the air in front of the disk [69, 70]. Successful compensation with active or adaptive mirrors has been demonstrated for both, spherical aberrations [71] and aspherical aberrations [72].

2.2.2 Fiber lasers

The beam quality of fiber lasers is defined by the waveguide and should in principle be independent of the output power. Properly designed, this allows stable fundamental-mode operation with excellent beam quality (M² ̴ 1.1). However, due to the radial heat flow, a power-dependent thermal lens is generated that affects the waveguide properties and may reduce the effective mode size in comparison to the one in the cold fiber [73, 74]. This is especially important if one wants to increase the mode-field diameter for fundamental-mode operation as much as possible to reduce the intensity.

The transverse-mode instability (TMI) was noticed as an additional thermally induced limit around 2010, for a review see [75]. The mechanism discussed is the following: The large-core fiber designs needed for high output powers as discussed above, also allow the propagation of higher-order modes (HOM), namely the LP₁₁ mode in addition to the fundamental LP₁₀ mode (FM). The superposition of these modes creates an interference pattern (MIP), which creates a refractive-index grating (RIG) induced by the thermo-optic effect. Depending on the phase shift between MIP and RIG, power flows between the FM and the HOM. For low powers, the laser runs stably and usually with most of its power in the FM. After a certain threshold, the power transfer grows exponentially, resulting in increasingly stronger fluctuations of the power content of the FM. Once a modulation of almost 100% is reached, the power fluctuates in a rather chaotic way. The heat source driving this effect is the quantum defect, but also photodarkening is discussed, although this effect has been reduced substantially over the years. Since the strength of TMI depends on a complex interplay between the fiber design and the amplification process, it is difficult to give simple scaling laws for this effect, but it seems clear that TMI is the dominant limitation for FM fiber lasers. An experimental rule of thumb for high-power low-gain multi-mode fiber amplifiers gives a heat load of 34 W/m as threshold for TMI. A modified diagram showing the dominant limitations as a function of the basic design parameters, core diameter and fiber length is given in [76]. Recently published simulations can be found in [77, 78]. Mitigation strategies include the reduction of photodarkening and the quantum defect to reduce the heat load [75], the reduction of dn/dT [79], the use of a fiber design that supports the FM only or has increased bend losses for HOMs, the application of counter- or bidirectional pumping [53], the increase of the power or linewidth of the seed [80], the modulation of the pump beam [53], or the control of the phase shift [81, 82]. For a detailed discussion of the various methods see [75] and from a simulation-based point of view [78] and references therein.

2.3 Nonlinear effects and limitations

There are a variety of nonlinear effects that can occur in lasers, the most important ones being:

• Stimulated Raman Scattering (SRS)

• Stimulated Brillouin Scattering (SBS)

• Amplified spontaneous emission (ASE)

• Self-phase modulation (SPM)

• Self-focusing

Since nonlinear effects depend on the intensity and the propagation length, they are especially important in fiber lasers due to the strong spatial confinement of the radiation and in ultrafast lasers due to the strong temporal confinement of the optical power in the individual pulses.

Inelastic scattering of photons can occur at optical phonons (Raman scattering) or acoustical phonons (Brillouin scattering). In the Stokes process, the generation of a phonon causes the wavelength of the interacting photon to be red-shifted. In the less-likely, temperature-dependent anti-Stokes process, the absorption of a phonon induces a blue-shift of the interacting photon.

Because of the linear dispersion relation of acoustical phonons, energy and momentum conservation, Brillouin scattering can only occur in the GHz spectral range and in back-reflection. There exist also the corresponding stimulated processes, where an already existing Stokes or anti-Stokes photon stimulates such a scattering process. Starting from noise, there is a threshold-like behavior, at which the exponential growth becomes macroscopically relevant. For SBS and lasers with a linewidth smaller than the Brillouin linewidth ν_B of approximately 20 MHz, the threshold is reached for $\frac{{P}_{\mathrm{opt}}}{{A}_{\mathrm{eff}}}=\frac{21}{{g}_{0}{ L}_{\mathrm{eff}}}$ [83] with ${g}_{0}$ of the order of 3 cm/GW. This limits the fiber length for a given power density or the maximum power that can be transported for a given mode cross section ${A}_{\mathrm{eff}}$ and fiber length ${L}_{\mathrm{eff}}$. As the SBS gain has a Lorentzian line shape, it strongly decreases for a signal radiation with linewidths Δv >  > v_B. Therefore, SBS is important for narrow-linewidth or single-frequency lasers only, and it can be reduced by increasing the signal linewidth by some kind of modulation or by broadening or varying the SBS frequency along or across the fiber. This can be achieved by temperature gradients, tapers, refractive-index variation, radial stress, etc. [84,85,86].

Unlike SBS, SRS can occur in any propagation direction—hence forward and backward inside a fiber—and may occur as a cascade in several orders. In each step, the red-shift is of the order of several hundred inverse centimeters, in silica by 13 THz. The Raman gain g_R in silica fibers is of the order of 10^–2 cm/GW. Since the original laser radiation and the Raman shifted radiation are spectrally well separated, SRS can be strongly reduced by applying spectral filters, e. g., by transmissive fiber Bragg gratings [87, 88]. Another option, both for SRS and SBS, could be to modify the material constants [79, 89, 90].

Amplified spontaneous emission is the process, which allows the laser oscillator to start lasing. For high gain coefficients combined with a long propagation length, the laser can in principle oscillate without the feedback of the resonator (so-called super-luminescent source). This effect can become especially relevant for both fiber and disk amplifiers. The fiber waveguide naturally confines the light in the direction of propagation, leading to directional ASE-emission. For thin-disks however, the gain length in the longitudinal direction is very short (due to the small thickness of the disk), but the gain length in the transversal plane normal to the axis of the laser grows with the diameter of the pumped spot, which is usually increased for power scaling. Depending on the geometry, this may lead to parasitic oscillation in the plane of the disk competing with the intended amplification of a given laser beam. Therefore, any feedback from the circumference of the disk has to be avoided by chamfering and by leaving an unpumped area in the outer area of the disk. Nonetheless, ASE opens an additional relaxation channel within the pump spot, which reduces the lifetime of the excited state with increasing (saturated) gain and thereby increases the pump power necessary to reach the laser threshold. According to a simplified analytical model in [50], the relaxation rate is approximately enhanced by the factor.

$$\frac{\tau }{{\tau }_{ASE}}=1+\frac{h}{D} {e}^{\gamma D},$$

where $h$ is the thickness of the disk, $D$ is the diameter of the pump spot, $D>>h$, and $\gamma$ is the (saturated) gain coefficient, in laser operation given by $\gamma 2h={L}_{\mathrm{tot}}$, where ${L}_{\mathrm{tot}}$ is the total round-trip loss of the laser cavity including the output-coupling. Assuming ${L}_{\mathrm{tot}}=4 \%$ and $h$ = 0.1 mm, the relaxation rate is doubled for a pump spot diameter $D \sim 30 \mathrm{mm}$ compared to the relaxation rate without ASE and grows nearly exponentially with increasing $D$. The maximum useful $D$ can be increased by reducing the output-coupling and hence ${L}_{\mathrm{tot}}$ and by increasing the thickness of the disk. If the laser is operated in fluorescence mode (with the resonator blocked) or in pulsed mode with the repetition rate near or below the inverse radiative lifetime τ, γ is no longer saturated and can assume much larger values. Assuming a single-pass gain of 15%, the maximum useful pump spot diameter, where the relaxation rate doubles, is approximately 2 mm. For high-energy laser systems, where high inversion is crucial, additional transparent, so called 'anti-ASE caps' are used to avoid trapping of the spontaneous emission within the amplifying disk. There are a number of publications on ASE in disk lasers, mostly relying on ray-tracing for the ASE and the rate equation for the laser process, for various geometries, sometimes also taking into account the temperature [50, 91,92,93,94,95,96,97,98,99].

Self-phase modulation and self-focusing both originate from the Kerr effect, which describes an almost instantaneous change of the refractive index with the intensity of the light. The spatial intensity distribution of the mode-profile transfers into spatially dependent refractive index, which for most glasses and optical crystals with a positive nonlinear refractive index, leads to a nonlinear focusing lens branding this effect as self-focusing. It is worth noting that the self-focusing threshold only depends on the power but not on the intensity of the pulse. The critical power is proportional to ${P}_{\mathrm{critical}}\propto {\lambda }_{0}^{2}/({n}_{0}{n}_{2})$ [100], where ${\lambda }_{0}$ is the vacuum wavelength, ${n}_{0}$ the refractive index, and ${n}_{2}$ the nonlinear refractive index. The critical power is 4 MW for linearly polarized light, and 6 MW for circularly polarized light in glass for a wavelength of approx. 1 µm [101]. As self-focusing leads to irreversible damage of the material, it ultimately limits the usable peak power of the pulse.

In a similar manner, the temporal intensity profile of the pulse leads to a temporal variation of the phase, effectively creating new frequencies. This results in a chirped pulse with an increased spectral bandwidth. While this effect has only minor impact on amplifiers, as it distorts the temporal profile of the pulse due to the acting dispersion, it limits the range of stable operation of mode-locked oscillators.

Although nonlinear effects often severely limit the performance of lasers, their unique properties can be put to use to alter the properties of laser radiation in beneficial ways. This e.g. can be the frequency conversion to remote spectral regions [102] or the controlled use of SPM to increase the spectral bandwidth of laser pulses to then reduce their pulse duration. As these effects rely on a significant intensity and/or propagation length for a high efficiency, they are often restricted to pulsed laser operation. Since nonlinear stages only depend on the injected pulse parameters and are independent of the laser architecture, we will not go into details, but point out relevant results where suited.

3 High-power disk lasers

3.1 Continuous-wave disk lasers

CW or pulsed thin-disk lasers with high average power are typically based on YAG or LuAG disks with a thickness ranging between 100 and 200 µm, doped with 5–10 at-% Yb³⁺. They are pumped with power densities (here defined as the pump power entering the pump optics, divided by the pump-spot area) of up to typically 10 kW/cm², ideally at a wavelength of 969 nm, with commonly 24–44 (single) passes of the pump beam through the disk (12–22 reflections of the pump beam at the rear facet of the disk). The disks are usually placed in a V-type cavity with an output coupling of 2–4%. This design allows to obtain a high pump efficiency and a high outcoupling efficiency (both around 95%) and to keep the disks at comparably low temperatures (100 °C), which ensures a low three- and four-level laser threshold of typically 1/20 of the maximum operating pump power.

Due to the comparatively low power density and very short amplification length of thin-disk lasers, SRS, SBS, SPM, and self-focusing can be neglected for cw operation. Only ASE and parasitic lasing need to be considered and possibly reduced by appropriate measures. To reduce competing laser emission in radial direction and in so-called whispery-gallery modes, the diameter of the disk is commonly chosen to be at least twice the diameter of the pump spot and the circumference of the disk is chamfered. Although thinner disks and/or a higher output coupling could slightly further increase the laser efficiency and reduce phase distortions, this would also strongly increase ASE and hence the laser threshold for pump-spot diameters above 1 cm due to the higher gain coefficient. An option to realize a thin active layer and at the same time a thick disk to reduce ASE is using an undoped so-called 'Anti-ASE cap' bonded on top of the (thin) doped disk. The undoped cap adds a thermal lens due to the radial heat flow, which could be used to compensate the focal power of the disk, but adds also rather strong aspherical distortions [93, 98, 103, 104]. Therefore, this does not seem to be a good choice for fundamental-mode lasers, neither for cw nor for mode-locked operation.

The highest cw powers so far have been achieved with Yb³⁺ doped YAG or LuAG. LuAG is similar to YAG, but has better thermal properties when doped. Sesquioxides like Lu₂O₃ may become an interesting alternative, when issues concerning crystal quality are solved. Hence, the first crystal used for thin-disk lasers is still among the best in terms of power scaling. The highest multi-mode power of 10 kW (M² ≈ 10, optical efficiency ≈ 60%) achieved with one disk was reported in 2016 without giving any details on the actual setup [105].

The highest output power reported so far with a close to diffraction-limited beam quality, M² < 1.4, was 4 kW [106]. Again, no experimental details have been published except that pumping wavelength was 969 nm. Obviously, the stability range of the cavity was optimized for an output power of 3–4 kW. With decreasing power between 3 to 1 kW, the beam propagation factor M² increased to 5. The optical efficiency was close to 55%. With an adaptive mirror in the resonator, the beam quality could be further improved to M² < 1.15 for the entire power range [107] with optical efficiencies around 50%. With conventional optics, but replacing the air at ambient pressure by a low pressure or He atmosphere to increase the stability range, an M² < 1.1 was demonstrated for an output-power range between 300 and 800 W [69]. For an overview see Table 1.

Table 1 High-power, high-brightness cw thin-disk lasers

3.2 Ultrafast disk lasers

Like with other approaches, ultrafast disk lasers can be setup as simple oscillators or in MOPA configuration. For oscillators (Fig. 6c), the most straight-forward approach is to start from a fundamental-mode cw oscillator in which a mode-locking mechanism is introduced, e. g., a saturable absorber like a SESAM, which has a geometry and scaling properties similar to that of the laser disk. For thin-disk laser amplifiers, mainly two concepts are used: regenerative amplifiers and multipass amplifiers. Both concepts increase the gain length by multiple passes of the amplified pulse over the disk. Regenerative amplifiers (Fig. 6b) use a cavity with an optical switch, multipass amplifiers a geometrical folding of the beam path (Fig. 6a). For an ultra-brief review, see, e. g. [108, 109].

Fig. 6

Schematic illustration of the different schemes for the generation of ultrashort pulses with hundreds of watts to kilowatts with thin-disk lasers. a multi-pass amplifier, b regenerative amplifier, c mode-locked oscillator (here illustrated is the case of SESAM mode-locking and without showing the pulse propagating inside the cavity with much higher peak power). Reprinted from [109], originally published by Springer

3.2.1 Thin-disk oscillators

High-power ultrafast thin-disk lasers are most commonly based on soliton mode-locking with SESAMs or KLM, which were first demonstrated by Aus der Au et al. [110] and Pronin et al. [111], respectively. The upper limit of the average power of these oscillators is set by the power, which can be extracted in cw fundamental-mode operation. For stable mode-locking with a single pulse circulating in the cavity, the pulse energy is inversely proportional to the pulse repetition rate, which is then given by the round-trip time of the cavity. With these techniques, average powers of up to a few hundred watts and pulse energies of up to a few tens of microjoule were demonstrated. For a review see, e. g., [112]. Table 2 lists a selection of milestone experiments of the recent years. The value of M² is close to 1, usually below 1.1. 'Active multipass cells' (AMPC) are used in some cases to increase the number of reflections at the disk within one roundtrip of the beam in the laser cavity.

Table 2 High-power ultra-fast thin-disk oscillators. KLM: Kerr-lens mode-locking; SESAM: semiconductor saturable absorber mirror; OC: output coupling; AMPC: active multipass cell; SPM: self-phase modulation

The management of nonlinear effects constitutes a main challenge in mode-locking. Among these, self-phase modulation (SPM) is the most important in soliton mode-locked thin-disk lasers. For ultrafast thin-disk lasers, nonlinear effects mainly arise from the propagation of the pulses in the air inside the laser cavity as the comparatively thin gain medium limits the interaction length to a few hundred micrometers per pass. Additionally, contributions from multilayer coatings are also often non-negligible [122].

For soliton mode-locking, the pulse-forming mechanism of a soliton are exploited to enable stable mode-locking of ultrashort pulses [123]. This requires that the nonlinear phase-shift introduced by SPM (usually positive) needs to be balanced by group-delay dispersion (GDD) of the opposite sign (usually negative), which is often done by adding several dielectric mirrors, designed to add the necessary GDD over a certain spectral range. This relation is expressed as [124]

$${\tau }_{p}\approx 1.76\cdot \frac{2|D|}{\left|{\gamma }_{SPM}\right|{E}_{p}},$$

where ${\tau }_{p}$ is the FWHM pulse duration, $|D|$ is the sum of the GDD of all elements per round-trip in the cavity, ${\gamma }_{\mathrm{SPM}}=\frac{4{n}_{2}d}{\lambda {w}^{2}}$ is the sum of the on-axis nonlinear phase-shift (in units of rad/W) of all elements per round-trip in the cavity for a Gaussian beam with radius $w$, wavelength $\lambda$, and pulse energy ${E}_{p}$, propagating through a nonlinear medium of thickness $d$ and nonlinear index ${n}_{2}$. This relation is a good approximation when the soliton pulse shaping effects are dominant and the pulse experiences the averaged effects of dispersion and nonlinearity, which requires that the discreteness of SPM and dispersion are weak. Hence, e. g., excessive nonlinear phase shifts, which lead to strong periodic disturbances, destabilize the pulse. As a rule of thumb, the phase-shift per roundtrip should be much lower than $\pi$. On the other hand, too small nonlinear phase shifts require a low cavity dispersion resulting in only weak soliton shaping effects, which makes the pulse vulnerable to disturbances from other pulse shaping mechanisms (e. g., gain-bandwidth or absorber action).

To reduce the nonlinear effects either the intensity $I$ or the nonlinear refractive index ${n}_{2}$ can be reduced. As the gain per reflection is low, thin-disk oscillators employ a low output coupling. As a consequence, the intensity of the pulse circulating inside the cavity is much higher than the one of the pulses that are coupled out. A common way to reduce the nonlinear effects is therefore to increase the roundtrip gain by employing several passes over the disk to allow for a larger output coupling. Bauer et al. [116] demonstrated the efficacy of this approach by employing a multipass setup inside the laser cavity. Still today, the extracted pulse energy of 41 µJ constitutes a record for thin-disk oscillators operated at ambient pressure.

Another approach consists in reducing the value of ${{\varvec{n}}}_{2}$ of the atmosphere in the resonator either by evacuation [119], reduction of the air pressure [115], or by employing a gas with a lower ${n}_{2}$ such as helium [122]. This also reduces thermal effects and is therefore helpful to achieve high average powers [69]. For a comparison of the relevant extra- and intra-cavity parameters see [112].

Furthermore, a reduction of the total nonlinear phase shift was demonstrated by introducing a component exhibiting a negative ${{\varvec{n}}}_{2}$, which counteracts self-phase modulation originating from material with a positive ${n}_{2}$ [117]. As high-power capable materials with this property that can be used for laser radiation at a wavelength of 1 µm are rare, the negative ${n}_{2}$ was artificially created using the cascaded quadratic nonlinearity [125] in a phase-mismatched second-harmonic generation process in lithium triborate.

If one wants to compare the maximum output power and efficiency of fundamental-mode cw lasers and mode-locked lasers, one has to consider that there exist several boundary conditions that reduce the optical efficiency of mode-locked lasers to typically 30%:

• o The laser is operated with comparably low pump and laser intensity and comparably high output coupling, reducing the maximum pump power with respect to the threshold pump power.

• o The intracavity losses are higher due to the SESAM or the Kerr-lens cavity, reducing the overall efficiency.

• o As a consequence, the thermal effects are stronger leading to a reduced stability range.

3.2.2 Thin-disk regenerative amplifiers

The basic design of a regenerative amplifier is similar to that of an oscillator with an additional (electro-) optical switch. This switch is used to couple the pulses from a master oscillator into the cavity of the regenerative amplifier and—after a certain number of roundtrips—to couple the amplified pulse out of the cavity again. This has a couple of advantages:

• o Since the repetition rate can be chosen much smaller than the repetition rates of oscillators, much higher pulse energies can be achieved with regenerative amplifiers at a given maximum average power.

• o In contrast to oscillators, there are no self-reproducing pulses per roundtrip needed. For moderate nonlinearity, there is no need to manage the nonlinear effects.

• o Many passes through the disk can be easily realized, compensating the inherently low gain of the thin disk.

• o With the cavity optimized for fundamental-mode operation, an M² close to one can be sustained during amplification.

• o There is no enhancement of the resonator-internal peak power due to the Q-factor of the cavity as in oscillators with an output coupling typically below 10%. However, because of the circulation of the pulse, the average power within a regenerative amplifier is higher by one or two orders of magnitude than the average power of the extracted beam.

• o Pulse broadening during propagation through the cavity can keep the peak intensity at a manageable level despite the increase of the pulse energy.

• o The spectral broadening may compensate gain narrowing or even increase the spectral bandwidth [126, 127].

• o If needed, the pulses can be pre-stretched before being injected into the regenerative amplifier.

However, the additional Pockels cell is the major limiting factor for power scaling of regenerative amplifiers because it sets a limit to the beam diameter, the peak intensity (damage threshold), average power (thermal effects), and the switching speed. BBO, the preferred electro-optical crystal for high power applications, needs a quarter-wave transverse voltage per diameter of the free aperture of U_λ/4 = 1.3 kV/mm, the capacitance is typically around C = 5 pF. Therefore, not only high voltage is required for Pockels cells with suitably large apertures, but the power for (dis)charging the Pockels cell also grows quadratically with the aperture and linearly with the modulation frequency f: $P=f C {U}_{\lambda /4}^{2}$. This limits the repetition rate of regenerative amplifiers to the order of 1 MHz. The maximum aperture depends on the maximum repetition rate and may be as large as 10 mm for repetition rates in the range of 1–10 kHz. By using two crystals in series on the optical path but electrically in parallel, the voltage can be halved, however, the capacitance and the optical losses are increased. Furthermore, the thick, rod-type crystals cause additional dispersion, SPM for high peak powers, and thermal distortions at high average powers. The damage threshold of the coatings may also limit the maximum peak-power or energy density. For sub-picosecond pulses, usually a pulse compressor and optionally a stretcher is needed to avoid some of these issues.

The first report on a Yb-thin-disk regenerative amplifier was published in 1997 [128] with a pump source similar to the one used for the very first cw thin-disk laser, i.e., seven 1-W fiber-coupled pump diodes. It used a pump optics with four double passes of the pump beam, realized with four spherical mirrors (see Fig. 3), allowing to use a thinner (300 µm) and less heavily doped (11%) disk than the first thin-disk laser. Starting from 750-fs long pulses, pulses with 180 µJ pulse energy and a duration of 2.3 ps at a repetition rate of 750 Hz were generated. No additional stretching or compressing of the pulses was applied.

Today's high-power regenerative amplifiers with average powers between 100 and 200 W are typically operated at much higher repetition rates in the range of 100 kHz to 1 MHz, which results in typical pulse energies between 2 mJ and 200 µJ, depending on the repetition rate. The pulse length after recompression is typically 1 ps, the beam quality close to diffraction limited (M² < 1.2 or 1.1). With repetition rates in the 1 to 5 kHz range, pulse energies up to approx. 200 mJ and average powers in the kilowatt range could be demonstrated. As with cw oscillators, two (or more) disks can be operated in series within the resonator to double the average power and pulse energy [129]. See Table 3 for an overview. However, if the pulse repetition rate is near or somewhat above the spontaneous recombination rate of the upper laser level, pulse to pulse instabilities can occur. The reason is that the pulse energy depends on the inversion and vice versa: A somewhat stronger inversion leads to a stronger pulse amplification, which results in a reduced inversion for the following pulse. The result is an oscillating pulse energy (bifurcation) and ultimately a chaotic behavior. By monitoring the energy of the circulating pulse, this effect can be easily suppressed [130].

Table 3 High-power ultrafast thin-disk regenerative amplifiers

Despite the somewhat more complex setup than simple pulsed oscillators, regenerative amplifiers provide higher powers and/or pulse energies and are meanwhile also commercially available as table-top boxes (Trumpf Lasers, TruMicro 5000 series; Trumpf Scientific, Dira series; Jenoptik JenLas femto).

3.2.3 Thin-disk multipass amplifiers

Multipass amplifiers are characterized by geometrical folding of the beam path to obtain multiple passes through the gain medium by means of an array of mirrors. Depending on the injected seed pulses and the gain medium of the amplifier usually 5 to 50 passes are used. In contrast to regenerative amplifiers, the number of passes is fixed by the geometrical layout and is not meant to be altered during operation. Multipass amplifiers exhibit several advantages:

• The optical layout can be all-reflective except for the laser gain medium. As a consequence, chromatic dispersion and nonlinear effects are low.

• The amplifier setup without any active switches enables a high flexibility in terms of pulse duration, repetition rate and polarization. There is no upper limit in terms of pulse duration (even continuous-wave or burst operation are possible) or repetition rate. However, as for all laser amplifiers, gain-dynamic effects occur for repetition rates close to or below the active medium's upper state relaxation rate. Depending on the gain material, multipass amplifiers can be built to work with any kind of polarization, even supporting cylindrical states of polarization [137].

• All the optical components are subject to comparably low optical powers and intensities, except for the disk, which is irradiated by the sum of the beams in the folded path. Some designs even prevent any enhancement of the optical power on folding optics, which reduces the likeliness of damage to the optics.

• Distortions of the pulse shape due to saturation of the gain are effectively prevented by the low gain per pass in combination with the multiple subsequent reflections.

These advantages are accompanied by some disadvantages:

• Depending on the number of passes, efficient operation (with strongly saturated gain) requires a sufficient level of seeded pulse energy or power.

• The number of passes is limited by the available space for the geometric folding and the increasing length of the beam path, which increases the sensitivity to misalignment.

• The beam quality factor is largely influenced by the quality of the optical elements and the alignment as there is no feedback of a cavity.

As the last two listed drawbacks are softened with a reduced number of passes and the advantages are especially high at a high average power or pulse energy, thin-disk multipass amplifiers are preferably used as final power boosters behind an eventual pre-amplifier, which often is a regenerative amplifier. So far, this combination delivered the highest average power with ultrashort pulses from a single laser reported to date and works for a large range of repetition rates and pulse lengths. The first demonstration of a high-power ultrafast thin-disk multipass amplifier in 2013 [138] triggered an amazing progress. Subsequent research efforts resulted in highly stable laser sources emitting up to multi-kW average powers, Joule-level pulse energies, and pulses with durations of few-hundred femtoseconds. The technology was further extended to vector beams with cylindrical states of polarization, and used for frequency conversion to the visible and UV. An overview is given in Table 4.

Table 4 High-power thin-disk multipass amplifiers (CPA: chirped-pulse amplification; MGA: monolithic glass assembly)

4 High-power fiber lasers

4.1 Continuous-wave fiber lasers

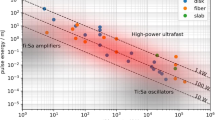
The challenge with high-power fundamental-mode (FM) fiber lasers is that the inelastic scattering effects (Raman- and Brillouin scattering) as well as transversal mode instabilities (TMI) need to be considered. The strategy of 'thermally' scaling the output power by increasing the fiber length is strongly limited by the nonlinear effects, in the first place SRS and—for narrow-linewidth lasers—SBS, which grow exponentially with the fiber length (in case of amplifiers, including the length of the transport fiber). Increasing the mode-field area to reduce the intensity and thereby reducing the nonlinear effects, on the other hand, is limited by TMI. However, over the years one has developed some strategies, as mentioned above, to shift these limits to quite impressive power levels. Figure 7 gives an idea of how SRS, TMI, and the pump source brightness limit the output power.

Fig. 7

Contour plot of power limits (in kW) due to pump brightness (blue area), SRS (green area), and TMI (orange), not taking into account SBS. Assumed are pump brightness B_p = 0.18 W/µm²/sr, η_laser = 85%, η_heat = 10%, G = 10 dB; α_{core, pump} = 250 dB/m. Reproduced from [74]

As with disk lasers, the most powerful FM fiber lasers have been realized by commercial companies with correspondingly little information on details of the design. Already since 2010, IPG Photonics Corporation offers single-mode fiber lasers with output powers of up to 10 kW. The data of some cw fiber lasers reported in the literature are given in Table 5. In ref. [147] and [148], Fujikura Ltd reported all-fiber oscillators with attached transport fiber with an essentially SBS- (and TMI-)free output power of 5 kW (M² = 1.3) at 6.3 kW pump power and 8 kW output power with M² = 1.5 at 10 kW pump power before the onset of SRS. A reviewed paper was published by Beier et al. [149] on two fiber amplifiers with effective mode cross section areas of 333 µm² and 405 µm², respectively, and output powers of 2.8 kW (small cross section, TMI limited), 3.5 kW (large cross section, SBS limited due to the narrow-band seed), and 4.3 kW (large cross section, two spectrally shifted seeds, pump limited).

Table 5 High-power cw fiber lasers. A_eff: effective mode-size area

4.2 Ultrafast fiber lasers

4.2.1 Fiber oscillators

Despite the high performance of ultrafast fiber amplifiers, mode-locked fiber oscillators usually deliver average powers of up to 1 W and pulse energies up to 200 nJ only. This significant difference to mode-locked thin-disk oscillators originates from the extremely increased nonlinearity due to the tight confinement in the fiber core. Therefore, in addition to self-phase modulation, stimulated Raman scattering and self-steepening need to be considered in the oscillator design [150, 151]. To reduce the peak-power in the cavity, mode-locked fiber oscillators are usually operated in a positive net-dispersion regime to produce chirped pulses (compare Fig. 5), which are later-on compressed with an external prism or grating optics. There are several ways to achieve stable pulse shapes per round-trip [152]:

• o Dissipative soliton: The linear spread from GVD is balanced by spectral loss from finite gain bandwidth or spectral filters (e. g. gratings). The max. accumulated phase shift can be as high as 10 π.

• o Passive and amplifier similariton: A parabolic pulse evolves self-similarly, broadening continuously in time and frequency space.

In either case, if this is to be taken advantage of in oscillators, a self-consistent evolution of the pulses through the cavity is needed. This can be done with an additional negative-dispersion fiber (passive similariton; soliton-similariton) or by adding a narrow-bandwidth Gaussian filter (e. g., free-space grating with subsequent coupling into a single-mode fiber; all-normal dispersion amplifier similariton). It makes sense to do this in a ring-cavity after coupling out the main part of the laser pulse from the cavity and before feeding the remaining pulse back into the gain fiber. In any case, a saturable absorber is needed for allowing the laser to start from noise, stabilizing it in the steady-state, and suppressing the cw background. Besides the SESAM, there exist also fiber-based saturable absorbers based on nonlinear polarization evolution (NPE) or nonlinear optical/amplifying loop mirrors (NOLM, NALM).

Alternatively, an effective self-amplitude modulation can be achieved with a combination of SPM induced spectral broadening and offset spectral filtering (Mamyshev oscillator) [153]. Two gain-fibers, each followed by a Gaussian offset-filter, make-up a (ring) cavity. The filters shape the pulses to narrow-bandwidth and short duration before injecting them as seed again into the fiber. These step-like filters suppress any cw background—but also the self-starting of the oscillation from noise—and should work with large phase shifts of the order of 100 π and high pulse energies of the order of 100 nJ in standard SMF.

For typical performance data, see Table 6 and references therein. A recent brief review of fiber oscillators and amplifiers can be also found in [154, 162].

Table 6 Performance summary of SMF-based ytterbium-doped fiber oscillators for different pulse evolutions. Adapted from [153]

4.2.2 Fiber amplifiers

Since the pulse energy of fiber oscillators is limited to some nanojoules, master-oscillator power-amplifiers are needed for higher pulse energies and average powers in the 10-W to kW range, see Fig. 8. This allows to use:

• o A pulse picker, e. g., an acousto-optical modulator (AOM) to reduce the repetition rate.

• o Chirped pulse amplification (CPA) to reduce peak power. The stretching is realized in free space with a grating pair or a chirped volume Bragg grating (CVBG), in an all-fiber system with a fiber Bragg grating (CFBG) or a polarization maintaining fiber providing the group-delay dispersion, to achieve pulse lengths in the nanosecond range. Compression after the amplification is usually in free space with grating pairs.

• o Divided pulse amplification (DPA) to reduce the peak power [161]. For details see chapter 6.

• o Coherent beam combination (CBC) to reduce the peak and average power. For details see chapter 6.

Fig. 8

Schematic setup of a fiber CPA system: IO, optical isolator; DL, diode laser. Reprinted with permission from [57] © The Optical Society

To further reduce the power density in the amplifying fiber, the mode-field area is maximized similar as in high power fiber oscillators. Catastrophic damage limits the peak power to some 4 MW.

Due to gain narrowing and residual dispersion mismatch one has to use additional measures to obtain pulses shorter than 200 fs. These can be an additional nonlinear pulse compression or to apply nonlinear amplification right from the beginning, where the interplay between SPM, gain and positive GVD results in a propagating parabolic similariton with a linear chirp that can be compressed to pulses as short as 50 fs to 100 fs. Additional pre-chirping helps to increase the average power from typically 10 W to the order of 100 W [154] and references therein. Additional spectral pulse shaping (e. g. by spectral filters) of the seeded laser pulses can be used to counteract gain-narrowing in the amplifier, which effectively increases the spectral bandwidth of the amplified pulses [163].

Similar to nonlinear amplification, nonlinear pulse compression stages are used to increase the spectral bandwidth of laser pulses to further shorten the pulse duration. The compression stage consists of a nonlinear broadening stage and usually a low-dispersion compressor. As only the parameters of the injected pulse need to be in a reasonable range to match the designed use of the stage, these stages are independent from the laser itself and can in principle be used with any architecture. Since this topic is out of the scope of this review, we recommend the review in reference [164] to the interested reader.

Typical pulse energies, average powers and pulse widths achieved so far are shown in Table 7.

Table 7 High-power ultrafast fiber amplifiers. PCF: photonic-crystal fiber; CPA: chirped-pulse amplification; MFD: mode-field diameter; ML: mode-locked; LMA: large mode area

5 Innoslab lasers

The characteristic dimensions of the laser crystal in Innoslab lasers with typical sizes of the Yb slabs of 1 × 10 × 10 mm³ and up to 1 × 25 × 10 mm³ for booster amplifiers range between the ones of disk and fiber lasers. Folding the beam path in the slab several times, the amplification length is much longer than in multipass disk lasers, whereas the mode size is larger than in fiber lasers and can be adapted to the increase of pulse energy during the zig-zag propagation through the slab (see Fig. 9). Although developed as a kind of alternative to the thin-disk, the Innoslab development was initially based on Nd³⁺ crystals, probably because of the active volume being larger than in disk and fiber lasers. Still, commercial cw and Q-switched Innoslab lasers, and also mode-locked lasers with multi-ps pulse width are based on Nd³⁺. Yb³⁺:YAG is used only for sub-ps pulses, because of its larger gain bandwidth. Some of the difficulties that needed to be addressed were the homogeneous longitudinal pumping and—particularly for the oscillator—the efficient extraction of the stored energy in an almost diffraction-limited beam. For a review see [18, 178].

Fig. 9

Schematic setup of an Innoslab amplifier. Reproduced from [179]

5.1 Ultrafast Innoslab amplifiers

Detailed design considerations for Yb Innoslab amplifiers as well as a comparison with disk and fiber lasers can be found in [179]. Typically, between 7 and 9 passes with a gain in the range of 2–10 per pass are used for the main amplifier. Optional booster amplifiers are operated with 1 or 2 passes. For pulse widths around 1 ps and repetition rates above 10 MHz, the nonlinearities are so low (B integral < 3) that no CPA is needed.

Selected results for sub-ps Yb-Innoslab lasers are given in Table 8.

Table 8 High-power ultrafast Innoslab amplifiers

With an additional spatial filter, it should be possible to reduce M² to below 1.1 in most cases at the expense of approximately 10% of the output power.

In order reach the 500-W, 50-mJ level [181], the experimental setup became quite complex:

Starting from an Yb fiber oscillator delivering 1-nJ pulses with 20 MHz repetition rate, a pulse picker reduced the repetition rate to 10 kHz. Subsequently, the pulse energy was increased by an Yb fiber pre-amplifier to 50 nJ and by an Yb rod amplifier to several Microjoule. From then on, between each amplification step a Faraday isolator prevents feedback from the following stages. The next steps included a Littrow grating compressor to compensate the previous GVD of 1,23 ps², resulting in 5-µJ pulses with a pulse width of 1 ps, a fiber Bragg grating stretcher to stretch the pulses to a length of 250 ps, another fiber amplifier, followed by another rod amplifier to increase the pulse energy to 100 µJ. The Innoslab amplifier with 7 passes increased the pulse energy to 15 mJ corresponding to an average power of 150 W, using a pump power density of 25 kW/cm². Finally, a two-pass booster amplifier pushed the average power to 630 W, using a pump power of 2.7 kW. The optical efficiency of the whole amplification chain amounted to 23%. A grating compressor with an efficiency of 86% restored approximately the original pulse duration, delivering 1.5-ps pulses with 530 W average power at 10 kHz. The wall-plug efficiency of the complete system was between 5 and 6%.

6 Coherent beam combining and divided pulse amplification.

6.1 Coherent beam combining (CBC)

A method that works in principle with any amplifier or (injection seeded) oscillator is to superimpose several beams coherently. This is done by dividing the seed beam in N beams, e. g., with a cascade of 50:50 beam splitters, and to combine the N amplified beams in one (diffraction-limited) beam ('filled aperture'), e. g., by using a similar set of beam splitters in reverse order. For this to work, the combined beams have to have identical positions, propagation directions and polarization, as well as nearly the same path and identical phase differences with respect to the seed. One possibility to optimize the phase is to modulate the power of each of the N channels except for one reference channel using a different frequency and then to maximize the power of the superimposed beams by adjusting the phase of the corresponding channel.

This was demonstrated with 12 high-power fiber amplifiers, each yielding approx. 900 W with 1.5 kW of pump power. The seed was generated with a fiber oscillator, followed by a pulse picker, a pulse stretcher (5.4 ns; 1040 nm to 1053 nm), a spatial-light modulator, low-power fiber preamps, and a high-power 150-W fiber preamp. After heating-up and manual pre-alignment, the fine-alignment was done electronically. The combination efficiency was η_comb = 96%, the combined power P = 10.4 kW, the beam quality comparable with that of a single beam: M² = 1.2, the pulse length τ = 254 fs was close to transform-limited (248 fs), the power fluctuations < 0.6% (1 Hz–1 MHz; including the dither), the wall-plug efficiency η_opt = 20% [66]. This result represents the highest average power of an ultrafast laser system reported to date.

The other option for spatial beam combining is to arrange the collimated beams in a hexagonal array with a fill factor close to one ('tiled aperture' or 'phased array') and to image it into the far field with a single lens. The phase control can be done here individually by superimposing a small fraction of the near field distribution with its individual lasers with an expanded reference beam onto a camera or detector array. Further phase adjustments can be done by dithering the individual phases and monitoring the peak power in the far field [182]. With 61 fibers and a total far-field power of 10 W, a power of 5.2 W in the central peak was recently demonstrated. However, with a total power of 1 kW and a total pulse energy of 0.5 mJ in the far field, the fraction in the central lobe dropped initially to 19% and after one hour to 12%, probably due to thermal problems in the fiber/lens array [183]. By using diffractive optical elements (DOEs) in the near and/or far field, the fraction of power in the central peak can be increased, experimentally, to 80–90%, in principle, up to 100% [184].

The array can also be realized within one fiber by placing several cores in one pump cladding. Using a 4 × 4 array with large core-core spacing, pumped by 190 W, and beam-splitters for splitting/combining, a combined average power of 70 W with ps pulses, M² < 1.2, and a combining efficiency of 80% was demonstrated [185].

Using a MCF with a closely spaced ring of 6 LMA cores in an amplifier setup, an output power of 44 W at 1070 nm was demonstrated, limited by self-lasing at 1045 nm. Here, the in-phase supermode is favored by seeding with an appropriately expanded Gaussian beam as demonstrated before in [186]. The resulting central lobe contained 53% of the far-field power and had an M² of 1.3 and 1.6 along the two axis [187]. With a similar fiber in an oscillator setup, 115 W with 61% slope efficiency was achieved. The central lobe contained close to 70% of the total power and had an M² of 1.43. The in-phase supermode was favored by using a kind of Talbot resonator that produced differently strong feed-back for the supermodes depending on the spacing between fiber end and mirror [188]. Using such MCF with strong coupling and tiled-aperture combining greatly simplifies the optical setup and does not need an external phase control, but so far it seems to be difficult to exceed the (diffraction-limited) powers that can be achieved with a single-core fiber.

As mentioned above, CBC is not limited to fiber lasers as long as the individual lasers operate in single transverse mode or, in the case of strongly coupled lasers, in a well-defined supermode. Using two 40 × 1 mm² Yb:YAG rods, so-called single-crystal fibers, as booster amplifiers, a combining efficiency of 94% independent of the output power could be demonstrated after the combination with a polarizing beam splitter and filtering of one polarization state. With a pump power of 2 times 65 W from high-brightness pump laser diodes, 3-mJ 700-fs pulses with an average power of 14 W could be generated [34].

6.2 Divided pulse amplification (DPA)

Divided pulse amplification [161] uses the temporal splitting of a single pulse into N time-delayed replicas to reduce the pulse peak power. After amplification these replicas are then coherently recombined into a single pulse. This strategy is relatively similar to coherent beam combination but uses a temporal separation of the pulses instead of a spatial separation. Often the optical setup for splitting is used in reverse order for the recombination. Since no active stabilization is required in this case to ensure the pulse overlap, the technique is often referred to as “passive DPA”. Using this technique with a delay of 1 ns in a 15-mm-long,1-mm-thick end-pumped Yb:YAG SCF, after compression, pulses with 2.3 mJ and 520 fs at a repetition rate of 10 kHz without damage could be demonstrated [30].

Actively stabilized DPA (ADPA) in contrast uses separate splitting and combination stages, which allows for more control over the pulses being injected into the amplifier by using amplitude pre-shaping but requires an active phase stabilization. This is especially interesting for fiber amplifiers to mitigate effects of gain saturation on the shape of the DPA pulse train as demonstrated in [189]. Since the splitting in ADPA occurs in a sequential manner, the pulses cannot be pre-shaped completely individually, which results in a reduced combination efficiency for a large number of pulse replicas. This drawback was solved by electro-optically controlled DPA (EDPA) [190], which allows for phase and amplitude pre-shaping of the individual pulse to increase the combination efficiency. While active DPA schemes enable an effective reduction of the pulse peak power with the number of replicas, the complexity of the temporal recombination stage increases as well with number of pulses. The experimental implementation of this technique in a CBC-based high-power laser system is described in [191]. The combination of both techniques enabled a very high pulse energy of 23 mJ and an average power of 674 W. This result and some more results achieved by coherently combining the beams of some fiber and single-crystal fiber amplifiers and/or using DPA are summarized in Table 9.

Table 9 High-power ultrafast amplifiers with coherent beam combination

7 Conclusion and outlook

To better appreciate the advances, let us briefly look back again at the era of lamp-pumped high-power lasers. The wall-plug efficiency was in the order of 2–3%. Since the effective focal length of the thermally induced distortions was close to the length of the rods, several rods were arranged as a kind of lens chain in the resonator of multi-kW lasers. Fibers with a core diameter of 600 µm were used to transport the laser radiation, as used today for diode lasers with comparable power. With the high-power diode lasers becoming available as pump sources, the goal was then to achieve comparable or higher laser power with significantly higher efficiency and better beam quality. The proposed concepts, based on the quasi-three-level system of Yb³⁺-doped materials, and an extremely small active volume of 1 mm³/kW—the thin-disk laser and the fiber laser—at that time received some skepticism about their aspired scalability over 3 or 4 orders of magnitude. However, along with the progress of the pump diodes, this goal has been convincingly achieved within one decade with both, the disk and fiber laser concepts.

Nowadays, commercial cw disk and fiber lasers are offered with output powers in the high multi-kW range and beam parameter products in the range of 2–8 mm·mrad, see Table 10. Fiber lasers tend to be more compact, more efficient, are inherently fiber-coupled, and are optionally offered with diffraction-limited beam quality. The nonlinear effects, however, strongly limit the possible length of the passive transport fibers, since the length of the transport fiber adds up to the already long interaction length of the generate beam inside the fiber laser itself. For this reason, disk lasers of comparable performance can be operated with significantly longer transport fibers. And especially when the beam is to be used at different work stations, it has anyway to be coupled into different transport fibers by means of a free-space switch requiring that the diameter of the transport fiber is at least twice the diameter of the original (multi-mode) feed fiber. Disk lasers, additionally, are less sensitive to feedback (reflections) into the cavity because of the highly reflective output-coupler. In addition, this highly reflective output coupler in combination with the high intra-cavity power density allows for very efficient intra-cavity frequency doubling.

Table 10 Commercial disk, fiber, and Innoslab laser systems

When the development of the high-power disk and fiber lasers started, probably not many could envision kW-class lasers with picosecond pulses. Meanwhile, ultrashort-pulsed lasers with very high average powers in excess of 2 kW using the disk architecture and up to 1 kW using the fiber architecture were demonstrated. Additional coherent beam combining allowed to increase the average output power from a system of fiber lasers to 10 kW. An overview of the performance of lasers with respect to their laser architecture is given in Fig. 9 in terms of pulse energy, pulse duration, and peak power versus average power.

Commercial ultrafast lasers with an average power exceeding 1 kW have already become available in the last few years, see Table 10.

Comparing the performance of fiber, disk, and Innoslab systems reveals the characteristics of the respective architectures (Table 11):

• Fiber lasers offer excellent beam quality even at very high average power, as well as short pulse durations on the order of a few hundred femtoseconds. However, nonlinear effects restrict the pulse energy to moderate values even when sophisticated techniques such as CPA and DPA are used. Thanks to the waveguide structure, efficient coherent combination of several fiber lasers is facilitated, which enables state-of-the-art performances. As seen in Fig. 10, fiber lasers dominate the lower end of the pulse duration range. Coherently combined systems additionally dominate the higher end of the average powers but then usually lack significant pulse energy.

• Disk lasers usually emit longer pulses with durations on the order of 1 ps but offer advantages when targeting very high pulse energies as nonlinear effects are much less dominant than in the fiber. This enables comparatively simple designs, which only in extreme cases require CPA. However, operation at very high average power usually is accompanied by slight degradation of the beam quality. These characteristics are illustrated in Fig. 10, where a dominance of disk lasers at high pulse energies and average powers on the order of 1 kW is visible.

• Innoslab amplifiers offer a good compromise between the disk and fiber architecture, delivering high pulse energies at a moderate complexity (CPA required) with a sweet spot at average powers in the range of several hundred watts up to 1 kW.

Table 11 Strengths and weaknesses of fiber, Innoslab, and thin-disk amplifiers. Reproduced from [179]

Fig. 10

Performance of (single-emitter) fiber lasers (Fiber), Innoslab amplifiers (Slab), thin-disk oscillators (TDO), thin-disk regenerative oscillators (TDR), thin-disk multi-pass amplifiers (TDMPA), coherently combined lasers (CBC). The numbers in the figure correspond to the numbers of the corresponding references. The references [197,198,199,200,201,202,203,204] only appear in Fig. 10

With respect to ultrafast laser systems, Innoslab amplifiers can be advantageously combined with fiber MOPA systems to generate medium-energy seed pulses for thin-disk multipass (booster) amplifiers for average powers of the order of and above 1 kW and correspondingly increased pulse energies, see Table 11.

In addition to well-established industrial laser applications of high-power cw lasers as, e. g., welding and cutting, kilowatt-class ultrafast lasers open up a whole new range of industrial and scientific applications.

The ability of lasers to generate extremely high intensities is exploited in basic research, for example, to drive nonlinear effects to an extreme level to create or enhance radiation sources with exotic properties to enable new applications. As the efficiency of these nonlinear processes is low, high average-power laser sources are used to increase the flux of these sources. Lasers combining high average powers and high peak powers are therefore especially interesting for these applications. Such an application can be the generation of attosecond pulses, which then are used to study matter on atomic scales [212]. Another (future) promising application could be the miniaturization of particle-based radiation sources by making use of the high accelerating gradients of beam-driven wakefields [213]. These sources would enable a variety of applications in the medical [214] and material sciences [215].

Industrially interesting applications are focused on high-throughput and high-precision micromachining [145, 216, 217] as used for, e. g., structuring, drilling, fine-cutting of metals or cutting of transparent materials (e. g., glasses). As these processes required different laser parameters usually different types of lasers were used until now. To reduce investment costs, it is, therefore, obvious to ask whether all this can be realized with one and the same laser. In fact, the modular structure of passive high-power laser amplifiers is well suited to use the power booster in combination with a variety of seed lasers or a single seed laser with flexible parameters. This would enable the realization of a flexible laser, which can emit CW, pulsed, or ultrashort-pulsed laser beams at average powers in the order of beyond one kilowatt and therefore would be suited for most of today’s manufacturing processes. Together with an intelligent control and a suitable laser machine, such flexible laser sources provide the opportunity to develop comprehensively versatile material processing systems meeting the requirements to consistently fulfill the vision of the fourth industrial revolution ('industry 4.0') [218].