1 Introduction

Optical atomic magnetometers (OAMs) can be used to detect time dependent fields (TDF) that can be fast varying, disadvantageously oriented and not necessarily small. Several kinds of optical magnetometers reach their best performance when measuring weak and quasi-static fields. These systems are often modelled and analyzed under these conditions, and their behaviour in the above mentioned, more general case is scarcely discussed and investigated.

The possibility of measuring magnetic fields using optical pumping and probing of alkali atoms was pointed out more than 60 years ago, in the works of Dehmelt [1] and Bell and Bloom [2, 3]. In the late Sixties and Seventies, important further steps were carried out by the group of Cohen-Tannoudji [4, 5]. The mentioned works demonstrated the potential for high resolution magnetometry based on magneto-optical effects which were known since the historical observations described by Michael Faraday [6] in non-resonant high density materials, and by Macaluso and Corbino [7, 8], who observed the enhancement of the Faraday effect under resonant conditions in low density material (atomic media).

Advances in laser technology and in laser spectroscopy, in conjunction with intense studies on optical pumping processes [9, 10] prepared a revival of optical magnetometry at the beginning of this millennium [11]. The practicality and the potential of this research in applications, was induced by further technological advances, making available easy-to-use (reliable, low-cost, low-power, small size, highly tunable and stable) solid state laser sources, and high-quality atomic samples with long ground-state relaxation times. Many research groups contributed to this new phase of optical magnetometry, and a panoramic view of that recent history can be found in [12].

Optical magnetometers are developed for a variety of applications [13] including fundamental research [14,15,16], characterization of magnetic anomalies and of their dynamics in space-physics [17, 18], geology [19], archaeology [20, 21], material science e.g. to detect diluted magnetic nano- and micro-particles [22] or induced eddy currents [23,24,25,26] (with potential in medical applications, in detection of biomagnetism [27] or in building apparatuses for nuclear magnetic resonance (for spectroscopy or imaging) in the ultra-low-field [28,29,30,31] and zero-to-ultra-low field regimes [32, 33].

Among the most attractive characteristics of OAMs is their robustness and the possibility of pushing to extreme levels many crucial parameters such as sensitivity, size, minimal power consumption, bandwidth, long-term operativity, etc. The high sensitivity of atomic magnetometers relies on the fact that light near-resonant with an optical transition may create long-lived magnetization in the atomic ground state that subsequently evolves under the effect of the magnetic field that is being measured. This precession in turn modifies the optical properties of the atomic medium, and can be detected by absorption and/or polarimetric measurements performed on a probe radiation propagated through the medium itself.

Regardless of the quantum or the classical approach to the problem, the evolution of a spin precessing in a magnetic field is well described by the Larmor equations, or by the Bloch equations when spin relaxation processes play an important role. This magnetic-resonance picture is actually the framework in which the spin dynamics in OAM can be described.

When dealing with time-dependent fields, the problem is often considered in the resonant regime, when a field component oscillates at the Larmor frequency (this is the case of radio-frequency magnetometers [34]). Other studies, concerning fast oscillating fields, consider the magnetic dressing phenomena, which address configurations with a strong field that oscillates at frequencies largely above the Larmor one. At the other extreme, the quasi-stationary regime is analyzed (e.g. in the case of light-modulated OAMs), which let detect slow and extremely weak field variations.

When considering a quasi-static TDF \(\mathbf {b}\) much weaker than the static field \(\mathbf {B}_L\) to which it is superimposed, the scalar nature of OAM makes them responsive only to the TDF component along the direction of the static field

The high sensitivity of OAM makes indeed these detectors excellent tools to detect very slow and extremely weak TDFs. The weak- and low-frequency field approximation is often implicitly assumed [35, 36]: the dynamic response to stronger, generically oriented and/or non quasi-static TDF remains overlooked. Only few works address operating conditions with TDF not necessarily small, with fast dynamics and generic orientation [35, 37], and this investigation—with emphasis to the system response—is at the focus of the present work.

If we consider a Bell and Bloom magnetometer driven at resonance, a slight change of the magnetic field modulus will bring the device to a near-resonant regime, with a correspondent new (near-resonant) steady state characterized by smaller and dephased atomic magnetization. However, we are not dealing with a linear time-invariant (LTI) system forced by a signal initially resonant and then out-of-resonance. The magnetometer should be rather regarded (see also the appendix in Ref. [38]) as a parametric system forced by a stationary term. Despite the inherent similarity at the steady state, the transient response of such a system cannot be studied in terms of a damped-forced (LTI) device.

Parametric systems are used in a variety of sensors e.g. for nanoscale mass and acceleration detectors [39], solid state gyroscopes [40], micropositioning [41]. In some cases instabilities of parametric oscillators can be used to sustain the sensor [42], which is viable technique when the equation ruling the dynamics makes it possible to provide the system with energy from the parameter modulation. This is the case of many parametric oscillators, but it is not a general feature and does not apply to the particular case of precessing spins. The dynamic response of a parametric system to the parameter(s) variation depends strictly on its nature and requires a dedicated analysis of the equations that rule its dynamics.

This work provides an accurate description of the dynamical behaviour of spins precessing in a TDF. Similarly to the case of Ref. [43], a Bell and Bloom magnetometer is considered as a test of the developed model, under conditions in which the driving field \(\mathbf {B}\) changes in time with TDF components both parallel and transverse with respect to the static (bias) term. The field is assumed to vary not necessarily slowly and by small but not necessarily vanishing amounts. Differing from Ref. [43], which reports a numerical study, in the Sect. 2 we develop an analytic perturbative model to evaluate the response of such system to TDFs.

In Sect. 3 we describe an experimental setup, where a weak synchronous optical pumping acting on an atomic vapour compensates the relaxation phenomena, rendering the evolution of the sample magnetization adequately described by the Larmor precession equation. Section 4 reports a quantitative analysis and experimental tests of the main outputs of the model. A synthesis of the main findings is finally drawn in Sect. 5.

2 Model

Table 1 Symbols
Full size table

The starting point in modeling of the spin response is the Larmor equation for the magnetization vector

$$\begin{aligned} \dot{\mathbf {M}} = - \Gamma \mathbf {M} + \gamma \mathbf {B}(t) \times \mathbf {M} + \mathbf {f}(t) \end{aligned}$$
(1)

where \(\gamma\) is the gyromagnetic factor and \(\mathbf {f}(t)\) represents the action of the circularly polarized pump radiation and it is modeled as a forcing term (a list of symbol definitions is reported in Table 1). The total magnetic field \(\mathbf {B}\) is composed of a large static one \(\mathbf {B}_L\) (bias field) perpendicular to the pump radiation wavevector and a small TDF \(\mathbf {b}(t)\). A simplified isotropic decay mechanism (\(- \Gamma \mathbf {M}\)) is included. This is a well justified approximation as discussed in [44]. Fixing the axis in such a way that the x axis is along the pump and the y axis is along the bias field \(\mathbf {B}_L\) one obtains the equations

$$\begin{aligned} {\dot{M}}_{+}&= - \Gamma M_{+} - i ( \omega _L + \omega _2(t) ) M_{+} + ( i \omega _1(t) - \omega _3(t) ) M_2 + f(t) \end{aligned}$$
(2a)
$$\begin{aligned} {\dot{M}}_{-}&= - \Gamma M_{-} + i ( \omega _L + \omega _2(t) ) M_- - ( i \omega _1(t) + \omega _3(t) ) M_2 + f(t) \end{aligned}$$
(2b)
$$\begin{aligned} {\dot{M}}_{2}&= - \Gamma M_{2} + \frac{1}{2}( i \omega _1(t) + \omega _3(t) ) M_+ -\frac{1}{2}( i \omega _1(t) - \omega _3(t) ) M_- \end{aligned}$$
(2c)

where \(\omega _L = \gamma B_L\) is the Larmor frequency associated at the static field, \(\omega _i(t) = \gamma b_i(t)\), and \(M_{\pm } = M_x \pm i M_z\), \(M_2 = M_y\). These equations must be solved in the regime of \(\omega _i(t) \ll \omega _L\), which can be rewritten in matrix form as

$$\begin{aligned} \begin{aligned} \dot{\mathbf {M}}&= - \Gamma \mathbf {M} + \begin{pmatrix} - i \omega _L &{} 0 &{} 0 \\ 0 &{} i \omega _L &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix} \mathbf {M} \\& \phantom{=}+ \epsilon \begin{pmatrix} - i \omega _2 &{} 0 &{} i \omega _+ \\ 0 &{} i \omega _2 &{} -i\omega _- \\ i \omega _-/2 &{} -i \omega _+/2 &{} 0 \end{pmatrix} \mathbf {M} + f(t)\begin{pmatrix} 1\\ 1\\ 0 \end{pmatrix} \\&= - \Gamma \mathbf {M} + ( A_0 + \epsilon A_1(t) ) \mathbf {M} + f(t) \mathbf {u} \end{aligned} \end{aligned}$$
(3)

here we have slightly redefined the magnetization as \(\mathbf {M} = ( M_+, M_-, M_2)\) and introduced \(\omega _{\pm }(t) = \omega _1(t) \pm i \omega _3(t)\). The parameter \(\epsilon\) is just a bookkeeping device for the perturbation theory. In fact writing \(\mathbf {M}= \mathbf {M}^{(0)}+ \epsilon \mathbf {M}^{(1)}+ \epsilon ^2 \mathbf {M}^{(2)}+ \cdots\) we have

$$\begin{aligned} \dot{ \mathbf {M} }^{(0)}&= - \Gamma \mathbf {M}^{(0)}+ A_0 \mathbf {M}^{(0)}+ \mathbf {u} f(t) \end{aligned}$$
(4a)
$$\begin{aligned} \dot{ \mathbf {M} }^{(1)}&= - \Gamma \mathbf {M}^{(1)}+ A_0 \mathbf {M}^{(1)}+ A_1(t) \mathbf {M}^{(0)}\end{aligned}$$
(4b)
$$\begin{aligned} \dot{ \mathbf {M} }^{(2)}&= - \Gamma \mathbf {M}^{(2)}+ A_0 \mathbf {M}^{(2)}+ A_1(t) \mathbf {M}^{(1)}\end{aligned}$$
(4c)

The steady-state solution for \(\mathbf {M}^{(0)}\)can be obtained noticing that the function f(t) is a real and periodic function (whose exact form is not important as it is shown below) which represents the modulated pumping

$$\begin{aligned} f(t) = \sum _n f_n {{\,\displaystyle\mathrm{ e}\,}}^{ i n \omega t} \end{aligned}$$
(5)

here \(\omega\) (\(\approx \omega _L\) in the experiment) is the frequency modulation of the pumping laser. With standard methods one finds

$$\begin{aligned} \mathbf {M}^{(0)}= \sum _n f_n \; \frac{1}{ \Gamma - A_0 + i n \omega } \mathbf {u} \; {{\,\displaystyle\mathrm{e}\,}}^{i n \omega t} \approx \begin{pmatrix} \frac{f_{-1}}{\Gamma + i\; \delta } {{\,\displaystyle\mathrm{e}\,}}^{- i \omega t} \\ \frac{f_{1}}{\Gamma - i \;\delta } {{\,\displaystyle\mathrm{e}\,}}^{ + i \omega t} \\ 0 \end{pmatrix} \end{aligned}$$
(6)

where \(\delta = \omega _L - \omega\) is the Larmor detuning and the second approximated form is obtained retaining only the resonant terms from the first. This solution represents the steady state magnetization due to the bias field \(\mathbf {B}_L\) only.

The quantity experimentally monitored is the phase of x component of the magnetization, that is if we write

$$\begin{aligned} M_+(t) = a(t){{\,\displaystyle\mathrm{e}\,}}^{i \varphi (t)} {{\,\displaystyle\mathrm{e}\,}}^{-i \omega t} \end{aligned}$$
(7)

then \(\varphi (t)\) is observed in the experiment. Accordingly with the perturbation theory we can write

$$\begin{aligned} \varphi (t)&= \varphi _0 + \epsilon \varphi _1(t) + \epsilon ^2 \varphi _2(t) + \cdots \end{aligned}$$
(8a)
$$\begin{aligned} a(t)&= a_0 + \epsilon a_1(t) + \epsilon ^2 a_2(t) + \cdots \end{aligned}$$
(8b)

Using (6) it follows that \(a_0 = |f_{-1}/(\Gamma + i \delta )|\) and \(\varphi _0 = \arg (f_{-1}/(\Gamma + i\delta ))\) which is not interesting because it is just an offset in the experimental signal.

2.1 First order solution

Substituting (6) into (4) the steady-state first order solution is found:

$$\begin{aligned} \mathbf {M}^{(1)}= {{\,\displaystyle\mathrm{e}\,}}^{-(\Gamma - A_0)t}\int _0^t {{\,\displaystyle\mathrm{e}\,}}^{(\Gamma - A_0)t'} A_1(t') \mathbf {M}^{(0)}(t') {{\,\displaystyle\mathrm{d}\,}}t' \end{aligned}$$
(9)

and due to the diagonal form of the \(A_0\) matrix the detailed expressions are

$$\begin{aligned} M_+^{(1)}&= -i \frac{f_{-1}}{\Gamma + i \delta } {{\,\displaystyle\mathrm{e}\,}}^{-(\Gamma + i \omega _L)t}\int _0^t {{\,\displaystyle\mathrm{e}\,}}^{(\Gamma + i \omega _L - i \omega )t'} \omega _2(t') {{\,\displaystyle\mathrm{d}\,}}t' \end{aligned}$$
(10a)
$$\begin{aligned} M_-^{(1)}&= ( M_+^{(1)} ) ^* \end{aligned}$$
(10b)
$$\begin{aligned} M_2^{(1)}&= \frac{i}{2} \frac{f_{-1}}{\Gamma + i \delta } {{\,\displaystyle\mathrm{e}\,}}^{-\Gamma t}\int _0^t {{\,\displaystyle\mathrm{e}\,}}^{(\Gamma - i \omega )t'} \omega _-(t') {{\,\displaystyle\mathrm{d}\,}}t' \\& \phantom{=}- \frac{i}{2} \frac{f_{1}}{\Gamma - i \delta } {{\,\displaystyle\mathrm{e}\,}}^{-\Gamma t}\int _0^t {{\,\displaystyle\mathrm{e}\,}}^{(\Gamma + i \omega )t'} \omega _+(t') {{\,\displaystyle\mathrm{d}\,}}t' . \end{aligned}$$
(10c)

From

$$\begin{aligned} \begin{aligned} M_+&\approx M_+^{(0)} + \epsilon M_+^{(1)} \\&=\frac{f_{-1}}{\Gamma + i \delta }{{\,\displaystyle\mathrm{e}\,}}^{-i \omega t} \left[ 1 - i \epsilon {{\,\displaystyle\mathrm{e}\,}}^{-(\Gamma + i \delta )t}\int _0^t {{\,\displaystyle\mathrm{e}\,}}^{(\Gamma + i \delta )t'} \omega _2(t') {{\,\displaystyle\mathrm{d}\,}}t' \right] \end{aligned} \end{aligned}$$
(11)

and using the relations

$$\begin{aligned} \arg \left[ z_0 ( 1 + \epsilon u_1 + \epsilon ^2 u_2) \right]&= \arg (z_0) + \mathrm {Im}(u_1) \epsilon + \mathrm {Im}( u_2 - u_1^2/2) \epsilon ^2 + \cdots \end{aligned}$$
(12a)
$$\begin{aligned} \left| z_0 ( 1 + \epsilon u_1 + \epsilon ^2 u_2) \right|&= |z_0| \bigg[ 1 + \mathrm {Re}(u_1) \epsilon \\ & \phantom{====} + \bigg( \mathrm {Re}(u_2) + \frac{|u_1|^2 - \mathrm {Re}(u_1)^2}{2} \bigg) \epsilon ^2 + \cdots \bigg] \end{aligned}$$
(12b)

one obtains

$$\begin{aligned} u&= - i {{\,\displaystyle\mathrm{e}\,}}^{-(\Gamma + i \delta )t}\int _0^t {{\,\displaystyle\mathrm{e}\,}}^{(\Gamma + i \delta )t'} \omega _2(t') {{\,\displaystyle\mathrm{d}\,}}t' \end{aligned}$$
(13a)
$$\begin{aligned} a_1(t)&= a_0 \mathrm {Re}( u) \end{aligned}$$
(13b)
$$\begin{aligned} \varphi _1(t)&= \mathrm {Im}( u ) = - \int _0^t {{\,\displaystyle\mathrm{e}\,}}^{-\Gamma ( t - t')} \cos ( \delta (t - t') ) \; \omega _2(t') {{\,\displaystyle\mathrm{d}\,}}t' \end{aligned}$$
(13c)

This result shows that the phase does not depend on the specific form of the pumping signal. In fact, the \(f_{\pm 1}\) coefficients do not appear in Eq. 13c. The same equation shows that the monitored phase can be obtained as a convolution between the “longitudinal” TDF \(\omega _2(t)\) and \({{\,\displaystyle\mathrm{e}\,}}^{-\Gamma t} \cos (\delta t)\), or, in other words \(\omega _2(t)\) and \(\varphi _1(t)\) can be thought as the input and output of a linear system with transfer function

$$\begin{aligned} T(s) = -\frac{s + \Gamma }{ (s+\Gamma )^2 + \delta ^2} = -\frac{1}{2} \left( \frac{1}{s + \Gamma - i \delta } + \frac{1}{s + \Gamma + i \delta } \right) \end{aligned}$$
(14)

Moreover to this perturbative order the spin response is driven only by the component of the small magnetic field parallel to the large bias. In the limit \(\delta \approx 0\), the expression for \(\varphi _1\) agrees with that reported in [44, 45].

For instance, for a sinusoidal field \(\omega _2(t) = w \cos ( \Omega t + \Phi )\) one obtains

$$\begin{aligned} \varphi _1(t) & = -\frac{w}{2} \left[ \frac{1}{[\Gamma ^2 + ( \delta + \Omega )^2]^{1/2}} \cos ( \Omega t + \Phi - \psi _+) + \right. \\ &\phantom{= -\frac{w}{2}} \left.\;\; \frac{1}{[\Gamma ^2 + ( \delta - \Omega )^2]^{1/2}} \cos ( \Omega t + \Phi + \psi _-) \right] \qquad t \gg 1/\Gamma \end{aligned}$$
(15)

where \(\psi _{\pm } = \arctan ( (\delta \pm \Omega )/\Gamma )\), which shows as the monitored phase is composed of two quantities oscillating at the same frequency, but with different amplitudes and phases.

2.2 Second order solution

The first order solution does not depend on the TDF component orthogonal to the bias field and one has to go one step further in the perturbative expansion which is not difficult in principle, but the algebra becomes quickly a burden, thus we introduce a simplifying hypothesis very close to the experiment. Let’s assume that the TDF corresponds to \(\omega _i(t)\) in the form

$$\begin{aligned} \omega _i(t) = \sum _k c_{i,k} {{\,\displaystyle\mathrm{e}\,}}^{i \Omega _{i,k} t} \qquad \Omega _{i, -k} = - \Omega _{i,k} \;\;\; c_{i,-k} = c_{i,k}^* \end{aligned}$$
(16)

and the frequencies satisfy \(\Omega _{i,k} \ll \omega\) (in the experiment \(\omega / 2 \pi \sim 10 \, \mathrm {kHz}\) range while \(\Omega _{i,k} / 2\pi \sim 100\) Hz range). With these assumptions we have for \(t \gg 1/\Gamma\)

$$\begin{aligned} M_+^{(1)}&= -i \frac{f_{-1}}{\Gamma + i \delta } {{\,\displaystyle\mathrm{e}\,}}^{-i \omega t} \sum _k \frac{c_{2,k}}{\Gamma + i \delta + i\Omega _{2,k}} {{\,\displaystyle\mathrm{e}\,}}^{i \Omega _{2,k}t} = W(t) {{\,\displaystyle\mathrm{e}\,}}^{-i \omega t} \end{aligned}$$
(17a)
$$\begin{aligned} M_2^{(1)}&= Z(t) {{\,\displaystyle\mathrm{e}\,}}^{-i \omega t } + Z^*(t) {{\,\displaystyle\mathrm{e}\,}}^ {i \omega t} \end{aligned}$$
(17b)
$$\begin{aligned} Z(t)&= \frac{1}{2} \frac{f_{-1}}{\Gamma + i \delta } \sum _k \left[ \frac{c_{3,k}}{\Gamma - i \omega + i \Omega _{3,k}} {{\,\displaystyle\mathrm{e}\,}}^{i \Omega _{3,k} t} + \frac{ i c_{1,k}}{\Gamma - i \omega + i \Omega _{1,k}} {{\,\displaystyle\mathrm{e}\,}}^{i \Omega _{1,k} t} \right] \end{aligned}$$
(17c)

where the functions Z(t) and W(t) change on a much slower timescale with respect to \({{\,\displaystyle\mathrm{e}\,}}^{\pm i \omega t}\).

Writing \(M_+^{(2)} = V(t) {{\,\displaystyle\mathrm{e}\,}}^{-i \omega t}\), the equation to solve reads as

$$\begin{aligned} \begin{aligned} {\dot{V}}&= -( \Gamma + i \delta ) V - i \omega _2 W + ( i \omega _1 - \omega _3) (Z + Z^*{{\,\displaystyle\mathrm{e}\,}}^{2i\omega t}) \\&\approx -( \Gamma + i \delta ) V - i \omega _2 W + ( i \omega _1 - \omega _3) Z , \end{aligned} \end{aligned}$$
(18)

where the neglected term is a fast oscillating quantity. The solution for \(t \gg 1/\Gamma\) is

$$\begin{aligned} V = \frac{1}{2} \frac{f_{-1}}{\Gamma + i \delta } ( v_1 + v_2 + v_3 + v_4 ) , \end{aligned}$$
(19)

where

$$\begin{aligned} v_1&= \sum _{k, k'} \frac{ -2 c_{2,k} c_{2,k'}}{(\Gamma + i\delta +i \Omega _{2,k}) (\Gamma + i\delta +i \Omega _{2,k'})} {{\,\displaystyle\mathrm{e}\,}}^{i (\Omega _{2,k} + \Omega _{2,k'}) t} \end{aligned}$$
(20a)
$$\begin{aligned} v_2&= \sum _{k, k'} \frac{ - c_{3,k} c_{3,k'}}{(\Gamma - i\omega +i \Omega _{3,k}) (\Gamma + i\delta +i (\Omega _{3,k} + \Omega _{3,k'}) )} {{\,\displaystyle\mathrm{e}\,}}^{i (\Omega _{3,k} + \Omega _{3,k'}) t} \end{aligned}$$
(20b)
$$\begin{aligned} v_3&= \sum _{k, k'} \frac{ - c_{1,k} c_{1,k'}}{(\Gamma - i\omega +i \Omega _{1,k}) (\Gamma + i\delta +i (\Omega _{1,k} + \Omega _{1,k'}) )} {{\,\displaystyle\mathrm{e}\,}}^{i (\Omega _{1,k} + \Omega _{1,k'}) t} \end{aligned}$$
(20c)
$$\begin{aligned} v_4&= \sum _{k, k'} \frac{ (\Omega _{3,k'} - \Omega _{1,k}) c_{1,k} c_{3,k'}}{(\Gamma - i\omega +i \Omega _{1,k})(\Gamma - i\omega +i \Omega _{3,k'}) (\Gamma + i\delta +i (\Omega _{1,k} + \Omega _{3,k'}) )} {{\,\displaystyle\mathrm{e}\,}}^{i (\Omega _{1,k} + \Omega _{3,k'}) t} \end{aligned}$$
(20d)

Using again the Eq. 12, after some algebra we find the second order phase

$$\begin{aligned} \varphi _2(t) = \mathrm {Im}\left( \frac{v_1}{4} + \frac{v_2 + v_3 + v_4 }{2} \right) . \end{aligned}$$
(21)

A close inspection shows that the \(v_1\) term “doubles” and mixes the frequencies present in y component of the small field (i.e. the TDF component along the bias field). A similar behaviour is observed in the terms \(v_2\) and \(v_3\): they double and mix the frequencies of TDF components along the z and x directions, respectively. Only the \(v_4\) term gives rise to frequencies mixing among orthogonal TDF components, and noticeably involves only x and z terms: no mixing occurs between transverse and longitudinal TDFs.

Notice also that, thanks to the structure of the denominators, in the regime \(\delta \approx 0\) the \(v_1\) term is greater than the others. Moreover the \(v_2\) and \(v_3\) terms depend on the modulation frequency approximately as \(1/\omega\) and the cross-component mixing term is furtherly depressed, being \(v_4 \sim 1/\omega ^2\).

Workable expressions can be obtained in the case of single frequency TDF applied along each axis. Substituting \(\omega _i(t) = w_i \cos ( \Omega _i t + \Phi _i) = ( w_i{{\,\displaystyle\mathrm{e}\,}}^{i \Phi _i} \; {{\,\displaystyle\mathrm{e}\,}}^{i \Omega _i t } + w_i{{\,\displaystyle\mathrm{e}\,}}^{-i \Phi _i} \; {{\,\displaystyle\mathrm{e}\,}}^{-i \Omega _i t })/2\) in Eq. 20 one obtains, for instance:

$$\begin{aligned} v_1 = -\frac{w_2^2}{2}\left( \frac{{{\,\displaystyle\mathrm{e}\,}}^{-2 i (\Omega _2 t + \Phi _2)}}{(\Gamma + i \delta - i \Omega _2)^2} + \frac{{{\,\displaystyle\mathrm{e}\,}}^{2 i (\Omega _2 t + \Phi _2)}}{(\Gamma + i \delta +i \Omega _2)^2} + \frac{2}{(\Gamma + i \delta )^2 + \Omega _2^2} \right) , \end{aligned}$$
(22)

which produces a peak at \(\Omega = 2 \Omega _2\) in the square modulus of the Fourier transform of \(\varphi _2(t)\):

$$\begin{aligned} | {\hat{\varphi }}_2( \Omega = 2\Omega _2) |^2 = \frac{w_2^4}{4} (\Gamma ^2 + \Omega _2^2)\; \frac{\delta ^2}{(\Gamma ^2 + (\delta -\Omega _2)^2)^2 (\Gamma ^2 + (\delta +\Omega _2)^2)^2}. \end{aligned}$$
(23)

Similarly,

$$\begin{aligned} | {\hat{\varphi }}_2( \Omega = 2\Omega _{1,3}) |^2 = \frac{w_{1,3}^4}{16} \frac{ \Gamma ^2 + 4 \Omega _{1,3}^2}{(\Gamma ^2 + (\delta -2\Omega _{1,3})^2) (\Gamma ^2 + (\delta +2\Omega _{1,3})^2)} \frac{1}{\omega ^2} + O( \frac{1}{\omega ^3}) \end{aligned}$$
(24)

and, defining \(\Omega _\pm =|\Omega _1\pm \Omega _3|\),

$$\begin{aligned} | {\hat{\varphi }}_2 ( \Omega = \Omega _{\pm }) |^2 = \frac{w_3^2 w_1^2}{16} \frac{\Omega _{\mp }^2 (\Gamma ^2 + \Omega _{\pm }^2 )}{( \Gamma ^2 + ( \delta - \Omega _{\pm })^2) ( \Gamma ^2 +( \delta + \Omega _{\pm })^2) } \frac{1}{\omega ^4} + O( \frac{1}{\omega ^5}). \end{aligned}$$
(25)

A quantity more relevant for comparison with experimental results is the square-amplitude ratio among sum-frequency and difference-frequency terms:

$$\begin{aligned} R=\frac{\Omega _+^2 (\Omega _-^2+\Gamma ^2) [\Gamma ^2+(\delta -\Omega _+)^2][\Gamma ^2+(\delta +\Omega _+)^2]}{\Omega _-^2 (\Omega _+^2+\Gamma ^2) [\Gamma ^2+(\delta -\Omega _-)^2][\Gamma ^2+(\delta +\Omega _-)^2]}, \end{aligned}$$
(26)

.

The Eqs. 23, 25 and 26 describe quadratic terms which scale differently with \(\omega\). The second harmonic response to TDF component along the bias field (Eq. 23) vanishes at \(\delta =0\), but does not scale with \(\omega\) and hence easily exceeds the others (Eq. 24) out of this condition. In contrast, being \(\omega \gg \Omega _{1,3}, \Gamma\) the cross-component mixing term described by the Eq. 25 is extremely weak compared to both the \(2\Omega _2\) and to the \(2\Omega _{1,3}\) terms.

2.2.1 Not exactly orthogonal fields

Suppose that the TDF applied transversely to the bias field are not exactly orthogonal to each other, but there is some tilting \(\delta \theta = \theta _1+\theta _3\). In formula

$$\begin{aligned} \omega _1(t)&= w_1 \cos (\Omega _1 t + \Phi _1) \cos \theta _1 + w_3 \cos (\Omega _3 t + \Phi _3) \sin \theta _3 \end{aligned}$$
(27)
$$\begin{aligned} \omega _3(t)&= w_1 \cos (\Omega _1 t + \Phi _1) \sin \theta _1 + w_3 \cos (\Omega _3 t + \Phi _3) \cos \theta _3 \end{aligned}$$
(28)

the previous result (Eq. 25) generalizes to

$$\begin{aligned} | {\hat{\varphi }}_2 ( \Omega = \Omega _{\pm }) |^2 = \frac{w_3^2 w_1^2}{32} \frac{\Omega _{\mp }^2 (\Gamma ^2 + \Omega _{\pm }^2 )(1 + \cos (2\theta _1 +2 \theta _3) )}{( \Gamma ^2 + ( \delta - \Omega _{\pm })^2) ( \Gamma ^2 +( \delta + \Omega _{\pm })^2) } \frac{1}{\omega ^4} + O( \frac{1}{\omega ^5}) \end{aligned}$$
(29)

while another mixing term appears:

$$\begin{aligned} | {\hat{\varphi }}_2 ( \Omega = \Omega _{\pm }) |^2 = \frac{w_3^2 w_1^2}{32} \frac{ (\Gamma ^2 + \Omega _{\pm }^2 )(1 - \cos (2\theta _1 +2 \theta _3) )}{( \Gamma ^2 + ( \delta - \Omega _{\pm })^2) ( \Gamma ^2 +( \delta + \Omega _{\pm })^2) } \frac{1}{\omega ^2} + O( \frac{1}{\omega ^3}). \end{aligned}$$
(30)

The latter scales with a lower power of \(1/\omega\) so that it may become easily dominant, also for small \(\delta \theta\) values. Interestingly, taking into account the mixing terms (Eq. 30), the ratio \(R^\prime\) does not depend on \(\delta \theta\) and reads

$$\begin{aligned} R^\prime =\frac{(\Omega _-^2+\Gamma ^2) [\Gamma ^2+(\delta -\Omega _+)^2][\Gamma ^2+(\delta +\Omega _+)^2]}{(\Omega _+^2+\Gamma ^2) [\Gamma ^2+(\delta -\Omega _-)^2][\Gamma ^2+(\delta +\Omega _-)^2]} \end{aligned}$$
(31)

that differs from R only for the factor \(\Omega _+^2/\Omega _-^2\).

3 Experimental setup

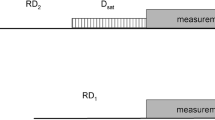
The dynamics of atomic spins precessing in a TDF is experimentally studied by means of one channel of the multi-channel Bell and Bloom magnetometer described in Ref. [44]. Basic information of the device is here summarized in Fig. 1.

Fig. 1
figure 1

Schematics of the magnetometer. Two laser sources (\(D_1L\) and \(D_2L\)) produce pump and probe radiations, at different wavelengths, which are combined (Mix) and coupled to a polarization maintaining fiber PMF. The \(D_1L\) wavelength is broadly modulated at \(\omega\) and maintained at milliwatt level, while \(D_2L\) is unmodulated and attenuated (Att) down to microwatt level. At the PMF output, a lens (L) collimates the radiation on a 10 mm diameter beam, whose polarization is reinforced by a polarizer (pol) and modified by a multi-order waveplate (WP). The latter renders the pump radiation circularly polarized while leaving the probe radiation linearly polarized. After the interaction with the atomic sample (Cs) the pump light is blocked by an interference filter (IF), and the probe polarization is analyzed by a balanced polarimeter made by a Wollaston prism (W) and a pair of silicon photodetectors (PD). The photocurrent imbalance is converted to a voltage signal by a transimpedance amplifier (TIA), to be acquired by a 16 bit 500 kS/s card for subsequent numerical elaboration. The Cs cell is in a magnetic field composed by a large static \(\mathbf {B}_L\) transverse to the laser beam and by a weaker, generically oriented, time dependent term \(\mathbf {b}\)

Full size image

Beside a self-oscillating mode [46, 47] not relevant for the scopes of this work, the magnetometer can be used under scan or forced modes. In the first case, the angular frequency \(\omega\) of the pump laser modulation is scanned around the atomic magnetic resonance, to characterize center, amplitude, width and shape of the resonance itself, while in the forced mode, the modulation is set at a (near) resonant frequency, and TDF is detected via the phase shifts induced in the polarimetric signal. The measurements described in this paper are obtained in the forced mode, after having run the system in the scan mode to determine the resonant modulation frequency and the resonance width \(\Gamma\).

The sensor is operated in a magnetically unshielded environment, where the Earth field is partially compensated by means of three mutually orthogonal Helmholtz coils. Additional coils complete the setup to apply variously oriented TDF that are normally used for the manipulation of atomic spins [31, 48, 49].

A solenoid surrounding the atomic cells is used to apply a homogeneous TDF along the propagation direction of the laser beams (x). Helmholtz pairs or far located dipoles are used to produce TDF components along the static field (y) and in the other perpendicular direction (z). These TDF sources can be supplied by RF generators configured as voltage generators with series resistors. The frequencies of the applied signals are low enough to make the inductive nature of the loads negligible. A simplified calibration is performed for each field source under magnetostatic conditions to determine the voltage-to-field conversion coefficients. The complete control of static and time-dependent field components enables the analysis of the system response at the focus of the present work.

4 Discussion

4.1 First-order approximation

The perturbative approach presented in Sect. 2 confirms that the response to small and quasi-static (\(\Omega \ll \Gamma\)) TDF is consistent with the approximation anticipated in the Introduction for weak and quasi-static TDF and extends the analysis to the case of TDF lower than \(\omega _L/\gamma\), but with a dynamics non-necessarily slower than \(\Gamma\) (i.e. not quasi-static). In other words, it is only required that the TDF is much weaker than the bias field. When this condition is strictly fulfilled (i.e. the TDF is extremely weak), the first perturbation order is sufficient to describe the system behaviour, and it shows that the system is still responsive to the longitudinal TDF component only. Additionally, in the first-order approximation the dynamics of the precessing spins can be described in terms of Eq. 14, referring to the notation commonly used for linear systems, despite the parametric nature of the problem.

At the steady state (\(s=i \Omega\)), the mentioned response function reads:

$$\begin{aligned} T( \Omega ) = -\frac{1}{2} \left( \frac{1}{ \Gamma + i (\Omega -\delta )} + \frac{1}{ \Gamma + i (\Omega +\delta )} \right) , \end{aligned}$$
(32)

which for \(\delta =0\), corresponds to the response of a 1-st order Butterworth low pass filter (the same as an RC circuit) [50, 51], while for non-zero values of \(\delta\) (particularly for \(|\delta | \gg \Gamma\)) the system responds as a bandpass filter approximately centered at \(\delta\).

Fig. 2
figure 2

Theoretical Bode plot of the first order response

Full size image

An interesting feature is obtained under an intermediate condition (\(\delta \approx \Gamma /2\)), which produces a nearly flat response up to a cut-off frequency set by \(\Gamma /2\) itself. Such extended flat bandwidth is obtained at expenses of a slight reduction of the response amplitude, if compared to the \(\delta =0\) case. Similarly, the condition \(\delta = \Gamma\) leads to a maximally extended constant-phase response. Figure 2 summarizes these aspects showing the theoretical Bode plot corresponding to the Eq. 32, for four relevant values of \(\delta\). Both the extended flat gain (\(\delta \approx \Gamma /2\)) and the extended flat phase (\(\delta \approx \Gamma\)) conditions can be of interest in magnetometric applications, e.g. in the detection of magnetic signals with spectral components which range from zero to (about) \(\Gamma\) or when the magnetometric signal is used to feed a closed-loop system for active field stabilization [52, 53].

Fig. 3
figure 3

Amplitude of the first order response, for different values (\(\delta /\Gamma\) increases in steps of 1/2) of the detuning \(\delta\). For large \(\delta\) the response has a maximum at \(\Omega _M \approx \delta\) and noticeably these maxima converge to the asymptotic value \(1/(2\Gamma )\) differing from the case \(\delta =0\) for which a low-pass (\(|T|\rightarrow 0\)) response is found. Notice that the maxima are higher than the low-pass curve (blue thick line)

Full size image

Finally, the large \(\delta\) regime can be of interest in applications that need an enhancement of the response to TDF oscillating at frequencies around \(\delta\).

As said, for small values of \(\delta\) the response modulus |T| is a monotonically decreasing function of \(\Omega\). Then, for \(\delta /\Gamma > \left( \sqrt{5}-2\right) ^{1/2} \approx 1/2\), |T| has a maximum located at \(\Omega _M=\left( \sqrt{\delta ^4+4\delta ^2\Gamma ^2}- \Gamma ^2\right) ^{1/2}\), which turns to \(\Omega _M \approx |\delta |\) if \(\delta \gg \Gamma\), i.e. when the band-pass regime occurs. The maximum value of |T| (let it be \(T_M\)) is

$$\begin{aligned} T_M^2 =\frac{1}{8 \Gamma ^2}\left( 1+\sqrt{1+\frac{4 \Gamma ^2}{\delta ^2}}\right) , \end{aligned}$$
(33)

which for large values of \(\delta\) (and hence for large \(\Omega _M\)) does not decrease to zero (as in the case of \(\delta =0\)), but approaches an asymptotic value \(1/(2\Gamma )\). Notice that in the band-pass regime the response obtained for \(\Omega \approx \delta\) exceeds the response for the same \(\Omega\) in the low-pass regime. This behaviour is summarized in Fig. 3, where a set of curves \(T(\Omega )\) corresponding to different detuning \(\delta\) are plotted together with the enveloping curve described by Eq. 33. The possibility of operating in a band-pass regime, with maximal system response centered at a selectable frequency has an evident relevance in magnetometric applications where narrowband signals must be detected. As an example, when an atomic magnetometer is used to detect nuclear precession [31, 54], the nuclear signal is narrowband in nature, with a predictable frequency. In such case, an appropriate selection of \(\delta\) let enhance the system response to the signal under investigation.

These predictions are validated with the apparatus described in Sect. 3. The Fig. 4 shows several experimental data sets (amplitude and phases) obtained with weak TDF applied along the static field direction, with frequencies ranging in a broad interval. Theoretical curves obtained from the model (solid lines) are drawn with the corresponding colours. Both amplitude and phase responses are considered for different values of \(\delta\), and particularly for \(\delta \ll \Gamma , \delta \sim \Gamma , \delta > \Gamma , \delta \gg \Gamma\), and excellent agreement is found for all the regimes.

Fig. 4
figure 4

Bode plots of the first order response, theoretical (solid lines) and experimental (points) results, as obtained for different values of \(\delta\). Experimental points at 50 Hz, 100 Hz and 150 Hz have been skipped, because affected by mains disturbance. The response passes progressively from a low-pass to a band-pass behaviour, with an interesting intermediate condition (\(\delta \approx \Gamma /2\)), where a nearly flat response extends from zero up to \(\approx \delta\): this is the case of the plot with \(\delta =2 \pi \cdot 13\) Hz)

Full size image

4.2 Second-order approximation

When more intense TDFs are applied, the second order perturbation terms start playing a role. We have experimentally tested the developed model by applying sinusoidal TDFs along one or two directions, which are nominally parallel or perpendicular to the bias field. When two oscillating components are applied, different frequencies are selected, in order to make their contributions spectrally distinguishable.

At the second-order approximation, the model shows that the system response contains quadratic terms of both the longitudinal (\(i=2\)) and transverse (\(i=1,3\)) TDF components. The simultaneous application of TDF with a single Fourier component along different directions i (\(i=1, 2, 3\), the direction 2 being that of the bias field) with different angular frequencies \(\Omega _{i}\), causes the presence of terms at \(2 \Omega _{i}\) and at \(|\Omega _{1} \pm \Omega _{3}|\), while no mixing between transverse and longitudinal TDF is expected.

It is worth noting that slight coil misalignments may lead to “spurious” mixing response as discussed at the end of Sect. 2 (Eqs. 29–31), and in applications this mixing can be used as a monitor tool, to refine the coil orthogonality.

On the basis of Eq. 24, second harmonic peaks at \(2\Omega _1\) and \(2\Omega _3\) are expected, when one single frequency TDF is applied along the x or z direction. The Fig. 5 shows experimental points and corresponding fitting curves obtained when a single frequency TDF is applied along x or z. The fitting are calculated for an assigned \(\Gamma =2 \pi \cdot 30\) Hz, with only one free parameter \(\delta\) that is determined to be \(\approx \Gamma\), consistently with the experimental conditions.

Fig. 5
figure 5

Quadratic response to the transverse fields. These plots report the second harmonic amplitude registered when an oscillating transverse field is applied. In the case (a) a 12.34 Hz field is applied along z (\(b_3\), see Eq. 24a), and in the case (b) a 15 Hz field is applied along x (\(b_1\), see Eq. 24b). A saturation effect appears above 300-400 \(\mu\)T, while the experimental points recorded at lower field intensity are perfectly fitted by a parabolic curve (solid line). Only the detuning \(\delta\) is varied in the best fit procedure, while \(\Gamma\) is set a \(2 \pi\)30 Hz. The arbitrary units used for the vertical scales are the same as for the Figs. 6 and 7

Full size image

When the TDF is applied in the same direction as the bias field, the system second-order response is described by the Eq. 23: the expected amplitude of second-harmonics peak may noticeably vary as a function of \(\delta\). In particular, it is expected to vanish for \(\delta =0\): a feature that may find application in stabilization systems aimed to maintain the static field correctly oriented and under resonant condition (\(\omega _L \approx \omega\)).

Figure 6 shows experimental points and a corresponding fitting parabola obtained when a TDF is applied along the bias field with different amplitudes. The fitting curve lets estimate \(\delta \approx 50\) rad/s, a value consistent with the experimental conditions.

Fig. 6
figure 6

In accordance with Eq. 23, provided that a detuning \(\delta\) exists, a second harmonic response with quadratically dependent amplitude is expected, in response to longitudinal TDF. This figure reports the \(2\Omega _2\) peak registered when a 12.34 Hz oscillating \(b_2\) field is applied. The relaxation rate is set at \(\Gamma =2\pi \cdot 30\) rad/s, and good fitting is found for \(\delta =\)50 Hz, which is consistent with the experimental conditions. In this case saturation is observed above 15 nT

Full size image

The Eqs. 25 and 30 describe a linear dependence of the sum- and difference-frequency peaks as a function of either the x or z TDF component. This behaviour is consistent with the data shown in Fig. 7, up to TDF amplitudes around 300 nT. Those data are recorded when applying two sinusoidal TDFs along the x and z directions, at 15 Hz and 12.34 Hz, respectively.

The linear slopes of the fitting curves largely exceed the amount expected from Eq. 25, suggesting that orthogonality imperfections (Eq. 30) play a dominant role in this case. The ratio between the sum- and difference-frequency slopes is approximately 1.4, which is well consistent with the values estimated from Eq. 31 for \(\delta \approx 0\) and \(\Gamma \approx 2\pi \cdot 30\) Hz.

Fig. 7
figure 7

Linear dependence of mixing terms on the \(b_1\) and \(b_3\) amplitude. The two plots are obtained when oscillating fields at 15 Hz and 12.34 Hz are simultaneously applied along the x and z directions, respectively. In the upper plot \(b_1\) is set at 435 nT and \(b_3\) is varied, while in the lower plot \(b_3\) is set at 270.6 nT and \(b_1\) is varied. Peaks at the sum and difference frequencies are recorded. Both the absolute amplitude of the peaks and their ratios indicate that these mixed frequency peaks do not originate from the second order term described in Eq. 25, but are rather caused by imperfect coil orthogonality. The ratio between sum- and difference-frequency peaks is indeed perfectly consistent with the square root of the ratio R expressed in Eq. 31. Similarly to the cases shown in Fig. 5, a saturation effect occurs above about 300 nT

Full size image

5 Conclusion

We have studied the dynamic response of a parametric system constituted by a light-modulated atomic magnetometer. Such kind of instrumentation is commonly used to detect extremely weak and slowly varying fields. Under these conditions, these devices are often analyzed with an implicit assumption, leading to treat them in analogy with linear time-invariant systems. We have developed a model that provides a more detailed analysis, and particularly let determine the response to TDFs that can range in a wider frequency interval and may have larger amplitudes.

In a first order approximation, which is valid for tiny TDF, we find that the system responds only to the TDF component along the bias field, and that it acts as a low-pass or a band-pass filter, in dependence of the frequency mismatch between the Larmor precession and the pump laser modulation signal. Conditions to achieve maximally flat spectral response, or frequency independent dephasing are identified.

Extending the model to the second order approximation enables the analysis of the system behaviour when larger TDFs are applied. Our findings show that the system responds quadratically to both longitudinal and transverse TDF components. The model provides quantitative evaluations of the diverse coefficients that describe amplitudes and phases of those nonlinear terms. In addition, frequency mixing may emerge between harmonic TDF components applied along the two transverse directions. The mixing occurs at different levels, depending on the relative orientation of the oscillating fields. In application (particularly when high resolution magnetometry is performed in the presence of narrow-band disturbances), this analysis will help to identify the origin of spurious spectral peaks that constitute artefacts in the detected signals.