Simple modelling of nonlinear losses induced by Kerr lensing effect

Abstract

This paper considers the calculation of the nonlinear losses induced in a circular aperture enlighten by a focused Gaussian beam (GB) subject to optical Kerr effect. Such a problem known since a long time typically requires the numerical calculation of a diffraction integral which becomes rapidly cumbersome in the case of repetitive applications. Alternatively, we propose a new simple modelling completely analytical. This method called as Non Gaussian Gaussian Beam modelling is based on the beam propagation factor $M^{2} > 1$ of the GB traversing the Kerr aberration. The $M^{2}$ is found to depend only on the nonlinear Kerr phase shift and independent of the wavelength and the width of the GB incident on the Kerr medium. This simple modelling has been applied to three applications: Kerr Lens Mode locking (KLM) mechanism, optical limitation, and Z-scan technique for a large nonlinearity.

Appendices

Appendix 1

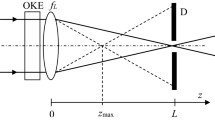
The direct calculation of $T_{D}$ the aperture transmission is based on the knowledge of $I_{d} (r,z) = \left| {E_{d} (r,z)} \right|^{2}$ the diffracted intensity distribution of the intensity beam of electrical field distribution $E_{{{\text{in}}}} (\rho )$ and having traversed the Kerr medium of transmittance (field ratio) $\exp [ - i\Delta \varphi (\rho )]$ followed by the thin focusing lens of transmittance $\exp [ik\rho ^{2} /(2f_{L} )]$; where r ($\rho$) is the radial coordinate in plane z (lens plane).

The collimated incident beam is assumed to be Gaussian and characterised by the electrical field given by:

$$E_{{in}} (\rho ) = \sqrt {\frac{{2P}}{{\pi W^{2} }}} \times \exp [ - \rho ^{2} /W^{2} ],$$

(31)

where W = 1 mm is the Gaussian beam width and P the beam power.

The diffracted field distribution $E_{d} (r,L)$ in the aperture plane is obtained using the Fresnel–Kirchhoff integral:

$$E_{d} (r,L) = \frac{{2\pi }}{{\lambda L}}\int\limits_{0}^{\infty } {E_{{{\text{in}}}} (\rho )\exp [ - i\Delta \varphi (\rho )]} \exp \left[ {\frac{{i\pi \rho ^{2} }}{\lambda }\left( {\frac{1}{{f_{L} }} - \frac{1}{L}} \right)} \right]J_{0} \left[ {\frac{{2\pi }}{{\lambda L}}r.\rho } \right]\rho d\rho .$$

(32)

Depending on the beam power, i.e. the on-axis nonlinear phase shift, the diffracted intensity distribution in the aperture plane is in general no longer Gaussian in shape, and has to be characterised by a beam width based on the second-order intensity moment noted $W_{D} (L)$, and defined as follows:

$$W_{D}^{2} (L) = \frac{{2\int\limits_{0}^{\infty } {I_{d} (r,L)r^{3} dr} }}{{\int\limits_{0}^{\infty } {I_{d} (r,L)rdr} }}.$$

(33)

Appendix 2

The aim of this appendix is to demonstrate that considering two laser beams having an intensity profile $I_{1} (\rho )$ and $I_{2} (\rho )$ characterised by the same width based on the second-order intensity moment, their transmissions through a given diaphragm can be very different. For that, we will consider the particular case where the two beams are $LG_{{00}}$ (Gaussian) and $LG_{{01}}$ (doughnut) beams having intensity profile given by:

$$I_{1} (\rho ) = I_{0} \times \exp \left[ { - \frac{{2\rho ^{2} }}{{W_{1}^{2} }}} \right],$$

(34)

$$I_{2} (\rho ) = I_{0} \times \left[ {\frac{{2\rho ^{2} }}{{W_{2}^{2} }}} \right] \times \exp \left[ { - \frac{{2\rho ^{2} }}{{W_{2}^{2} }}} \right].$$

(35)

The Gaussian (doughnut) beam has a width $W_{1}$ ($W_{2}$). As pointed out above, we will assume the same width for the two beams, and consequently we have the following relationship:

$$W_{1} = 2W_{2} .$$

(36)

By definition, the transmission (ratio of powers) through a circular aperture of radius $R_{D}$ of a laser beam having an intensity profile $I(\rho )$ is given by:

$$T = \frac{{\int\limits_{0}^{{R_{D} }} {I(\rho )\rho d\rho } }}{{\int\limits_{0}^{\infty } {I(\rho )\rho d\rho } }}.$$

(37)

The integral in Eq. (37) for the $LG_{{01}}$ beam involves the product of a Gaussian function and a polynomial. Its calculation can be found using a table of integrals [32] which provides the following result:

$$\int {x^{m} \exp \left[ {ax^{n} } \right]dx = } \frac{{\exp \left[ {ax^{n} } \right]}}{n}\left[ {\frac{{x^{n} }}{a} - \frac{1}{{a^{2} }}} \right]\,a \ne 0\,{\text{if}}\,\gamma = \frac{{m + 1}}{n} = 2.$$

(38)

If we set $Y = R_{D} /W_{2}$, then we obtain the transmission $T_{1}$ ($T_{2}$) for the Gaussian (doughnut) beam:

$$T_{1} = 1 - \exp \left[ { - Y^{2} /2} \right],$$

(39)

$$T_{2} = 1 - \left[ {1 + Y^{2} } \right]\exp \left[ { - 2Y^{2} } \right].$$

(40)

Figure 

Fig. 18

Variations of the transmissions $T_{1}$ (Gaussian beam) and $T_{2}$ (doughnut beam) versus $Y = R_{D} /W_{2}$. The width of the two beams is $2W_{2}$

18 shows the variations of $T_{1}$ and $T_{2}$ versus Y, and it is seen that, except for Y close to 0.6, $T_{1} \ne T_{2}$ although the two beams have the same width based on the second-order intensity moment.