The significance of beam steering on laser-induced incandescence measurements in laminar counterflow flames

Abstract

Beam steering is often encountered in laser diagnostic measurements, especially in flame environments, due to changes in refractive index caused by thermal and species gradients. It can negatively affect the accuracy of the results. In this work, the effects of beam steering on laser-induced incandescence (LII) measurements of pre-vaporized-liquid counterflow flames are assessed. The focus on counterflow flames is to facilitate future detailed experimental campaigns on one-dimensional nonpremixed sooty flames. It is found that the temperature and species gradients in the counterflow configuration have a much more significant impact on the beam profile than in laminar flat flames, especially for heavier fuels. As a result of the changes in the beam profile, for the same applied laser energy, the local fluence shifts markedly with fuel type, therefore, having a direct impact on the LII measurements. A procedure is developed for ensuring accurate measurements and it is shown that, for a specific fuel, it is possible to tailor the laser energy, such that the collected LII signal in the counterflow flames is nearly independent of beam-steering effects.

1 Introduction

The control of soot in flames requires understanding of its formation and oxidation. In particular, the further development of improved models of flames containing soot requires new measurements in well-controlled environments. A canonical configuration for the fundamental study of nonpremixed flames and soot formation is the counterflow arrangement. Counterflow burners to establish nonpremixed flames consist of two opposed jets, one with a fuel and the other with an oxidizer. Apart from nonpremixed flames, the counterflow configuration can also be used for premixed flames [1] and partially premixed flames [2, 3] by introducing fuel–air mixtures with different degrees of premixing through the opposed nozzles. For top-hat velocity profiles at the exit of the opposed nozzles, similarity formulations enable the prediction of the flame by one-dimensional simulations, therefore, making counterflow flames amenable to simplified modeling [4].

For the investigation of soot formation and oxidation processes, various experimental techniques, including extractive sampling and laser diagnostics, are extensively employed, yielding a wide range of important quantities, such as soot volume fraction ($f_\mathrm{v}$), particle number, size, and mass. In particular, the laser-induced incandescence (LII) technique is widely used for the in-situ and non-intrusive measurement of $f_\mathrm{v}$ [5]. It has been applied in a range of laminar and turbulent, premixed, and nonpremixed flames [6,7,8,9], as well as specifically in counterflow flames [10,11,12]. The LII technique has also been extended to provide a measure of soot primary particle size, both at a single point [13, 14] and two-dimensional imaging [15, 16].

Laser-based measurement techniques, including LII, are widely known to be subjected to beam-steering effects due to gradients in refractive index caused by local changes in gas composition as well as temperature [17,18,19,20]. In the case of Rayleigh scattering, an approach to correct for beam-steering effects has been proposed [17]. Fortuitously, with Rayleigh scattering imaging, it is possible to image the laser sheet throughout the entire flow field and, therefore, enables ray tracing to facilitate correction in the post-processing. In the case of LII, the laser path is only imaged, where soot is present—the propagation of the laser elsewhere is unknown. While it is conceivable to implement a separate Rayleigh scattering detection system to enable ray tracing of the LII laser sheet to account for beam steering, the Mie scattering from the soot in the measurement volume would overwhelm the Rayleigh signal. Instead, other approaches have been suggested to mitigate the effects of beam steering, such as using diffused back-light illumination to measure soot concentration [21].

The extent of beam steering in LII measurements has been reported in depth by Zerbs et al. [18] and Sun et al. [19] for turbulent ethylene jet flames, reporting that $f_\mathrm{v}$ can be underestimated by 30% because of variation in the local fluence. This effect even occurs in the plateau excitation regime [19], where the effect could be expected to be less significant due to the reduced impact of the fluence. Furthermore, the impact of beam steering is significant in both reacting and non-reacting flows [19] and is substantial at higher pressures, because the gradient in the refractive index becomes steeper [18]. In addition, the effect of beam steering has been identified as the dominant factor for asymmetries in some LII measurements [22, 23] as the laser fluence tends to decrease across the flame. This effect is exacerbated with a Gaussian laser energy profile [19].

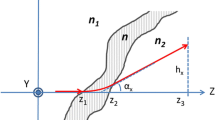
The previous works investigating the impact of beam steering have used methane [17] or ethylene [18, 19] as the fuel. The effect of beam steering due to altering refractive indices with other fuels, such as vaporized n-heptane, is expected to be more pronounced. Figure 1 shows the refractivity, N, of some gases, where $N=(n-1)\times 10^6$ and n is the refractive index [24]. For a 1064-nm wavelength, the ratio in refractivity between hot exhaust gases (2273 K) to ambient temperature air (288 K) is $\sim$1:8; to ethylene (288 K) is $\sim$1:20; and to n-heptane vapor (371 K) the ratio is almost 1:50. It is, therefore, apparent that n-heptane and, similarly other heavier fuels, are particularly prone to beam steering due to the potential for a high gradient in refractive index across the transition from pure fuel to the burnt gases.

Fig. 1

Refractivity, N of selected gases at different temperatures

While the role of beam steering and its impact on LII measurements has been shown to be of significant importance in turbulent flows [19], where gradients exist due to the vortices, the extent of beam steering in laminar flames has not been assessed yet. The laminar counterflow configuration inherently induces high spatial gradients and differences in refractive indices, such that beam steering might be substantial. Moreover, the variation in experimental boundary conditions, such as fuel type, fuel dilution, and strain rate, might result in differing effects of beam steering. Although these aspects are of particular concern and may lead to substantial uncertainties, especially for soot measurements in counterflow flames by means of LII, the beam-steering effects in the counterflow configuration have not been analyzed. Thus, the consequences of beam steering on the uncertainty of soot measurements in counterflow flames are so far unknown. Potential approaches to compensate for beam steering have not been reported. Therefore, the objective of this paper is first to identify the level of beam steering in laminar counterflow flames by means of laser energy profile measurements after the beam has propagated through the burner. For an assessment of the beam-steering impact, results are also compared to beam profiles recorded behind a laminar premixed flat flame. Then, an approach to overcome potential issues due to beam steering is proposed and its applicability is evaluated for various boundary conditions. Uncertainties in measurements of $f_\mathrm{v}$ induced by local laser fluence fluctuations as a result of beam steering are estimated.

2 Experimental details

The counterflow burner used in this study has been described previously [25]. A schematic of the counterflow setup is shown in Fig. 2. Briefly, it consisted of two 27.6-mm-diameter opposed pipes, separated by 13.75 mm. The ducts featured an area contraction ratio of nine upstream of the exit, and multiple fine mesh layers to ensure an axisymmetric laminar flow from each jet with a constant velocity profile across the exit plane of the jet. Fuel issued from the bottom jet, air from the top, and the flows were momentum-balanced to establish a stagnation plane mid-way between the nozzles. The strain rate was controlled by adjusting the flow rates. The fuel and oxidizer jets were surrounded by an annular coflow of nitrogen to shroud the disc-shaped flame.

Fig. 2

Schematic of counterflow burner setup and quantitative soot distribution in counterflow flame

For comparison with the counterflow burner, soot measurements were also performed in a McKenna-type burner fueled with an ethylene/air mixture. The laminar flat premixed flame was established above a water-cooled sintered bronze matrix with a 60-mm diameter. A metal plate 21-mm downstream of the burner stabilized the flame. The inner flame was shrouded by an annular nitrogen coflow.

For both burner configurations, the gas streams were adjusted by laminar flow element mass flow controllers from Alicat, with an accuracy of 0.8% of the set point and 0.2% of the maximum flow rate. To evaluate the fuel’s impact on beam steering in the counterflow burner, three typical gasoline surrogate components were used, namely, n-heptane, iso-octane, and toluene. The liquid fuels were heated in a controlled evaporator-mixer (DLI Vaporizing System, Brooks), and were transported to the burner with a nitrogen carrier gas. The evaporator, tubes, and burner were electrically heated to 398 K to prevent condensation. At this temperature, thermal decomposition of the fuel is negligible. In addition, ethylene was also used as a fuel.

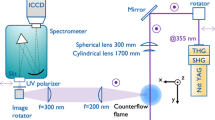
The optical system for $f_\mathrm{v}$ detection is shown in Fig. 3. The 1064-nm output from an Nd:YAG laser (Brilliant B, Quantel) was used as the light source for the LII measurements. The laser energy was controlled by passing the beam through an adjustable half-wave plate and a polarizing filter to ensure the beam energy distribution remained constant with the changes in laser energy. A pinhole was mounted behind the half-wave plate to only allow the homogeneous part of the laser beam to pass through. A combination of a concave cylindrical lens ($f = -80$ mm) and a convex spherical lens ($f = 500$ mm) was used to form a vertically parallel light sheet. To reduce the expansion of the light sheet width across the flame, a convex cylindrical lens ($f = 100$ mm) was positioned in front of the burner. The dimensions of the sheet were controlled with knife edges to give a Gaussian sheet profile. The height of the light sheet was 13 mm and 19 mm in the counterflow and McKenna-type burner, respectively. Throughout both burner configurations, the thickness of the light sheet remained constant at 0.3 mm. The maximum laser energy behind the counterflow burner was measured to be 33.9 mJ/pulse. Due to the larger light sheet, the pulse energy behind the flat-flame burner was increased to 49 mJ/pulse. The resultant profile was recorded with a beam-profiling camera (Ophir, model BGP-USB-L11059), approximately 300 mm after the burner, where the light sheet width had increased to 1 mm. Therefore, the reported laser fluences were significantly lower than in the LII measurement volume between the opposed nozzles. The impact of the distance between beam profiler and burner on the light sheet deformation has been carefully evaluated and was found to be negligible. Prior to the soot experiments, the fluence distribution within the light sheet was measured at the burner centerline. In the subsequent discussion, we report averaged fluence values $F_{\mathrm{avg}}$ with respect to the undisturbed light sheet at the burner centerline.

Fig. 3

Optical setup for laser-induced incandescence measurements. 1: Nd:YAG laser; 2: half-wave plate combined with polarization filter; 3: mirror; 4: pinhole; 5: cylindrical lens ($f = - 80$ mm); 6: vertical knife edge; 7: spherical lens ($f = 500$ mm); 8: horizontal knife edge; 9: cylindrical lens ($f = 100$ mm); 10: counterflow burner; 11: beam splitter; 12: beam profiler; 13: band pass filter (400 nm, FWHM 5 nm); 14: ICCD camera; 15: beam dump

Detection of the LII signal was normal to the propagation of the light sheet through a $400\pm 5$ nm bandpass filter, a 50-mm f/1.2 lens, and an intensified CCD (ICCD) camera (Andor iStar 334) yielding an in-plane spatial resolution of 0.04 mm/pixel. The camera gate width was 40 ns and prompt with the laser pulse. Quantification of the LII measurements was achieved by calibrating the LII signal against laser extinction (LE) measurements. The energy of the LII laser was reduced by the adjustable half-wave plate and polarizing filter to 1 mJ/pulse and a pinhole was used to form a beam with a diameter of 1 mm. Light extinction along the laser beam was measured in ethylene flames at 13 mm above the burner exit and 6 mm above the fuel nozzle in the flat-flame burner and the counterflow configuration, respectively.

To verify the applied LII setup, profiles of $f_\mathrm{v}$ in a laminar premixed ethylene/air flat flame, $\Phi =2.34$ and a gas exit velocity of 6.44 cm/s at 1 atm and 298 K, on a McKenna-type burner were compared to those previously obtained with a laser extinction technique by De Iuliis et al. [26]. The flame condition is consistent with that from the International Sooting Flames (ISF) workshop. As both profiles are in excellent agreement, Fig. 4 demonstrates the reliability of the optical system to give results consistent with the literature. The strong decrease in the $f_\mathrm{v}$ profile evident at $x\ge 16$ mm above the burner is predominantly attributed to the stabilizing plate located 21 mm above the burner surface. The non-zero soot emission for $x \le 5$ mm is a residual of the post-processing, where the background was not fully removed.

Fig. 4

Comparison of $f_\mathrm{v}$ from LII measurements and LE measurements from the literature (De Iuliis et al. [26]) obtained in laminar premixed ethylene/air flame, gas exit velocity 6.44 cm/s at a pressure of 1 atm and a temperature of 298 K [26]

3 Results

3.1 Beam steering in a laminar flat flame

First, the relevance of beam-steering effects is evaluated based on the beam profiles obtained behind the McKenna-type burner. Figure 5a, b shows a two-dimensional cross-sectional image of the laser beam energy profile collected by the beam-profiling camera, after the beam had passed above the burner surface. For LII measurements in the McKenna-type burner, the laser fluence has been set to 0.26 J/cm$^2$ with respect to the light sheet dimensions at the burner centerline. Figure 5a shows the beam profile in the absence of any flow or flame, while Fig. 5b shows the profile after the beam propagated through the laminar ethylene/air flat flame, as described in Sect. 2.

In Fig. 5a, b, diffraction patterns are observed and attributed to the knife edges used to shape the beam. Without the flame, the beam appears homogeneous and symmetric. This is supported by Fig. 5c, which shows the mean vertical energy profile across the full-width half-maximum portion of the beam. It is apparent that the central portion of the beam has a uniform intensity without the flame, while towards the wings of the beam, the diffraction effects become distinct. With the flame, the laser energy is seen to slightly decrease with increasing distance above the burner ($x \ge 13$ mm), due to absorption by the soot. Although the presence of soot from $x \ge 5$ mm is expected to attenuate the laser fluence behind the flame, the local fluence with flame is found to be slightly higher (5 mm $\le x \le$ 12 mm) as compared with the fluence without flame. This observation is attributed to small temporal changes in the overall laser output energy during the experiments. However, the similarity of both beam profiles suggests that beam-steering effects are minor in the region that is typically relevant for soot studies (7 mm $\le x \le$ 16 mm). Here, temperature gradients, and thereby changes of the refractive index, are small and the impact of the stabilization plate on the flame is assumed to be negligible. For $x \ge 18$ mm, differences between the two laser fluence profiles are observed. With flame on, thermal gradients from the flame towards the stabilizing plate and the deposition of soot on the stabilizing plate surface disturb the light sheet.

Fig. 5

Laser beam energy distribution behind a McKenna burner. a Cross-sectional view without flame, b cross-sectional view behind a laminar ethylene/air flat flame ($\Phi =2.34$, $v_{\mathrm{exit}} = 6.44$ cm/s), c vertical profile along sheet height with and without flame. a Without flame. b With flame. c Vertical profile

3.2 Beam steering in counterflow diffusion flames

This section reveals the strong influence of fuel distribution and combustion on beam steering in counterflow flames. It is shown that, despite beam-steering effects and laser absorption, a region of nearly homogeneous laser fluence is located around the reaction and soot formation zone. A procedure to overcome beam-steering effects to allow for accurate soot measurements in counterflow flames is proposed. The performance of the approach is discussed for different fuels and different soot loadings, including an estimation of the uncertainties of soot measurements in counterflow flames.

3.2.1 Laser energy distribution in the counterflow burner

To assess the impact of local variation in the refractive indices introduced either by changes in the local gas composition or by temperature gradients, the burner is operated with and without a flame, as well as with a range of operating conditions. The corresponding beam profiles behind the burner are compared in Fig. 6. The beam profile obtained under ambient condition without flow through the nozzles serves as a reference and is shown in Fig. 6a. Apart from a different burner and a reduced light sheet height, the optical setup remained unchanged compared to measurements in the flat-flame burner yielding the same beam profile as that presented in Fig. 5a. A homogeneous energy profile distribution with some minor diffraction patterns at the sheet edges is obtained.

Fig. 6

Cross-sectional view of laser energy distribution after beam has passed through the counterflow burner. For case d and e, n-C$_7$H$_{16}$ was balanced with N$_2$ and the flow temperature was 398 K

Figure 6b shows the corresponding energy distribution in the light sheet when a nitrogen flow heated to 398 K is introduced from the bottom nozzle, while cool air is flowing from the top. For this condition, a flame is absent. Therefore, the change in refractive index is predominately attributed to the change in local temperature, since the effects of differences in the refractive index between air and nitrogen are minor. Figure 6b reveals that the change in refractive index due to the heating is sufficient to affect the beam profile. Even though the temperature of the heated gas flow is quite low, the induced thermal gradient causes a more significant variation in the laser beam uniformity as compared with the effect from the flat flame, as shown in Fig. 5b.

To evaluate the impact of changes in the local gas composition on the beam profile, pre-vaporized n-heptane is added to the fuel nozzle, along with the nitrogen carrier gas, heated to 398 K. The fuel mass fraction is $Y_\mathrm{F}=0.5$, and the flow is not ignited. The presence of the unreacted vaporized fuel, which has a significantly higher refractive index relative to the air, has an enormous impact on the beam profile, as presented in Fig. 6c. Near the stagnation plane (around 7 mm from the fuel nozzle), the laser fluence is much lower: the beam is refracted towards the fuel nozzle.

Figure 6d shows the beam profile when the flame is ignited (same conditions as Fig. 6c, but with reaction). The laser energy in the fuel stream remains high, but within the central region between the nozzles, where the presence of the flame induces high gradients in the refractive index, the laser fluence is much lower. Hence, when performing LII measurements, the local laser fluence is significantly lower in the soot formation region of the flame (approximately at 4–8 mm distance from the fuel nozzle) compared with the fluence of an undisturbed light sheet. The selection of the laser energy for LII measurements often assumes a homogeneous light sheet. However, these results demonstrate that it is significantly different from the local fluence inside the flame.

Figure 6e shows the same features noted in Fig. 6d when the mass fraction of fuel is increased to $Y_\mathrm{F}=0.8$. The subsequent change in refractive index slightly affects the laser fluence distribution compared to the profile, as shown in Fig. 6d. The differences in the fluence distribution between $Y_\mathrm{F} = 0.5$ and $Y_\mathrm{F} = 0.8$ is distinct at the light sheet edges, whereas differences in the central section of the light sheet are barely detectable. The impacts of variation in fuel mass fraction are discussed in more detail in Sect. 3.2.2.

From Fig. 6, it is noted that in all cases, the laser sheet thickness (width in the horizontal direction) remains nearly constant. This is expected, because the gradients are steepest along the centerline of the counterflow configuration.

Figure 7 shows the vertical laser energy distribution averaged in the horizontal direction across the full-width half-maximum region of the sheet for the various cases, as presented in Fig. 6. It is apparent from Fig. 7 that the local fluence can change by more than a factor of two as a result of beam steering. Even when operating LII in the so-called plateau regime, it may be difficult to accomplish LII signals independent of laser fluence [5, 27].

Fig. 7

Horizontally averaged laser fluence profiles as a function of height above fuel nozzle in counterflow burner for the cases presented in Fig. 6

3.2.2 Soot measurements in counterflow flames

The previous subsection has demonstrated a substantial redistribution of energy within the sheet due to beam steering caused by steep gradients of temperature and gas composition in counterflow flames. These characteristics are exploited to develop an approach to overcome beam-steering effects. The beam-steering effects are analyzed for three liquid fuels, n-heptane (C$_{7}$H$_{16}$), iso-octane (C$_{8}$H$_{18}$) and toluene (C$_{7}$H$_{8}$), as well as for a gaseous fuel, namely ethylene (C$_{2}$H$_{4}$). The following discussion is predominately based on the results from C$_{8}$H$_{18}$-flames, as it yields the intermediate soot emission of the liquid fuels and its soot emission level is similar to that of C$_{2}$H$_{4}$.

To relate the local fluence to the location of the reaction zone and the soot region, Fig. 8 presents the fluence along the sheet height, the normalized signal intensity of OH* chemiluminescence, and the $f_\mathrm{v}$ profiles along the burner centerline. It is apparent that the reaction zone and the soot layer correspond to a location, where the local fluence is 20% of the peak value. Nevertheless, throughout the region of interest, the fluence is relatively constant, with fluctuations of $\sim$ 15% around the mean fluence in this region. To compensate for the decreased laser fluence in the soot formation region, a reasonable approach is the increase of the LII laser energy to ensure that the relevant part of the laser sheet within the soot layer is at the required fluence, even though the local fluence values outside the soot layer at the sheet edges exceed the desired fluence level. The approach is evaluated in detail in the following paragraph.

Fig. 8

Location of OH* and LII signal relative to laser energy distribution indicated by the $f_\mathrm{v}$ profile (left y-axis) and the normalized OH* and laser fluence distribution (right y-axis) obtained in an iso-octane flame with $Y_\mathrm{F}=0.8$, $a_2=40$/s and $F_{\mathrm{avg}} = 0.52$ J/cm$^2$

In the context of LII measurements, it is necessary to identify the relationship between laser fluence and the resultant LII signal: a so-called LII fluence curve. Note that the qualitative sheet profiles behind the burner are independent of the selected beam energy. Within the region of interest, it is mandatory to judiciously select the correct laser energy to minimize the effects of both absorption along the beam path and excessive sublimation on the LII signal, due to the laser fluence being too low or high, respectively. In either case, the $f_\mathrm{v}$ data will be biased. In light of the beam profile variations that have been identified in Sect. 3.2.1, generating fluence curves is especially important, because the local fluence within the soot layer is known to be continuously affected by beam steering, sublimation, and absorption across the flame. Hence, the local fluence in the flame is significantly altered relative to the fluence without flame.

Figure 9 shows the normalized LII signal as a function of laser fluence for the four investigated fuels. The normalized LII signal is the mean value along the centerline of the burner ($r\pm 0.5$ mm). By averaging the LII signal over the entire soot layer, differences in the soot loading and soot properties are neglected. However, in Sect. 3.2.3, it is shown that the fluence curves are independent of these quantities. Due to beam steering and absorption across the flame, the local fluence is unknown. Therefore, the fluence values are reported as the mean fluence ($F_{\mathrm{avg}}$) with respect to the undisturbed light sheet dimensions at the burner centerline. It is apparent that the fluence curve peak varies with respect to the fuel. Similar curves are observed for ethylene and toluene, whereas the peaks for iso-octane and n-heptane are shifted towards higher fluence values. The fuel-dependent variations of the fluence curve peaks are attributed to the combined effects of beam steering and light absorption. These effects occur to different levels, depending on the fuel stream composition and thus the index of refraction and soot volume fraction. For constant $F_{\mathrm{avg}}$, the local fluence within the probe volume changes with the fuel; hence, different mean fluences are required to achieve the fluence curve peak. It is also noted that a plateau in the LII fluence curve is not achieved, even if expected for a Gaussian sheet [27].

Fig. 9

Normalized LII signal along centerline of the burner ($r\pm 0.5$ mm) as a function of averaged laser fluence for n-heptane (C$_{7}$H$_{16}$, $f_{\mathrm{v,peak}} = 0.01$ ppm), iso-octane (C$_{8}$H$_{18}$, $f_{\mathrm{v,peak}} = 0.06$ ppm), toluene (C$_{7}$H$_{8}$, $f_{\mathrm{v,peak}} = 0.20$ ppm), and ethylene (C$_{2}$H$_{4}$, $f_{\mathrm{v,peak}} = 0.15$ ppm). Note that the mean fluence values, $F_{\mathrm{avg}}$, are based on the undisturbed light sheet dimensions at the burner centerline

The impact of $F_{\mathrm{avg}}$ variation is further assessed in Fig. 10 by means of normalized radial profiles obtained in an iso-octane flame ($Y_\mathrm{F}=0.8$, $a_2=40$/s). The LII signals for each laser energy are vertically averaged over the soot formation zone of the flame and normalized to the centerline signal intensity of $F_{\mathrm{avg}}$ yielding the peak in the fluence curves of Fig. 9. The laser propagation is from left to right along the abscissa. The soot volume fraction is nominally axisymmetric across the width of the central portion of the flame, with a slight increase towards the edges which are outside of the controlled flow field. Therefore, any deviation from a constant LII signal in the central portion of the profiles in Fig. 10 is due to changes in the local laser fluence. For $F_{\mathrm{avg}} = 0.17$ J/cm$^2$ and $F_{\mathrm{avg}} = 0.35$ J/cm$^2$, the averaged LII signal profiles constantly decrease from the beam entrance side towards the beam exit. Note that these fluence values are below the mean fluence for which the peak in the LII curve is obtained. In addition to beam steering, absorption of laser energy across the soot layer causes the reduction of the LII signal in the radial direction. The mean fluence above the plateau region, $F_{\mathrm{avg}} = 0.70$ J/cm$^2$, results in an opposite trend—the LII signal gradually increases along the beam propagation direction. It is expected that the high fluence at the beam entrance side increases the sublimation of soot particles, hence lowering the LII signal near the beam entrance. Across the flame, beam steering and laser energy absorption reduce the local fluence and lead to a signal increase. The same observations are made for C$_{2}$H$_{4}$, C$_{7}$H$_{8}$, and n-C$_{7}$H$_{16}$. The corresponding plots are summarized in Fig. 1 of the Supplementary Material. When the laser energy is increased to a level, such that it results in a uniform distribution, the effects of beam steering, absorption, and sublimation are balanced yielding a constant radial LII signal. The laser energy that results in a near-constant LII signal in Fig. 10 corresponds to the laser energy at the peak of the LII fluence curve (Fig. 9). The approach of tailoring the laser energy to accomplish a flat intensity profile relies on the assumption that the flame is indeed flat; this needs to be verified by independent means before adopting this approach.

Fig. 10

Radial profile of LII signal (vertically averaged over the soot formation zone of the flame) obtained in an iso-octane flame ($Y_\mathrm{F}=0.8$, $a_2=40$/s) for various $F_{\mathrm{avg}}$

To assess the impact of different flame conditions on the fluence curve, Fig. 11 presents the normalized LII signal as a function of $F_{\mathrm{avg}}$ for iso-octane flames with various fuel mass fractions and strain rate conditions. Note that the non-linear dependence of soot formation on time scales and mixture fraction results in a reduction of the peak $f_\mathrm{v}$ by 60% from $Y_\mathrm{F}=0.95$, $a_2=30$/s to $Y_\mathrm{F}=0.80$, $a_2=40$/s. Despite the change in soot loading, neither fuel mass fraction nor strain rate change the location of the peak in the fluence curve by an appreciable amount. Hence, when determining the optimal laser energy, it is reasonable to generate an LII fluence curve for each fuel, and when subsequently varying fuel mass fraction or strain rate, a consistent laser energy can be maintained. The effect of soot loading on the fluence curve is further analyzed in Sect. 3.2.3.

Fig. 11

Normalized LII signal as a function of $F_{\mathrm{avg}}$ for N$_{2}$-diluted iso-octane flames with different fuel mass fraction and strain rates

This observation is supported by Fig. 12 that shows the radial LII signal profiles for the different flame conditions of Fig. 11. The mean fluence was 0.52 J/cm$^2$, which achieved the best trade-off between maximum signal and most homogeneous radial signal profile.

Fig. 12

Radial profiles of LII signals for iso-octane flames with different fuel mass fraction and strain rates, $F_{\mathrm{avg}} = 0.52$ J/cm$^2$. The signals are integrated in the vertical direction over the entire soot region and normalized to the centerline signal value

3.2.3 Impact of local soot loading on LII measurement accuracy

In the previous section, it was demonstrated that beam steering causes significant shifts in the location of the fluence plateau region, which could induce remarkable measurement errors if this effect is not properly considered. The method to correct for the plateau shift is based on selecting the laser fluence, such that the processes of sublimation and absorption, as well as beam steering, are balanced to achieve a flat radial soot profile around the centerline. In Sect. 3.2.2, it was shown that the correction is applicable for different fuels and boundary conditions.

Thus far, the discussion was based on LII signals averaged over the entire soot layer neglecting the variation of soot loading and soot maturity within the flame. Soot loading and soot maturity can have a substantial effect on the optical properties of soot [28]. To further assess the resulting impact on the LII fluence curve, Fig. 13 presents LII fluence curves obtained at various locations in an iso-octane flame ($Y_\mathrm{F}=0.8$, $a_2=40$/s). The locations are 6.4 mm, 6.2 mm, and 5.7 mm above the fuel nozzle, where $f_\mathrm{v}$ has decreased to 25%, 50%, and 75% of the peak, respectively. The peak $f_\mathrm{v}$ of 0.06 ppm is located 5 mm downstream of the fuel nozzle. Figure 13 shows that the normalized LII fluence curve is essentially independent of the local soot loading and soot property. The fluence peak is at $F_{\mathrm{avg}} = 0.52$ J/cm$^2$, which is consistent with the optimal value determined from the mean across the entire centerline (Fig. 9).

Fig. 13

Normalized LII signal as a function of $F_{\mathrm{avg}}$ for an iso-octane flame ($Y_\mathrm{F}=0.8$, $a_2=40$/s, $f_{\mathrm{v,peak}} = 0.06$ ppm) at various locations in the flame corresponding to different $f_\mathrm{v}$, where the position is defined relative to the peak of $f_\mathrm{v}$

Figure 14 presents the radial LII signal profiles at 6.2 mm and 5.7 mm above the fuel nozzle, where the soot has reduced to 50% and 75% of the peak soot loading, respectively. For $F_{\mathrm{avg}} = 0.17$ J/cm$^2$ and $F_{\mathrm{avg}} = 0.7$ J/cm$^2$, the radial profiles of both soot loadings are strongly affected by absorption or sublimation, respectively. For $F_{\mathrm{avg}} = 0.35$ J/cm$^2$, the soot profiles appear flat at 6.2 mm, but for high soot loading at 5.7 mm, the radial profile is affect by absorption. Therefore, Fig. 14 demonstrates that $F_{\mathrm{avg}} = 0.52$ J/cm$^2$, which has been identified to be the optimal value for iso-octane flames, balances the impact of sublimation and absorption, as well as beam steering, and yields flat signal profiles independent of the soot loading and maturity. This finding is supported by the radial LII signal profiles obtained at 6.4 mm and 5 mm above the fuel nozzle. The corresponding radial profiles are summarized in the Supplementary Material.

Fig. 14

Radial profile of LII at the position, where the soot volume fraction is 50% and 75% of the peak soot loading for iso-octane flame, $Y_\mathrm{F}=0.8$, $a_2=40$/s. a Radial profiles at 0.50 $f_{\mathrm{v,max}}$. b Radial profiles at 0.75 $f_{\mathrm{v,max}}$

In the case of iso-octane, $F_{\mathrm{avg}} = 0.52$ J/cm$^2$ has been identified as the optimal value; however, local fluctuations in the laser fluence might occur and bias the LII signal. The fluence curves at different flame locations presented in Fig. 13 allow an estimate of the error induced by light sheet deformation. From Fig. 8, it is apparent that the minimum and maximum fluence values in the soot region deviate by less than ± 15% from the mean fluence value. Differences in the local fluence of 15% behind the burner at $F_{\mathrm{avg}} = 0.52$ J/cm$^2$ correspond to mean fluences in the range of $F_{\mathrm{avg}} = 0.43$ J/cm$^2$ to $F_{\mathrm{avg}} = 0.61$ J/cm$^2$. From the fluence curves presented in Fig. 13, it becomes evident that the induced error is well below 10%.

In combination, the results give confidence in identifying a reference point near the peak in the LII fluence curve as a means of ensuring near-uniform signal across the region of interest in the flame. The importance of the LII fluence curve for each fuel is not only to ensure that the soot profile is accurately determined, but also to balance the effects of beam steering, absorption, and sublimation throughout the flame. While it appears feasible to reach a compromise in these laminar flames, in a turbulent flame, it would be difficult to accurately determine the necessary laser energy on an instantaneous basis.

4 Conclusions

Beam steering is known to affect laser diagnostic measurements in flames. The laser-induced incandescence technique is particularly susceptible to beam steering. In a flat-flame burner, the beam-steering effects were shown to be relatively minor. In contrast, the high spatial gradients of the refractive index encountered in the counterflow configuration lead to extensive beam steering, which is further exacerbated when vaporized liquid fuels are used, due to their high refractive indices. The beam-steering effects in counterflow flames with vaporized liquid fuels have been assessed, and the following conclusions are drawn:

• 1. Beam steering is more pronounced in a non-reacting counterflow configuration with a gently heated gas stream than it is in a reacting sooty flat-flame.

• 2. The presence of fuel vapor can cause a deviation from a uniform beam profile by more than a factor of two.

• 3. In counterflow flames, the local fluence in the vicinity of the reaction zone is much lower than in the absence of a flame, but the fluence profile is nearly uniform and stable. Away from the reaction zone, beam steering is more pronounced and found to be less stable, despite a laminar flame condition.

• 4. The fuel type influences the fluence curve, with the peak LII signal being obtained for a different laser energy. In the current experimental arrangement, for a given fuel, the fluence curve is independent of the fuel mass fraction and the strain rate.

• 5. By judiciously selecting a laser energy for each fuel based on the peak of an LII fluence curve, it is possible to obtain LII measurements of soot volume fraction that are nearly independent of the beam-steering effects.

• 6. The laser energy corresponding to the peak LII signal balances the effects of sublimation, beam steering and absorption such that a flat soot profile is obtained.

• 7. The fluence curves are independent of the local soot loading in the flame.

• 8. The local fluence fluctuations in the light sheet induced errors in the soot volume fraction measurements below 10%.