1 Introduction

Laser frequency difference stabilization is indispensable in multiple modern experimental schemes. Applications range from quantum optics, cold atomic physics and off-resonant light–atom interfaces [1,2,3,4,5], through frequency comb stabilization [6,7,8,9] to precision spectroscopy and sensing [10, 11].

In multiple applications, phase coherence of the two laser fields locked at a frequency offset is not required [2,3,4,5,6,7,8,9,10,11] and a mere frequency lock is a sufficient solution. Nevertheless, one of the most commonly used solutions is the optical phase locked loop (OPLL) [12,13,14,15]. In a generic OPLL the master laser (ML) and the slave laser (SL) are combined and the beat note is measured on a fast photodiode (PD), compared with a reference value and then the difference is fed through the loop filter and used to tune SL by employing a fast current modulator. However, phase difference has to be kept within tight margins for OPLLs to work, rendering them impractical for broad-line lasers.

If the OPLL is constructed to ensure only the frequency drift stabilization and not the phase coherence, it constitutes an optical frequency locked loop (OFLL). Such approach has been presented previously in Ref. [16]; however, it was applied to narrow-line external cavity diodes lasers (ECDL) and was based on a frequency voltage converter, allowing only up to 8 MHz offsets between SL and ML. OPLL setups involving phase-frequency detectors (PFD) have been presented in Refs. [17] or [18] but for frequency offsets only up to 7 GHz. Both works were concerned with phase coherence requiring complicated loop filters and either field programmable gate array (FPGA) implementation or two parallel proportional-integral (PI) controllers. Ivanov et. al. [18] apply their setup to DFB lasers albeit of narrower line (1 MHz) than in our case. They also present a detailed analysis of OPLL performance in the presence of frequency dividers.

Here we present an OFLL designed for the stabilization of the long-term (>100 \(\upmu\)s) frequency drift. Our setup is based on an integrated PFD chip that compares the beat note signal of ML and SL with low-frequency reference. The PD and PFD are specifically matched to provide the simplicity of setup construction and usage.

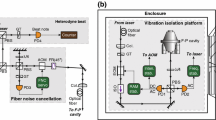
The PFD delivers current pulses (phase error) which are averaged and converted to a voltage signal on a low-pass filter (LPF). After subtracting the programmable reference voltage (Vref in Fig. 1), the signal (error signal) becomes proportional to the measured phase difference.

We design a single-stage loop filter as a proportional controller with only a small integral term to keep the phase difference in the detector range. The PFD chip may detect very large phase differences and thus can be applied to broad-line laser diodes. The error signal is fed back to a simple current controller with relatively slow response.

Several other methods had been developed for the purpose of frequency locking. These include feedback loops involving Mach–Zehnder interferometer with coaxial cable delay lines [19] or the application of electrical frequency filters [20, 21] performing frequency to amplitude conversion. These methods suffer from several significant limitations, including: less compact design, susceptibility to the environmental conditions as well as limited tunability of laser frequency difference.

We address these issues by employing a method that yields excellent phase stabilization [13] to the regime of long-term frequency stabilization of broad-line lasers, such as DFB laser diodes applicable in harsh environmental conditions [2, 9]. Additionally, a compact design is achieved using an integrated PFD chip. Long-term stability of our method is limited by the reference frequency generator, voltage source stability (DAC and inside LPF, see Fig. 1) as well as by PFD noise and hysteresis. The tuning of the setup can be performed in a real time by reprogramming the PFD chip and the generator.

Finally, we use an I/Q mixer to recover a full phase trace of the beat note signal. This method constitutes a new approach to laser phase-lock characterization and yields very informative data that allow us to recover phase variance and Allan deviation.

Fig. 1
figure 1

OFLL and a phase \(\phi (t)\) measurement setup. Broad-line (10 MHz) distributed feedback (DFB) master laser (ML) and slave laser (SL) frequency difference (RF) is measured as a beat note on a fast photodiode (PD) and fed to a programmable ADF41020 phase-frequency detector (PFD) where its frequency is divided (N) and compared with a frequency divided (R) reference local oscillator (LO). PFD output current signal (phase error) is averaged and converted to a voltage signal with a low-pass filter (LPF). A PC-controlled reference voltage from a digital analog converter (DAC) is then subtracted from the signal. Resulting error signal is then fed through a proportional-integral controller (PI) to slow laser current controller (Ictrl) closing the feedback loop. In a configuration RF signal is fed to in-phase quadrature (I/Q) mixer along with high-frequency local oscillator (LO’). The two local oscillators (LO and LO’) share a common 10 MHz clock reference. Relative phase of I/Q outputs comprises the RF to LO’ phase difference \(\phi (t)\)

Full size image

This paper is organized as follows: Sects. 2 and 3 discuss limitations of the OPLL operation and how these are addressed in our solution. Section 4 describes a simple theoretical model we have developed to simplify the setup and optimization of the OFLL using generic hardware. The process is then described in Sect. 5 in the form of a step-by-step procedure requiring merely simple time domain measurements. Section 6 describes how to modify the model to account for specific hardware characteristics. Section 7 shows the experimental performance of our OFLL realization and shows the results of I/Q mixer-based phase measurements. Section 8 concludes our work.

2 OPLL limitations

In a typical OPLL the beat note of ML and SL is registered with a photodiode detector (PD) and then an electronic mixer is used for comparison of the phase with the reference local oscillator (LO) [22, 23]. Such construction imposes severe limitations on the maximal phase error \(|\phi | < {\pi }/{2}\) rad due to periodic response of the mixer. This limitation can be safely neglected in phase coherence-oriented applications where \(\left<\phi ^2\right>\ll 1\) and loop bandwidth exceeds laser linewidth. However, in the regime of slowly reacting broad-line lasers \(\left<\phi ^2\right>\) can reach thousands. This is caused by the intrinsic laser frequency drift within the closed-loop response time.

In feedback loop systems, unavoidable delays limit the reaction time of the loop. In the frequency domain this corresponds to the loop bandwidth \(f_\mathrm{u}\)—the maximal frequency at which the loop gains G(f) is above unity. The loop bandwidth \(f_\mathrm{u}\) is bound by \(1/(2\Delta \tau )\), where \(\Delta \tau\) is the open-loop delay.

The phase fluctuations at frequencies above \(f_u\) cannot be compensated by the loop. Therefore, the open-loop delay is the main reason why the state-of-the-art, high-speed electronics is needed to maintain sufficiently high \(f_\mathrm{u}\) and thus sufficiently low \(\left<\phi ^2\right>\) for a typical OPLL to function correctly.

3 Optical frequency locked loop

If one is concerned merely with a long-term frequency drift compensation, a slow loop is sufficient, provided it can process relatively large phase fluctuations \(\left<\phi ^2\right>\). This is enabled by replacing a simple mixer with a commercial PFD, integrated with programmable dividers in a single chip. If the beat note signal is divided by N, the maximum phase difference for linear PFD regime becomes \(N\pi\). Allowing for larger phase detours \(\left<\phi ^2\right>\), the loop bandwidth \(f_u\) is no longer required to exceed the laser linewidth. It results in larger acceptable open-loop delay \(\Delta \tau\) enabling the usage of commercially available slow laser current controllers in the loop.

Fig. 2
figure 2

Error signal (see Fig. 1 and Sect. 3) in OFLL for three different locking points during broad \(\pm 17\,\text {GHz}\) laser frequency scan with the loop opened. Note an extreme span of unambiguous error signal. Sharp slopes in the error signal indicate that up to \(15 \,\text {GHz}\) beat note signals (RF) can be stabilized in this OFLL configuration

Full size image

In the experiment we use two distributed feedback (DFB) lasers (Toptica DL100). The master laser (ML) is free running during all measurements. The slave laser (SL) and ML are controlled by two Toptica current controllers (DCC110). The PI controller is built using a single LM358N operational amplifier with several passive components. About 100 \(\upmu\)W power from each laser is combined with a fiber coupler (Thorlabs FC780-50B) and the resulting beat note is monitored by a \(\sim\)10 GHz photodiode (PD) (Finisar HFD6380-418) as depicted in Fig. 1. The signal from complementary microwave outputs of the photodiode is guided by roughly 7-mm-long coplanar lines realized on standard FR4 laminate (0.15 mm clearance between 1 mm RF trace and surrounding ground, 1.6-mm-thick laminate, ground stitched to continuous plane on the bottom of a board with 0.3 mm vias spaced 0.6 mm apart) and directed to PFD chip (ADF41020, see [24]) and diagnostic SMA output. The PFD uses a charge pump to sink or source current pulses. Their width is proportional to the absolute value of the phase difference of the divided inputs, and the flow direction indicates its sign. Current pulses then pass through a low-pass filter (LPF) consisting of a parallel RC pair (\(R = 390~{\Omega }\), \(C=330\) pF) connected to ground and a resistor (\(R=390~{\Omega }\)) connected to stabilized voltage of \(3~\text {V}\). The current impulses are averaged and converted to a voltage signal. In the next step the Vref voltage from a PC-controlled digital analog converter (DAC) is subtracted from the signal by an operational amplifier. The resulting error signal is proportional to the phase difference. The photodiode saturates at about 500 \(\upmu\)W total optical power, providing approximately −10 dBm RF power at 6 GHz. In this arrangement the PFD operates reliably between 4 and 15 GHz as depicted in Fig. 2 delivering unambiguous error signal in the entire range. Operation range is limited from above by the bandwidth of the photodiode and from below by the construction of input stage amplifiers in the PFD [24].

4 Simplified loop model

Fig. 3
figure 3

OPLL equivalent schematic showing loop elements as transfer functions. Perturbation is added to the loop filter L(f) output. Closed-loop response H(f) is gathered just after the summation, at the current controller D(f) input

Full size image

In this section we present a model of the OFLL used to select optimal loop parameters. We assume an OFLL as sketched in Fig. 3. The transfer function of the open loop G(f) is the product of constituent transfer functions \(G(f) = {AD(f) L(f)}/{2 \pi i f},\) where A is the overall gain constant, accounting for the product of individual gains, D(f) and L(f) are unity gain transfer functions for laser and loop filter, respectively. The integration due to the frequency-phase conversion is explicitly included.

In optimization procedure we consider the closed loop which transfers function is given by \(H(f)=1/(1+G(f))\). In turn the eigenfrequencies of the closed loop are given by the roots of the H(f) denominator. Their location on the complex plane determines the time response as well as the stability of the loop. The necessary condition for non-oscillatory behavior is that all roots lay in the negative real half-plane. The denominator root of interest for optimization purposes is the one with the highest real part as that is approximately equal the inverse of the closed-loop response time.

To maintain generality and simplicity we assume laser response D(f) to be flat with dominant open-loop delay \(\Delta \tau\), \(D(f) = \exp \left( - i 2 \pi f \Delta \tau \right) .\) We first consider a purely proportional loop filter, i.e., \(L(f)=1\) with proportional gain constant included in A. The optimal gain in this case is found to be \(A_{P,\mathrm {opt}} = 1/({e\Delta \tau })\). For the sake of further optimization considerations, we also note that when the gain is increased up to the stability margin, oscillations emerge at a frequency \(f_{P,u} = {1}/{(4 \Delta \tau )}\) depending only on the open-loop delay \(\Delta \tau\). The dependence originates from the stability condition requiring the gain to be below unity at \(180^{\circ }\) phase shift. Upon the condition violation, the overall integration factor is responsible for the first \(90^{\circ }\) and the open-loop delay factor \(\exp \left( -i 2\pi f \Delta \tau \right)\) for the second introducing the overall \(\frac{1}{4}\) factor. A purely proportional loop can stabilize at an arbitrary loop filter output voltage level. In particular, the level may gradually increase over several hours and reach the maximum rendering the loop partially unresponsive. An addition of the integral term to the loop filter ensures the loop stabilizes at the 0 V level. Thus, it compensates, otherwise steadily accumulating, total phase error, which in turn can be kept within the finite operating range of the phase detector. In this case the loop filter L(f), shown in Fig. 3, is characterized by a large DC gain \(\kappa\) and filter zero-frequency \(f_\mathrm{z}\) having a unity proportional gain at high frequencies:

$$\begin{aligned} L(f) = \kappa \frac{1+{i f}/{f_\mathrm{z} }}{1+{i f \kappa }/{ f_\mathrm{z} }}. \end{aligned}$$
(1)

At \(f_\mathrm{z}\) the gain contributions from the proportional and integral terms are equal.

The presented model can be used to predict open-loop time response and optimize \(f_\mathrm{z}\) and A for a given \(\Delta \tau\) aiming at the quickest, non-oscillatory response. For large DC gains (\(\kappa \gg 1\)) the optimal parameters do not depend on \(\kappa\). They are found to be very close to \(A = 1/(2 \Delta \tau )\) and \(f_\mathrm{z} = {1}/({10\pi \Delta \tau })\).

The model definitions and optimization calculations can be found in a Mathematica worksheet in attached supplementary materials, allowing easy extension and adaptation to parameters measured in particular experimental scenario.

5 Setting up and optimization

An experimental procedure to quickly set up the OFLL relies solely on the measurements in the time domain thus eliminating the need for specialized devices such as network analyzers. The procedure aims at establishing the open-loop delay \(\Delta \tau\) and its total gain. During the measurement, a care should be taken to ensure a wide PFD phase detection range by setting a high N divisor value. This prevents loop oscillations originating from PFD overflow. Indications of these can be observed as discontinuities in the PFD output signal.

First, a proportional amplifier is used to close the loop with a gain P chosen to avoid oscillations. The proportional constant P should be subsequently increased until the loop develops oscillations. When these arise the total gain of the loop equals 1 and their frequency corresponds to the open-loop delay \(f_{P,u} = {1}/{(4 \Delta \tau )}\). This allows us to immediately use the optimal PI parameters by merely correcting for the gain \(P_P\) used to arrive at oscillations. The derived model parameters correspond to the proportional gain \(P_{\mathrm{PI}} = A P_P / (2 \pi f_{P,u})\) and integral gain \(I = 2 \pi P_{\mathrm{PI}} f_\mathrm{z}\). These equations can be combined with derived optimal parameter values to obtain a formula for the optimal PI gains in terms of used \(P_P\) and measured \(\Delta \tau\): \(P_{\mathrm{PI}} = P_P / \pi\), \(I = P_{P}/(5 \pi \Delta \tau )\).

If N is to be later altered the resulting change in the total open-loop delay must be considered. Working at RF frequency \(f_{\text {RF}}\) the additional delay, due to the PFD response time, is \(2N/f_{\text {RF}}\). In the regime where \(\Delta N \ll f_{\text {RF}} \Delta \tau / 2 + N\) the change \(\Delta N\) in N will merely affect proportional loop gain. Otherwise re-optimization with a new open-loop delay value may be required. It does not, however, require further measurements as the delay change may be calculated and accounted for.

6 Tailoring the model

Fig. 4
figure 4

Experimental and theoretical closed-loop time response for unit step perturbation. The signal was measured at the current controller (Ictrl) input. Optimal response (a) occurs for parameters \(f_\mathrm{z} = 800~\text {Hz}\), \(A = 12.5~\text {kHz}\). Upon increasing A damping period is prolonged (b). If the A is lowered too much to suppress oscillatory behavior one may obtain slow sub-optimal response (c)

Full size image

The simplicity of the model presented in Sect. 4 provides its usability in a generic case. This, however, comes at the cost of omitting details in the loop element description. It is quite straightforward to adjust the model if the details of the involved transfer functions are known. As depicted in Fig. 4, we have compared the experimental data (RF freq. \(6~\text {GHz}\), \(N=5120\)) with model predictions before and after accounting for the measured laser current controller response. In our case it comprised both \(\Delta \tau = 10~\upmu \text {s}\) delay and a double pole at \(f=12.8~\text {kHz}\). The models are used with the open-loop delay \(\Delta \tau = 10~\upmu \text {s}\) and PI parameters (A, \(f_\mathrm{z}\)) optimal according to Eq. 2 with \(\Delta \tau = 10~\upmu \text {s}\). In Fig. 4b it is evident that in such conditions the simple model does not capture details of the loop time response. Here, according to the simple model, an increase in the loop gain relative to the situation depicted in Fig. 4a shall only improve the response time while the extended model properly predicts the appearance of the unwanted oscillatory behavior. The comparison is done under the assumption that the real open-loop delay \(\Delta \tau\) is known and used in both models. If this is not the case the procedure described in Sect. 5 can be used. However, the formula \(f_{P,u} = {1}/{(4 \Delta \tau )}\) holds exactly only for the simple model. If the real loop constituent transfer functions are more complicated it merely provides an approximation. Therefore, \(\Delta \tau \approx 36~\upmu \text {s}\) obtained in the procedure would not be a real open-loop delay. Nevertheless, when used in the simple model, it compensates to some extent the neglected details of the transfer functions. In such case the optimal PI parameters can be estimated from the simple model formulae with \(\Delta \tau \approx 36~\upmu \text {s}\). The simple model supplied with these parameters would provide a good approximation of the loop response. If the loop details are already accounted for in the model the open-loop delay should be measured independently (e.g., using I/Q mixer, vide Sect. 7). Then the full model can employed to obtain optimal PI parameters.

The most prominent alterations to the model can be made by adjusting the laser response D(f). To construct the corresponding transfer function, its complex poles and zeros may be located. This can be achieved by subsequently applying harmonic perturbations at different frequencies to the loop and recording the phase shift and amplification of the response. D(f) can be established either directly from the measurements of microwave phase or inferred from the loop response. The former requires additional apparatus depicted in Fig. 1a while the latter assumes D(f) to be the only unknown transfer function in the model. We have applied the former method. Validity of any alteration of the model can be verified to some extent by measuring the loop time response.

Additional phase shifts are introduced, in our setup, due to D(f) double pole. Accounting for these we find the optimal gain and PI zero parameter values reduced by a factor of 4 compared to the predictions of the simple model:

$$\begin{aligned} A = {1}/{(8 \Delta \tau )}, \quad f_\mathrm{z} = {1}/({40\pi \Delta \tau }). \end{aligned}$$
(2)

Therefore, we advise to use reduced gain A and zero-frequency \(f_\mathrm{z}\). In terms of \(P_{\mathrm{PI}}\) and I the corrected values read \(P_{\mathrm{PI}} = P_P/(4\pi)\), \(I = P_P/(80\pi \Delta \tau)\).

Similar methods of optimization based on time series analysis exist. Basic Ziegler–Nichols (ZN) approach [25] and Refined Ziegler–Nichols [26] constrain their analysis to processes without integration while our method accounts for integration by the PFD. Other methods such as [27] ignore open-loop delay and require trial-and-error parameter tuning. In contrast our method is fully systematic and accounts for the open-loop delay. The well-acknowledged ZN method provides the following PI parameters \(I_{\mathrm{ZN}} = 0.6 \pi / \Delta \tau\), \(P_{\mathrm{PI,ZN}} = P_P/2.2\). Our method requires exactly the same information as ZN; however, it provides I that depends on \(P_P\). Thus, it is more specific than Ziegler–Nichols method, while remaining equally simple yet less universal.

7 Performance

Here we discuss the system performance after application of the optimization procedures. In our configuration, with \(\Delta \tau = 10~\upmu \text {s}\), the closed-loop time response was found to be around 100 \(\upmu\)s as depicted in Fig. 4a.

Performance and short-term stability is well characterized by the phase evolution of the system. As depicted in Fig. 1a the phase \(\phi (t)\) has been measured using the apparatus consisting of an in-phase quadrature mixer (I/Q mixer) ADL5380 fed with a reference signal (LO’) from HMC833 high-frequency generator. The mixer measures the in-phase \(I_\mathrm {iq}\) and \(90 ^{\circ }\) shifted \(Q_\mathrm {iq}\) components of the RF signal enabling the retrieval of the phase \(\phi (t) = \mathrm {arctan}\left( Q_\mathrm {iq}/I_\mathrm {iq}\right)\) relative to the LO’. We collected many 1-ms-long (\(0 \le \Delta t \le 1~\text {ms}\)) records \(\phi (\Delta t - t_0)\) of \(\phi (t)\), each starting at a different \(t = t_0\). After application of the phase unwrapping algorithm, we subtracted \(\phi (t_0)\) from each record and obtained a record of many \(\phi (\Delta t - t_0)-\phi (t_0)\). The records were subsequently used to obtain a probability density map \(p(\phi )\) (histogram) of phase difference \(\phi (\Delta t - t_0)-\phi (t_0)\) for each delay time \(\Delta t\) depicted in Fig. 5. The histogram confirms that the phase distributions relative to \(t_0\) are symmetric and virtually constant for times over \(100~\upmu\)s.

Fig. 5
figure 5

Phase evolution of the closed-loop system: a time evolution of histograms \(p(\phi )\) of lasers beat note phase deviations \(\phi (\Delta t-t_0)\) after subtracting \(\phi (t_0)\) from each realization and b phase variance \(\langle \phi (\Delta t-t_0)^2\rangle\) time evolution. We infer the closed-loop response time \(\approx 100 \,\upmu \text {s}\) and the typical phase deviation \(\approx 270 \,\text {rad}\) from the curve plateau

Full size image

Since the average \(\left<\phi (t_0)\right>= 0\) the phase variance \(\left<(\phi (\Delta t-t_0)-\left<\phi (t_0)\right>)^2\right> = \left<\phi (\Delta t - t_0)^2\right>\). As depicted in Fig. 5b it reaches a constant value of \(75\times 10^3 \,\text {rad}^2\) after the settling time of 100 \(\upmu\)s confirming the correct functioning of the OFLL. The N divider was set to be \(N=12{,}800\). This corresponds to the PFD range of approx. \(4 \times 10^4 \,\text {rad}\). Thus, the PFD range was kept far above the average phase deviation, allowing simple adjustments of the loop gain by altering N values.

Finally, we characterize the long-term stability of the system. A convenient tool is the overlapping Allan variance, which is calculated using three separate phase measurements—two for locked laser and one for unlocked laser. To obtain the result for short averaging times, we acquired a single 1.4-s-long record of phase using the I/Q mixer (Fig. 1a). Since this measurement requires high sampling rate, the total time is limited by oscilloscope memory. For longer averaging times we use another technique and continuously measure average PFD output signal (error signal in Fig. 1) for 1800 s and calculate the corresponding phase. Allan variances inferred from these two measurements are consistent in the overlapping region.

Fig. 6
figure 6

a Power spectrum of the open-loop beat note signal (sweep time 1 ms, RBW = 910 kHz, VBW = 910 kHz) and b the overlapping Allan deviation for locked and free-running SL showing the effect of the feedback loop for averaging times over 100 \(\upmu \mathrm {s}\). We observe excellent behavior at long averaging times corresponding to a strong noise suppression at low frequencies. Dashed orange line corresponds to the \(\tau ^{-1}\) trend due to phase white noise

Full size image

Figure 6b depicts the result for the overlapping Allan deviation for locked and unlocked (free-running) laser. For the unlocked laser only data obtained with mixer-based measurement is presented. For the case of locked laser, long averaging times region is dominated by the phase white noise as inferred from the observed \(\tau ^{-1}\) power-law dependence. In this region, starting from \(\tau \approx 100\ \upmu \mathrm {s}\) we clearly see the effect of the OFLL. In particular, the long-term stability of our system is guaranteed by an intrinsically environmentally insensitive frequency detection, resulting in <0.1 Hz frequency deviation after 500 s averaging time. For much longer times we expect that electronic instabilities such as drift of voltage reference will cause the trend to collapse. At small averaging times the \(\tau ^{-1}\) trend discontinues due to internal frequency characteristics of the laser, such as white or flicker frequency noise [13, 18, 28]. This kind of noise dominates in the case of unlocked laser.

8 Conclusions

In conclusion, we have presented a laser difference stabilization technique extending the optical phase locked loop methods to the regime of broad-line lasers. We have discussed the OFLL operation, constructing a simple model which enabled us to present a simple method of OFLL optimization, relying merely on a straightforward time domain measurement. Furthermore, the loop diagnostic methods have been presented.

Our setup provides an excellent long-term frequency stability, yet providing a broad lock set point frequency range (4–15 GHz) with unambiguous error signal in the entire range, promising a variety of applications in quantum optics and cold atomic physics. If smaller offset frequencies are required, similar PFD chip suitable for smaller frequencies can be used. Furthermore, a phase variance measurement on the PFD output provides a simple method to eliminate an unwanted locking at zero-frequency offset thus extending the effective frequency range of unambiguous error signal to nearly 30 GHz.

Exploiting an integrated phase-frequency detector ADF41020 on an ordinary PCB with merely one microwave track, our design remains simple and readily compatible with generic laser current controllers. Digitally controlled ADF41020 frequency divisors and lock setpoint (e.g., by DDS AD9959) allow for easy regulation. The ADF41020 can independently output the divided measured frequency, which enables construction of fully automated, self-diagnosing systems with standard counters.