Skip to main content
SpringerLink
Log in

Porous flexoelectric cylindrical nanoshell based on the non-classical continuum theory

  • Published:
Applied Physics A Aims and scope Submit manuscript

Abstract

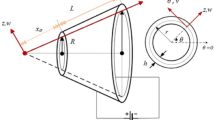
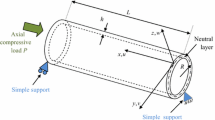
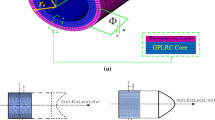
In this paper, the coupling equations dependent on the size of the functionally graded porous flexoelectric cylindrical nanoshell are extracted based on non-classical theory. The electromechanical coupling equations dependent on the size of the functionally graded porous flexoelectric cylindrical nanoshell are a purpose of this paper and these coupling equations are extracted with polarization (independent of electrical potential) which is the underlying innovation of the current study. When flexoelectricity and porosity are not considered, the shell model developed in this paper is reduced to the simple classical first-order shell model. The law of power distribution has been used to model the changes of the constituent material in the shell thickness, and three different porosity distributions have been considered. The effects of microstructure are considered using modified flexoelectric strain gradient theory. Finally, to investigate the application of the formulation performed in this paper, the problem is solved for a specific case such as free vibrations. In free vibration analysis, the geometric and material effects of porous flexoelectric nanotubes have been investigated. According to the obtained results, it can be noted that in the case of positive external voltage, by increasing the flexoelectric coefficient of the material, the natural frequency of the nanotube increases. Also, increasing the porosity of the flexoelectric cylindrical nanoshell increases the frequencies. Also, in the presence of the flexoelectric effect, the modified strain gradient theory, by considering three size parameters, predicts higher results numerically than the couple and classical stress theories.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. H. Zeighampour, Y.T. Beni, A shear deformable cylindrical shell model based on couple stress theory. Arch. Appl. Mech. 85(4), 539–553 (2015)

    MATH  ADS  Google Scholar 

  2. H. Safarpour, Z.E. Hajilak, M. Habibi, A size-dependent exact theory for thermal buckling, free and forced vibration analysis of temperature dependent FG multilayer GPLRC composite nanostructures restring on elastic foundation. Int. J. Mech. Mater. Des. 15, 1–15 (2018)

    Google Scholar 

  3. A. Pourjabari, Z.E. Hajilak, A. Mohammadi, M. Habibi, H. Safarpour, Effect of porosity on free and forced vibration characteristics of the GPL reinforcement composite nanostructures. Comput. Math. Appl. 77(10), 2608–2626 (2019)

    MathSciNet  MATH  Google Scholar 

  4. A. Li, S. Zhou, L. Qi, X. Chen, A reformulated flexoelectric theory for isotropic dielectrics. J. Phys. D Appl. Phys. 48(46), 465502 (2015)

    ADS  Google Scholar 

  5. N. Ebrahimi, Y.T. Beni, Electro-mechanical vibration of nanoshells using consistent size-dependent piezoelectric theory. Steel Compos. Struct. 22(6), 1301–1336 (2016)

    Google Scholar 

  6. F. Mehralian, Y.T. Beni, R. Ansari, Size dependent buckling analysis of functionally graded piezoelectric cylindrical nanoshell. Compos. Struct. 152, 45–61 (2016)

    Google Scholar 

  7. L. Qi, S. Huang, G. Fu, A. Li, S. Zhou, X. Jiang, Modeling of the flexoelectric annular microplate based on strain gradient elasticity theory. Mech. Adv. Mater. Struct. 26, 1–11 (2018)

    Google Scholar 

  8. A. Ghobadi, Y.T. Beni, H. Golestanian, Size dependent thermo-electro-mechanical nonlinear bending analysis of flexoelectric nanoplate in the presence of magnetic field. Int. J. Mech. Sci. 152, 118–137 (2019)

    Google Scholar 

  9. A. Ghobadi, Y. Tadi Beni, H. Golestanian, Size dependent nonlinear bending analysis of a flexoelectric functionally graded nano-plate under thermo-electro-mechanical loads. J. Solid Mech. 12(1), 33–56 (2020)

    MATH  Google Scholar 

  10. J. Kim, K.K. Żur, J.N. Reddy, Bending, free vibration, and buckling of modified couples stress-based functionally graded porous microplates. Compos. Struct. 209, 879–888 (2019)

    Google Scholar 

  11. L.L. Ke, Y.S. Wang, J.N. Reddy, Thermo-electro-mechanical vibration of size dependent piezoelectric cylindrical nanoshells under various boundary conditions. Compos. Struct. 116(1), 626–636 (2014)

    Google Scholar 

  12. Y. Wang, D. Wu, Free vibration of functionally graded porous cylindrical shell using a sinusoidal shear deformation theory. Aerosp. Sci. Technol. 66, 83–91 (2017)

    Google Scholar 

  13. M. Ghadiri, H. SafarPour, Free vibration analysis of size-dependent functionally graded porous cylindrical microshells in thermal environment. J. Therm. Stress 40(1), 55–71 (2017)

    Google Scholar 

  14. H. Li, F. Pang, H. Chen, Y. Du, Vibration analysis of functionally graded porous cylindrical shell with arbitrary boundary restraints by using a semi analytical method. Compos. B Eng. 164, 249–264 (2019)

    Google Scholar 

  15. J. Zhao, F. Xie, A. Wang, C. Shuai, J. Tang, Q. Wang, A unified solution for the vibration analysis of functionally graded porous (FGP) shallow shells with general boundary conditions. Compos. B Eng. 156, 406–424 (2019)

    Google Scholar 

  16. S. Zeng, B.L. Wang, K.F. Wang, Analyses of natural frequency and electromechanical behavior of flexoelectric cylindrical nanoshells under modified couple stress theory. J. Vib. Control 25(3), 559–570 (2019)

    MathSciNet  Google Scholar 

  17. S.F. Dehkordi, Y.T. Beni, Electro-mechanical free vibration of single-walled piezoelectric/flexoelectric nano cones using consistent couple stress theory. Int. J. Mech. Sci. 128, 125–139 (2017)

    Google Scholar 

  18. H. Qiu, M. Fan, D. Wang, H. Tzou, Flexoelectric actuation and control of conical shells. In 2019 14th Symposium on Piezoelectricity, Acoustic Waves and Device Applications (SPAWDA) (IEEE, 2019), pp. 1–5‏

  19. S.A. Faghidian, Integro-differential nonlocal theory of elasticity. Int. J. Eng. Sci. 129, 96–110 (2018)

    MathSciNet  MATH  Google Scholar 

  20. S.A. Faghidian, Higher-order nonlocal gradient elasticity: a consistent variational theory. Int. J. Eng. Sci. 154, 103337 (2020)

    MathSciNet  MATH  Google Scholar 

  21. S.A. Faghidian, Two-phase local/nonlocal gradient mechanics of elastic torsion. Math. Methods Appl. Sci. (2020). https://doi.org/10.1002/mma.6877

    Article  Google Scholar 

  22. S.A. Faghidian, Higher order mixture nonlocal gradient theory of wave propagation. Math. Methods Appl. Sci. (2020). https://doi.org/10.1002/mma.6885

    Article  MATH  Google Scholar 

  23. R. Ansari, M. Faraji Oskouie, S. Nesarhosseini, H. Rouhi, Flexoelectricity effect on the size-dependent bending of piezoelectric nanobeams resting on elastic foundation. Appl. Phys. A 127, 518 (2021)

    ADS  Google Scholar 

  24. K.K. Żur, M. Arefi, J. Kim, J.N. Reddy, Free vibration and buckling analyses of magneto-electro-elastic FGM nanoplates based on nonlocal modified higher-order sinusoidal shear deformation theory. Compos. B Eng. 182, 107601 (2020)

    Google Scholar 

  25. Ç. Demir, Ö. Civalek, On the analysis of microbeams. Int. J. Eng. Sci. 121, 14–33 (2017)

    MathSciNet  MATH  Google Scholar 

  26. H. Metin, N. Oğlu, B. Akgöz, Ö. Civalek, On dynamic analysis of nanorods. Int. J. Eng. Sci. 130, 33–50 (2018)

    Google Scholar 

  27. B. Akgöz, Ö. Civalek, A size-dependent shear deformation beam model based on the strain gradient elasticity theory. Int. J. Eng. Sci. 70, 1–14 (2013)

    MathSciNet  MATH  Google Scholar 

  28. B. Akgöz, Ö. Civalek, Bending analysis of embedded carbon nanotubes resting on an elastic foundation using strain gradient theory. Acta Astronaut. 119, 1–12 (2016)

    ADS  Google Scholar 

  29. M.H. Jalaei, Ӧ Civalek, On dynamic instability of magnetically embedded viscoelastic porous FG nanobeam. Int. J. Eng. Sci. 143, 14–32 (2019)

    MathSciNet  MATH  Google Scholar 

  30. A. Norouzzadeh, R. Ansari, H. Rouhi, Pre-buckling responses of Timoshenko nanobeams based on the integral and differential models of nonlocal elasticity: an isogeometric approach. Appl. Phys. A 123, 330 (2017)

    ADS  Google Scholar 

  31. A.E. Abouelregal, H. Mohammad-Sedighi, S.A. Faghidian, A.H. Shirazi, Temperature-dependent physical characteristics of the rotating nonlocal nanobeams subject to a varying heat source and a dynamic load. Facta Univ. Ser. Mech. Eng. 19(4), 633–656 (2021)

    Google Scholar 

  32. E. Abouelregal, H. Mohammad-Sedighi, The effect of variable properties and rotation in a visco-thermoelastic orthotropic annular cylinder under the Moore–Gibson–Thompson heat conduction model. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 235(5), 1004–1020 (2021)

    Google Scholar 

  33. A.E. Abouelregal, H. Mohammad-Sedighi, A.H. Shirazi, M. Malikan, V.A. Eremeyev, Computational analysis of an infinite magneto-thermoelastic solid periodically dispersed with varying heat flow based on non-local Moore–Gibson–Thompson approach. Contin. Mech. Thermodyn. 29, 1–9 (2021)

    Google Scholar 

  34. A. Singhal, H. Mohammad Sedighi, F. Ebrahimi, I. Kuznetsova, Comparative study of the flexoelectricity effect with a highly/weakly interface in distinct piezoelectric materials (PZT-2, PZT-4, PZT-5H, LiNbO3, BaTiO3). Waves Random Complex Media 31(6), 1780–1798 (2021)

    MathSciNet  MATH  ADS  Google Scholar 

  35. D. Hieu, N. Hoa, L. Duy, N. Kim Thoa, Nonlinear vibration of an electrostatically actuated functionally graded microbeam under longitudinal magnetic field. J. Appl. Comput. Mech. 7(3), 1537–1549 (2021)

    Google Scholar 

  36. A. Ghobadi, H. Golestanian, Y. Tadi Beni, K. Kamil Żur, On the size-dependent nonlinear thermo-electro-mechanical free vibration analysis of functionally graded flexoelectric nanoplate. Commun. Nonlinear Sci. Numer. Simul. 95, 105585 (2021). https://doi.org/10.1016/j.cnsns.2020.105585

    Article  MATH  Google Scholar 

  37. A. Ghobadi, H. Golestanian, B.Y. Tadi, Nonlinear thermo-electromechanical vibration analysis of size-dependent functionally graded flexoelectric nano-plate exposed magnetic field. Arch. Appl. Mech. 90, 2025–2070 (2020). https://doi.org/10.1007/s00419-020-01708-0

    Article  MATH  Google Scholar 

  38. A. Ghobadi, Y. Tadi Beni, K. Kamil Żur, Porosity distribution effect on stress, electric field and nonlinear vibration of functionally graded nanostructures with direct and inverse flexoelectric phenomenon. Compos. Struct. 259, 113220 (2021)

  39. A. Faramarzi Babadi, Y. Tadi Beni, Size-dependent continuum-based model of a flexoelectric functionally graded cylindrical nanoshells. Math. Methods Appl. Sci. (2020). https://doi.org/10.1002/mma.6928

    Article  Google Scholar 

  40. Y. Tadi Beni, Size-dependent electromechanical bending, buckling, and free vibration analysis of functionally graded piezoelectric nanobeams. J. Intell. Mater. Syst. Struct. 27(16), 2199–2215 (2016)

    Google Scholar 

  41. Y. Tadi Beni, Size-dependent analysis of piezoelectric nanobeams including electro-mechanical coupling. Mech. Res. Commun. 75, 67–80 (2016)

    Google Scholar 

  42. M.S. Ebnali Samani, Y. Tadi Beni, Size dependent thermo-mechanical buckling of the flexoelectric nanobeam. Mater. Res. Express (2018). https://doi.org/10.1088/2053-1591/aad2ca

    Article  Google Scholar 

  43. R. Omidian, Y.T. Beni, F. Mehralian, Analysis of size-dependent smart flexoelectric nanobeams. Eur. Phys. J. Plus 132(11), 481 (2017)

    Google Scholar 

  44. R. Bagheri, Y. Tadi Beni, On the size-dependent nonlinear dynamics of viscoelastic/flexoelectric nanobeams. J. Vib. Control. 27(17–18), 2018–2033 (2021)

  45. M. Esmaeili, Y. Tadi Beni, Vibration and buckling analysis of functionally graded flexoelectric smart beam. J. Appl. Comput. Mech. 5(5), 900–917 (2019)

    Google Scholar 

  46. S. Fattaheian Dehkordi, Y. Tadi Beni, Size-dependent continuum-based model of a truncated flexoelectric/flexomagnetic functionally graded conical nano/microshells. Appl. Phys. A 128, 320 (2022)

    ADS  Google Scholar 

  47. R. Toupin, The elastic dielectric. J. Ration. Mech. Anal. 5(6), 849–915 (1956)

    MathSciNet  MATH  Google Scholar 

  48. J. Lu, Xu. Liang, Hu. Shuling, Flexoelectricity in solid dielectrics: from theory to application. Comput. Mater. Contin. 45(3), 145–162 (2015)

    Google Scholar 

  49. G.H. Farrahi, S.A. Faghidian, D.J. Smith, Reconstruction of residual stresses in autofrettaged thick-walled tubes from limited measurements. Int. J. Press. Vessel Pip. 86(11), 777–784 (2009)

    Google Scholar 

  50. S. Ali Faghidian, Inverse determination of the regularized residual stress and eigenstrain fields due to surface peening. J. Strain Anal. Eng. Des. 50(2), 84–91 (2015)

    Google Scholar 

  51. J.N. Reddy, R.A. Arciniega, Shear deformation plate and shell theories: from Stavsky to present. Mech. Adv. Mater. Struct. 11, 535–582 (2004)

    Google Scholar 

  52. S. Ali Faghidian, Unified formulations of the shear coefficients in Timoshenko beam theory. J. Eng. Mech. 143(9), 06017013-1:8 (2017)

Download references

Funding

No funding was received for conducting this study.

Author information

Authors and Affiliations

  1. Mechanical Engineering Department, Shahrekord University, Shahrekord, Iran

    Ashkan Ashrafi Dehkordi & Reza Jahanbazi Goojani

  2. Faculty of Engineering, Shahrekord University, Shahrekord, Iran

    Yaghoub Tadi Beni

  3. Nanotechnology Research Institute, Shahrekord University, Shahrekord, 8818634141, Iran

    Yaghoub Tadi Beni

Authors
  1. Ashkan Ashrafi Dehkordi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Reza Jahanbazi Goojani
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yaghoub Tadi Beni
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yaghoub Tadi Beni.

Ethics declarations

Conflict of interest

The author declares that there is no any conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

$$\begin{aligned} A_{11} & = \int_{ - h/2}^{h/2} {\left( { - 2{\mkern 1mu} k(z) - 8/3{\mkern 1mu} \mu (z) - f_{1} } \right){\text{d}}z} \\ A_{12} & = \int_{ - h/2}^{h/2} {4/5{\mkern 1mu} \mu (z)\left( {5{\mkern 1mu} l_{0}^{2} + 2{\mkern 1mu} l_{1}^{2} } \right){\text{d}}z} \\ A_{13} & = \int_{ - h/2}^{h/2} {2/3{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} \left( {3{\mkern 1mu} R^{2} + 4{\mkern 1mu} l_{1}^{2} + 6{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{4} }}{\text{d}}z} \\ A_{14} & = \int_{ - h/2}^{h/2} {1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} \left( {27{\mkern 1mu} l_{0}^{2} + 16{\mkern 1mu} l_{1}^{2} + 15{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{4} }}{\text{d}}z} \\ A_{15} & = \int_{ - h/2}^{h/2} {\left( {1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} \left( {87{\mkern 1mu} l_{0}^{2} + 64{\mkern 1mu} l_{1}^{2} + 15{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{2} }} - 8/5{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} l_{1}^{2} }}{{R^{2} }}} \right){\text{d}}z} \\ A_{16} & = \int_{ - h/2}^{h/2} {\left( {2{\mkern 1mu} \frac{{\left( {R^{2} + 4/3{\mkern 1mu} l_{1}^{2} - l_{2}^{2} } \right)\mu (z){\mkern 1mu} }}{{R^{3} }} - 2/3{\mkern 1mu} \frac{{3{\mkern 1mu} k(z){\mkern 1mu} - 2{\mkern 1mu} \mu (z){\mkern 1mu} }}{R} + 1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {27{\mkern 1mu} l_{0}^{2} + 8{\mkern 1mu} l_{1}^{2} - 15{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{3} }} - \frac{{f_{1} }}{R}} \right){\text{d}}z} \\ A_{17} & = \int_{ - h/2}^{h/2} {\left( { - 8/5{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} l_{1}^{2} }}{{R^{3} }} - 1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {27l_{0}^{2} - 32{\mkern 1mu} l_{1}^{2} + 15{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{3} }}} \right){\text{d}}z} \\ A_{18} & = \int_{ - h/2}^{h/2} {\left( { - 1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {27{\mkern 1mu} l_{0}^{2} - 32{\mkern 1mu} l_{1}^{2} + 15{\mkern 1mu} l_{2}^{2} } \right)}}{R} - 8/5{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} l_{1}^{2} }}{R}} \right){\text{d}}z} \\ A_{19} & = \int_{ - h/2}^{h/2} {\left( { - 2/3{\mkern 1mu} \frac{{3{\mkern 1mu} k(z){\mkern 1mu} - 2{\mkern 1mu} \mu (z){\mkern 1mu} }}{R} - \frac{{f_{1} }}{R}} \right){\text{d}}z} \\ A_{110} & = \int_{ - h/2}^{h/2} {8/5{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} l_{1}^{2} }}{R}{\text{d}}z} \\ A_{111} & = \int_{ - h/2}^{h/2} {\left( {8/3{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {l_{1}^{2} - 3/4{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{3} }} - 1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {27{\mkern 1mu} l_{0}^{2} + 32l_{1}^{2} - 15{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{3} }} - 1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {27{\mkern 1mu} l_{0}^{2} - 32l_{1}^{2} + 15{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{3} }}} \right){\text{d}}z} \\ A_{112} & = \int_{ - h/2}^{h/2} {\left( { - 4/5{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} l_{1}^{2} }}{R} - f_{1} {\mkern 1mu} z} \right){\text{d}}z} \\ A_{113} & = \int_{ - h/2}^{h/2} {\left( {8/3{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {l_{1}^{2} + 3/2{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{3} }} + 1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {27l_{0}^{2} + 16l_{1}^{2} + 15{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{3} }}} \right){\text{d}}z} \\ A_{114} & = \int_{ - h/2}^{h/2} {\left( {8/3{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {l_{1}^{2} - 3/4{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{2} }} - 1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {27{\mkern 1mu} l_{0}^{2} + 8{\mkern 1mu} l_{1}^{2} - 15l_{2}^{2} } \right)}}{{R^{2} }} - \frac{{f_{{1{\mkern 1mu} }} z}}{R}} \right){\text{d}}z} \\ A_{115} & = - R \\ \end{aligned}$$
$$\begin{aligned} {B_{21}} & = \int_{ - h/2}^{h/2} {\left( { - 2 {{\left( {{R^2} + 4/3 {l_1}^2 - {l_2}^2} \right)\mu (z) } \over {{R^3}}} - 2/3 {{3 k(z) - 2 \mu (z) } \over R} + 1/15 {{\mu (z) \left( {27 {l_0}^2 + 8 {l_1}^2 - 15 {l_2}^2} \right)} \over {{R^3}}} - {{{f_1}} \over {{R^2}}}} \right){\rm{d}}z} \\ {B_{22}} & = \int_{ - h/2}^{h/2} {\left( { - 8/5 {{\mu (z) {l_1}^2} \over {{R^3}}} - 1/15 {{\mu (z) \left( {27 {l_0}^2 - 32{l_1}^2 + 15 {l_2}^2} \right)} \over {{R^3}}}} \right){\rm{d}}z} \\ {B_{23}} & = \int_{ - h/2}^{h/2} {\left( { - 1/15 {{\mu (z) \left( {27 {l_1}^2 - 32 {l_1}^2 + 15 {l_2}^2} \right)} \over R} - 8/5 {{\mu (z) {l_1}^2} \over R}} \right){\rm{d}}z} \\ {B_{24}} & = \int_{ - h/2}^{h/2} {1/15 {{\mu (z) \left( {30 {R^2} + 27 {l_0}^2 + 136 {l_1}^2 + 15{l_2}^2} \right)} \over {{R^4}}}{\rm{d}}z} \\ {B_{25}} & = \int_{ - h/2}^{h/2} {\left( { - 2/3 {{\mu (z) \left( {3 {R^2} + 4 {l_1}^2 + 6 {l_2}^2} \right)} \over {{R^2}}} - 2/15 {{\mu (z) \left( {27 {l_0}^2 - 4{l_1}^2 - 15 {l_2}^2} \right)} \over {{R^2}}}} \right){\rm{d}}z} \\ {B_{26}} & = \int_{ - h/2}^{h/2} {1/15 \mu (z) \left( {27 {l_0}^2 + 16 {l_1}^2 + 15 {l_2}^2} \right){\rm{d}}z} \\ {B_{27}} & = \int_{ - h/2}^{h/2} {\left( { - 2 {1 \over {{R^4}}}\left( {\left( {4/3 {R^2} + {{19{l_0}^2} \over 5} + {{128 {l_1}^2} \over {15}} + {l_2}^2} \right)\mu (z) + {R^2}k(z) } \right) - {{32 \mu (z) {l_1}^2} \over {5 {R^4}}} - {{{f_1}} \over {{R^3}}}} \right){\rm{d}}z} \\ {B_{28}} & = \int_{ - h/2}^{h/2} {4/5 {{\mu (z) \left( {5 {l_0}^2 + 2{l_1}^2} \right)} \over {{R^4}}}dz} \\ {B_{29}} & = \int_{ - h/2}^{h/2} {\left( {1/15 {{\mu (z) \left( {87 {l_0}^2 + 64{l_1}^2 + 15 {l_2}^2} \right)} \over {{R^2}}} - 8/5 {{\mu (z) {l_1}^2} \over {{R^2}}}} \right){\rm{d}}z} \\ {B_{210}} & = \int_{ - h/2}^{h/2} {\left( { - 2 {{\mu (z) } \over {{R^2}}} - 1/15 {{\mu (z) \left( {27 {l_0}^2 + 184 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^4}}} - 2 {1 \over {{R^4}}}\left( {\left( {k(z) + 4/3 \mu (z) } \right){R^2} + {{32 \mu (z) {l_1}^2} \over 5}} \right) - {{{f_1}} \over {{R^3}}}} \right)dz} \\ {B_{211}} & = \int_{ - h/2}^{h/2} {\left( {2/15 {{\mu (z) \left( {27 {l_0}^2 + 32{l_1}^2 + 15{l_2}^2} \right)} \over {{R^4}}} + {{24 \mu (z) {l_1}^2} \over {5 {R^4}}}} \right){\rm{d}}z} \\ {B_{212}} & = \int_{ - h/2}^{h/2} {\left( {1/30 {{\mu (z) \left( {81 {l_0}^2 - 32{l_1}^2 - 45 {l_2}^2} \right)} \over {{R^2}}} + 1/15 {{\mu (z) \left( {27 {l_0}^2 + 64 {l_1}^2 + 15{l_2}^2} \right)} \over {{R^2}}} + 8/3 {{\mu (z) \left( {{l_1}^2 + 3/2{l_2}^2} \right)} \over {{R^2}}} + 1/15 {{\mu (z) \left( {27 {l_0}^2 - 16{l_1}^2 - 15{l_2}^2} \right)} \over {{R^2}}}} \right){\rm{d}}z} \\ {B_{213}} & = \int_{ - h/2}^{h/2} {\left( {8/3 {{\mu (z) {l_1}^2} \over {{R^2}}} - 1/30 {{\mu (z) \left( {81 {l_0}^2 + 64{l_1}^2 - 45 {l_2}^2} \right)} \over {{R^2}}} - 2 {{\mu (z) {l_2}^2} \over {{R^2}}} - 1/15 {{\mu (z) \left( {27{l_0}^2 - 32 {l_1}^2 + 15{l_2}^2} \right)} \over {{R^2}}} - {{{f_{1 }}z} \over {{R^2}}}} \right){\rm{d}}z} \\ {B_{214}} & = \int_{ - h/2}^{h/2} {\left( { - 2 {{\mu (z) } \over R} - 1/15 {{\mu (z) \left( {27 {l_0}^2 + 136 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^3}}}} \right){\rm{d}}z} \\ {B_{215}} & = \int_{ - h/2}^{h/2} {\left( {8/3 {{\mu (z) \left( {{l_1}^2 - 3/4 {l_2}^2} \right)} \over R} + 1/5 {{\mu (z) \left( {9 {l_0}^2 - 5 {l_2}^2} \right)} \over R} - {{4 \mu (z) {l_1}^2} \over {15 R}}} \right){\rm{d}}z} \\ {B_{216}} & = \int_{ - h/2}^{h/2} {\left( { - 2/15 {{\mu (z) \left( {27 {l_0}^2 - 64 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^3}}} + {{16 \mu (z) {l_1}^2} \over {5 {R^3}}} - {{{f_1} z} \over {{R^3}}}} \right){\rm{d}}z} \\ {B_{217}} & = - R \end{aligned}$$
$$\begin{aligned} {C_{31}} & = \int_{ - h/2}^{h/2} {2/3 {{\left( {3 k(z) - 2 \mu (z) } \right)} \over R}{\rm{d}}z} \\ {C_{32}} & = \int_{ - h/2}^{h/2} {8/5 {{\mu (z) {l_1}^2} \over R}{\rm{d}}z} \\ {C_{33}} & = \int_{ - h/2}^{h/2} {\left( { - 1/15 {{\mu (z) \left( {27 {l_0}^2 + 32 {l_1}^2 - 15 {l_2}^2} \right)} \over {{R^3}}} - 1/15 {{\mu (z) \left( {27 {l_0}^2 - 32 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^3}}}} \right){\rm{d}}z} \\ {C_{34}} & = \int_{ - h/2}^{h/2} { - 8/3 {{\mu (z) \left( {{l_1}^2 - 3/4 {l_2}^2} \right)} \over {{R^3}}}{\rm{d}}z} \\ {C_{35}} & = \int_{ - h/2}^{h/2} {\left( {2 {{\mu (z) } \over {{R^2}}} + 1/15 {{\mu (z) \left( {27 {l_0}^2 + 184 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^4}}} + 2 {1 \over {{R^4}}}\left( {\left( {k(z) + 4/3 \mu (z) } \right){R^2} + {{32 \mu (z) {l_1}^2} \over 5}} \right)} \right){\rm{d}}z} \\ {C_{36}} & = \int_{ - h/2}^{h/2} {\left( { - 2/15 {{\mu (z) \left( {27 {l_0}^2 + 32 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^4}}} - {{24 \mu (z) {l_1}^2} \over {5 {R^4}}}} \right){\rm{d}}z} \\ {C_{37}} & = \int_{ - h/2}^{h/2} {\left( { - 1/30 {{\mu (z) \left( {81 {l_0}^2 - 32 {l_1}^2 - 45 {l_2}^2} \right)} \over {{R^2}}} - 1/15 {{\mu (z) \left( {27 {l_0}^2 + 64 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^2}}} - 8/3 {{\mu (z) \left( {{l_1}^2 + 3/2 {l_2}^2} \right)} \over {{R^2}}} - 1/15 {{\mu (z) \left( {27 {l_0}^2 - 16 {l_1}^2 - 15 {l_2}^2} \right)} \over {{R^2}}}} \right){\rm{d}}z} \\ {C_{38}} & = \int_{ - h/2}^{h/2} {{2 \over {{R^4}}}\left( {\left( {4/3 {R^2} + 2 {l_0}^2 + {{24 {l_1}^2} \over 5}} \right)\mu (z) + {R^2}k(z) } \right){\rm{d}}z} \\ {C_{39}} & = \int_{ - h/2}^{h/2} {\left( { - 1/15 {{\mu (z) \left( {30 {R^2} + 87 {l_0}^2 + 64 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^2}}} + 8/5 {{\mu (z) {l_1}^2} \over {{R^2}}}} \right){\rm{d}}z} \\ {C_{310}} & = \int_{ - h/2}^{h/2} {1/15 \mu (z) \left( {27 {l_0}^2 + 16 {l_1}^2 + 15 {l_2}^2} \right){\rm{d}}z} \\ {C_{311}} & = \int_{ - h/2}^{h/2} {\left( { - 1/15 {{\mu (z) \left( {30 {R^2} + 87 {l_0}^2 + 256 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^4}}} - {{32 \mu (z) {l_1}^2} \over {5 {R^4}}}} \right){\rm{d}}z} \\ {C_{312}} & = \int_{ - h/2}^{h/2} {2/15 {{\mu (z) \left( {27 {l_0}^2 + 8 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^4}}}{\rm{d}}z} \\ {C_{313}} & = \int_{ - h/2}^{h/2} {\left( {8/3 {{\left( {{l_1}^2 + 3/2 {l_2}^2} \right)\mu (z) } \over {{R^2}}} + 1/15 {{\mu (z) \left( {81 {l_0}^2 - 8 {l_1}^2 - 45 {l_2}^2} \right)} \over {{R^2}}}} \right){\rm{d}}z} \\ {C_{314}} & = \int_{ - h/2}^{h/2} {\left( { - 1/15 {{\mu (z) \left( {30 {R^2} - 27 {l_0}^2 + 32 {l_1}^2 - 15 {l_2}^2} \right)} \over {{R^2}}} + 8/5 {{\mu (z) {l_1}^2} \over {{R^2}}}} \right){\rm{d}}z} \\ {C_{315}} & = \int_{ - h/2}^{h/2} { - 1/15 \mu (z) \left( {27 {l_0}^2 - 32 {l_1}^2 + 15 {l_2}^2} \right){\rm{d}}z} \\ {C_{316}} & = \int_{ - h/2}^{h/2} {\left( { - {{32 \mu (z) {l_1}^2} \over {5 {R^3}}} - 1/15 {{\mu (z) \left( {30 {R^2} + 27 {l_0}^2 + 184 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^3}}}} \right){\rm{d}}z} \\ {C_{317}} & = \int_{ - h/2}^{h/2} {\left( {8/3 {{\left( {{l_1}^2 - 3/4 {l_2}^2} \right)\mu (z) } \over {{R^2}}} - 1/30 {{\mu (z) \left( {81 {l_0}^2 + 16 {l_1}^2 - 45 {l_2}^2} \right)} \over {{R^2}}}} \right){\rm{d}}z} \\ {C_{318}} & = \int_{ - h/2}^{h/2} { - 2/15 {{\mu (z) \left( {27 {l_0}^2 - 16 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^3}}}{\rm{d}}z} \\ {C_{319}} & = \int_{ - h/2}^{h/2} {\left( { - 1/30 {{\mu (z) \left( {81 {l_0}^2 + 16 {l_1}^2 - 45 {l_2}^2} \right)} \over R} + 8/3 {{\left( {{l_1}^2 - 3/4 {l_2}^2} \right)\mu (z) } \over R}} \right){\rm{d}}z} \\ {C_{320}} & = - R \end{aligned}$$
$$\begin{aligned} D_{41} & = \int_{ - h/2}^{h/2} {\left( { - 4/5{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} l_{1}^{2} }}{R} - zf_{1} } \right){\text{d}}z} \\ D_{42} & = \int_{ - h/2}^{h/2} {\left( {8/3{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {l_{1}^{2} + 3/2{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{3} }} + 1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {27{\mkern 1mu} l_{0}^{2} + 16{\mkern 1mu} l_{1}^{2} + 15{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{3} }}} \right){\text{d}}z} \\ D_{43} & = \int_{ - h/2}^{h/2} {\left( {8/3{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} l_{1}^{2} }}{{R^{2} }} - 1/30{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {81{\mkern 1mu} l_{0}^{2} + 64{\mkern 1mu} l_{1}^{2} - 45{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{2} }} - 2{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} l_{2}^{2} }}{{R^{2} }} - 1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {27{\mkern 1mu} l_{0}^{2} - 32{\mkern 1mu} l_{1}^{2} + 15{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{2} }} - \frac{{zf_{1} }}{R}} \right){\text{d}}z} \\ D_{44} & = \int_{ - h/2}^{h/2} {\left( {1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {30{\mkern 1mu} R^{2} - 27{\mkern 1mu} l_{0}^{2} + 32{\mkern 1mu} l_{1}^{2} - 15{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{2} }} - 8/5{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} l_{1}^{2} }}{{R^{2} }} - \frac{{zf_{1} }}{R}} \right){\text{d}}z} \\ D_{45} & = \int_{ - h/2}^{h/2} {1/15\mu (z){\mkern 1mu} {\mkern 1mu} \left( {27{\mkern 1mu} l_{0}^{2} - 32{\mkern 1mu} l_{1}^{2} + 15{\mkern 1mu} l_{2}^{2} } \right){\text{d}}z} \\ D_{46} & = \int_{ - h/2}^{h/2} {\left( { - 8/3{\mkern 1mu} \frac{{\left( {l_{1}^{2} - 3/4{\mkern 1mu} l_{2}^{2} } \right)\mu (z){\mkern 1mu} }}{{R^{2} }} + 1/30{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {81{\mkern 1mu} l_{0}^{2} + 16{\mkern 1mu} l_{1}^{2} - 45{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{2} }}} \right){\text{d}}z} \\ D_{47} & = \int_{ - h/2}^{h/2} {1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} \left( {30{\mkern 1mu} R^{2} + 27{\mkern 1mu} l_{0}^{2} + 16{\mkern 1mu} l_{1}^{2} + 15{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{2} }}{\text{d}}z} \\ D_{48} & = \int_{ - h/2}^{h/2} {\left( { - 1/15{\mkern 1mu} \left( {87{\mkern 1mu} l_{0}^{2} + 64{\mkern 1mu} l_{1}^{2} + 15{\mkern 1mu} l_{2}^{2} + 40{\mkern 1mu} z^{2} } \right)\mu (z){\mkern 1mu} - 2{\mkern 1mu} z^{2} k(z){\mkern 1mu} - f_{1} {\mkern 1mu} z^{2} } \right){\text{d}}z} \\ D_{49} & = \int_{ - h/2}^{h/2} {4/5{\mkern 1mu} \mu (z){\mkern 1mu} {\mkern 1mu} \left( {5{\mkern 1mu} l_{0}^{2} + 2{\mkern 1mu} l_{1}^{2} } \right)z^{2} {\text{d}}z} \\ D_{410} & = \int_{ - h/2}^{h/2} { - 2{\mkern 1mu} \frac{{\left( {\left( {z^{2} + 4/3{\mkern 1mu} l_{1}^{2} + 2{\mkern 1mu} l_{2}^{2} } \right)R^{2} + 4/3{\mkern 1mu} l_{1}^{2} z^{2} } \right)\mu (z){\mkern 1mu} }}{{R^{4} }}{\text{d}}z} \\ D_{411} & = \int_{ - h/2}^{h/2} {1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} z^{2} \left( {27{\mkern 1mu} l_{0}^{2} + 16{\mkern 1mu} l_{1}^{2} + 15{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{4} }}{\text{d}}z} \\ D_{412} & = \int_{ - h/2}^{h/2} {\left( {1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} z^{2} \left( {87{\mkern 1mu} l_{0}^{2} + 64{\mkern 1mu} l_{1}^{2} + 15{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{2} }} - 8/5{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} l_{1}^{2} z^{2} }}{{R^{2} }}} \right){\text{d}}z} \\ D_{413} & = \int_{ - h/2}^{h/2} { - 2{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} \left( {\left( {z^{2} + 4/3{\mkern 1mu} l_{1}^{2} - l_{2}^{2} } \right)R^{2} + 4/3{\mkern 1mu} l_{1}^{2} z^{2} } \right)}}{{R^{3} }} - 2{\mkern 1mu} \frac{1}{R}\left( {\left( { - 2/3{\mkern 1mu} z^{2} + \frac{{27{\mkern 1mu} l_{0}^{2} }}{20} - \frac{{8{\mkern 1mu} l_{1}^{2} }}{15} - 3/4{\mkern 1mu} l_{2}^{2} } \right)\mu (z){\mkern 1mu} + z^{2} k(z){\mkern 1mu} } \right) + \frac{{8{\mkern 1mu} \mu (z){\mkern 1mu} {\mkern 1mu} l_{1}^{2} z^{2} }}{{15{\mkern 1mu} R^{3} }} - \frac{{f_{1} {\mkern 1mu} z^{2} }}{R}{\text{d}}z} \\ D_{414} & = \int_{ - h/2}^{h/2} {\left( { - 8/5{\mkern 1mu} \frac{{l_{1}^{2} z^{2} }}{{R^{3} }} - 1/15{\mkern 1mu} \frac{{\mu (z){\mkern 1mu} {\mkern 1mu} z^{2} \left( {27{\mkern 1mu} l_{0}^{2} - 32{\mkern 1mu} l_{1}^{2} + 15{\mkern 1mu} l_{2}^{2} } \right)}}{{R^{3} }}} \right){\text{d}}z} \\ D_{415} & = \int_{ - h/2}^{h/2} {\left( { - 9/5{\mkern 1mu} \frac{{\left( {l_{0}^{2} + 5/9{\mkern 1mu} l_{2}^{2} } \right)z^{2} \mu (z){\mkern 1mu} }}{R} + \frac{{8{\mkern 1mu} \mu (z){\mkern 1mu} l_{1}^{2} z^{2} }}{{15{\mkern 1mu} R}}} \right){\text{d}}z} \\ D_{416} & = - 2R \\ \end{aligned}$$
$$\begin{aligned} {E_{51}} & = \int_{ - h/2}^{h/2} {\left( {8/3 {{\mu (z) \left( {{l_1}^2 - 3/4 {l_2}^2} \right)} \over {{R^2}}} - 1/15 {{\mu (z) \left( {27 {l_{{0^2}}} + 8 {l_1}^2 - 15 {l_2}^2} \right)} \over {{R^2}}} - {{z{f_1}} \over {{R^2}}}} \right){\rm{d}}z} \\ {E_{52}} & = \int_{ - h/2}^{h/2} {\left( { - 2 {{\mu (z) } \over R} - 1/15 {{\mu (z) \left( {27 {l_0}^2 + 136 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^3}}}} \right){\rm{d}}z} \\ {E_{53}} & = \int_{ - h/2}^{h/2} {\left( {8/3 {{\mu (z) \left( {{l_1}^2 - 3/4 {l_2}^2} \right)} \over R} + 1/5 {{\mu (z) \left( {9 {l_0}^2 - 5 {l_2}^2} \right)} \over R} - {{4 \mu (z) {l_1}^2} \over {15 R}}} \right){\rm{d}}z} \\ {E_{54}} & = \int_{ - h/2}^{h/2} {\left( { - 2/15 {{\mu (z) \left( {27 {l_0}^2 - 64 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^3}}} + {{16 \mu (z) {l_1}^2} \over {5 {R^3}}} - {{z{f_1}} \over {{R^3}}}} \right){\rm{d}}z} \\ {E_{55}} & = \int_{ - h/2}^{h/2} {\left( {1/15 {{\mu (z) \left( {30 {R^2} + 27 {l_0}^2 + 184 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^3}}} + {{32 \mu (z) {l_1}^2} \over {5 {R^3}}} - {{z{f_1}} \over {{R^3}}}} \right){\rm{d}}z} \\ {E_{56}} & = \int_{ - h/2}^{h/2} {2/15 {{\mu (z) \left( {27 {l_0}^2 - 16 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^3}}}{\rm{d}}z} \\ {E_{57}} & = \int_{ - h/2}^{h/2} {\left( { - 8/3 {{\mu (z) \left( {{l_1}^2 - 3/4 {l_2}^2} \right)} \over R} + 1/30 {{\mu (z) \left( {81 {l_0}^2 + 16 {l_1}^2 - 45 {l_2}^2} \right)} \over R}} \right){\rm{d}}z} \\ {E_{58}} & = \int_{ - h/2}^{h/2} {\left( {2 {{\mu (z) \left( {\left( {{z^2} + 4/3 {l_1}^2 - {l_2}^2} \right){R^2} + 4/3 {l_1}^2{z^2}} \right)} \over {{R^3}}} - 2 {1 \over R}\left( {\left( { - 2/3 {z^2} + {{27 {l_0}^2} \over {20}} - {{8 {l_1}^2} \over {15}} - 3/4 {l_2}^2} \right)\mu (z) + {z^2}k(z) } \right) + {{8 \mu (z) {l_1}^2{z^2}} \over {15 {R^3}}} - {{{f_{1 }}{z^2}} \over {{R^2}}}} \right){\rm{d}}z} \\ {E_{59}} & = \int_{ - h/2}^{h/2} {\left( { - 8/5 {{{l_1}^2{z^2}} \over {{R^3}}} - 1/15 {{\mu (z) {z^2}\left( {27 {l_0}^2 - 32 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^3}}}} \right){\rm{d}}z} \\ {E_{510}} & = \int_{ - h/2}^{h/2} {\left( { - 9/5 {{\left( {{l_0}^2 + 5/9 {l_2}^2} \right){z^2}\mu (z) } \over R} + {{8 \mu (z) {l_1}^2{z^2}} \over {15 R}}} \right){\rm{d}}z} \\ {E_{511}} & = \int_{ - h/2}^{h/2} {1/15 {{\mu (z) \left( {30 {R^4} + 27 {l_0}^2{R^2} + 136 {R^2}{l_1}^2 + 15 {R^2}{l_2}^2 + 136 {l_1}^2{z^2}} \right)} \over {{R^4}}}{\rm{d}}z} \\ {E_{512}} & = \int_{ - h/2}^{h/2} {\left( { - 4 {{\mu (z) \left( {\left( {{z^2} + 2/3 {l_1}^2 + {l_2}^2} \right){R^2} + 2/3 \left( {{l_1}^2 + 1/2 {l_2}^2} \right){z^2}} \right)} \over {{R^2}}} + {{8 \mu (z) {l_1}^2{z^2}} \over {15 {R^2}}}} \right){\rm{d}}z} \\ {E_{513}} & = \int_{ - h/2}^{h/2} {1/15 \mu (z) {z^2}\left( {27 {l_0}^2 + 16 {l_1}^2 + 15 {l_2}^2} \right){\rm{d}}z} \\ {E_{514}} & = \int_{ - h/2}^{h/2} {\left( {2 {1 \over {{R^4}}}\left( {\left( {\left( {4/3 {z^2} + {{19 {l_0}^2} \over 5} + {{32 {l_1}^2} \over {15}} + {l_2}^2} \right){R^2} + 2 {z^2}\left( {{l_0}^2 + {{64 {l_1}^2} \over {15}}} \right)} \right)\mu (z) + {R^2}k(z) {z^2}} \right) - {{32 \mu (z) {l_1}^2{z^2}} \over {5 {R^4}}} - {{{f_{1 }}{z^2}} \over {{R^3}}}} \right){\rm{d}}z} \\ {E_{515}} & = \int_{ - h/2}^{h/2} {4/5 {{\mu (z) {z^2}\left( {5 {l_0}^2 + 2 {l_1}^2} \right)} \over {{R^4}}}{\rm{d}}z} \\ {E_{516}} & = \int_{ - h/2}^{h/2} {\left( {1/15 {{\mu (z) {z^2}\left( {87 {l_0}^2 + 64 {l_1}^2 + 15 {l_2}^2} \right)} \over {{R^2}}} - 8/5 {{{l_1}^2{z^2}} \over {{R^2}}}} \right){\rm{d}}z} \\ {E_{517}} & = - 2R. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ashrafi Dehkordi, A., Jahanbazi Goojani, R. & Tadi Beni, Y. Porous flexoelectric cylindrical nanoshell based on the non-classical continuum theory. Appl. Phys. A 128, 478 (2022). https://doi.org/10.1007/s00339-022-05584-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00339-022-05584-z

Keywords

Search

Navigation